On Multi-Scale Entropy Analysis of Order-Tracking Measurement for Bearing Fault Diagnosis under Variable Speed
Abstract
:1. Introduction
2. Vibration Signal Analysis
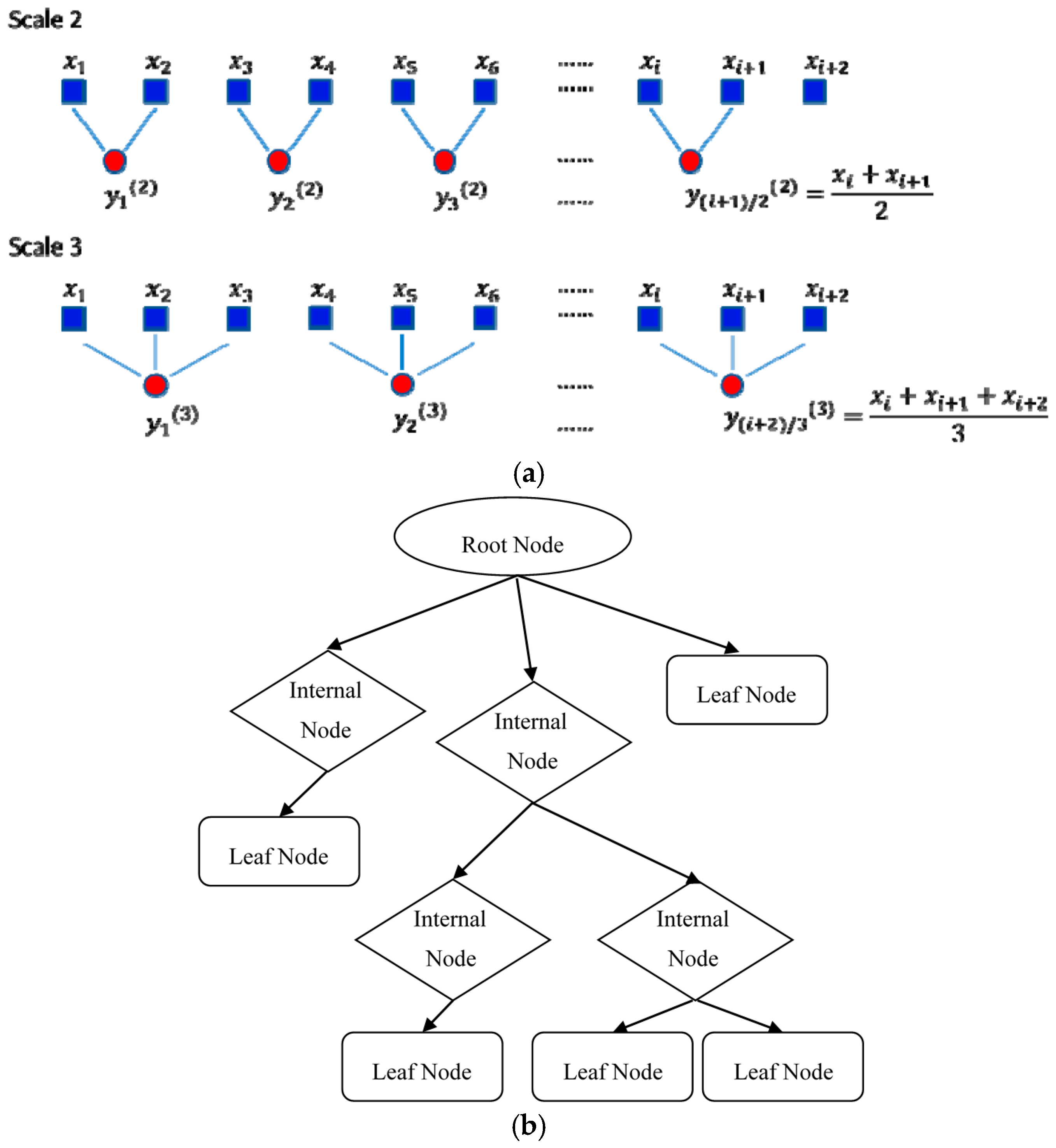
2.1. Signal Decomposition
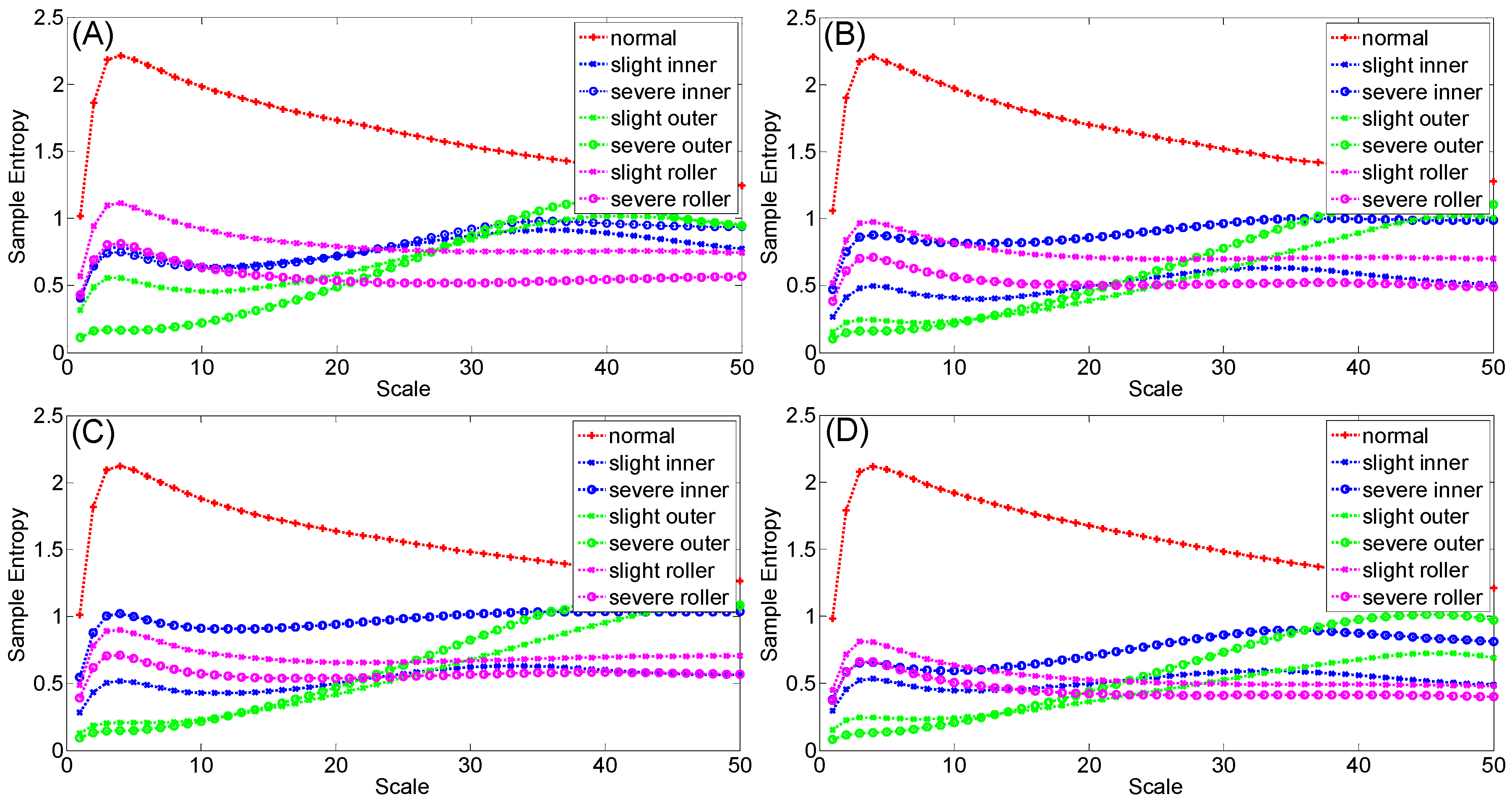
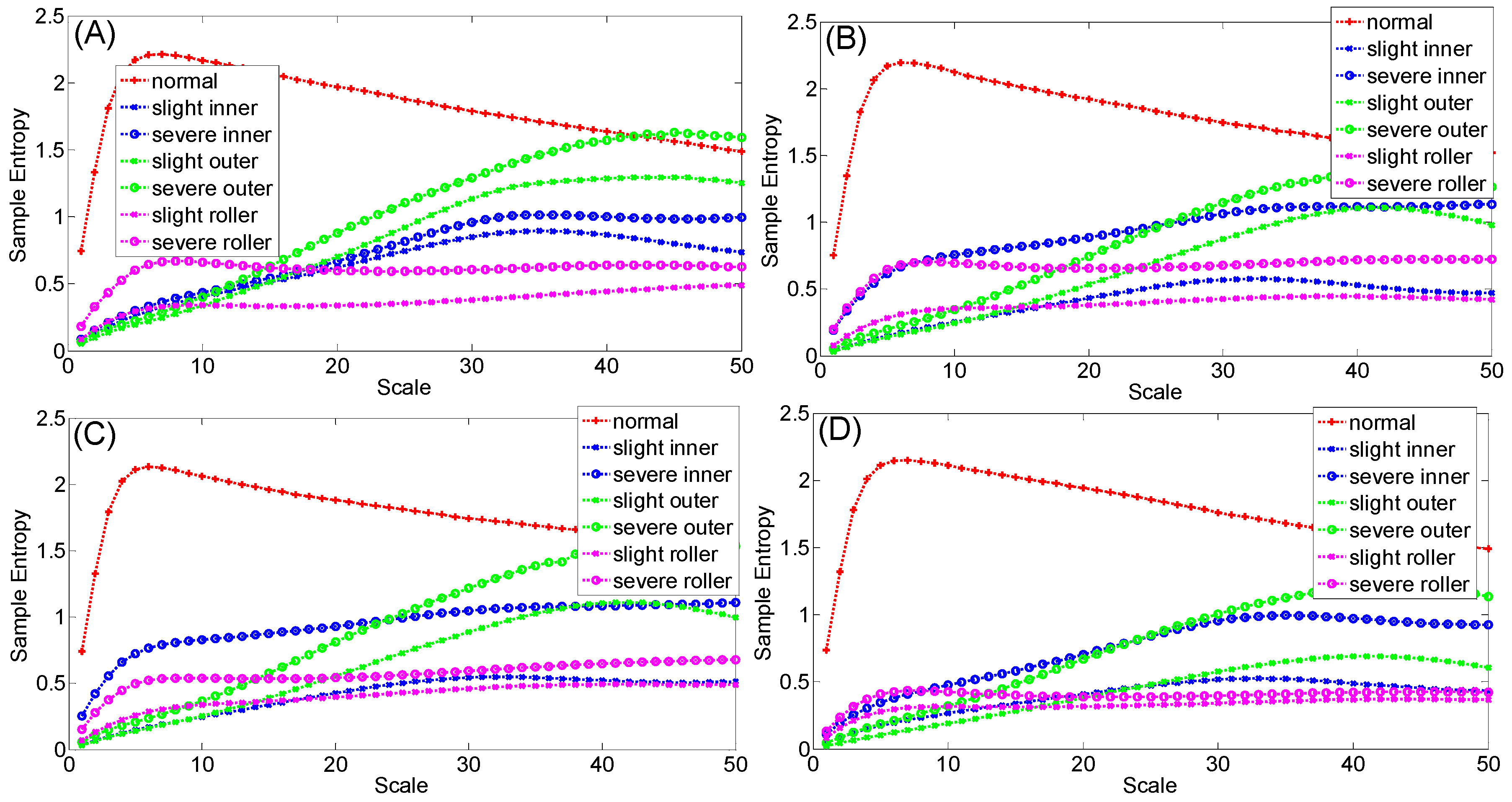
2.2. Computation of Multi-Scale Entropy
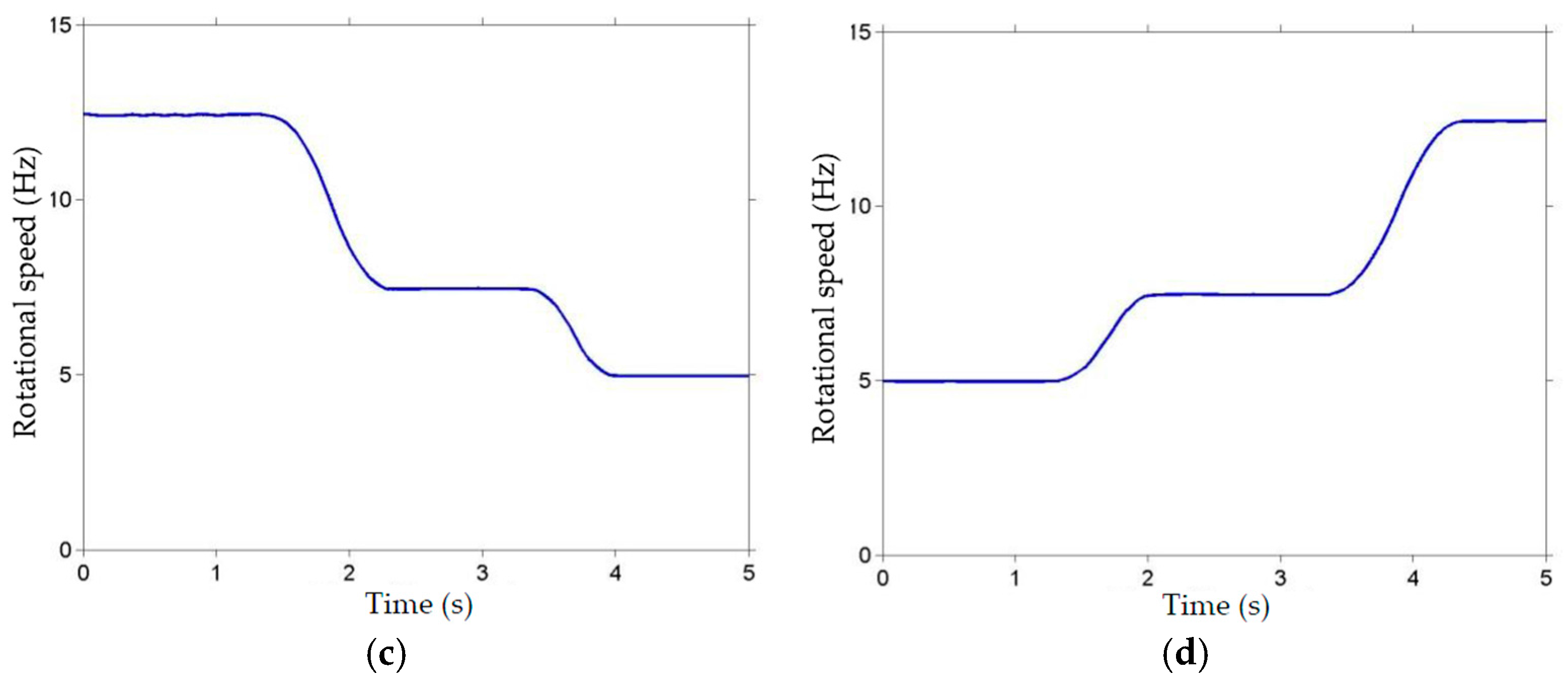
2.3. Decision Tree Classification
- (1)
- The source set of features start training at the root node of the decision tree.
- (2)
- If the features have the same outcome values of attributes at the same node, then this node is the leaf node and all of the features at the node are classified as the same class label.
- (3)
- If the features at the node have different outcome values of attributes, then this node belongs to the internal node and the most distinguishable attribute among the features is estimated to discriminate the features. The estimation criteria of this attribute are employed for the decision rule at this node.
- (4)
- The above steps go through recursively to form the decision tree model.
- (5)
- The stoppage conditions of the steps include:
- (i)
- For all nodes in the decision tree, all of the features at the same node have the same outcome values of attributes. Namely, all the nodes go to Step 2.
- (ii)
- The features at the same node do not consist of attribute to be utilized for further separation.
3. Experiment Verification
3.1. Experiment Setup
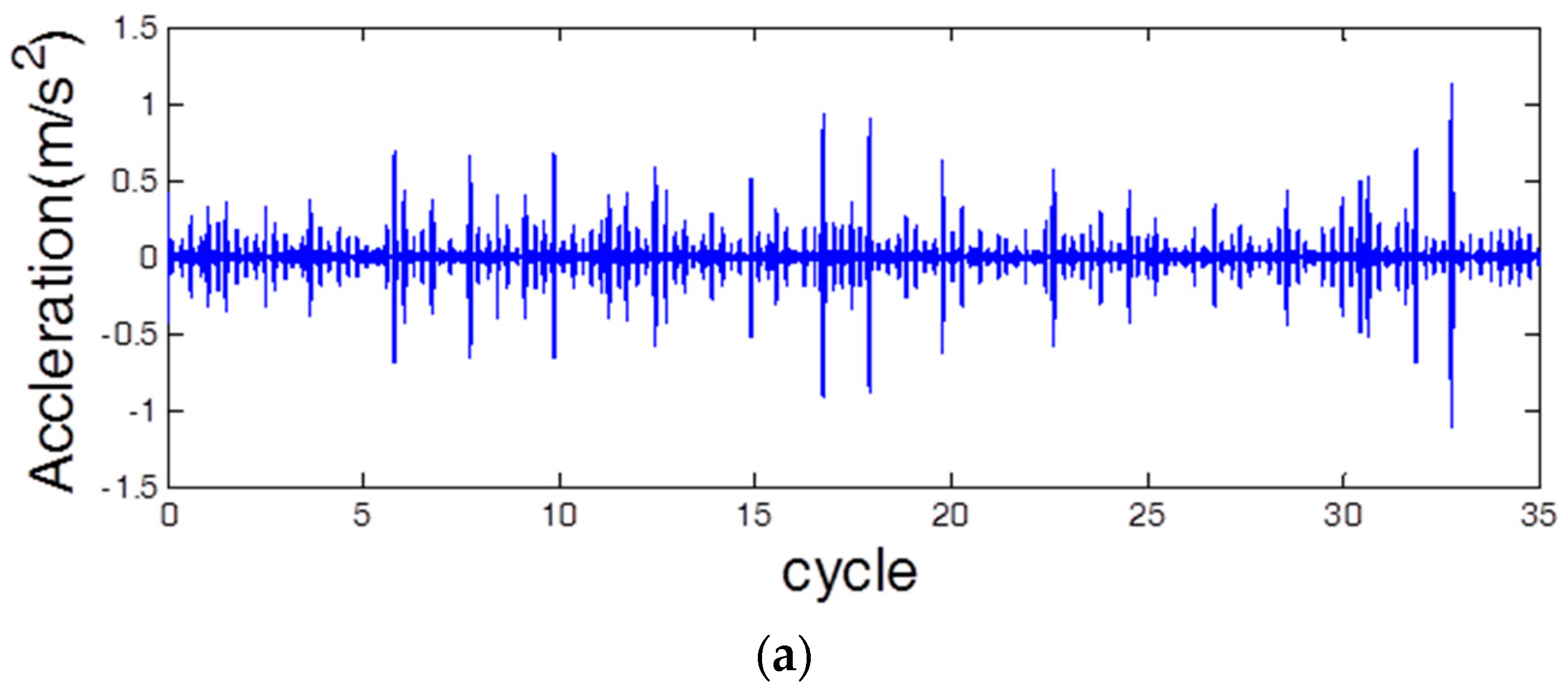
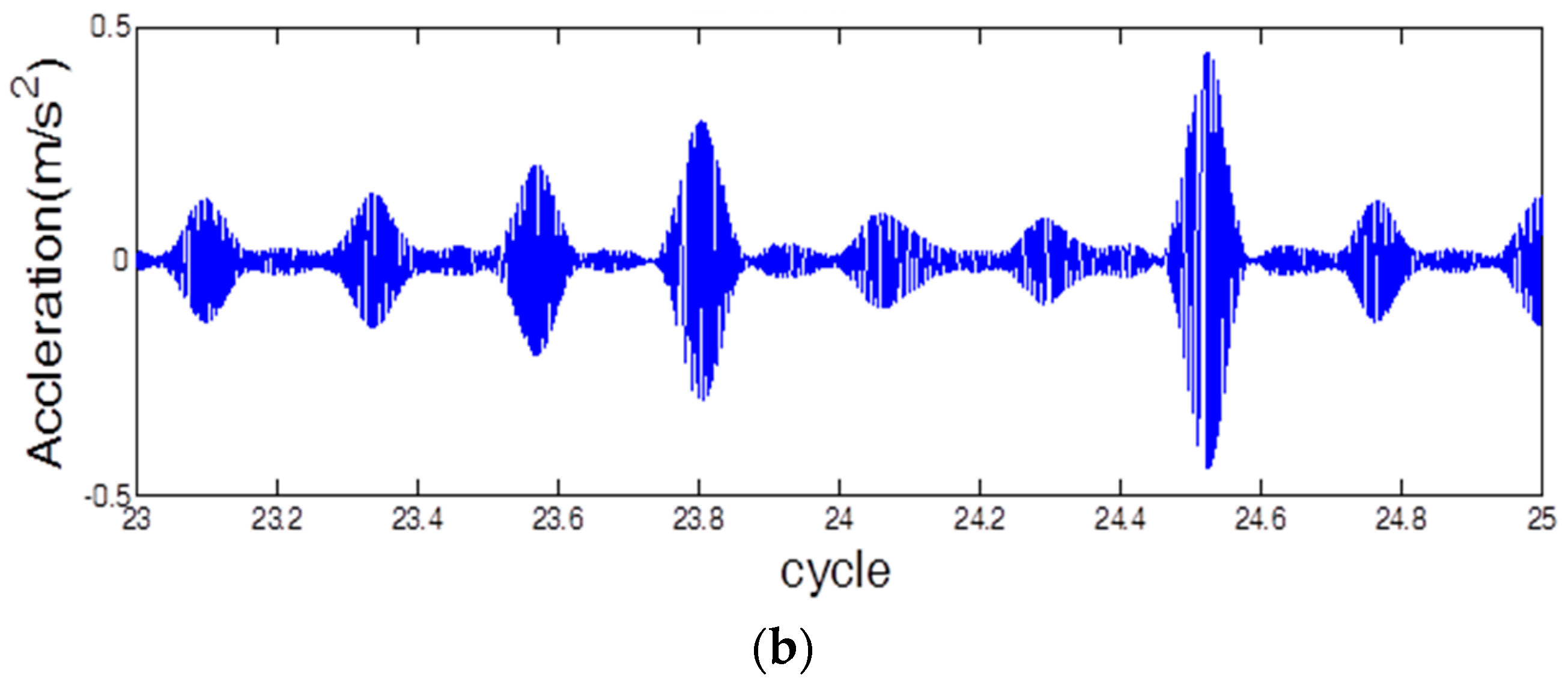
3.2. Vibration Signal Analysis and Processing
3.3. Signal Feature Extraction
3.4. Bearing Defect Classification through Decision Tree
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [PubMed]
- Han, M.H.; Pan, J.L. A fault diagnosis method combined with FEEMD, sample entropy and energy ratio for roller bearings. Measurement 2015, 75, 7–19. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X. Approximate entropy as a diagnosis tool for machine health monitoring. Mech. Syst. Signal Process. 2007, 21, 824–839. [Google Scholar] [CrossRef]
- Pen, Y.N.; Chen, J.; Li, X.L. Spectral entropy: A complementary index for rolling element bearing performance degradation assessment. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 1223–1231. [Google Scholar] [CrossRef]
- Hao, R.; Peng, Z.; Feng, Z.; Chu, F. Application of support vector machine based on pattern spectrum entropy in fault diagnostics of rolling element bearings. Meas. Sci. Technol. 2011, 22. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, P.H.; Wu, C.W.; Ding, J.J.; Wang, C.C. Bearing fault diagnosis based on multiscale permutation entropy and support vector machine. Entropy 2012, 14, 1343–1356. [Google Scholar] [CrossRef]
- Shi, Z.L.; Song, W.Q.; Taheri, S. Improved LMD, Permutation Entropy and Optimized K-Means to Fault Diagnosis for Roller Bearings. Entropy 2016, 18, 70. [Google Scholar] [CrossRef]
- Lei, Y.G.; Zuo, M.J.; He, Z.J.; Zi, Y.Y. A multidimensional hybrid intelligent method for gear fault diagnosis. Expert Syst. Appl. 2010, 37, 1419–1430. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.D.; Wu, C.W.; Wu, T.Y.; Wang, C.C. Multi-scale analysis based ball bearing defect diagnostics using Mahalanobis distance and support vector machine. Entropy 2013, 15, 416–433. [Google Scholar] [CrossRef]
- Hsieh, N.K.; Lin, W.Y.; Young, H.T. High-speed spindle fault diagnosis with the empirical mode decomposition and multiscale entropy method. Entropy 2015, 17, 2170–2183. [Google Scholar] [CrossRef]
- Fyfe, K.R.; Munck, E.D.S. Analysis of computed order tracking. Mech. Syst. Signal Process. 1997, 11, 187–205. [Google Scholar] [CrossRef]
- Bai, M.R.; Huang, J.; Hong, M.; Su, F. Fault diagnosis of rotating machinery using an intelligent order tracking system. J. Sound Vib. 2005, 280, 699–718. [Google Scholar] [CrossRef]
- Wu, J.D.; Huang, C.W.; Chen, J.C. An order-tracking technique for the diagnosis of faults in rotating machineries using a variable step-size affine projection algorithm. NDT E Int. 2005, 38, 119–127. [Google Scholar] [CrossRef]
- Vibration Measurements for Bearing Defect Diagnosis through Hardware-Implemented Order-Tracking Technique. Available online: http://web.nchu.edu.tw/~tianyauwu/data/bearing/identical_theta/web_data_expression.htm (accessed on 9 August 2016).
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Costa, M.; Peng, C.K.; Goldberger, A.L.; Hausdorff, J.M. Multiscale entropy analysis of human gait dynamics. Physica A 2003, 330, 53–60. [Google Scholar] [CrossRef]
- Saravanan, N.; Ramachandran, K.I. Fault diagnosis of spur bevel gear box using discrete wavelet features and Decision Tree classification. Expert Syst. Appl. 2009, 36, 9564–9573. [Google Scholar] [CrossRef]
- Jin, C.; Li, F.; Li, Y. A generalized fuzzy ID3 algorithm using generalized information entropy. Knowl. Based Syst. 2014, 64, 13–21. [Google Scholar] [CrossRef]
- Quinlan, J.R. Improved use of continuous attributes in C4.5. J. Artif. Intell. Res. 1996, 4, 77–90. [Google Scholar]
- Althuwaynee, O.F.; Pradhan, B.; Lee, S. A novel integrated model for assessing landslide susceptibility mapping using CHAID and AHP pair-wise comparison. Int. J. Remote Sens. 2016, 37, 1190–1209. [Google Scholar] [CrossRef]
- Wickramarachchi, D.C.; Robertson, B.L.; Reale, M.; Price, C.J.; Brown, J. HHCART: An oblique decision tree. Comput. Stat. Data Anal. 2016, 96, 12–23. [Google Scholar] [CrossRef]
- Chou, J.S. Comparison of multilabel classification models to forecast project dispute resolutions. Expert Syst. Appl. 2012, 39, 10202–10211. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers: San Mateo, CA, USA, 1993. [Google Scholar]


| Dimension Specification | |||
|---|---|---|---|
| Inner diameter (mm) | 17 | Roller diameter (mm) | 6.5 |
| Outer diameter (mm) | 40 | No. of roller | 10 |
| Cage diameter (mm) | 28.6 | ||
| Characteristics | order | ||
| Cage rotating order (Oc) | 0.39 | ||
| Roller spin order (Obs) | 2.09 | ||
| Order of roller passing through an outer race point (Obpo) | 3.86 | ||
| Order of a roller point passing through inner and outer race (Orp) | 4.17 | ||
| Order of roller passing through an inner race point (Obpi) | 6.14 | ||
| Class | Defect Expression | Notch Dimension |
|---|---|---|
| C1 | Normal | |
| C2 | Slight outer race defect | 0.4 mm × 0.3 mm |
| C3 | Severe outer race defect | 0.8 mm × 0.3 mm |
| C4 | Slight inner race defect | 0.4 mm × 0.3 mm |
| C5 | Severe inner race defect | 0.8 mm × 0.3 mm |
| C6 | Slight roller defect | 0.1 mm × 0.3 mm |
| C7 | Severe roller defect | 0.4 mm × 0.3 mm |
| Number of Data Set | Classified Fault Class | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | Accuracy | ||
| True experimental class | C1 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| C2 | 0 | 95 | 5 | 0 | 0 | 0 | 0 | 95% | |
| C3 | 0 | 4 | 96 | 0 | 0 | 0 | 0 | 96% | |
| C4 | 0 | 0 | 0 | 97 | 1 | 1 | 1 | 97% | |
| C5 | 1 | 0 | 0 | 3 | 93 | 2 | 0 | 93% | |
| C6 | 0 | 0 | 0 | 2 | 1 | 83 | 14 | 83% | |
| C7 | 0 | 0 | 0 | 0 | 0 | 10 | 90 | 90% | |
| Overall accuracy | 93.4% | ||||||||
| Consolidate different levels of roller defects | 96.9% | ||||||||
| Number of Data Set | Classified Fault Class | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | Accuracy | ||
| True experimental class | C1 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| C2 | 0 | 99 | 1 | 0 | 0 | 0 | 0 | 99% | |
| C3 | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100% | |
| C4 | 0 | 0 | 0 | 98 | 1 | 0 | 1 | 98% | |
| C5 | 2 | 1 | 0 | 2 | 92 | 0 | 3 | 92% | |
| C6 | 0 | 0 | 0 | 0 | 0 | 86 | 14 | 86% | |
| C7 | 0 | 0 | 2 | 2 | 0 | 13 | 83 | 83% | |
| Overall accuracy | 94.0% | ||||||||
| Consolidate different levels of roller defects | 97.9% | ||||||||
| Number of Data Set | Classified Fault Class | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | Accuracy | ||
| True experimental class | C1 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| C2 | 0 | 90 | 0 | 2 | 4 | 2 | 2 | 90% | |
| C3 | 0 | 24 | 76 | 0 | 0 | 0 | 0 | 76% | |
| C4 | 0 | 0 | 0 | 100 | 0 | 0 | 0 | 100% | |
| C5 | 0 | 12 | 0 | 16 | 68 | 2 | 2 | 68% | |
| C6 | 0 | 0 | 0 | 0 | 4 | 69 | 27 | 69% | |
| C7 | 0 | 0 | 0 | 0 | 4 | 29 | 67 | 67% | |
| Overall accuracy | 81.4% | ||||||||
| Consolidate different levels of roller defects | 88.3% | ||||||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, T.-Y.; Yu, C.-L.; Liu, D.-C. On Multi-Scale Entropy Analysis of Order-Tracking Measurement for Bearing Fault Diagnosis under Variable Speed. Entropy 2016, 18, 292. https://doi.org/10.3390/e18080292
Wu T-Y, Yu C-L, Liu D-C. On Multi-Scale Entropy Analysis of Order-Tracking Measurement for Bearing Fault Diagnosis under Variable Speed. Entropy. 2016; 18(8):292. https://doi.org/10.3390/e18080292
Chicago/Turabian StyleWu, Tian-Yau, Chang-Ling Yu, and Da-Chun Liu. 2016. "On Multi-Scale Entropy Analysis of Order-Tracking Measurement for Bearing Fault Diagnosis under Variable Speed" Entropy 18, no. 8: 292. https://doi.org/10.3390/e18080292







