A Critical Reassessment of the Hess–Murray Law

Abstract

The Hess–Murray law is a correlation between the radii of successive branchings in bi/trifurcated vessels in biological tissues. First proposed by the Swiss physiologist and Nobel laureate Walter Rudolf Hess in his 1914 doctoral thesis and published in 1917, the law was “rediscovered” by the American physiologist Cecil Dunmore Murray in 1926. The law is based on the assumption that blood or lymph circulation in living organisms is governed by a “work minimization” principle that—under a certain set of specified conditions—leads to an “optimal branching ratio” of $\frac{{\mathrm{r}}_{i+1}}{{\mathrm{r}}_i}=\frac{1}{\sqrt[3]{2}}=0.7937$. This “cubic root of 2” correlation underwent extensive theoretical and experimental reassessment in the second half of the 20th century, and the results indicate that—under a well-defined series of conditions—the law is sufficiently accurate for the smallest vessels (r of the order of fractions of millimeter) but fails for the larger ones; moreover, it cannot be successfully extended to turbulent flows. Recent comparisons with numerical investigations of branched flows led to similar conclusions. More recently, the Hess–Murray law came back into the limelight when it was taken as a founding paradigm of the Constructal Law, a theory that employs physical intuition and mathematical reasoning to derive “optimal paths” for the transport of matter and energy between a source and a sink, regardless of the mode of transportation (continuous, like in convection and conduction, or discrete, like in the transportation of goods and people). This paper examines the foundation of the law and argues that both for natural flows and for engineering designs, a minimization of the irreversibility under physically sound boundary conditions leads to somewhat different results. It is also shown that, in the light of an exergy-based resource analysis, an amended version of the Hess–Murray law may still hold an important position in engineering and biological sciences.

1. Introduction

In this paper, the history of the Hess–Murray law, a correlation that relates the diameters of successive bifurcations in blood flow, is briefly revisited, its major consequences analyzed and its applicability to real (natural or artificial) artefacts examined. It is then argued that an exergy-based reinterpretation of the law may lead to more rigorously based and more general applications.

1.1. The Original Formulation by Hess

The Hess–Murray’s law is a formula for relating the radii of daughter branches to the radii of the parent branch of a bi- or multi-furcated circulatory or respiratory system. The original formulation was published by Hess (1949 Nobel laureate in Physiology) [1,2]. Hess stated his law in its final form his 1914 thesis: as a historical remark, it must be mentioned though that in his 1808 Croonian Lecture [3], Thomas Young, though, in a rather obscure wording and without providing any theoretical justification, had already stated a “cubic root of 2” law. Hess’ intent was to determine the vessel radius that required minimum expenditure of energy by the organism. This approach, novel for his times, led him to adopt an “energy minimization” procedure to derive the optimal ratio between the radii of two successive branchings in vascular tissue. In Hess’ words,

(The optimal ratio) between the main and the secondary branch is reached when the tendency to control the blood flow is such that the regulatory action leads to the smallest possible reduction of the cross-section. This ratio is attained when the main- and secondary branch have the same effect on the resistance to the flow.

—Walter Rudolf Hess [2] (p. 473)

Hess provided an explicit proof of the “$2^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}=0.7937$ratio”, which he obtained in three quite simple steps:

(a)

In a symmetric branching (Figure 1) the mass flowrate is equally split between the secondary branches: $m_{i+1}=0.5m_i$, and, for an incompressible fluid, $Q_{i+1}=0.5Q_i$, i.e., the two volumetric flowrates in the bifurcated sections are each equal to half the total volumetric flowrate in the main branch. Hess first relates the pressure drop ∆p in both the main and the secondary branches to the respective flow rates through a “viscous resistance” R, and then calculates a “total work expenditure” as the sum of the metabolic work related to the blood flow and the pumping work needed to overcome the frictional pressure drop;

(b)

The resistance to the flow in a circular tube of length L and cross-sectional area A is given by Poiseuille’s formula, which Hess rearranges to obtain $R=\frac{\Delta p}{Q}=\frac{8\pi \mu L}{A^2}$ kg/(s∙m⁴). He argues that, for a fixed flowrate and for the laminar isothermal flow of an incompressible newtonian fluid with constant properties, the “optimal control” is established when the variations of the hydraulic resistance induced by an infinitesimal variation in the flow area attain the same value in the main and in the daughter branches, i.e., when:

$$\frac{d}{d{A}_i}\left(\frac{1}{A_i^2}\right)=\frac{d}{2d{A}_{i+1}}\left[\frac{2}{(2A_{i+1}^2)}\right]$$

(1)

(c)

Since $\frac{A_{i+1}}{A_i}={\left(\frac{r_{i+1}}{r_i}\right)}^2$, it follows that:

$${\delta }_{i+1}=\frac{r_{i+1}}{r_i}=\frac{1}{\sqrt[3]{2}}$$

(2)

It is noteworthy that Hess was the first scientist to make explicit mention of the teleology of blood transport: he wrote ”…(the bifurcation) splits the blood flow delivered from the central system in such a way that the supply requested by the internal organs is ensured with the minimum possible flow volume of blood” [2].

1.2. Murray’s Rediscovery of the Hess’ Law

Murray’s analysis [4] was originally aimed at the identification of the most efficient oxygen transport in man. Since oxygen is supplied to the body organs by the blood through the vascular system, he was faced with the problem of, as he put it, “the cost of blood volume”. In line with the logical empiricism of his time, he explicitly remarks that the most suitable model for the analysis of metabolic processes is one based on an energy (power) balance, “all other factors remaining constant”. Following Hess’ ideas, Murray states “If the vessels are too small, the work required to drive the blood through them becomes too great; if the volume of the vessels is too large, the volume of blood, being equally large, becomes a burden to the whole body” [4] (p. 210). By a procedure slightly different from that proposed by Hess, he re-derived the same “cubic root of 2” rule:

(a)

Murray [4] starts by expressing the total power involved in the circulation of blood as the sum of two terms: the first needed to overcome the frictional resistance through the vessel and the second corresponding to the metabolic effort needed to “create and maintain” the blood volume therein:

$$P=Q\Delta p+c_b\pi r^{2}L$$

(3)

(b)

In line with Hess, the pressure drop is expressed by the Hagen–Poiseuille’s law:

$$\Delta p=\left(\frac{8\mu L}{\pi r^4}\right)Q=RQ$$

(4)

(c)

Murray then uses Equation (3) to compute the metabolic cost c_b, and then equates the total resistances R₀ and R₁₊₂ w.r.t. the flow area to derive his “cubic root of 2” law. Notice that the appearance of the cubic root does not depend on the value of the “specific metabolic cost of blood” c_b, which is assumed constant;

(d)

By differentiating Equation (4) w.r.t. r and equating the result to 0, Murray argues that, for given c_b and L, Q is proportional to r³;

(e)

If the above point is correct, and since the flow obeys Poiseuille’s law, the pressure gradient in successive branchings is proportional to r⁻¹:

$$\frac{\Delta p_{i+1}}{L_{i+1}}\frac{L_i}{\Delta p_i}=\frac{1}{\delta }=\sqrt[3]{2}$$

(5)

(f)

Under the same stipulation, the flow velocity correspondingly decreases:

$$\frac{U_{i+1}}{U_i}=\delta =\frac{1}{\sqrt[3]{2}}$$

(6)

(g)

Correspondingly, the Reynolds number Re scales with the radius ratio as:

$$\frac{R{e}_{i+1}}{R{e}_i}={\delta }^2=\frac{1}{2^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}$$

(7)

and also decreases along successive branchings.

Murray was aware of Hess’ work, but considered it preliminary and incomplete, and made only one reference in passing to it [4]. Although his derivation does not make use of an “optimal control” assumption (he reasons purely in terms of metabolic energy needed to maintain the blood flow and energy dissipation by friction generated by the bifurcation), his equations indeed derive, contrary to what he wrote, from Hess’ formulae, because both derivations are equivalent to the assumption of the constancy of the wall stress along successive branches (see Section 1.5 below). In spite of this slip, Murray’s papers contain genuine novelty and are quite propositive: he uses the “cubic root of 2” paradigm to draw some inference about the correspondence between the results of his law and the experimental oxygen rates in capillary and pulmonary vessels available at that time. He states that, while the experimental results are in satisfactory agreement with the law for capillary flow, for larger vessels the agreement is weak, and attributes this discrepancy to “side effects” like turbulence and vessel wall structure.

In [5] he also provides an original formula for the branching angle, given the splitting point and the two endpoints of the branchings (Figure 2), extends the treatment to non-symmetric branchings and to trifurcations, and remarks that the results ought to apply equally well (and with the same limitations) to the branchings of xylems, the sap transport system in plants.

An interesting finding in Murray’s analysis is the correlation between the branching angle and the radius ratio, which he derived using a constrained optimization of the pumping work: while referring readers to [5] for the details, the formulae he derives are:

$$\cos {\alpha }_1=\frac{r_0^4+r_1^4-{\left(r_0^3-r_1^3\right)}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{2r_0^2{r}_1^2}$$

(8)

$$\cos {\alpha }_2=\frac{r_0^4+r_2^4-{\left(r_0^3-r_2^3\right)}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{2r_0^2{r}_2^2}$$

(9)

which in the case of symmetric splitting become:

$$\cos {\alpha }_1=\cos {\alpha }_2=\frac{1+{\delta }_1^4-{\left(1-{\delta }_1^3\right)}^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{2{\delta }_1^2}$$

(10)

which, upon substitution of ${\delta }_1=\frac{1}{\sqrt[3]{2}}$, provides α₁ = α₂ = 37.5°. Note that, though Murray’s original drawing shows different lengths for the branches, nowhere in his derivation is the length L related to the vessel diameter: he posits no “slenderness ratio” for the vessels.

1.3. A brief Summary of Experimental Results and of Other Allometric Laws

As remarked by Sherman [6] in a very well-documented review, the Hess–Murray law (H-M in the following) is only approximately valid for natural branched systems (animal tissues and tree structures): the exponent in the root is found experimentally to range between 2 and 3 (though some experimental findings seem to substantially widen this range, [7]) and the introduction of a correction for turbulent effects leads to a 7/3 = 2.3 value [8]. Confirming the previous findings by Murray, the predictions of the H-M law are closer to reality for the smaller vessels (arterioles and capillaries). Additional deductions from—or comments & modifications to—the law were made by different authors:

(a)

Assuming thin-walled vessels, the external radius does not play any significant role, because it is—at the considered scales—negligibly larger than the internal radius [6];

(b)

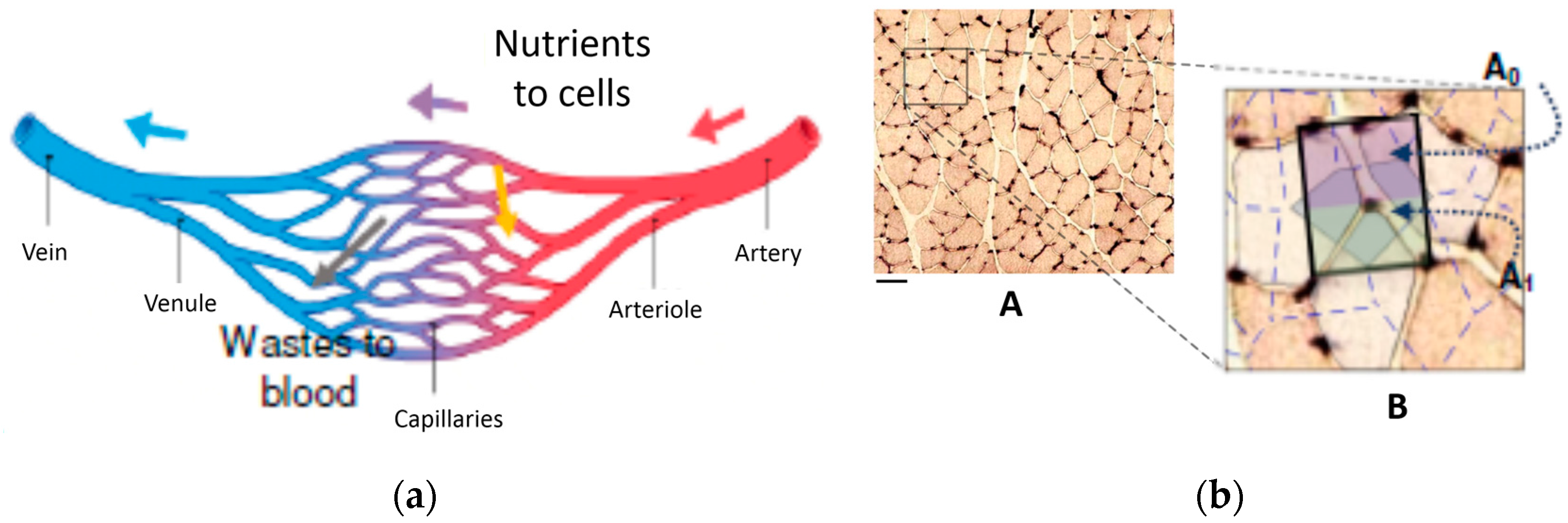
For 3-D branchings, the H-M still applies, because over 90% of the bifurcations are experimentally found to be coplanar [9];

(c)

A different “optimal branching ratio” can be derived by using fractals [10,11]: however, even for the smallest pulmonary alveoli (for which values 0.4 < δ < 0.85 are found experimentally) its value is not in agreement with the H-M law;

(d)

Both experimental and numerical findings show that while the H-M law leads—under the above stated assumptions—to an optimal value of δ = 0.7937 for laminar flow, for turbulent flow in veins and arteries the result becomes 0.74 and for the largest arteries, 0.77. Moreover, contrary to Hess & Murray’s result of an inverse scaling of the pressure gradient in successive branchings with δ (∆p/L = δ⁻¹, see Equation (4)), radius-dependent slenderness factors are found experimentally: L/r = 15.75r^1.10 for arterioles with r ≥ 50 μm, 1.79r^0.47 for arterioles with r ≤ 50 μm, 14.54r for veins with r ≤ 2000 μm, [12,13]. Notice that the fundamental deviation of Huang’s results [12] from the H-M law depend also on the different ordering of “successive branches” adopted therein, whose classification cannot be directly extended to capillary networks. Nevertheless, their findings contradict the H-M predictions in arterioles and veins (see also Table 3). Notice that [14] the H-M law is independent of the slenderness ratio r/L. Very well documented critiques of the H-M law are presented in [7,15];

(e)

The H-M law assumes impervious vessel walls: this is bound to cause a discrepancy with real lymph and blood flows, in which a major transport mechanism is through selectively permeable walls [14,16,17,18];

(f)

Nothing in the derivation of the H-M. law makes explicit reference to biological vessels: in principle, the law should hold also for human artefacts (pipes and any other kind of conduit) [6]: if the cross-sectional area is not circular, the law of the area $\frac{A_{i+1}}{A_i}={\left(\frac{r_{i+1}}{r_i}\right)}^2$ still approximately holds if the hydraulic radius r_h is substituted for r and a proper correction is introduced [19];

(g)

The law has important consequences when the growth of a biological organism is taken into account: if it holds, then the radii of the individual vessels in the vascular system must “grow” according to cubic root of 2 because the volume flow rate of the organism grows as well, and so does r₀, the radius of the primary stem [6,20]. This applies also to stress situations: when a higher rate of blood (or sap) flow is needed, the existence (or the emergence) of a self-regulatory response which suitably adjusts the vessels radii, as originally proposed by Hess, seems reasonable [15];

(h)

The H-M law also allows for an “allometric scaling” between different species [20]: if the relative sizes of the respective blood (or sap) vessels scale according to this law, then the physical dimensions depend on the radius of the main branch, which in turn depends on the metabolic rate of the species [21];

(i)

If blood is modelled as a non-Newtonian fluid, the 2^−1/3 law does not apply anymore, because—as expected—the exponent is found to have a non negligible dependence on the viscosity law (from 1 to 2.5 in [22,23]). Miguel [17,18] analyzed the irreversibility in branched flows of a power fluid and showed that (a) the “optimal” radius ratio depends on the “degree of non-newtonianity” of the fluid, ω; (b) that in the limit of Newtonian behavior, ω tends to 1 and the H-M law is recovered;

(j)

It is also possible to derive the optimal radius ratio in a dendritic structure by reformulating the problem as a constrained multi-variable optimization [11,24,25]: this approach, useful as it may be in engineering applications, loses somewhat of its significance in biological investigations.

On the basis of the above remarks, we can state that although the H-M law represents an innovative and theoretically interesting approach to the scaling in dendritic structures, its experimental confirmation and its generality are not completely satisfactory. We shall return to this point in Section 3.

1.4. Bejan’s Constructal Law

In 1997 Adrian Bejan [26] presented a reinterpretation and a very clever extension of the H-M law: expanding one of Murray’s statements (see comment to Figure 2 above) he reasoned that, if the law holds, then every bifurcated stream that carries some material (sap, blood, particles) or immaterial (energy under any form) flow from one point to two (or more) others in a given domain can—in an evolutionary sense—only develop along a global structure exactly specified by the “cubic root of 2” rule. This intuition forms the basis for his Constructal Theory (CT in the following), which has since seen a plethora of applications in a wide range of fields (see for instance [20,27]). Though CT is surely not as omni-comprehensive as it is being represented, its greatest merit is to have shown that—in the words of Bejan—“Nature is not fractal”: real structures follow from goals (Hess’ and Murray’s teleology!) rather than from fractal exponents, the goals being determined by external factors related, in nature, to evolutional pressures, and in engineering, to design specifications. Contrary to previous applications of the H-M law, Bejan’s findings are in a real sense “engineering” findings, not only qualitative but quantitative: they lead on the one side to a better interpretation and classification of natural (abiotic and biological) structures, and on the other side to measurable and repeatable design procedures for engineered artefacts. For the purpose of this paper, it suffices here to report one of the clearest definitions of the CT “thought procedure”:

The flow path was constructed in a sequence of steps that started with the smallest building block (elemental area) and continued in time with larger building blocks (assemblies, or constructs). The mode of transport with the highest resistivity (slow flow, diffusions, walking, and high cost) was placed on the smallest scales, completely filling the smallest elements. Modes of transport with successively lower resistivities (fast flow, streams, vehicles and low cost) were placed in the larger constructs, where they were used to connect the area-point or volume-point flows integrated over the constituents. The geometry of each building block was optimised for area-point access.

— Wishsanuruk Wechsatol, et al. [28]

When applied to bifurcating flows, this translates into “higher pressure gradients in the smallest vessels”, in complete agreement with the H-M law. In the next sections, it will be though argued that:

(a)

This very same “construction” derives in fact from a single principle, namely that of minimizing irreversibility in the transport of a certain mass flow rate of fluid from one point to a pair of a triplet of “users”;

(b)

The objective function whose minimum identifies the optimal configuration is the specific irreversible entropy generation rate;

(c)

That both natural and artificial dendritic flow structures do not admit of a single “optimal radius ratio” or of an “optimal splitting angle”, because both of these quantities are determined by the imposed boundary conditions. Therefore, in an evolutionary sense, it is the random variation of the latter that determines the “shape” of the winning configuration.

1.5. A fluiddynamic Interpretation

For the laminar flow of a Newtonian, single-phase, incompressible fluid in a circular tube with a rigid non-permeable skin, the Hagen–Poiseuille law (Equation (4) above) relates the pressure drop over a length L of tube to the volumetric flowrate:

$$\frac{\Delta p}{L}=\frac{8\mathsf{\mu }\mathrm{Q}}{\mathsf{\pi }{r}^4}$$

Under the same stipulations, the wall shear stress is given by:

$${\tau }_w=\frac{r\Delta p}{2L}=\frac{4\mathsf{\mu }\mathrm{Q}}{\mathsf{\pi }{r}^3}$$

(11)

In a symmetric bifurcation as those shown in Figure 1, Q₁ = Q₂ = 0.5Q₀, and the ratio of the wall stresses in the main and in the daughter branches depends on the radius ratio:

$$\frac{{\tau }_{w,1}}{{\tau }_{w,0}}=\frac{r_0^3}{2r_1^3}$$

(12)

The required pumping power is proportional to the wall stress and to the flowrate:

$$\frac{2P_1}{P_0}=\frac{{\tau }_{w,1}{L}_1{r}_0}{{\tau }_{w,0}{L}_0{r}_1}$$

(13)

Now, if we denote as θ the wall stress ratio τ_w,1/τ_w,0, by δ the radius ratio r₁/r₀ and by λ the length ratio L₁/L₀, the total pumping power required to deliver the flow from the bifurcation inlet (point O in Figure 1) to its two outlets (points A & B) is:

$$P_{tot}=P_0+2P_1={\tau }_{w,0}{L}_0{r}_1+{\tau }_{w,1}{L}_1{r}_0$$

(14)

For a given bifurcation (L₀, r₀, Q₀ assigned, so that τ_w,0 is known), one obtains:

$$\frac{P_{tot}}{P_0}=\mathrm{\Pi }=1+2\frac{P_1}{P_0}=1+2\frac{{\tau }_{w,1}{L}_1{r}_0}{{\tau }_{w,0}{L}_0{r}_1}=1+2\frac{\mathsf{\theta }\lambda }{\delta }$$

(15)

For the purpose of the present paper, it is useful to examine Equations (11) and (14) jointly: the H-M law is equivalent to the assumption of a constant τ_w along successive branches. But Equation (15) shows that τ_w is not the only factor influencing the total power expenditure (what Hess and Murray call “the pumping work”), because there are several possible cases, based on different assumptions, that are relevant to the problem:

(a)

θ = 1 (this is the H-M law): $1=\frac{Q_1}{r_1^3}\frac{r_0^3}{Q_0}$, which results in δ = 2^−1/3 (and, incidentally, in $\mathrm{\Pi }=1+2^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\lambda$);

(b)

V₀ = 2V₁ (the volume of fluid in the main branch is equal to the sum of the two volumes of the daughter branches): now δ = 1/(2λ) and $\Pi =1+\frac{1}{2{\delta }^3}$;

(c)

Re₀ = Re₁, from which δ = 0.5, θ = 4 and Π = 1 + 16λ;

(d)

U₀ = U₁ (constant fluid velocity in successive branchings): δ = 2^−1/2, θ = 0.1768, and Π = 0.5λ.

Other cases may be of importance in physiological flows, like for instance a lower velocity in smaller branches, to facilitate nutrients absorption from the permeable wall [14,16,17], or wall thickness proportional to radius, which may be convenient for sap flow on plants, but they are outside of the goals of the present study and will not be considered here.

1.6. Scope of This Work

In conclusion, the scope of this work is to prove that:

• The Hess–Murray law is only one of several possible instantiations of a class of rules that can be derived from irreversibility minimization;
• That there are therefore different structures that can develop if one or more of the assumptions are modified;
• That if an exergy-based resource cost paradigm is employed, the Hess–Murray law is amenable to a more fundamental and interesting interpretation that complements and extends the henceforth published results.

Since our goal is to demonstrate that the “configurator” of branched structures is the specific entropy generation rate, which depends on the shape of the domain, on the fluid properties and on the physical characteristics of the material of the vessel walls and of the surrounding tissues, only symmetric bifurcations will be considered here. Including non-symmetric cases would introduce additional geometric parameters that would complicate the treatment while adding nothing to the phenomenological significance of the model and to the interpretation of the results. For the same reason, the bifurcation losses, i.e., the viscous loss generated at the cusp, was omitted as well. For a more complete discussion on the effects of localized entropy generation, see [29].

2. Irreversibility in Viscous Isothermal Flows

Consider the flow of a viscous Newtonian fluid through a circular vessel: the irreversibility of the flow can be measured by its specific entropy generation rate (per unit mass). Following [30] we can separate the viscous and thermal effects, and in cylindrical coordinates (r,x) we obtain:

$$s_v\left(x,r,t\right)=\frac{\nu }{T}\left\{2\left[{\left(\frac{\partial V}{\partial r}\right)}^2+{\left(\frac{V}{r}\right)}^2+{\left(\frac{\partial U}{\partial x}\right)}^2\right]+{\left(\frac{\partial U}{\partial r}+\frac{\partial V}{\partial x}\right)}^2\right\}$$

(16)

$$s_t\left(x,r,t\right)=\frac{k}{\rho T^2}\left[\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)+{\left(\frac{\partial T}{\partial x}\right)}^2\right]$$

(17)

where U and V are the axial and radial velocity respectively and tangential periodicity is assumed. U, V and T are local and time-dependent quantities, and therefore in the context of the present analysis it at the moment is irrelevant whether the flow is turbulent or laminar. The derivative in the axial direction has been maintained to include entrance length effects, which will though be neglected for the moment. Let us consider, in line with Murray’s original suggestion, that the scope of the branching is to deliver the fluid from an origin or source (point O in Figure 1) to two endpoints or sinks (A & B). Our goal is to show that, whether the “basin of influence” of the branching is a rectangle or a circular sector, the total entropy generation within the region where the bifurcation appears is an explicit function of, among other parameters, the aspect ratio of the surrounding domain [14,29]. The first step is to relate the values of L₀ and L₁ (a similar derivation applies to any L_i+1) to the splitting angle α₁ and to the aspect ratio of the area “served” by the flow, which may be defined as a = H/L or a = 2α₀ for rectangular and triangular domains respectively. A first relevant finding is that for triangular domains (circular sectors, a geometry relevant to heat exchanger design), Murray’s angle law does not apply, because α₀ ≤ α₁. Figure 1 shows the respective formulae, derived using elementary trigonometry. We shall henceforth present the calculations for a single bifurcation in rectangular domains, as a function of the aspect ratio a = H/L that defines the domain in which the bifurcation takes place. A remark is in order here: all calculations presented in this paper are related to steady flow, and pulsating effects and compliant walls are excluded from this model: the emphasis is placed here on rigorous fundamental principles rather than on a higher degree of complexity.

Let us first assume, in accordance with the premises of the Hess–Murray law, that the flow structure ”evolves” so as to minimize the irreversibility: this is equivalent to Hess’ statement of minimizing the pressure loss per unit length, except that now, by means of Equations (16) and (17) we could also reformulate it in terms of total enthalpy. This paper deals though only with isothermal, fully developed laminar flows, for which Equation (17) vanishes identically, and so do the terms ∂/∂x in Equation (16). It is convenient to introduce dimensionless quantities: u = U/U₀, v = V/U₀, $\tilde{r}$ = r/r₀, $\tilde{x}$ = x/L, etc., with r₀ and U₀ respectively the radius of the main stem (the first branch) and the average velocity therein, and L the length of the domain shown in Figure 1. Then, substituting the Poiseuille velocity profile and integrating Equation (16) from r = 0 to r = 1, and then again from x = 0 to x = L₀/L, we obtain for the entropy generation rate for a circular vessel of length L₀:

$$S_0=\frac{\nu m_0^2}{{\pi }^{2}T{\rho }_0{r}_0^4}=K{m}_0^2\frac{L_0}{r_0^4} \left[\mathrm{W}/\mathrm{K}\right]$$

(18)

Notice that in Equation (18) entrance length effects are neglected: a detailed investigation [29] shows that, as long as the flow is isothermal, they do not significantly modify the results. Under the first stipulation of the H-M law, let us now consider only symmetric bifurcations in which each daughter branch carries m_i+1 = 0.5m_i kg/s. Denoting as δ_i the ratio r_i+1/r_i and as λ_i = L_i+1/L_i (δ₀ = 1, λ₀ = L₀/L), the viscous entropy generation rates in successive branches are shown in

Table 1. Viscous entropy generation rate in successive symmetrical branchings.

Branching Rank	Total Number of Branches	Entropy Generation Rate in the Branches	Total Entropy Generation Rate from the Initial Stem to the n-th Branching Included
Main stem	1	$S_0=K{m}_0^2\frac{L_0}{r_0^4}$	$S_0$	(19)
First bifurcation	2	$\frac{S_0}{2}\frac{{\lambda }_1}{{\delta }_1^4}$	$S_0\left(1+\frac{{\lambda }_1}{2{\delta }_1^4}\right)$
Second bifurcation	4	$\frac{S_0}{4}\frac{{\lambda }_2}{{\delta }_2^4}$	$S_0\left(1+\frac{{\lambda }_1}{2{\delta }_1^4}+\frac{{\lambda }_2}{4{\delta }_2^4}\right)$
Third bifurcation	8	$\frac{S_0}{8}\frac{{\lambda }_3}{{\delta }_3^4}$	$S_0\left(1+\frac{{\lambda }_1}{2{\delta }_1^4}+\frac{{\lambda }_2}{4{\delta }_2^4}+\frac{{\lambda }_3}{8{\delta }_3^4}\right)$
…	…	…	…
n-th bifurcation	2n	$\frac{S_0}{2^n}\frac{{\lambda }_n}{{\delta }_n^4}$	$S_0\left(1+{\displaystyle \sum _1^n}\frac{{\lambda }_n}{2^n{\delta }_n^4}\right)$

:

Here, S₀ denotes the entropy generation rate in a tube of length L₀ = L and of radius r₀ (no splitting).

In the line of thought explained in Section 1.5 above, four cases are of interest:

• The velocity remains the same before and after the bifurcation, U_i+1 = U_i: thence ${\delta }_i=\frac{r_{i+1}}{r_i}=\frac{1}{\sqrt{2}}$;
• The Reynolds number remains the same before and after the bifurcation, Re₁ = Re₀: ${\delta }_i=\frac{r_{i+1}}{r_i}=\frac{1}{2}$;
• The sum of the volumes of the daughter branches equals the volume of the main stem: $L_0{r}_0^2=2L_1{r}_1^2$, in which case $\frac{r_{i+1}}{r_i}=\sqrt{\frac{L_i}{2L_{i+1}}}$, or ${\delta }_i=\sqrt{\frac{1}{2{\lambda }_i}}$;
• The pressure drop in the daughter branches equals that in the main stem and the radius ratio is dictated by the Hess–Murray law (${\delta }_i={\lambda }_i=\frac{1}{\sqrt[3]{2}}$).

To better understand the premises of this study, it is important to remark once more that there is no a priori physical reason for either one of the four above choices: their occurrence may be in fact facilitated by evolutionary pressures in nature and imposed by designer’s choice in engineered artefacts. For instance, a constant velocity may be preferred if the volume to be “fed” by the fluid varies with the cross section of the vessel (as in a leaf) or when a constant residence time in the vessel is more efficient in an evolutionary sense; a constant Reynolds number leads to a constant heat exchange rate per unit length; a “constant volume” law implies that the daughter branches use roughly the same biological material as the main branch. This remark is in line with the argument presented in [19], in which a branching parameter X is introduced and the radius ratio is defined as ${\delta }_i=\frac{1}{\sqrt[3]{2X}}$: the authors show that values of X different from 1 (X = 1 recovers the H-M limit) give origin to different flow configurations, some of which may be “optimal” in vivo.

Notice that in Equation (19) the length ratio between successive branches appears as well, and since—except for case 4—Murray’s “optimal angle” relations do not apply, we need to use some different physical reasoning (cases 1,2,3 above) to establish a direct link between the radius—and the length ratio. In practice, we shall use the general geometric derivation shown in Figure 1 and select α₁ as the running variable.

The results for the first bifurcation in a rectangular domain are shown in Figure 3: for slender domains (a = 0.2) the constant volume case (case 3 above) is the one that generates the least irreversibility for bifurcation angles lower than about 20°, and thereafter the CT case 4 is the least irreversible one. For a = 0.5 the constant volume case 3 is again the most efficient one up to α₁ = 35°, beyond which the CT case is again less dissipative. For a = 0.75, the constant volume and the CT are in practice equivalent beyond α₁ = 40°, while for lower angles the constant volume configuration is the least dissipative. This simple example demonstrates that in practical (albeit quite idealized) cases the failure of the Hess–Murray law to consider the “teleological” aspects of the structure (i.e., the goal for which a bifurcation should occur in nature or by design) makes its application questionable: a radius ratio equal to $\frac{1}{\sqrt[3]{2}}$ is indeed a feasible option, but other values are equally feasible on physical grounds and, with the possible exception of the constant velocity case (not included in Figure 3), all are more or less compatible with the experimental measurements.

Along the same line of reasoning it is possible to calculate, with a larger computational effort but with no substantial methodological change, the entropy generation in the successive n > 1 branchings (Figure 4 and Table 1).

3. Is the Hess-Murray Energy Balance the Correct One?

Hess and Murray derived their “cubic root of 2” formula on the basis of an energy (power) balance applied to two different situations:

(a)

Hess assumed that the variation of the hydraulic viscous resistance w.r.t. a small change in the blood flow is the same in the parent and daughter branches. Today we know that blood supply pressure is regulated also in the arterioles, upstream of the capillaries, and that the latter may function also as temporary “blood reservoirs”, and therefore Hess’ balance cannot be applied to derive the radius ratio of capillary bifurcations;

(b)

Murray starts by calculating the total power (which he calls cost) of blood circulation as the sum of the power dissipated by friction losses and of a “metabolic cost” of the blood, calculated as the pumping power requested of the heart. This calculation is though inaccurate, because it neglects for instance the work needed to deliver the blood through the veins back to the heart (in fact, Murray [4,31] obtains three different values for his metabolic cost depending on the different assumptions he posits). Thus, his balance between the blood pumping work (proportional to the vessels radius) and the friction work is completely contingent on the rather arbitrary assumptions he posits to calculate the “pumping power” of the heart.

Neither Hess nor Murray explicitly formulated their law in its simplest form (which is likely to be the sense of Young’s statement mentioned in Section 1.1): for laminar flow, and assuming a Poiseuille profile, the wall shear stress is ${\tau }_w={\left(\frac{du}{dr}\right)}_{r=R}=\frac{4\mu Q}{\pi R^3}$, and if one imposes for τ_w to remain constant across a symmetric bifurcation, a radius ratio 2^−1/3 results (in Murray’s derivation, the statement that Q is proportional to R³—point d in Section 1.2—is in practice equivalent to assuming a constant wall stress; see Section 1.5 above). Their “energy based” approach, though, is completely sound and cannot be discarded: considering the evolutionary pressures that favor selective competition, it is very likely that the circulatory system has evolved in such a way as to increase its “efficiency”, however defined. Let us then reconsider the original scenario under which the H-M law was derived: a net of capillaries (Figure 5) carries a nutrients-laden fluid to a portion of a biological structure. Such a net performs two functions: first, by selective permeability on the outer wall of the vessels, it provides the surrounding organic material with the chemicals it needs; and second, possibly in a different region, absorbs from the surrounding tissue organic detritus and other discharges and delivers them to a different portion of the organism. Globally, in the assumption of steady-state conditions, the in- and out- flows from the walls compensate, and thus the mass flowrate through the individual vessels may be considered constant over their respective lengths. Therefore, in a very real sense, each bifurcation “serves” a small region of its surroundings, the one Al-Shammari [16] correctly identifies as “the supply region”.

If we observe the detailed pictures of some natural occurrences of such nets (Figure 6), the most striking character of each structure is without any doubt its connectivity: all images resemble “networks” rather than “dendrites”. Therefore, it seems reasonable to assume a simplified rectangular geometry for the basin of influence of a single bifurcation, and since the permeability of the wall tissues remains constant, the evolution-driven efficiency of natural structures suggests that each branch drains or provides a mass flow rate proportional to the immediate surrounding portion of the domain.

With reference to schematic representation of Figure 5a, the process may be thus described as follows (Figure 7): the mass flow rate of the permeate from (or to) the vessel wall area 2πL₀r₀ is proportional to the domain portion A₀, while that of the permeate from (or to) area 4πr₁L₁ is proportional to A₁ (similar considerations are made in the detailed numerical simulation presented in [31]). This simple apportioning is based on the assumption of a uniform “specific absorbance” by the surrounding cells, and leads to a calculation of the radius ratio based on the function of the net rather than on the “energy balance” proposed by Hess and Murray:

$${\delta }_1=\frac{r_1}{r_0}=0.5\cos {\alpha }_1$$

(20)

The rationale of the apportioning of the delivery of nutrients is the following:

(a)

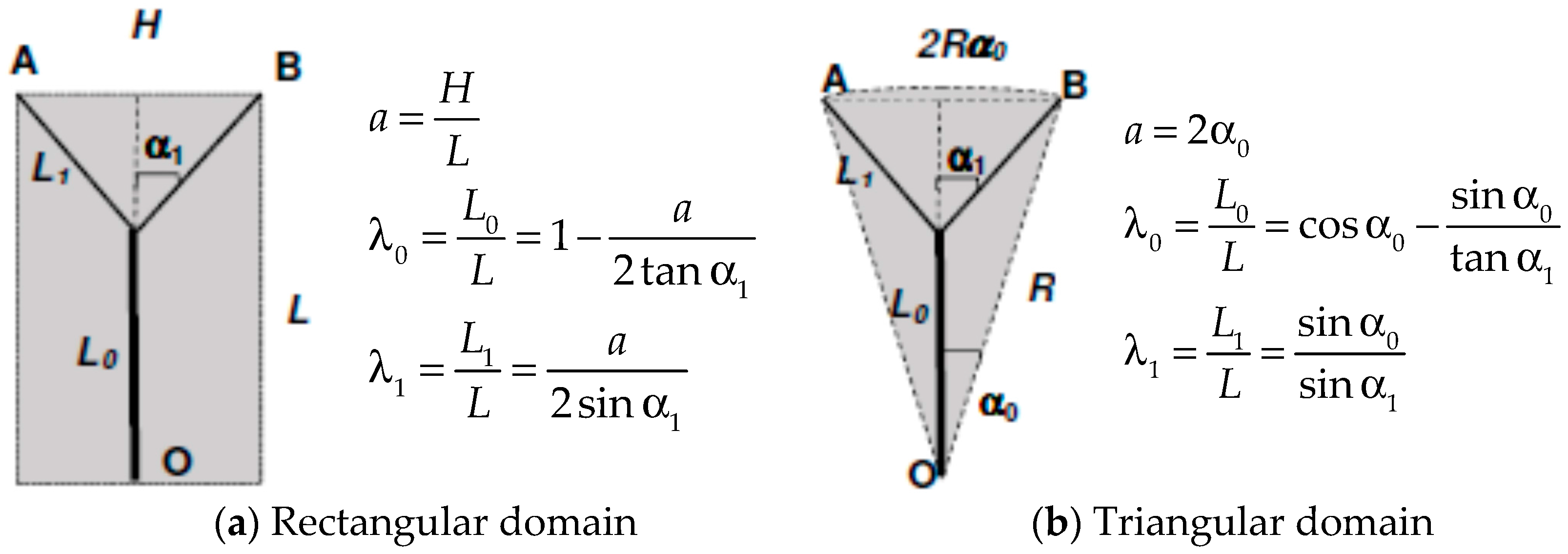
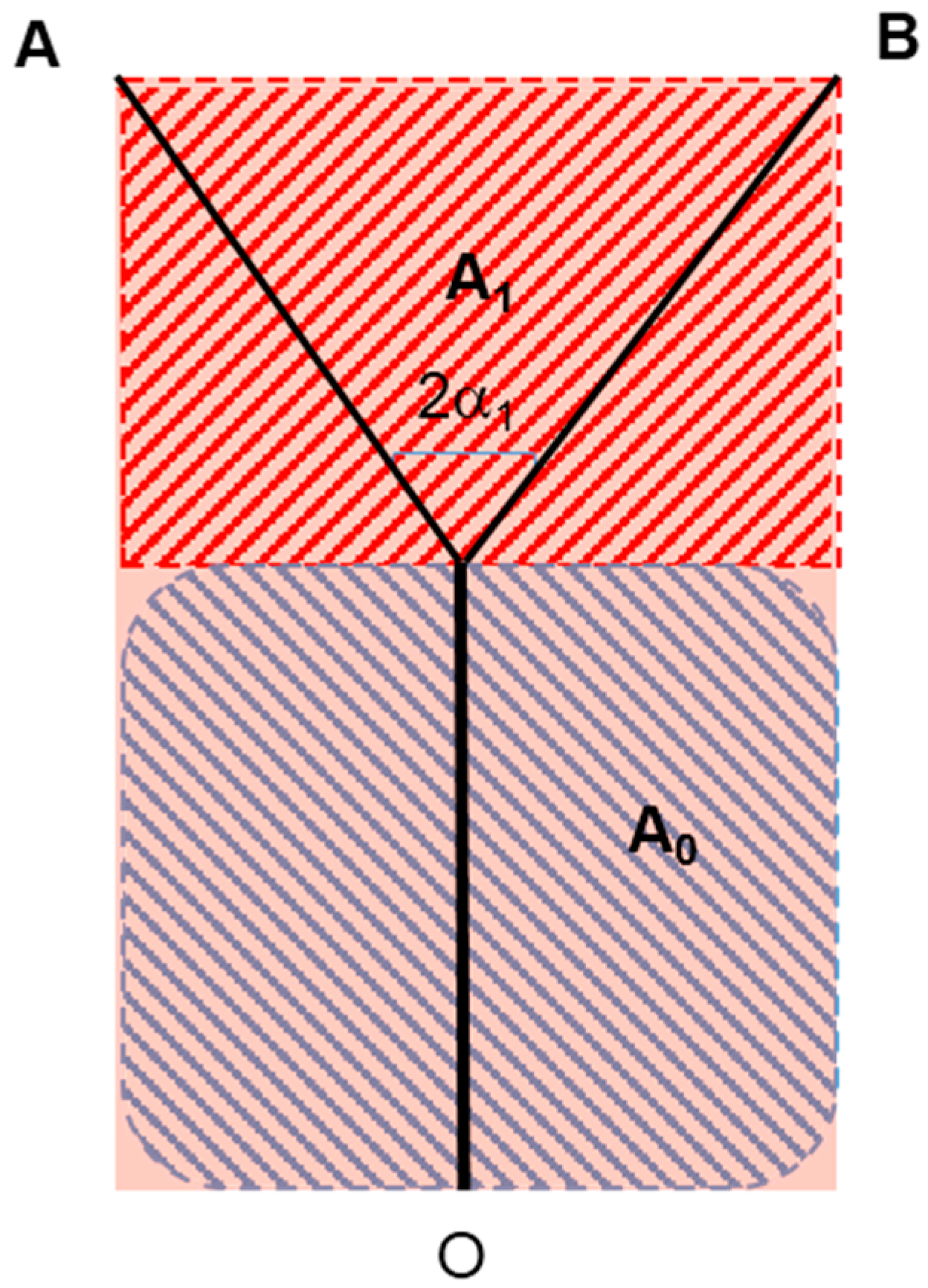
The portion of the supply region denoted as A₀ receives all of (and only) the nutrients permeated through the main branch: ${\dot{m}}_{A0}=2\pi {\mathrm{r}}_0{\mathrm{L}}_0\mu$, where μ is the wall permeability (kg/(m²s)), assumed to remain constant throughout. By analogy for the remaining portion A₁, ${\dot{m}}_{A1}=4\pi {\mathrm{r}}_1{\mathrm{L}}_1\mu$;

(b)

The “costs” of the irreversibility, S₀ and S₁, must be attributed to the mass flow rates m₀ and m₁ respectively;

(c)

And the objective function becomes

$$f_{objective}=\frac{S_0}{{\mathrm{r}}_0{\mathrm{L}}_0}+\frac{S_1}{{\mathrm{r}}_1{\mathrm{L}}_1}$$

Equation (20), together with the formulae that link λ₀ and λ₁ to the splitting angle α₁ (half of bifurcation angle, Figure 1), sheds new light on the phenomenology: the structure of the capillary network is dictated by the instantaneous local balance between the drained or absorbed mass flowrate of nutrients and the permeability of the capillary walls (notice that the introduction of this “wall permeability” is in contrast with one of the initial assumptions, namely, that the walls are non-permeable. The relaxation of this constraint is acceptable for the case in study though, where the mass fraction of the permeate is of orders of magnitude smaller than the main flow rate of fluid in the vessel). In a very real sense, this is a “form from function” derivation! And since, in an evolutionary competition, conversion efficiency is a bonus, it is to be expected that structures will prevail that generate the minimum possible irreversibility per unit mass of supplied or absorbed fluid (same product, less resources used). The formula for the total entropy generation rate in the vessels is (second line of Equation (19)):

$$S_L\left({\lambda }_0+\frac{{\lambda }_1}{2{\delta }_1^4}\right)$$

(21)

where $S_L=\frac{8\mu L{Q}_0^2}{\pi r_0^4{T}_0}$ is the irreversible entropy generation rate, in W/K, in a vessel of radius r₀ bisecting the domain for its entire length L.

The total drained/leaked mass flowrate is:

$$m_{dr}=m_{dr, L0}\left({\lambda }_0+2{\delta }_1{\lambda }_1\right)$$

(22)

And the most efficient configuration, i.e., the one that requires the least pumping power to ensure the survival of the cells in the domain, is that for which the ratio ∆S/m_dr is lowest.

Table 2. Radius ratio δ₁ and optimal splitting angle for different domain aspect ratios.

a = H/L	0.2	0.4	0.5	0.6	0.75	1
α1,opt	27°	29°	30°	31°	32°	34°
β1,opt	0.445	0.437	0.433	0.428	0.424	0.414
λ0	0.804	0.639	0.567	0.5	0.4	0.259
λ1	0.22	0.412	0.5	0.582	0.708	0.894
$\mathsf{\sigma }=\frac{\Delta S/\Delta S_L}{\Delta m_d/\Delta m_d,L}$	4.039	7.878	10.176	12.778	17.338	27.21
(∆p0L1)/(∆p1L0)	0.157	0.146	0.14	0.135	0.129	0.118
∆p0/∆p1	0.575	0.227	0.159	0.116	0.073	0.046

displays the values obtained for the dimensionless ratio $\mathsf{\sigma }=\frac{\raisebox{1ex}{$\Delta S$}\!\left/ \!\raisebox{-1ex}{$\Delta S_L$}\right.}{\raisebox{1ex}{$\Delta m_d$}\!\left/ \!\raisebox{-1ex}{$\Delta m_d,L$}\right.}$.

The corresponding geometries are displayed in Figure 8.

Some consequences of the above derivation are noteworthy:

(1)

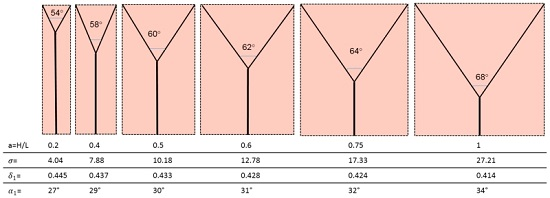
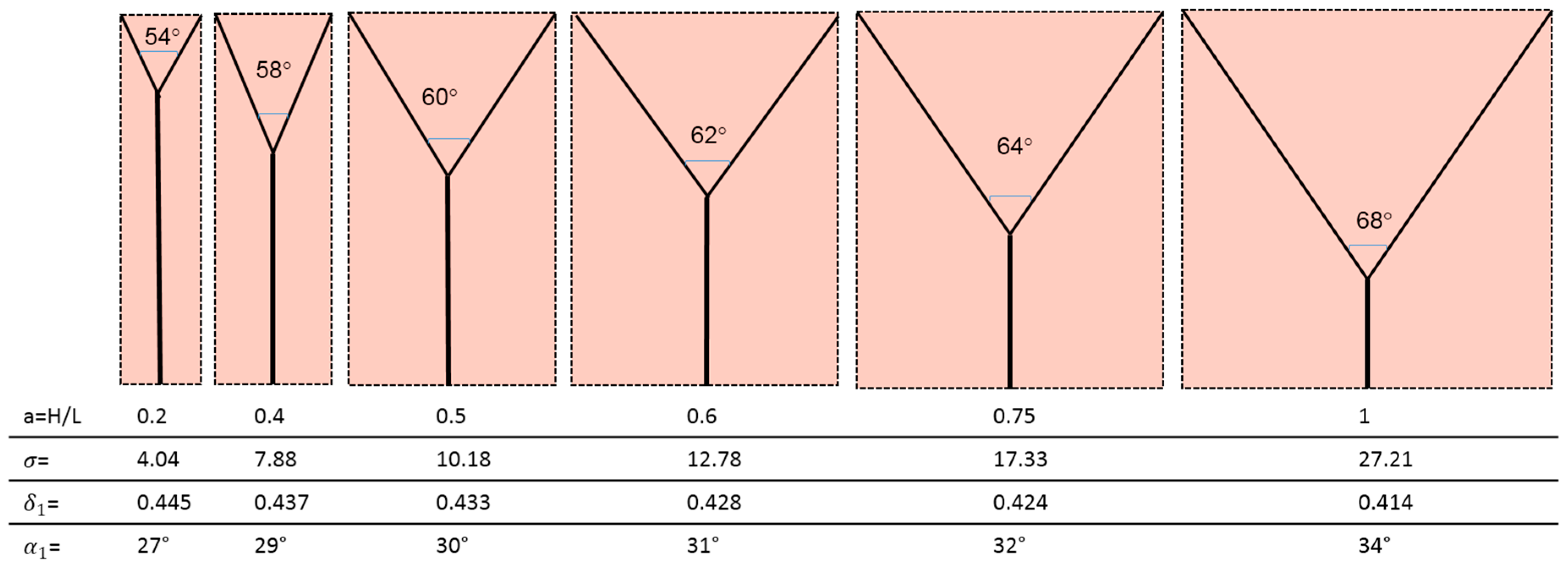
The bifurcation angle (2α₁) varies between 54° and 68° and is a function of the domain aspect ratio. This is not in agreement with Murray’s cosine rule for the “optimal angle”, that predicts 2α₁ = 75°;

(2)

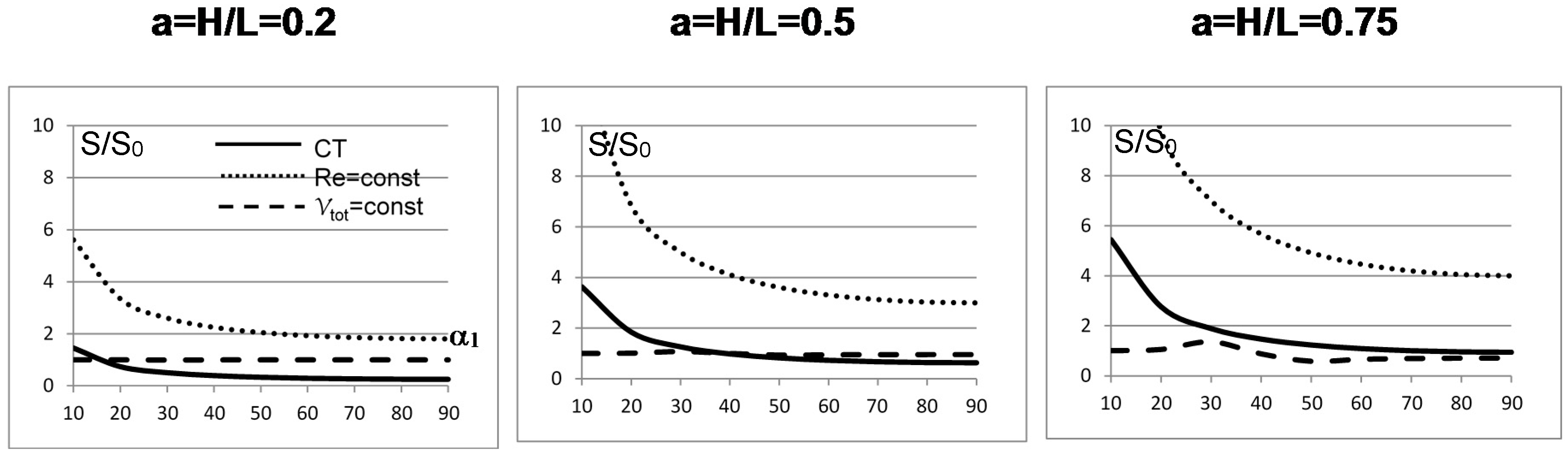
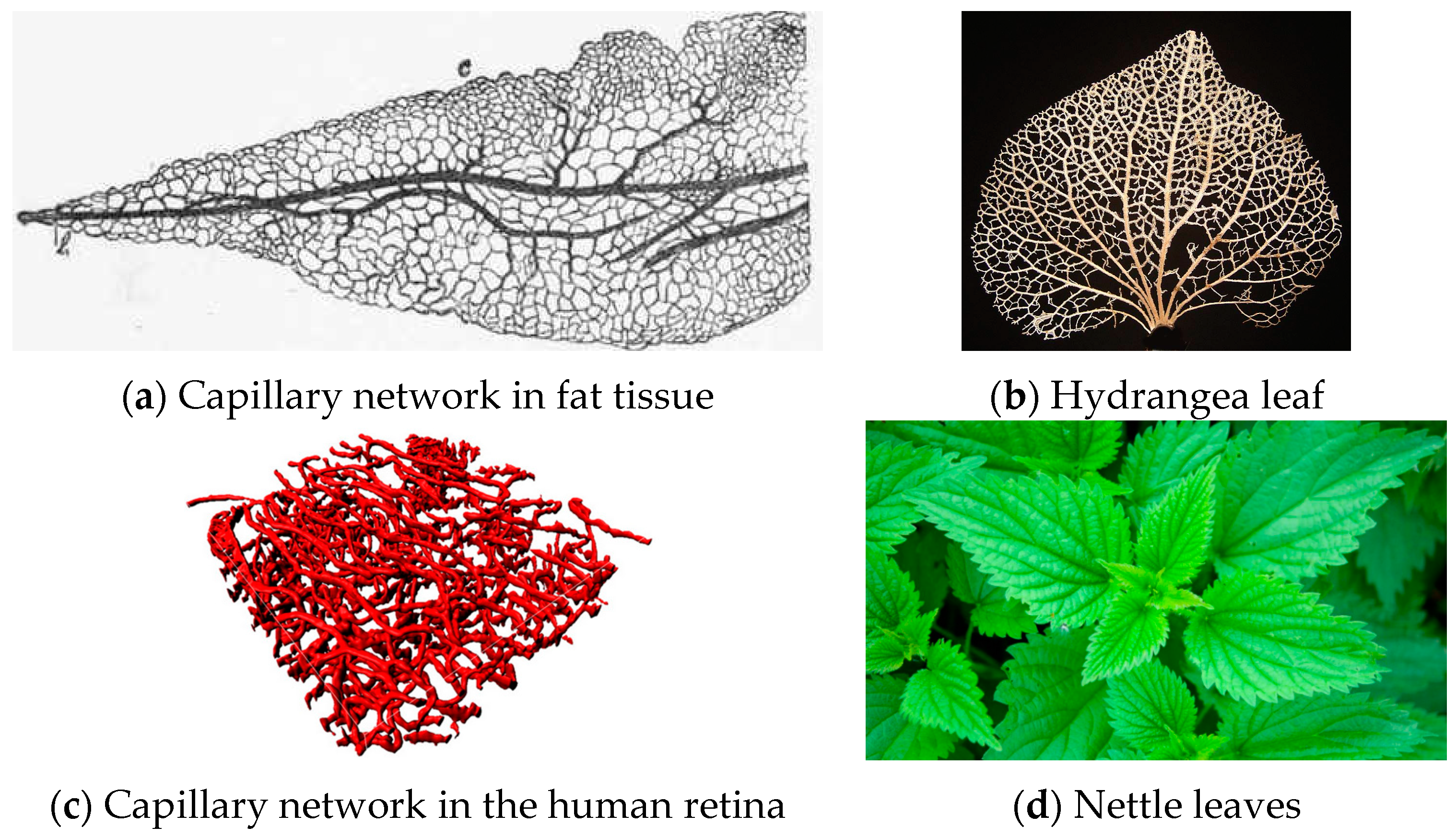
The radius ratio is a function of the splitting angle only, which is a remarkable result, because it was derived from a wall suction/drainage balance which in fact minimizes irreversible effects. Though much lower than that (0.7937) predicted by the H-M law, the values of δ₁ shown in Table 2 are within the range of the available experimental data: a series of indicative measurements on the images displayed in see Figure 6a,b,d show that the radius ratio of the first bifurcation is in the range 0.3 ÷ 0.75;

(3)

The more slender the domain (lower aspect ratio), the shorter λ₁ and the higher δ₁. This implies that the pressure gradient in the main and in the daughter branches is also a function of the splitting angle, and (Table 2) it is higher in the latter, as predicted also by the H-M law;

(4)

The pressure drop is also a function of the aspect ratio and it does not assume equal values in the parent and daughter branches, its value being always higher in the latter: while for lower aspect ratios the total pressure drop is almost equally allocated, for square domains the ∆p₁ is 25 times higher than the ∆p₀. Incidentally, this also negates the assumption of “equal pumping work” that is at the basis of the H-M law, but agrees with the dictates of Constructal Theory;

(5)

Considering that entropy generation rate per unit mass of transported fluid is proportional to the “lost pumping power”, the present model predicts that non-slender domains (aspect ratio a > 0.5) generate a much higher “cost” of the blood or sap distribution.

Table 3. “Optimal” ratios and angles in the present and in some previous studies.

Source	Radius Ratio δ = r1/r0	Length Ratio λ = L1/L0	Half-Splitting Angle α1
Hess and Murray [1,4,18], symmetrical & laminar	0.7937	-	37.5°
Present work, symmetrical & laminar	0.414 if a = 1 0.445 if a = 0.2	30 if a = 1 0.225 if a = 0.2	27° ÷ 34°
Grunert [37], fractal	0.707	0.7937	-
Huang [12], experimental	0.58 veins 0.555 arteries	0.846 0.619	-
Miguel [17], Newtonian limit, symmetrical	0.7937	0.7937	-
Uylings [8]	0.7937 laminar 0.198 turbulent	-	37.5° laminar 25° turbulent
Zamir [9], experimental, symmetric limit	0.8	-	-

shows the “optimal” ratios and angles in the present and in some previous studies.

4. Conclusions

The Hess/Murray law was revisited on the basis of the most modern representations of capillary nets. If the structures are represented as bifurcations, it is possible to show that the “cubic root of 2” rule derived for the radius ratio from the H-M law is not the unique optimum that can be obtained under physically sound assumptions. In particular, there is no a priori reason for a natural structure to bifurcate under constant volume, constant Reynolds number, or constant velocity constraints (though this latter case is almost surely at odds with experimental observations). The original energy balance proposed by Hess & Murray is then scrutinized, and an alternative form based on the functionality of the capillary network is developed: this new energy balance shows that both the “optimal splitting angle” and the “optimal radius ratio” depend on the shape of the domain “served” by the bifurcation. In this new representation, the general features of the capillary structure depend thus on its function and are in complete agreement with an evolution-driven adaptive model based on a minimum dissipation principle: in nature, organisms show a tendency to minimize the energy dissipation by friction for a given delivered mass flowrate of nutrients; for artificial artifacts, engineers may follow the same guideline to design optimal distribution networks for material and energy flows. A more rational “economic” approach than Murray’s “cost of blood” is certainly the amount of entropy generation per unit mass of delivered blood or sap. If the goal is to carry fluid to a “user”, and the transportation is affected by irreversible entropy generation, then the most efficient transportation network is the one that displays the lowest entropy generation rate per unit mass of transported fluid. In thermodynamics, the degree of irreversibility is best measured by a parameter called exergy destruction, Ex_δ, proportional to ∆S_irr. Since exergy-based optimization procedures are well known in engineering and thermal sciences, it is likely that a systematic exergy analysis of fluid-carrying networks may shed more light on the evolution of living organisms, as it has on the design of energy systems and heat exchangers.

As a final remark, it is necessary to recall that the study presented herein was conducted assuming stationary flow and domain conditions: pulsating and compliant wall effects are therefore neglected. While this obviously detracts of the direct applicability of the theory to real flows, the existence of a rigorously based steady model may help future investigations.