A Critical Reassessment of the Hess–Murray Law
Abstract
:1. Introduction
1.1. The Original Formulation by Hess
(The optimal ratio) between the main and the secondary branch is reached when the tendency to control the blood flow is such that the regulatory action leads to the smallest possible reduction of the cross-section. This ratio is attained when the main- and secondary branch have the same effect on the resistance to the flow.—Walter Rudolf Hess [2] (p. 473)
- (a)
- In a symmetric branching (Figure 1) the mass flowrate is equally split between the secondary branches: , and, for an incompressible fluid, , i.e., the two volumetric flowrates in the bifurcated sections are each equal to half the total volumetric flowrate in the main branch. Hess first relates the pressure drop ∆p in both the main and the secondary branches to the respective flow rates through a “viscous resistance” R, and then calculates a “total work expenditure” as the sum of the metabolic work related to the blood flow and the pumping work needed to overcome the frictional pressure drop;
- (b)
- The resistance to the flow in a circular tube of length L and cross-sectional area A is given by Poiseuille’s formula, which Hess rearranges to obtain kg/(s∙m4). He argues that, for a fixed flowrate and for the laminar isothermal flow of an incompressible newtonian fluid with constant properties, the “optimal control” is established when the variations of the hydraulic resistance induced by an infinitesimal variation in the flow area attain the same value in the main and in the daughter branches, i.e., when:
- (c)
- Since , it follows that:
1.2. Murray’s Rediscovery of the Hess’ Law
- (a)
- Murray [4] starts by expressing the total power involved in the circulation of blood as the sum of two terms: the first needed to overcome the frictional resistance through the vessel and the second corresponding to the metabolic effort needed to “create and maintain” the blood volume therein:
- (b)
- In line with Hess, the pressure drop is expressed by the Hagen–Poiseuille’s law:
- (c)
- Murray then uses Equation (3) to compute the metabolic cost cb, and then equates the total resistances R0 and R1+2 w.r.t. the flow area to derive his “cubic root of 2” law. Notice that the appearance of the cubic root does not depend on the value of the “specific metabolic cost of blood” cb, which is assumed constant;
- (d)
- By differentiating Equation (4) w.r.t. r and equating the result to 0, Murray argues that, for given cb and L, Q is proportional to r3;
- (e)
- If the above point is correct, and since the flow obeys Poiseuille’s law, the pressure gradient in successive branchings is proportional to r−1:
- (f)
- Under the same stipulation, the flow velocity correspondingly decreases:
- (g)
- Correspondingly, the Reynolds number Re scales with the radius ratio as:
1.3. A brief Summary of Experimental Results and of Other Allometric Laws
- (a)
- Assuming thin-walled vessels, the external radius does not play any significant role, because it is—at the considered scales—negligibly larger than the internal radius [6];
- (b)
- For 3-D branchings, the H-M still applies, because over 90% of the bifurcations are experimentally found to be coplanar [9];
- (c)
- (d)
- Both experimental and numerical findings show that while the H-M law leads—under the above stated assumptions—to an optimal value of δ = 0.7937 for laminar flow, for turbulent flow in veins and arteries the result becomes 0.74 and for the largest arteries, 0.77. Moreover, contrary to Hess & Murray’s result of an inverse scaling of the pressure gradient in successive branchings with δ (∆p/L = δ−1, see Equation (4)), radius-dependent slenderness factors are found experimentally: L/r = 15.75r1.10 for arterioles with r ≥ 50 μm, 1.79r0.47 for arterioles with r ≤ 50 μm, 14.54r for veins with r ≤ 2000 μm, [12,13]. Notice that the fundamental deviation of Huang’s results [12] from the H-M law depend also on the different ordering of “successive branches” adopted therein, whose classification cannot be directly extended to capillary networks. Nevertheless, their findings contradict the H-M predictions in arterioles and veins (see also Table 3). Notice that [14] the H-M law is independent of the slenderness ratio r/L. Very well documented critiques of the H-M law are presented in [7,15];
- (e)
- (f)
- Nothing in the derivation of the H-M. law makes explicit reference to biological vessels: in principle, the law should hold also for human artefacts (pipes and any other kind of conduit) [6]: if the cross-sectional area is not circular, the law of the area still approximately holds if the hydraulic radius rh is substituted for r and a proper correction is introduced [19];
- (g)
- The law has important consequences when the growth of a biological organism is taken into account: if it holds, then the radii of the individual vessels in the vascular system must “grow” according to cubic root of 2 because the volume flow rate of the organism grows as well, and so does r0, the radius of the primary stem [6,20]. This applies also to stress situations: when a higher rate of blood (or sap) flow is needed, the existence (or the emergence) of a self-regulatory response which suitably adjusts the vessels radii, as originally proposed by Hess, seems reasonable [15];
- (h)
- The H-M law also allows for an “allometric scaling” between different species [20]: if the relative sizes of the respective blood (or sap) vessels scale according to this law, then the physical dimensions depend on the radius of the main branch, which in turn depends on the metabolic rate of the species [21];
- (i)
- If blood is modelled as a non-Newtonian fluid, the 2−1/3 law does not apply anymore, because—as expected—the exponent is found to have a non negligible dependence on the viscosity law (from 1 to 2.5 in [22,23]). Miguel [17,18] analyzed the irreversibility in branched flows of a power fluid and showed that (a) the “optimal” radius ratio depends on the “degree of non-newtonianity” of the fluid, ω; (b) that in the limit of Newtonian behavior, ω tends to 1 and the H-M law is recovered;
- (j)
1.4. Bejan’s Constructal Law
The flow path was constructed in a sequence of steps that started with the smallest building block (elemental area) and continued in time with larger building blocks (assemblies, or constructs). The mode of transport with the highest resistivity (slow flow, diffusions, walking, and high cost) was placed on the smallest scales, completely filling the smallest elements. Modes of transport with successively lower resistivities (fast flow, streams, vehicles and low cost) were placed in the larger constructs, where they were used to connect the area-point or volume-point flows integrated over the constituents. The geometry of each building block was optimised for area-point access.— Wishsanuruk Wechsatol, et al. [28]
- (a)
- This very same “construction” derives in fact from a single principle, namely that of minimizing irreversibility in the transport of a certain mass flow rate of fluid from one point to a pair of a triplet of “users”;
- (b)
- The objective function whose minimum identifies the optimal configuration is the specific irreversible entropy generation rate;
- (c)
- That both natural and artificial dendritic flow structures do not admit of a single “optimal radius ratio” or of an “optimal splitting angle”, because both of these quantities are determined by the imposed boundary conditions. Therefore, in an evolutionary sense, it is the random variation of the latter that determines the “shape” of the winning configuration.
1.5. A fluiddynamic Interpretation
- (a)
- θ = 1 (this is the H-M law): , which results in δ = 2−1/3 (and, incidentally, in );
- (b)
- V0 = 2V1 (the volume of fluid in the main branch is equal to the sum of the two volumes of the daughter branches): now δ = 1/(2λ) and ;
- (c)
- Re0 = Re1, from which δ = 0.5, θ = 4 and Π = 1 + 16λ;
- (d)
- U0 = U1 (constant fluid velocity in successive branchings): δ = 2−1/2, θ = 0.1768, and Π = 0.5λ.
1.6. Scope of This Work
- The Hess–Murray law is only one of several possible instantiations of a class of rules that can be derived from irreversibility minimization;
- That there are therefore different structures that can develop if one or more of the assumptions are modified;
- That if an exergy-based resource cost paradigm is employed, the Hess–Murray law is amenable to a more fundamental and interesting interpretation that complements and extends the henceforth published results.
2. Irreversibility in Viscous Isothermal Flows
- The velocity remains the same before and after the bifurcation, Ui+1 = Ui: thence ;
- The Reynolds number remains the same before and after the bifurcation, Re1 = Re0: ;
- The sum of the volumes of the daughter branches equals the volume of the main stem: , in which case , or ;
- The pressure drop in the daughter branches equals that in the main stem and the radius ratio is dictated by the Hess–Murray law ().
3. Is the Hess-Murray Energy Balance the Correct One?
- (a)
- Hess assumed that the variation of the hydraulic viscous resistance w.r.t. a small change in the blood flow is the same in the parent and daughter branches. Today we know that blood supply pressure is regulated also in the arterioles, upstream of the capillaries, and that the latter may function also as temporary “blood reservoirs”, and therefore Hess’ balance cannot be applied to derive the radius ratio of capillary bifurcations;
- (b)
- Murray starts by calculating the total power (which he calls cost) of blood circulation as the sum of the power dissipated by friction losses and of a “metabolic cost” of the blood, calculated as the pumping power requested of the heart. This calculation is though inaccurate, because it neglects for instance the work needed to deliver the blood through the veins back to the heart (in fact, Murray [4,31] obtains three different values for his metabolic cost depending on the different assumptions he posits). Thus, his balance between the blood pumping work (proportional to the vessels radius) and the friction work is completely contingent on the rather arbitrary assumptions he posits to calculate the “pumping power” of the heart.
- (a)
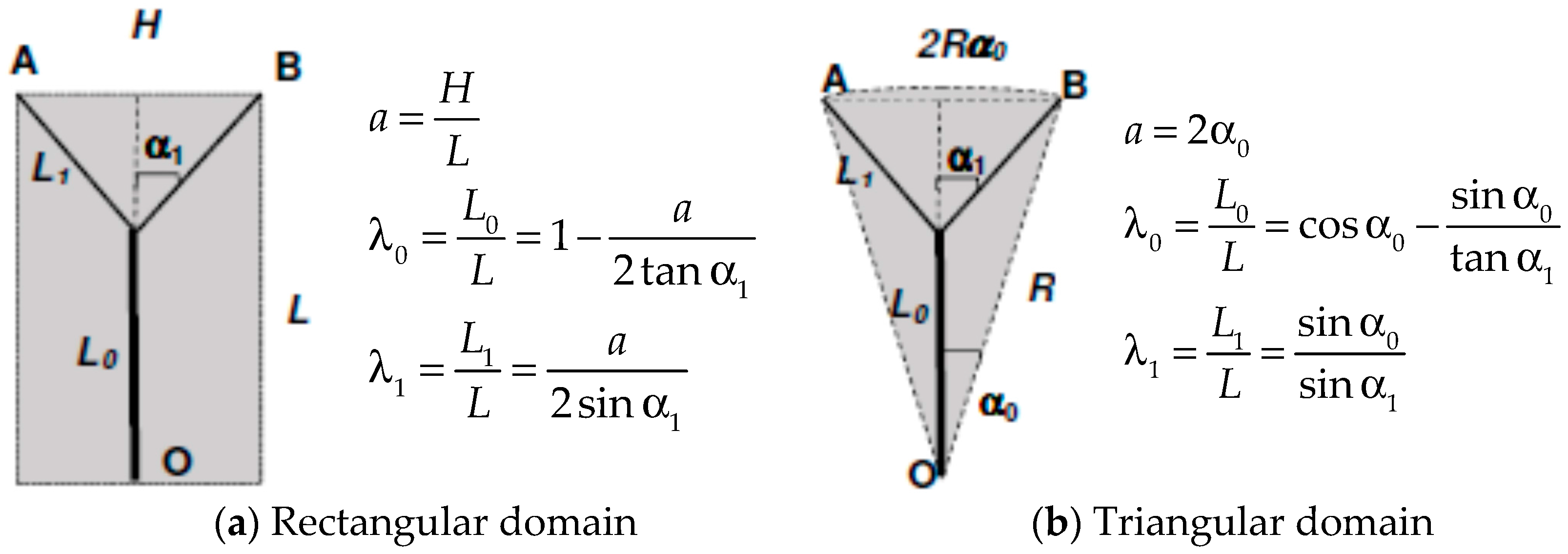
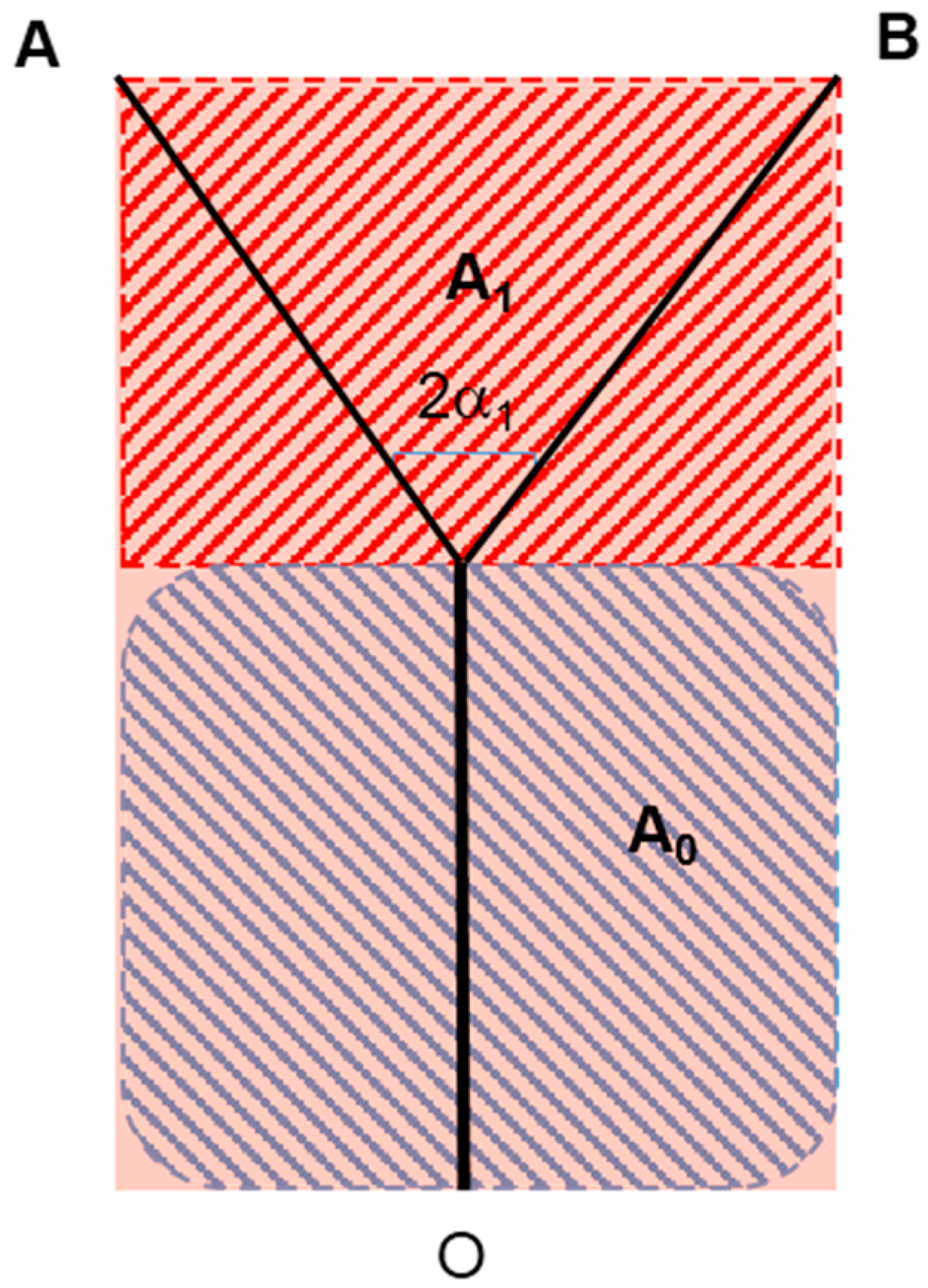
- The portion of the supply region denoted as A0 receives all of (and only) the nutrients permeated through the main branch: , where μ is the wall permeability (kg/(m2s)), assumed to remain constant throughout. By analogy for the remaining portion A1, ;
- (b)
- The “costs” of the irreversibility, S0 and S1, must be attributed to the mass flow rates m0 and m1 respectively;
- (c)
- And the objective function becomes
- (1)
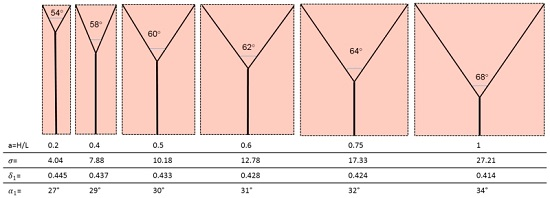
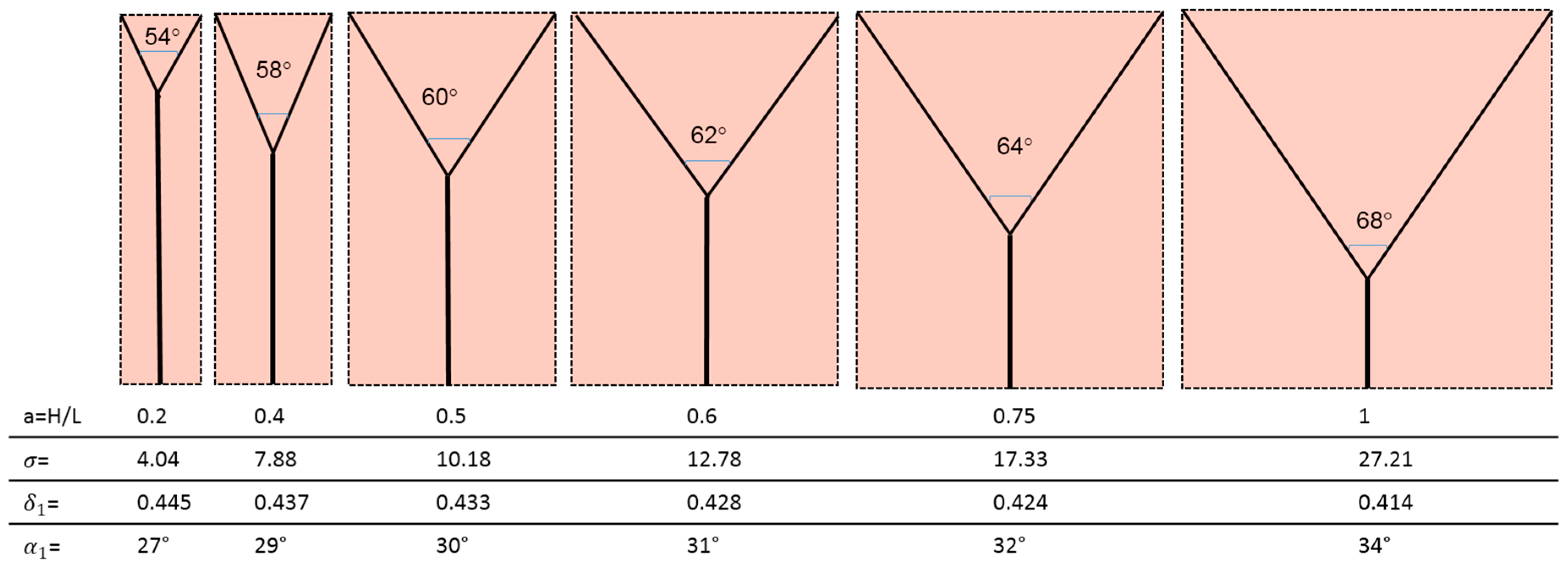
- The bifurcation angle (2α1) varies between 54° and 68° and is a function of the domain aspect ratio. This is not in agreement with Murray’s cosine rule for the “optimal angle”, that predicts 2α1 = 75°;
- (2)
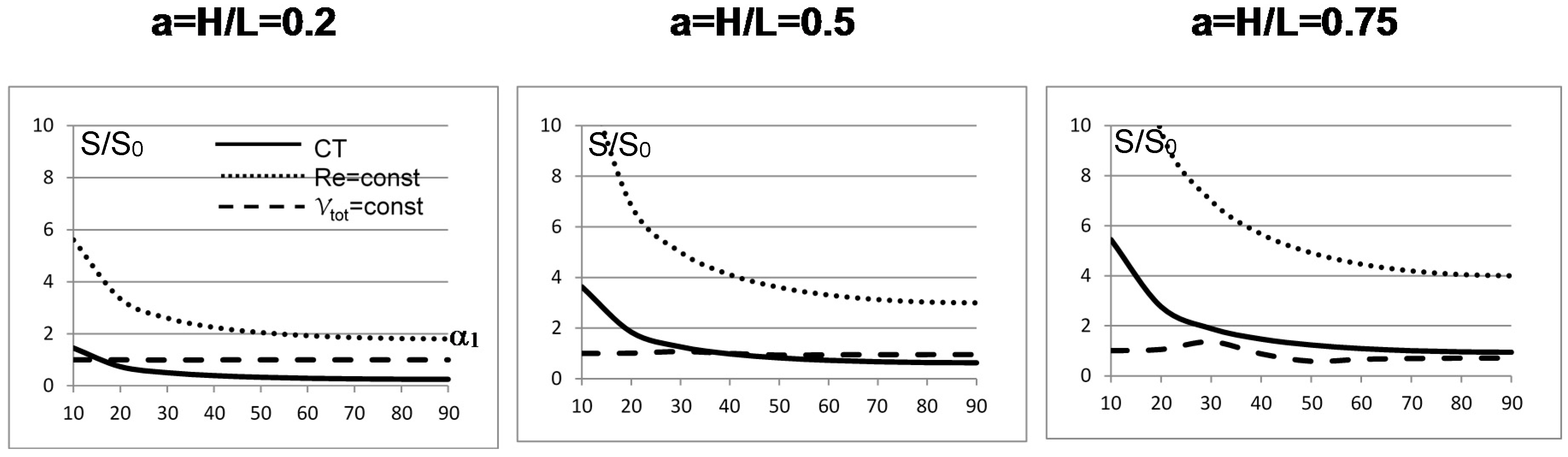
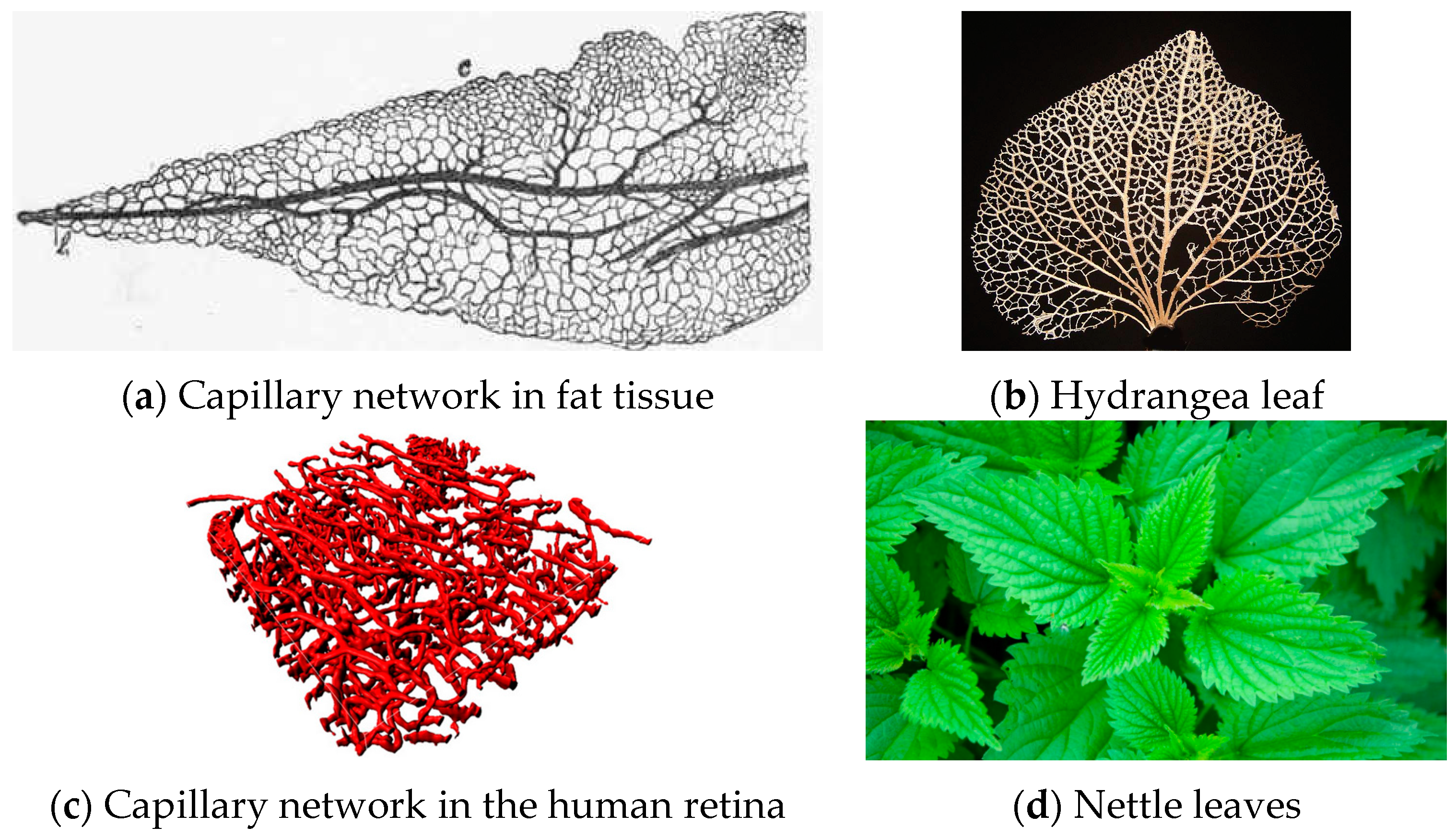
- The radius ratio is a function of the splitting angle only, which is a remarkable result, because it was derived from a wall suction/drainage balance which in fact minimizes irreversible effects. Though much lower than that (0.7937) predicted by the H-M law, the values of δ1 shown in Table 2 are within the range of the available experimental data: a series of indicative measurements on the images displayed in see Figure 6a,b,d show that the radius ratio of the first bifurcation is in the range 0.3 ÷ 0.75;
- (3)
- The more slender the domain (lower aspect ratio), the shorter λ1 and the higher δ1. This implies that the pressure gradient in the main and in the daughter branches is also a function of the splitting angle, and (Table 2) it is higher in the latter, as predicted also by the H-M law;
- (4)
- The pressure drop is also a function of the aspect ratio and it does not assume equal values in the parent and daughter branches, its value being always higher in the latter: while for lower aspect ratios the total pressure drop is almost equally allocated, for square domains the ∆p1 is 25 times higher than the ∆p0. Incidentally, this also negates the assumption of “equal pumping work” that is at the basis of the H-M law, but agrees with the dictates of Constructal Theory;
- (5)
- Considering that entropy generation rate per unit mass of transported fluid is proportional to the “lost pumping power”, the present model predicts that non-slender domains (aspect ratio a > 0.5) generate a much higher “cost” of the blood or sap distribution.
4. Conclusions
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Domain aspect ratio |
| A | Area, m2 |
| c | Energy cost of the unit flow, W/kg |
| H | Domain height, m |
| L | Domain width, m |
| m | Mass flowrate, kg/s |
| p | Pressure, N/m2 |
| Q | Volume flowrate, m3/s |
| r | Radius, m |
| V | Volume, m3 |
| α | Splitting angle, ° |
| S | Entropy generation rate, W/K |
| T | Temperature, °, K |
| U | Velocity components, m/s |
| δ | Radius ratio |
| θ | Wall stress ratio |
| λ | Branching ratio |
| μ | Wall permeability coefficient, kg/(m2s) |
| ν | Kinematic viscosity, m2/s |
| Π | Pumping power ratio |
| ρ | Density, kg/m3 |
| τw | Wall stress, N/m2 |
References
- Hess, W.R. Eine mechanisch bedingte Gesetzmäßigkeit im Bau des Blutgefäßsystems. Archiv für Entwicklungsmechanik der Organismen 1903, 16, 632–641. (In German) [Google Scholar] [CrossRef]
- Hess, W.R. Über die periphere Regulierung der Blutzirkulation. Pflüger’s Archiv für die Gesamte Physiologie des Menschen und der Tiere 1917, 168, 439–490. (In German) [Google Scholar] [CrossRef]
- Young, T. Hydraulic investigations, subservient to an intended Croonian lecture on the motion of the blood. Philos. Trans. R. Soc. Lond. 1808, 98, 164–186. [Google Scholar] [CrossRef]
- Murray, C.D. The physiological principle of minimum work—I: The vascular system and the cost of blood volume. Proc. Natl. Acad. Sci. USA 1926, 12, 207–214. [Google Scholar] [CrossRef] [PubMed]
- Murray, C.D. The physiological principle of minimum work applied to the angle of branching of arteries. J. Gen. Physiol. 1926, 9, 835–841. [Google Scholar] [CrossRef] [PubMed]
- Sherman, T.F. On Connecting Large Vessels to Small: The Meaning of Murray’s Law. J. Gen. Physiol. 1981, 78, 431–453. [Google Scholar] [CrossRef] [PubMed]
- Roy, A.G.; Woldenberg, M.J. A generalization of the optimal models of arterial branching. Bull. Math. Biol. 1982, 44, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Uylings, H.B.M. Optimization of diameters and bifurcation angles in lung and vascular tree structures. Bull. Math. Biol. 1977, 39, 509–520. [Google Scholar] [CrossRef]
- Zamir, M.; Wrigley, S.M.; Langille, B.L. Arterial bifurcations in the cardiovascular system of a rat. J. Gen. Phys. 1983, 81, 325–335. [Google Scholar] [CrossRef]
- Mauroy, B.; Filoche, M.; Weibel, E.R.; Sapoval, B. An optimal bronchial tree may be dangerous, letters to Nature. Nature 2004, 427, 633–636. [Google Scholar] [CrossRef] [PubMed]
- Tesch, K. On some extensions of Murray’s law. Task Q. 2010, 14, 227–235. [Google Scholar]
- Huang, W.; Yen, R.T.; Mclaurine, M.; Bledsoe, G. Morphometry of the human pulmonary vasculature. J. Appl. Physiol. 1996, 81, 2123–2133. [Google Scholar] [PubMed]
- Qureshi, M.U.; Vaughan, G.D.A.; Sainsbury, C.; Johnson, M.; Peskin, C.S.; Olufsen, M.S.; Hill, N.A. Numerical simulation of blood flow and pressure drop in the pulmonary arterial and venous circulation. Biomech. Model. Mechanobiol. 2014, 13, 1137–1154. [Google Scholar] [CrossRef] [PubMed]
- Sciubba, E. Entropy Generation Minimization as a Design Tool. Part 1: Analysis of Different Configurations of Branched and Non-branched Laminar Isothermal Flow through a Circular Pipe. Int. J. Thermodyn. 2011, 14, 11–20. [Google Scholar]
- West, G.B.; Brown, J.H. The origin of allometric scaling laws in biology from genomes to ecosystems: towards a quantitative unifying theory of biological structure and organization. J. Exp. Biol. 2005, 208, 1575–1592. [Google Scholar] [CrossRef] [PubMed]
- Al-Shammari, A.A.; Gaffney, E.A.; Egginton, S. Modelling capillary oxygen supply capacity in mixed muscles: Capillary domains revisited. J. Theor. Biol. 2014, 356, 47–61. [Google Scholar] [CrossRef] [PubMed]
- Miguel, A.F. A study of entropy generation in tree-shaped flow structures. Int. J. Heat Mass Transf. 2016, 92, 349–359. [Google Scholar] [CrossRef]
- Miguel, A.F. Toward an optimal design principle in symmetric and asymmetric tree flow networks. J. Theor. Biol. 2016, 389, 101–109. [Google Scholar] [CrossRef] [PubMed]
- Barber, R.W.; Emerson, D.R. Biomimetic design of artificial micro-vasculatures for tissue engineering. ATLA 2010, 38 (Suppl. S1), 67–79. [Google Scholar] [PubMed]
- Bejan, A.; Zane, J.P. Design in Nature, How the Constructal Law Governs Evolution in Biology, Physics, Technology, and Social Organization; Knopf Doubleday Publishing Group: New York, NY, USA, 2012. [Google Scholar]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Revellin, R.; Rousset, F.; Baud, D.; Bonjour, J. Extension of Murray’s law using a non-Newtonian model of blood flow. Theor. Biol. Med. Model. 2009, 6. [Google Scholar] [CrossRef] [PubMed]
- Westerhof, N.; Stergiopulos, N.; Noble, M.I.M. Snapshots of Hemodynamics: An Aid for Clinical Research and Graduate Education; Springer: New York, NY, USA, 2010. [Google Scholar]
- Robbe, M.; Sciubba, E.A. 2-D Constructal Configuration Genetic Optimization Method. In Proceedings of the ASME 2008 International Mechanical Engineering Congress and Exposition (IMECE 2008), Boston, MA, USA, 31 October–6 November 2008.
- Robbe, M.; Sciubba, E. Derivation of the optimal internal cooling geometry of a prismatic slab: Comparison of constructal and non-constructal geometries. Energy 2009, 34, 2167–2174. [Google Scholar] [CrossRef]
- Bejan, A. Constructal-theory network of conducting paths for cooling a heat generating volume. Int. J. Heat Mass Transf. 1997, 40, 799–816. [Google Scholar] [CrossRef]
- Heitor Reis, A. Constructal Theory: From Engineering to Physics, and How Flow Systems Develop Shape and Structure. ASME Appl. Mech. Rev. 2006, 59, 269–282. [Google Scholar] [CrossRef]
- Wechsatol, W.; Lorente, S.; Bejan, A. Dendritic convection on a disc. Int. J. Heat Math Transf. 2003, 46, 4381–4391. [Google Scholar] [CrossRef]
- Sciubba, E. Entropy Generation Minima in Different Configurations of the Branching of a Fluid-Carrying Pipe in Laminar Isothermal Flow. Entropy 2010, 12, 1855–1866. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Murray, C.D. The physiological principle of minimum work II: Oxygen exchange in capillaries. Proc. Natl. Acad. Sci. USA 1926, 12, 299–304. [Google Scholar] [CrossRef] [PubMed]
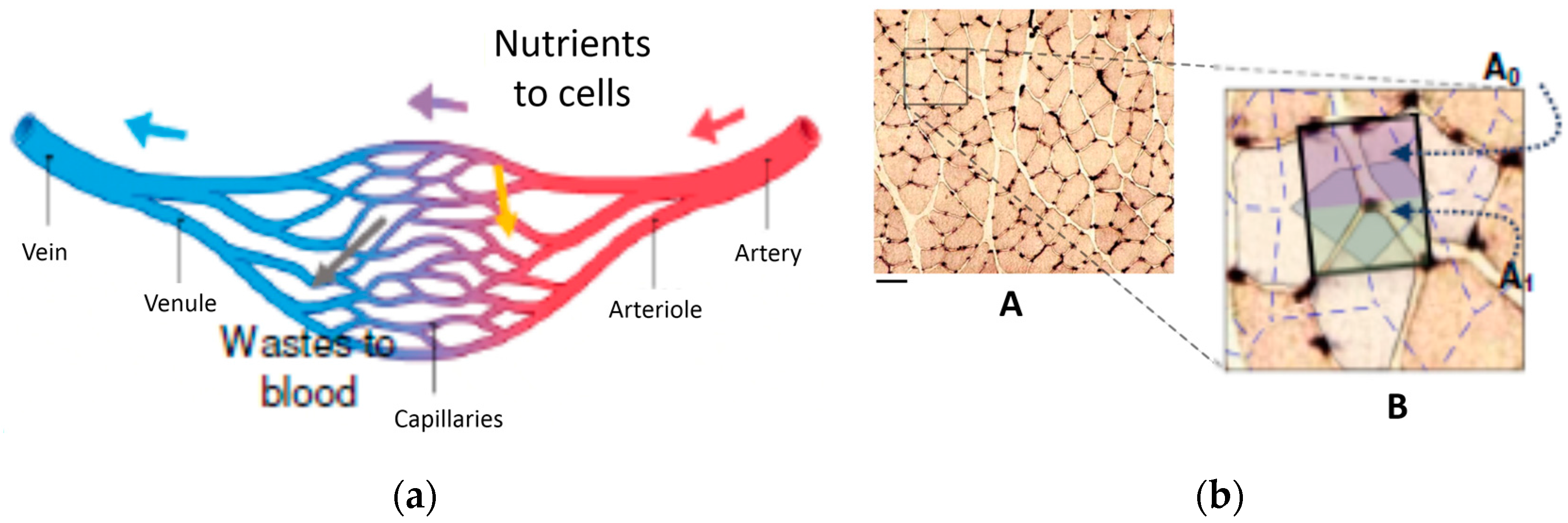
- Functional Scheme of a Capillary Network. Available online: http://www.evolvingsciences.com/wpimages/wpbd1d7154_06.png (accessed on 1 August 2016).
- Capillary Network in Fat Tissue. Available online: http://chestofbooks.com/health/physiology/Manual/images/Capillary-Network-of-Fat-Tissue-Klein.jpg (accessed on 1 August 2016).
- Hydrangea Leaf. Available online: https://nl.wikibooks.org/wiki/Leer_jezelf_ecologisch_tuinieren/Plantkunde/Blad#/media/File:Vein_sceleton_hydrangea_ies.jpg (accessed on 1 August 2016).
- Capillary Network in the Human Retina. Available online: http://iovs.arvojournals.org/data/Journals/IOVS/933252/i1552-5783-53-9-5502-f04.jpeg (accessed on 1 August 2016).
- Nettle Leaves. Available online: http://tvoje-zdorovja.com/wp-content/uploads/2013/07/39343_0.jpg (accessed on 1 August 2016).
- Grunert, M. Allometric Scaling Laws and the Derivation of the Scaling Exponent. Available online: http://jaguar.biologie.hu-berlin.de/~wolfram/pages/seminar_theoretische_biologie_2007/ausarbeitungen/grunert.pdf (accessed on 26 July 2016).

| Branching Rank | Total Number of Branches | Entropy Generation Rate in the Branches | Total Entropy Generation Rate from the Initial Stem to the n-th Branching Included | |
|---|---|---|---|---|
| Main stem | 1 | (19) | ||
| First bifurcation | 2 | |||
| Second bifurcation | 4 | |||
| Third bifurcation | 8 | |||
| … | … | … | … | |
| n-th bifurcation | 2n | |||
| a = H/L | 0.2 | 0.4 | 0.5 | 0.6 | 0.75 | 1 |
|---|---|---|---|---|---|---|
| α1,opt | 27° | 29° | 30° | 31° | 32° | 34° |
| β1,opt | 0.445 | 0.437 | 0.433 | 0.428 | 0.424 | 0.414 |
| λ0 | 0.804 | 0.639 | 0.567 | 0.5 | 0.4 | 0.259 |
| λ1 | 0.22 | 0.412 | 0.5 | 0.582 | 0.708 | 0.894 |
| 4.039 | 7.878 | 10.176 | 12.778 | 17.338 | 27.21 | |
| (∆p0L1)/(∆p1L0) | 0.157 | 0.146 | 0.14 | 0.135 | 0.129 | 0.118 |
| ∆p0/∆p1 | 0.575 | 0.227 | 0.159 | 0.116 | 0.073 | 0.046 |
| Source | Radius Ratio δ = r1/r0 | Length Ratio λ = L1/L0 | Half-Splitting Angle α1 |
|---|---|---|---|
| Hess and Murray [1,4,18], symmetrical & laminar | 0.7937 | - | 37.5° |
| Present work, symmetrical & laminar | 0.414 if a = 1 0.445 if a = 0.2 | 30 if a = 1 0.225 if a = 0.2 | 27° ÷ 34° |
| Grunert [37], fractal | 0.707 | 0.7937 | - |
| Huang [12], experimental | 0.58 veins 0.555 arteries | 0.846 0.619 | - |
| Miguel [17], Newtonian limit, symmetrical | 0.7937 | 0.7937 | - |
| Uylings [8] | 0.7937 laminar 0.198 turbulent | - | 37.5° laminar 25° turbulent |
| Zamir [9], experimental, symmetric limit | 0.8 | - | - |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sciubba, E. A Critical Reassessment of the Hess–Murray Law. Entropy 2016, 18, 283. https://doi.org/10.3390/e18080283
Sciubba E. A Critical Reassessment of the Hess–Murray Law. Entropy. 2016; 18(8):283. https://doi.org/10.3390/e18080283
Chicago/Turabian StyleSciubba, Enrico. 2016. "A Critical Reassessment of the Hess–Murray Law" Entropy 18, no. 8: 283. https://doi.org/10.3390/e18080283