1. Introduction
In this work, we consider finite precision representations of probabilistic models. Suppose the original model, or target distribution, has n non-zero mass points and is given by . We wish to approximate it by a distribution of which each entry is a rational number with a fixed denominator. In other words, for every i, for some non-negative integer . The distribution is called an M-type distribution, and the positive integer is the precision of the approximation. The problem is non-trivial, since computing the numerator by rounding to the nearest integer in general fails to yield a distribution.
M-type approximations have many practical applications, e.g., in political apportionments,
M seats in a parliament need to be distributed to
n parties according to the result of some vote
. This problem led, e.g., to the development of
multiplier methods [
1]. In communications engineering, example applications are finite precision implementations of probabilistic data compression [
2], distribution matching [
3], and finite-precision implementations of Bayesian networks [
4,
5]. In all of these applications, the
M-type approximation
should be close to the target distribution
in the sense of an appropriate error measure. Common choices for this approximation error are the variational distance and the informational divergences:
where log denotes the natural logarithm.
Variational distance and informational divergence Equation (1b) have been considered by Reznik [
6] and Böcherer [
7], respectively, who presented algorithms for optimal
M-type approximation and developed bounds on the approximation error. In a recent manuscript [
8], we extended the existing works on Equation (1a,b) to target distributions with infinite support (
) and refined the bounds from [
6,
7].
In this work, we focus on the approximation error Equation (1c). It is an appropriate cost function for data compression [
9] (Theorem 5.4.3) and seems appropriate for the approximation of parameters in Bayesian networks (see
Section 4). Nevertheless, to the best of the authors’ knowledge, the characterization of
M-type approximations minimizing
has not received much attention in literature so far.
Our contributions are as follows. In
Section 2, we present an efficient greedy algorithm to find
M-type distributions minimizing Equation (1c). We then discuss in
Section 3 the properties of the optimal
M-type approximation and bound the approximation error Equation (1c). Our bound incorporates a reverse Pinsker inequality recently suggested in [
10] (Theorem 7). The algorithm we present is an instance of a greedy algorithm similar to
steepest ascent hill climbing [
11] (Chapter 2.6). As a byproduct, we unify this work with [
6,
7,
8] by showing that also the algorithms optimal w.r.t. variational distance Equation (1a) and informational divergence Equation (1b) are instances of the same general greedy algorithm, see
Section 2.
2. Greedy Optimization
In this section, we define a class of problems that can be optimally solved by a greedy algorithm. Consider the following example:
Example 1. Suppose there are n queues with jobs, and you have to select M jobs minimizing the total time spent. A greedy algorithm suggests to select successively the job with the shortest duration, among the jobs that are at the front of their queues. If the jobs in each queue are ordered by increasing duration, then this greedy algorithm is optimal.
We now make this precise: Let
M be a positive integer, e.g., the number of jobs that have to be completed, and let
,
, be a set of functions, e.g.,
is the duration of the
k-th job in the
i-th queue. Let furthermore
be a
pre-allocation, representing a constraint that has to be fulfilled (e.g., in the
i-th queue at least
jobs have to be completed) or a chosen initialization. Then, the goal is to minimize
i.e., to find a
final allocation satisfying
and, for every
i,
. A greedy method to obtain such a final allocation is presented in Algorithm 1. We show in
Appendix A.1. that this algorithm is optimal if the functions
satisfy certain conditions:
| Algorithm 1: Greedy Algorithm |
| Initialize |
| repeat times |
| Compute |
| Compute // (choose one minimal element) Update |
| end repeat |
| Return c = (k1, ⋯, kn). |
Proposition 1. If the functions are non-decreasing in k, Algorithm 1 achieves a global minimum for a given pre-allocation and a given M.
Remark 1. The minimum of may not be unique.
Remark 2. If a function is convex, the difference is non-decreasing in k. Hence, Algorithm 1 also minimizes Remark 3. Note that the functions need not be non-negative, i.e., in the view of Example 1, jobs may have negative duration. The functions are non-negative, though, if in Remark 2 is convex and non-decreasing.
Remark 2 connects Algorithm 1 to steepest ascent hill climbing [
11] (Chapter 2.6) with fixed step size and a constrained number of
M steps.
We now show that instances of Algorithm 1 can find
M-type approximations
minimizing each of the cost functions in Equation (1). Noting that
for some non-negative integer
, we can rewrite the cost functions as follows:
where
denotes entropy in nats.
Ignoring constant terms, these cost functions are all instances of Remark 2 for convex functions
(see
Table 1). Hence, the three different
M-type approximation problems set up by Equation (1) can all be solved by instances of Algorithm 1, for a trivial pre-allocation
and after taking
M steps. The final allocation
simply defines the
M-type approximation by
.
For variational distance optimal approximation, we showed in [
8] (Lemma 3), that every optimal
M-type approximation satisfies
, hence one may speed up the algorithm by pre-allocating
. We furthermore show in Lemma 1 below that the support of the optimal
M-type approximation in terms of Equation (1c) equals the support of
(if
). Assuming that
is positive, one can pre-allocate the algorithm with
. We summarize these instantiations of Algorithm 1 in
Table 1.
This list of instances of Algorithm 1 minimizing information-theoretic or probabilistic cost functions can be extended. For example, the -divergences and can also be minimized, since the functions inside the respective sums are convex. However, Rényi divergences of orders cannot be minimized by applying Algorithm 1.
3. -Type Approximation Minimizing
As shown in the previous section, Algorithm 1 presents a minimizer of the problem
if instantiated according to
Table 1. Let us call this minimizer
. Recall that
is positive and that
. The support of
must contain the support of
, since otherwise
. Note further that the costs
are negative if
and zero if
; hence, if
, the index
i cannot be chosen by Algorithm 1, thus also
. This proves:
Lemma 1. If , the supports of and coincide, i.e., .
The assumption that
is positive and that
hence comes without loss of generality. In contrast, neither variational distance nor informational divergence Equation (1b) require
: As we show in [
8], the
M-type approximation problem remains interesting even if
.
Based on Lemma 1, the following example explains why the optimal M-type approximation does not necessarily result in a “small” approximation error:
Example 2. Let and , hence by Lemma 1, . It follows that , which can be made arbitrarily close to by choosing a small positive ε.
In
Table 1 we made use of [
8] (Lemma 3), which says that every
minimizing the variational distance
satisfies
, to speed up the corresponding instance of Algorithm 1 by proper pre-allocation. Initialization by rounding is not possible when minimizing
, as shown in the following two examples:
Example 3. Let and . The optimal M-type approximation is , hence . Initialization via rounding off fails.
Example 4. Let and . The optimal M-type approximation is , hence . Initialization via rounding up fails.
To show that informational divergence vanishes for
, assume that
for all
i. Since the variational distance optimal approximation
satisfies
for every
i,
has the same support as
, which ensures that
. By similar arguments as in the proof of [
8] (Proposition 4), we obtain
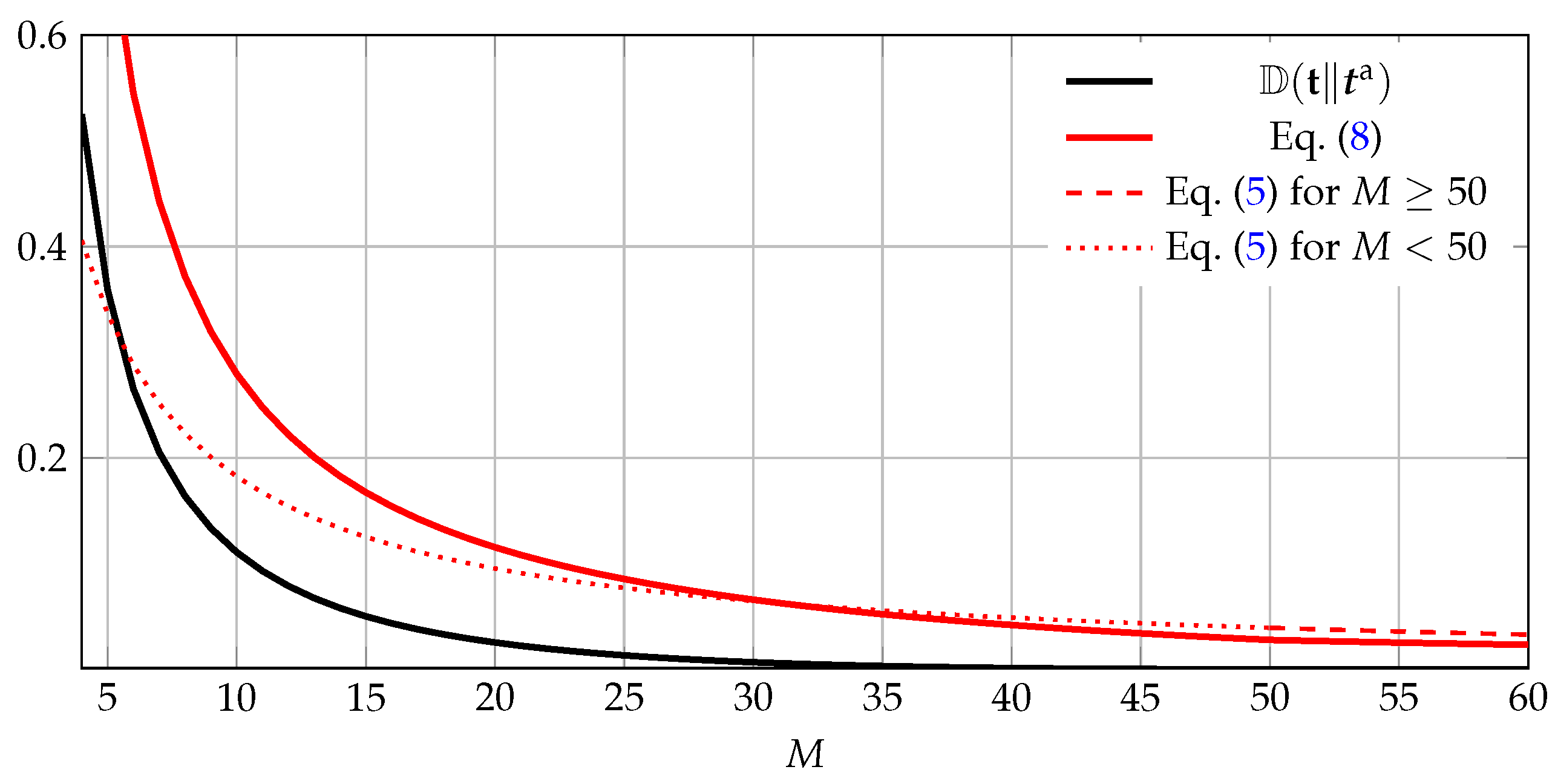
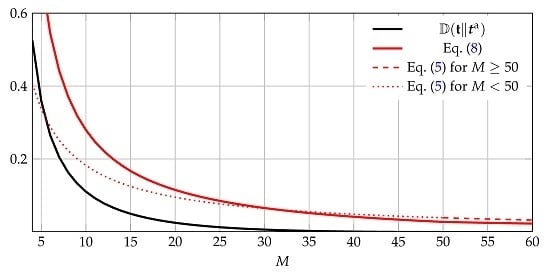
Note that this bound is universal, i.e., it prescribes the same convergence rate for every target distribution with n mass points.
We now develop an upper bound on
that holds for every
M. To this end, we first approximate
by a distribution
in
that minimizes
. If
is unique, then it is called the
reverse I-projection [
12] (Section I.A) of
onto
. Since
, its variational distance optimal approximation
has the same support as
, which allows us to bound
by
.
Lemma 2. Let minimize . Then,where is such that , and where . Let
,
, and
. The parameter
must scale the mass
such that it equals
, i.e., we have
If, for all i, , then , hence is feasible and . One can show that decreases with M.
The first term on the right-hand side of Equation (8) accounts for the error caused by first approximating
by
(in the sense of Lemma 2). The second term accounts for the additional error caused by the
M-type approximation of
and incorporates the reverse Pinsker inequality [
10] (Theorem 7). If
for every
i, hence
, then
and the bound simplifies to
For
M sufficiently large, Equation (8) thus yields better results than Equation (5), which approximates to
. Moreover, for
M sufficiently large, our bound Equation (8) is uniform, i.e., it prescribes the same convergence rate for every target distribution with
n mass points. We illustrate the bounds for an example in
Figure 1.
4. Applications and Outlook
Arithmetic coding uses a probabilistic model to compress a source sequence. Applying Algorithm 1 with cost Equation (1c) to the empirical distribution of the source sequence provides an
M-type distribution as a probabilistic model. The parameter
M can be choosen small for reduced complexity. Another application of Algorithm 1 can be found in [
3], which considers the problem of generating length-
M sequences according to a desired distribution. Since a length-
M sequence has an
M-type empirical distribution, the Reference [
3] applies Algorithm 1 with cost Equation () to pre-calculate the
M-type approximation of the desired distribution.
Algorithm 1 can also be used to calculate the
M-type approximation of Markov models, i.e., approximating the transition matrix
of an
n-state, irreducible Markov chain with invariant distribution vectors
μ by a transition matrix
containing only
M-type probabilities. Generalizing Equation (1c), the approximation error can be measured by the informational divergence rate [
13]
The optimal M-type approximation is found by applying the instance of Algorithm 1 to each row separately, and Lemma 1 ensures that the transition graph of equals that of , i.e., the approximating Markov chain is irreducible. Future work shall extend this analysis to hidden Markov models and should investigate the performance of these algorithms in practical scenarios, e.g., speech processing with finite-precision arithmetic.
Another possible application is the approximation of Bayesian network parameters. The authors of [
4] approximated the true parameters using a stationary multiplier method from [
14]. Since rounding probabilities to zero led to bad classification performance, they replaced zeros in the approximating distribution afterwards by small values. This in turn led to the problem that probabilities that are in fact zero, were approximated by a non-zero probability. We believe that these problems can be removed by instantiating Algorithm 1 for cost Equation (1c). This automatically prevents approximating non-zero probabilities with zeros and vice-versa, see Lemma 1.
Finally, for approximating Bayesian network parameters, recent work suggests rounding
log-probabilities, i.e., to approximate
by
for a non-negative integer
[
5]. Finding an optimal approximation that corresponds to a true distribution is equivalent to solving
where
denotes any of the considered cost functions Equation (1). If
and
using the binary logarithm, the constraint translates to the requirement that
is approximated by a complete binary tree. Then, the optimal approximation is the Huffman code for
.