Entropy-Based Incomplete Cholesky Decomposition for a Scalable Spectral Clustering Algorithm: Computational Studies and Sensitivity Analysis
Abstract
:1. Introduction
2. Spectral Clustering
- is called the normalized Laplacian;
- S is the similarity matrix, which describes the topology of the graph;
- , with and , denotes the degree matrix;
- is the matrix containing the normalized cluster indicator vectors ;
- , with , is the cluster indicator vector for the l-th cluster. It has a 1 in the entries corresponding to the nodes in the l-th cluster and 0 otherwise. Moreover, the cluster indicator matrix can be defined as ;
- denotes the identity matrix.
2.1. Incomplete Cholesky Decomposition
2.2. A Reduced Eigenvalue Problem
3. Proposed Algorithm
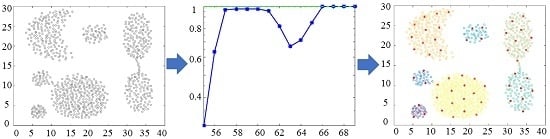
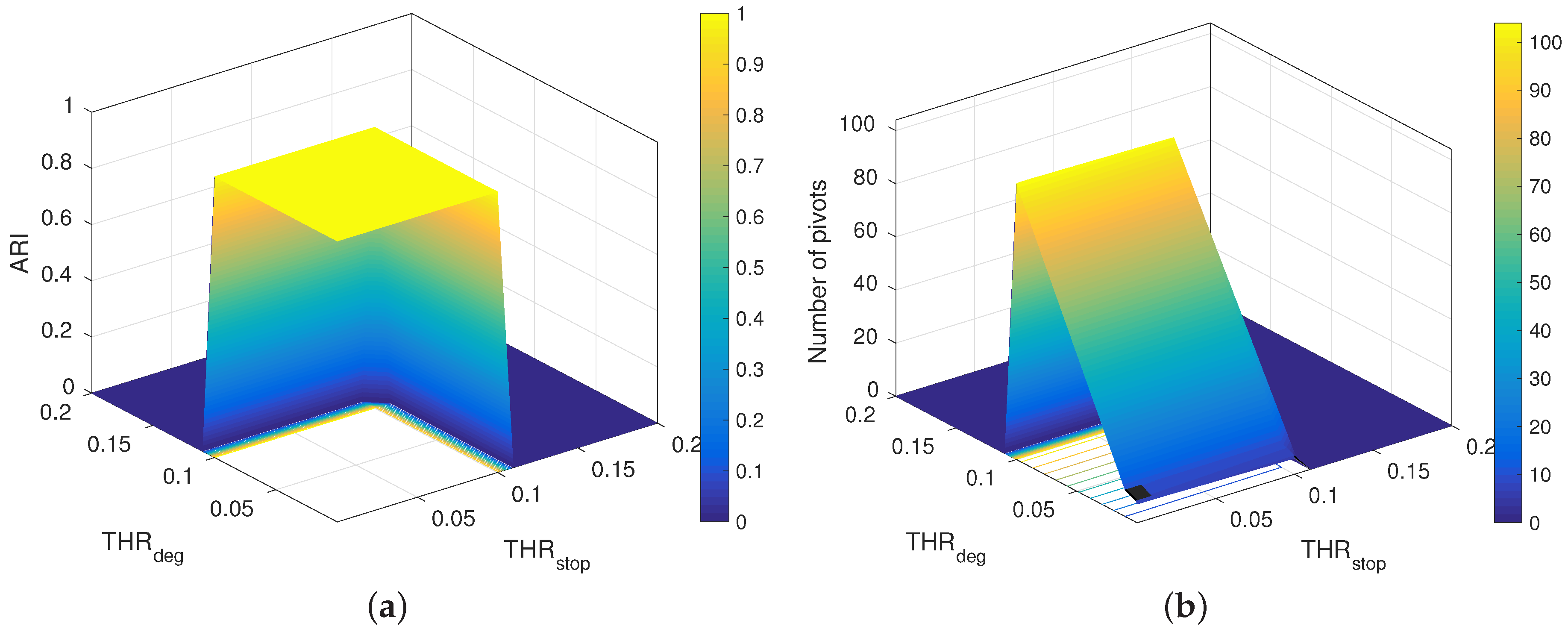
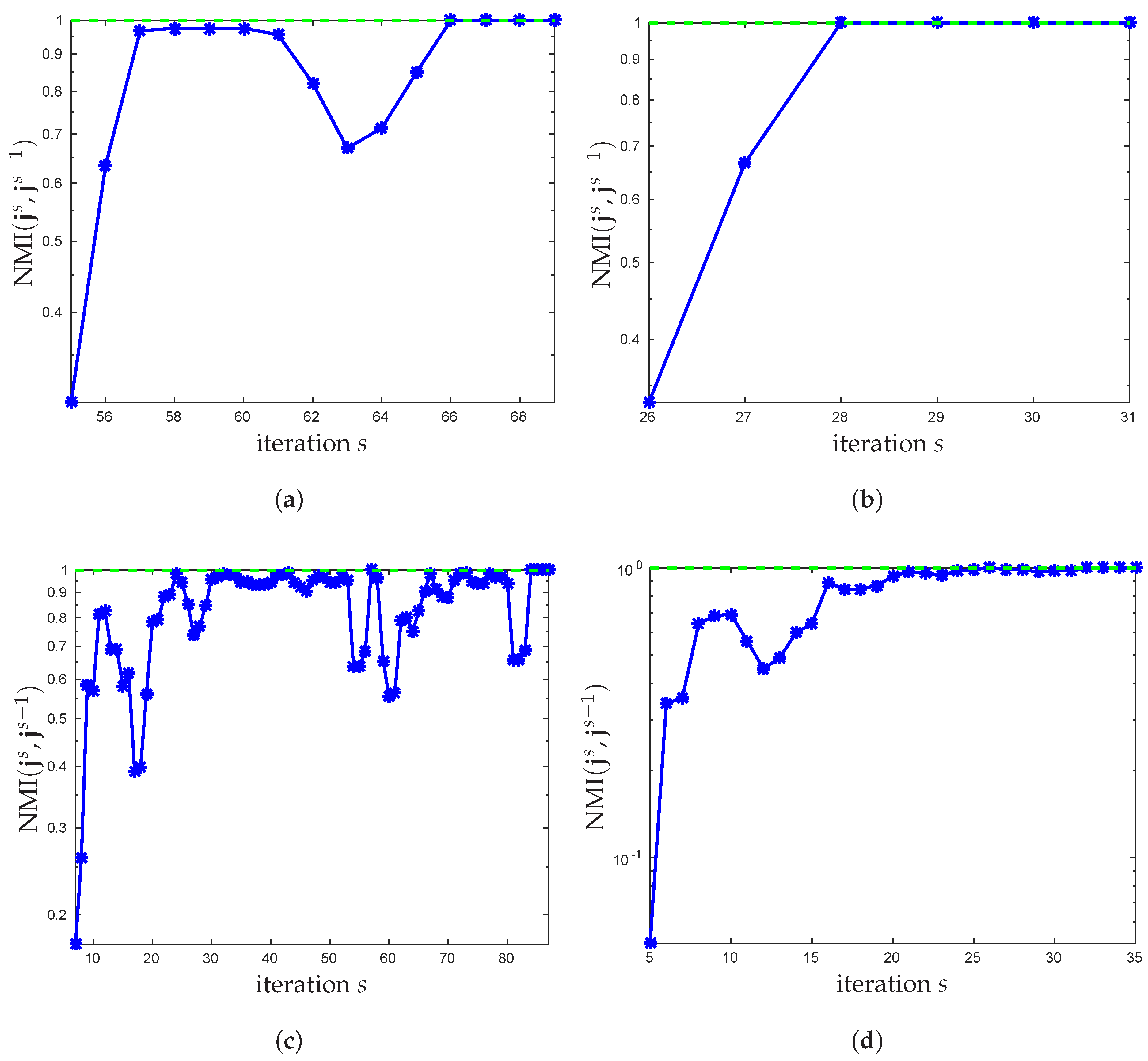
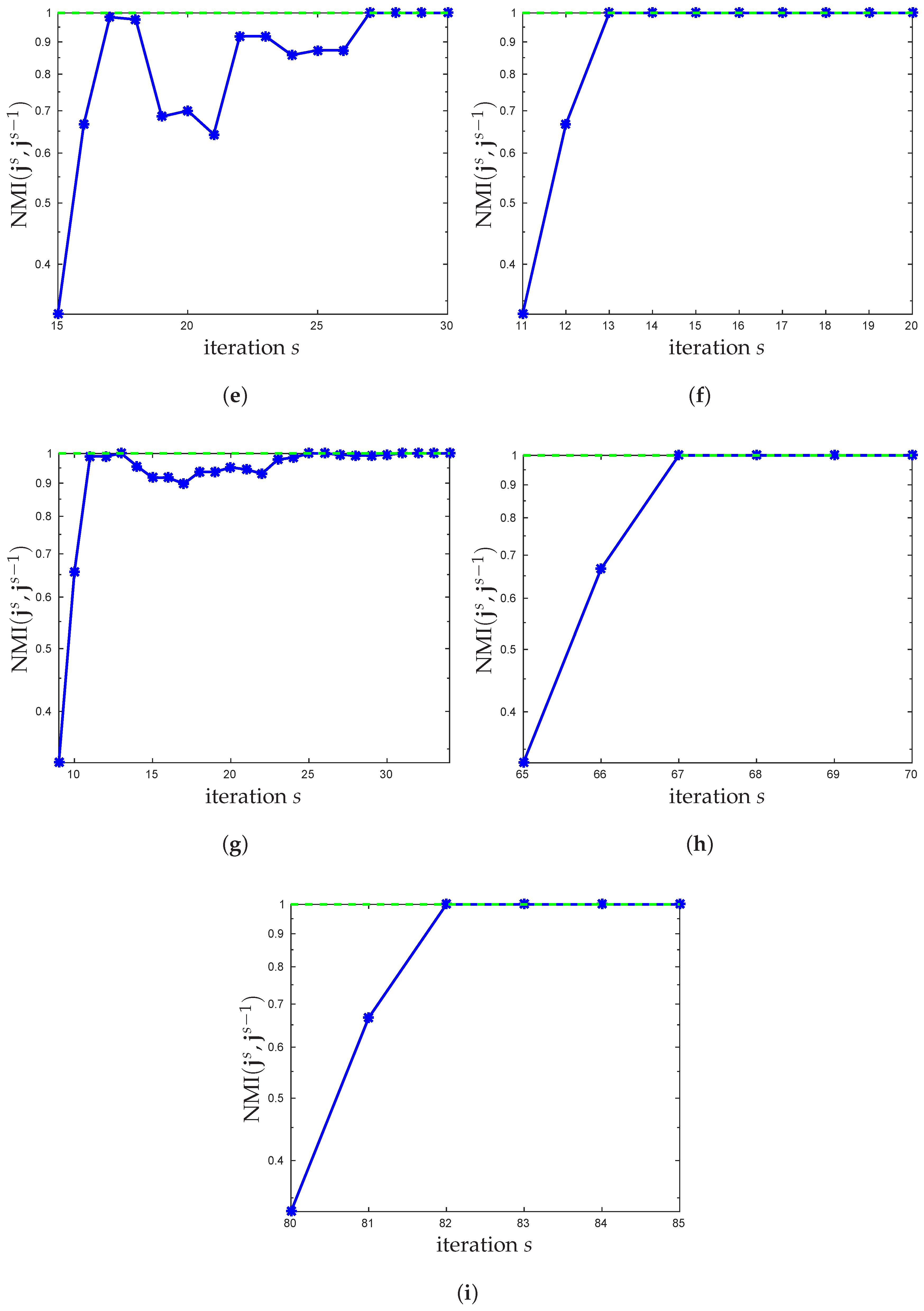
3.1. New Stopping Criterion
3.2. Choosing the Number of Clusters

4. Experimental Results
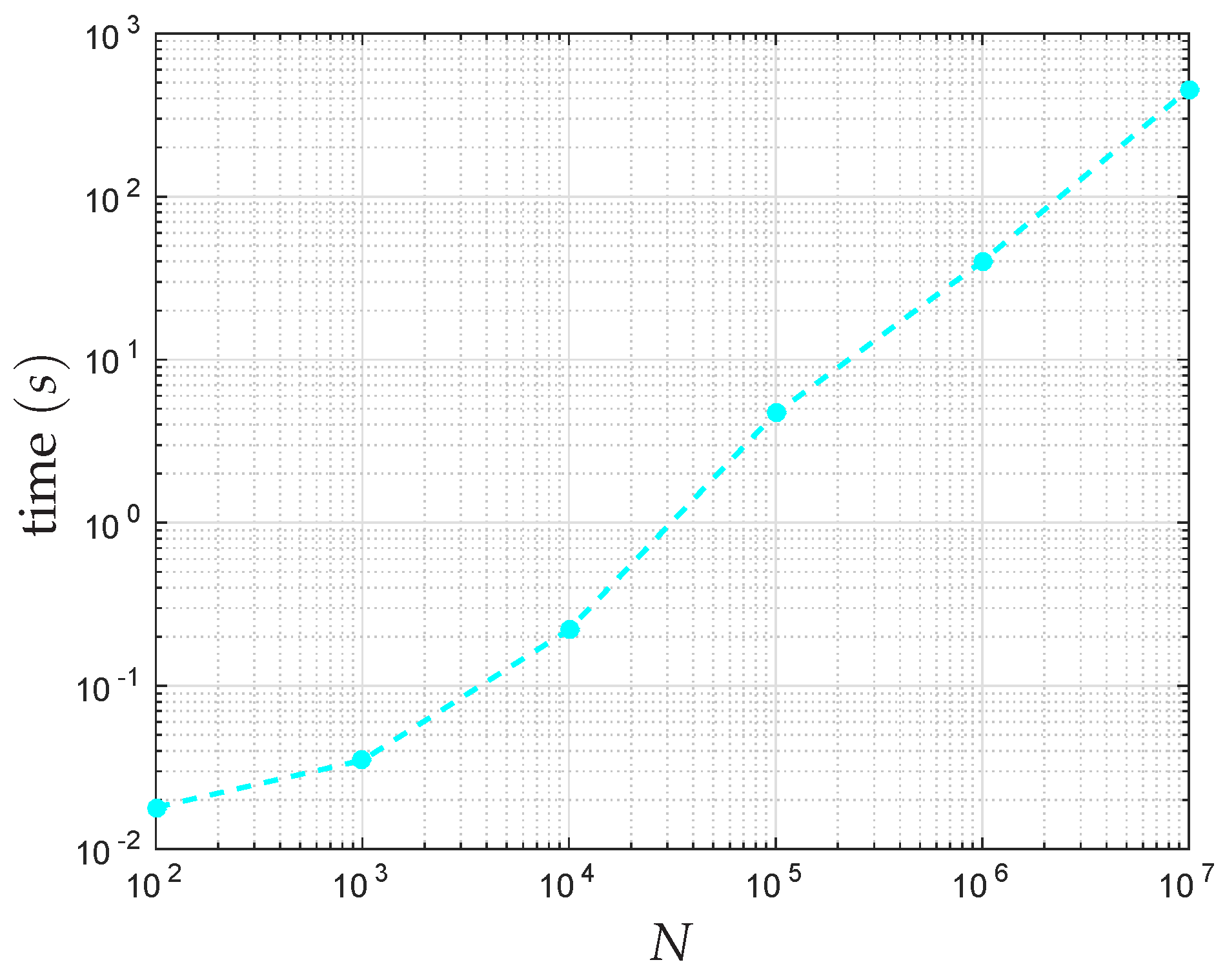
5. Computational Complexity and Memory Requirements
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recogn. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Chung, F.R.K. Spectral Graph Theory; American Mathematical Society: Providence, RI, USA, 1997. [Google Scholar]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Advances in Neural Information Processing Systems 14; Dietterich, T.G., Becker, S., Ghahramani, Z., Eds.; MIT Press: Cambridge, MA, USA, 2001; pp. 849–856. [Google Scholar]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Jia, H.; Ding, S.; Xu, X.; Nie, R. The latest research progress on spectral clustering. Neural Comput. Appl. 2014, 24, 1477–1486. [Google Scholar] [CrossRef]
- Lin, F.; Cohen, W.W. Power Iteration Clustering. In Proceedings of the 27th International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; pp. 655–662.
- Fowlkes, C.; Belongie, S.; Chung, F.; Malik, J. Spectral Grouping Using the Nyström Method. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 214–225. [Google Scholar] [CrossRef] [PubMed]
- Ning, H.; Xu, W.; Chi, Y.; Gong, Y.; Huang, T. Incremental Spectral Clustering With Application to Monitoring of Evolving Blog Communities. In Proceedings of the 2007 SIAM International Conference on Data Mining, Minneapolis, MN, USA, 26–28 April 2007.
- Dhanjal, C.; Gaudel, R.; Clemençon, S. Efficient Eigen-Updating for Spectral Graph Clustering. Neurocomputing 2013, 131, 440–452. [Google Scholar] [CrossRef] [Green Version]
- Langone, R.; Agudelo, O.M.; de Moor, B.; Suykens, J.A.K. Incremental kernel spectral clustering for online learning of non-stationary data. Neurocomputing 2014, 139, 246–260. [Google Scholar] [CrossRef]
- Alzate, C.; Suykens, J.A.K. Multiway spectral clustering with out-of-sample extensions through weighted kernel PCA. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 335–347. [Google Scholar] [CrossRef] [PubMed]
- Mall, R.; Langone, R.; Suykens, J.A.K. Kernel spectral clustering for big data networks. Entropy 2013, 15, 1567–1586. [Google Scholar] [CrossRef]
- Novák, M.; Alzate, C.; Langone, R.; Suykens, J.A.K. Fast Kernel Spectral Clustering Based on Incomplete Cholesky Factorization for Large Scale Data Analysis. Available online: http://www.esat.kuleuven.be/stadius/ADB/novak/kscicdinternal.pdf (accessed on 11 May 2016).
- Chen, W.Y.; Song, Y.; Bai, H.; Lin, C.J.; Chang, E. Parallel Spectral Clustering in Distributed Systems. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 568–586. [Google Scholar] [CrossRef] [PubMed]
- Luo, D.; Ding, C.; Huang, H.; Nie, F. Consensus spectral clustering in near-linear time. In Proceedings of the 2011 IEEE 27th International Conference on Data Engineering (ICDE), Hannover, Germany, 11–16 April 2011; pp. 1079–1090.
- Taşdemir, K. Vector quantization based approximate spectral clustering of large datasets. Pattern Recogn. 2012, 45, 3034–3044. [Google Scholar] [CrossRef]
- Wang, L.; Leckie, C.; Kotagiri, R.; Bezdek, J. Approximate pairwise clustering for large data sets via sampling plus extension. Pattern Recogn. 2011, 44, 222–235. [Google Scholar] [CrossRef]
- Frederix, K.; van Barel, M. Sparse spectral clustering method based on the incomplete Cholesky decomposition. J. Comput. Appl. Math. 2013, 237, 145–161. [Google Scholar] [CrossRef]
- Stoer, M.; Wagner, F. A Simple Min-cut Algorithm. J. ACM 1997, 44, 585–591. [Google Scholar] [CrossRef]
- Golub, G.H.; van Loan, C.F. Matrix Computations; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Bach, F.R.; Jordan, M.I. Kernel Independent Component Analysis. J. Mach. Learn. Res. 2002, 3, 1–48. [Google Scholar] [CrossRef]
- Alzate, C.; Suykens, J.A.K. Sparse Kernel Models for Spectral Clustering Using the Incomplete Cholesky Decomposition. In Proceedings of the 2008 International Joint Conference on Neural Networks, Hong Kong, China, 1–8 June 2008; pp. 3555–3562.
- Zha, H.; Ding, C.; Gu, M.; He, X.; Simon, H. Spectral Relaxation for K-means Clustering. In Advances in Neural Information Processing Systems 14; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar]
- Mall, R.; Mehrkanoon, S.; Suykens, J.A. Identifying intervals for hierarchical clustering using the Gershgorin circle theorem. Pattern Recogn. Lett. 2015, 55, 1–7. [Google Scholar] [CrossRef]
- Scalable Spectral Clustering. Available online: http://www.esat.kuleuven.be/stadius/ADB/langone/scalableSC.php (accessed on 12 May 2016).
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman & Hall: New York, NY, USA, 1986. [Google Scholar]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 1, 193–218. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [CrossRef] [PubMed]
- Blackard, J.A.; Dean, D.J. Comparative accuracies of artificial neural networks and discriminant analysis in predicting forest cover types from cartographic variables. Comput. Electron. Agric. 1999, 24, 131–151. [Google Scholar] [CrossRef]
- Lintott, C.; Schawinski, K.; Bamford, S.; Slosar, A.; Land, K.; Thomas, D.; Edmondson, E.; Masters, K.; Nichol, R.C.; Raddick, M.J.; et al. Galaxy Zoo 1: Data release of morphological classifications for nearly 900,000 galaxies. Mon. Not. R. Astron. Soc. 2011, 410, 166–178. [Google Scholar] [CrossRef] [Green Version]
- Cattral, R.; Oppacher, F. Evolutionary Data Mining: Classifying Poker Hands. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007.
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; Le Cam, L.M., Neyman, J., Eds.; University of California Press: Oakland, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- Zhang, K.; Kwok, J. Clustered Nyström Method for Large Scale Manifold Learning and Dimension Reduction. IEEE Trans. Neural Netw. 2010, 21, 1576–1587. [Google Scholar] [CrossRef] [PubMed]

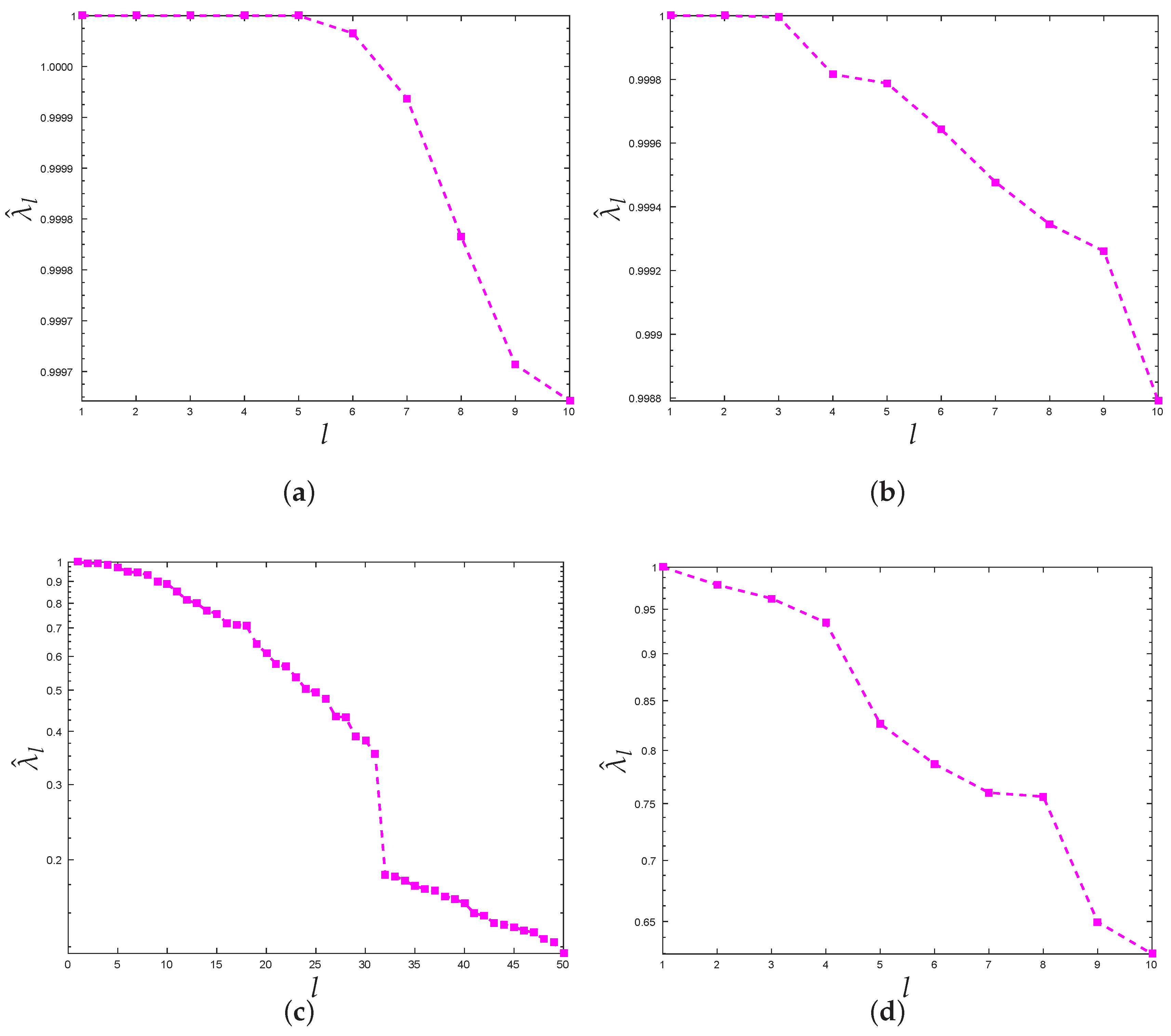
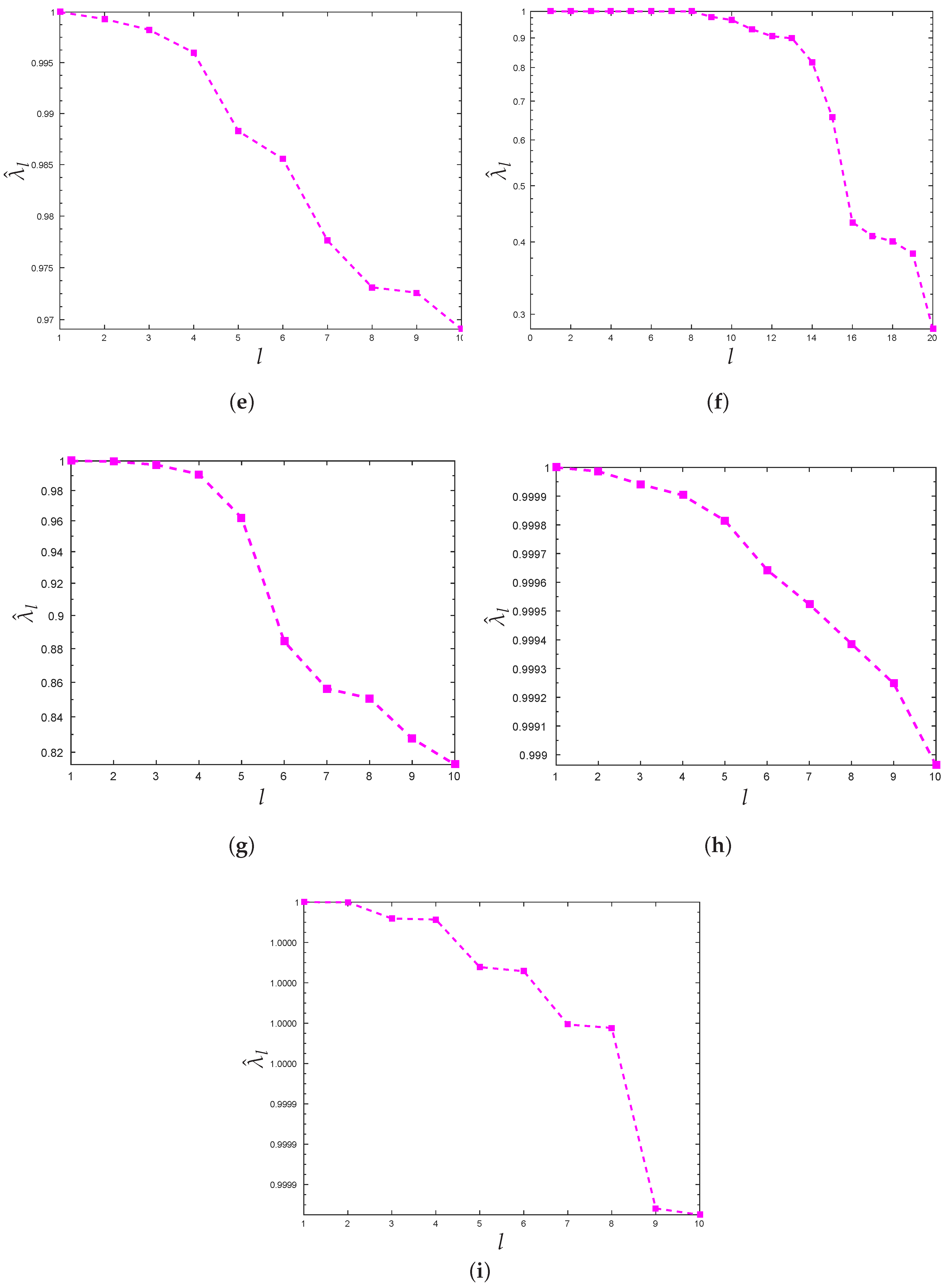
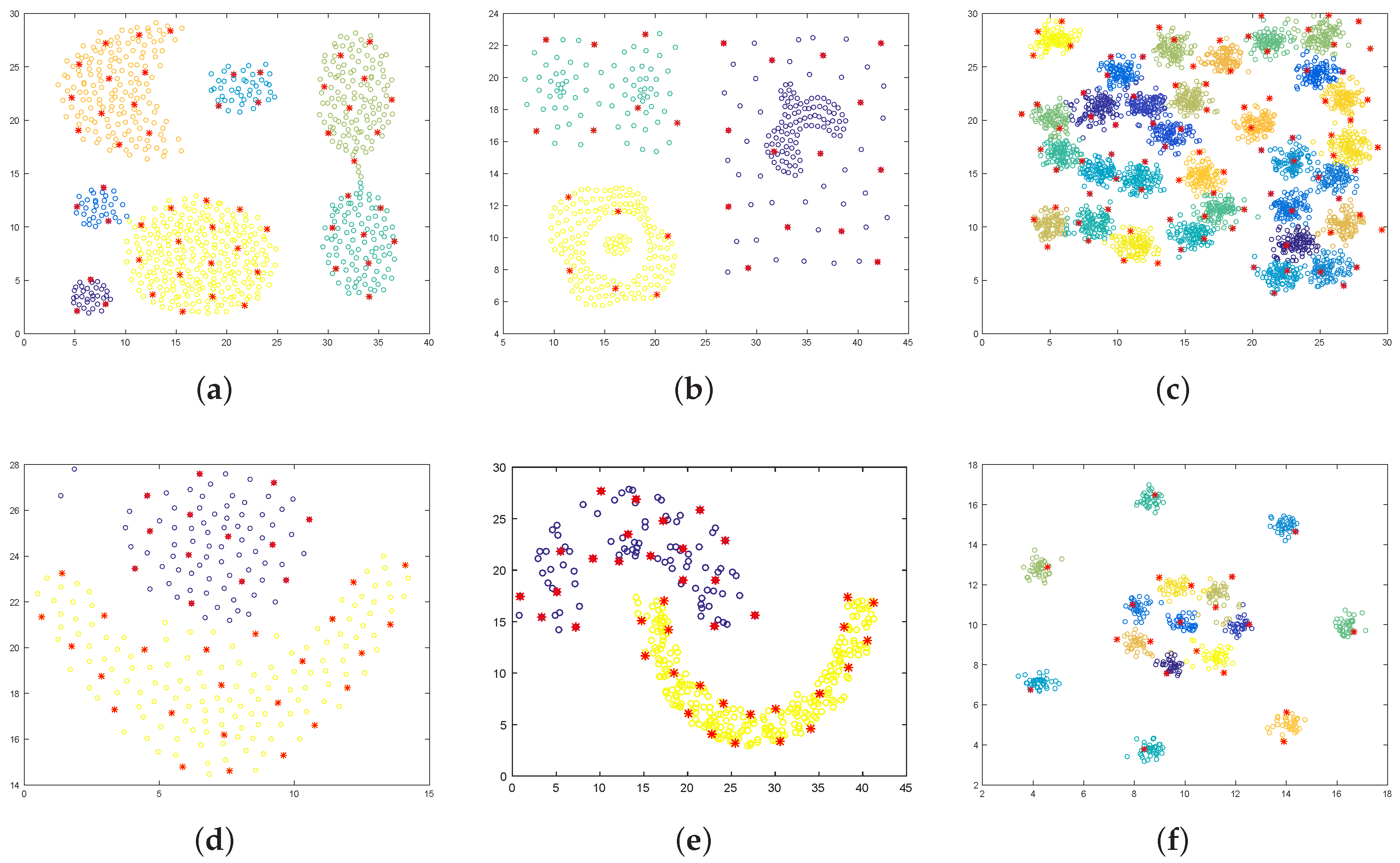
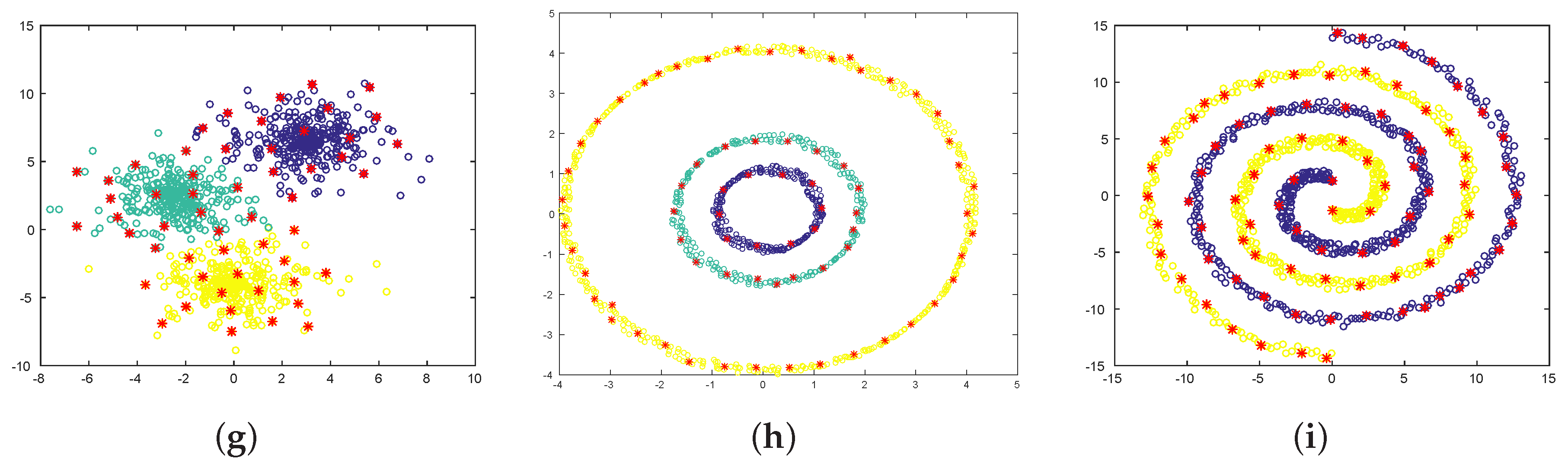

| Dataset | Algorithm | Number of Pivots | ARI |
|---|---|---|---|
| Two spirals | ICD-NMI | 1 | |
| [22] | 129 | 1 | |
| [18] | 94 | 1 | |
| Three rings | ICD-NMI | ||
| [22] | 93 | ||
| [18] | 87 | ||
| Three 2D Gaussians | ICD-NMI | 9 | 1 |
| [22] | 21 | 1 | |
| [18] | 9 | 1 |
| Algorithm | Covertype [31] | GalaxyZoo [32] | PokerHand [33] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| N | d | N | d | N | d | ||||
| 54 | 9 | 10 | |||||||
| Sil | DB | time (s) | Sil | DB | time (s) | Sil | DB | time (s) | |
| ICD-NMI | |||||||||
| k-means [34] | |||||||||
| Clustered Nyström [35] | |||||||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Langone, R.; Van Barel, M.; Suykens, J.A.K. Entropy-Based Incomplete Cholesky Decomposition for a Scalable Spectral Clustering Algorithm: Computational Studies and Sensitivity Analysis. Entropy 2016, 18, 182. https://doi.org/10.3390/e18050182
Langone R, Van Barel M, Suykens JAK. Entropy-Based Incomplete Cholesky Decomposition for a Scalable Spectral Clustering Algorithm: Computational Studies and Sensitivity Analysis. Entropy. 2016; 18(5):182. https://doi.org/10.3390/e18050182
Chicago/Turabian StyleLangone, Rocco, Marc Van Barel, and Johan A. K. Suykens. 2016. "Entropy-Based Incomplete Cholesky Decomposition for a Scalable Spectral Clustering Algorithm: Computational Studies and Sensitivity Analysis" Entropy 18, no. 5: 182. https://doi.org/10.3390/e18050182