Abstract
Tribology involves the study of friction, wear, lubrication, and adhesion, including biomimetic superhydrophobic and icephobic surfaces. The three aspects of icephobicity are the low ice adhesion, repulsion of incoming water droplets prior to freezing, and delayed frost formation. Although superhydrophobic surfaces are not always icephobic, the theoretical mechanisms behind icephobicity are similar to the entropically driven hydrophobic interactions. The growth of ice crystals in saturated vapor is partially governed by entropically driven diffusion of water molecules to definite locations similarly to hydrophobic interactions. The ice crystal formation can be compared to protein folding controlled by hydrophobic forces. Surface topography and surface energy can affect both the icephobicity and hydrophobicity. By controlling these properties, micro/nanostructured icephobic concrete was developed. The concrete showed ice adhesion strength one order of magnitude lower than regular concrete and could repel incoming water droplets at −5 °C. The icephobic performance of the concrete can be optimized by controlling the sand and polyvinyl alcohol fiber content.
1. Introduction
Tribology covers the study of friction, wear, lubrication, and adhesion. A topic of active investigation in the area of adhesion is the superhydrophobicity. Closely correlated to hydrophobicity is the phenomenon of icephobicity. Concepts related to entropy have been actively used in tribology [1,2,3] and may be applied to study hydrophobicity and icephobicity [4].
Undesirable ice formation, accretion and adhesion causes various problems ranging from slippery sidewalks and roadways, cracked concrete structures, to icing of airplane wings and windmill propeller blades. Various approaches are used for ice control and removal including active methods, for example, electro-thermal systems or mechanical actuators, and passive methods, for example, adding antifreeze/freezing point depressants (e.g., a salt) or applying surface coatings. However, active ice removal methods consume energy, and freezing point depressants are not environmentally friendly. This is why surface coatings that prevent ice buildup or reduce ice adhesion have become a focus of active research [5]. In cold conditions, a functional icephobic surface should prevent freezing of condensing and incoming water droplets, and upon freezing should result in a weak adhesion with ice when it forms. Surfaces or surface coatings that satisfy one of the above-mentioned criteria are often called icephobic. The icephobicity is analogous to the hydrophobicity, although an exact accepted definition of the icephobicity is still missing from the literature.
There are three features required to define an ideal icephobic surface. These three features deal with surface’s interaction with the solid, liquid, and vaporous states of water. The first condition is to have a low adhesive strength of the ice to the surface [6,7]. The second is the ability of the surface to repel incoming supercooled water droplets before these freeze at the surface [8,9]. The third is the ability of expelling water condensate before it undergoes nucleation or delaying the nucleation of ice on the surface from the saturated vapor, thereby delaying the frost formation [10,11]. The first property is analogous to the adhesion of water droplet to a surface. The second is similar to the ability of a superhydrophobic surface to repel incoming water droplets [12]. We review and discuss these three approaches in the following section. An ideal icephobic surface should prevent the condensation of water, delay ice nucleation, and induce a weak bond with ice.
In cold conditions, the precipitation of water can result in sleet, snow, hail, or freezing rain. When the ambient temperature is below the freezing point, there are two ways of how ice can form: by the heterogeneous and homogeneous nucleation. The nucleation occurs when the energy gained in forming the new phase is greater than the energy cost due to creation of a new interface. The rate of nucleation is related to the nucleation energy barrier. The heterogeneous ice nucleation is caused by a seed of the new phase which may be a foreign object (e.g., a particle) in liquid water or vapor that acts as a preferential nucleation site. The homogenous ice nucleation occurs spontaneously and randomly for supercooled (metastable) water in the absence of foreign nucleation sites [13]. The heterogeneous ice nucleation in a droplet deposited on a surface starts at the edge of droplets or at surface heterogeneities (chemical or morphological). An important consideration while designing the icephobic surfaces is to delay the heterogeneous ice nucleation so that the supercooled water droplet may be removed by some means (such as the vibration or moving air) before it freezes.
Ice formation is correlated to the hydrophobic/philic properties of a surface. Li et al. [14] showed that at the same temperature, ice nucleation rates on hydrophilic surfaces are about one order higher than those on hydrophobic surfaces. It was also shown that at low relative humidity, superhydrophobic surfaces have higher nucleation barriers for temperatures ≥ −20 °C, thereby considerably slowing down the formation of ice [15]. However, superhydrophobic surfaces rely on the surface roughness. Although surface roughness does not play a significant role in ice nucleation from liquid water [16], the roughness can promote ice formation from vapor since the details of rough profile could serve as seeds for heterogeneous nucleation. Therefore, hydrophobicity does not always translate into icephobicity [17]. In addition, the icephobicity of a hydrophobic surface decreases significantly in humid environments [18].
It has been shown that at low humidity, fluorosilicone containing block copolymer can increase the delay in ice formation, as well as decrease the adhesion strength of ice on the surface [19,20]. Fluoroalkyl silane coating was seen to reduce ice adhesion compared to just hydrophobic nanoparticle coating [21]. Stainless steel rendered superhydrophobic using nanoparticles and a fluoropolymer was seen to retain its superhydrophobicity after several cycles of icing/deicing [22].
Several new ideas in designing of non-adhesive surfaces were inspired by nature [23]. This includes the “lotus effect” [24] and the so-called “Slippery Liquid-Infused Porous Surfaces (SLIPS)” inspired by the pitcher plant (Nepenthes) [25]. The latter showed icephobic properties at 60% relative humidity [11,26]. Bilayer anti-icing coatings inspired by the stimuli-responsive skin of poison dart frogs, have an outer porous superhydrophobic surface over an antifreeze-infused superhydrophilic surface. These coatings repel incoming water droplets and delay frost formation because ice or water comes into contact with the underlying antifreeze liquid [27]. It was also suggested to mimic thermogenic plants, such as lotus or the skunk cabbage (Symplocarpus foetidus). The latter is found in cold climates and it is known for its ability to melt the snow [28].
In this paper, we discuss the fundamental physical interactions related to ice adhesion and nucleation and their similarity to the hydrophobic interactions. We also report experimental results on icephobic properties of a superhydrophobic concrete and suggest how the icephobic properties can be improved and optimized.
2. Hydrophobic Interactions Essential for Ice Repulsion
Hydrophobic forces play an important role for both wetting and ice adhesion to solids. These forces are believed to be of entropic nature and they have several important properties including the embedded ability for the self-organization through the effect called “self-organized criticality”, which leads to the formation of fractal structures, such as snowflakes, and has parallels with effects such as polymer chain folding.
2.1. Entropic and Hydrophobic Forces
The classical example of an entropic force is the elasticity of a polymer chain. Unlike in other materials, the elastic force of a polymer chain is caused by maximizing the configurational entropy (attaining the most probable state). An ideal polymer chain is a simple model with N monomers connected in series with bonds that are linear and free to orient at any angle and also intersect other bonds any number of times. Thus, the chain is assumed to be a random walk consisting a succession of random steps. Consider an ideal chain, where the bond between any two monomer units is represented by the vector (Figure 1). The end-to-end displacement along the chain is given by the vector . For a freely fluctuating polymer chain with large N, the mean (over time) end-to-end vector as the chain is free to fluctuate in any positive or negative direction with equal probability. The root mean square end-to-end distance (mean size) of the chain is given by where r is the size of the bond between monomers. For a non-ideal chain (without self-intersections), the effect of the excluded volume should be considered, which leads to the power exponent of R~N3/5 [29].
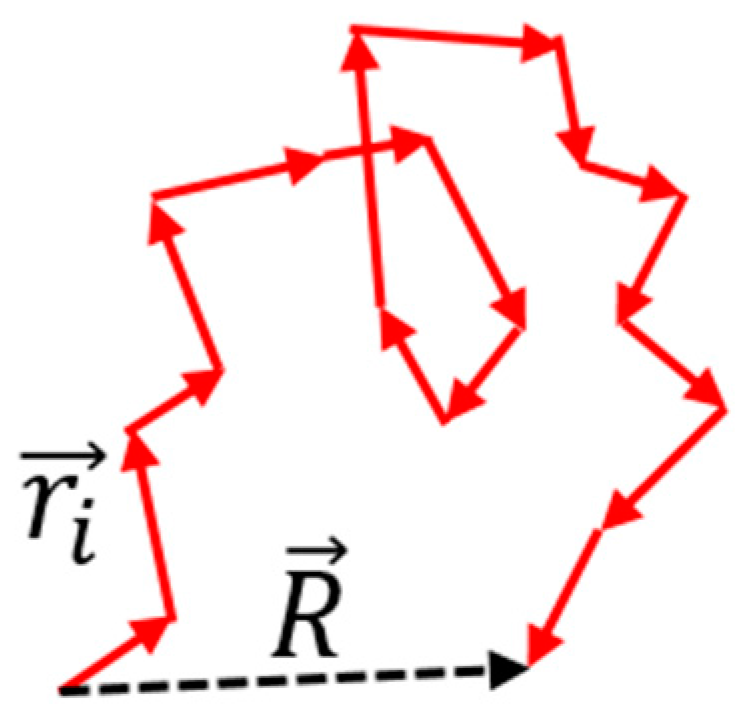
Figure 1.
Random walk along an ideal polymer chain. The chain attains the most probable configuration.
When an ideal polymer chain is isothermally stretched from its natural state (entropy S1) to a taut state (entropy S2), the number of configurations it can take is vastly reduced. The change in entropy is . From the Helmholtz free energy relation where A, U and T are the free energy, internal energy, and temperature, respectively, . This implies work done on the system. The force required to do this mechanical work is purely entropic in nature. The force required to isothermally stretch the polymer chain to larger values of is:
The entropy of the chain can be written using the Boltzmann’s relation as:
where kB is the Boltzmann’s constant and is the probability of finding a polymer chain of end-to-end distance R. In three dimensions given by the Gaussian distribution function
Using Equations (1)–(3), the restoring entropic force is:
Thus, a change in configurational entropy can manifest as an effective force.
Similarly to the polymer chain elasticity, entropic effects are responsible for the so-called hydrophobic force. When a hydrophobic molecule (for example, a hydrocarbon immiscible with water, such as decane) is added to water, the water molecules arrange themselves around it to form a “clathrate cage”. This arrangement allows a maximum number of hydrogen bonds between neighboring water molecules, thus achieving a minimum energy state [30]. However, despite the energetic profitability of such a configuration in terms of the bond energy, the molecules that form the cage are constricted in their motion, thus forming an entropically unfavorable ordered (less random) state. At ambient temperatures, the entropic effect overcomes the energy gain. As a result, when two hydrophobic molecules are introduced, the system is forced to spontaneously reduce the size of the cage by pushing the molecules to aggregate together (Figure 2a).
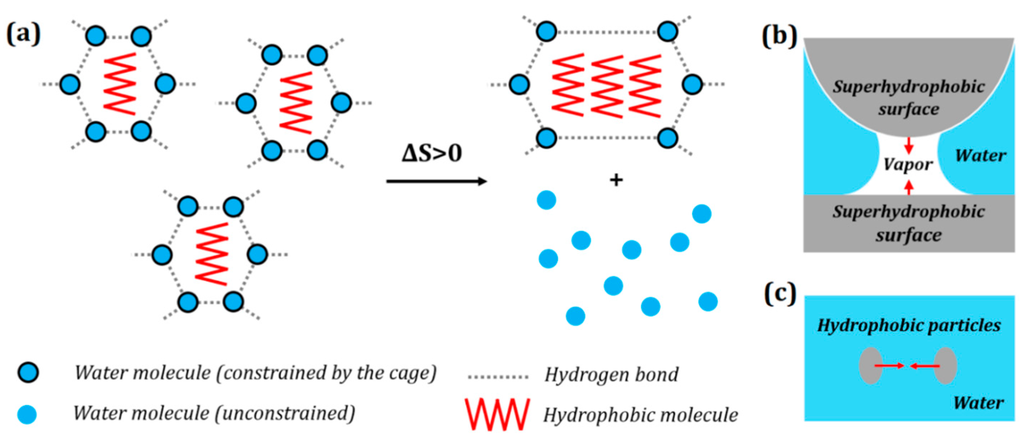
Figure 2.
(a) Entropic origin of hydrophobic interaction. Aggregation of hydrophobic molecules frees up water molecules to increase the configurational entropy of the system (attaining the most probable configuration). Hydrophobic interaction is manifested as a hydrophobic force which results in (b) clustering of hydrophobic particles in water; and (c) attraction of hydrophobic particles towards a hydrophobic surface in water.
The urge for aggregation of hydrophobic molecules or particles in water is called the hydrophobic interaction or hydrophobic force [31]. It should be noted that the hydrophobic force is not a result of attraction between hydrophobic molecules, but the result of increase in configurational entropy of the system, similarly to the elastic force in a polymer chain. Hydrophobic forces increase with increasing temperature [32]. Although there is a general consensus that hydrophobic interactions act over long ranges compared to van der Wall’s forces, there is still a debate on the exact range of these forces. Hydrophobic forces over distance of several microns between superhydrophobic surfaces have been reported due to formation of cavitation bubbles between the surfaces (Figure 2b) [33]. These forces, however, are similar to the capillary force and they may have complex molecular origin. Israelachvili et al. reports the range of hydrophobic forces as 10–20 nm with exponential decay [34]. The hydrophobic force also leads to the preferential attraction of hydrophobic particles towards each other (Figure 2c), as well as a hydrophobic surface in water [31].
2.2. Self-Organized Criticality and Hysteresis of the Contact Angle
An important effect associated with the hydrophobic forced is self-organized criticality (SOC). Bak et al. [35] demonstrated that many dynamical systems can evolve naturally into stable critical points which separate two states of the system. In other words, the system is spontaneously attracted to this critical point irrespective of its starting point. A commonly cited example is SOC in a sand pile. As the sand is poured, it falls in a heap. At some point adding a grain of sand, which is a minor event, can trigger an avalanche, a major event, leading to the pile being flattened, and thus the sand pile maintains a certain critical angle dependent on the coefficient of friction between the sand grains. The value of the critical angle is the critical point, separating between the state with the sand flow and a stable pile. Further addition of sand leads to formation of a pile until the next avalanche is triggered. The intensity and the frequency of avalanches follows a power law distribution. SOC has characteristic properties by which it can be detected: The power law distribution of the magnitudes of the avalanche events, the formation of fractal structures, and the “one-over-frequency noise” [35].
Another example of SOC is wetting of a rough or chemically heterogeneous surface and certain types of nanoscale friction [36,37]. If a surface with a sessile droplet on it is tilted, the solid-liquid-vapor triple line advances in intermittent steps (Figure 3a). Each of these steps are the result of the energy barriers associated with surface defects (Figure 3b). As the surface tilts, gravitational potential energy is added to the droplet which at some point causes triple line to overcome the energy barrier due to surface defects and results in an advance of the triple line (analogous to an avalanche of the sand pile). The advancing triple line then halts at another surface defect until the critical point is reached again [38]. This leads to contact angle hysteresis, the difference between the larger contact angle at the front and the smaller contact angle at the rear of a moving droplet. There are various thermodynamic theories predicting the values of contact angle hysteresis [39,40,41,42,43,44].
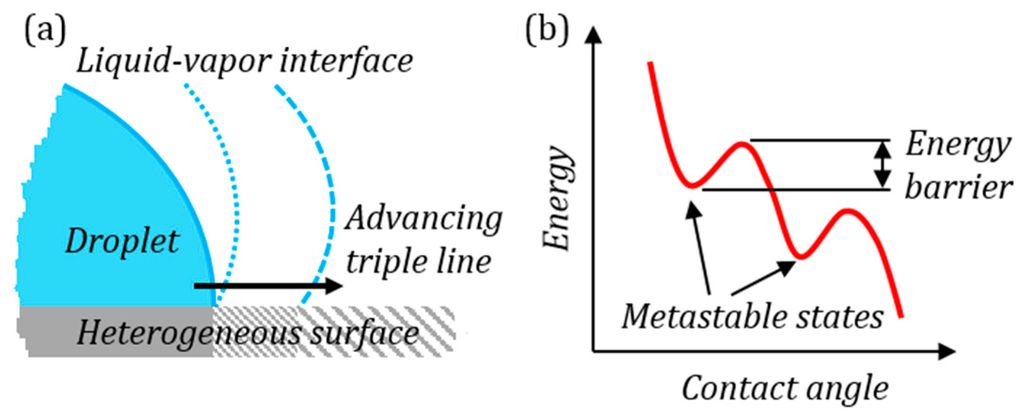
Figure 3.
(a) Intermittent pinning and advancing of the triple line; (b) energy barriers associated with contact angle hysteresis.
An important function of hydrophobic forces is in protein folding. Proteins are long chains molecules made of amino acids (AA), and the sequence of the amino acids (the primary structure of the protein) is encoded by genes in the DNA. A protein molecule folds, somewhat similarly to a polymer chain. However, unlike a polymer chain, which folds randomly, a protein molecule forms a stable 3D “native configuration” (a so-called “tertiary structure”).
The amino acids can be hydrophobic or hydrophilic. The interaction of these hydrophobic or hydrophilic side chains with each other and the surrounding aqueous medium governs the folded shape of the protein. The folded shape in turn governs function of the protein. The protein chain clusters such that the hydrophobic side chains are attracted to each other and away from water (Figure 4a). This behavior is similar to the hydrophobic interaction observed between hydrophobic molecules in water. Thus, entropic forces lead to folding of the protein.
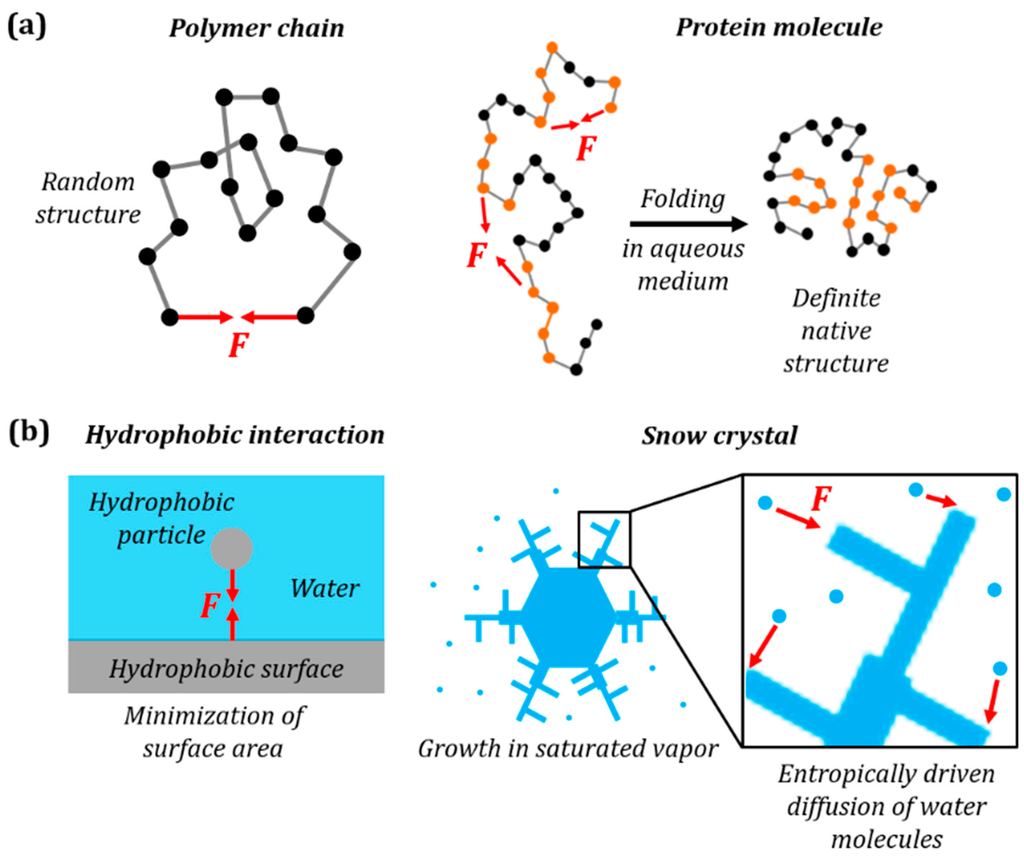
Figure 4.
(a) Folding of protein molecule from a linear primary structure to 3D tertiary (native) structure is similar to the elastic force in a polymer chain. For a polymer chain the force can be attractive or repulsive depending on the end-to-end distance. For a protein molecule the attractive hydrophobic force causes the hydrophobic side chains to retract to the interior of the cluster; (b) parallelism with snow crystal growth as opposed to the hydrophobic interaction of a particle and a surface. The red vectors denote the entropic force F in each case.
According to the authors of [45,46], protein folding governed by the hydrophobic forces is controlled by SOC, which is a universal feature of hydrophobic interactions present during both wetting of hydrophobic surfaces and protein folding. Furthermore, folding of proteins is thought to be the main driving force of the evolution on the gene level [47], which also demonstrates power law and fractal quantitative behavior [48]. The formation of ice (snow) crystals also demonstrates fractal characteristics typical for SOC.
2.3. Ice Crystal Formation
Ice (snow) crystal formation is another process governed by interactions, which are similar to the hydrophobic forces. It is similar to the hydrophobic interaction between a particle and a surface in water. However, ice crystals can form very complex structures, as opposed to a simple spherical shape formed by a hydrophobic substance in water. This is partially similar to how a protein forms a complex 3D structure as opposed to the random folding of a simple polymer chain (Figure 4). For a simple polymer chain, the most probable configuration does not depend on the shape of the polymer chain (but only on the distance between its ends). However, much more complex protein folding depends on the interaction between amino acids, and thus on the 3D shape of the molecule. Similarly, in the case of the hydrophobic attraction of two particles the shape formed by the hydrophobic phase does not matter, since only its surface area is minimized. However, a more complex interaction of a vapor molecule with solid / ice favors certain directions or shapes (Figure 4b).
Another parallel between the random polymer versus protein folding and the hydrophobic attraction versus ice crystal formation is in the fractal geometry of both the snow crystals and the protein globules. In a non-ideal polymer chain (using the excluded volume approach), the end-to-end displacement and the radius of gyration are scaled as R~N3/5 [29]. More accurate estimates using the renormalization group predict the power exponent of 0.588. For the folded polymer chain forming a sphere, the radius of gyration is proportional to the power 1/3 of the volume, R~N1/3. However, folded proteins tend to show the power exponent of 0.4 rather than 0.333 [49] thus demonstrating scaling of a fractal object. Similarly, hydrophobic liquid droplets in water would form spheres (with a two dimensional surface), whereas snow crystals, according to the literature, may have a fractal shape with the fractal dimension of about 1.85 [50].
A snow crystal is a single crystal of water molecules arranged in a hexagonal crystal lattice, while many snow crystals clustered together make a snow flake. A snow crystal is formed when water molecules from the vapor attaches to a dust nucleus in a supersaturated atmosphere. The crystal grows as more water molecules from vapor phase hydrogen bond to the water molecules already on the nucleus. The crystal may start out as a spherical particle. Smooth surfaces of a crystal have fewer free sites for incoming water molecules to form hydrogen bonds, while irregular rough surfaces have many. Thus, rough surfaces grow relatively fast compared to smooth surfaces. This process leads to evolution of snow crystals into hexagonal prisms with two basal and six prismatic planes or facets. When prismatic facets grow faster than basal facets, plate-like snow crystals are produced. When prismatic facets grow slower than basal facets, columnar snow crystals are produced (Figure 5a). Snow crystals formed in very cold and dry conditions are small and have simple geometries due to their slow growth [51].
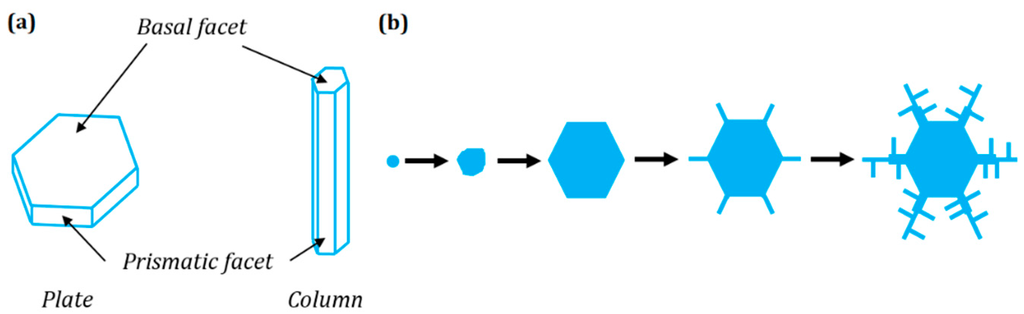
Figure 5.
(a) Simple snow crystals are either plate-like or columnar; (b) evolution of intricate shapes in a snow crystal by diffusion-limited aggregation and Mullins-Sekerka growth instability.
It is easier for water molecules from air to diffuse to the corners rather than face centers in a hexagonal prism. Thus corners grow faster (instability) leaving behind irregular steps on the face centers. This irregularity causes face centers to grow fast and catch up with the corners, thereby minimizing the interfacial energy. This balance between the diffusion and minimization of the interfacial energy helps maintain the hexagonal structure as the crystal grows. Therefore the hexagonal structure acts as a stable critical point in the SOC of a growing snow crystal.
At some limiting value of roughness of the face centers, the corners grow much faster due to the Mullins-Sekerka growth instability. The perturbations at the corners due to diffusion of water molecules (as well as latent heat) can no longer be stabilized by minimizing the interfacial energy of the crystal. This results in hexagonal prisms sprouting digits (instabilities) at the corners. These digits continue to grow until they come under the influence of the growth instability when they start sprouting branches [52]. As a result, fractal geometries are produced in snow crystals. Note that fractal shapes are a characteristic of SOC. Figure 5b shows the evolution of an intricate geometry as a result of diffusion and Mullins-Sekerka growth instability.
Ukichiro Nakaya extensively studied the shapes of snow crystals and summarized the relationship between the shapes and atmospheric conditions (temperature, and supersaturation of atmosphere) in the form of the so-called “Nakaya diagram” (Figure 6) [53]. He found that the shape of snow crystals change as they pass through regions of different temperature and supersaturation. This is known as “habit change”, which can be explained by Kuroda-Lacmann model [54]. The complexity of the crystal structure increases with the supersaturation in atmosphere. Colder and dryer atmosphere promote the growth of simple geometric structures. Natural snow crystals are not always symmetrical. But the intricate shape of a snow crystal suggests an apparent synchronization between the branches of the crystal as it falls through different regions of temperature and supersaturation in the atmosphere. This can, perhaps, be explained by an “icephobic interaction” of entropic origin as shown in Figure 4b, similar to the hydrophobic interaction.
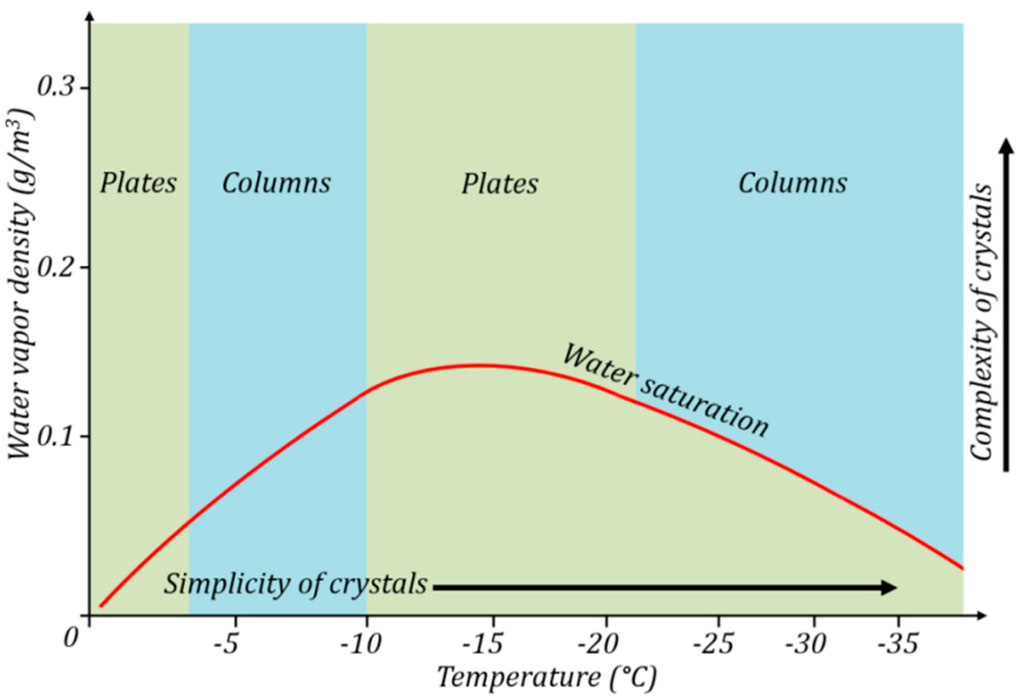
Figure 6.
The Nakaya diagram. The geometry of a snow crystal is dependent on the supersaturation and temperature of the atmosphere in which it grows.
The shape and direction of snow/ice crystal growth is governed by the roughening transition which happens above a critical roughening temperature. The equilibrium surface configuration depends on the minimization of free energy of the surface. The change of Gibb’s free energy is given by where is the change in enthalpy. At temperatures above the roughening temperature, the entropic contribution to the free energy dominates, thereby resulting in a rough equilibrium surface configuration. Thus, the growth of snow/ice crystals is governed entropically, similar to the aggregation of hydrophobic molecules in water.
We discussed the fundamental physical interaction related to ice nucleation and adhesion. These interactions are believed to be of entropic nature, and are similar to hydrophobic interactions. There are several similarities between the hydrophobicity and the icephobicity phenomenon as summarized in Table 1. In the following section we discuss the three aspects of the icephobicity.

Table 1.
Similarities between the hydrophobicity and the icephobicity.
3. Three Approaches to Icephobic Surfaces
In the preceding section we have discussed the superhydrophobicity (very low adhesion of water to a solid) and “icephobic interactions” governing vapor water molecule interaction with a solid surface, such as an ice surface. In this section, we concentrate on the three approaches to the icephobicity: low ice adhesion to solid, bouncing off water droplets, and suppressing frost formation from vapor that can be utilized for anti-icing surfaces.
3.1. Ice Adhesion to Solids
High contact angle does not always yield low ice adhesion. The adhesion of ice to solid surfaces is a result of the synergetic effect of van der Wall’s forces, chemical bonding, and direct electrostatic interactions. Hydrogen bonding between the surface groups and the water molecules can enhance ice adhesion [5,55]. The electrostatic interactions are the significant factor for metals because charges on the ice surface induce mirror charges, thus causing adhesion. Whereas these mirror charges can be reduced by dielectrics [56], the ice adhesion decreases significantly only at low values of the dielectric constant. Thus, superhydrophobic surfaces coated with polytetrafluoroethylene with the dielectric constant of about 2 demonstrated negligible ice adhesion [57]. According to Kulinich and Farzaneh, the ice adhesion to a superhydrophobic surface is correlated with contact angle hysteresis, rather than contact angle itself, which can be explained by the reduction of the ice-solid contact area [7]. High valued of the contact angle coupled with low contact angle hysteresis imply the Cassie wetting state with air pockets on the surface [58]. The cavities or voids with air pockets can act as stress concentrators at the ice-solid interface. In this case, the size of the microvoids and cracks at the ice-solid interface becomes a critical parameter controlling the ice adhesion on a surface. According to the analysis of Hejazi and Nosonovsky, who applied the linear fracture mechanics model, if the cracks are not sufficiently large, the superhydrophobic surface may exhibit strong ice adhesion [17].
Another effect which should be taken into account is the latent heat released during freezing of a droplet. This heat tends to increase the vapor pressure near the solid-ice-vapor contact line resulting in the desublimation of supersaturated water vapor referred to as a “frost halo” surrounding the three phase contact line, thus increasing the ice-solid interfacial area and eventually the adhesion force between ice and the solid surface [59].
The quantitative parameter characterizing ice adhesion to a solid surface is the adhesion strength. There are several method for measuring the adhesion strength. One method is the centrifuge adhesion test [60]. Samples with ice are rotated and the adhesion strength is calculated from the speed at which ice detaches from the sample surface [61,62]. Another method is by shear ice adhesion test. A shear stress can be applied to the interface so that the maximum shear strength at which the ice detaches is measured experimentally. Li et al. [19,20] used this method to study the icephobicity of block copolymer coatings. A variation of this method was used by Fu et al. [21], where a piston was used to shear off the ice from the sample surface. Aizenberg and colleagues reported ice adhesion measurement on SLIPS coated aluminum and found that it was two orders of magnitude lower than for aluminum without the coating [11]. Interestingly, a study by Varanasi and colleagues [63] demonstrated that the low ice adhesion force on lubricant-infused surfaces was a result of a thick layer of a lubricant on top of a textured surface. For a surface with a stable lubricant film, the ice adhesion strength decreases with increasing surface texture density increases. Ice adhesion strength of some surfaces and coatings from the literature are listed in Table 2.

Table 2.
Ice adhesion strength of some materials from literature.
3.2. Decreasing Contact Time for Droplets Approaching the Solid Surface
Icephobic surfaces should be able to prevent or delay freezing of incoming water droplets. This can be by bouncing off or breaking up. Minimizing the duration of contact when a droplet interacts with a surface can reduce the heat transfer time and the probability of heterogeneous ice nucleation. Hydrophobic and superhydrophobic self-cleaning surfaces can easily repel incoming water droplets at room temperature. However, the increase in viscosity of supercooled water below 0 °C prevails over the increase in surface forces and increases the contact time with the surface [64]. High contact angles together with low contact angle hysteresis help minimizing the time of contact and, thus, maximizing droplet shedding.
Water pressure during the impact can cause the Cassie-Wenzel wetting regime transition, which is usually undesirable because it increases the solid ice contact area and contact time due to pinning of the incoming droplet. This, in turn, increases the rate of heat transfer at the interface [65]. Asymmetric and oblique impacts can reduce chances of this wetting transition, as well as droplet pinning [9,66]. Functionalized carbon nanotube superhydrophobic surfaces repel obliquely impacting water droplets at −8 °C [67]. Mishchenko et al. showed that nanostructured silicon superhydrophobic surface could repel low velocity supercooled water droplets at −25 °C and thus remain ice free. Despite droplets freezing at temperatures under −25 °C, their removal was easy because the droplets remained in the Cassie-Baxter wetting state before they froze [8]. In our previous study we showed that hydrophobic fiber-reinforced concrete can repel impacting water droplets (Weber number ~55) in an oblique manner at 20 °C and −5 °C [9].
3.3. Suppression of Frost Formation
Water vapor condenses below the dew point temperature. Humid and supercooled conditions can cause water to condense and freeze on a surface. Therefore, the ability to expel condensing water droplets and delay the process of frost formation and ice nucleation on a surface is important for icephobic surfaces. Water droplets that condense in capillaries of a superhydrophobic surface may undergo the Cassie-Wenzel wetting transition, and adhere strongly to the surface [68]. The energy released during droplet coalescence can eject condensing water droplets spontaneously [69]. Condensation frosting occurs on a surface as a result of formation of inter droplet frost bridges. This makes eventual frost formation on superhydrophobic surfaces inevitable. However, jumping-drop superhydrophobic surfaces can slow down frost formation by ejecting condensate droplets at −20 °C before they undergo nucleation, and by lowering the chance of frost bridge formation between droplets [70]. Chen et al. reported a hierarchical superhydrophobic surface that can delay ice nucleation and suppress in the inter droplet frost bridge formation [71].
Ice nucleation being a molecular scale phenomenon, is difficult to notice. However, the freezing front in a droplet can be observed by a change in opacity of the droplet. Water droplets are placed on supercooled test surfaces, and the time taken for a freezing front to appear is noted to quantify the icephobicity [19,61]. Eberle et al. [10] showed that the delay in ice nucleation can constitute up to 25 h for a droplet at −21 °C if nanoscale roughness of the surface is carefully controlled. The SLIPS coated surfaces were seen to exhibit delayed ice nucleation for longer time than textured or regular hydrophobic surfaces. This may be because the smooth and chemically heterogeneous surface of the impregnating liquid in SLIPS offers fewer sites for heterogeneous nucleation of ice [26]. Water droplets condensing and coalescing on tilted SLIPS at −10 °C rolled off before freezing [11].
The nucleation and formation of frost on a surface is similar to the formation of snow crystals. The entropic force and the growth instability are instrumental in the formation of dendritic structures in snow crystals. Water vapor molecules diffuse from the saturated atmosphere to a supercooled surface due to the entropic (icephobic) forces that minimize the surface energy of the clustered water molecules. This leads to a buildup of ice on surfaces with roughness greater than the critical value for ice nucleation.
Having discussed the theoretical foundations of the icephobicity we found that the solid-ice interaction is governed by mechanisms similar to the solid-water interactions, in particular, by entropic and hydrophobic forces. We also found that the superhydrophobicity can be utilized to make icephobic surfaces. In the following section, we demonstrate the icephobic characteristics of rough heterogeneous surfaces. For this purpose, we use concrete substrates. Regular concrete, being porous and hydrophilic, imbibes water. The imbibed water expands on freezing and initiates the cracks within cementitious matrix. This limits the material’s durability required for many civil engineering applications, especially in northern climates, where concrete is exposed to numerous freezing–thawing cycles. Therefore, there is the need to make concrete hydrophobic and also icephobic. We induce the icephobic properties of superhydrophobic concrete using two approaches—by minimization of ice adhesion strength, and by minimizing the contact time for incoming droplets.
4. Materials and Methods
In this section, we make an effort to estimate the icephobic characteristics of rough heterogenic surfaces based on concrete mortars. We study the icephobicity of concrete using two approaches described previously by measuring the ice adhesion strength, and studying the interaction of incoming water droplets with the surface.
4.1. Materials
In this study, portland cement Type I (PC) supplied by Lafarge (Alpena, MI, USA) was used to prepare the mortar specimens. All the required characteristics of the cement, according to the ASTM150, are presented in Table 3. Standard quartz sand with an average particle size of 425 µm, according to the ASTM C778 and a regular tap water were used to produce the mortar samples. The Kuralon K-II RECS15x12 polyvinyl alcohol (PVA) fibers (supplied by Kuraray Co., Osaka, Japan) were used to modify mortar mixes and induce a certain “self-reproducing” surface structure, important for icephobic properties. The PVA fibers also have a low dielectric constant which may weaken ice adhesion to the surface. The fibers had diameter of 45 μm with the length of 12 mm. It order to improve the workability of fiber reinforced mortars, polycarboxylate ether (PCE) high-range water-reducing admixture, supplied by Handy Chemicals (Montreal, QC, Canada), was used.

Table 3.
Chemical and physical properties of portland cement.
“Shell type” water-based siloxane emulsion was used in this study for hydrophobic modification of the mortars surfaces. Polymethylhydroxysilane (PMHS) was used for emulsion preparation as a hydrophobic agent and polyvinyl alcohol (PVA) with molecular weight of 16,000 (supplied by Acros Organics, Geel, Belgium) was used as a surfactant. Silica fume particles were incorporated in order to stabilize the emulsion and also to serve as micro-roughness forming elements when attached to the rough mortar surface coated by the emulsion. For the experiment two emulsions with different concentrations of hydrophobic agent and silica fume were prepared at proportions of 25%:5% and 5%:1%, by weight, respectively. The concentration of the PVA surfactant in water was kept constant at 5% for both types of emulsions. The procedure of emulsion preparation was described in detail in our previous study [72,73,74].
4.2. Contact Angle and Roll-Off Angle
The hydrophobic characteristics were estimated for samples by measuring the contact angle (CA) and roll-off angles (ROA) of water droplets on the mortar tiles and cubes using Krüss Drop Shape Analysis System DSA100.
4.3. Ice Adhesion Strength
Ice adhesion strength on mortar samples was measured using the shear test [58]. Contact angle (CA) values, roll-off angle of water droplets, as well as concrete mortar formulation, were the main parameters for the icephobicity assessment. Three sets of samples of 10 different formulations were used in the experiment. The first set was used without any treatment as a reference, and two others were differently modified with hydrophobic “shell type” emulsions, as discussed in our previous study [73].
In order to estimate the icephobicity, which was defined by the adhesion strength between the ice and concrete samples, PASCO CI-6746 stress-strain apparatus was employed to test the adhesion strength by measuring the shear force, applied to a cylindrical mold filled with ice and attached to the surface of a tile.
All mortar tiles and cylindrical molds were placed into freezing room and stored at −18 °C for 24 h. After that, molds were placed on the top on the tiles and filled with cool water (0 °C). The samples with attached cylinders were cooled for an additional 5 h at −18 °C to achieve the complete crystallization of ice. Three sets of the specimens with different hydrophobic surfaces were tested for icephobic characteristics. Two specimens of each composition were prepared and tested and the average value of the shear strength was calculated and reported. The shear test, including settling of a sample and applying force, was conducted at a temperature of 0 ± 2 °C for 2 min in order to avoid melting of ice.
4.4. Interaction of Incoming Droplets
In this section, the second aspect of the icephobicity of a surface, i.e., minimizing the contact time for incoming droplets, was studied using concrete mortars. The interaction of incoming droplets with the concrete surfaces were studied at −5 °C and 20 °C. Qualitative observations were made if the droplets got pinned, bounced off or froze on the surface. It was observed that droplets bouncing off generally had very low contact time with the surfaces.
The interaction between the incoming droplets and concrete surfaces were studied at −5 °C and 20 °C, which was shown in supplementary Video S1. Distilled water droplets (14 μL) were dropped using a micro syringe from a height of 50 mm onto the samples set at 45° inclination. The samples were then precooled for two hours at −20 °C. Distilled water droplets (14 μL) stored at 0 °C were dropped from 50 mm height onto the samples inclined at 45°, at an ambient temperature of −5 °C and relative humidity of 34%. The experiments were performed carefully and quickly at −5 °C, so that the water at 0 °C could not freeze in the dispensing syringe. The interactions were video recorded at 420 fps, using a Canon EX-FH25 camera, in both cases. Stacked images were prepared using the frames captured from the videos to show the trajectories of droplets after impact at −5 °C and 20 °C.
4.5. Sample Preparation
For studying the ice adhesion strength, 3 sets of 10 different compositions of fiber reinforced concrete (compositions M1–M5)/mortar (compositions M6–M10) samples were prepared in laboratory conditions with component proportions presented in Table 4.

Table 4.
The composition of concrete/mortar specimen.
Small tile specimens of 10 mm × 10 mm × 5 mm were cast, compacted using a shaking table and placed in a curing room for 24 h. These were then demolded and placed in a moist room (RH = 90% ± 5%) for total of 28 days of curing. Later, the tiles were dried in an oven for 2 days at 70 °C. The dried samples were sealed in ziplock bags filled with paper to adsorb extra water (if any), and stored at laboratory conditions (22 ± 3 °C and RH = 55%) before further testing.
Before coating with hydrophobic emulsions tile surfaces were subjected to mechanical abrasion using 60 grit sand paper for 30 s. Prepared samples were treated with two hydrophobic emulsions, with different concentration of hydrophobic agent and silica fume. Upon coating, the samples were cured for 48 h at a room temperature of 22 ± 3 °C and relative humidity of 55%.
In addition to these specimens, for water droplet bouncing tests, the fiber-reinforced concrete cubes with composition M11–M14 were also used. The concrete mortar cubes compositions are shown in Table 4.
The procedure involved the production of 40 mm × 40 mm × 160 mm beams using the same approach as described above. These beams were cut into cubes of 40 mm × 40 mm × 40 mm with a diamond saw. The difference between these two types of samples (tiles and cubes) was that for the M1–M10 samples, the top side of the sample was used as a testing surface, and for the M11–M14 samples, a newly cut side was used. Therefore, the direction of imbedded fibers was observed to be different.
4.6. Surface Roughness
Uncoated mortar samples M1, M5, M6 and M10 were observed at 20× using a Laser Confocal microscope Olympus Lext OLS4100 (Tokyo, Japan). The average surface roughness (Sa), and average line roughness (Ra) were obtained. The uncoated samples were chosen for microscopy to study the roughness imparted by the sand, and PVA fibers after the abrasion treatment. The samples M1, M5, M6 and M10 were selected to study the effect of PVA fibers and sand on surface roughness.
5. Results and Discussions
The controlling parameters of CA and ROA for the tile and cube surfaces were measured before the shear tests and droplet impact tests.
5.1. Surface Roughness
The 2D optical images and 3D surface topographies of the mortar surfaces are reported in Figure 7 and Figure 8, respectively. The average surface roughness (Sa) of the samples are listed in Table 5. The PVA fibers are visible in samples M1 (Figure 7a and Figure 8a) and M5 (Figure 7b and Figure 8b), emerging from the mortar surface. The surfaces of M5 (Figure 8b) and M10 (Figure 8d) are wavy due to the presence of sand grains. The sample M6 (Figure 8c), which lacks PVA fibers, as well as sand, has the lowest value of Sa at 2.218 μm. Sample M1, which has PVA fibers but no sand, has an Sa of 9.929 μm. This increase in roughness can be attributed to the effect of PVA fibers.

Figure 7.
Optical images of M1, M5, M6, and M10. The blue broken arrows show the PVA fibers, while the red arrows show the sand grains. The scale bar for M1, M5 and M6 is 100 μm, and for M10 it is 200 μm.

Figure 8.
The surface topographies of samples M1, M5, M6, and M10. The PVA fibers are highlighted in blue, while the sand grains are highlighted in red. (a) PVA fiber is visible in M1 emerging from the surface; (b) PVA fibers, as well as sand grains, are observed in M5. The sand creates roughness on the surface (c) M6 has the lowest roughness due to absence of sand and PVA fibers; (d) the presence of sand creates distributed roughness in M10.

Table 5.
Average surface roughness (Sa) of the samples in μm, and the controlling parameters such as PVA fiber content and sand to cement ratio.
The mortar sample, M10, without fibers has the highest Sa of 19.155 μm, whereas M5, which has both sand and fibers, has an Sa of 18.054 μm. Thus, the presence of sand in the mortar significantly increases the surface roughness. While the surfaces are prepared by abrasion treatment using sandpaper, the areas with stronger sand grains exposed wear differently when compared to cement matrix zones due to differences in hardness. This explains the approach used to induce required roughness observed on samples containing sand.
Using the surface roughness data, and the mixture composition parameters as two independent variables, namely —the PVA fiber content and —the sand to cement ratio, a second degree polynomial model can be derived for the average surface roughness Sa.
Although the surface roughness is a function of several parameters related to the mortar composition, Equation (5) serves to demonstrate that the surface roughness of mortar can be controlled.
5.2. Ice Adhesion Strength
In this study the assessment of icephobic characteristics of surfaces with hydrophobic properties was conducted using 3 sets of fiber-reinforced concrete and mortar tiles with different coatings: (a) reference tiles without hydrophobic treatment (Set A); (b) tiles treated with the emulsion containing 5% and 1% of hydrophobic agent and silica fume, respectively (Set B); and (c) tiles treated with the emulsion based on 25% and 5% of components (Set C). The test results of CA and ROA values are presented in Table 6.

Table 6.
Contact angle (CA), roll-off angle, and ice adhesion strength for concrete and mortar tiles.
The reference set of samples (A) without hydrophobic treatment has hydrophilic properties with the values of CA barely exceeding 25°; at the same time, some of the samples demonstrate zero CA, which can be explained by a high absorption capability induced by the capillary porous structure of concrete. Because of hydrophilicity, the roll-off angle parameter for those samples cannot be measured.
The set B treated with emulsion containing low concentration of hydrophobic agent and silica fume (5% and 1%, respectively) demonstrated the best results for CA of up to 151° and roll-off angle of less than 1°. The lowest values of roll-off angle <1° within the set belong to the fiber reinforced samples with higher surface roughness, which correlates with the CA data for the same samples. This approach for surface treatment results in over- and superhydrophobic characteristics. Herein, it is important to note that the lowest values of roll-off angle belong to the fiber reinforced samples, produced at low W/C and S/C ratios.
The set C, with tiles treated with high concentration emulsion demonstrated the hydrophobic and over-hydrophobic (water CA between 120° and 150°) characteristics, which can be explained by low surface energy of siloxane hydrophobic agent, covering the hydrophilic surface of the tiles. The best results were demonstrated by the samples with higher water to cement (W/C) 0.4–0.5 and sand to cement (S/C) 2.5–3 ratios, which induce beneficial roughness of the surface. High roll-off angle can be observed, however, some of the samples reached the maximum value 90°.
The cube samples M11–M14, which were treated with the emulsion based on 5% and 1% of hydrophobic agent and silica fume, respectively, had over-hydrophobic characteristics with quite equal CA values of average 138. 5° and, comparatively, low ROA values for all the cube samples.
Based on the shear strength test, a linear dependence of ice adhesion strength on CA can be observed (Figure 9a). The higher the CA, the lower the shear force that has to be applied to separate the ice from a sample surface and, thus, the lower the adhesion strength of ice to a surface. Comparing set A of the samples, which are hydrophilic, to sets B and C, which are hydrophobic, the ice adhesion strength is seen to differ by a factor of 10.
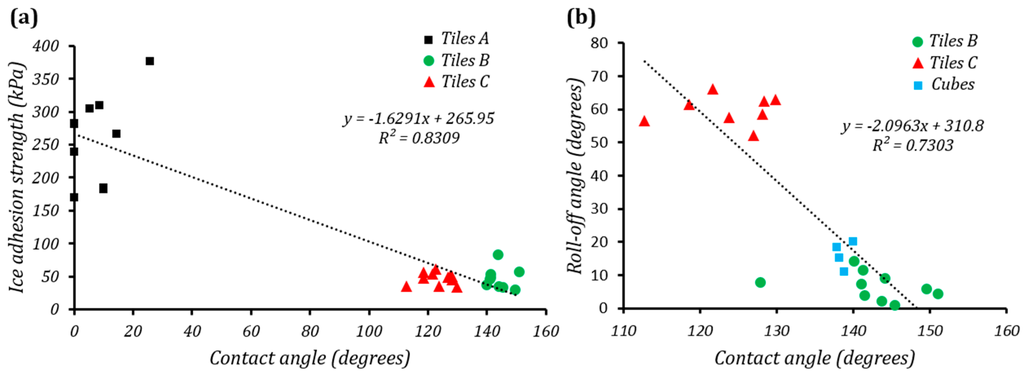
Figure 9.
(a) The correlation of water contact angle and ice adhesion strength for the samples; (b) The correlation of water contact angle and the roll-off angle for the samples.
At the same time, a slightly weaker ice adhesion to the surfaces of M6–M10 tiles treated with the emulsion containing higher concentration of hydrophobic agent (set C) can be observed. Therefore, lower adhesion strength in the case of set C of specimens is due to a thicker hydrophobic layer, which covers the surface roughness and to some extent and makes it smooth. This allows ice sliding more easily on the surface while applying the shearing force.
There is no correlation between the roll-off angle values and adhesion strength. The correlation between roll-off angles of the samples and their CAs is shown in Figure 9b. The tile specimen set C show high roll-off angles, whereas the cube specimens and the tile specimen set B, which were hydrophobized using low concentration emulsion, show both high CA, as well as a low roll-off angle.
The investigations carried out on the icephobic capability of the concrete tiles with different hydrophobic coatings allows to make the conclusion that the controlling parameters governing the adhesion of ice are the CA values, the thickness of a hydrophobic layer, as well as the roughness and structure of a surface. Fine tuning of these parameters can result in the concrete surfaces with an adhesion strength of 10 times less than the reference.
This finding can lead to the design of ice-free roads and runways, and meeting extreme durability and extended service life objectives.
5.3. Interaction of Incoming Droplets
For the bouncing droplet test, tiles M1 and M2 from set B were chosen, because of they had the best CA and ROA results. The M11–M14 cube samples, treated with the emulsion containing 5% and 1% of hydrophobic agent and silica fume, respectively, were also tested in this experiment.
Figure 10 shows stacked images for various samples. The droplets before impact at −5 °C and the droplets after impact at 20 °C are represented as clear shapes. The droplets after impact at −5 °C are represented in red. The trajectories of the droplets after impact at −5 °C and 20 °C are distinct. The droplets bounce further at 20 °C. In the case of M1, the droplets at −5 °C bounce off without freezing, while, in the case of M2, the droplets freeze. Droplets either bounce off or roll off after impacting all the samples except M2.

Figure 10.
Stacked images showing the trajectory of water droplets falling from 50 mm, impinging on concrete samples inclined at 45° at 0 °C and 20 °C. The trajectory of droplets at −5 °C after bouncing is shown in red.
The marked difference in trajectories at 0 °C and 20 °C indicate a higher dissipation of energy of droplet at −5 °C. This can be accounted for by the change in density, viscosity, and surface tension of water, as well as the change in adhesion with the concrete surface. The surface is sticky at −5 °C, resulting in a longer time of contact with the droplet. This results in heat transfer and heterogeneous nucleation of ice in the droplet, followed by freezing, as seen in the case of sample M2.
The difference in the interaction of water droplets with samples M1 and M2 could be related to the extent of surface roughness or relief caused by variation in W/C and S/C ratios of fiber reinforced concrete or mortar formulations. Surface density and porosity are key parameters of the substrate material. At the same time, both of the mentioned parameters significantly affect the height of incorporated PVA fibers, which emerge from the surface after abrasion treatment. Comparing two samples, M1 and M2, the surface roughness of M2 is greater because of higher W/C and S/C ratios, as well as lower surface density and higher porosity.
The trajectory of a droplet after impact depends on the wetting state of the droplet on impact. The roughness of the concrete surface, as well as the energy of incoming droplets, can influence Cassie-Baxter to Wenzel wetting transition on impact. To prevent the wetting transition and resulting ice formation, the surface roughness and porosity needs to be optimized. This can be achieved by changing the W/C and S/C ratios, and the PVA fiber content.
6. Optimization of Icephobic Surfaces
In this section we discuss how the three aspects of the icephobicity of a surface can be optimized by controlling surface and material parameters.
6.1. Ice Adhesion to Solids
As discussed in Section 3.1, dielectric materials can reduce ice adhesion because of the induction of less mirror charges. The surface charge density of ice is = 1.6 × 10−2 C/m2 [75]. Following Ryzhkin and Petrenko [56], the induced surface charge density on the dielectric coating in contact with the ice can be written as:
where is dielectric constant of the coating material. The electrostatic interaction force scales as . The electrostatic interactions are thought to be one of the major causes of ice adhesion, therefore, one can assume that the adhesion strength of the ice-dielectric interface scales similarly to . Figure 11 shows the variation of the ice adhesion strength with dielectric constants assuming a proportionality constant of the unity. The trend is similar to the experimental results reported by Saleema et al. [57] There is no appreciable decrease in ice adhesion strength when the dielectric constant is larger than 10. However, for the ice adhesion strength decreases considerably.
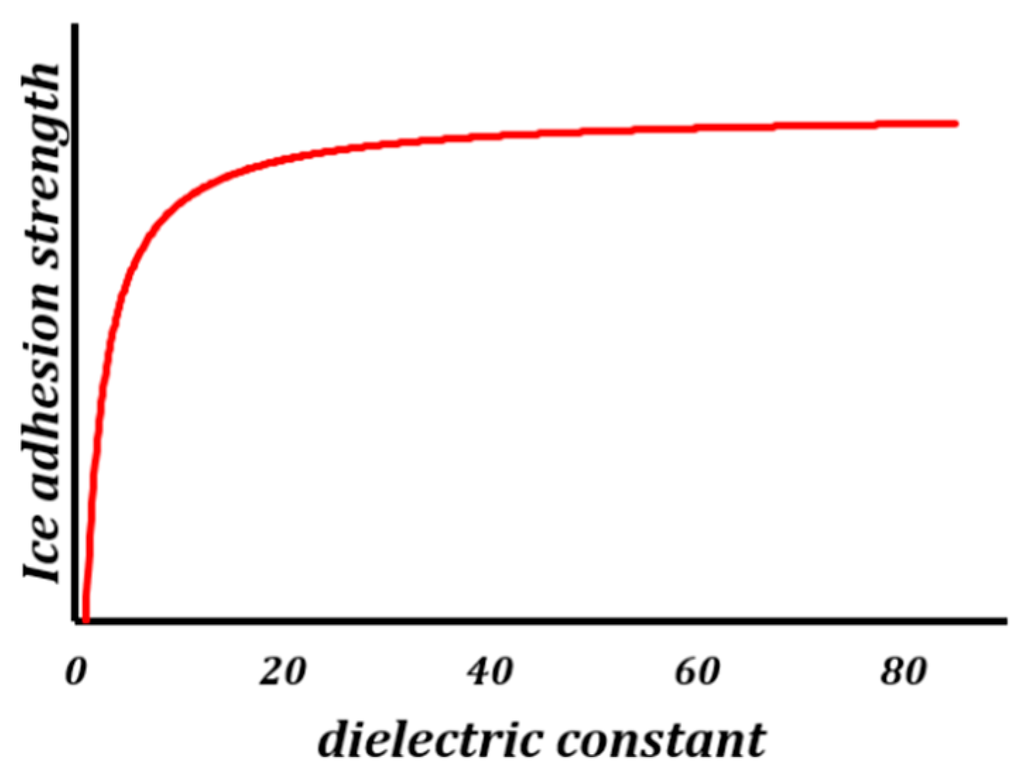
Figure 11.
Variation of ice adhesion strength with dielectric constant of the icephobic coating.
For water, , while for air, . Thus, having air pockets is favorable to lower the ice adhesion strength. Therefore, the Wenzel state is unfavorable for the icephobicity, whereas the Cassie-Baxter state, with air pockets between the solid and water, will lead to low ice adhesion strength when water freezes. The PVA fibers, which were used to increase concrete roughness, as described in the preceding sections, have a dielectric constant of about [76], which, therefore, helps in minimizing the ice adhesion strength.
As we discussed in the preceding section, the ice adhesion strength of hydrophobic concrete is lower than that of uncoated concrete. We attribute this, at least partially, to the synergistic effect of the air pockets due to the hydrophobization, as well as the exposed PVA fibers. Both these factors minimize the mirrored charges on ice, thereby weakening ice adhesion.
6.2. Suppression of Frost Formation
Nucleation occurs when the energy gained in forming a nucleus is greater than the energy cost due to creation of a new interface. The rate of nucleation is related to the nucleation energy barrier (ΔG*) as . The nucleation energy barrier for homogeneous nucleation is
where Δμ is the difference in chemical potentials between the surrounding phase and the nucleating phase, γ, is the interfacial tension of the nucleus, and the number density of the nucleating phase, , is the number of possible nucleation sites per unit volume. Ice nucleation occurs when the critical radius of the nucleus is equal to or greater than [77]:
The nucleation energy barrier for heterogeneous nucleation at a surface is less than the energy barrier for homogeneous nucleation. The heterogeneous nucleation energy barrier on a flat surface [78] is:
while the heterogeneous nucleation energy barrier in a wedge [79] with a characteristic length greater than the critical radius is:
where θ is the contact angle of the nucleus at the surface, α is the angle of the wedge, and (Figure 12a). The Equation (10) is valid for and . When α = 180°, .
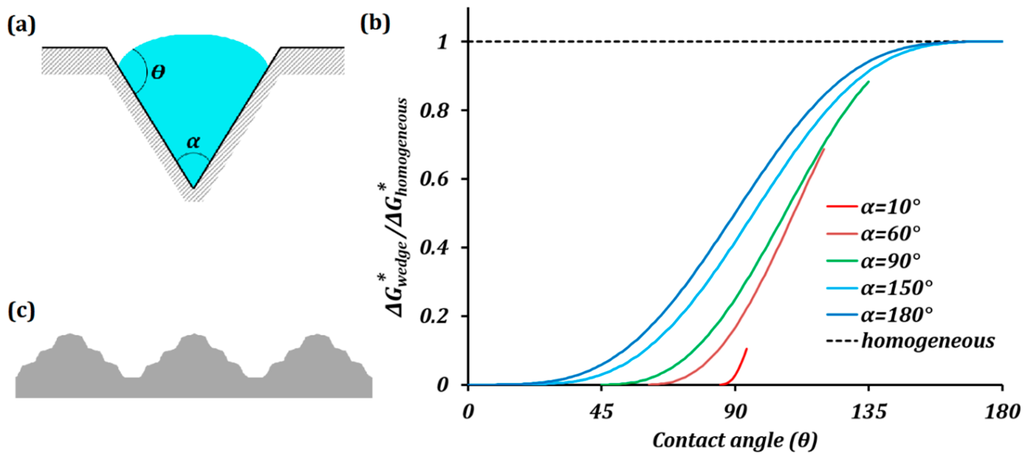
Figure 12.
(a) Water droplet making a contact angle θ inside a wedge of angle α; (b) normalized nucleation energy barrier versus contact angle. The energy barrier increases as the wedge angle increases; (c) surface topography with wide corners will have the highest possible nucleation energy barrier.
Nucleation energy barrier for a wedge normalized using the homogeneous nucleation energy barrier varies with contact angle and wedge angle, as shown in Figure 12b. The narrow wedges lower the energy barrier for nucleation. Thus, ice nucleation occurs readily at concave sites compared to flat or convex sites. For hydrophilic surfaces, the nucleation energy barrier is low whereas for hydrophobic surfaces the nucleation energy barrier is high. Thus, theoretically, a smooth superhydrophobic surface should provide the highest energy barrier for heterogeneous nucleation and frost formation. Molecularly smooth surfaces exhibit delayed ice nucleation in humid conditions compared to rough superhydrophobic surfaces [80].
The highest possible contact angle on any smooth surface is 119° [81]. Multiscale surface roughness is essential for large values of macroscopic contact angles. The critical radius of the ice nucleus R* is of the order of a few nanometers. The characteristic length scale of the surface features on a superhydrophobic surface is usually greater than R*. Therefore, the local contact angle θ of the material is critical for the ice nucleation energy barrier than the macroscopic contact angle.
For rough surfaces, the aim must be to have the wedge angles as large as possible. For a surface topography, as shown in Figure 12c, both the micro and nano scale features maintain wide angle corners to have high nucleation energy barriers.
For the concrete samples studied here, the surface topography is influenced by the sand to cement ratio and the PVA fiber content. The effect of these parameters on the surface roughness is given by Equation (5). The mechanical abrasion of concrete prior to coating with emulsion also affects the surface topography. An appropriate grit sandpaper can be selected so that the prepared surface has a topography resembling that in Figure 12c.
6.3. Minimizing Contact Time for Incoming Droplets
It was seen in the experiments with impinging droplets that the surface tends to be sticky at −5 °C. The stickiness of the surface can be explained by the spontaneous condensation of water from vapor into the cracks and pores on the concrete surface. The equilibrium curvature of the condensate meniscus is given by the Kelvin equation [30].
where is the Kelvin radius, is the surface tension, is the molar volume, is the vapor pressure and is the saturated vapor pressure at temperature T. For supercooled water at −5 °C, 18.026 × 10−6 m3/mol, 0.0764 N/m, and 0.62 nm. At saturated conditions . At 34% relative humidity , −0.57 nm. The negative value of curvature implies that condensation can occur at undersaturated conditions. The geometry of the surface topographical features plays an important role in the formation of thermodynamically stable interface. Spontaneous condensation can occur in hydrophilic pores of size greater than .
The condensate formed in nano and micro pores of the concrete surface results in the modification of the surface energy of concrete. An incoming liquid droplet encountering a condensate liquid film on the surface will experience an adhesion force [30]:
where R is the radius of the undeformed droplet and is the contact angle of the condensate film with the surface. The energy required to overcome this adhesion will scale as where X is the size of the flattened face of the droplet on impact. Consider the concrete surface wetted by the nano scale condensate film . For a 14 μL water droplet at −5 °C impacting the concrete surface at 0.99 m/s, the kinetic energy at impact is of the order 10−6 J. If the droplet deformation is of the same order as R, the energy required to overcome adhesion and bounce off the surface is of the order 10−6 J. The significant energy loss incurred by the droplet results in the droplet wetting the surface followed by freezing.
To minimize the contact time between the incoming droplets and a surface, it is essential to control the surface topography as well as the contact angle. Hydrophobizing the surface pores will result in a reduction of the adhesion force . Sample M1, with no sand content, demonstrated the best ability to repel incoming water droplets. The absence of sand resulted in smaller pores, which do not sustain a thermodynamically stable continuous condensate film. The hydrophobic coating ensured a low adhesion force. The surface roughness of concrete can be optimized by controlling the parameters in Equation (5).
7. Conclusions
We have discussed the theoretical mechanisms of ice-repellence and found that the interactions involved are similar to hydrophobic interactions. Furthermore, the requirements for an icephobic surface are analogous to the requirements for a superhydrophobic surface, as summarized in Table 1. Although it is well known that not all the superhydrophobic surfaces are icephobic, most surface properties needed to design a superhydrophobic surface, such as the surface roughness and free energy, affect the icephobic performance. This finding led us to develop an icephobic surface using the same approaches, which were used for the superhydrophobic modification. For our study, we selected one of the most challenging materials for the hydrophobization, concrete, which is typically hydrophilic and wicks water. Only recently, hydrophobic and superhydrophobic types of concrete were synthesized. Concrete is a very common material in civil engineering and construction; therefore, addition of an icephobic property can have a significant impact on many applications.
The three aspects of the icephobicity are the reduced ice adhesion, repulsion of incoming droplets prior to freezing, and delayed frost formation. We studied two aspects of the icephobicity, namely, the ice adhesion to concrete and the repulsion of incoming droplets. The icephobicity of concrete was achieved by hydrophobizing the surface so that it can maintain the Cassi state with air pockets between the solid and water, by using dielectric coatings, and by modifying the surface topography. Uncoated concrete samples were hydrophilic, and showed ice adhesion strength in the range 170–376 kPa. Concrete samples coated with hydrophobic emulsion showed water contact angle as high as 151° and roll-off angle as low as 1°. The ice adhesion strength of the coated samples were one order lower in the range 29–83 kPa. The PVA fibers, as well as the air pockets on the surface, due to their low dielectric constants, can minimize the mirror charges on the ice surface, thereby reducing the ice adhesion strength. The addition of PVA fibers and sand to concrete resulted in a significant increase in surface roughness. The coated concrete samples could repel incoming water droplets at 20 °C, as well as −5 °C. We found that icephobic performance of concrete depends on these parameters—the hydrophobic emulsion concentration, the PVA fiber content, the water to cement ratio, and sand to cement ratio.
The surface roughness of concrete can be optimized by controlling the sand and PVA fiber content. An optimally rough surface could prevent wetting transition for incoming droplets and minimize the resulting ice accretion, as well as delay the ice nucleation and frost formation by increasing the ice nucleation energy barrier for the surface.
Supplementary Materials
The following are available online at www.mdpi.com/1099-4300/18/4/132/s1, Video S1: Impact of water droplets on fiber-reinforced concrete with superhydrophobic siloxane-based top layer.
Acknowledgments
The work was partially supported by the University of Wisconsin-Milwaukee (UWM) Research Growth Initiative (RGI) grant 101X245. The authors thank Ryoichi S. Amano (UWM) for the high-speed camera.
Author Contributions
Michael Nosonovsky suggested the idea of the entropic approach; Konstantin Sobolev proposed and realized the concept of superhydrophobic concrete with engineered roughness; Rahul Ramachandran performed the incoming droplet experiments, microscopy, wrote a major part of the manuscript, and prepared the figures; Marina Kozhukhova performed the ice adhesion tests, measured contact angles and wrote a majority of the experimental section; Konstantin Sobolev and Michael Nosonovsky supervised the research and wrote parts of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SOC | Self-organized criticality |
| CA | Contact angle |
| PMHS | Polymethylhydroxysilane |
| PVA | Polyvinyl alcohol |
| W/C | Water to cement ratio |
| S/C | Sand to cement ratio |
References
- Nosonovsky, M. Entropy in Tribology: In the Search for Applications. Entropy 2010, 12, 1345–1390. [Google Scholar] [CrossRef]
- Bryant, M. Unification of Friction and Wear. In Recent Developments in Wear Prevention, Friction and Lubrication; Nikas, G., Ed.; Research Signpost: Kerala, India, 2010. [Google Scholar]
- Amiri, M.; Khonsari, M.M. On the Thermodynamics of Friction and Wear-A Review. Entropy 2010, 12, 1021–1049. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Ramachandran, R. Geometric Interpretation of Surface Tension Equilibrium in Superhydrophobic Systems. Entropy 2015, 17, 4684–4700. [Google Scholar] [CrossRef]
- Kreder, M.J.; Alvarenga, J.; Kim, P.; Aizenberg, J. Design of Anti-Icing Surfaces: Smooth, Textured or Slippery? Nat. Rev. Mater. 2016, 1, 15003. [Google Scholar] [CrossRef]
- Blackburn, C.; Laforte, C.; Laforte, J.L. Apparatus for Measuring the Adhesion Force of a Thin Ice Sheet on a Substrate. In Proceedings of the International Workshop on Atmospheric Icing of Structures (IWAIS), Chester, UK, 5–8 June 2000.
- Kulinich, S.A.; Farzaneh, M. How Wetting Hysteresis Influences Ice Adhesion Strength on Superhydrophobic Surfaces. Langmuir 2009, 25, 8854–8856. [Google Scholar] [CrossRef] [PubMed]
- Mishchenko, L.; Hatton, B.; Bahadur, V.; Taylor, J.A.; Krupenkin, T.; Aizenberg, J. Design of Ice-Free Nanostructured Surfaces Based on Repulsion of Impacting Water Droplets. ACS Nano 2010, 4, 7699–7707. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, R.; Sobolev, K.; Nosonovsky, M. Dynamics of Droplet Impact on Hydrophobic/Icephobic Concrete with the Potential for Superhydrophobicity. Langmuir 2015, 31, 1437–1444. [Google Scholar] [CrossRef] [PubMed]
- Eberle, P.; Tiwari, M.K.; Maitra, T.; Poulikakos, D. Rational Nanostructuring of Surfaces for Extraordinary Icephobicity. Nanoscale 2014, 6, 4874–4881. [Google Scholar] [CrossRef] [PubMed]
- Kim, P.; Wong, T.; Alvarenga, J.; Kreder, M.J.; Adorno-Martinez, W.; Aizenberg, J. Liquid-Infused Nanostructured Surfaces with Extreme Anti-Ice and Anti-Frost Performance. ACS Nano 2012, 6, 6569–6577. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Whyman, G.; Bormashenko, E.; Hao, C.; Wang, Z. Controlling Drop Bouncing using Surfaces with Gradient Features. Appl. Phys. Lett. 2015, 107, 051604. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Klett, J.D. Microphysics of Clouds and Precipitation, 1st ed.; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Li, K.; Xu, S.; Shi, W.; He, M.; Li, H.; Li, S.; Zhou, X.; Wang, J.; Song, Y. Investigating the Effects of Solid Surfaces on Ice Nucleation. Langmuir 2012, 28, 10749–10754. [Google Scholar] [CrossRef] [PubMed]
- Alizadeh, A.; Yamada, M.; Li, R.; Shang, W.; Otta, S.; Zhong, S.; Ge, L.; Dhinojwala, A.; Conway, K.R.; Bahadur, V.; et al. Dynamics of Ice Nucleation on Water Repellent Surfaces. Langmuir 2012, 28, 3180–3186. [Google Scholar] [CrossRef] [PubMed]
- Campbell, J.M.; Meldrum, F.C.; Christenson, H.K. Is Ice Nucleation from Supercooled Water Insensitive to Surface Roughness? J. Phys. Chem. C 2015, 119, 1164–1169. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Hejazi, V. Why Superhydrophobic Surfaces are Not always Icephobic. ACS Nano 2012, 6, 8488–8491. [Google Scholar] [CrossRef] [PubMed]
- Farhadi, S.; Farzaneh, M.; Kulinich, S.A. Anti-Icing Performance of Superhydrophobic Surfaces. Appl. Surf. Sci. 2011, 257, 6264–6269. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Luo, C.; Zhao, Y.; Yuan, X. Icephobicity of Polydimethylsiloxane-b-Poly (Fluorinated Acrylate). Thin Solid Films 2014, 573, 67–73. [Google Scholar] [CrossRef]
- Li, X.; Zhao, Y.; Li, H.; Yuan, X. Preparation and Icephobic Properties of Polymethyltrifluoropropylsiloxane-Polyacrylate Block Copolymers. Appl. Surf. Sci. 2014, 316, 222–231. [Google Scholar] [CrossRef]
- Fu, Q.; Wu, X.; Kumar, D.; Ho, J.W.C.; Kanhere, P.D.; Srikanth, N.; Liu, E.; Wilson, P.; Chen, Z. Development of Sol-Gel Icephobic Coatings: Effect of Surface Roughness and Surface Energy. ACS Appl. Mater. Interfaces 2014, 6, 20685–20692. [Google Scholar] [CrossRef] [PubMed]
- Boinovich, L.B.; Emelyanenko, A.M.; Ivanov, V.K.; Pashinin, A.S. Durable Icephobic Coating for Stainless Steel. ACS Appl. Mater. Interfaces 2013, 5, 2549–2554. [Google Scholar] [CrossRef] [PubMed]
- Horgnies, M.; Chen, J.J. Superhydrophobic Concrete Surfaces with Integrated Microtexture. Cem. Concr. Compos. 2014, 52, 81–90. [Google Scholar] [CrossRef]
- Barthlott, W.; Neinhuis, C. Purity of the Sacred Lotus, or Escape from Contamination in Biological Surfaces. Planta 1997, 202, 1–8. [Google Scholar] [CrossRef]
- Wong, T.; Kang, S.H.; Tang, S.K.Y.; Smythe, E.J.; Hatton, B.D.; Grinthal, A.; Aizenberg, J. Bioinspired Self-Repairing Slippery Surfaces with Pressure-Stable Omniphobicity. Nature 2011, 477, 443–447. [Google Scholar] [CrossRef] [PubMed]
- Wilson, P.W.; Lu, W.; Xu, H.; Kim, P.; Kreder, M.J.; Alvarenga, J.; Aizenberg, J. Inhibition of Ice Nucleation by Slippery Liquid-Infused Porous Surfaces (SLIPS). Phys. Chem. Chem. Phys. 2013, 15, 581–585. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Damle, V.G.; Liu, S.; Rykaczewski, K. Bioinspired Stimuli-Responsive and Antifreeze-Secreting Anti-Icing Coatings. Adv. Mater. Interfaces 2015, 2. [Google Scholar] [CrossRef]
- Ramachandran, R.; Nosonovsky, M. Surface micro/nanotopography, Wetting Properties and the Potential for Biomimetic Icephobicity of Skunk Cabbage Symplocarpus Foetidus. Soft Matter 2014, 10, 7797–7803. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Statistical Mechanics of Chain Molecules; Interscience: New York, NY, USA, 1969. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Waltham, MA, USA, 2011. [Google Scholar]
- Donaldson, S.H., Jr.; Royne, A.; Kristiansen, K.; Rapp, M.V.; Das, S.; Gebbie, M.A.; Lee, D.W.; Stock, P.; Valtiner, M.; Israelachvili, J. Developing a General Interaction Potential for Hydrophobic and Hydrophilic Interactions. Langmuir 2015, 31, 2051–2064. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D. Interfaces and the Driving Force of Hydrophobic Assembly. Nature 2005, 437, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Houston, J.; van Swol, F.; Brinker, C.J. Superhydrophobicity—Drying Transition of Confined Water. Nature 2006, 442, 526–526. [Google Scholar] [CrossRef] [PubMed]
- Hammer, M.U.; Anderson, T.H.; Chaimovich, A.; Shell, M.S.; Israelachvili, J. The Search for the Hydrophobic Force Law. Faraday Discuss. 2010, 146, 299–308. [Google Scholar] [CrossRef] [PubMed]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-Organized Criticality—An Explanation of 1/f Noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef] [PubMed]
- Zypman, F.R.; Ferrante, J.; Jansen, M.; Scanlon, K.; Abel, P. Evidence of Self-Organized Criticality in Dry Sliding Friction. J. Phys. Condensed Matter 2003, 15, L191–L196. [Google Scholar] [CrossRef]
- Creeger, P.; Zypman, F. Entropy Content during Nanometric Stick-Slip Motion. Entropy 2014, 16, 3062–3073. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Bhushan, B. Do Hierarchical Mechanisms of Superhydrophobicity Lead to Self-Organized Criticality? Scr. Mater. 2008, 59, 941–944. [Google Scholar] [CrossRef]
- Tadmor, R. Line Energy and the Relation between Advancing, Receding, and Young Contact Angles. Langmuir 2004, 20, 7659–7664. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Lee, J.; Patankar, N.A. Contact Angle Hysteresis on Rough Hydrophobic Surfaces. Colloids Surfaces A-Physicochem. Eng. Asp. 2004, 248, 101–104. [Google Scholar] [CrossRef]
- Krasovitski, B.; Marmur, A. Drops Down the Hill: Theoretical Study of Limiting Contact Angles and the Hysteresis Range on a Tilted Plate. Langmuir 2005, 21, 3881–3885. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Amirfazli, A. A Thermodynamic Approach for Determining the Contact Angle Hysteresis for Superhydrophobic Surfaces. J. Colloid Interface Sci. 2005, 292, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Nosonovsky, M. Model for Solid-Liquid and Solid-Solid Friction of Rough Surfaces with Adhesion Hysteresis. J. Chem. Phys. 2007, 126, 224701. [Google Scholar] [CrossRef] [PubMed]
- Bormashenko, E.Y. Wetting of Real Surfaces; De Gruyter: Berlin, Germany; Boston, MA, USA, 2013. [Google Scholar]
- Phillips, J.C. Scaling and Self-Organized Criticality in Proteins I. Proc. Natl. Acad. Sci. USA 2009, 106, 3107–3112. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C. Hydropathic Self-Organized Criticality: A Magic Wand for Protein Physics. Protein Peptide Lett. 2012, 19, 1089–1093. [Google Scholar] [CrossRef]
- Lobkovsky, A.E.; Wolf, Y.I.; Koonin, E.V. Universal Distribution of Protein Evolution Rates as a Consequence of Protein Folding Physics. Proc. Natl. Acad. Sci. USA 2010, 107, 2983–2988. [Google Scholar] [CrossRef] [PubMed]
- Koonin, E.V. The Logic of Chance: The Nature and Origin of Biological Evolution; FT Press: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Hong, L.; Lei, J. Scaling Law for the Radius of Gyration of Proteins and its Dependence on Hydrophobicity. J. Poly. Sci. Part B Polym. Phys. 2009, 47, 207–214. [Google Scholar] [CrossRef]
- Nittmann, J.; Stanley, H.E. Nondeterministic Approach to Anisotropic Growth-Patterns with Continuously Tunable Morphology—The Fractal Properties of some Real Snowflakes. J. Phys. A Math. Gen. 1987, 20, L1185–L1191. [Google Scholar] [CrossRef]
- Libbrecht, K.G. Morphogenesis on Ice: The Physics of Snow Crystals. Eng. Sci. 2001, 64, 10–19. [Google Scholar]
- Libbrecht, K.G. The Physics of Snow Crystals. Rep. Progr. Phys. 2005, 68, 855–895. [Google Scholar] [CrossRef]
- Furukawa, Y.; Wettlaufer, J.S. Snow and Ice Crystals. Phys. Today 2007, 60, 70–71. [Google Scholar] [CrossRef]
- Furukawa, Y. Snow and ice crystal growth. In Handbook of Crystal Growth: Fundamentals: Thermodynamics and Kinetics. Volume 1A, 2nd ed.; Nishinaga, T., Ed.; Elsevier: Waltham, MA, USA, 2015; p. 1061. [Google Scholar]
- Petrenko, V.F.; Peng, S. Reduction of Ice Adhesion to Metal by using Self-Assembling Monolayers (SAMs). Can. J. Phys. 2003, 81, 387–393. [Google Scholar] [CrossRef]
- Ryzhkin, I.A.; Petrenko, V.F. Physical Mechanisms Responsible for Ice Adhesion. J. Phys. Chem. B 1997, 101, 6267–6270. [Google Scholar] [CrossRef]
- Saleema, N.; Farzaneh, M.; Paynter, R.W.; Sarkar, D.K. Prevention of Ice Accretion on Aluminum Surfaces by Enhancing their Hydrophobic Properties. J. Adhes. Sci. Technol. 2011, 25, 27–40. [Google Scholar] [CrossRef]
- Hejazi, V.; Sobolev, K.; Nosonovsky, M. From Superhydrophobicity to Icephobicity: Forces and Interaction Analysis. Sci. Rep. 2013, 3, 2194. [Google Scholar] [CrossRef] [PubMed]
- Boinovich, L.; Emelyanenko, A.M. Role of Water Vapor Desublimation in the Adhesion of an Iced Droplet to a Superhydrophobic Surface. Langmuir 2014, 30, 12596–12601. [Google Scholar] [CrossRef] [PubMed]
- Laforte, C.; Beisswenger, A. Icephobic Material Centrifuge Adhesion Test. In Proceedings of the 11th International Workshop on Atmospheric Icing of Structures, IWAIS, Montreal, QC, Canada, 12–16 June 2005.
- Li, W.; Zhang, X.; Yang, J.; Miao, F. In Situ Growth of Superbydrophobic and Icephobic Films with micro/nanoscale Hierarchical Structures on the Aluminum Substrate. J. Colloid Interface Sci. 2013, 410, 165–171. [Google Scholar] [CrossRef] [PubMed]
- Mobarakeh, L.F.; Jafari, R.; Farzaneh, M. The Ice Repellency of Plasma Polymerized Hexamethyldisiloxane Coating. Appl. Surf. Sci. 2013, 284, 459–463. [Google Scholar] [CrossRef]
- Subramanyam, S.B.; Rykaczewski, K.; Varanasi, K.K. Ice Adhesion on Lubricant-Impregnated Textured Surfaces. Langmuir 2013, 29, 13414–13418. [Google Scholar] [CrossRef] [PubMed]
- Maitra, T.; Antonini, C.; Tiwari, M.K.; Mularczyk, A.; Imeri, Z.; Schoch, P.; Poulikakos, D. Supercooled Water Drops Impacting Superhydrophobic Textures. Langmuir 2014, 30, 10855–10861. [Google Scholar] [CrossRef] [PubMed]
- Kwon, H.; Paxson, A.T.; Varanasi, K.K.; Patankar, N.A. Rapid Deceleration-Driven Wetting Transition during Pendant Drop Deposition on Superhydrophobic Surfaces. Phys. Rev. Lett. 2011, 106, 036102. [Google Scholar] [CrossRef] [PubMed]
- Bird, J.C.; Dhiman, R.; Kwon, H.; Varanasi, K.K. Reducing the Contact Time of a Bouncing Drop. Nature 2013, 503, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Li, Z.; Bourdo, S.; Khedir, K.R.; Asar, M.P.; Ryerson, C.C.; Biris, A.S. Exceptional Superhydrophobicity and Low Velocity Impact Icephobicity of Acetone-Functionalized Carbon Nanotube Films. Langmuir 2011, 27, 9936–9943. [Google Scholar] [CrossRef] [PubMed]
- Lafuma, A.; Quere, D. Superhydrophobic States. Nat. Mater. 2003, 2, 457–460. [Google Scholar] [CrossRef] [PubMed]
- Boreyko, J.B.; Chen, C. Self-Propelled Dropwise Condensate on Superhydrophobic Surfaces. Phys. Rev. Lett. 2009, 103, 184501. [Google Scholar] [CrossRef] [PubMed]
- Boreyko, J.B.; Collier, C.P. Delayed Frost Growth on Jumping-Drop Superhydrophobic Surfaces. ACS Nano 2013, 7, 1618–1627. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Ma, R.; Zhou, H.; Zhou, X.; Che, L.; Yao, S.; Wang, Z. Activating the Microscale Edge Effect in a Hierarchical Surface for Frosting Suppression and Defrosting Promotion. Sci. Rep. 2013, 3, 2515. [Google Scholar] [CrossRef] [PubMed]
- Muzenski, S.; Flores-Vivian, I.; Sobolev, K. Freeze-Thaw Resistance of Fiber Reinforced Composites with Superhydrophobic Admixtures. In Proceedings of the Mechanics and Physics of Creep, Shrinkage, and Durability of Concrete, Cambridge, MA, USA, 2013; pp. 269–276.
- Flores-Vivian, I.; Hejazi, V.; Kozhukhova, M.I.; Nosonovsky, M.; Sobolev, K. Self-Assembling Particle-Siloxane Coatings for Superhydrophobic Concrete. ACS Appl. Mater. Interfaces 2013, 5, 13284–13294. [Google Scholar] [CrossRef] [PubMed]
- Muzenski, S.; Flores-Vivian, I.; Sobolev, K. Hydrophobic Engineered Cementitious Composites for Highway Applications. Cem. Concr. Compos. 2015, 57, 68–74. [Google Scholar] [CrossRef]
- Petrenko, V.F. The Surface of Ice; Special Report for US Army Corps of Engineers Cold Regions Research and Engineering Laboratory: Washington, DC, USA, August 1994. [Google Scholar]
- Dielectric Constant Values. Available online: http://www.clippercontrols.com/pages/Dielectric-Constant-Values.html (accessed on 5 January 2016).
- Sear, R.P. Nucleation: Theory and Applications to Protein Solutions and Colloidal Suspensions. J. Phys. Condens. Matter 2007, 19, 033101. [Google Scholar] [CrossRef]
- Volmer, M. Über keimbildung und keimwirkung als spezialfälle der heterogenen katalyse. Z. Elektrochem. Angew. Phys. Chem. 1929, 35, 555–561. [Google Scholar]
- Sholl, C.A.; Fletcher, N.H. Decoration Criteria for Surface Steps. Acta Metall. 1970, 18, 1083–1086. [Google Scholar] [CrossRef]
- Heydari, G.; Sedighi Moghaddam, M.; Tuominen, M.; Fielden, M.; Haapanen, J.; Mäkelä, J.M.; Claesson, P.M. Wetting Hysteresis Induced by Temperature Changes: Supercooled Water on Hydrophobic Surfaces. J. Colloid Interface Sci. 2016, 468, 21–33. [Google Scholar] [CrossRef] [PubMed]
- Nishino, T.; Meguro, M.; Nakamae, K.; Matsushita, M.; Ueda, Y. The Lowest Surface Free Energy Based on -CF3 Alignment. Langmuir 1999, 15, 4321–4323. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).