1. Introduction
In information retrieval, a typical post-query process is relevance feedback, which builds a refined query model (often a term distribution) based on a set of feedback documents, in order to have a better representation of the user’s information need [
1]. There are three types of relevance feedback methods,
i.e., explicit, implicit and pseudo-relevance feedback. Among them, pseudo-relevance feedback (PRF) is a fully automatic approach to the query expansion, by assuming that the top ranked documents returned by an information retrieval (IR) system are relevant. A widely-used PRF method is the relevance model (RM) [
2], which utilizes top ranked documents
D to construct a relevance term distribution
R. One limitation of RM-based methods is that the feedback document set
D is often a mixture of relevant and irrelevant documents, so that
R is very likely to be a mixture distribution rather than the true relevance distribution that is supposed to be derivable from the truly relevant documents only.
Recent research on negative relevance feedback has attempted to make use of irrelevant documents to improve the retrieval performance [
3,
4,
5]. By assuming that a set of seed irrelevant documents is available, a distribution separation method (DSM) has been proposed in our earlier work [
6]. Essentially, given a mixture distribution and a seed irrelevance distribution, DSM aims to derive an approximation of the true relevance distribution, in other words to separate the irrelevance distribution from the mixture one. It has been shown in [
6] that, compared to the direct removal of irrelevant documents, separating the irrelevance distribution from the mixture distribution is theoretically more general and practically has led to a better performance.
The formulation of DSM was based on two assumptions, namely the linear combination assumption and the minimum correlation assumption. The former assumes that the mixture term distribution is a linear combination of the relevance and irrelevance distributions, while the latter assumes that the relevance distribution should have a minimum correlation with the irrelevance distribution. DSM provided a lower bound analysis for the linear combination coefficient, based on which the desired relevance distribution can be estimated. It was also proven that the lower bound of the linear combination coefficient corresponds to the condition of the minimum Pearson correlation coefficient between DSM’s output relevance distribution and the input seed irrelevance distribution.
Although initially developed in the context of IR, DSM is indeed a general mathematical formulation for probability distribution separation. The separation algorithm and analysis of DSM are not restricted to query term distributions or any other distributions for IR tasks. It is thus important to further investigate its theoretical properties and make it become more general.
In this article, we propose to generalize DSM’s theoretical analysis, which was originally based on the Pearson correlation coefficient, to entropy-related measurements, specifically the KL-divergence and two variants. In addition, we investigate the distribution separation idea in a widely-used method,
i.e., the mixture model feedback (MMF) approach [
7]. Theoretical analysis has shown that the linear separation algorithm in DSM can be applied to simplify the EM-algorithm in MMF. The specific descriptions of the above contributions are as follows.
First, we explore the effect of DSM on the KL-divergence between the DSM’s estimated relevance distribution and the seed irrelevance distribution. In
Section 3, we prove that DSM’s lower bound analysis can also be extended to KL-divergence, and the minimum correlation coefficient corresponds to the maximum KL-divergence. We further prove that the decreasing correlation coefficient also leads to the maximum symmetrized KL-divergence, as well as the maximum JS-divergence between DSM’s output distribution and the seed irrelevance distribution. These extended analyses enrich DSM’s own theoretical properties.
Second, we investigate the relationship between DSM and the mixture model feedback (MMF) approach [
7]. In
Section 4, we show that the linear combination assumption is valid in MMF, and the EM-based iterative algorithm of MMF is essentially a distribution separation process. Thus, its iterative steps can be largely simplified by the linear separation algorithm (see Equation (
2)) developed in DSM. Furthermore, compared to MMF with an empirically-assigned combination coefficient, DSM’s combination coefficient is analytically derived and is adaptive for each query. The experimental results in terms of the retrieval performance and running time costs have demonstrated the advantages of our DSM approach.
2. Basic Analysis of DSM
In this section, we briefly describe the basic analysis of DSM [
6]. Some basic notations are summarized in
Table 1. We use
M to represent the mixture term distribution derived from all of the feedback documents, where
M is a mixture of relevance term distribution
R and irrelevance term distribution
I. In addition, we assume that only part of the irrelevance distribution
(also called the seed irrelevance distribution) is available, while the other part of irrelevance distribution is unknown (denoted as
).
The task of DSM is defined as: given a mixture distribution
M and a seed irrelevance distribution
, derive an output distribution that can approximate the
R as closely as possible. Specifically, as shown in
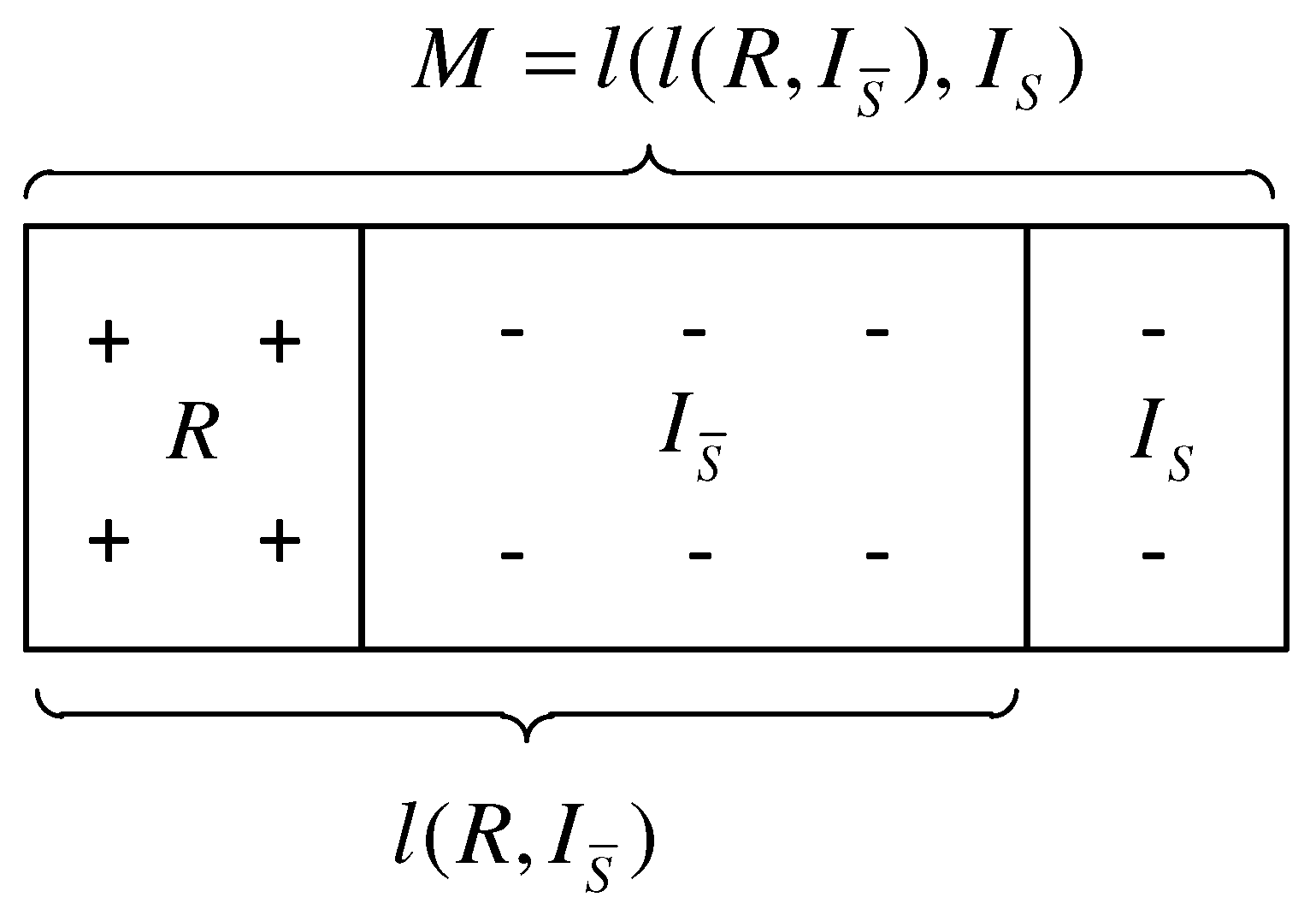
Figure 1, the task of DSM can be divided into two problems: (1) how to separate
from
M and derive a less noisy distribution
, which is mixed by
R and
; (2) how to further refine
to approximate
R as closely as possible. In this article, we will be focused on the first problem and the linear separation algorithm to derive
. Note that
is also an estimate of
R, depending on how much irrelevance data are available. The theoretical analysis proposed in this article will be mainly related to the linear separation algorithm and its lower bound analysis.
2.1. Linear Combination Analysis
DSM adopts a linear combination assumption, which states that the mixture term distribution is a linear combination of the relevance and irrelevance distributions. Under such a condition, the mixture distribution
M can be a linear combination of
R and
I. As shown in
Figure 1,
M can also be a linear combination of two distributions
and
, where
is a linear combination of
R and
. We have:
where
λ is the linear coefficient. The problem of estimating
does not have a unique solution generally, since the value of the coefficient
λ is unknown. Therefore, the key is to estimate
λ. Let
denote an estimate of
λ, and correspondingly, let
be the estimation of the desired distribution
. According to Equation (
1), we have:
Once the right
is obtained, Equation (
2) is the main equation to construct the distribution separation in linear time. However, there can be infinite possible choices of
and its corresponding
. To get the solution of
, we need to find its lower bound, by introducing a constraint that values in the distribution should be nonnegative [
6]. Based on this constraint and Equation (
2), we have:
Effectively, Equation (
3) sets a lower bound
of
:
where
stands for a vector in which all of the entries are one,
denotes the entry-wise division of
M by
and
denotes the max value in the resultant vector
. The lower bound
itself also determines an estimation of
, denoted as
.
The calculation of the lower bound is critical to the estimation of λ. Now, we present an important property of in Lemma 1. Lemma 1 guarantees that if the distribution contains a zero value, then , leading to the distribution w.r.t. being exactly the desired distribution w.r.t. λ.
Lemma 1. If there exists a zero value in , then , leading to .
The proof can be found in [
6]. In a density estimation problem or a specific IR model estimation task, with a smoothing method used, there would be many small values instead of zero values, in
. In this case,
is still approximately equal to
, which guarantees that
can still be equal to
λ. The detailed description of this remark can be found in [
6].
2.2. Minimum Correlation Analysis
In this section, we go in-depth to study another property of the combination coefficient and its lower bound. Specifically, we analyse the correlation between
and
, along with the decreasing coefficient
. Pearson product-moment correlation coefficient
ρ [
8] is used as the correlation measurement.
Proposition 1. If decreases, the correlation coefficient between and , i.e., , will decrease.
The proof of Proposition 1 can be found in [
6]. According to Proposition 1, among all
,
corresponds to the minimum correlation coefficient between
and
,
i.e.,
. We can also change the
minimum correlation coefficient (
i.e.,
) to the
minimum squared correlation coefficient (
i.e.,
). To solve this optimization problem, please refer to [
6] for more details.
3. Extended Analysis of DSM on Entropy-Related Measurements
As we can see from the previous section, although DSM was proposed in the pseudo-relevance feedback scenario, its algorithm and analysis are not restricted to query term distributions derived by PRF techniques. DSM is actually a mathematical formulation for probability distribution separation, and it is important to further investigate its theoretical properties.
In this section, we describe the generalization of DSM’s analysis in terms of some entropy-related measures. Specifically, we will extend the aforementioned minimum correlation analysis to the analysis of the maximum KL-divergence, the maximum symmetrized KL-divergence and the maximum JS-divergence.
3.1. Effect of DSM on KL-Divergence
Recall that in
Section 2.2, Proposition 1 shows that after the distribution separation process, the Pearson correlation coefficient between DSM’s output distribution
and the seed irrelevance distribution
can be minimized. Here, we further analyse the effect of DSM on the KL-divergence between
and
.
Specifically, we propose the following Proposition 2, which proves that if decreases, the KL-divergence between and will be increased monotonously.
Proposition 2. If decreases, the KL-divergence between and will increase.
Proof. Using the simplified notations in
Table 2, let the KL-divergence of between
and
be formulated as:
Now, let
as we did in the proof of Proposition 1 (see [
6]). According to Equation (
2), we have
. It then turns out that:
Based on Equations (
5) and (
6), we get:
Let
. The derivative of
can be calculated as:
Since
and
,
becomes zero. We then have:
Let the
i-th term in the summation of Equation (
9) be:
It turns out that when or , is greater than zero. When , is zero. However, does not always equal to . Therefore, is greater than zero.
In conclusion, we have . This means that (i.e., ) increases after ξ increases. Since , after decreases, will increase. ☐
According to Proposition 2, if λ is reduced to its lower bound , then the corresponding KL-divergence will be the maximum value for all of the legal (). In this case, the output distribution of DSM will have the maximum KL-divergence with the seed irrelevance distribution.
3.2. Effect of DSM on Symmetrized KL-Divergence
Having shown the effect of reducing the coefficient on the KL-divergence between and , we now investigate the effect on the symmetrized KL-divergence between two involved distributions by proving the following proposition.
Proposition 3. If decreases, the symmetrized KL-divergence between and will increase.
The proof of Proposition 3 can be found in
Appendix A.1. According to the above proposition, if
λ is reduced to its lower bound
, the corresponding symmetrized KL-divergence
will be the maximum value for all of the legal
(
). This means that the output distribution of DSM given this lower bound estimation has the maximum symmetrized KL-divergence with the seed irrelevance distribution.
3.3. Effect of DSM on JS-Divergence
Now, let us further study the reduction of the coefficient in terms of its role in maximizing the JS-divergence between DSM’s output distribution and the seed irrelevance distribution , by presenting the following proposition.
Proposition 4. If decreases, the JS-divergence between and will increase.
The proof of Proposition 4 can be found in
Appendix A.2. Based on the above proposition, if
λ is reduced to its lower bound
, then the corresponding JS-divergence
will be the maximum value for all of the legal
(
).
In summary, we have extended the analysis of DSM’s lower bound combination coefficient, from the minimum correlation analysis, to the maximum KL-divergence analysis, the maximum symmetrized KL-divergence analysis and the maximum JS-divergence analysis. These extended analyses enrich DSM’s own theoretical properties.
These above theoretical properties of DSM are based on one basis condition, i.e., the linear combination assumption. In the next section, we will investigate how to apply the distribution separation idea/algorithm in other methods. The main idea is to verify if the well-known mixture model feedback (MMF) approach complies with this linear combination assumption. If yes, the idea of DSM’s linear separation algorithm can be applied in MMF, and the associated theoretical properties of DSM can be valid for MMF’s solution, as well.
4. Generalized Analysis of DSM’s Linear Combination Condition in MMF
Now, we will investigate the relation between DSM and a related PRF model, namely the mixture model feedback (MMF) approach [
7]. MMF assumes that feedback documents are generated from a mixture model with two multinomial components,
i.e., the query topic model and the collection model [
7].
The estimation of the output “relevant” query model of MMF is trying to purify the feedback document by eliminating the effect of the collection model, since the collection model contains background noise, which can be regarded as the “irrelevant” content in the feedback document [
7]. In this sense, similar to DSM, the task of MMF can also be regarded as a process that removes the irrelevant part in the mixture model. However, to our knowledge, researchers have not investigated whether the linear combination assumption is valid or not in MMF. We will prove that the mixture model in MMF is indeed a linear combination of “relevant” and “irrelevant” parts. This theoretical result can lead to a simplified version of MMF based on the linear separation equation (see Equation (
2)) of DSM.
4.1. Review of the Mixture Model Feedback Approach
Now, we first review the mixture model feedback approach, where the likelihood of feedback documents (
) can be written as:
where
is the count of a term
w in a document
d,
is the query topic model, which can be regarded as the relevance distribution to be estimated, and
is the collection model (
i.e., the distribution of term frequency in the whole document collection), which is considered as the background distribution/noise. The empirically-assigned parameter
λ is the amount of the true relevance distribution, and
indicates the amount of background noise,
i.e., the influence of
C in the feedback documents. An EM method [
7] is developed to estimate the relevance distribution via maximizing the likelihood in Equation (
10). It contains iterations of two steps [
9]:
where
is the probability that the word
w is from the background distribution, given the current estimation of the relevance distribution (
). This estimation can be regarded as a procedure to obtain relevant information from feedback documents while filtering the influence of collection distribution, leading to a more discriminative relevance model. It should be noted that in Equation (
10), due to the log operator within the summations (
i.e.,
), it does not directly show that the mixture model is a linear combination of the collection model and the query topic model. Therefore, an EM algorithm is adopted to estimate the query topic model
.
4.2. The Simplification of the EM Algorithm in MMF via DSM’s Linear Separation Algorithm
Now, we explore the connections between DSM and MMF. In both methods, once λ is given (either by the estimation in DSM or by an assigned value in MMF), the next step is to estimate the true relevance distribution R. We will first demonstrate that if the EM algorithm (in MMF) converges, the mixture model of the feedback documents is a linear combination of the collection model and the output model of the EM iterative algorithm.
Proposition 5. If the EM algorithm (in MMF) converges, the mixture model of the feedback documents is a linear combination of the collection model and the output relevance model of the EM iterative algorithm.
The proof of Proposition 5 can be found in
Appendix A.3. Based on such a proof, it is shown that:
where
is the mixture model, which represents the term frequency in the feedback documents,
is the collection model and
is the estimated relevance model output by the
n-th step of the EM iterative algorithm in MMF. It shows that the mixture model
is a linear combination of the collection model
and the output relevance model
of the EM iterative algorithm.
The above equation can be changed to:
Now, if we regard
as an estimated relevance distribution,
as a kind of mixture distribution and
as a kind of irrelevance distribution, then Equation (
13) fits Equation (
1), and Equation (
14) is the same distribution separation process as Equation (
2), where
is the estimated relevance distribution. It demonstrates that the EM iterative steps in MMF can actually be simplified by the linear separation solution in Equation (
14), which has the same distribution separation idea in Equation (
2).
5. Comparisons between DSM and Related Models
In this section, we will compare DSM with other related works, including mixture model feedback (MMF) [
7], fast mixture model feedback (FMMF) [
10], regularized mixture model feedback (RMMF) [
11], as well as a mixture multinomial distribution framework and a query-specific mixture modelling feedback (QMMF) approach [
12]. Since the above models are implemented on two basic relevance feedback models,
i.e., relevance model (RM) and mixture model feedback (MMF), we will also compare RM (we use RM to denote RM1 in [
2]) and MMF. These comparative discussions and analyses are described in the following, in order to clarify the position of DSM in the IR literature and our contributions for the IR community.
5.1. DSM and MMF
As discussed in the previous section, DSM and MMF share a similar strategy that the irrelevant part should be eliminated from the mixture model, and then, the output relevant query model can be purified. In MMF, the collection model is considered as the irrelevance model that contains background noise, and an EM iterative method [
7] is developed to estimate the relevance distribution via maximizing the likelihood in Equation (
10).
To our knowledge, researchers have not investigated whether the linear combination assumption is valid or not in MMF. We, for the first time, prove Proposition 5, which shows that if the EM algorithm (in MMF) converges, the mixture model of the feedback documents is a linear combination of the collection model and the output model of the EM iterative algorithm. This proposition directly results in a simplified solution for MMF, by replacing the EM iterative steps in MMF with DSM’s linear distribution separation solution (see Equation (
14)).
Besides providing a simplified solution with linear complexity to the EM method in MMF, DSM shows an essential difference regarding the coefficient
λ. In MMF, the proportion of relevance model in the assumed mixture model
is controlled by
λ, which is a free parameter and is empirically assigned to a fixed value before running the EM algorithm. On the other hand, in DSM, as previously mentioned in
Section 2,
λ for each query is estimated adaptively via an analytical procedure based on its linear combination analysis (see
Section 2.1), a minimum correlation analysis (see
Section 2.2) and a maximal KL-divergence analysis (described in
Section 3.1).
5.2. DSM and FMMF
Another simplified solution to MMF was proposed in [
10]. This solution is derived by the Lagrange multiplier method, and the complexity of its divide and conquer algorithm is
(on average) to
(the worst case). On the other hand, our simplified solution in Equation (
14) was analytically derived from the convergence condition of the EM method in the MMF approach, and the complexity of the linear combination algorithm in Equation (
14) is further reduced to a fixed linear complexity,
i.e.,
.
5.3. DSM and RMMF
To deal with the problems of the manually-tuned interpolation coefficient
λ in MMF (see also the discussions in
Section 5.1), Tao and Zhai [
11] proposed a regularized MMF (RMMF), which yields an adaptive solution for estimating
λ and achieves good performance. Specifically, RMMF added a conjugate Dirichlet prior function to the original objective function in MMF, and the original query model is used as the prior. In RMMF, a regularized EM method is developed to adapt the linear coefficients and the prior confident value. The main strategy in this EM method is to gradually lower the prior confident value
μ starting with a very high value, and the learned interpolation coefficient
λ (in [
11,
λ is denoted by
) varies with different queries.
Although both RMMF and DSM can estimate an adaptive interpolation coefficient
λ for the mixture model MMF, their algorithms are quite different. In RMMF, an EM iterative algorithm is still used, like in the original MMF. Therefore, the computational cost is relatively time consuming. On the other hand, as described in
Section 5.1, the adaptive solution of the interpolation coefficient of MMF can be obtained in linear time via an analytical procedure, with a minimum correlation analysis and a maximal KL-divergence analysis guaranteed. Moreover, for the estimation of the output relevance distribution, different from the iteratively-learned solution in RMMF, the solution of MMF can be obtained by a closed-form solution in Equation (
14).
5.4. DSM and Mixture Multinomial Distribution Framework
Chen
[
12] proposed a unified framework by considering several query expansion models, e.g., RM and MMF, as mixture multinomial distributions. In addition, they built a query-specific mixture model feedback (QMMF) approach, which modifies RMMF by replacing the original query model with the relevance model (actually RM1) in the prior function of RMMF. QMMF was then successfully applied in speech recognition and summarization tasks.
Although Chen
have summarized RM and MMF in the mixture multinomial distribution [
12], they have not shown that both RM and MMF comply with the linear combination assumption. With the proof in
Appendix A.3, we demonstrate Proposition 5, which shows that MMF complies with the linear combination assumption. This theoretical result leads to a simplified solution for MMF (see Equation (
14)). In
Appendix A.4, we also show the validity of the linear combination assumption in RM. Therefore, to some extent, DSM unifies RM and MMF from another point of view,
i.e., the linear combination assumption and DSM’s analysis and algorithm can be applied to both of them.
With regard to QMMF, since it is actually based on RMMF and MMF, the difference between QMMF and DSM is also related to the EM algorithm’s solution in MMF-based methods
versus the linear separation solution in DSM, as we discussed in
Section 5.1 and
Section 5.3.
Indeed, in RMMF and QMMF, it brings obvious benefits to adopt the original query model or the relevance model as a prior to constrain the estimation of the interpolation coefficient and the relevance feedback distribution. In our future work, we are going to investigate if it is possible to adopt similar relevance information to regularize the separation algorithm in DSM.
5.5. RM and MMF
Exploiting relevance feedback for query expansion [
13] is a popular strategy in the information retrieval area to improve the retrieval performance [
14]. Many models with relevance feedback have been proposed [
2,
7,
11,
15,
16,
17], among which the relevance model (RM) [
2] and the mixture model feedback (MMF) [
7] are two basic models on which many other models are built.
RM extends the original query with an expanded term distribution generated from the feedback documents. The resultant distribution of RM is calculated by combining the distributions of each feedback document with the normalized query likelihood as its document weight. Therefore, the effectiveness of RM is dependent on the quality of feedback documents. Since feedback documents may contain collection noise, which affects the quality of the relevance model, the mixture model approach [
7] is proposed to handle this problem. It assumes that the relevance documents are generated from a mixture model of the relevance information and collection noise, and an EM iterative method is used to learn a relevance feedback distribution.
Although empirical results have shown that MMF can perform better than RM on some collections [
14], we cannot say which one is definitely better or worse than the other, since the retrieval performance of a feedback-based query model is dependent on the quality of the feedback documents. Low quality feedback documents may not reflect the user’s information need well, which affects the effectiveness of the feedback document-based models.
With respect to the time complexity, due to an EM learning procedure in MMF [
7,
9], MMF is more time consuming than RM. In this paper, we provide a simplified solution for MMF in
Section 4.2. Equipped with this linear separation algorithm, MMF can be also implemented efficiently.
As discussed in
Section 5.4, DSM’s generalized analysis can unify RM and MMF, since the linear combination assumption holds in both models, and DSM’s analysis and algorithm can be applied to both of them. Moreover, DSM can guide the improvements of both of them. Specifically, for RM, DSM can separate an irrelevant distribution from the mixture model to approach the pure relevance distribution, and for MMF, the linear separation algorithm of DSM can be utilized to simplify the solution of MMF, significantly reducing its algorithm complexity.
5.6. Contributions of DSM in Information Retrieval
Based on the above comparisons between DSM and other related models, we summarize our contributions as follows:
We, for the first time, prove that mixture model feedback (MMF) complies with the linear combination assumption.
Based on the above proof, MMF’s EM algorithm can be simplified by a linear separation algorithm in DSM.
DSM can unify RM and MMF, in the sense that DSM’s analysis and algorithm can be applied to both of them.
The solution of DSM is associated with solid mathematical proofs in the linear combination analysis, the minimum correlation analysis, as well the analyses with the maximal KL-divergence, the maximal symmetric KL-divergence and the maximal JS-divergence.
We believe that compared to the empirical contributions on the retrieval performance improvements, the theoretical contributions of DSM are also important in the IR community. The generalized analyses of DSM are validated by the mathematical proofs, and its validity is to some extent independent of different parameters or different test collections. Although many feedback-based query expansion models have been proposed, relatively less attention has been paid to the rigorous analysis (through the proof of lemmas or propositions) of a retrieval model. There are a few works on the theoretical analysis of relevance feedback. For example, recently, Clinchant and Gaussier [
18] studied the statistical characteristics of the terms selected by several pseudo-relevance feedback methods, and proposed properties that may be helpful for effective relevance feedback models. However, to our knowledge, in the literature, there is a lack of a generalized analysis for DSM and an investigation on the linear combination condition in MMF.
6. Experiments
We have theoretically described the relation between the mixture model feedback (MMF) approach and our DSM method. The main experiments in this section provide empirical comparisons of these two methods in an
ad hoc retrieval task. In addition, since we compare RM and DSM in
Section 5.4 and
Section 5.5, we will conduct an implicit feedback task with RM as the baseline (for the empirical comparison between RM and DSM in the
ad hoc retrieval task, please refer to [
6]). It is expected that this additional experiment can show the flexibility of DSM on different tasks.
6.1. Experimental Setup
The evaluation involves four standard TREC (Text REtrieval Conference) collections, including WSJ (87–92, 173,252 documents), AP (88–89, 164,597 documents) in TREC Disk 1 and 2, ROBUST 2004 (528,155 documents) in TREC Disk 4 and 5 and WT10G (1,692,096 documents). These datasets involve a variety of texts, ranging from newswire articles to web/blog data. Both WSJ and AP datasets are tested on Queries 151–200, while the ROBUST 2004 and WT10G collections are tested on Queries 601–700 and 501–550, respectively. The
title field of the queries is used to reflect the typical keyword-based search scenarios. In query expansion models, the top 100 terms in the corresponding distributions are selected as expanded terms. The top 50 documents in the initial ranked list obtained by the query likelihood approach are selected as the feedback documents. The top 1000 documents retrieved by the negative KL-divergence between the expanded query model and the document language model [
19] are used for retrieval performance evaluation. The Lemur 4.7 toolkit [
20] is used for indexing and retrieval. All collections are stemmed using the Porter stemmer, and stop words are removed in the indexing process.
As for the evaluation metric for the retrieval performance, we use the mean average precision (MAP), which is the mean value of average precision over all queries. In addition, we use the Wilcoxon significance test to examine the statistical significance of the improvements over the baseline (baseline model and significant test results are shown in the result tables).
6.2. Evaluation on Retrieval Performance
As previously mentioned, the EM iteration algorithm of MMF can be simplified as a distribution separation procedure (see Equation (
14)) whose inputs are two distributions
(
for short) and
, where
is the mixture distribution for which the probability of a term is its frequency in feedback documents, and
C is the distribution of the term frequency in the whole document collection. It has been shown in
Section 4 that Equation (
14) is actually a special case of DSM, when
and
C are DSM’s input distributions and
λ is assigned empirically without principled estimation. We denote this special case as DSM (
λ fixed). Now, we compare MMF (to the EM algorithm) and DSM (
λ fixed) to test Proposition 5 empirically.
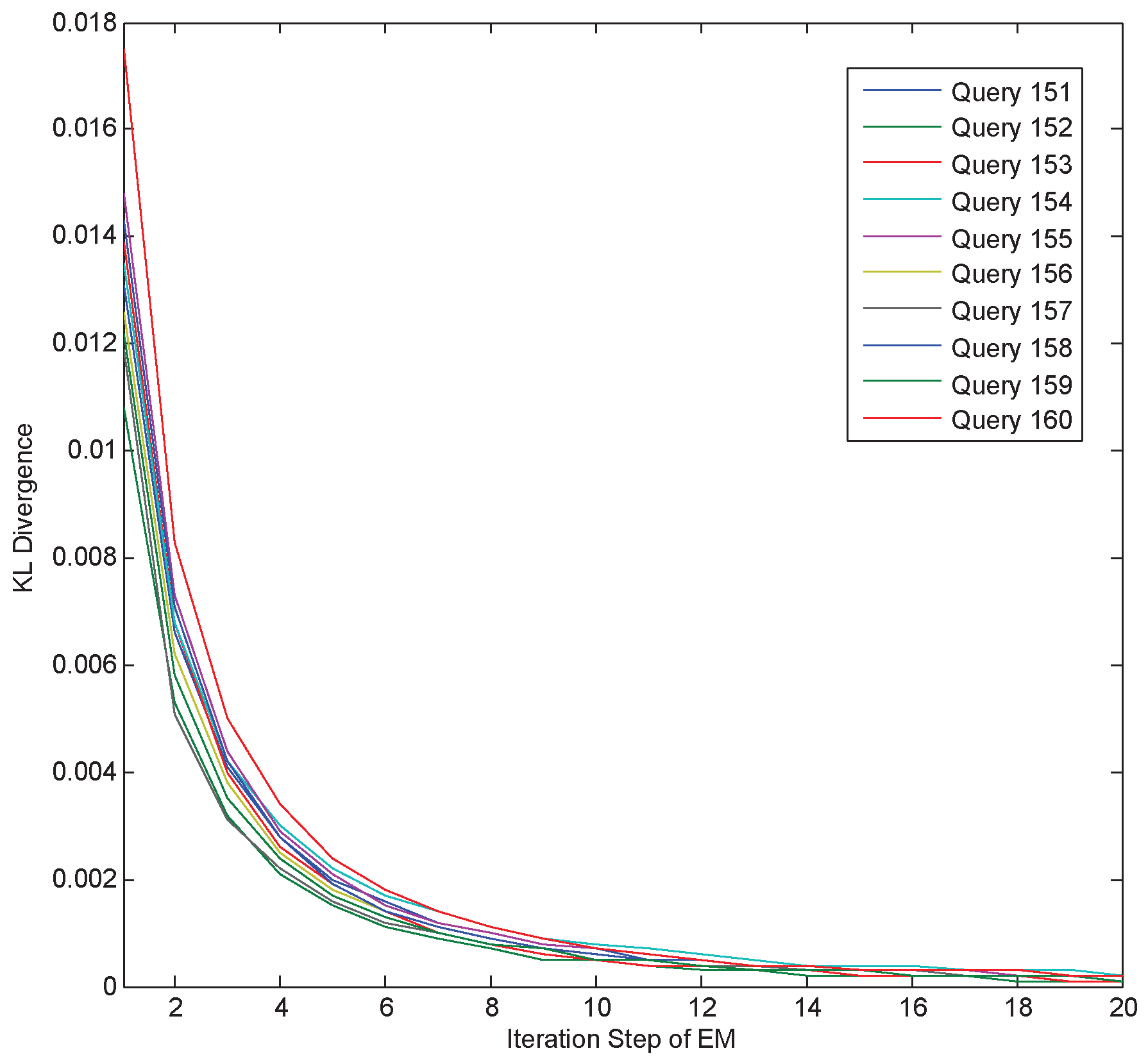
At first, we directly measure the KL-divergence between the resultant distributions of MMF and DSM (
λ fixed). We report the results of Queries 151–160 on WSJ 87-92 with
in
Figure 2, and the results of other queries/datasets show the same trends. It can be observed in
Figure 2 that the KL-divergence between the resultant distributions of MMF and DSM (
λ fixed) tends to zero, when the EM algorithm (of MMF) converges (as the iteration steps are going to 20). The above observation supports the proof of their equivalence illustrated in Proposition 5.
Next, we compare the retrieval performance of MMF and DSM (
λ fixed). For MMF, we set
λ to the value with the best retrieval performance, and this optimal value is also used in DSM (
λ fixed). Experimental results are shown in
Table 3. We can find that the performances of these two methods are very close, which is consistent with the analysis in
Section 4. The results again confirm that the EM algorithm in MMF can be simplified by Equation (14), which is a linear separation algorithm used in DSM.
As previously mentioned, DSM (
λ fixed) is just a special case of DSM when the
λ is empirically assigned. This
λ is the same for all of the concerned queries. For DSM, we can use the lower bound of
λ and this estimation (
i.e., the lower bound
) is computed adaptively for each query. In addition, DSM involves a refinement step for the input distributions (see the algorithm in [
6]). In
Table 3, we denote DSM with the lower bound of
λ as DSM (
) and denote DSM with the refinement step as DSM (+refine).
We now test DSM (
) and DSM (+refine) when
and
C are the mixture distribution and seed irrelevance distribution, respectively, as used in DSM (
λ fixed). It is demonstrated in
Table 3 that the performances of both DSM (
) and DSM (+refine) are significantly better than MMF. This is because although MMF and DSM (
λ fixed) empirically tune
λ for each collection, the value of
λ is the same for each query. On the contrary, DSM (
) and DSM (+refine) adopt the principled estimation of
λ for each concerned query
adaptively based on the linear combination analysis, the minimum correlation analysis and maximum KL-divergence analysis. This set of experiments demonstrates that the estimation method for
λ in the DSM method is crucial and effective for the irrelevance distribution elimination.
6.3. Evaluation on Running Time
Now, we report the running time of the DSM in comparison with the MMF’s EM iterative methods. The running times are recorded on a Dell PowerEdge R730 with one six-core CPU. Each recorded time is computed over a number of topical queries, and this number is 50, 50, 100 and 50 for WS J8-792, AP 88-89, ROBUS 2004T and WT10G, respectively. We run each method 100 times and report the average running time of the MATLAB code. The number of iterations used in the EM algorithm of MMF is set to 20, since in our experiments, the EM algorithm cannot converge well with less than 20 iterations.
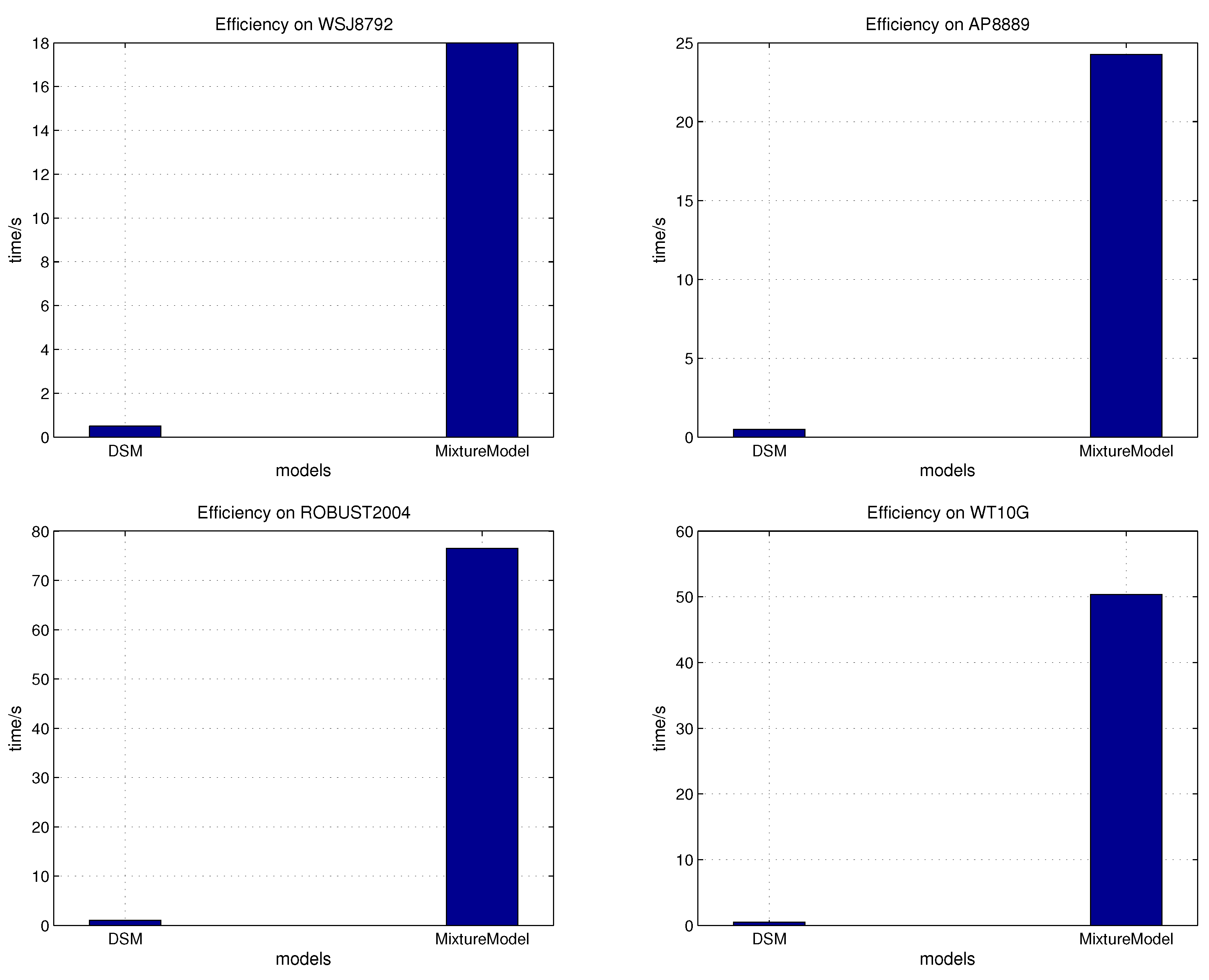
The running time comparisons between DSM and MMF are shown in
Figure 3. For each figure, the left column is for the DSM method (with distribution refinement), which has more computation steps and is thus slower than DSM (with
λ fixed) and DSM (with lower bound
) described in the previous experiment; while the right column is for the EM algorithm used in MMF. These results demonstrate the acceleration effect of DSM for MMF. It is clear that DSM with a linear time complexity is much more efficient than the EM’s iterative algorithm used for MMF.
6.4. Application of DSM on Implicit Irrelevant Feedback Using Commercial Query Logs
To further show DSM’s flexibility, in this section, we will give the empirical evaluation of DSM in implicit irrelevant feedback using query log data from a real commercial search engine. Since users’ behaviour can be exploited in implicit feedback to infer their preference [
21], it can be used here for identifying seed irrelevant documents. Without loss of generality, we assume that each query is part of a searching session, which consists of a sequence of queries with a time interval (30 min in our case). A list of returned documents is associated with each query, and whether or not the documents were clicked is recorded. Besides, the clicked documents can also be divided into satisfied clicked and unsatisfied clicked according to the hovering time over the document. We call the clicked documents with a short hovering time (e.g., less than 30 s) as “unsatisfied”, because we believe that a user clicking a document, but closing it really quickly, gives a hint that the user is not interested in this document [
22,
23,
24].
Now, we can obtain the seed irrelevant document set, which consists of the unsatisfied clicked documents in the history appearing in the current returned documents list, recorded as
. The corresponding seed irrelevance distribution is:
where
.
We obtain the seed irrelevance distribution from unsatisfied clicked (USC) documents as the implicit feedback documents. As for the mixture term distribution, we use the term distribution derived from RM as an input for DSM. The detailed calculation for this mixture distribution can be found in
Appendix A.4. We compare DSM to the initial result of the search engine. In addition, we compare DSM to two kinds of relevance feedback methods: pseudo-relevance feedback using all of the returned documents for query expansion and implicit relevance feedback using the clicked document in the log (the number of pseudo-relevant documents is not a constant, since the number for each query’s returned documents is different; some sessions may have no unsatisfied clicked documents, and to handle this problem, we simply ignore these sessions). For implicit irrelevance feedback, the top 50 terms are selected as expanded terms in query expansion models, and performance evaluations are conducted on all of the returned documents.
We sort all of the sessions based on the current query’s query click entropy [
25,
26], which is a metric for the variability in click results from different users. Low click entropy means that clicks from the most users are within a small number of returned documents, which leads to less potential to benefit from user’s implicit feedback and little improvement space. To clearly compare different implicit feedback-based re-ranking methods, we take the top
n (
) sessions with the largest click entropy. In
Table 4, each column records the result for the top
n sessions with the largest click entropy.
In
Table 4, “Initial” denotes the initial performance of the search engine. “Pseudo-Relevance Feedback” and “Implicit Relevance Feedback” denote the cases when we use all of the returned documents and clicked documents, respectively, as the feedback documents, based on which we carry out query expansion using RM.
From
Table 4, we can observe that DSM with unsatisfied clicked (USC) documents (as the seed irrelevance documents) can largely improve the initial ranking performanceand works better than both pseudo-relevance feedback and implicit relevance feedback. The above results demonstrate that DSM is effective for implicit irrelevance feedback.
7. Conclusions and Future Work
In this paper, we have systematically investigated the theoretical properties of the distribution separation method (DSM). Specifically, we have proven that the minimum correlation analysis in DSM is generalizable to maximum (original and symmetrized) KL-divergence analysis, as well as JS-divergence. We also proved that the solution to the well-known mixture model feedback (MMF) can be simplified using the linear combination technique in DSM, and this is also empirically verified using standard TREC datasets. We summarize the theoretical contributions of DSM for the IR research in
Section 5.6.
The experimental results on the ad hoc retrieval task show that the DSM with an analytically-derived combination coefficient λ can not only achieve better retrieval performance, but also can largely reduce the running time, compared to the EM algorithm used in MMF. An additional experiment on the query log shows that DSM can also work well in the implicit feedback task, which indicates the flexibility of DSM on different tasks.
In our future work, we are going to investigate if it is possible to adopt the original query model (or other relevance information) to regularize the separation algorithm in DSM. The empirical evaluation will then be based on RMMF and QMMF as the baselines, in order to compare different regularization strategies, given the same prior information for the regularization. Moreover, since the EM algorithm is widely used in many fields, e.g., machine learning, data mining, etc., it is interesting to investigate the distribution separation idea in certain applications of EM algorithms (e.g., the Gaussian mixture model). In our future work, we will endeavour to make DSM be more applicable to various methods/tasks.