Selecting Video Key Frames Based on Relative Entropy and the Extreme Studentized Deviate Test †
Abstract
:1. Introduction
2. Related Work
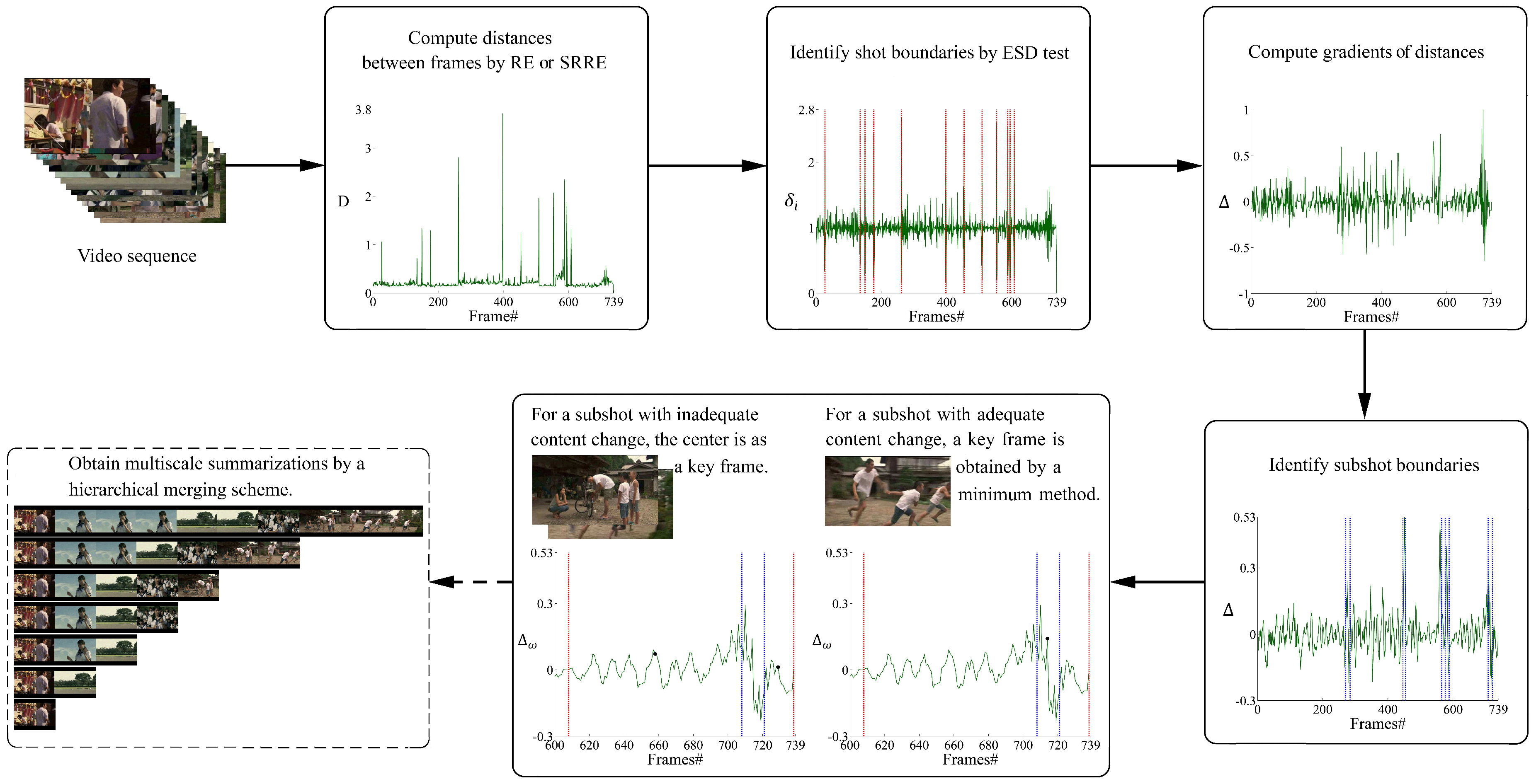
3. Proposed Approach for Key Frame Selection
3.1. Distance Measure
3.2. Shot Boundary Detection
3.3. Sub-Shot Location
3.4. Key Frame Selection
4. Multiscale Video Summarizations
| Algorithm 1: Hierarchical merging scheme for obtaining multiscale summarizations. |
 |
5. Experimental Results and Discussion
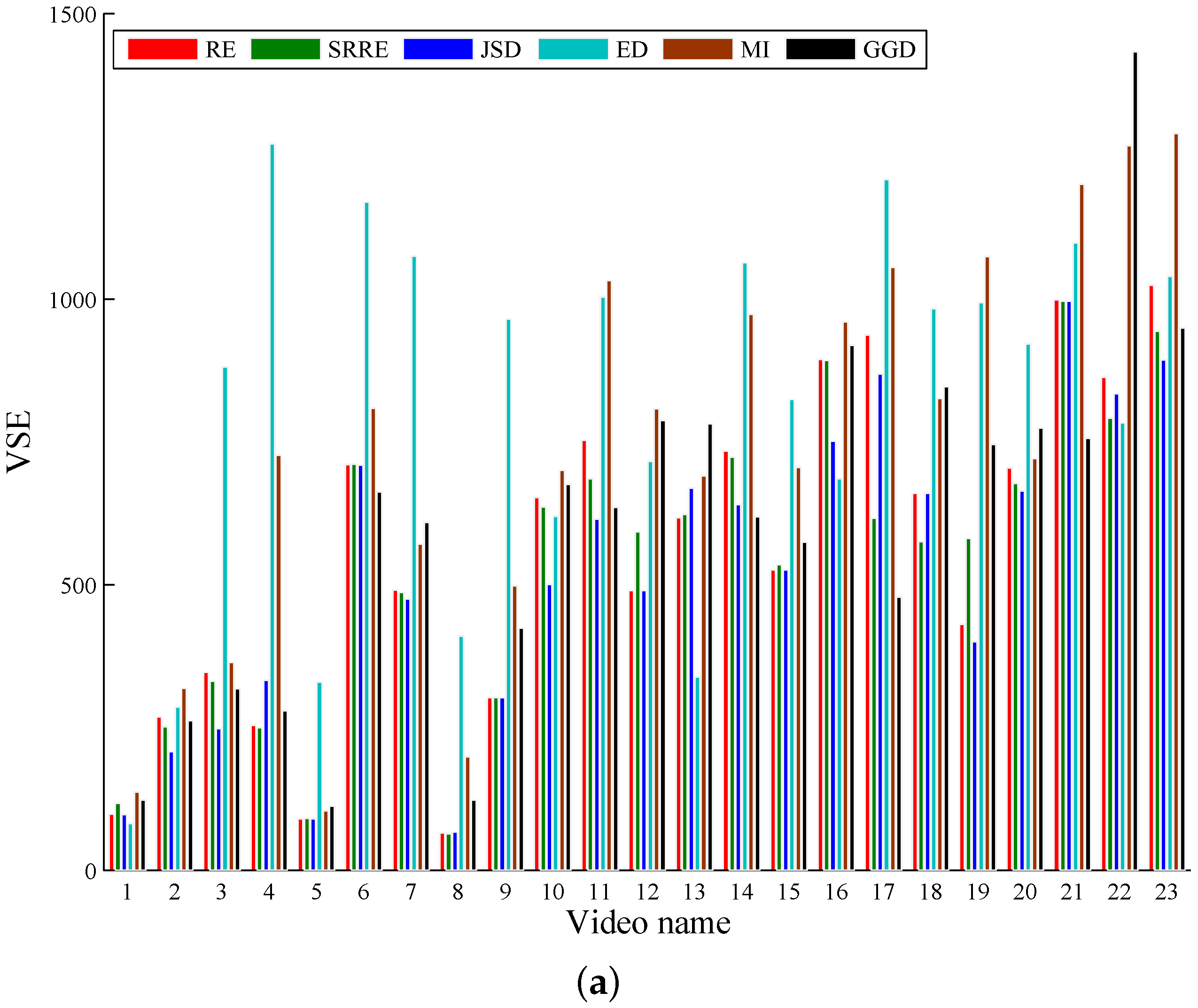
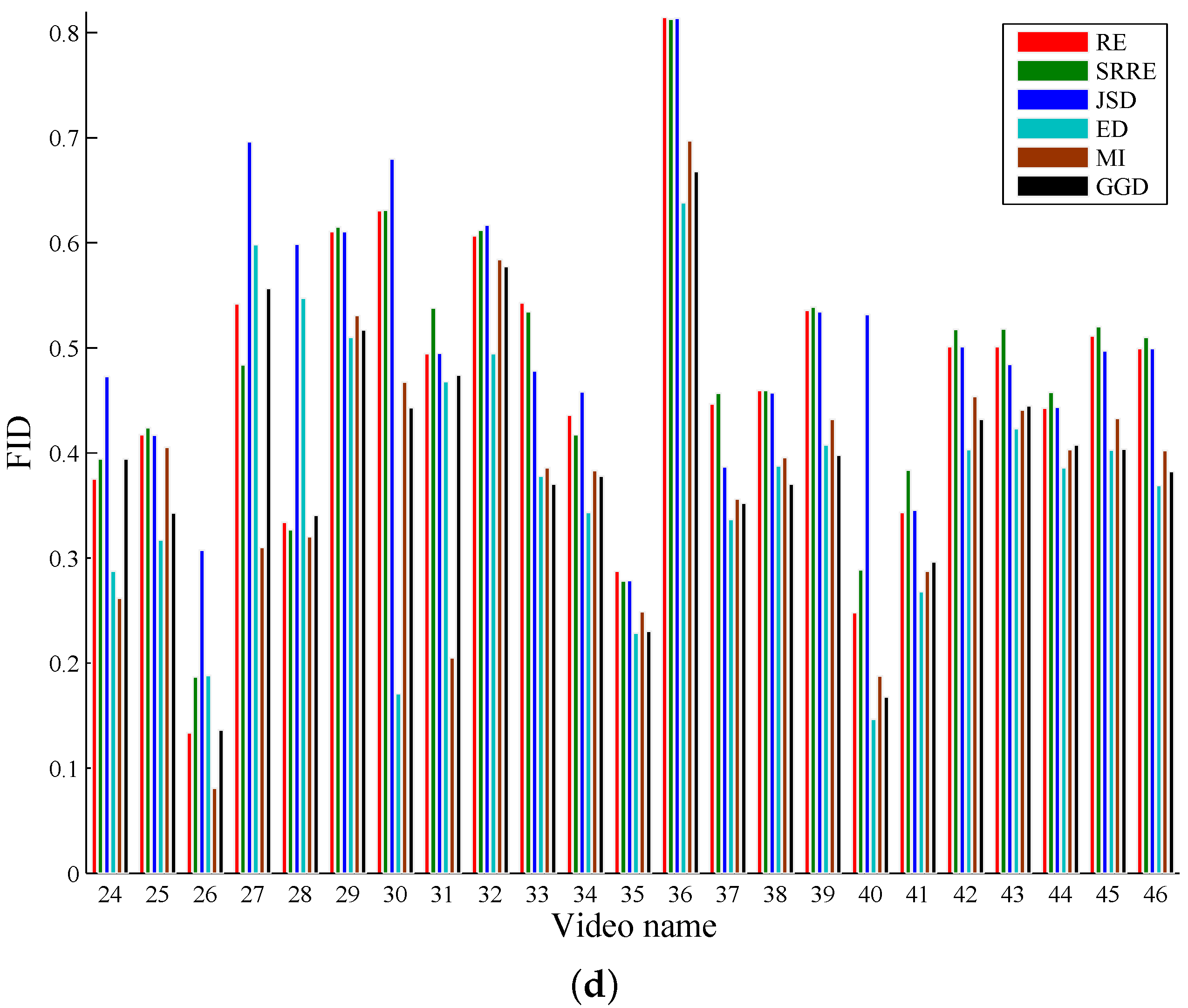
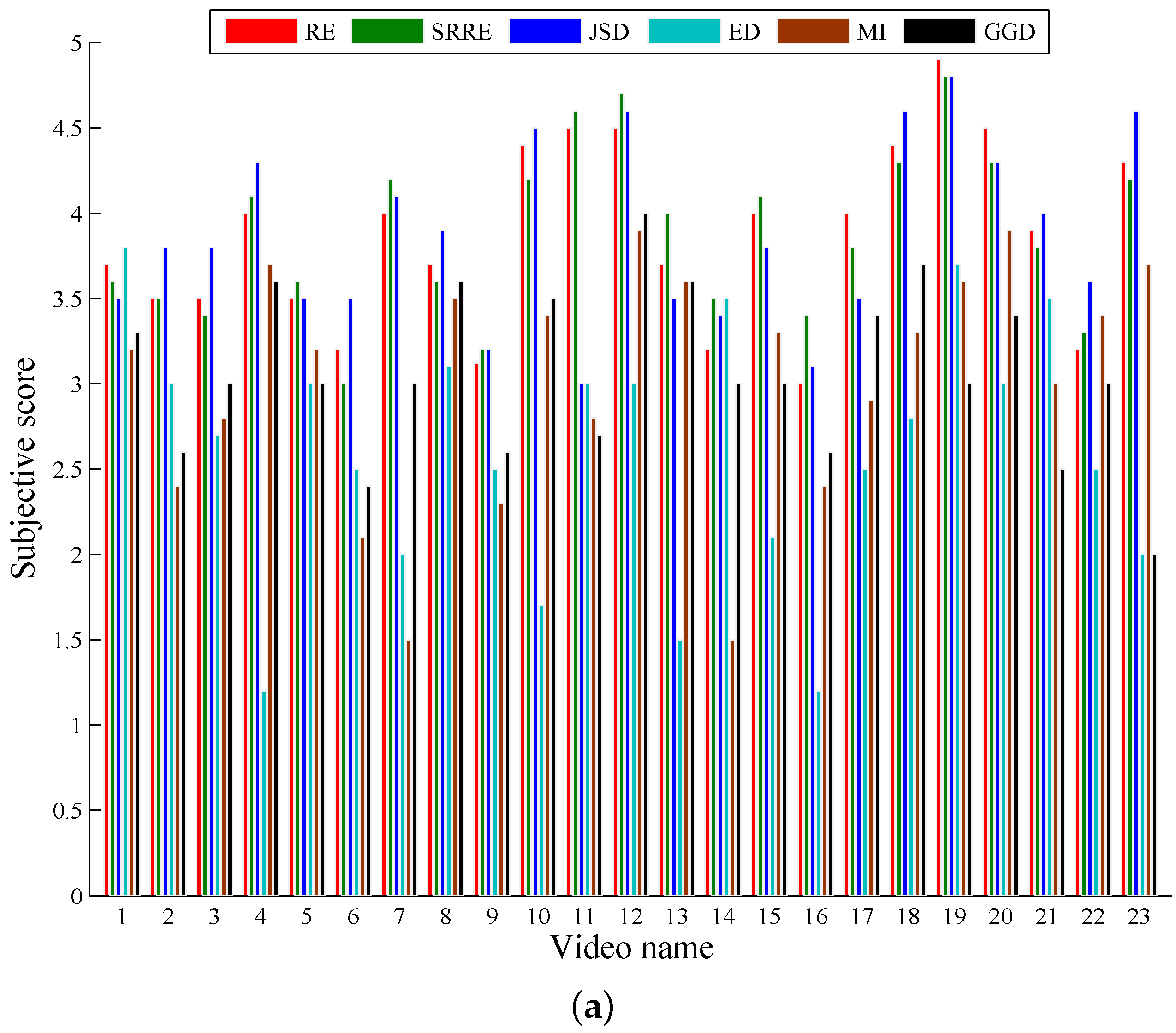
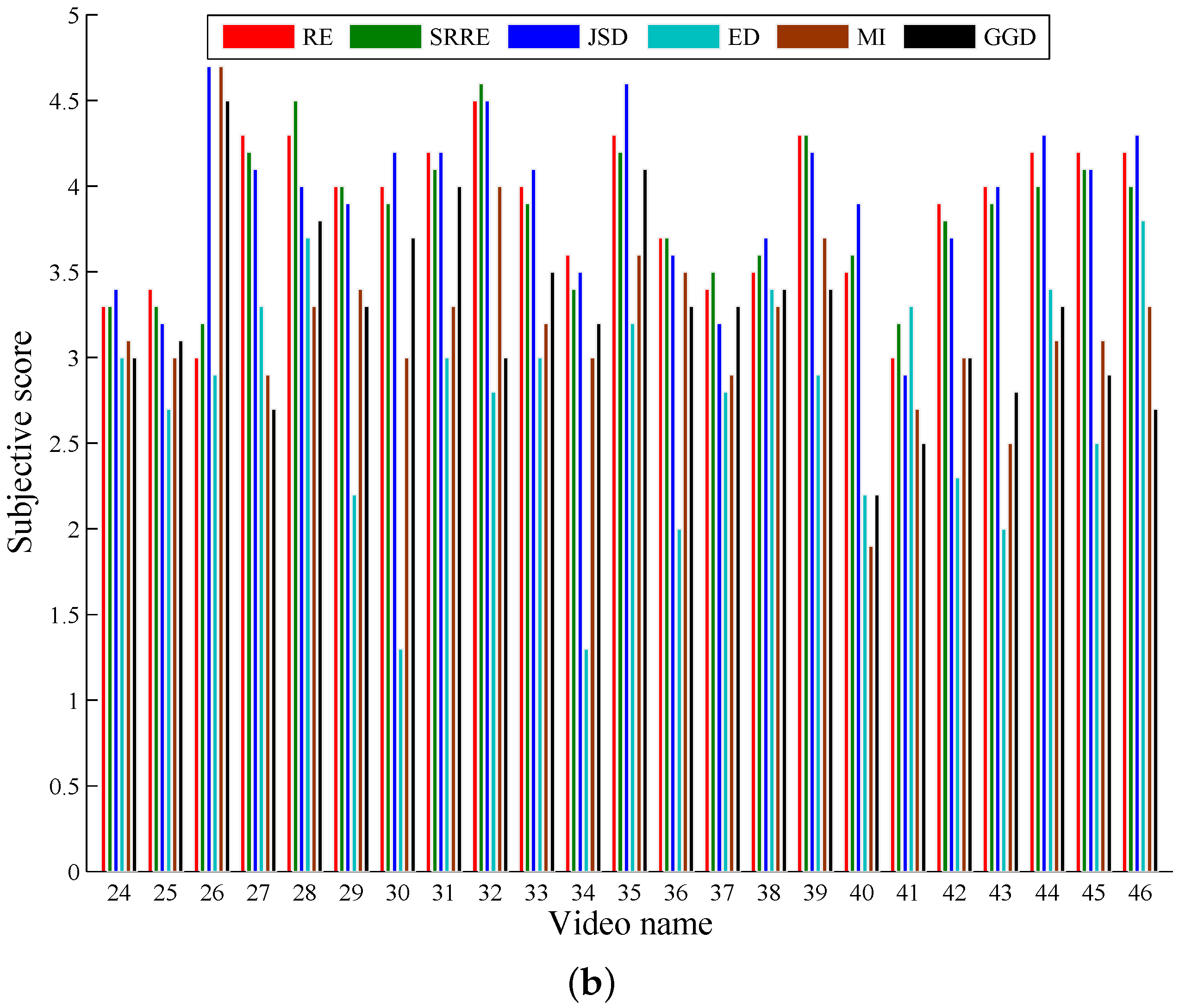
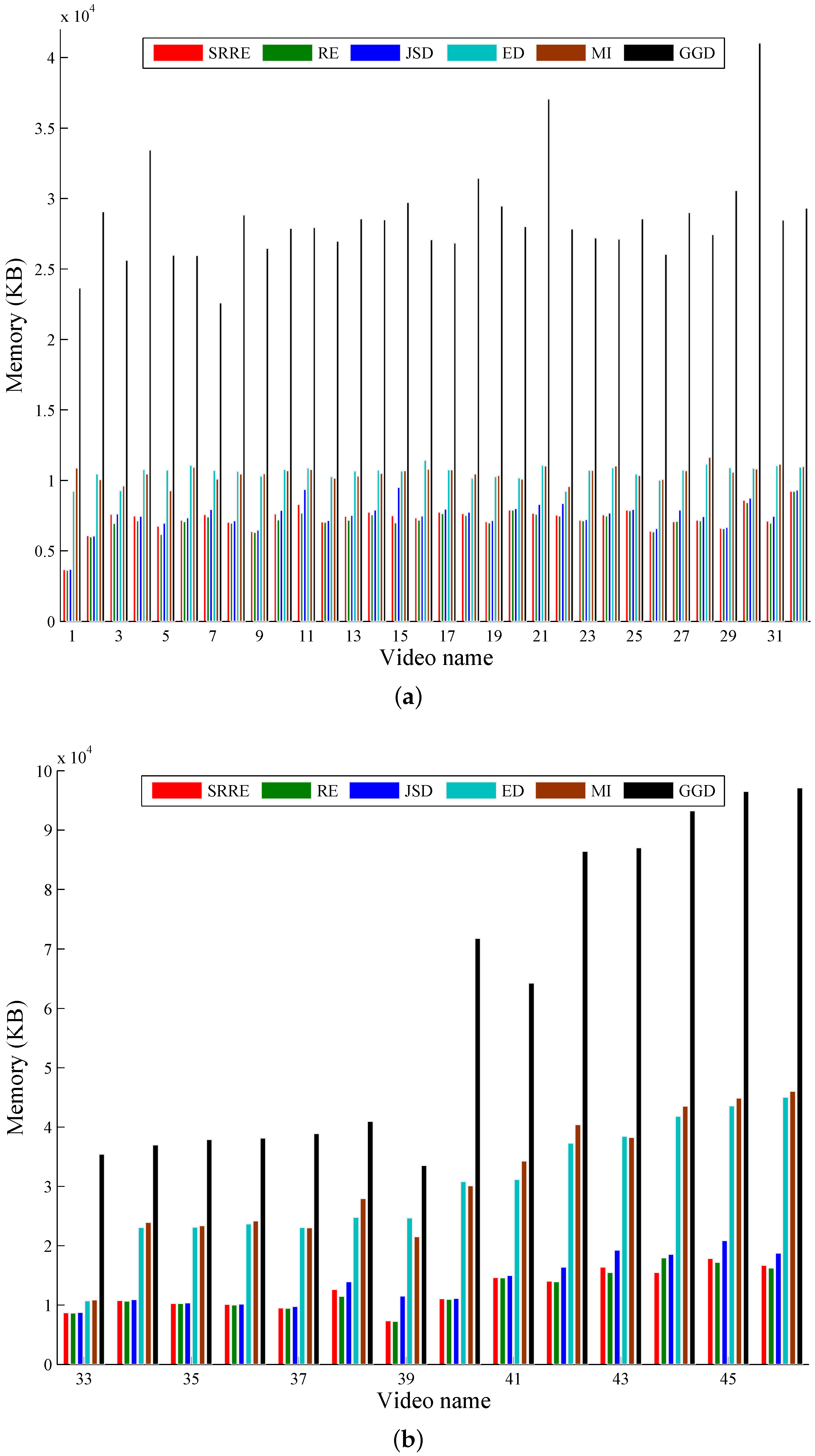
5.1. A Performance Comparison Based on Common Test Videos
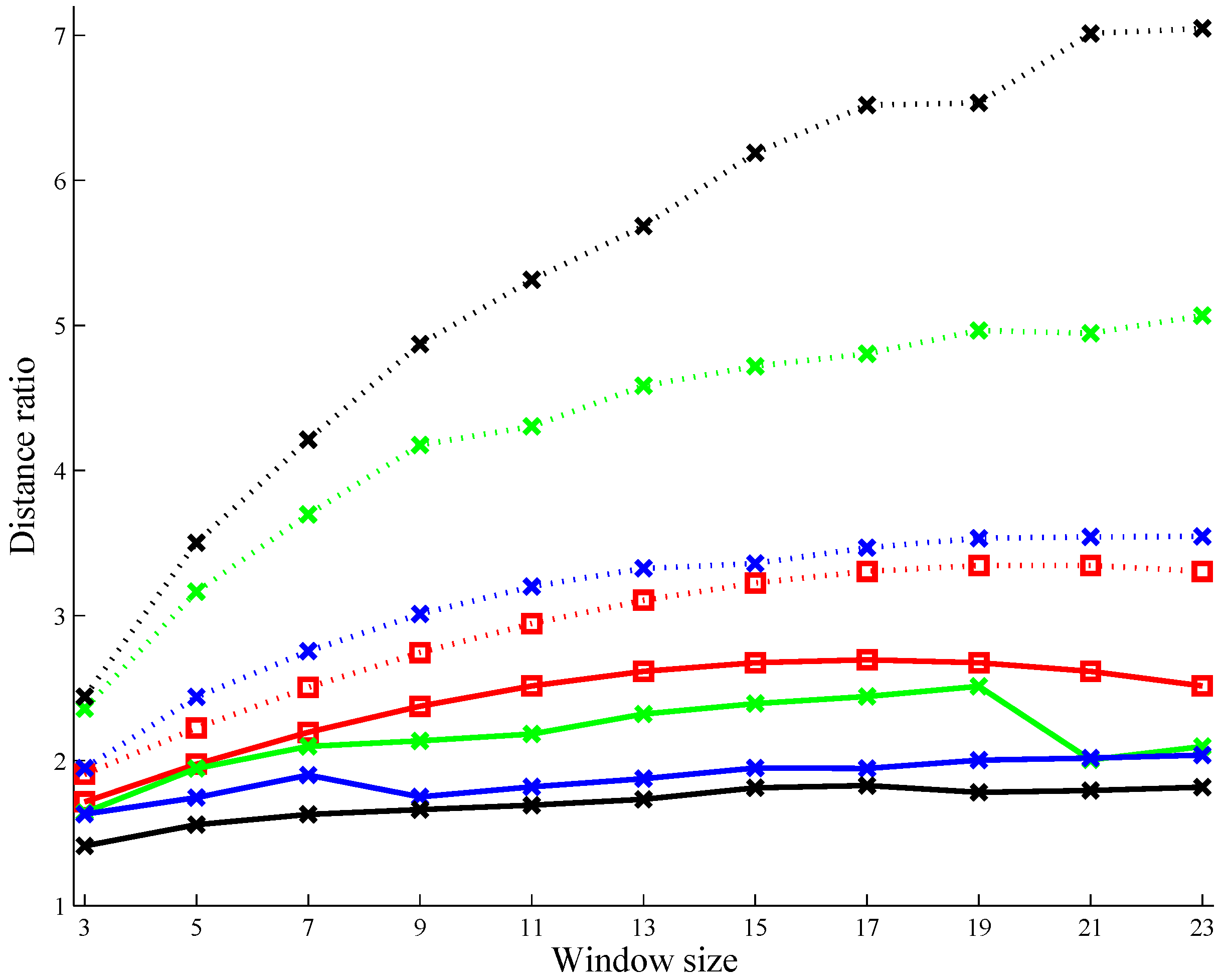
5.2. A Performance Analysis on the Use of the Square Root Function
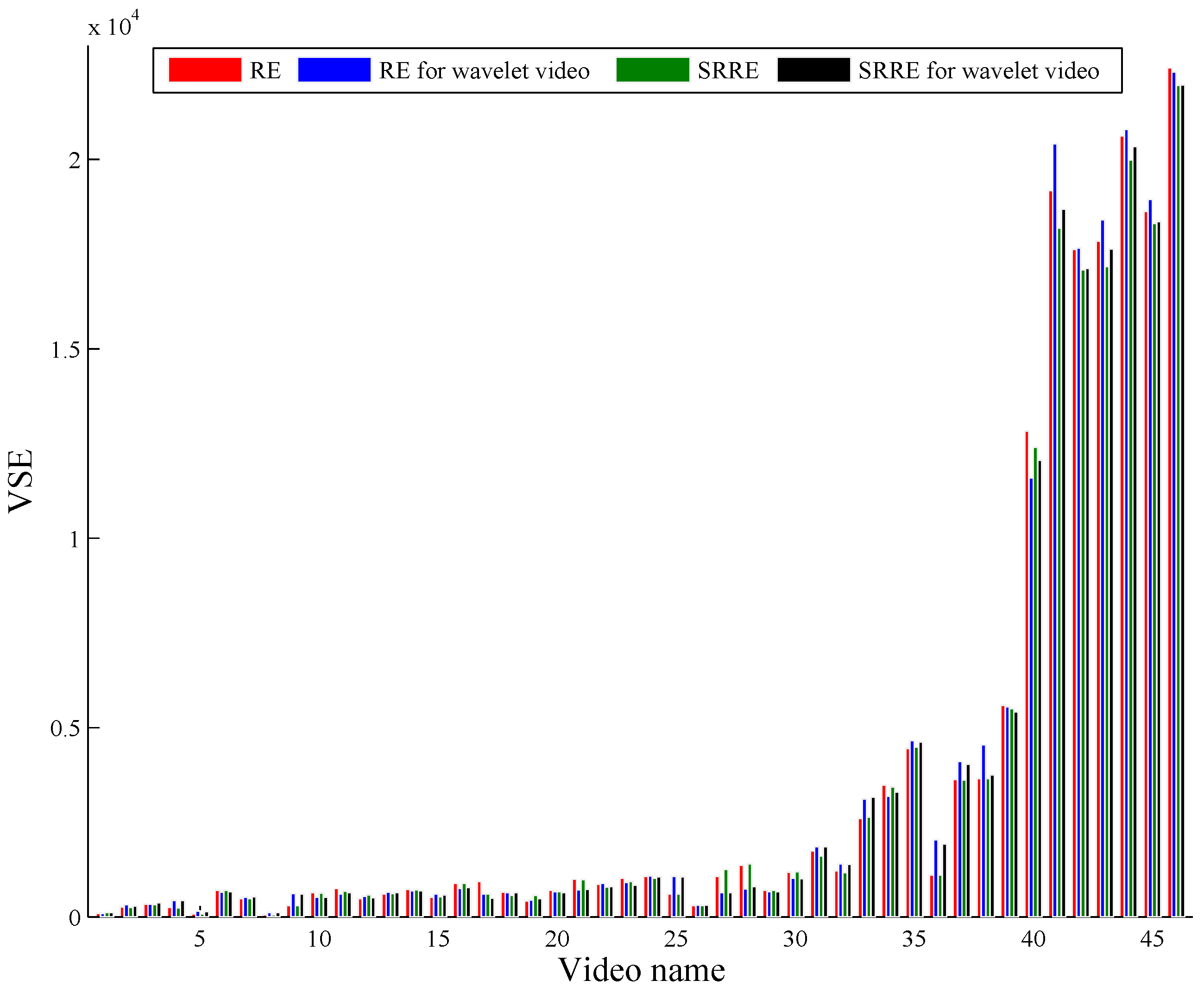
5.3. A Discussion on Dealing with Wavelet Video by RE and SRRE
6. Conclusion and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Comparison of Video Hosting Services. Available online: http://en.wikipedia.org/wiki/comparison_of_video_hosting_services (accessed on 8 January 2016).
- Barnes, C.; Goldman, D.B.; Shechtman, E.; Finkelstein, A. Video tapestries with continuous temporal zoom. ACM Trans. Graph. 2010. [Google Scholar] [CrossRef]
- Assa, J.; Caspi, Y.; Cohen-Or, D. Action synopsis: Pose selection and illustration. ACM Trans. Graph. 2005, 24, 667–676. [Google Scholar] [CrossRef]
- Schoeffmann, K.; Hudelist, M.A.; Huber, J. Video interaction tools: A survey of recent work. ACM Comput. Surv. 2015. [Google Scholar] [CrossRef]
- Truong, B.T.; Venkatesh, S. Video abstraction: A systematic review and classification. ACM Trans. Multimed. Comput. Commun. Appl. 2007. [Google Scholar] [CrossRef]
- Money, A.G.; Agius, H. Video summarisation: A conceptual framework and survey of the state of the art. J. Vis. Commun. Image Represent. 2008, 19, 121–143. [Google Scholar] [CrossRef]
- Ouellet, J.N.; Randrianarisoa, V. To watch or not to watch: Video summarization with explicit duplicate elimination. In Proceedings of the 2011 Canadian Conference on Computer and Robot Vision, St. John’s, NL, Canada, 25–27 May 2011; pp. 340–346.
- Souza, C.L.; Pádua, F.L.C.; Nunes, C.F.G.; Assis, G.T.; Silva, G.D. A unified approach to content-based indexing and retrieval of digital videos from television archives. Artif. Intell. Res. 2014, 3, 49–61. [Google Scholar] [CrossRef]
- Escolano, F.; Suau, P.; Bonev, B. Information Theory in Computer Vision and Pattern Recognition; Springer: London, UK, 2009. [Google Scholar]
- Feixas, M.; Bardera, A.; Rigau, J.; Xu, Q.; Sbert, M. Information Theory Tools for Image Processing; Morgan & Claypool: San Rafael, CA, USA, 2014. [Google Scholar]
- Mentzelopoulos, M.; Psarrou, A. Key-frame extraction algorithm using entropy difference. In Proceedings of the 6th ACM SIGMM International Workshop on Multimedia Information Retrieval, New York, NY, USA, 15–16 October 2004; ACM: New York, NY, USA, 2004; pp. 39–45. [Google Scholar]
- C̆erneková, Z.; Pitas, I.; Nikou, C. Information theory-based shot cut/fade detection and video summarization. IEEE Trans. Circuits Syst. Video Technol. 2006, 16, 82–91. [Google Scholar] [CrossRef]
- Omidyeganeh, M.; Ghaemmaghami, S.; Shirmohammadi, S. Video keyframe analysis using a segment-based statistical metric in a visually sensitive parametric space. IEEE Trans. Image Process. 2011, 20, 2730–2737. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Liu, Y.; Li, X.; Yang, Z.; Wang, J.; Sbert, M.; Scopigno, R. Browsing and exploration of video sequences: A new scheme for key frame extraction and 3D visualization using entropy based Jensen divergence. Inf. Sci. 2014, 278, 736–756. [Google Scholar] [CrossRef]
- Chen, W.; Chang, S.F. Motion trajectory matching of video objects. Proc. SPIE 1999. [Google Scholar] [CrossRef]
- Li, L.; Xu, Q.; Luo, X.; Sun, S. Key frame selection based on KL-divergence. In Proceedings of the 2015 IEEE International Conference on Multimedia Big Data, Beijing, China, 20–22 April 2015; pp. 337–341.
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Rosner, B. On the detection of many outliers. Technometrics 1975, 17, 221–227. [Google Scholar] [CrossRef]
- Lienhart, R.; Pfeiffer, S.; Effelsberg, W. Video abstracting. Commun. ACM 1997, 40, 54–62. [Google Scholar] [CrossRef]
- Cotsaces, C.; Nikolaidis, N.; Pitas, I. Video shot detection and condensed representation: A review. IEEE Signal Process. Mag. 2006, 23, 28–37. [Google Scholar] [CrossRef]
- Vila, M.; Bardera, A.; Feixas, M.; Sbert, M. Tsallis mutual information for document classification. Entropy 2011, 13, 1694–1707. [Google Scholar] [CrossRef]
- Li, Y.; Lee, S.H.; Yeh, C.H.; Kuo, C.J. Techniques for movie content analysis and skimming: Tutorial and overview on video abstraction techniques. IEEE Signal Process. Mag. 2006, 23, 79–89. [Google Scholar]
- Liang, K.C.; Kuo, C.J. Retrival and progressive transmission of wavelet compressed images. In Proceedings of the 1997 IEEE International Symposium on Circuits and Systems, Hong Kong, China, 9–12 June 1997; Volume 2, pp. 1467–1467.
- Johnson, D.H. Information Theory and Neural Information Processing. IEEE Trans. Inf. Theory 2010, 56, 653–666. [Google Scholar] [CrossRef]
- Johnson, D.H.; Gruner, C.M.; Baggerly, K.; Seshagiri, C. Information-theoretic analysis of neural coding. J. Comput. Neurosci. 2001, 10, 47–69. [Google Scholar] [CrossRef] [PubMed]
- Lin, J. Divergence Measures Based on the Shannon Entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Yang, Y.; Barron, A. Information theoretic determination of minimax rates of convergence. Ann. Stat. 1999, 27, 1546–1599. [Google Scholar]
- Hanjalic, A. Shot-boundary detection: Unraveled and resolved? IEEE Trans. Circuits Syst. Video Technol. 2002, 12, 90–105. [Google Scholar] [CrossRef]
- Grubbs, F.E. Sample Criteria for Testing Outlying Observations. Ann. Math. Stat. 1950, 21, 27–58. [Google Scholar] [CrossRef]
- Verma, S.P.; Quiroz-Ruiz, A. Critical values for six Dixon tests for outliers in normal samples up to sizes 100, and applications in science and engineering. Rev. Mex. Cienc. Geol. 2006, 23, 133–161. [Google Scholar]
- Stigler, S.M. Gergonne’s 1815 paper on the design and analysis of polynomial regression experiments. Hist. Math. 1974, 1, 431–439. [Google Scholar] [CrossRef]
- Yeo, B.L.; Liu, B. Rapid Scene Analysis on Compressed Video. IEEE Trans. Circuits Syst. Video Technol. 1995, 5, 533–544. [Google Scholar]
- Koprinska, I.; Carrato, S. Video segmentation of MPEG compressed data. In Proceedings of the IEEE International Conference on Electronics, Circuits and Systems, Lisboa, Portugal, 7–10 September 1998; Volume 2, pp. 243–246.
- Hürst, W.; Hoet, M. Sliders versus storyboards—Investigating interaction design for mobile video browsing. In MultiMedia Modeling; Springer International Publishing: Cham, Switzerland, 2015; Volume 8936, pp. 123–134. [Google Scholar]
- Starch, D. A demonstration of the trial and error method of learning. Psychol. Bull. 1910, 7, 20–23. [Google Scholar] [CrossRef]
- Open-Video. Available online: http://www.open-video.org/index.php (accessed on 10 October 2012).
- Liu, T.; Kender, J.R. Computational Approaches to Temporal Sampling of Video Sequences. ACM Trans. Multimed. Comput. Commun. Appl. 2007, 3, 217–218. [Google Scholar] [CrossRef]
- Chang, H.S.; Sull, S.; Lee, S.U. Efficient video indexing scheme for content-based retrieval. IEEE Trans. Circuits Syst. Video Technol. 1999, 9, 1269–1279. [Google Scholar] [CrossRef]
- Gianluigi, C.; Raimondo, S. An innovative algorithm for key frame extraction in video summarization. J. Real-Time Image Process. 2006, 1, 69–88. [Google Scholar] [CrossRef]
- Stricker, M.A.; Orengo, M. Similarity of color images. In Proceedings of the IS&T/SPIE’s Symposium on Electronic Imaging: Science & Technology; International Society for Optics and Photonics, San Jose, CA, 27 January–2 February 1996; Volume 2420, pp. 381–392.
- Gangeh, M.J.; Sadeghi-Naini, A.; Diu, M.; Tadayyon, H.; Kamel, M.S.; Czarnota, G.J. Categorizing Extent of Tumour Cell Death Response to Cancer Therapy Using Quantitative Ultrasound Spectroscopy and Maximum Mean Discrepancy. IEEE Trans. Med. Imaging 2014, 33, 1390–1400. [Google Scholar] [CrossRef] [PubMed]
- Geusebroek, J.M.; van den Boomgaard, R.; Smeulders, A.W.M.; Dev, A. Color and scale: The spatial structure of color images. In Computer Vision-ECCV 2000; Springer: Berlin, Germany, 2000; Volume 1842, pp. 331–341. [Google Scholar]
- May, R.; Hanrahan, P.; Keim, D.A.; Shneiderman, B.; Card, S. The state of visual analytics: Views on what visual analytics is and where it is going. In Proceedings of the 2010 IEEE Symposium on Visual Analytics Science and Technology (VAST), Salt Lake City, UT, USA, 25–26 October 2010; pp. 257–259.











| No. | Length(s) | Frame Amount | Resolution | No. | Length(s) | Frame Amount | Resolution |
|---|---|---|---|---|---|---|---|
| 1 | 8 | 192 | 240 × 180 | 24 | 55 | 1673 | 352 × 240 |
| 2 | 16 | 502 | 320 × 240 | 25 | 58 | 1052 | 320 × 240 |
| 3 | 24 | 720 | 352 × 240 | 26 | 58 | 871 | 176 × 144 |
| 4 | 28 | 850 | 352 × 240 | 27 | 59 | 1798 | 320 × 240 |
| 5 | 29 | 436 | 320 × 240 | 28 | 59 | 1796 | 320 × 240 |
| 6 | 30 | 913 | 320 × 240 | 29 | 60 | 1181 | 368 × 480 |
| 7 | 30 | 751 | 320 × 240 | 30 | 87 | 2308 | 352 × 240 |
| 8 | 30 | 738 | 320 × 240 | 31 | 97 | 2917 | 352 × 240 |
| 9 | 30 | 901 | 368 × 480 | 32 | 120 | 2881 | 176 × 144 |
| 10 | 31 | 930 | 352 × 240 | 33 | 155 | 4650 | 352 × 240 |
| 11 | 35 | 1049 | 352 × 240 | 34 | 189 | 5688 | 352 × 264 |
| 12 | 35 | 1056 | 352 × 240 | 35 | 195 | 5856 | 352 × 264 |
| 13 | 36 | 1097 | 352 × 240 | 36 | 196 | 5878 | 352 × 264 |
| 14 | 36 | 1097 | 320 × 240 | 37 | 199 | 5991 | 352 × 240 |
| 15 | 39 | 1186 | 352 × 240 | 38 | 213 | 6388 | 352 × 264 |
| 16 | 39 | 1169 | 320 × 240 | 39 | 380 | 11388 | 352 × 264 |
| 17 | 39 | 1169 | 352 × 240 | 40 | 513 | 15400 | 320 × 240 |
| 18 | 39 | 1186 | 352 × 240 | 41 | 871 | 26114 | 352 × 240 |
| 19 | 41 | 1237 | 368 × 480 | 42 | 1419 | 34027 | 512 × 384 |
| 20 | 42 | 1288 | 352 × 264 | 43 | 1431 | 34311 | 512 × 384 |
| 21 | 48 | 1460 | 320 × 240 | 44 | 1479 | 35461 | 512 × 384 |
| 22 | 49 | 1491 | 352 × 240 | 45 | 1520 | 36504 | 512 × 384 |
| 23 | 50 | 1097 | 320 × 240 | 46 | 1778 | 42635 | 512 × 384 |
| RE | SRRE | JSD | ED | MI | GGD | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FID | VSE | FID | VSE | FID | VSE | FID | VSE | FID | VSE | FID | VSE | |
| Avg | 0.4838 | 3824.8 | 0.4958 | 3724.7 | 0.5145 | 3719.6 | 0.3754 | 4998.3 | 0.3748 | 4421.9 | 0.4311 | 4643.8 |
| SE | 0.0204 | 953.4882 | 0.0198 | 923.6689 | 0.0181 | 950.707 | 0.0197 | 1188.3 | 0.0196 | 1074.3 | 0.0194 | 1192.1 |
| RE | SRRE | JSD | ED | MI | GGD | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg | SE | Avg | SE | Avg | SE | Avg | SE | Avg | SE | Avg | SE | |
| Score | 3.8591 | 0.0713 | 3.8587 | 0.0658 | 3.8957 | 0.0726 | 2.6696 | 0.1046 | 3.1065 | 0.0917 | 3.1565 | 0.0761 |
| RE | SRRE | JSD | ED | MI | GGD | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg | SE | Avg | SE | Avg | SE | vg | SE | Avg | SE | Avg | SE | |
| Runtime | 56.3199 | 17.6052 | 57.8966 | 17.9796 | 63.6442 | 18.7679 | 787.1878 | 237.6665 | 838.5448 | 251.6437 | 103.8613 | 30.0365 |
| Memory | 8742.7 | 466.8184 | 8891.6 | 460.2758 | 9513.3 | 562.7364 | 16,513 | 1556.3 | 16718 | 1630.3 | 38,529 | 3094.1 |
| RE | RE for Wavelet Video | SRRE | SRRE for Wavelet Video | |||||
|---|---|---|---|---|---|---|---|---|
| FID | VSE | FID | VSE | FID | VSE | FID | VSE | |
| Avg | 0.4838 | 3824.8 | 0.491 | 3889.1 | 0.4958 | 3724.7 | 0.4973 | 3775.4 |
| SE | 0.0204 | 953.4882 | 0.0174 | 965.125 | 0.0198 | 923.6689 | 0.0175 | 932.663 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Xu, Q.; Sun, S.; Luo, X.; Sbert, M. Selecting Video Key Frames Based on Relative Entropy and the Extreme Studentized Deviate Test. Entropy 2016, 18, 73. https://doi.org/10.3390/e18030073
Guo Y, Xu Q, Sun S, Luo X, Sbert M. Selecting Video Key Frames Based on Relative Entropy and the Extreme Studentized Deviate Test. Entropy. 2016; 18(3):73. https://doi.org/10.3390/e18030073
Chicago/Turabian StyleGuo, Yuejun, Qing Xu, Shihua Sun, Xiaoxiao Luo, and Mateu Sbert. 2016. "Selecting Video Key Frames Based on Relative Entropy and the Extreme Studentized Deviate Test" Entropy 18, no. 3: 73. https://doi.org/10.3390/e18030073
APA StyleGuo, Y., Xu, Q., Sun, S., Luo, X., & Sbert, M. (2016). Selecting Video Key Frames Based on Relative Entropy and the Extreme Studentized Deviate Test. Entropy, 18(3), 73. https://doi.org/10.3390/e18030073






