Angular Spectral Density and Information Entropy for Eddy Current Distribution

Abstract

Here, a new method is proposed to quantitatively evaluate the eddy current distribution induced by different exciting coils of an eddy current probe. Probability of energy allocation of a vector field is modeled via conservation of energy and imitating the wave function in quantum mechanics. The idea of quantization and the principle of circuit sampling is utilized to discretize the space of the vector field. Then, a method to calculate angular spectral density and Shannon information entropy is proposed. Eddy current induced by three different exciting coils is evaluated with this method, and the specific nature of eddy current testing is discussed.

1. Introduction

Improving the performance of eddy current (EC) non-destructive testing (NDT) systems is important for enhancing the accuracy of such measurement devices, and the innovation in EC probes is one of the most important ways to achieve this goal. An EC probe is mainly composed of exciting coils and a pick-up element, and carries a non-uniform current that induces the eddy current in conductive materials. Depending on applications, different pick-up elements, coils, and sensors such as Superconducting Quantum Interference Device (SQUID), Hall, Anisotropic Magnetoresistance (AMR), Giant Magneto-impedance (GMI), Giant Magnetoresistance (GMR) [1,2,3,4,5,6], and Tunnel MagnetoResistance (TMR) [7] are used.

However, depending on the goal, many publications propose the use of different waveforms of exciting current. The conventional EC testing method is based on the single-frequency current exciting waveform and is used in many fields, such as defect detection and stress measurement. Multi-frequency EC testing [8] was proposed to detect defects in different depths, and pulse current exciting current [9] was proposed to enrich the frequency component. Chirp excitation [10], whose frequency changes with time, was used for frequency sweep. In short, the innovations in exciting current waveforms only improved the eddy current distribution over time at a certain position. However, the sensitivity of an EC probe depends on the relationship between the EC direction and the defect direction, so different exciting coils were proposed to improve the eddy current distribution, such as the meandering magnetometer (MWM) [11,12], rosette-like [13], fractal Koch curve [14,15], and rectangular exciting coil. Moreover, a rotating field EC planar probe [2,4,6] was proposed to generate an eddy current that can automatically rotate in the time domain. Thus, eddy current direction both in time and in space domains is of vital importance to a probe’s sensitivity.

To improve the performance of an EC probe, optimizing the eddy current distribution induced by the EC probe is a promising approach. However, the eddy current distribution can only be observed by the eyes and there is no appropriate index to be considered as an objective function. Shannon information entropy measures the uniformity of the distribution of information distribution. In 2016, Zhang et al. [16] first used the Shannon information entropy to evaluate eddy current in a plane distributed in different directions. To improve this method, a theoretical approach is proposed in this paper.

In general, probability density of energy allocation of a multidimensional vector in multidimensional space is modeled via the conservation of energy. Probability density discretization is described in Section 2 and Section 3, describing the discretization method for space utilizing the idea of quantization and sampling from circuit principle. Moreover, in Section 4, the method is applied to EC distribution evaluation, and an angular spectral method is proposed. Section 5 presents the method to calculate information entropy. Section 6 briefly describes the method of eddy current acquisition. In Section 7, the main results are presented and analyzed. Conclusions and future studies are addressed in the last section.

2. Energy of Field Distribution Density of a Multidimensional Vector in a Multidimensional Space

Without loss of generality, a multidimensional vector in a multidimensional space is investigated in this section. In general, a vector field includes two kinds of information: position vector and field vector. Assuming $\mathrm{\Omega }$ is an m-dimensional space (i.e., the position vector space), vector $\mathit{x}=\left(x_1,x_2,\cdots ,x_i,\cdots ,x_m\right)$ in $\mathrm{\Omega }$ represents a point in $\mathrm{\Omega }$ and is in a position of the position vector space. Similarly, assuming $\mathrm{\Gamma }$ is n-dimensional space (i.e., the field vector space) the vector $\mathit{X}=\left(X_1,X_2,\cdots ,X_k,\cdots ,X_n\right)$ in $\mathrm{\Gamma }$ represents a field vector in $\mathrm{\Gamma }$ in one position vector. In the position vector space $\mathrm{\Omega }$, if m = 0, $\mathrm{\Omega }$ is a 0-dimensional space, like a point; if m = 2 or 3, $\mathrm{\Omega }$ is a 2-dimensional planar space and a 3-dimensional cubic space; if m = 4, $\mathrm{\Omega }$ is a time–space. In the field vector space $\mathrm{\Gamma }$, if n = 1, $\mathit{X}$ is a scalar vector; if n = 2, $\mathit{X}$ is a 2-dimensional vector, like the EC vector $\left({\mathit{J}}_{\mathit{x}},{\mathit{J}}_{\mathit{y}}\right)$ studied in this paper; if n = 3, $\mathit{X}$ is a 3-dimensional electric field, magnetic field or a gradient field for temperature field. Different kinds of fields are distributed in different ways, such as a uniform field and a radial field, among others, so the different field distribution may carry different amounts of information.

Assume the function $F\left(\mathit{x},\mathit{X}\right)$ about position vector $\mathit{x}$ and field vector $\mathit{X}$, $F\left(\mathit{x},\mathit{X}\right)$ has the following property

$$F^2\left(\mathit{x},\mathit{X}\right)\ge 0$$

(1)

where $F^2\left(\mathit{x},\mathit{X}\right)$ is the energy allocation at position $\mathit{x}$ when the field vector is $\mathit{X}$. For example, in a 2-dimensional EC vector field

$$\mathit{J}\left(x,y\right)=\left(J_x\left(x,y\right),J_y\left(x,y\right)\right)$$

(2)

$J^2=J_x^2+J_y^2$ is the energy allocation of EC at position $\left(x,y\right)$, where the EC vector is $\left(J_x,J_y\right)$.

For Equation (1), the total energy of a field in the whole position vector space and the field vector space is

$$E_{total}={\displaystyle ∯}{F}^2\left(\mathit{x},\mathit{X}\right)d\mathrm{\Omega }d\mathrm{\Gamma }$$

(3)

here $d\mathrm{\Omega }$ is the infinitesimal position vector space and $d\mathrm{\Gamma }$ is the infinitesimal field vector space. Dividing both sides of Equation (3) gives

$$\frac{∯F^2\left(\mathit{x},\mathit{X}\right)d\mathrm{\Omega }d\mathrm{\Gamma }}{E_{total}}={\displaystyle ∯}\frac{F^2\left(\mathit{x},\mathit{X}\right)}{E_{total}}d\mathrm{\Omega }d\mathrm{\Gamma }=1$$

(4)

Function $f\left(\mathit{x},\mathit{X}\right)$ is defined as

$$f\left(\mathit{x},\mathit{X}\right)=\frac{F^2\left(\mathit{x},\mathit{X}\right)}{E_{total}}$$

(5)

$f\left(\mathit{x},\mathit{X}\right)$ is a percentage of the energy allocation of field at position $\mathit{x}$ where the field vector is $\mathit{X}$. By substituting Equation (5) into Equation (4) one obtains

$${\displaystyle ∯}f\left(\mathit{x},\mathit{X}\right)d\mathrm{\Omega }d\mathrm{\Gamma }=1$$

(6)

According to Equation (1)

$$f\left(\mathit{x},\mathit{X}\right)\ge 0$$

(7)

The aforementioned Equations (6) and (7) represent the normalization condition and the non-negative condition, respectively and $f\left(\mathit{x},\mathit{X}\right)$ is additive. Thus, $f\left(\mathit{x},\mathit{X}\right)$ is defined as a probability density of field energy allocation at position $\mathit{x}$ where the field vector is $\mathit{X}$.

By ignoring information of $\mathit{X}$ and only considering the position of field energy allocation, marginal probability density

$$f\left(\mathit{x}\right)={{\displaystyle \oint }}^{\text{}}{F}^2\left(\mathit{x},\mathit{X}\right)d\Gamma$$

(8)

represents the probability of field energy allocation at position $\mathit{x}$.

Similarly, by ignoring the information of position $\mathit{x}$ and only considering the vector of field energy allocation, marginal probability density

$$f\left(\mathit{X}\right)={{\displaystyle \oint }}^{\text{}}{F}^2\left(\mathit{x},\mathit{X}\right)d\Omega$$

(9)

represents the probability of field energy allocation for anywhere when the field vector is $\mathit{X}$.

Certainly, if the same component of vectors $\mathit{x}$ and $\mathit{X}$ is only considered, $2^{m+n}-2$ types of marginal probability densities exist, each of which has their own obvious physical meaning.

The probability density function in this study is modeled by imitating the wave function of quantum mechanics. In quantum mechanics [17], the wave function $\psi$ obeys the superposition of the principle to explain the phenomenon of interference, diffraction and others; however ${\left|\psi \right|}^2$ is considered as a probability. Similarly, the eddy current distribution vector induced by different coils obeys the superposition principle. For example, $\mathit{J}={\mathit{J}}_{\mathbf{1}}+{\mathit{J}}_{\mathbf{2}}$, ${\mathit{J}}_{\mathbf{1}}$ and ${\mathit{J}}_{\mathbf{2}}$ are eddy current density distributions induced by two different coils, and $\mathit{J}$ is the eventual eddy current distribution. Due to ${\left|\mathit{J}\right|}^2={\left|{\mathit{J}}_{\mathbf{1}}+{\mathit{J}}_{\mathbf{2}}\right|}^2$ and $\left|\mathit{J}\right|\ne \left|{\mathit{J}}_{\mathbf{1}}\right|+\left|{\mathit{J}}_{\mathbf{2}}\right|$, ${\left|\mathit{J}\right|}^2$ is selected to model the probability density function.

3. Probability Density Discretization

To calculate the information entropy of the field, probability density described in Section 1 must be discretized. Borrowing the idea of an analog-to-digital converter (ADC) in circuit principle, the position vector space $\mathrm{\Omega }$ and the field vector space $\mathrm{\Gamma }$ are discretized by equal interval sampling. Thus, the continuous spaces $\mathrm{\Omega }$ and $\mathrm{\Gamma }$ are converted to discretized spaces. The combination of one point in the discretized position vector space and one point in the discretized field vector space is defined as a discrete random variable. All discrete random variables form the probability density of space. Thus, the probability of the discretized random variable is

$$p\left(\mathit{x},\mathit{X}\right)=\frac{F^2\left(\mathit{x},\mathit{X}\right)}{{{\displaystyle \sum }}^{\text{}}{F}^2\left(\mathit{x},\mathit{X}\right)}=\frac{F^2\left(\mathit{x},\mathit{X}\right)}{E_{total}}$$

(10)

here $E_{total}={{\displaystyle \sum }}^{\text{}}{F}^2\left(\mathit{x},\mathit{X}\right)$, $p\left(\mathit{x},\mathit{X}\right)$ is the probability of event ($\mathit{x},\mathit{X}$) and the energy allocation percentage of the field at position $\mathit{x}$ when the field vector is $\mathit{X}$. Similar to Equation (5) in Section 1, $p\left(\mathit{x},\mathit{X}\right)$ is the normalization condition, non-negative and additive.

Similar to Section 1, $p\left(\mathit{x},\mathit{X}\right)$ is a joint probability density function for the m + n dimensional discrete random variable. $p\left(\mathit{x},\mathit{X}\right)$ has $2^{m+n}-2$ types of marginal probability density functions. If the information of field vector $\mathit{X}$ is ignored and the position of field energy allocation is only considered, a marginal probability density of the discrete random variable is given by

$$p\left(\mathit{x}\right)={\displaystyle \sum }_{\Gamma }\frac{F^2\left(\mathit{x},\mathit{X}\right)}{E_{total}}$$

(11)

here, $p\left(\mathit{x}\right)$ is called space spectral density.

Similarly, by ignoring the information of position $\mathit{x}$ and only considering the vector of field energy allocation, a marginal probability density of the discrete random variable is expressed as

$$p\left(\mathit{X}\right)={\displaystyle \sum }_{\Omega }\frac{F^2\left(\mathit{x},\mathit{X}\right)}{E_{total}}$$

(12)

here, $p\left(\mathit{X}\right)$ is called gesture spectral density.

4. Information Entropy of Energy Allocation of a Vector Field

Shannon information entropy is the expected value of self-information of a discrete random variable. In this study, information entropy of energy allocation of a vector field in the whole position vector space and the whole field vector field space is defined as

$$H=-{\displaystyle \sum }_{\begin{array}{c}x\in \Omega \\ X\in \Gamma \end{array}}p\left(\mathit{x},\mathit{X}\right)\log p\left(\mathit{x},\mathit{X}\right)$$

(13)

where $-\log p\left(\mathit{x},\mathit{X}\right)=\log \frac{1}{p\left(\mathit{x},\mathit{X}\right)}$ is the self-information for event $\left(\mathit{x},\mathit{X}\right)$, the base of the logarithmic function is 2 in this study. The physical meaning of $\log \frac{1}{p\left(\mathit{x},\mathit{X}\right)}$ is the following: if the probability of event $\left(\mathit{x},\mathit{X}\right)$ is strong, the event $\left(\mathit{x},\mathit{X}\right)$ is more decided, so the self-information of event $\log \frac{1}{p\left(\mathit{x},\mathit{X}\right)}$ is small, and vice versa; if the probability of event $\left(\mathit{x},\mathit{X}\right)$ equals 1, the event $\left(\mathit{x},\mathit{X}\right)$ is absolutely certain, so its self-information is 0.

If the information entropy in position vector space is only considered, the special entropy is defined as

$$H_{\mathit{x}}=-{\displaystyle \sum }_{\mathit{x}}p\left(\mathit{x}\right)\log p\left(\mathit{x}\right)$$

(14)

Similarly, if the information entropy in the field vector space is only considered, the special entropy is defined as

$$H_{\mathit{X}}=-{\displaystyle \sum }_{\mathit{X}}p\left(\mathit{X}\right)\log p\left(\mathit{X}\right)$$

(15)

Certainly, information entropy of other marginal probability densities can be calculated. For example,

$$H_{\mathit{X}}\left(\mathit{x}\right)=-{\displaystyle \sum }_{\mathit{X}}p\left(\mathit{x},\mathit{X}\right)\log p\left(\mathit{x},\mathit{X}\right)$$

(16)

where $H_{\mathit{X}}\left(\mathit{x}\right)$ is the information entropy of the field vector space $\mathit{X}$ at the particular position $\mathit{x}$.

5. Two-Dimensional EC Vector in a Two-Dimensional Plane

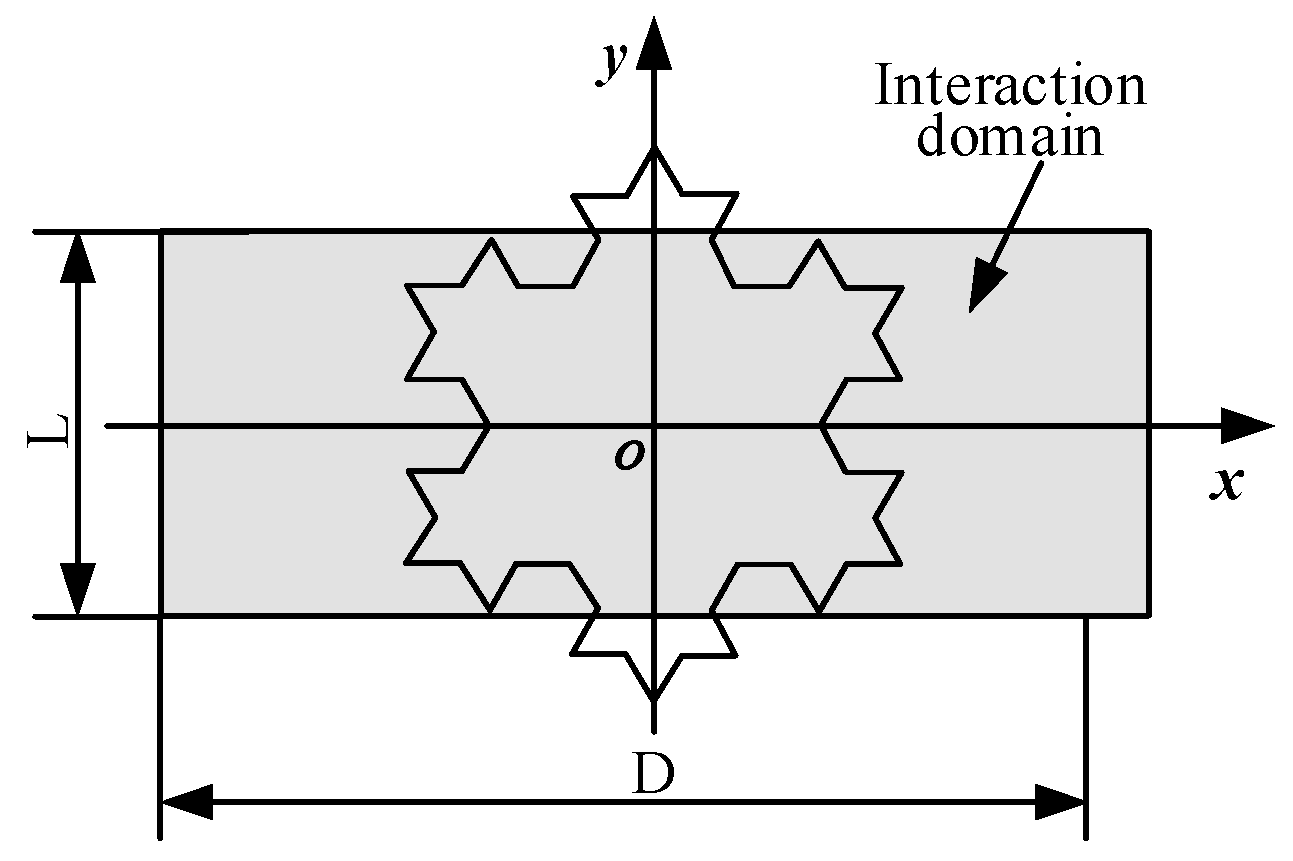
In EC non-destructive testing, the direction of EC vector distribution is very important because it is related to the sensitivity of the probe. In this study, the information entropy of the 2-dimensional EC in a 2-dimensional plane induced by three different exciting coils is calculated and analyzed.

The EC and defect interaction domain is considered as $\left(x,y\right)\in {\mathrm{\Omega }}_1$, the 2D field vector space in Cartesian coordinates is $\left(J_x,J_y\right)\in {\mathrm{\Omega }}_2$, and the 2D field vector space in polar coordinates is $\left(J,\theta \right)\in {\mathrm{\Omega }}_3$.

According to Equation (1), EC energy allocation at $\left(x,y\right)$ where the EC is $\left(J_x,J_y\right)$ is defined as

$$F^2=F^2\left(x,y,J_x,J_y\right)\ge 0$$

(17)

However, EC energy allocation at $\left(x,y\right)$ where the EC in polar coordinates is $\left(J,\theta \right)$ is defined as

$$G^2=G^2\left(x,y,J,\theta \right)\ge 0$$

(18)

According to the law of conservation of energy

$$E_{total}={{\displaystyle \int }}_{{\mathrm{\Omega }}_1}{{\displaystyle \int }}_{{\mathrm{\Omega }}_2}{F}^2\left(x,y,J_x,J_y\right)d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_2={{\displaystyle \int }}_{{\mathrm{\Omega }}_1}{{\displaystyle \int }}_{{\mathrm{\Omega }}_3}{G}^2\left(x,y,J,\theta \right)d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_2$$

(19)

Dividing both sides of Equation (19) by $E_{total}$ results in

$${{\displaystyle \int }}_{{\mathrm{\Omega }}_1}{{\displaystyle \int }}_{{\mathrm{\Omega }}_2}\frac{F^2\left(x,y,J_x,J_y\right)}{E_{total}}d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_2=1$$

(20)

$${{\displaystyle \int }}_{{\mathrm{\Omega }}_1}{{\displaystyle \int }}_{{\mathrm{\Omega }}_3}\frac{G^2\left(x,y,J,\theta \right)}{E_{total}}d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_3=1$$

(21)

Probability density function of the field can be defined as

$$f\left(x,y,J_x,J_y\right)=\frac{F^2\left(x,y,J_x,J_y\right)}{E_{total}}\ge 0$$

(22)

$$g\left(x,y,J,\theta \right)=\frac{G^2\left(x,y,J,\theta \right)}{E_{total}}\ge 0$$

(23)

Equations (22) and (23) express the non-negativity condition of two kinds of the probability density functions $f\left(x,y,J_x,J_y\right)$ and $g\left(x,y,J,\theta \right)$.

According to Equations (17) and (18), $f\left(x,y,J_x,J_y\right)$ and $g\left(x,y,J,\theta \right)$ are complete:

$${{\displaystyle \int }}_{{\mathrm{\Omega }}_1}{{\displaystyle \int }}_{{\mathrm{\Omega }}_2}f\left(x,y,J_x,J_y\right)d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_2=1$$

(24)

$${{\displaystyle \int }}_{{\mathrm{\Omega }}_1}{{\displaystyle \int }}_{{\mathrm{\Omega }}_3}g\left(x,y,J,\theta \right)d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_3=1$$

(25)

In this study, marginal probability densities $g\left(\theta \right)$ and $g\left(x,\theta \right)$ are studied first; $g\left(\theta \right)$ and $g\left(x,\theta \right)$ are defined as angular spectral density and angular spectral density along the x-axis, respectively. $g\left(\theta \right)$ represents the EC’s energy of the whole space allocated in different directions. However, $g\left(x,\theta \right)$ is the energy of EC at position $x$ allocated in different directions. Then, the information entropy $H\left(x\right)$ and $H$ of $g\left(\theta \right)$ and $g\left(x,\theta \right)$ are studied.

6. Acquisition of EC Vector

According to [16], three finite element models were studied and their EC distributions were acquired. The studied exciting coils were a line, a circle, and a second-order Koch curve, respectively, the centers of which were all located in the origin of coordinates and the line was along the y-axis. The eddy current in a hypothetical defect-eddy current interaction domain was sampled at equal intervals. The interaction domain, shown in Figure 1, was a $\mathrm{D}\times \mathrm{L}$ rectangle with axial symmetry along both the x-axis and y-axis. For all cases $D=52\mathrm{mm}$ and the x-axis were sampled with 0.5 mm-long steps. However, different values were chosen to simulate different lengths of defects. In the y direction, EC sampling was of 64 points uniformly distributed within $\mathrm{L}$. Angle and magnitude of eddy current were calculated by

$$\{\begin{array}{c}\theta \left(x,y\right)=arctan\left|\frac{J_y\left(x,y\right)}{J_x\left(x,y\right)}\right|\\ J\left(x,y\right)=\sqrt{J_x{\left(x,y\right)}^2+J_y{\left(x,y\right)}^2}\end{array}$$

(26)

where $J_x\left(x,y\right)$ and $J_y\left(x,y\right)$ are the $x$ component and $y$ component of the EC vector at position $\left(x,y\right)$, respectively; $\theta \left(x,y\right)$ and $J\left(x,y\right)$ are the angle to the x-axis and magnitude of the EC vector at position $\left(x,y\right)$.

7. Results and Discussion

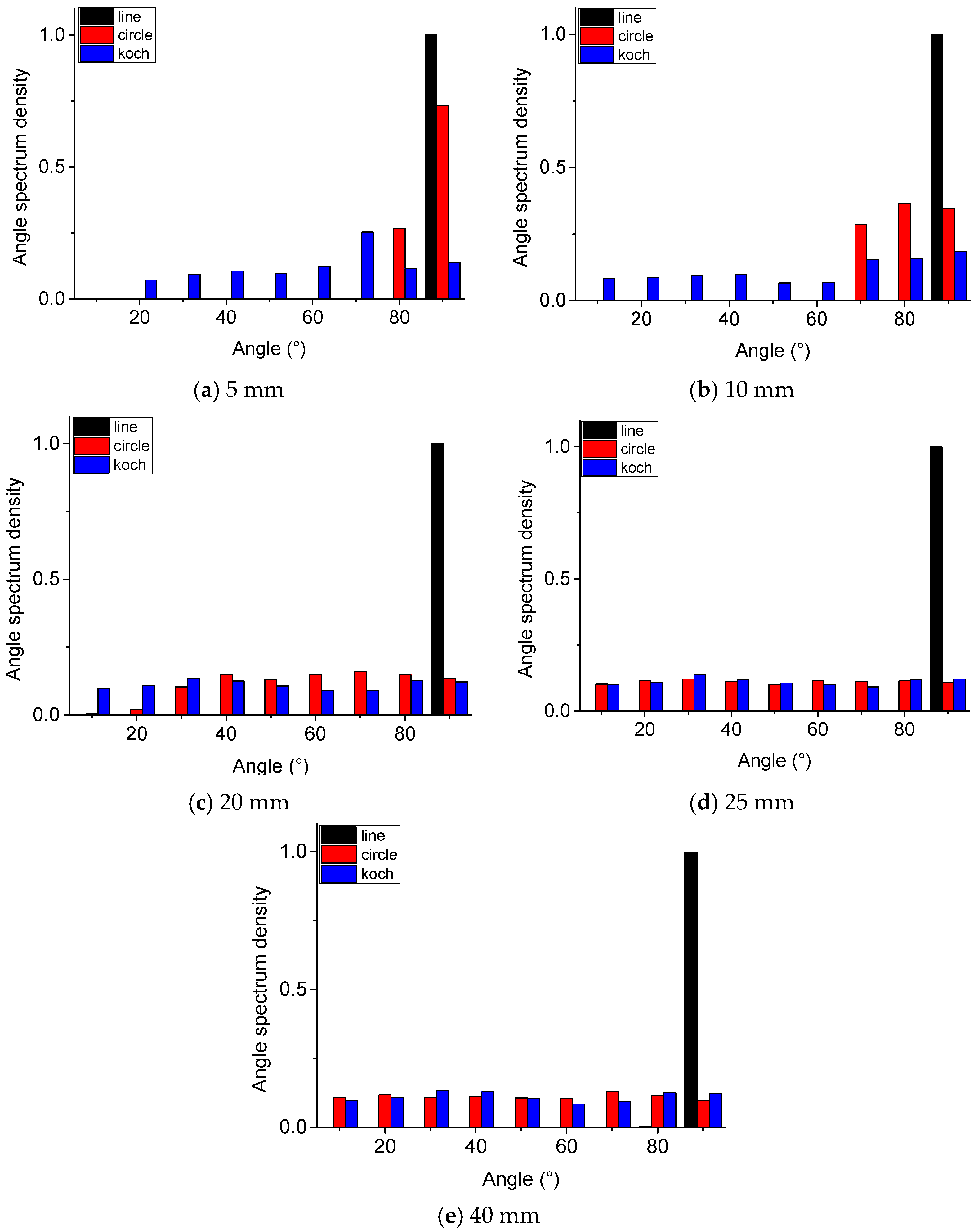
Angular spectral densities along the x-axis of the EC distribution induced by different exciting coils of different widths of the interaction domain are shown in Figure 2. Angular spectral densities $g\left(\theta \right)$ are shown in Figure 3. Information entropy $H\left(x\right)$ and $H$ are shown in Figure 4 and Figure 5, respectively.

7.1. Analysis of Angular Spectral Density along the x-Axis

The exciting coils and the width of the interaction domain influence the analysis of angular spectral density along the x-axis. As detailed in Figure 2a–e, angular spectral densities along the x-axis of the EC induced by a linear inducer in different width interaction domains are centrally concentrated on 90°.

For a circular exciting coil, the distribution of angular spectral density along the x-axis is shown in Figure 2f–j. As the interaction domain width increases, angular spectrum density along the x-axis distributes to different angles. When the width of the interaction is 5 mm, the angular spectral density along the x-axis is only distributed to 90°, but at 25 mm or 40 mm, the eddy current density ranges from 0° to 90° angles. Note that the angular spectrum is concentrated in a narrow angle at a certain x because the EC induced by one winding is distributed on the position underneath the coil.

For the Koch exciting coil, differences in angular spectrum density along the x-axis can be seen in Figure 2k–o: angular spectral density along the x-axis ranges from 0° to 90°, and at a certain value x, it is located in a large angle range. For linear and circular exciting coils, it is distributed on a certain angle at a certain x.

7.2. Angular Spectral Density

As shown in Figure 3, angular spectral density represents the EC distribution in different angles on the whole interaction domain. Similar to the cases described in Section 7.1, the angular spectral density for linear exciting coils is distributed in a narrow range. For a circular coil, its range increases with the width of the interaction domain. For a Koch coil, when the width of the interaction is 5 mm, angular spectral density ranges from 30° to 90°. However, when the widths of the interaction are larger than 10 mm, the density is distributed in all angles, and the larger the width, the more uniform the angular spectral density. In summary, when the interaction width is smaller, the angular spectral density of a circular coil is similar to that of the linear coil shown in Figure 3a. However, when the interaction width is larger, the angular spectral density is similar to that of a Koch coil, shown in Figure 3b.

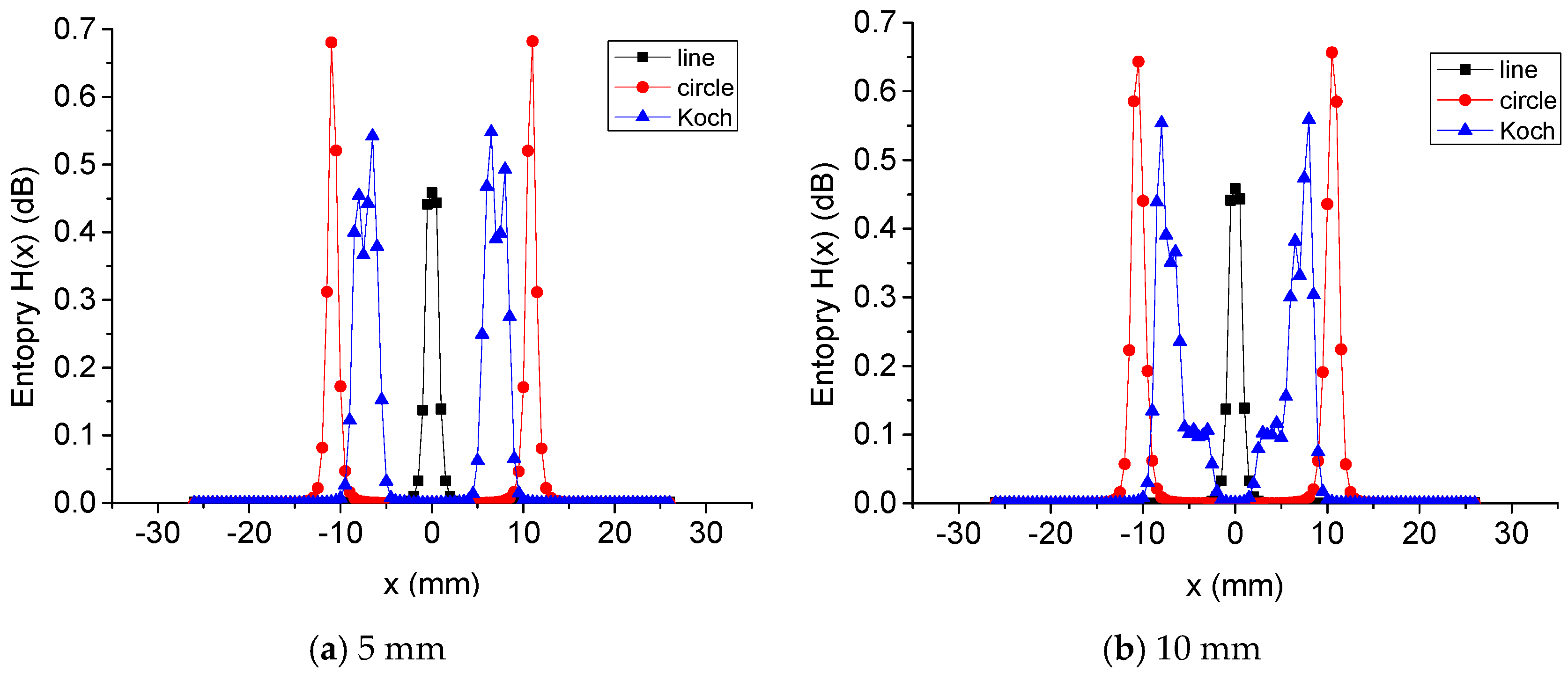
7.3. Information Entropy along the x-Axis

The information entropy for the EC distributed in different angles along the x-axis is shown in Figure 4. For linear exciting coils, $H_{\theta }\left(x\right)$ has only one peak and the peak value remains almost constant with the increasing width of the interaction domain.

For a circular coil, $H_{\theta }\left(x\right)$ has two peaks. As the width of the interaction domain increases, the peak value decreases but the value of $H_{\theta }\left(x\right)$ between the two peaks increases.

For Koch coils, the number and the position of the peaks of $H_{\theta }\left(x\right)$ change with the width of the interaction domain. The peak value decreases with the increasing of the width of the interaction domain, but the value between the peaks also increases.

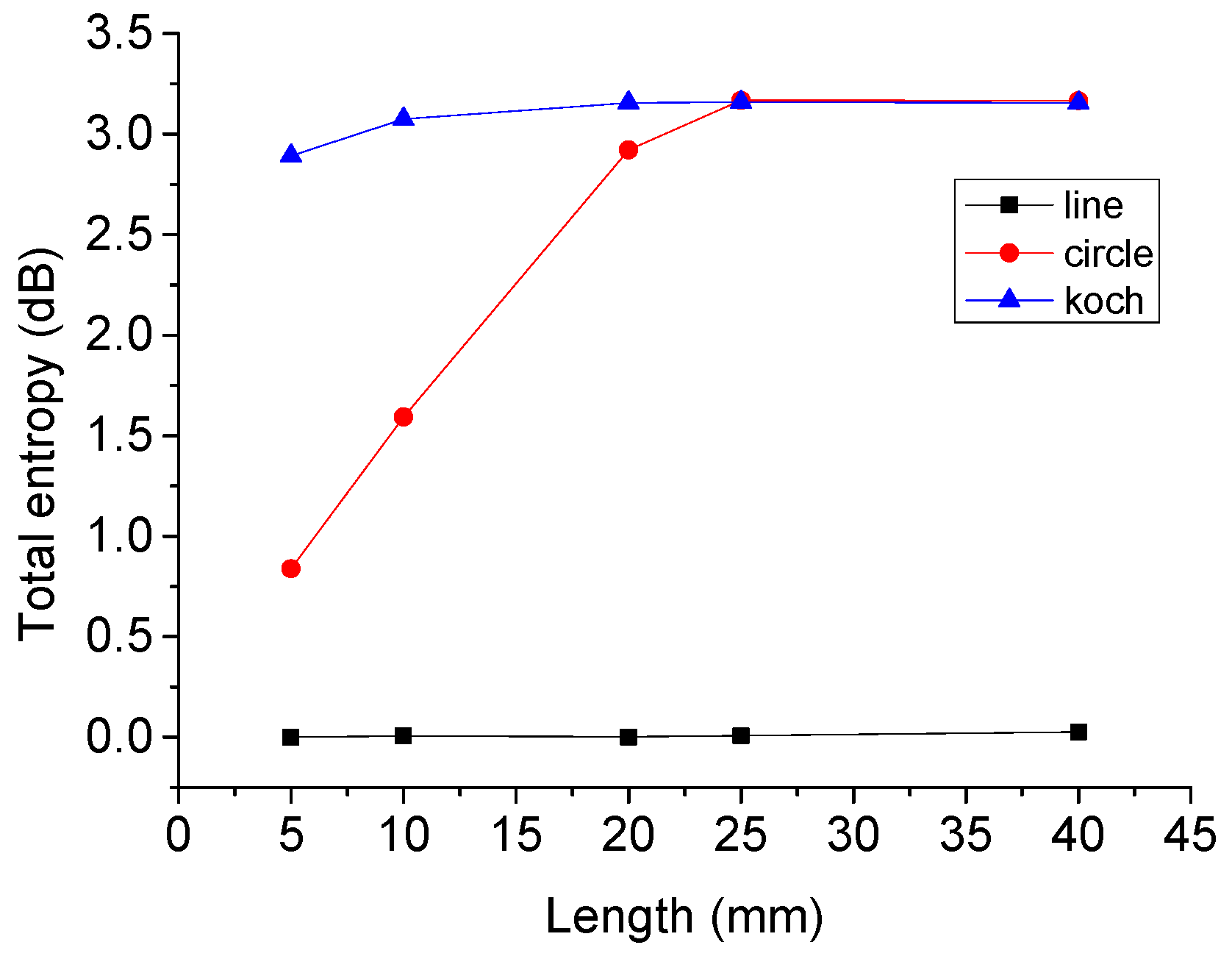
7.4. Information Entropy of the Whole Interaction Domain

The information entropy of the whole interaction domain is shown in Figure 5, measuring the complexity of the EC distribution at different angles. For the EC induced by a linear coil, its information entropy for different widths of interaction domains is nearly zero. Angular spectrum density for linear exciting coils is concentrated in a narrow angle range, so $p\left(\theta =90°\right)\approx 1$. In this case, the EC is a high-certainty event, and its self-information is almost zero $H_{\theta }\approx 0$.

For other exciting coils, when the width of the interaction domain is larger than 25 mm, the entropy of the circular and Koch coils approaches its maximum value of 3.1699. In this case, the interaction domain covers the whole exciting coil, and the angular spectral density is almost uniformly distributed; therefore, the information entropy reaches its maximum value $H=-{\displaystyle \sum }_{i=1}^9\frac{1}{9}\log \frac{1}{9}=3.1699$. When the width of the interaction domain is smaller than 25 mm, the total information entropy of the EC distributed in more than one angle increases with the width of the interaction domain. However, the rate of change of the information entropy of the Koch coil is larger than that of the circular coil. Therefore, when the width of interaction is 5 mm, the total information entropy of the Koch coil is more than three times higher than that of the circular coil. This validates the idea of using a Koch exciting coil as its induced EC is allocated in a larger angle range of a smaller domain compared to circular and linear exciting coils.

8. Conclusions

Without loss of generality, energy allocation density of a multi-dimensional vector field in a multidimensional space is proposed using conservation of energy. Via the method of quantization and sampling from circuit theory, the position vector space and field vector space are discretized. Then, the quantity of information of the field, using information entropy, is proposed. Finally, the proposed method is applied to evaluate two-dimensional eddy currents in a plane. Angular spectral density is proposed to illustrate the EC allocated in different directions, and the complexity of EC distribution in different directions is calculated by using information entropy. The EC induced by three typical exciting coils, i.e., linear, circular and Koch, is evaluated. Results highlight that angular spectral and information entropy can intrinsically and quantitatively reveal the disturbance principle of EC NDT.

In the next study, the EC in time–space, induced by the rotating field EC method and pulse EC testing method will be evaluated and analyzed.