Abstract
One of the fundamental questions about human language is whether its entropy rate is positive. The entropy rate measures the average amount of information communicated per unit time. The question about the entropy of language dates back to experiments by Shannon in 1951, but in 1990 Hilberg raised doubt regarding a correct interpretation of these experiments. This article provides an in-depth empirical analysis, using 20 corpora of up to 7.8 gigabytes across six languages (English, French, Russian, Korean, Chinese, and Japanese), to conclude that the entropy rate is positive. To obtain the estimates for data length tending to infinity, we use an extrapolation function given by an ansatz. Whereas some ansatzes were proposed previously, here we use a new stretched exponential extrapolation function that has a smaller error of fit. Thus, we conclude that the entropy rates of human languages are positive but approximately 20% smaller than without extrapolation. Although the entropy rate estimates depend on the script kind, the exponent of the ansatz function turns out to be constant across different languages and governs the complexity of natural language in general. In other words, in spite of typological differences, all languages seem equally hard to learn, which partly confirms Hilberg’s hypothesis.
1. Introduction
Estimation of the entropy rate of natural language is a challenge originally set up by Shannon [1,2]. The entropy rate quantifies the complexity of language, precisely the rate how fast the amount of information grows in our communication with respect to the text length. Today, the entropy rate provides an important target for data compression algorithms, where the speed of convergence of the compression rate to the entropy rate is an informative benchmark. Measuring the entropy rate is also the first step in answering what kind of a stochastic process can model generation of texts in natural language, an important question for many practical tasks of natural language engineering.
An important theoretical question concerning the entropy rate, which has also been noted in the domains of computational linguistics [3] and speech processing [4], is whether the entropy rate of human language is a strictly positive constant. The overwhelming evidence collected so far suggests that it is so—in particular, the amount of information communicated per unit time in English text is generally agreed to be about 1 bpc (bit per character) [2,5,6,7,8]. Although this is what we might intuitively expect, in 1990, Hilberg formulated a hypothesis that the entropy rate of natural language is zero [9]. Zero entropy rate does not imply that the amount of information in texts is not growing, but that it grows with a speed slower than linear. Although Hilberg’s hypothesis may seem unlikely, the results of recent experiments concerning the scaling of maximal repetition in human language [10] may be explained exactly by a hypothesis that the entropy rate is zero. Whereas zero entropy rate need not be the sole possible explanation of these experiments, it is advisable to perform another large scale experiment in which entropy rate would be estimated as precisely as possible.
Precise estimation of the entropy rate is a challenging task mainly because, mathematically speaking, the sought parameter is a limit for text length tending to infinity. To alleviate this problem, previous great minds proposed estimation methods based on human cognitive testing [2,5]. Since human testing is costly, however, such attempts remain limited in terms of the scale and number of tested languages. In contrast, although any conceivable data size can only be finite, today’s language data have become so large in scale that we may reconsider estimation of the entropy rate using big data computation. This point was already raised by [1], which led to important previous works such as [6] in the domain of computational linguistics. Both of these articles and many others that followed, however, mostly considered the English language only.
This article disproves Hilberg’s hypothesis by providing stronger empirical evidence that the entropy rate is positive. We investigate six languages using large, state-of-the-art 20 corpora of up to 7.8 gigabytes, across six languages: English, French, Russian, Korean, Chinese, and Japanese. We try to estimate the entropy rate by compressing these data sets using the standard PPM (Prediction by Partial Match) algorithm and extrapolating the data points with a new carefully selected ansatz function. Whereas a couple of ansatz functions were previously proposed in [8,9,11,12], here we introduce another function, which is a stretched exponential function and enjoys the same number of parameters as previous proposals. The new functions yields a smaller error of fit. As a result, we arrive at the entropy rate estimates which are approximately 20% smaller than without extrapolation, yet positive.
There remains something true in the original hypothesis of Hilberg, however. Hilberg [9] seemed to suppose that complexity of natural language, as expressed by some parameters of the ansatz function, is approximately constant across different languages. Our experimental data confirm this statement. Our ansatz function has three parameters: the limiting entropy rate, a proportionality constant, and an exponent β, which determines the speed of convergence of compression rate to the entropy rate. Although the entropy rate estimates depend on the kind of the script, the exponent β turns out to be approximately constant across different languages. Thus, we suppose that this exponent is a language universal. Let us note that entropy rate quantifies how difficult it is to predict the text once the optimal prediction scheme has been learned. In contrast, exponent β quantifies how difficult it is to learn to predict the text. Claiming constancy of exponent β, we provide some evidence that despite huge typological differences, all languages are equally hard to learn.
We can legitimately ask whether language can be modeled as a stationary ergodic process, which is a precondition for statistical identifiability of a unique entropy rate and other parameters of the underlying stochastic process, such as the exponent β. In report [7] it was observed that different written sources in the the same literary language give rise to somewhat different entropy rates. In our paper, we will further confirm this observation. Thus natural language is somewhat nonergodic. Still, if we speak of statistics pertaining to universal coding, there seem to be some cross-linguistic and cross-textual universals, like the mentioned exponent β. As we will see further in this paper, artificial random sources obey a different decay of the entropy rate estimates, so the constancy of exponent β, reported in this paper, does say something about complexity of natural language.
The organization of the article is as follows: In Section 2, we recall the notion of the entropy rate. In Section 3, we discuss methods of entropy estimation. In Section 4, we review the extrapolation functions. Section 5 details our experimental procedure, whereas Section 6 describes our experimental results. Section 7 contains the concluding remarks.
2. Entropy Rate
Let be a stochastic process, i.e., an infinite sequence of random variables with each random variable assuming values , where is a certain set of countably many symbols. For natural language, for instance, can be a set of characters, whereas is an infinite corpus of texts. Let , where , denote a finite subsequence of and let denote a probability function of the subsequence . The Shannon entropy of a finite subsequence is defined as:
where sequences are instances of [1]. In contrast, the entropy rate of the infinite sequence X is defined as [13]:
The entropy rate is the amount of information per element for the data length tending to infinity.
Let us note that the entropy rate quantifies the asymptotic growth of the number of possible values of an infinite sequence . Roughly speaking, there are effectively only possible values for a subsequence , where n is the sequence length. In other words, condition is tantamount to an exponential growth of the number of possible sequences with respect to n. Value need not mean that the number of possibilities does not grow. For instance, for a sequence whose number of possibilities grows like , as supposed by Hilberg [9], we have . Although the number of possibilities for such a sequence of random variables grows quite fast, the speed of the growth cannot be properly measured by the entropy rate.
The entropy rate thus quantifies, to some extent, the degree of randomness or freedom underlying the text characters to follow one another. (To make things more subtle, the randomness quantified by the entropy of a sequence is a sort of statistical randomness, which should be distinguished from algorithmic randomness of a sequence , quantified by the Kolmogorov complexity. These two concepts are closely related, however. It can be shown that the rate of Kolmogorov complexity and the entropy rate are almost surely equal for any stationary ergodic process [14].) For human languages, the occurrence of a linguistic element, such as a word or character, depends on the previous elements, and there are many long repetitions [10]. This results in a lower value of the entropy rate than for a random sequence, but the ultimate degree of randomness in natural language is hard to simply guess. Whereas Hilberg [9] supposed that holds for natural language, this is only a minority view. According to the overwhelming experimental evidence the entropy of natural language is strictly positive [2,5,6,7,8]. We may ask however whether these known estimates are credible. In fact, if convergence of to the entropy rate is very slow, this need not be so. For this reason, while estimating the entropy rate, it is important to investigate the speed of the estimate convergence.
3. Direct Estimation Methods
There are several methods to estimate the entropy rate of natural language. These can be largely divided into methods based on human cognitive testing and methods based on machine computation. Estimation via human cognitive testing is mainly conducted by showing a substring of a text to a human examinee and having him or her guess the character to follow the substring. This method was introduced by Shannon [2]. He tested an unmentioned number of examinees with the text of Dumas Malone’s “Jefferson the Virginian” and obtained bpc. This method was improved by Cover and King [5] as a sort of gambling. The results with 12 examinees produced an average of bpc. Human cognitive testing has the advantage over methods based on machine computations that the estimates of entropy rate converge faster. Unfortunately, such human cognitive testing is costly, so the number of examinees involved is small and the samples are rather short. It is also unclear whether human examinees guess the text characters according to the true probability distribution.
In contrast, today, estimation of the entropy rate can be performed by big data computation. For this paradigm, we can mention the following specific approaches:
- The first approach is to compress the text using a data compression algorithm. Let denote the size in bits of text after the compression. Then the code length per unit, , is always larger than the entropy rate [13],We call the encoding rate. In our application, we are interested in universal compression methods. A universal text compressor guarantees that the encoding rate converges to the entropy rate, provided that the stochastic process is stationary and ergodic, i.e., equalityholds with probability 1.
- The second approach is to estimate the probabilistic language models underlying formula (2). A representative classic work is [6], who reported bpc, by estimating the probability of trigrams in the Brown National Corpus.
- Besides that, a bunch of different entropy estimation methods has been proposed in information theory. There are lower bounds of entropy such as the plug-in estimator [15], there are estimators which work under assumption that the process is Markovian [16,17,18], and there are a few other methods such as Context Tree Weighting [15,19].
In the following we will apply the first approach: since our data are very large, we are obliged to use efficient and reliable tools only, so we use some off-the-shelf programs that are thoroughly tested and can manage large scale data efficiently. Among important known universal compressors we can name: the Lempel-Ziv (LZ) code [20], the PPM (Prediction by Partial Match) code [21], and a wide class of grammar-based codes [22], with many particular instances such as Sequitur [23] and NSRPS (Non-Sequential Recursive Pair Substitution) [12,24]. Whereas all these codes are universal, they are not equal—being based on different principles. The LZ code and the grammar-based codes compress texts roughly by detecting repeated substrings and replacing them with shorter identifiers. A proof of universality of the LZ code can be found in [13], whereas the proof of universality of grammar-based codes can be found in [22]. In contrast, the PPM code is an n-gram based language modeling method [21] which applies variable length n-grams and arithmetic coding. The PPM code is guaranteed to be universal when the length of the n-gram is considered up to the length of the maximal repetition of the input text [25,26].
A very important question for our application is the scaling of the encoding rate of off-the-shelf implementations of universal codes for finite real data. Since the probabilistic model of natural language remains unknown, the notion of universality may serve only as a possible standard to obtain a stringent upper bound. One may raise some doubt that natural language is strictly stationary since the word frequencies exhibit formidable long-memory effects, as indicated, e.g., by [27,28,29]. Moreover, many off-the-shelf compressors are not strictly universal, since they are truncated in various ways to gain the computational speed. Such truncations usually take form of a bounded traversing window length, so the respective compressors converge to the entropy of the traversing window rather than to the true entropy rate. Still, it is possible to implement a compressor that does not have this deficiency and there exist such off-the-shelf compressors. The simplest way to identify suitable compressors is by experimental inspection, excluding those for which the encoding rate is too large.
Among state-of-the-art compressors, we have considered zip, lzh, tar.xz, and 7-zip LZMA for the LZ methods and 7-zip PPMd for the PPM code. In Figure 1 (right panel) we show how the encoding rate depends on the data length for a Bernoulli process with (left panel, listed later in the first line of the third block of Table 1) and for natural language data of Wall Street Journal corpus (right panel, listed in the third line of the third block of Table 1). First, let us consider the Bernoulli process, which is a simple artificial source. Formally, the Bernoulli process is a sequence of independent random variables taking the value of 1 with probability p and 0 with probability . There are two known theoretical results for this process: The theoretically proven encoding rate of the LZ code is as much as [30], whereas the encoding rate for the PPM code is proved to be only [31,32]. Thus the convergence is extremely slow for the LZ code and quite fast for the PPM code. This exactly can be seen in Figure 1a, where all data points for the LZ code remain way above 1.0 bpc, the true entropy rate, while the data points for the PPM code practically converge to 1.0 bpc.
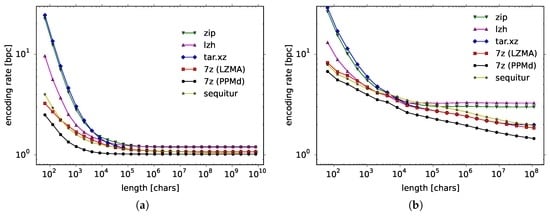
Figure 1.
Compression results for (a) a Bernoulli process () and (b) the Wall Street Journal for Lempel-Ziv (LZ), PPM (Prediction by Partial Match), and Sequitur.

Table 1.
Data used in this work, its size, its encoding rate, entropy rate and the error.
As for natural language data, whereas the empirical speed of convergence is much slower for the Wall Street Journal, the gradation of the compression algorithms remains the same. Algorithms such as zip and lzh get saturated probably because they are truncated in some way, whereas Sequitur, 7-zip LZMA and 7-zip PPMd gradually improve their compression rate the more data they read in. Since the encoding rate is visibly the smallest for 7-zip PPMd, in the following, we will use this compressor to estimate the entropy rate for other natural language data. Let us stress that we will be using an off-the-shelf compressor, 7-zip PPMd, since we are going to work with very large data and we need a computationally efficient and well-tested implementation of a universal code.
4. Extrapolation Functions
Many have attempted to estimate the entropy rate via compression. For example, paper [21] reported bpc for the collected works of Shakespeare in English. Majority of the previous works, however, reported only a single value of the encoding rate for the maximal size of the available data. Whereas any computation can handle only a finite amount of data, the true entropy rate is defined in formula (2) as a limit for infinite data. The later fact should be somehow taken into consideration, especially if convergence (4) is slow, which is the case of natural language. One way to fill this gap between the finite data and the infinite limit is to use extrapolation. In other words, the encoding rate is calculated for many n and the plots are extrapolated using some function . One possibility could be to consider in the form of polynomial series, but this does not describe the nature behind the problem in a functional form. Previously, function has been considered so far in form of an ansatz, since the probabilistic model of natural language is unknown.
Previously, two ansatzes have been proposed, to the best of our knowledge. The first one was proposed by Hilberg [9]. He examined the original paper of Shannon [2], which gives a plot of some upper and lower bounds of . Since Hilberg believed that the entropy rate vanishes, , his ansatz was
with , which apparently fits to the data by [2], according to Hilberg. However, if we do not believe in a vanishing entropy rate, the above formula can be easily modified as
so that it converges to an arbitrary value of the entropy rate, cf., [11]. Another ansatz was given in papers [12] and [8]. It reads
Using this ansatz, paper [8] obtained bpc for the collected works of Shakespeare and bpc for the LOB corpus of English.
We have used up to 7.8 gigabytes of data for six different languages and quite many plots were available for fitting, as compared to previous works. As will be shown in Section 6.2, function does not fit well to our plots. Function , however, is no more than some ansatz. If we can devise another ansatz that fits better, then this should rather be used to estimate the entropy rate. In fact we have come across a better ansatz. The function we consider in this article is a stretched exponential function:
which embeds function in an exponential function and yields the entropy rate . In fact, function converges to h slower than . In a way, this is desirable since slow convergence of the encoding rate is some general tendency of the natural language data. As a by-product, using function we will obtain smaller estimates of the entropy rate than using function .
Hilberg [9] and a few other researchers [11,12,33] seemed to suppose that exponent β is does not depend on a particular corpus of texts, i.e., it is some language universal which determines how hard it is to learn to predict the text. Exponent β is thus some important parameter of language, which is complementary to the entropy rate, which determines how hard it is to predict the text once the optimal prediction scheme has been learned. Let us note, that if the exponent β does not depend on a particular corpus of texts, then for all three functions , , and we can draw a diagnostic linear plot with axes: and for , and for , and and for , respectively. In these diagnostic plots, the entropy rate corresponds to the intercept of the straight line on which the data points lie approximately. In fact we observe that exponent β is indeed some language universal. For this reason we will use these diagnostic linear plots to compare different text corpora in Section 6.4.
5. Experimental Procedure
5.1. Data Preparation
Table 1 lists our data, including each text, its language and size in the number of characters, its encoding rate using the full data set (the minimal observed encoding rate), and the extrapolation results for the entropy rate h, including the error of the estimates—as defined in Section 5.2 and analyzed later. We carefully chose our data by examining the redundancies. Many of the freely available large-scale corpora suffer from poor quality. In particular, they often contain artificially long repetitions. Since such repetitions affect the entropy rate estimates, we have only used corpora of a carefully checked quality, making sure that they do not contain large chunks of a repeated text.
The table contains three blocks. The first block contains state-of-the-art large-scale corpora of texts. As will be shown in our experiments, the plots for the raw corpora often oscillated due to the topic change. To overcome this problem we have performed randomization and averaging. First, we have shuffled the corpora at the level of documents and, second, we have averaged ten different random permutations for each corpus. The experimental results shown from the fourth column to the last one of Table 1 pertain to so processed language data. As for the Japanese and Chinese data, in addition to the original texts of the Mainichi and People’s Daily newspapers, the Romanized versions were generated. (Kakasi and Pinyin Python library were used to Romanize Japanese and Chinese, respectively.) In contrast, the second block of Table 1 contains long literary works in five different languages. These data have not been randomized.
The data in the first and second blocks encompass six different languages. For discussion in the following sections, the six languages are grouped into three categories:
- English English;
- Chinese Chinese; and
- Others French, Russian, Japanese, Korean and Romanized Chinese and Japanese.
In the following, when results for all natural languages are shown in a figure, the colors black, red, and blue represent the English, Chinese, and other categories, respectively.
The third block of Table 1 contains some additional random data to provide the baseline. The first two lines of the block present data for the Bernoulli process with and the unigram Zipf process. The Zipf process is a sequence of independent random variables taking values in natural numbers according to the power-law Zipf distribution, mimicking the marginal distribution of words in natural language. The unigram Zipf process data was generated so that it were similar to the Wall Street Journal (WSJ) data (seventh line, first block), having exactly the same total number of words and character kinds (95), and almost the same numbers of different words. A word in this process is originally a large integer, transformed into ASCII characters with a 95 base. The next four lines present Wall Street Journal corpus (WSJ) randomized in four different ways: non-randomized, randomized by characters, randomized by words, and randomized by sentences. Note that the results for the WSJ corpus in the seventh line of the first block and the third line of the third block are different, since in the first case the WSJ corpus was randomized by documents.
5.2. Detailed Procedure
To estimate the entropy rate, we have used the 7-zip compressor, which implements the PPMd algorithm. As discussed in Section 3, this compressor seems the best among state-of-the-art methods. It compresses best not only the real Wall Street Journal corpus but also the artificial Bernoulli process. For this reason, we have used this compressor. Further detailed options of the PPMd algorithm were carefully chosen. Since the 7-zip program compresses by recording statistics for file names as well, the input text was fed to the compressor via a Unix pipe so that the compression was conducted without a file name. We also carefully excluded the header of the compressed file (which includes the name of the compressor etc.). This header is included in the compressed file but does not count to the proper compression length.
Another important option of the 7-zip program concerns the maximal n-gram length used by the PPM, called here MAX. As noted in Section 3, when MAX is greater than the length of the maximal repetition of the input text then the compression method is universal. But the larger MAX is, the slower the compression procedure becomes. Therefore, any available PPM compressor sets an upper bound on MAX, whereas the user can choose the MAX value smaller than this bound (the bound equals 32 in the case of 7-zip PPMd). However, even within this preset range, it was not always the case that a larger MAX resulted in a better encoding rate. Therefore, in our work, for each full data set, we searched for the value of MAX that achieved the best encoding rate and consistently used those best encoding rates for different subsets of the full data set.
Having clarified these specific issues, our detailed experimental procedure, applied to each data set from Table 1, was as follows. First, for every , where (data size), the first n characters of the full text were taken. This subsequence, denoted , was then compressed using the 7-zip program, and its size in bits was measured to calculate the encoding rate . The obtained encoding rates for different n were fitted to the ansatz functions , where . When encoding rates for K distinct values of were obtained, the fit was conducted by minimizing the square error as follows:
The logarithm was taken here to ascribe a larger weight to the errors of the larger n, since we were particularly interested in the tail behavior of the data points.
6. Experimental Results
6.1. Effects of Randomization by Documents
First, we will discuss how randomization by documents, applied throughout our data, affects the decay of the encoding rate and the estimates of entropy rate. Although, in principle randomization increases the estimates of entropy rate, simultaneously it removes certain oscillations in the decay of the encoding rate, thus leading to entropy rate estimates which are more stable and credible.
Figure 2 shows our results for the Wall Street Journal (WSJ) corpus (Table 1, first block, seventh line), which is the benchmark corpus most typically used in the computational processing of human language. The figure shows the encoding rate (vertical axis) as a function of the text size in characters n (horizontal axis). The left panel of Figure 2 shows the results obtained from the original text. The encoding rates tend to oscillate, which is due to topic changes in the corpus. Such oscillation is visible in majority of the natural language data, where some data can oscillate much worse than WSJ. In the context of entropy rate estimation such oscillation was already reported in paper [8].
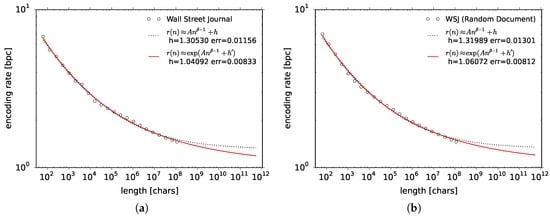
Figure 2.
Encoding rates for the Wall Street Journal corpus (in English). Panel (a) is for the original data, whereas (b) is the average of the data 10-fold shuffled by documents. To these results we fit functions and .
A possible method to cope with the problem of oscillation is to shuffle the text at the level of documents. The right panel of Figure 2 shows the average encoding rate for the data 10-fold shuffled by documents. The data points in the right panel oscillate less than in the left panel. At the same time, since shuffling the documents introduces some randomness, the entropy rate estimate is about 1% larger for the randomized data than for the original corpus. We found the 1% systematic error to be not much compared to the removal of oscillations which affect the fitting error. For this reason, we have applied randomization by documents to all text corpora mentioned in Table 1.
6.2. Comparison of the Error of Fit
In the next step, we will compare extrapolation functions to decide which one fits the data the best. We first consider our initial example of the Wall Street Journal corpus. Both panels of Figure 2 show two fits of the encoding rate, to extrapolation functions and —given by formulae (6) and (8), respectively. Whereas, visually, it is difficult to say which of the functions fits better, we can decide on that using the value of error (9). The estimates of the entropy rate are with error being 0.0130 for and with error being 0.00812 for . We can suppose that function in general yields both a smaller entropy rate estimate and a smaller fitting error.
The hypothesis that function yields the smallest fitting error can be confirmed by considering all text corpora mentioned in Table 1. We conducted fitting to all our data sets for three ansatz functions , , and . The fitted values of h and error for and , for both 10-fold randomized corpora and non-randomized texts are listed in Table 1 in the last four columns. The tendencies of h and error for the natural language data (first two blocks of Table 1) and all three ansatz functions , , and are summarized in Figure 3. The horizontal axis indicates h and the vertical axis indicates error, with each point representing one data set of natural language. As noted previously, the colors black, red, and blue indicate the English, Chinese, and Other language categories, respectively. An oval is drawn in the graph for each ansatz for the English and the Chinese data separately, with the center and the radius representing the mean and the standard deviation (SD in the figure) of h and error. The dotted, dashed, and solid ovals correspond to the results for , , and . The ovals are located lower when the error is smaller. The average values of the error for , and were 0.0113, 0.0194, and 0.00842 across all data sets, respectively. The plots therefore fit the best to . Among the three ansatz functions, function is the worst choice. In contrast, the stretched exponential function seems better than the modified Hilberg function and it consistently yields smaller estimates of the entropy rate.
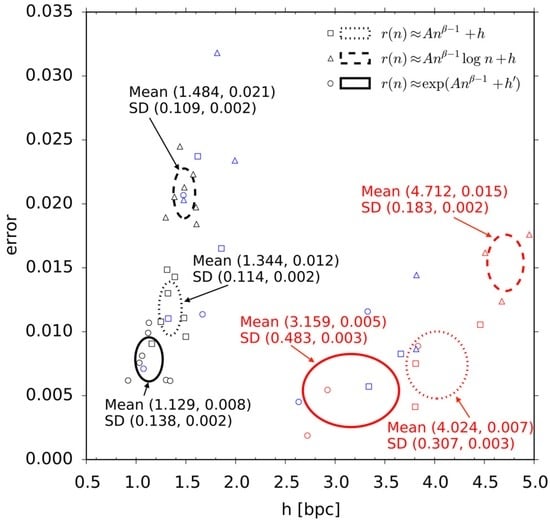
Figure 3.
The values of error and h for all natural language data sets in Table 1 and the three ansatz functions , , and . Each data point corresponds to a distinct corpus or a distinct text, where black is English, red is Chinese, and blue for other languages. The squares are the fitting results for , triangles—for , and circles—for . The means and the standard deviations of h (left) and error (right) are indicated in the figure next to the ovals, which show the range of standard deviation—dotted for , dashed for , and solid for .
6.3. Universality of the Estimates of Exponent β
We have also investigated the β exponents of the three ansatz functions , , and . In general, the β exponents determine how hard it is to learn to predict a given corpus of texts. As implicitly or explicitly supposed in [9,11,12,33], the β exponents could be some language universals, which is tantamount to saying that all human languages are equally hard to learn. Universality of exponent on much smaller data sets for the English, German, and French languages using ansatz has been previously reported in paper [33] in case of the Lempel-Ziv code rather than the PPM code. Our experimental data further corroborate universality of β, across a larger set of languages and a different universal code. The respective results are visualized in Figure 4, which is organized in the same fashion as Figure 3. For the functions , , and , the respective mean values of β were 0.771, 0.613, and 0.876, with standard deviations being 0.0511, 0.0587, and 0.0340. It is surprising that the variance of exponent β is so small for the best function . In view of our experimental results, we suppose that exponent β for the stretched exponential function is indeed a language universal.
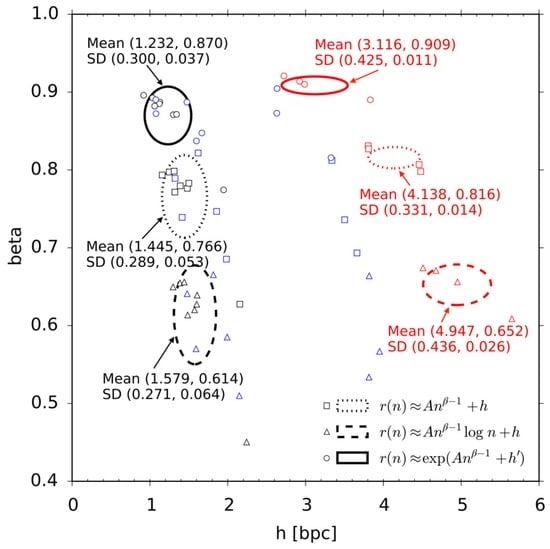
Figure 4.
The values of β and h for all natural language data sets in Table 1 and the ansatz functions , , and . Each data point corresponds to a distinct corpus or a distinct text, where black is English, red is Chinese, and blue for other languages. The squares are the fitting results for , triangles—for , and circles—for . The means and the standard deviations of h (left) and β (right) are indicated in the figure next to the ovals, which show the range of standard deviation—dotted for , dashed for , and solid for .
6.4. A Linear Perspective onto the Decay of the Encoding Rate
As described in Section 4, ansatzes , , and can be analyzed as a form of linear regression. Let us focus on , the function that yields the minimal fitting error. If we put as the vertical axis and as the horizontal axis where , the average value for the fit to , then the plots for all large scale natural language data (first block of Table 1) can be transformed as shown in Figure 5. It can be seen that each set of data points is roughly assembled in a linear manner. The quality of the linear fit appears to be visually satisfactory.
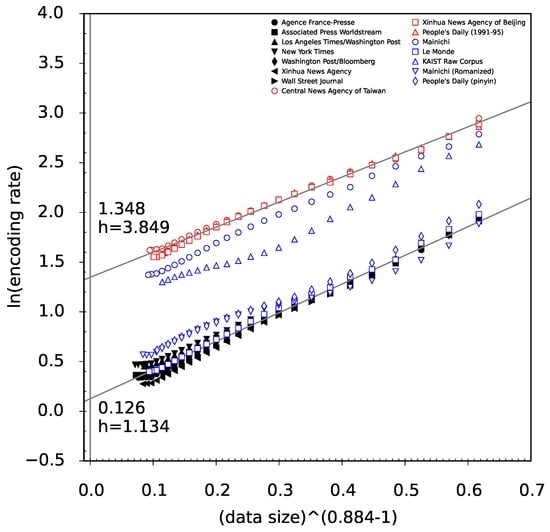
Figure 5.
All large scale natural language data (first block of Table 1) from a linear perspective for function . The axes are and , where . The black points are English, the red ones are Chinese, and the blue ones are other languages. The two linear fit lines are for English (lower) and Chinese (upper).
Two main groups of plots can be seen in Figure 5, one lower and one upper, where the lower plots in black are for English and the upper plots in red are for Chinese, as grouped in Section 5.1. The results for other languages, shown in blue, are located somewhere between English and Chinese. The blue plots appearing amidst the lower group indicate Romanized Japanese and Chinese. These results show that the script type distinguishes the amount of information per character. The scripts can be typically classified on some continuum from purely phonographic to purely logographic scripts, with other scripts located somewhere between [34].
Two straight lines were obtained in Figure 5 for the English and Chinese groups by least squares fitting to all data points from each group, respectively. Since the horizontal axis indicates variable , condition corresponds to condition . The intercept of a fitted straight line is thus the logarithm of the entropy rate. The intercepts are and , with the corresponding entropy rates bpc and bpc, for the English and Chinese groups, respectively. Compared to the minimal observed encoding rate, the entropy rate estimate h is smaller by approximately 20%. Interestingly, a similar analysis can be conducted for ansatz . For this function, by using the average of , the final h was found to be 1.304 and 4.634 for English and Chinese, respectively, which is similar to previous reports. Therefore, the estimate of the entropy rate depends on the used ansatz, with the better fitting ansatz yielding estimates smaller than generally agreed.
6.5. Discriminative Power the Decay of the Encoding Rate
An legitimate objection can be made whether the stretched exponential decay rate of the encoding rate is some generic property of the PPM code. In fact, the linear alignment of the data points in the plane, where and is highly specific to natural language. If we take into consideration a few instances of random and randomized sources, we can no longer observe this linear alignment. Figure 6 shows the plots obtained for data in the third block of Table 1. The black square points are the original WSJ data (third line of the third block), while the magenta points are its randomized versions and the blue points are two stochastic processes—the Bernoulli and Zipf processes, respectively. We can see that the plot for the Bernoulli process is located much lower and rapidly converges to bpc, following the theory. In contrast, the Zipf process data points coalesce with the WSJ corpus randomized by characters. This effect has to do with our particular construction of the Zipf process.
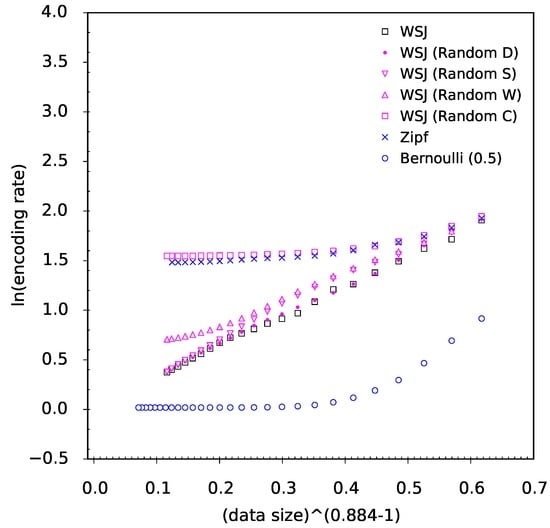
In general, in Figure 6, the data points for the randomized WSJ corpora partially overlap with the data points for the non-randomized WSJ corpus, and the randomized data (in magenta) approximate the non-randomized data (in black) the better the less randomized the source is. For randomization by characters and words the entropy rate estimates are visibly larger than for the original WSJ corpus. As for randomization by sentences and documents, the respective plots coalesce with the original WSJ data, especially for large data sizes. This is an expected result, since the PPM code is an n-gram based compression method, whereas the data with randomized sentences and documents preserve the majority of n-grams from the original texts.
As mentioned in Section 6.1, the entropy rate estimates are about 1% larger for the WSJ corpus shuffled by documents than for the non-randomized WSJ corpus. This 1% difference could be attributed to some long-range correlations in the text topics and style, ranging beyond single documents. In the results presented in the first block of Table 1, we have ignored these long-range correlations since we performed randomization by documents. Our main concern there was to smooth the plots to obtain a better fit to the extrapolation ansatz. Here, we recall this issue to remark that the entropy rate estimates in the first block of Table 1 may be about 1% larger than the true values.
6.6. Stability of the Entropy Rate Estimates
Finally, we have examined how the estimates of entropy rate change with respect to the data size. Figure 7 shows the change in the fitted values of the entropy rate h (vertical axis) for the English and Chinese groups of corpora when the fit to ansatz was conducted up to the data size n (horizontal axis). The plots present a horizontal alignment, which suggests that the obtained estimates practically converge to the true values for characters. Possible changes of the trend for larger n cannot be completely excluded, but the observed stability of estimates suggests that the data amount is sufficient, and that the value of the entropy rate as estimated using compression is 1.134 bpc for English and 3.849 bpc for Chinese. Whereas paper [35] reported how difficult it is to obtain a stable estimate of the entropy rate, the present results indicate that it is indeed possible.
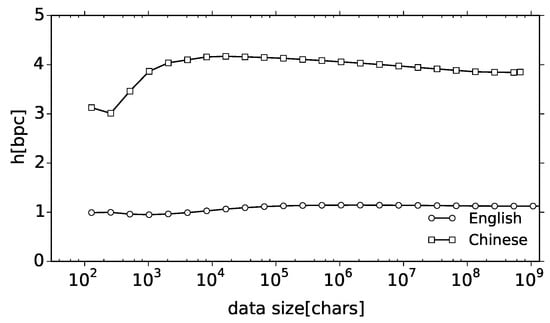
Figure 7.
Stability of the entropy rate estimates obtained with the ansatz function .
Given our results, we may revisit the question whether the entropy rate of natural language is a strictly positive constant. Our estimates of the entropy were obtained through extrapolation. Thus, the possibility of a zero entropy rate cannot be completely excluded but it seems highly unlikely in view of the following remark. Namely, if the entropy rate is zero, then the data points should head towards negative infinity in Figure 5. However, the plots do not show such a rapid decrease for data size of the order of several gigabytes. On the contrary, all endings of the plots for large data sizes are slightly bent upwards. Moreover, given the stability of the entropy rate shown in Figure 7, it is likely that this tendency would not change for larger data. Hence we are inclined to believe that the true entropy rate of natural language is positive and close to our estimates. Of course, a far larger amount of data would be required to witness the behavior of the plots in the margin between the infinite limit and the largest data size considered in our experiment.
7. Conclusions
Motivated by some controversy whether the entropy rate of natural language is zero [9,10] or not [2,5,6,7,8], in this article, we have evaluated the entropy rates of several human languages using the PPM algorithm, a state-of-the-art compression method. Compared to previous works, our contribution can be summarized as follows. First, we have calculated the compression rates for six different languages by using much larger, state-of-the-art corpora with sizes of up to 7.8 gigabytes. Second, we have extrapolated the empirical compression rates to some estimates of the entropy rate using a novel ansatz, which takes form of a stretched exponential function. This new ansatz function fits better than the previously proposed ansatzes and predicts entropy rates which are approximately 20% smaller than without extrapolation. Nonetheless, since these estimates are clearly positive, we falsify the original hypothesis by Hilberg [9].
Still, we observe that there remains something true in Hilberg’s original hypothesis. Our newly proposed stretched exponential function ansatz has three parameters: the limiting entropy rate, a proportionality constant, and an exponent β. Here, exponent β controls the speed of convergence of the compression rate to the entropy rate. In simple words, whereas entropy rate measures how hard it is to predict the text, exponent β measures how hard it is to learn to predict the text. Whereas the entropy rate strongly depends on the kind of the script, the exponent β turned out to be approximately constant, , across six languages, as supposed in [9,11,12,33]. Thus we suppose that the exponent β is a language universal and it characterizes the general complexity of learning of natural language, all languages being equally hard to learn in spite of apparent differences.
Considering the stretched exponential decay rate of entropy estimates, an objection can be made whether this decay is a property of language itself or a property of the PPM code. A quick look at Figure 6 asserts that the decay rate for randomized data is ruled by very different functions. Thus the decay rate ruled by the stretched exponential decay is a specific joint property of natural language and the PPM code. Whereas the decay of entropy rate estimates is different for simple stochastic sources, we suppose that the reported cross-linguistic and cross-textual universality of exponent β does say something about complexity of natural language.
Some future extension of our work might be to simply enlarge the data, but it will not be trivial to obtain a uniform corpus of a larger scale. In the future work, it may be advisable to look for other computational approaches to the problem of entropy estimation.
Acknowledgments
We like to thank Japan Science and Technology Agency (JST, Precursory Research for Embryonic Science and Technology) for financial support.
Author Contributions
Ryosuke Takahira and Kumiko Tanaka-Ishii produced the experimental results. Kumiko Tanaka-Ishii and Łukasz Dębowski worked on the theoretical interpretations. Three authors contributed equally to proposing the ansatz for the entropy convergence. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shannon, S. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Shannon, C. Prediction and entropy of printed English. Bell Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Genzel, D.; Charniak, E. Entropy Rate Constancy in Text. In Proceedings of the 40th Annual Meeting of the Association for the ACL, Philadelphia, PA, USA, 7–12 July 2002; pp. 199–206.
- Levy, R.; Jaeger, T.F. Speakers Optimize Information Density through Syntactic Reduction. In Proceedings of the 19th International Conference on Neural Information Processing Systems, Doha, Qatar, 12–15 November 2012.
- Cover, T.M.; King, R.C. A Convergent Gambling Estimate of the Entropy of English. IEEE Trans. Inf. Theory 1978, 24, 413–421. [Google Scholar] [CrossRef]
- Brown, P.F.; Pietra, S.A.D.; Pietra, V.J.D.; Lai, J.C.; Mercer, R.L. An Estimate of an Upper Bound for the Entropy of English. Comput. Linguist. 1983, 18, 31–40. [Google Scholar]
- Kontoyiannis, I. The Complexity and Entropy of Literary Styles; Technical Report 97; Department of Statistics, Stanford University: Stanford, CA, USA, 1997. [Google Scholar]
- Schümann, T.; Grassberger, P. Entropy estimation of symbol sequences. Chaos 1996, 6, 414–427. [Google Scholar] [CrossRef] [PubMed]
- Hilberg, W. Der Bekannte Grenzwert der Redundanzfreien Information in Texten—Eine Fehlinterpretation der Shannonschen Experimente? Frequenz 1990, 44, 243–248. [Google Scholar] [CrossRef]
- Dębowski, Ł. Maximal Repetitions in Written Texts: Finite Energy Hypothesis vs. Strong Hilberg Conjecture. Entropy 2015, 17, 5903–5919. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P. Regularities unseen, randomness observed: The entropy convergence hierarchy. Chaos 2003, 15, 25–54. [Google Scholar] [CrossRef]
- Ebeling, W.; Nicolis, G. Entropy of Symbolic Sequences: The Role of Correlations. Europhys. Lett. 1991, 14, 191–196. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Brudno, A.A. Entropy and the complexity of trajectories of a dynamical system. Trans. Moscovian Math. Soc. 1982, 44, 124–149. [Google Scholar]
- Gao, Y.; Kontoyiannis, I.; Bienenstock, E. Estimating the Entropy of Binary Time Series: Methodology, Some Theory and a Simulation Study. Entropy 2008, 10, 71–99. [Google Scholar] [CrossRef]
- Grassberger, P. Estimating the information content of symbol sequences and efficient codes. IEEE Trans. Inf. Theory 1989, 35, 669–675. [Google Scholar] [CrossRef]
- Farach, M.; Noordewier, M.; Savari, S.; Shepp, L.; Wyner, A.; Ziv, J. On the Entropy of DNA: Algorithms and Measurements Based on Memory and Rapid Convergence. In Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, CA, USA, 22–24 January 1995; pp. 48–57.
- Shields, P.C. Entropy and Prefixes. Ann. Probab. 1992, 20, 403–409. [Google Scholar] [CrossRef]
- Willems, F.M.J.; Shtarkov, Y.M.; Tjalkens, T.J. The Context Tree Weighting Method: Basic Properties. IEEE Trans. Inf. Theory 1995, 41, 653–664. [Google Scholar] [CrossRef]
- Ziv, J.; Lempel, A. A Universal Algorithm for Sequential Data Compression. IEEE Trans. Inf. Theory 1977, 23, 337–343. [Google Scholar] [CrossRef]
- Bell, T.C.; Cleary, J.G.; Witten, I.H. Text Compression; Prentice Hall: Upper Saddle River, NJ, USA, 1990. [Google Scholar]
- Kieffer, J.C.; Yang, E. Grammar-based codes: A new class of universal lossless source codes. IEEE Trans. Inf. Theory 2000, 46, 737–754. [Google Scholar] [CrossRef]
- Nevill-Manning, C.G.; Witten, I.H. Identifying hierarchical structure in sequences: A linear-time algorithm. J. Artif. Intell. Res. 1997, 7, 67–82. [Google Scholar]
- Grassberger, P. Data Compression and Entropy Estimates by Non-Sequential Recursive Pair Substitution. 2002; arXiv:physics/0207023. [Google Scholar]
- Ryabko, B. Applications of Universal Source Coding to Statistical Analysis of Time Series. In Selected Topics in Information and Coding Theory; Woungang, I., Misra, S., Misra, S.C., Eds.; Series on Coding and Cryptology; World Scientific Publishing: Singapore, 2010. [Google Scholar]
- Dębowski, Ł. A Preadapted Universal Switch Distribution for Testing Hilberg’s Conjecture. IEEE Trans. Inf. Theory 2015, 61, 5708–5715. [Google Scholar] [CrossRef]
- Baayen, R.H. Word Frequency Distributions; Kluwer Academic Publishers: Berlin, Germany, 2001. [Google Scholar]
- Katz, S.M. Distribution of content words and phrases in text and language modelling. Nat. Lang. Eng. 1996, 2, 15–59. [Google Scholar] [CrossRef]
- Altmann, E.G.; Pierrehumbert, J.B.; Motter, A.E. Beyond Word Frequency: Bursts, Lulls, and Scaling in the Temporal Distributions of Words. PLoS ONE 2009, 4, e7678. [Google Scholar] [CrossRef] [PubMed]
- Louchard, G.; Szpankowski, W. On the average redundancy rate of the Lempel-Ziv code. IEEE Trans. Inf. Theory 1997, 43, 2–8. [Google Scholar] [CrossRef]
- Barron, A.; Rissanen, J.; Yu, B. The Minimum Description Length Principle in Coding and Modeling. IEEE Trans. Inf. Theory 1998, 44, 2743–2760. [Google Scholar] [CrossRef]
- Atteson, K. The Asymptotic Redundancy of Bayes Rules for Markov Chains. IEEE Trans. Inf. Theory 1999, 45, 2104–2109. [Google Scholar] [CrossRef]
- Dębowski, Ł. The Relaxed Hilberg Conjecture: A Review and New Experimental Support. J. Quant. Linguist. 2015, 22, 311–337. [Google Scholar] [CrossRef]
- Daniels, P.T.; Bright, W. The World’s Writing Systems; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Tanaka-Ishii, K.; Shunsuke, A. Computational Constancy Measures of Texts—Yule’s K and Rényi’s Entropy. Comput. Linguist. 2015, 41, 481–502. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).