1. Introduction
Open quantum systems is currently a very active field of research due to the fact that the interaction with the environment can hardly be ignored in many physical, chemical, and biological processes [
1,
2,
3]. One of the most standard ways of analyzing the corresponding dynamics is by considering the system of interest and the environment as forming a whole closed system (the Universe). The so-called Caldeira–Leggett Hamiltonian [
4] is a very illustrative and convenient starting point for an open dynamics. When tracing out the degrees of freedom of the environment in that dynamics, the resulting equations of motion for the system (in the Heisenberg picture of quantum mechanics) lead to some sort of coupled equations, one of them being a generalized Langevin equation. The presence of environmental fluctuations makes the system dynamical variables behave like stochastic processes. The generalized Langevin equation is transformed into a standard one when Ohmic (constant) friction is assumed.
An alternative approach can also be analyzed in terms of nonlinear quantum equations. One of them it is the well known logarithmic nonlinear Schrödinger equation proposed for an open dynamics due to Kostin [
5]; in particular, for the Brownian motion (linear dissipation). This equation is known as the Schrödinger–Langevin, or Kostin, equation. Recently, an application of this equation to the harmonic oscillator under the presence of thermal fluctuations (white and colored) has been reported [
6]. A generalized equation for nonlinear dissipation has also been proposed [
7,
8]. As pointed out by Schuch, Chung, and Hartmann [
9], this equation does not give the correct reduced frequency of the dissipative harmonic oscillator. Their proposed equation—also reported by Nassar [
10] and Nassar and Miret-Artés [
11] in a different context, the continuous quantum measurement—tries to avoid this inconvenience. Beretta also used the new proposal within the formalism of density matrix in his version of quantum thermodynamics [
12].
On the other hand, the description of many phenomena in terms of a two-level system (TLS) can also be found in the same fields of research mentioned before [
13], going from chiral molecules, electron transfer reactions, high energy physics, quantum optics, and computation to biological homochirality. Concerning molecular chirality, the pioneering work of Harris and Stodolsky [
14] considered the effect of parity violation on the tunneling dynamics of chiral molecules, relating it to their optical activity (see also [
15]). Based on this approach, the so-called parity violating energy difference (PVED) is considered to be one of the possible origins of molecular homochirality, referring to the almost exclusive one-handedness of chiral molecules found in living systems (D-sugars and L-amino acids). This is one of the fundamental problems of science which still remains unsolved [
16]. Thus, chiral molecules could be used as a test for parity violating interactions, since inconclusive results for electroweak parity violation would allow us to put some stringent bounds on parity-violating interactions different from the electroweak one. In particular, in the light of the recent advances in molecular PVEDs, some spin-dependent gravitational theories can be devised and studied [
17,
18].
In a series of papers [
19,
20,
21,
22], the authors have studied a chiral TLS in the presence of an environment (harmonic bath) leading to a more realistic analysis of chiral dynamics. The TLS is modeled by a two-well (asymmetric) potential within the Born–Oppenheimer approximation. A canonical formalism has been proposed where populations and coherences (by means of phase differences) are seen as stochastic processes, both of them being related to their optical properties. The time evolution of the non-isolated chiral TLS has provided information about coherent and incoherent tunneling. This theoretical analysis has also allowed us to successfully reproduce some thermodynamical properties of these systems from a stochastic dynamics. In general, there are several routes to reach thermodynamical properties such as partition functions, thermal averages, heat capacity, entropy, etc. Very likely, the most popular one is that based on the thermodynamic method coming from the path–integral formalism. An extensive account of this formalism can be found in Weiss’s book [
1]. However, numerical instability problems from the analytic continuation of certain functions lead to some drawbacks. As an alternative way to avoid such problems, the computation of thermodynamic functions from a stochastic dynamics is carried out here, presenting some advantages. Thus, canonical thermal averages are then calculated when carrying out dynamical calculations for different bias or asymmetry. Analogously, one can also obtain the main equilibrium thermodynamics properties of the non-isolated TLS from the stochastic dynamics at asymptotic times (if the dynamics is ergodic) for a given bias and different temperatures. Furthermore, it is worth stressing that the thermodynamic functions are independent of the friction coefficient in the weak coupling limit. Therefore, our thermodynamic average values coming from solving the corresponding stochastic dynamics are independent of the friction coefficient as time goes to infinity; that is, when the thermal equilibrium with the bath is reached. In the strong coupling limit, this fact no longer holds [
23]. A dynamical viewpoint has also been proposed within the density matrix formalism [
24].
As a new extension of our work, the so-called quantum stochastic resonance (QSR) [
25] provides a natural scenario to apply our canonical formalism. Very briefly, this process refers to the amplification of the response to an external periodic signal at a certain value of the noise strength, being a cooperative effect of friction, noise and periodic driving occurring in a bistable system. Classically, the output signal is maximum when the thermal hopping rate is in resonance with the frequency of the driving force. However, the quantum counterpart of this process seems to reveal new features [
26]. Time-dependent bias effects have been used to enhance the very elusive parity violation effects in previously mentioned molecules. In particular, a proposal to detect parity violation effects in diatomic molecules by DeMille et al. [
27] is currently ongoing and seems to be very promising (see [
28] and references therein). In addition, a very recent work by Harris and Walls [
29] proposes the use of an AC electric field that is resonantly modulated at the Larmor frequency to enhance the chiral term effects which appear when an electric field is coupled to nuclear magnetic resonance effects in chiral molecules [
30]. In this spirit, QSR would constitute a good playground where parity violating effects in chiral molecules could be tested. In a previous work [
31] within the linear response regime, we have shown that an external driving field that lowers and rises each of the minima of the well alternatively, a QSR signal should be observed only in the case that the PVED is different from zero, the resonance condition being independent of tunneling between the two enantiomers.
In this work, we mainly focus on the observation of QSR in chiral molecules within the previously developed canonical formalism. From this simple analysis, some important consequences on the possible detection of the PVED between chiral molecules are directly deduced. The manuscript is organized as follows. In
Section 2, the dynamical theory of quantum thermodynamics previously developed by the authors is briefly summarized.
Section 3 deals with the quantum stochastic resonance to be applied to chiral molecules. This section presents the main quantities of interest for the study of this singular resonance mechanism. In
Section 4, these quantities are evaluated by numerically solving the coupled differential equations issued from this canonical formalism, with special emphasis on the signals of parity violation between enantiomers. Finally, some concluding remarks are found in
Section 5.
3. Quantum Stochastic Resonance for an Open Chiral Two Level System
Although we have assumed so far that both
δ and
ϵ are time-independent variables, a richer dynamics is obtained when considering one of them (or both) time dependent. In order to simplify the discussion, only a time varying bias is going to be considered here. As previously mentioned, time-dependent bias effects have been proposed to enhance the very elusive parity violation effects in molecules [
27,
28,
29]. When the driving field enters the dynamics by making the replacement
where
ω and
are the corresponding frequency and amplitude of the driving field, the Hamiltonian function for the isolated TLS is modified according to
where the time dependence is now also in the bias term, modulating then the competing mechanism between the tunneling and the asymmetry of the TLS. The driving field proposed in Equation (
4) describes the case of a monochromatic periodic bias modulation [
1].
Within the Markovian regime, the corresponding stochastic dynamics is now given by the following coupled differential equations
which can be seen as a straightforward extension of Equation (
3) to an external driving field. In the deep tunneling regime, the TLS approximation is particularly useful, and the quantity of interest is the so-called power spectrum [
1]
where
is the time-averaged steady-state (asymptotic) population autocorrelation function
which can be expressed as
being the Fourier coefficients of the asymptotic population
Taking into account Equations (
7) and (
9), the power spectrum is expressed as
where
are known as the power amplitudes
which correspond to the different harmonics of the driving frequency. This is the way to observe the QSR. Classically, the stochastic resonance is maximal for the symmetric system (
) whereas, in the deep quantum regime, the QSR is only effective for the asymmetric system or static bias [
1]. Moreover, at low temperatures (coherent regime), the QSR occurs when the frequency of the driving force is near to fractional values of the static bias (
with
). At these values, the amplitude of the fundamental frequency in the power spectrum is reinforced, and the coherent motion induced by the driving force is amplified [
1]. Even more, when the amplitude of the driving force is smaller than the static bias, the power spectrum shows an amplification as a function of the temperature.
Furthermore, other magnitudes derived from the asymptotic behavior of the population also display the same behavior with time as, for instance, the internal energy
and the specific heat
where
. In general, we have that
and
with
.
In the linear response regime, which is the appropriate regime to study the tiny P-odd effect predicted, only the first two contributions,
and
1 of
are important. Following the standard procedure [
1], the zeroth-order contribution gives the population difference in thermal equilibrium without external driving field. The non-zero optical activity derived from this result is due to the PVED between enantiomers,
ϵ. The second contribution given by
is related by Kubo’s formula to the linear susceptibility of the system,
. Following the standard procedure [
1], assuming small friction and the restrictions
,
, and
, this contribution of the response of our system to the external amplitude
is expressed as [
31]
where
and
,
being a cutoff frequency. As a function of the temperature,
displays a maximum when
leading to a critical temperature of
which means that, due to the fact that the
ϵ parameter is extremely small, the maximum lies in the ultracold regime and is also independent of the tunneling rate.
4. Results
In order to study the dynamics of the QSR, the coupled differential equations given by Equation (
6) have to be solved. Units along this work are dimensionless. By doing this, we are considering a general dynamics where any chiral molecule can be represented. For example, if for a given chiral molecule
meV, we set this value to be 1 after passing the tunneling rate to inverse of atomic units of time,
. In all the calculation, we have further assumed that
in order to properly analyze the competition between tunneling and asymmetry or between delocalization and localization. For time integration, the time step used is optimized for an Ohmic friction of
or
(dimensionless rate). When working on thermodynamic functions, reduced units have also been employed; that is, energies and temperatures are divided by Δ. As mentioned previously, at high temperatures,
, thermal effects are going to be predominant over quantum effects which become relevant, in general, at times on the order of or less than the so-called thermal time,
β (in atomic units). However, at very low temperatures,
, the noise is usually colored and its auto-correlation function is complex, our approach being no longer valid. Here, a anonical (Maxwell–Boltzman) distribution is assumed, and only classical noise is considered since the ultracold regime is not going to be analyzed. On the other hand, the role of initial conditions has been extensively discussed in the literature (see, for example, [
1,
2]); for practical purposes, the chiral system will be prepared in one of its two states, left or right (
or
in order to avoid initial singularities, and very far from the equilibrium condition), and the initial phase difference
will be uniformly distributed around the interval
. The stochastic trajectories issued then from solving Equation (
6) are dependent on the five dimensional parameter space
, apart from
and
. When running trajectories, there are some of them visiting
nonphysical regions; that is,
. This drawback is mainly associated with the intensity of the noise, since for large values of it (which depends on both the temperature and the friction coefficient), the stochastic
z-trajectories can become unbounded. To overcome this problem, we have implemented a
reflecting boundary condition such that when the trajectory reaches
, we replace its value by
(or when
, by
). The number of such pathological trajectories is found to be very small, and over a very large number of trajectories, their weight is totally negligible.
The general strategy consists of solving the pair of non-linear coupled Equations (
6) for the canonical variables under the action of a Gaussian white noise, which is implemented by using an Ermak-like approach [
35,
36]. Note that in the Langevin-like coupled equations to be solved, the noise term only appears in the equation of motion of the
z-variable. The time step used is
(dimensionless units) for all the cases analyzed. For a given
, unstable trajectories can also be found for certain values of
ϵ,
δ, and
γ in the simple case of dissipative (non-noisy) dynamics [
19]. As this problem persists in case of dealing with stochastic trajectories, not every triplet
gives place to a stable trajectory. In these cases, the time evolution of each individual trajectory is not possible, and a previous stability analysis is mandatory. However, in the stable case, a satisfactory description of population differences and coherences, average energies, and heat capacity have been achieved by running up to
trajectories (as previously used) [
21,
22]. The friction coefficient used is finally
(dimensionless rate), and a canonical (Maxwell–Boltzmann) distribution is assumed, only classical noise being considered.
The numerical uncertainty when solving Equation (
6) has been calculated to be
for
z and
radians for Φ, where
is the time step. From simple arguments, we have estimated that the error in
z is
. For other magnitudes, such as the heat capacity, we have that
(in our reduced units).
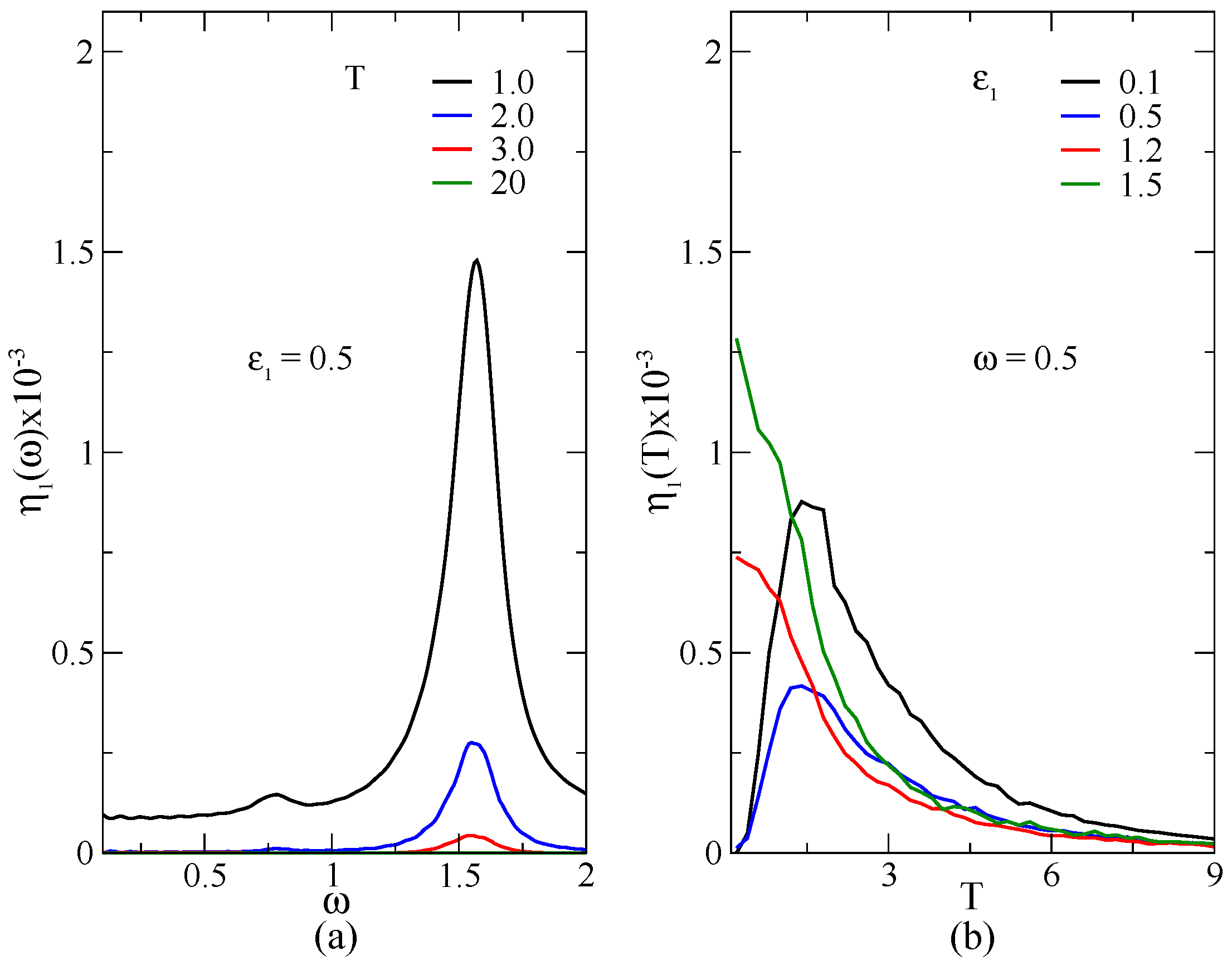
The QSR can be observed from the power amplitudes. In
Figure 1, the power amplitude
of the power spectrum as a function of the frequency of the external driving force (
Figure 1a) and the temperature (
Figure 1b) are plotted. The results are obtained for
,
, and
. In
Figure 1b, three different regimes are clearly displayed for a given driving frequency, as a function of the temperature. In the case of
, the power amplitude exhibits a more or less exponential decay as the temperature increases. When
, a maximum (quantum stochastic resonance) is observed at low temperatures, around the critical temperature
. Finally, if
, the resonance maximum is clearly enhanced. The evolution of the system could be described in the framework of the linear response theory [
1]. Moreover, in
Figure 1a where
is plotted as a function of
ω for different temperatures, a large peak near
and a smaller one around
(
) are observed, as also predicted by different theories. We also note that these peaks disappear as temperature increases. From Equation (
17), a simple analytical expression can be easily deduced from this power amplitude.
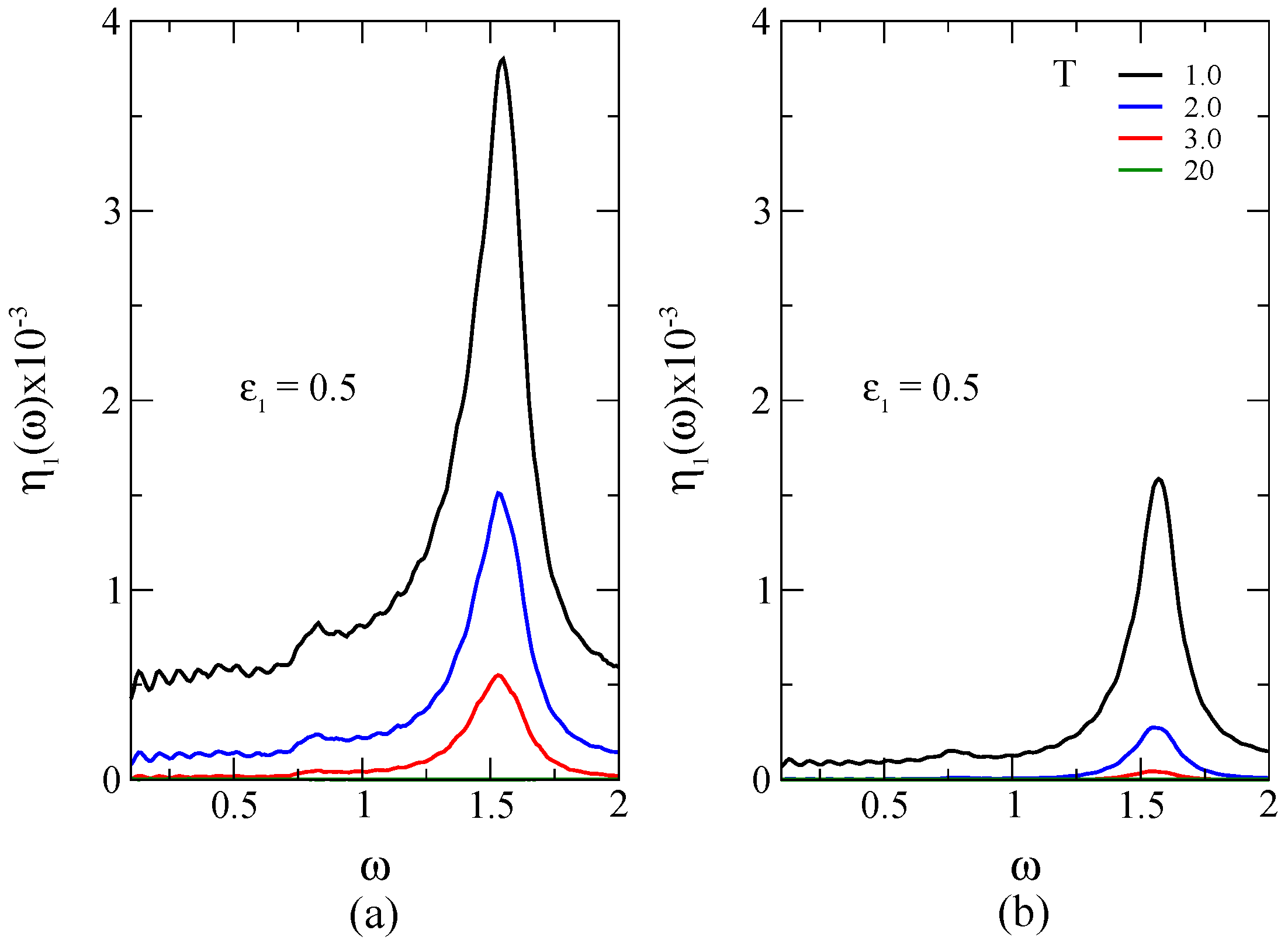
A very interesting and distinguishing feature between biased and unbiased systems is shown clearly in
Figure 2. The second Fourier coefficient of the power spectrum is completely suppressed for a symmetric (unbiased) potential. In
Figure 2a (b), the dynamics is starting from (out of) the thermodynamical equilibrium. In both cases, the parameters are
,
,
, and
. According to these results, the presence of
peak in the power spectrum could be used as an unambiguous signal of parity violation in chiral molecules.
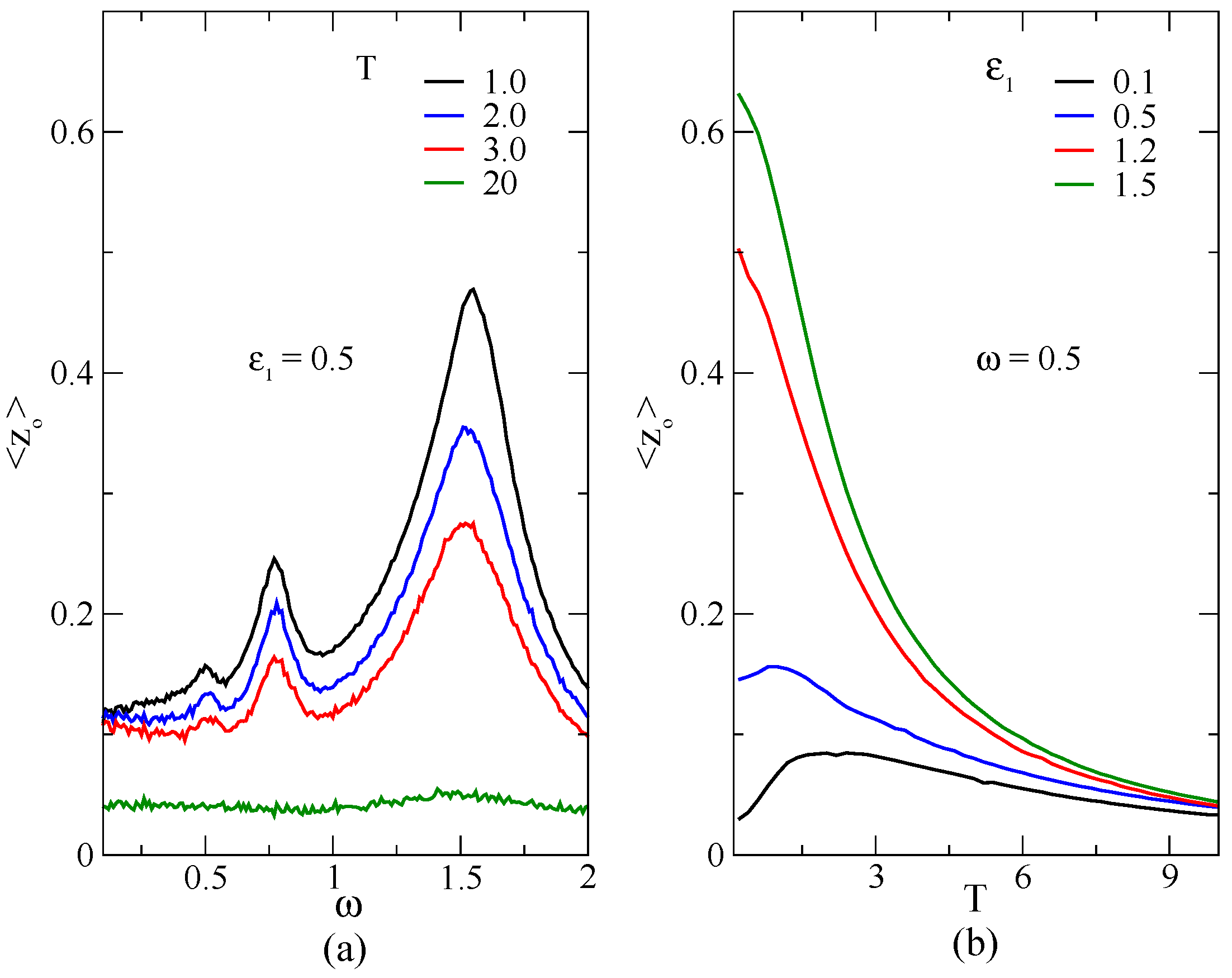
Interestingly enough, the features observed in the amplitude of the fundamental frequency of the power spectrum are also revealed in the behavior of other magnitudes, such as the population difference. In
Figure 3, average population differences,
, as a function of the frequency of the external driving force (
Figure 3a) and as a function of the temperature (
Figure 3b) are displayed for
,
, and
. It is clearly observed that the population difference exhibits well defined peaks around the fractional values of the static bias even for frequency values around
. When the temperature is increased more and more, an incoherent regime is rapidly established. For the same cases, in
Figure 4, the power amplitude
of the fundamental frequency in the power spectrum is plotted when propagation is starting far from thermodynamical equilibrium values (
Figure 4a) and close to them (
Figure 4b). When simulations start far from the thermodynamical equilibrium, the quantum stochastic resonance features observed in
are shown to be larger than those obtained starting closer.
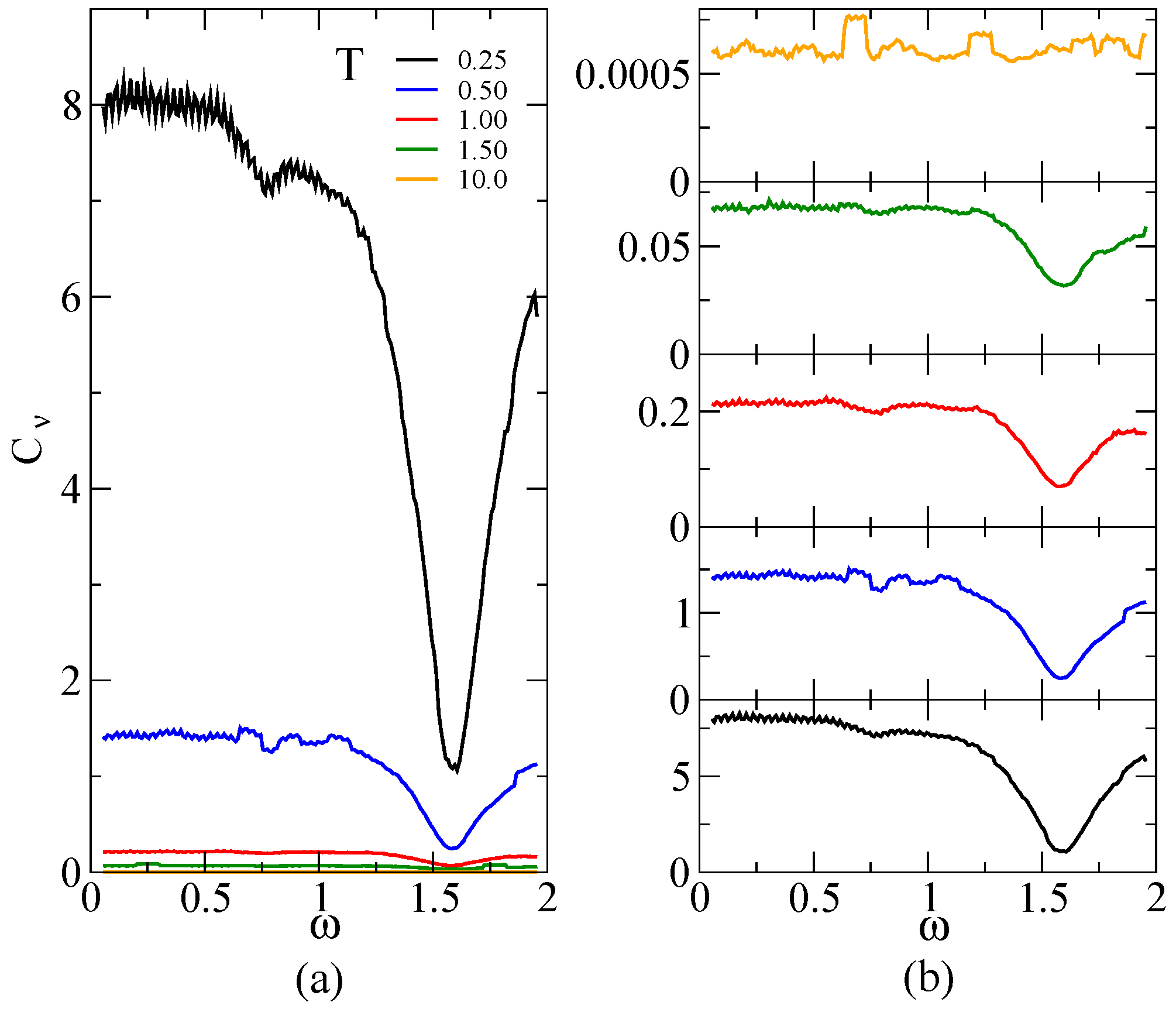
Finally, in
Figure 5, the heat capacity as a function of the frequency of the external bias for different temperatures is displayed. In these calculations,
,
,
, and
. This thermodynamical function shows a strong dependence on this frequency with temperature. It is important to note the appearance of extrema in the same regions where average population differences display a maximum (see
Figure 3). The same behavior is observed when starting the dynamics from non-equilibrium initial conditions. Different plots of the Fourier components of the internal energy and heat capacity at asymptotic times can also be easily analyzed in the light of Equations (
14)–(
16).