1. Introduction
In this paper, we will consider the following high (
d-) dimensional parabolic Volterra integro-differential equation with memory kernel
in the infinite domain [
1]:
which satisfies the initial condition and boundary conditions below,
where function
and memory kernel function
are assumed to be sufficiently smooth functions, and
is the
d-dimensional Laplacian operator.
Parabolic Volterra integro-differential equations present an important model to simulate the effects of the “memory” of the system. The model is based on a partial differential equation, combining the partial differentiation and integral term containing the unknown kernel function that leads to parabolic Volterra integro-differential equations. In general, the model nonlocal effects of the memory of past history cannot be described by partial differential equations. Therefore, more and more researchers have studied the solution of integro-differential equations.
Diffusion is one of the most important and ubiquitous phenomena in nature. The parabolic Volterra integro-differential equation model Equation (1) can be also describe anomalous diffusion; see references [
2,
3]. The reaction diffusion level most depends on the choice of the kernel
present in the nonlocal reaction diffusion (integral) term.
Parabolic Volterra integro-differential equations have many important physical applications to model dynamical systems, such as in compression of viscoelastic media [
4], nuclear reactor dynamics [
5], blow-up problems [
6], reaction diffusion problems [
7] and heat conduction materials with memory functional [
8], etc. So far, the analysis of numerical solution of Volterra integral-differential equations has been carried out by many authors. Avazzadeh et al. [
9] proposed radial basis functions through the finite difference method to find a nonlinear Volterra integro-differential equation’s numerical solution. Aguilar et al. [
10] proposed collocation methods to solve second-order parabolic Volterra integro-differential equations. Dehghan et al. [
8] studied numerical solution of parabolic integro-differential equations using the variational iteration method. Han et al. [
1] proposed the artificial boundary method to solve parabolic Volterra integro differential equations (one/two-dimensional) in infinite spatial domains. Fakhar-Izadi et al. [
11] considered the parabolic Volterra integro-differential equation in one-dimensional finite and infinite spatial domains using spectral collocation methods. Vasudeva Murthy et al. [
12] investigated parabolic integro-differential equations through explicit integration and the Runge-Kutta-Chebyshev method.
However, to the authors’ knowledge, there are no studies on analytical solutions of parabolic partial Volterra integro-differential equation in the infinite domain. In this article, our goal is mainly to discuss analytical solutions of Equation (1) with three different kinds of memory kernel functions in the infinite domain.
This paper is organized as follows. In
Section 2, some definitions and lemmas are introduced. In
Section 3, the analytical solutions of parabolic Volterra integro-differential equation with three different kinds of memory kernel are demonstrated in the infinite domain. In
Section 4, a typical example and some graphical representations of the solution are presented. Some conclusions are given in
Section 5.
2. Preliminaries
In this section, we present some fundamental definitions and lemmas that are used throughout this paper.
Definition 1. A four-parameter Mittag-Leffler (M-L) function is defined as [13]where , max , with Pochammer’s symbol can be expressed as It is worth noting that when
, the three-parameter Mittag-Leffler function can be expressed as
[
13,
14]:
where
, and
is the Pochhammer symbol.
Note the relation between generalized the Mittag-Leffler function and the Fox-H function:
where
[
15] is a Fox-H function, and
.
Note that, when
, we can obtain a two-parameter Mittag-Leffler function
[
16], there
where
,
. Note that
reduces to Mittag-Leffler function
when
, then
where
,
. In particular, we can obtain a regular exponential function when
.
Definition 2. An integral operator is defined as [17,18] It is worth noting that, when
and
, integral operator
would correspond to the Riemann-Liouville integral operator [
13].
In this section, we will introduce some fundamental lemmas for the Laplace transform (), which will be help us handle some problems in the next section.
Lemma 1. Let s, b, α, , and then the following inverse Laplace transform () is true [18].where Lemma 2. The Laplace transform of a three-parameter Mittag-Leffler function is given by [18,19]where . Lemma 3. The Laplace transform of is given by the following [19]:where . It is worth noting that in case , the structure of Lemma 3 is equivalent to Lemma 2.
Lemma 4 gives one important d-dimensional integral formula for the Mittag-Leffler function.
Lemma 4. For arbitrary α > 0, β is an arbitrary complex number, , and , establishing the following formula: [20] In fact, here
is a Bessel function, and
denotes the
n-th derivatives of the two-parameter Mittag-Leffler function.
n-th derivatives of the two-parameter Mittag-Leffler function can be expressed in terms of the Fox-H function as
Furthermore, on the right of Equation (10) is the following:
where
[
15] is the Fox-H function.
3. Analytical Solution of a Parabolic Volterra Integro-Differential Equation in the Infinite Domain
3.1. Analytical Solution with Frictional Memory Kernel of M-L type
In this case, Equation (1) can be written as follows:
where
,
is the memory time.
Theorem 1. The analytical solution of parabolic Volterra integro-differential Equation (11) with boundary conditions and initial condition (2) can be expressed as the following analytical form In which
is the Green function and reads as
In general, this denotes as the Fourier transform of with respect to the spatial variable . The Laplace transform of a function with regard to the time variable is defined as
Proof. This denotes
as the Fourier transform of
with respect to variable
, and
as the Laplace transform of
with respect to variable
. Taking the Laplace transform with respect to the time variable
t and the Fourier transform with respect to the spatial variable
x to Equation (11), we obtain a nonhomogeneous equation, which can be written as the following:
Using the initial condition, it yields:
Employing Lemma 2, we can get
Substituting Equations (15) and (16) into the first term of Equation (14), we have
By applying inverse Laplace transform (
), the convolution definition of a Laplace transform and Definition 2, we can obtain the inverse Laplace transform of the first term in Equation (14) as follows:
It follows that the inverse Laplace transform of the second term in Equation (14) is
According to Equations (18) and (19), we can obtain
from Equation (14)
Equation (20) can be further manipulated by employing an inverse Fourier transform:
We need and we presented that the series and integrals (21) are convergent. And is generalization of the Mittag-Leffler function.
The second term in Equation (21) can be further manipulated as follows
Denote Green function
is
Therefore, we complete the proof of Theorem 1. □
3.2. Analytical Solution with a Frictional Memory Kernel of Power-Law Type ,
In this case, Equation (1) can be written as the following:
Theorem 2. The analytical solution of parabolic Volterra integro-differential Equation (23) with boundary conditions and initial condition (2) can be expressed as The Green function
is given as
Note that and are the Fourier transform of and , respectively.
Remark. Employing the properties of the Fox-H functions, Green function can be expressed as a power series expansion [15] For
, therefore, the power-law asymptotics behavior is given by
Proof. Employing the Laplace transform with respect to variable
and Fourier transform with respect to variable
, respectively. We obtain the following nonhomogeneous equation
☐
Taking into account the initial condition, we obtain the following nonhomogeneous differential equation, and Equation (25) can be rewritten as
Using the technique introduced by [
18], we have
Expanding the third section on the right of Equation (27) and simplifying, one can easily get
Employing Lemma 2 in Equation (28), the first term of Equation (26) can be expressed as
We need and showed that series (29) is convergent. Also, is a generalization of the three-parameter Mittag-Leffler function.
According to the three-parameter Mittag-Leffler function definition, from Equation (29), we get
Applying the convolution property of the Laplace transform and integral operator
Definition 2, the inverse Laplace transform of the first term in Equation (26) can be obtained as follows:
Considering the relationship between the generalized Mittag-Leffler function and the Fox-H function, the inverse Laplace transform of the second term in Equation (26) can be expressed as [
15]
Using the inverse Fourier transform (
) in Equation (33), we can obtain
Using Lemma 4, we get the following result from Equation (35)
Employing a Hankel transform and the properties of the Fox-H functions [
15,
21,
22], Equation (36) can be written as
Substituting Equation (37) into the inverse Fourier transform of Equation (34), we can obtain
Then Equation (32) can also be written formally as
Applying an inverse Laplace transform to Equation (26), we can finally find
Equation (39) can be further manipulated by employing inverse Fourier transform and Fourier convolution theorem, respectively. Accordingly, the Theorem 2 is clearly demonstrated.
3.3. Analytical Solution with Frictional Memory Kernel of Exponential Factor Type ,
In this case, Equation (1) can be written in the following form
Theorem 3. The analytical solution of parabolic Volterra integro-differential Equation (40) with boundary conditions and initial condition (2) can be expressed as the following analysis formula: Letting
, using the asterisk (
) to denote a Laplace convolution, the Green function
is given by
Proof. Applying the Laplace and Fourier transform with respect to the time variable
and spatial variable
to Equation (40), and using the initial conditions, Equation (40) can be written as
☐
From Equation (42), we have
Applying power series expansion, one obtains
Combining with Lemma 3, Equation (44) can be expressed as
We need and showed that series (45) is convergent. In addition, is a generalization of the Mittag-Leffler function.
Through Equation (45), the first term in Equation (43) can be formally written as
Finally, the inverse Laplace transform of the first term in Equation(43) can be rewritten as
After analogous manipulation, the inverse Laplace transform of the second term of Equation (43) can be expressed as
Performing an inverse Laplace transform in Equation (43), we finally get
The solution is now obtained by performing an inverse Fourier transform in Equation (49), which produces
where the Green function is denoted as
Therefore, we complete the proof of Theorem 3.
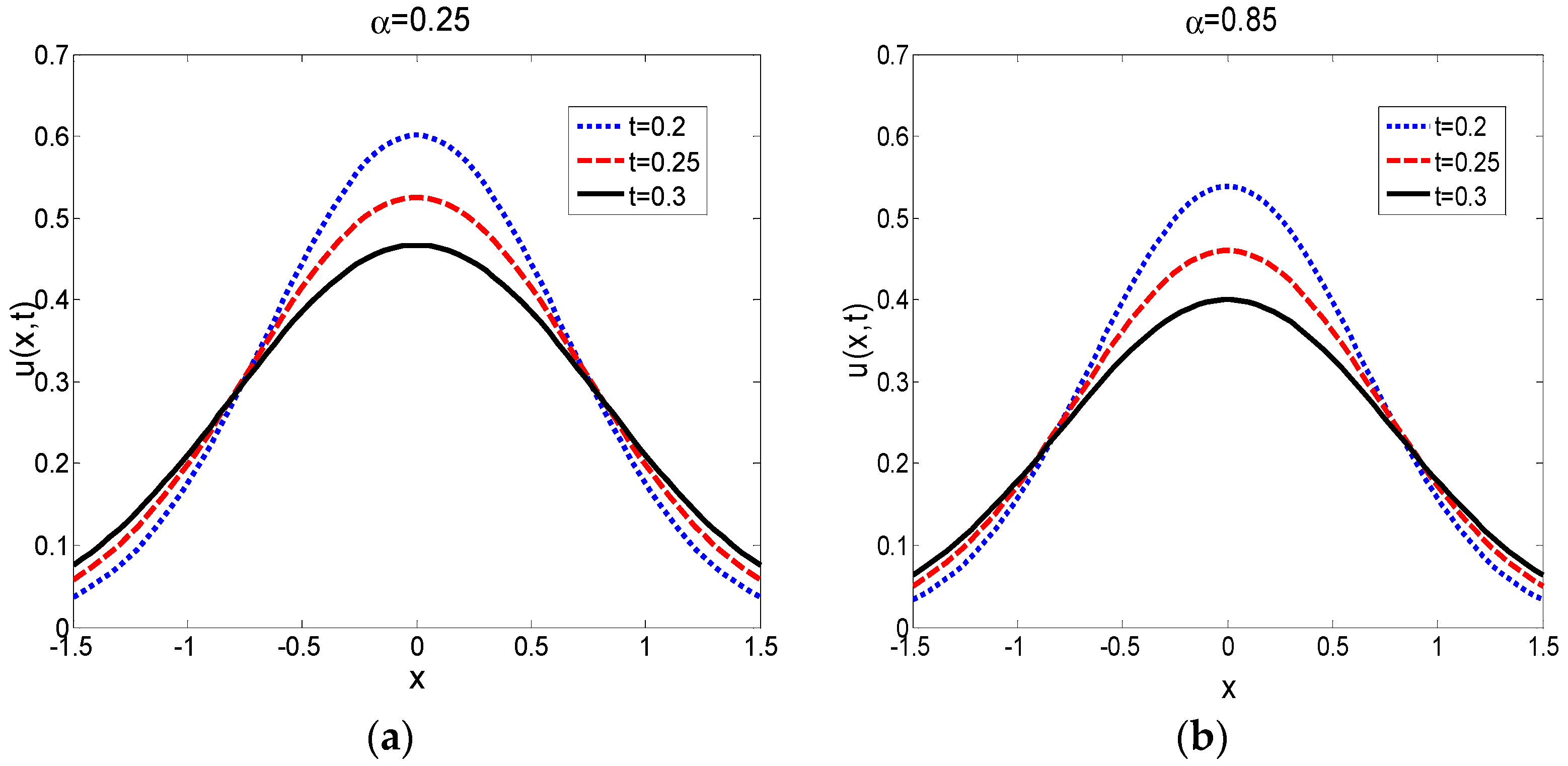
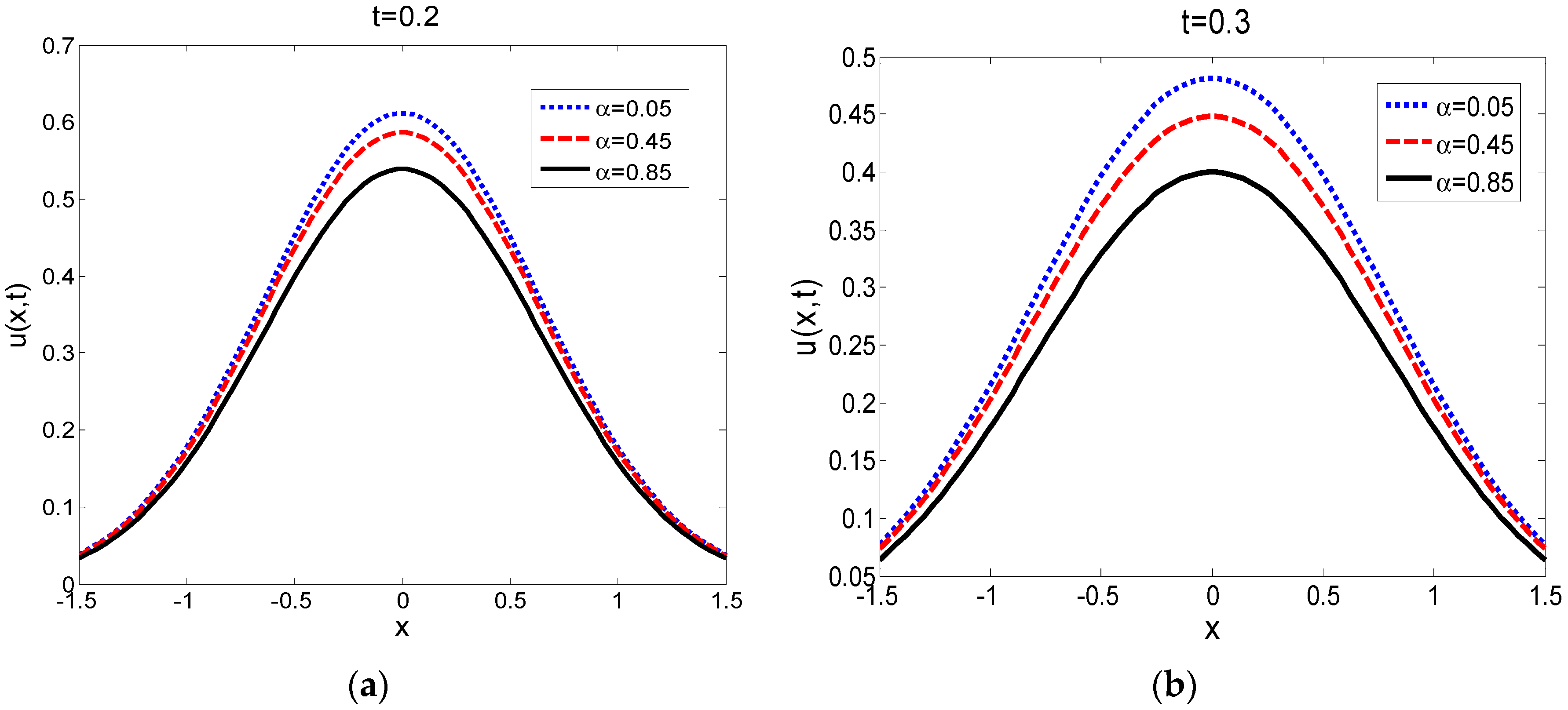
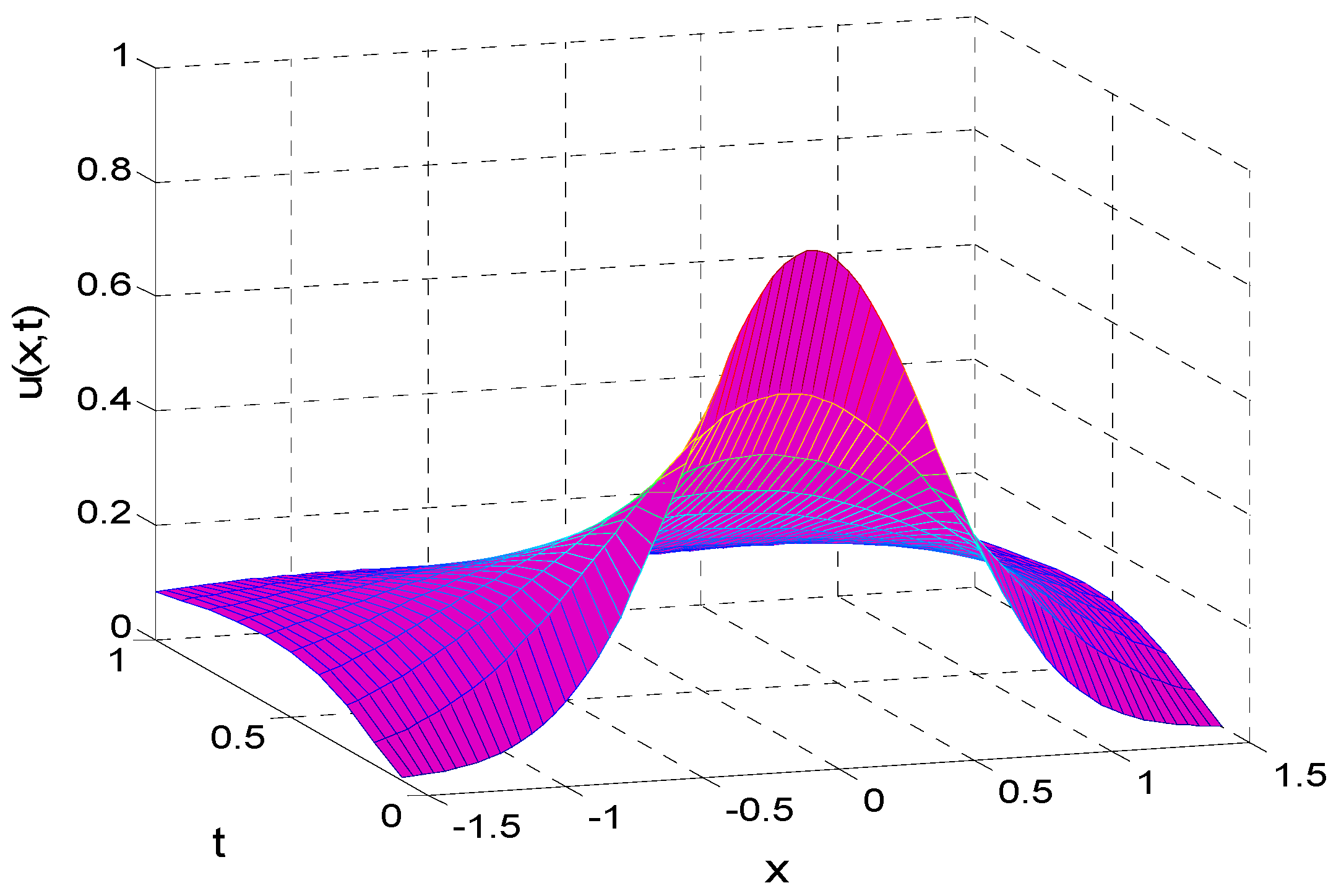
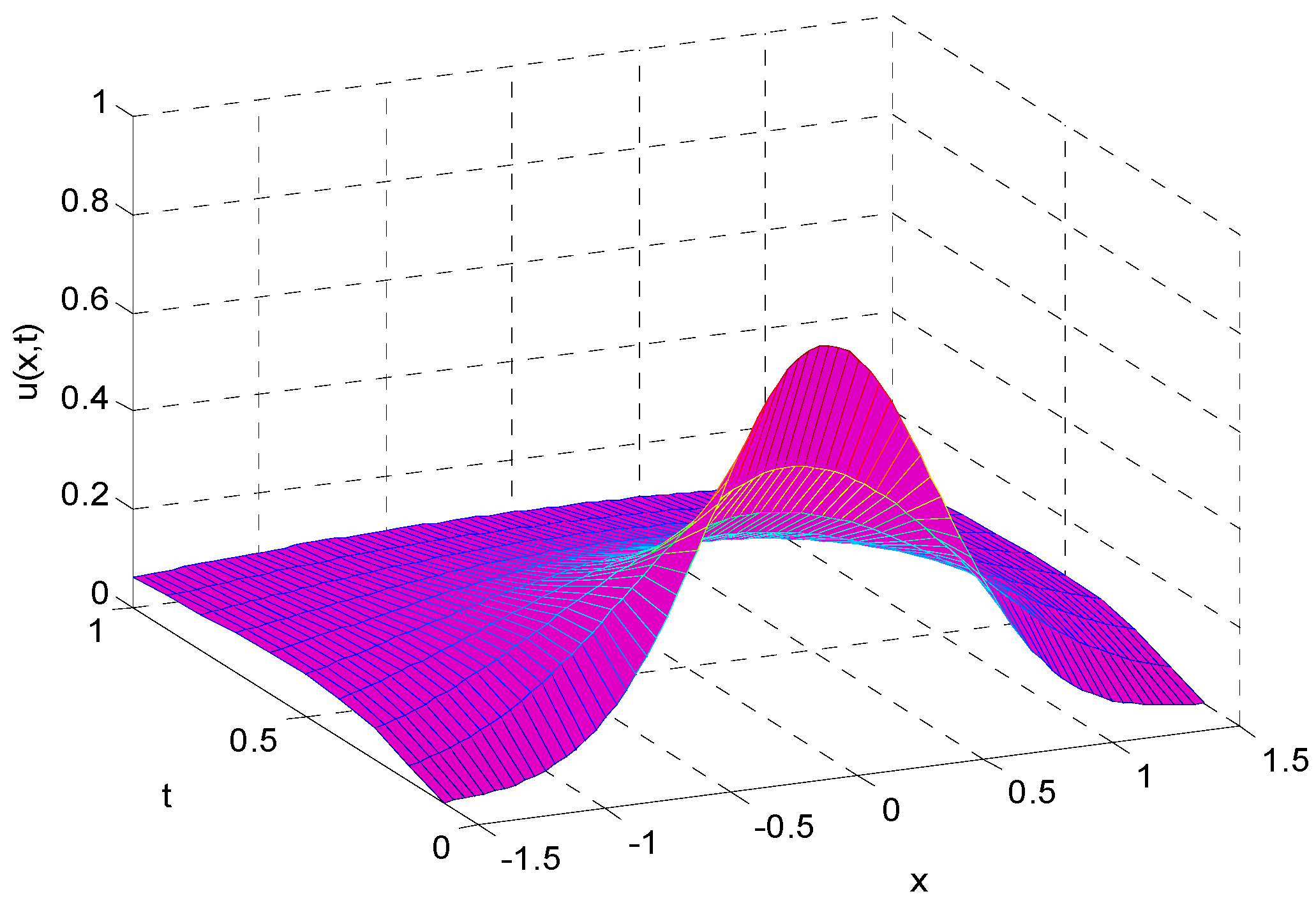
5. Conclusions
In practical applications, different types of the frictional memory kernel
have been used to describe a wide variety of complex dynamics and physical phenomena with memory effects. In this paper, by applying the Laplace transform method to the time variable and the Fourier transform to the spatial variable, we obtained analytical solutions to parabolic Volterra integro-differential equations with three different kinds of memory kernel in the infinite domain. The analytical solutions to the parabolic Volterra integro-differential equation consist of some special functions, such as the multi-parameter Mittag-Leffler function and Fox-H function. It is worth mentioning that the analytical solution provided in Equation (24) can also be obtained by applying the references method [
23,
24,
25] to Equation (23). In the end, some curves of the analytical solution are given, and the curves exhibit a long tail behavior for a large time. We found that a parabolic Volterra integro-differential equation with a power-law memory kernel is characterized by anomalous diffusion. The analytic solution of (1) can be found in some special cases, but in general it is difficult to obtain because of the non-local property of the integral term. Thus, in many cases, the more reasonable option is to find its numerical solution. Meanwhile, the analytical solutions we obtained from parabolic Volterra integro-differential equations with different types of frictional memory kernel provide great convenience for practical applications.