Information-Theoretic Neuro-Correlates Boost Evolution of Cognitive Systems
Abstract
:1. Introduction
2. Background
2.1. Network-Theoretic Neuro-Correlates
2.1.1. Minimum-Description-Length
2.1.2. Topological Complexity
2.1.3. Connectivity and Sparseness
2.1.4. Representations
2.1.5. Information Integration
2.1.6. Predictive Information
2.2. Complex Environments
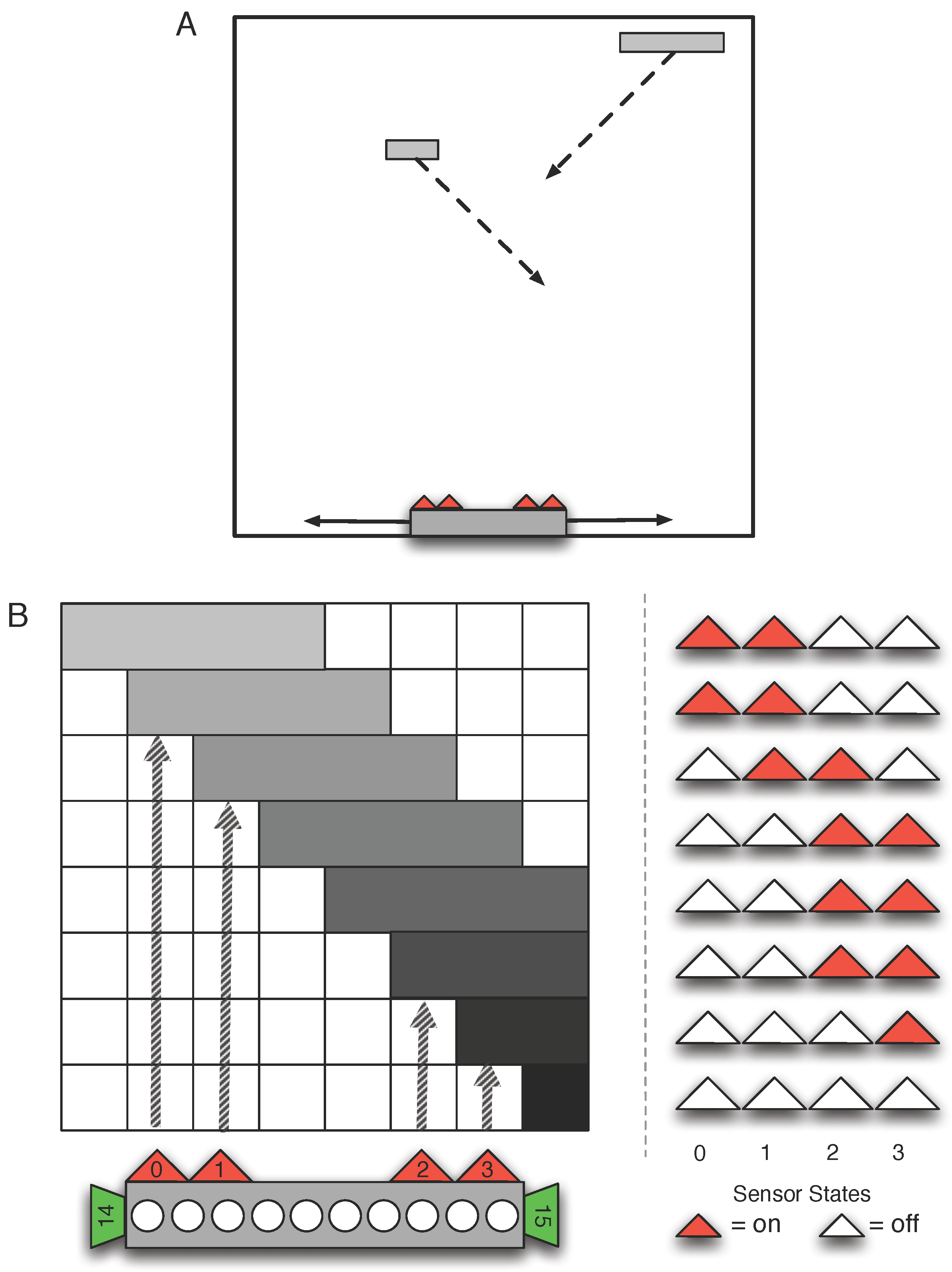
3. Methods
4. Results and Discussion
 ), with Gamma Index (★), with sparseness (+), with (◇), and with (
), with Gamma Index (★), with sparseness (+), with (◇), and with (  ) on task performance.
) on task performance.
 ), with Gamma Index (★), with sparseness (+), with (◇), and with (
), with Gamma Index (★), with sparseness (+), with (◇), and with (  ) on task performance.
) on task performance.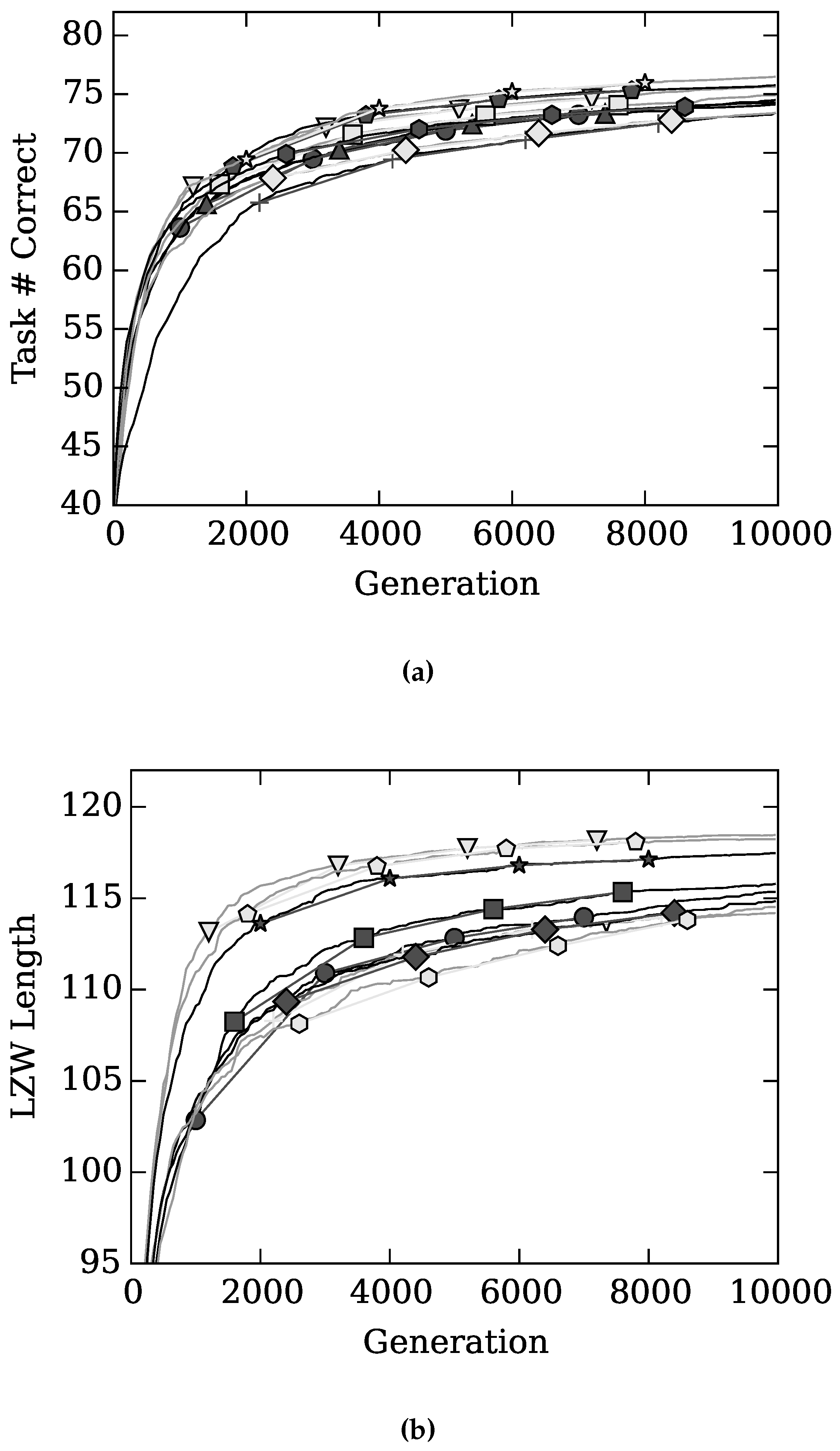
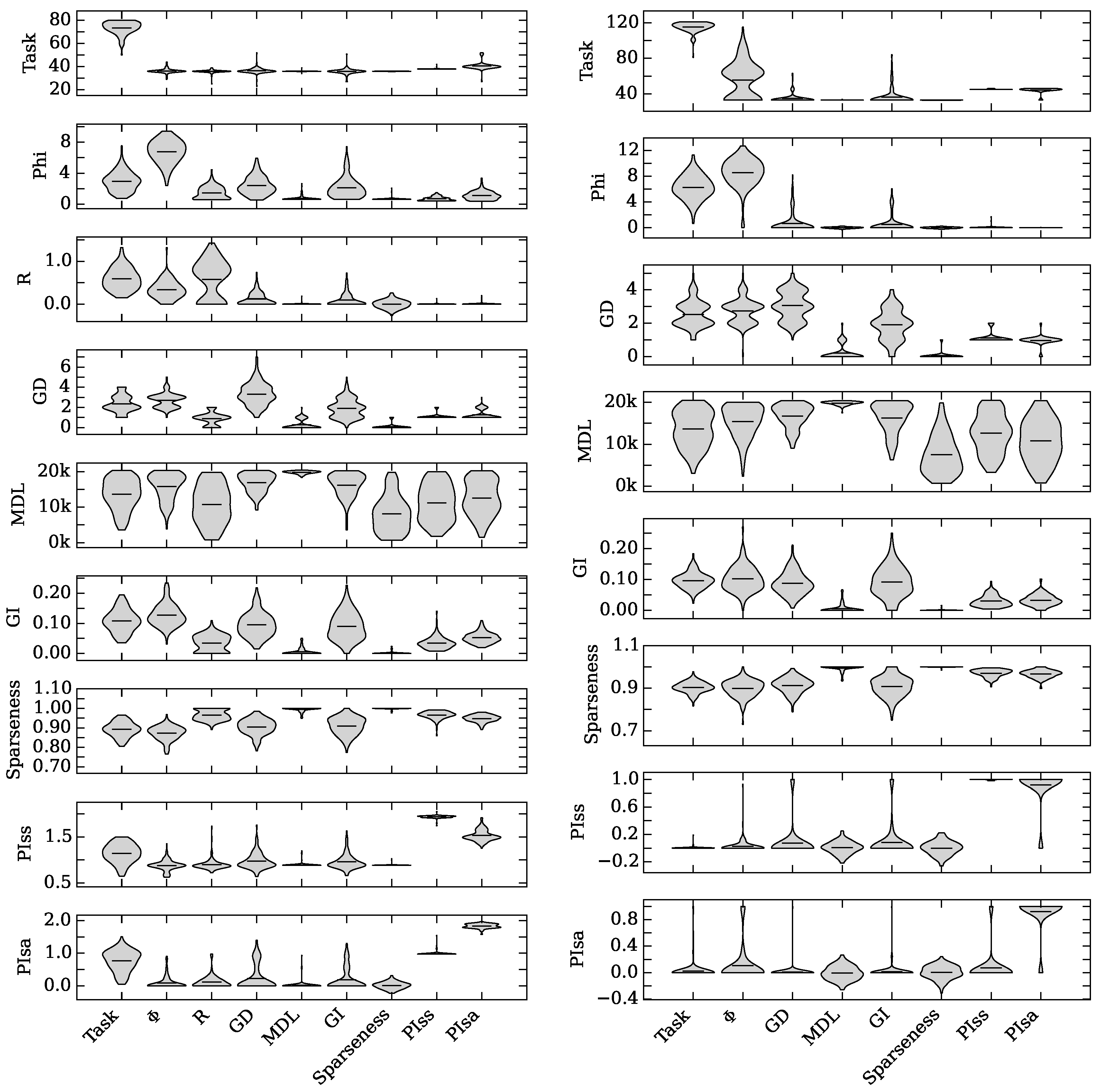
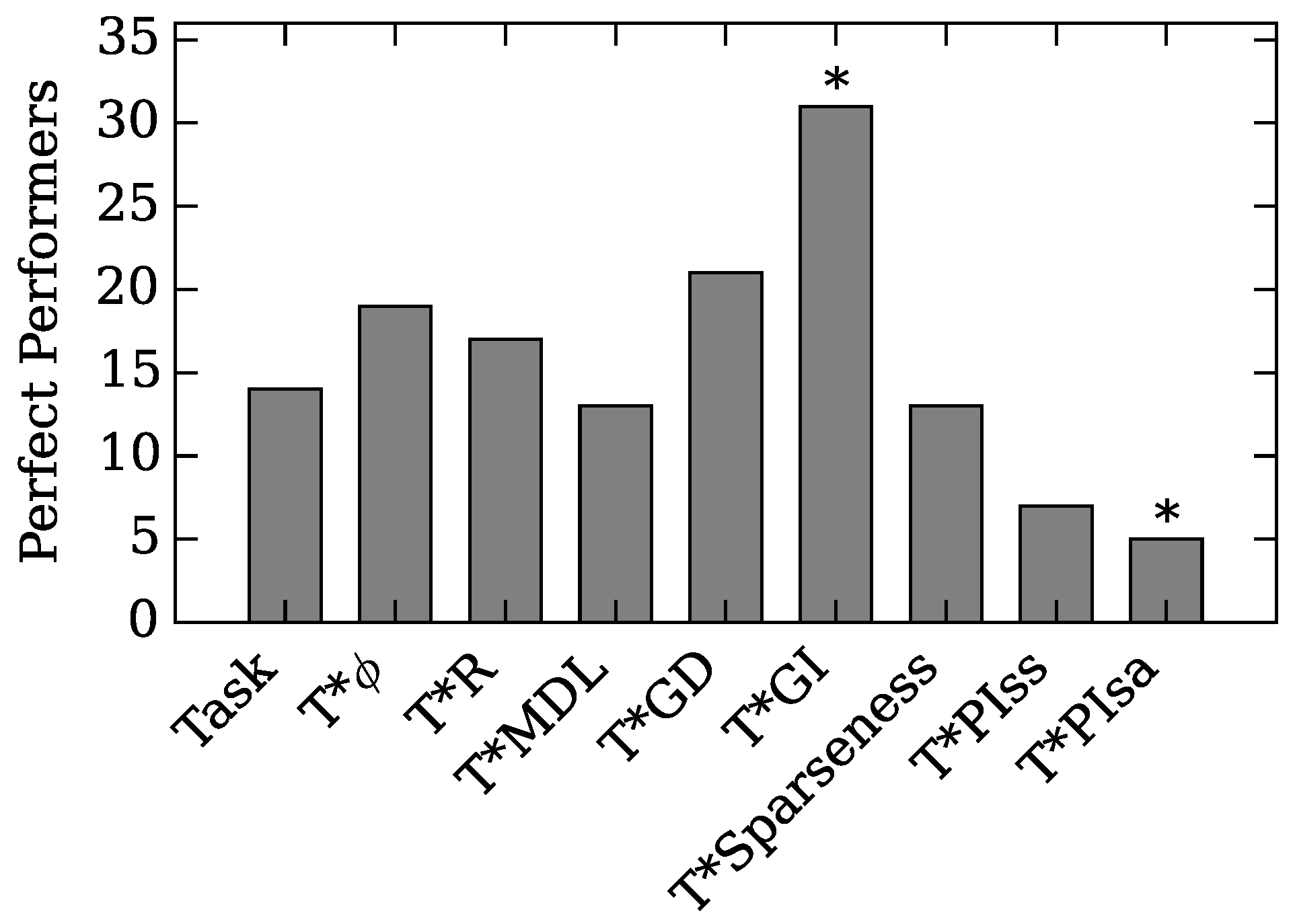
4.1. Augmented Selection and Its Effect on Other Neuro-Correlates


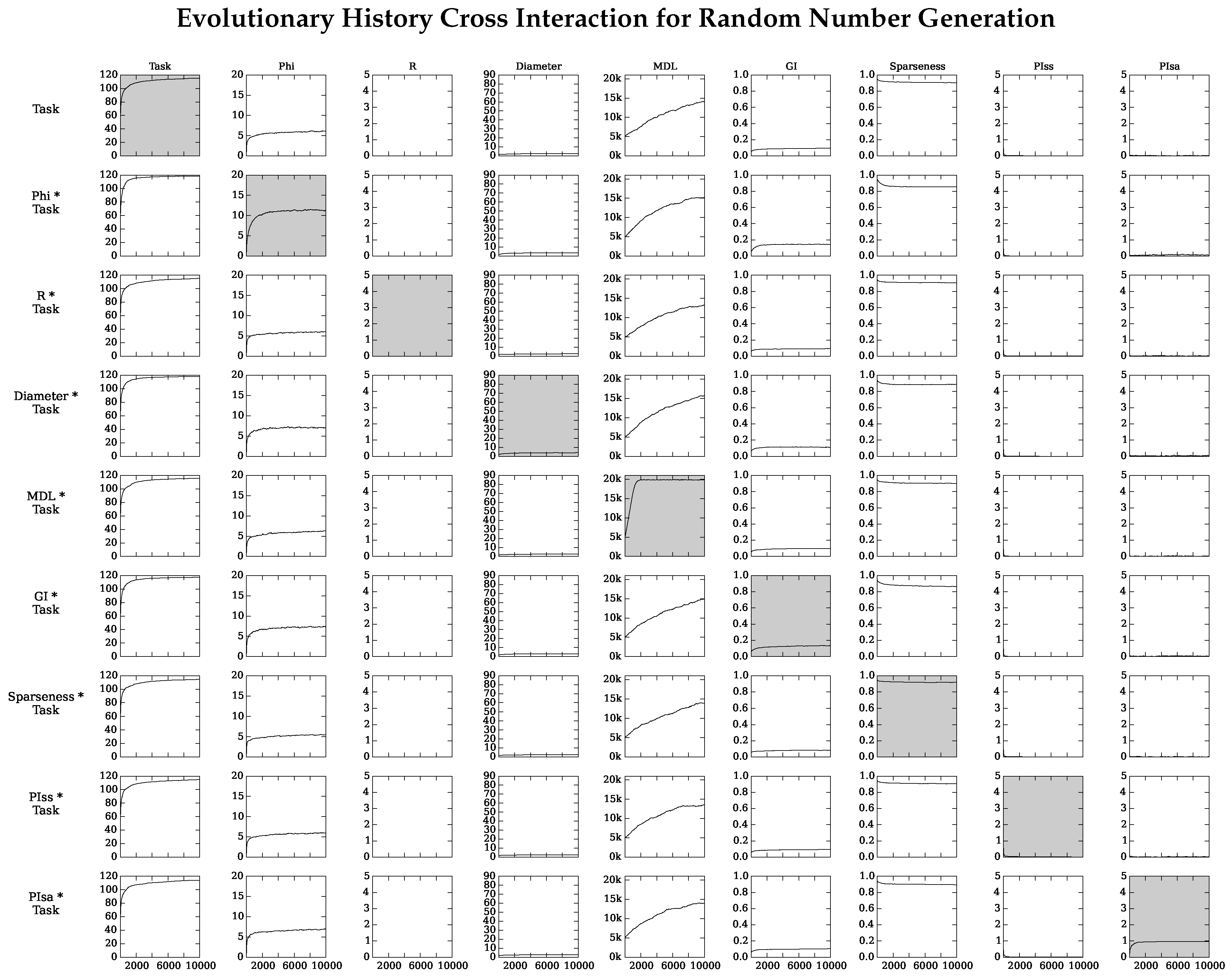
4.2. Neuro-Correlate Interactions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A


References
- Nguyen, A.; Yosinski, J.; Clune, J. Deep Neural Networks are Easily Fooled: High Confidence Predictions for Unrecognizable Images. In Proceedings of the IEEE 2015 Computer Vision and Pattern Recognition (CVPR ’15), Cambridge, MA, USA, 7–12 June 2015.
- Yao, X. Evolving artificial neural networks. Proc. IEEE 1999, 87, 1423–1447. [Google Scholar]
- Floreano, D.; Dürr, P.; Mattiussi, C. Neuroevolution: From architectures to learning. Evolut. Intell. 2008, 1, 47–62. [Google Scholar] [CrossRef]
- Michalewicz, Z. Genetic Algorithms + Data Strucures = Evolution Programs; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- De Jong, K.A. An Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1975. [Google Scholar]
- Whitley, D.; Rana, S.; Heckendorn, R.B. The Island Model Genetic Algorithm: On Separability, Population Size and Convergence. J. Comput. Inf. Technol. 1998, 7, 33–48. [Google Scholar]
- Bitbol, A.-F.; Schwab, D.J. Quantifying the role of population subdivision in evolution on rugged fitness landscapes. PLoS Comput. Biol. 2014, 10, e1003778. [Google Scholar] [CrossRef] [PubMed]
- Lehman, J.; Stanley, K.O. Exploiting Open-Endedness to Solve Problems Through the Search for Novelty. In Proceedings of the Eleventh International Conference on Artificial Life (ALIFE XI), Winchester, UK, 30–31 July 2008; MIT Press: Cambridge, MA, USA.
- Zhou, A.; Qu, B.-Y.; Li, H.; Zhao, S.-Z.; Suganthan, P.N.; Zhang, Q. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Clune, J.; Mouret, J.-B.; Lipson, H. The evolutionary origins of modularity. Proc. R. Soc. Lond. B Biol. Sci. 2013, 280. [Google Scholar] [CrossRef] [PubMed]
- Deb, K. Multi-Objective Optimization. In Search Methodologies; Springer: Berlin/Heidelberg, Germany, 2014; pp. 403–449. [Google Scholar]
- Beer, R.D. Toward the Evolution of Dynamical Neural Networks for Minimally Cognitive Behavior. In From Animals to Animats 4; Maes, P., Mataric, M., Meyer, J.-A., Pollack, J., Wilson, S., Eds.; MIT Press: Cambridge, MA, USA, 1996; pp. 421–429. [Google Scholar]
- Beer, R.D. The dynamics of active categorical perception in an evolved model agent. Adapt. Behav. 2003, 11, 209–243. [Google Scholar] [CrossRef]
- Van Dartel, M.; Sprinkhuizen-Kuyper, I.; Postma, E.; van Den Herik, J. Reactive Agents and Perceptual Ambiguity. Adapt. Behav. 2005, 13, 227–242. [Google Scholar] [CrossRef]
- Marstaller, L.; Hintze, A.; Adami, C. The evolution of representation in simple cognitive networks. Neural Comput. 2013, 25, 2079–2107. [Google Scholar] [CrossRef] [PubMed]
- Welch, T.A. A technique for high-performance data compression. Computer 1984, 6, 8–19. [Google Scholar] [CrossRef]
- Brugger, P.; Monsch, A.U.; Salmon, D.P.; Butters, N. Random number generation in dementia of the Alzheimer type: A test of frontal executive functions. Neuropsychologia 1996, 34, 97–103. [Google Scholar] [CrossRef]
- Baddeley, A. Random generation and the executive control of working memory. Q. J. Exp. Psychol. A 1998, 51, 819–852. [Google Scholar] [CrossRef] [PubMed]
- Jahanshahi, M.; Saleem, T.; Ho, A.K.; Dirnberger, G.; Fuller, R. Random number generation as an index of controlled processing. Neuropsychology 2006, 20, 391–399. [Google Scholar] [CrossRef] [PubMed]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Albantakis, L.; Hintze, A.; Koch, C.; Adami, C.; Tononi, G. Evolution of integrated causal structures in animats exposed to environments of increasing complexity. PLoS Comput. Biol. 2014, 10, e1003966. [Google Scholar] [CrossRef] [PubMed]
- Edlund, J.A.; Chaumont, N.; Hintze, A.; Koch, C.; Tononi, G.; Adami, C. Integrated information increases with fitness in the evolution of animats. PLoS Comput. Biol. 2011, 7, e1002236. [Google Scholar] [CrossRef] [PubMed]
- Olson, R.S.; Knoester, D.B.; Adami, C. Critical Interplay Between Density-Dependent Predation and Evolution of the Selfish Herd. In Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation, Amsterdam, The Netherlands, 6–10 July 2013; ACM: New York, NY, USA, 2013; pp. 247–254. [Google Scholar]
- Chapman, S.; Knoester, D.; Hintze, A.; Adami, C. Evolution of an Artificial Visual Cortex for Image Recognition. In Proceedings of the 20th European Conference on the Synthesis and Simulation of Living Systems, Taormina, Italy, 2–6 September 2013; pp. 1067–1074.
- Haley, P.B.; Olson, R.S.; Dyer, F.C.; Adami, C. Exploring Conditions that Select for the Evolution of Cooperative Group Foraging. In Proceedings of the 14th Conference on the Synthesis and Simulation of Living Systems (ALIFE 14), New York, NY, USA, 30 July–2 August 2014; pp. 310–311.
- Olson, R.S.; Haley, P.B.; Dyer, F.C.; Adami, C. Exploring the evolution of a trade-off between vigilance and foraging in group-living organisms. R. Soc. Open Sci. 2015, 2. [Google Scholar] [CrossRef] [PubMed]
- Kvam, P.; Cesario, J.; Schossau, J.; Eisthen, H.; Hintze, A. Computational Evolution of Decision-Making Strategies. In Proceedings of the 37th Annual Conference of the Cognitive Science Society, Pasadena, CA, USA, 23–25 July 2015; pp. 1225–1230.
- Olson, R.S.; Knoester, D.B.; Adami, C. Evolution of swarming behavior is shaped by how predators attack. 2013; arXiv:1310.6012. [Google Scholar]
- Stanley, K.O.; Miikkulainen, R. Evolving neural networks through augmenting topologies. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef] [PubMed]
- Brooks, R.A. A robust layered control system for a mobile robot. IEEE J. Robot. Autom. 1986, 2, 14–23. [Google Scholar] [CrossRef]
- Clune, J.; Stanley, K.O.; Pennock, R.T.; Ofria, C. On the performance of indirect encoding across the continuum of regularity. IEEE Trans. Evol. Comput. 2011, 15, 346–367. [Google Scholar] [CrossRef]
- D’Ambrosio, D.B.; Lehman, J.; Risi, S.; Stanley, K.O. Task Switching in Multiagent Learning Through Indirect Encoding. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS 2011), Piscataway, NJ, USA, 25–30 September 2011.
- Gauci, J.; Stanley, K.O. Indirect Encoding of Neural Networks for Scalable Go. In Parallel Problem Solving from Nature, PPSN XI; Springer: Berlin/Heidelberg, Germany, 2010; pp. 354–363. [Google Scholar]
- Marstaller, L.; Hintze, A.; Adami, C. Measuring Representation. In Proceedings of the 9th Conference of the Australasian Society for Cognitive Science, North Ryde, Austrlia, 30 September–2 October 2009.
- Hintze, A.; Miromeni, M. Evolution of Autonomous Hierarchy Formation and Maintenance. In Proceedings of the the 14th International Conference on the Synthesis and Simulation of Living Systems (ALIFE 14), New York, NY, USA, 30 July–2 August 2014; pp. 366–367.
- Vapnik, V.N.; Chervonenkis, A.Y. On the Uniform Convergence of Relative Frequencies of Events to Their Probabilities. Theory Probab. Appl. 1971, 16, 264–280. [Google Scholar] [CrossRef]
- McCabe, T.J. A Complexity Measure. IEEE Trans. Softw. Eng. 1976, 308, 308–320. [Google Scholar] [CrossRef]
- Ahn, Y.-Y.; Jeong, H.; Kim, B.J. Wiring cost in the organization of a biological neuronal network. Physica A 2006, 367, 531–537. [Google Scholar] [CrossRef]
- Cherniak, C.; Mokhtarzada, Z.; Rodriguez-Esteban, R.; Changizi, K. Global optimization of cerebral cortex layout. Proc. Natl. Acad. Sci. USA 2004, 101, 1081–1086. [Google Scholar] [CrossRef] [PubMed]
- Huizinga, J.; Clune, J.; Mouret, J.-B. Evolving Neural Networks That Are Both Modular and Regular: HyperNeat Plus the Connection Cost Technique. In Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, Nanchang, China, 18–20 October 2014; pp. 697–704.
- Schneidman, E.; Still, S.; Berry, M.J.; Bialek, W. Network information and connected correlations. Phys. Rev. Lett. 2003, 91, 238701. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G. Consciousness as integrated information: A provisional manifesto. Biol. Bull. 2008, 215, 216–242. [Google Scholar] [CrossRef] [PubMed]
- Balduzzi, D.; Tononi, G. Integrated information in discrete dynamical systems: Motivation and theoretical framework. PLoS Comput. Biol. 2008, 4, e1000091. [Google Scholar] [CrossRef] [PubMed]
- Balduzzi, D.; Tononi, G. Qualia: The geometry of integrated information. PLoS Comput. Biol. 2009, 5, e1000462. [Google Scholar] [CrossRef] [PubMed]
- Barrett, A.B.; Seth, A.K. Practical Measures of Integrated Information for Time-Series Data. PLoS Comput. Biol. 2011, 7, e1001052. [Google Scholar] [CrossRef] [PubMed]
- Ay, N. Information Geometry on Complexity and Stochastic Interaction. Entropy 2015, 17, 2432–2458. [Google Scholar] [CrossRef]
- McGill, W.J. Multivariate information transmission. Psychometrika 1954, 19, 97–116. [Google Scholar] [CrossRef]
- Tononi, G.; Sporns, O.; Edelman, G.M. A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. USA 1994, 91, 5033–5037. [Google Scholar] [CrossRef] [PubMed]
- Lungarella, M.; Pegors, T.; Bulwinkle, D.; Sporns, O. Methods for quantifying the informational structure of sensory and motor data. Neuroinformatics 2005, 3, 243–262. [Google Scholar] [CrossRef]
- Lungarella, M.; Sporns, O. Mapping information flow in sensorimotor networks. PLoS Comput. Biol. 2006, 2, e144. [Google Scholar] [CrossRef] [PubMed]
- Joshi, N.J.; Tononi, G.; Koch, C. The minimal complexity of adapting agents increases with fitness. PLoS Comput. Biol. 2013, 9, e1003111. [Google Scholar] [CrossRef] [PubMed]
- Bialek, W.; Nemenman, I.; Tishby, N. Predictability, complexity, and learning. Neural Comput. 2001, 13, 2409–2463. [Google Scholar] [CrossRef] [PubMed]
- Ay, N.; Bertschinger, N.; Der, R.; Güttler, F.; Olbrich, E. Predictive information and explorative behavior of autonomous robots. Eur. Phys. J. B 2008, 63, 329–339. [Google Scholar] [CrossRef]
- Rinehart, N.J.; Bradshaw, J.L.; Moss, S.A.; Brereton, A.V.; Tonge, B.J. Pseudo-random number generation in children with high-functioning autism and Asperger’s disorder. Autism 2006, 10, 70–85. [Google Scholar] [CrossRef] [PubMed]
- Zlotowski, M.; Bakan, P. Behavioral variability of process and reactive schizophrenics in a binary guessing task. J. Abnorm. Soc. Psychol. 1963, 66, 185–187. [Google Scholar] [CrossRef] [PubMed]
- Wagenaar, W.A. Generation of random sequences by human subjects: A critical survey of literature. Psychol. Bull. 1972, 77, 65–72. [Google Scholar] [CrossRef]
- Williams, M.A.; Moss, S.A.; Bradshaw, J.L.; Rinehart, N.J. Brief report: Random number generation in autism. J. Autism Dev. Disord. 2002, 32, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Olson, R.S.; Hintze, A.; Dyer, F.C.; Knoester, D.B.; Adami, C. Predator confusion is sufficient to evolve swarming behaviour. J. R. Soc. Interface 2013, 10, 20130305. [Google Scholar] [CrossRef] [PubMed]
- Lenski, R.E.; Ofria, C.; Pennock, R.T.; Adami, C. The evolutionary origin of complex features. Nature 2003, 423, 139–144. [Google Scholar] [CrossRef] [PubMed]
- Zahedi, K.; Martius, G.; Ay, N. Linear combination of one-step predictive information with an external reward in an episodic policy gradient setting: A critical analysis. Front. Psychol. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Rivoire, O.; Leibler, S. The value of information for populations in varying environments. J. Stat. Phys. 2011, 142, 1124–1166. [Google Scholar] [CrossRef]
- Knowles, J.D.; Watson, R.A.; Corne, D.W. Reducing Local Optima in Single-Objective Problems by Multi-Objectivization. In Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2001; pp. 269–283. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schossau, J.; Adami, C.; Hintze, A. Information-Theoretic Neuro-Correlates Boost Evolution of Cognitive Systems. Entropy 2016, 18, 6. https://doi.org/10.3390/e18010006
Schossau J, Adami C, Hintze A. Information-Theoretic Neuro-Correlates Boost Evolution of Cognitive Systems. Entropy. 2016; 18(1):6. https://doi.org/10.3390/e18010006
Chicago/Turabian StyleSchossau, Jory, Christoph Adami, and Arend Hintze. 2016. "Information-Theoretic Neuro-Correlates Boost Evolution of Cognitive Systems" Entropy 18, no. 1: 6. https://doi.org/10.3390/e18010006
APA StyleSchossau, J., Adami, C., & Hintze, A. (2016). Information-Theoretic Neuro-Correlates Boost Evolution of Cognitive Systems. Entropy, 18(1), 6. https://doi.org/10.3390/e18010006





