Predicting Traffic Flow in Local Area Networks by the Largest Lyapunov Exponent
Abstract
:1. Introduction
2. Fundamental Theories
2.1. Phase Space Reconstructions for Time Sequences in Networks
- Suppose there is a time sequence, x(t) = (x(t1), x(t2), …, x(tn)), here x(t) is the sample, n the number of samples, t the time and Δt the sampling interval. The Euclidean subspace with m-dimensions can be constructed by the time sequence as a proper time lag τ = kΔt is chosen, and here k is a positive integer. The first point of the m-dimensional subspace includes m values, in which x(t1) is the first element of the vector, x(t1 + τ) is the next one, and the last one is x(t1 + (m − 1)τ), so the first point in vector form in the phase space is defined as follows:
- Then let x(t2) be the first element in the vector, the second point in the m-dimensional subspace can be obtained further using the same method, that is:
- The number of points in m-dimensional subspace is N = n − (m − 1)k, and all the points of the subspace are:where Yi can be considered as a point in the reconstructed phase space, including m elements.
2.2. C-C Method
2.3. Physical Meaning of the Largest Lyapunov Exponent in Network
- As λ > 0, two trajectories diverge rapidly in phase space, and the long time behaviors of the dynamic system are sensitive to the initial conditions, implying the system is in a chaotic state.
- As λ = 0, two trajectories will not diverge or converge implying there is no chaos.
- As λ < 0, two trajectories in phase space converge, and the long time behaviors of dynamic system are not sensitive to the initial conditions, implying there is no chaos and the system is stable.
2.4. Small Data Sets Method
2.5. Longest Predictable Duration
2.6. Prediction Method Based on the Largest Lyaponov Exponent
3. Numerical Examples and Analysis
3.1. Largest Lyapunov Exponent of LAN Traffic
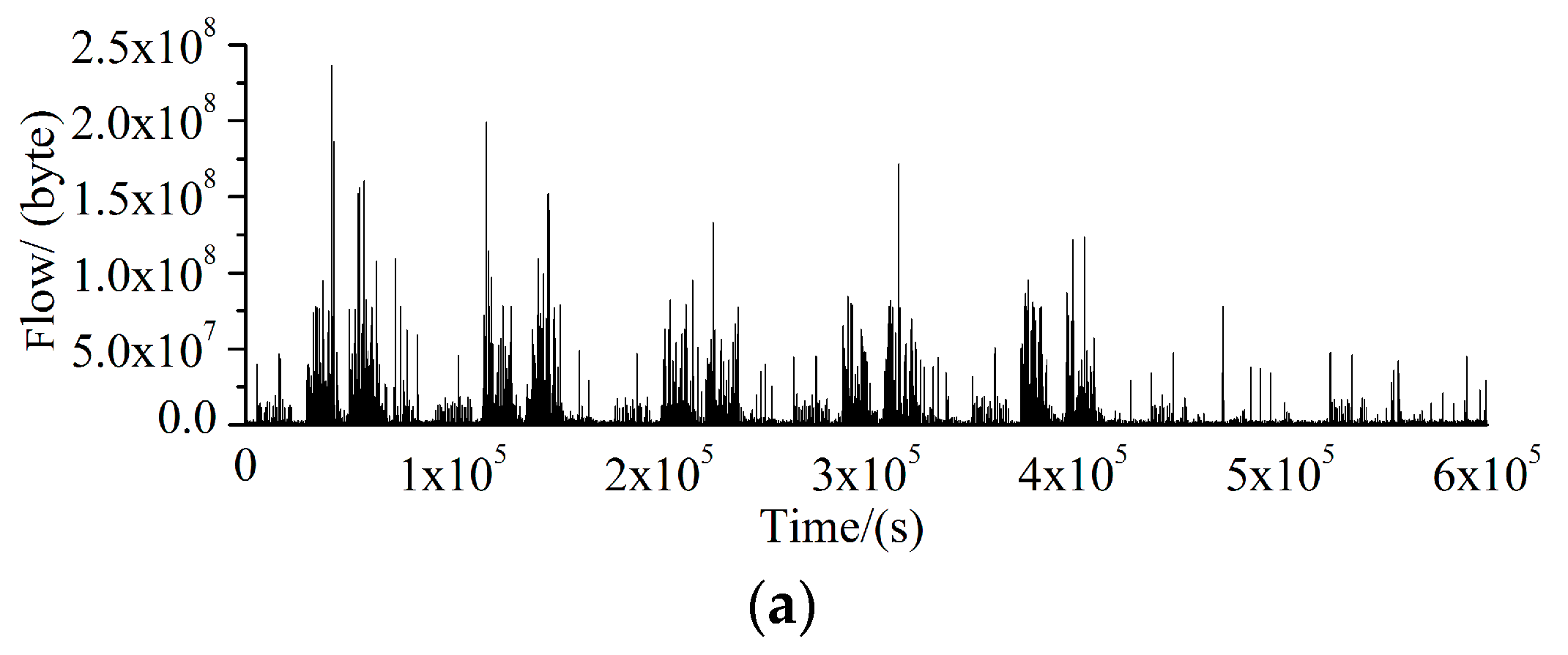
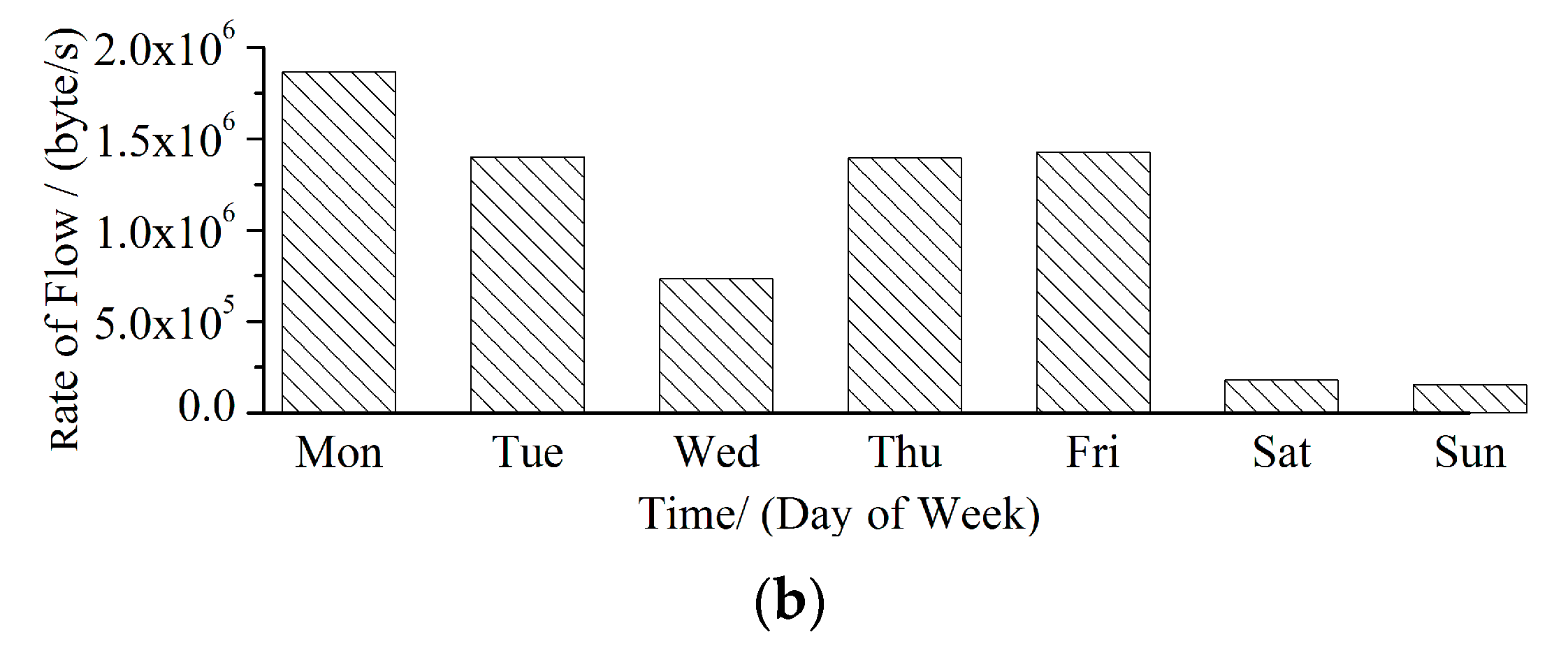
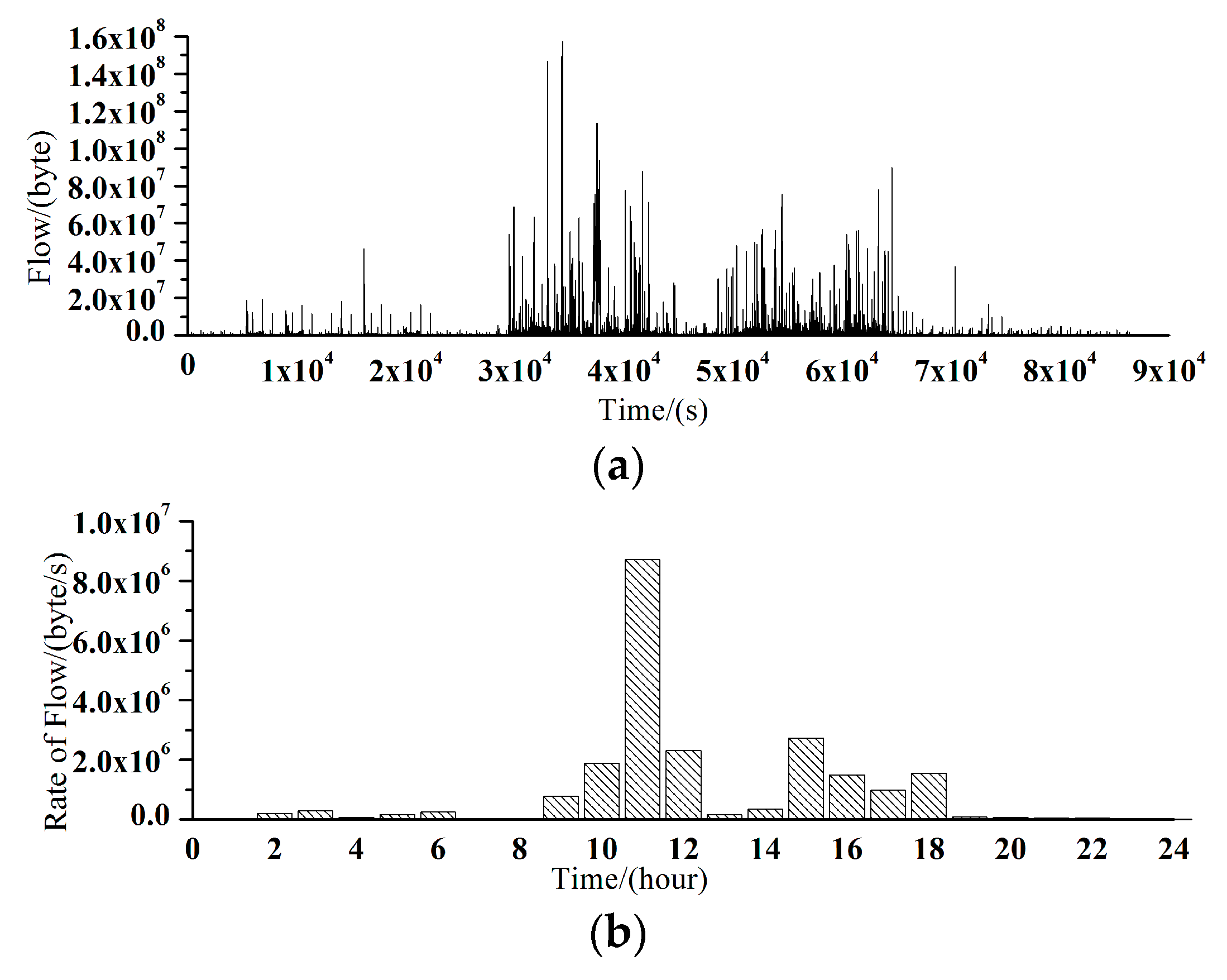
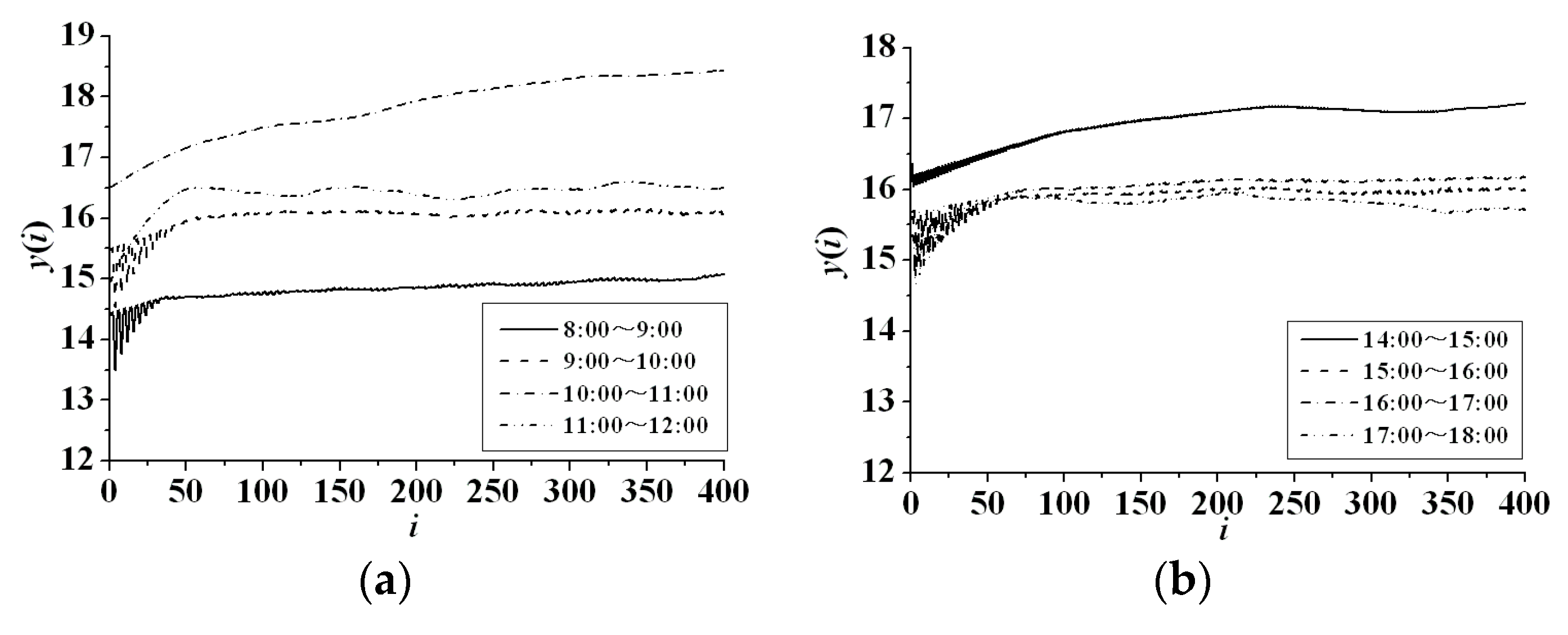
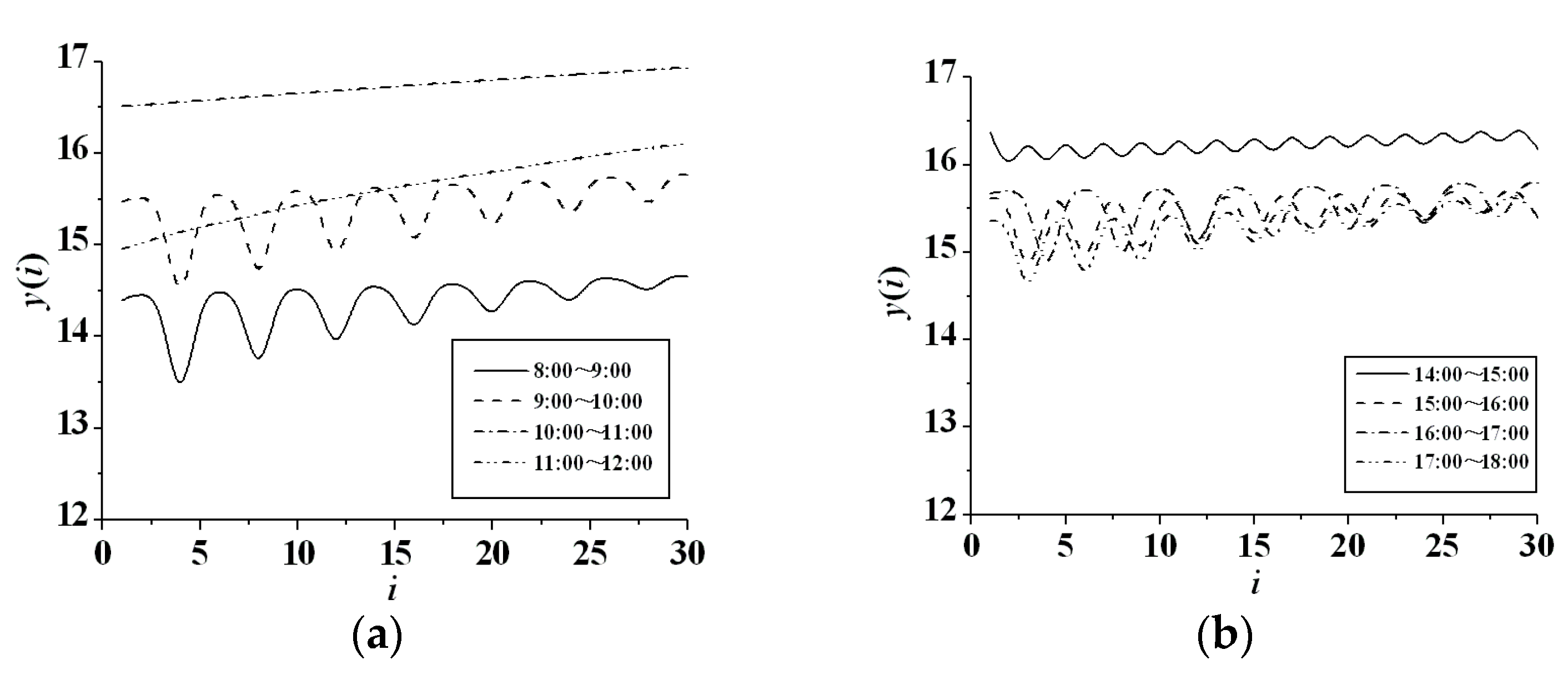
| Working Periods | 8:00–9:00 | 9:00–10:00 | 10:00–11:00 | 11:00–12:00 | 14:00–15:00 | 15:00–16:00 | 16:00–17:00 | 17:00–18:00 |
|---|---|---|---|---|---|---|---|---|
| Average traffic (byte/s) | 772,602 | 1,881,664 | 8,721,630 | 2,313,709 | 2,731,960 | 1,504,641 | 985,395 | 1,555,366 |
| τw | 32 | 48 | 99 | 40 | 100 | 51 | 72 | 42 |
| τ | 4 | 4 | 1 | 1 | 2 | 3 | 4 | 3 |
| m | 9 | 13 | 100 | 41 | 51 | 18 | 19 | 15 |
| λ1 | 0.0169 | 0.0171 | 0.0147 | 0.0386 | 0.0065 | 0.0103 | 0.0076 | 0.0178 |
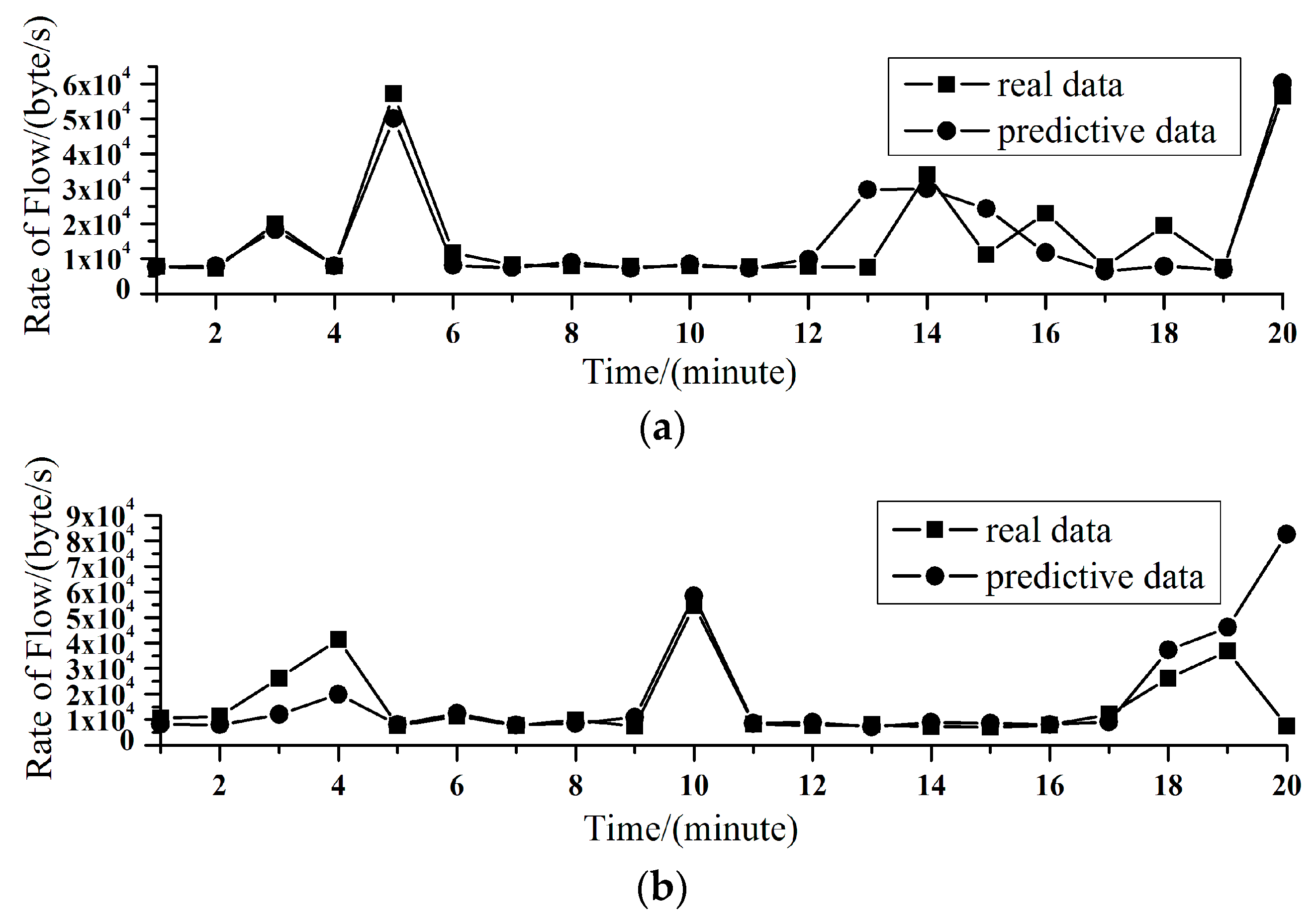
3.2. Prediction
3.2.1. Dot Prediction
| Date | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
|---|---|---|---|---|---|---|---|
| rate of flow (byte/s) | 1.86538 × 106 | 1.40022 × 106 | 7.35079 × 105 | 1.39503 × 106 | 1.42701 × 106 | 1.80545 × 105 | 1.55155 × 105 |
| τ | 4 | 2 | 3 | 7 | 2 | 2 | 4 |
| m | 6 | 12 | 3 | 3 | 19 | 27 | 8 |
| λ1 | 0.1848 | 0.0475 | 0.146 | 0.1562 | 0.044 | 0.1557 | 0.0606 |
| n | 5 | 21 | 7 | 6 | 23 | 6 | 17 |
| f1(%) | 60 | 71 | 57 | 67 | 52 | 83 | 41 |
| f2(%) | 80 | 90 | 86 | 100 | 91 | 100 | 71 |
3.2.2. Interval Prediction
| Date | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
|---|---|---|---|---|---|---|---|
| n3 | 3 | 16 | 18 | 4 | 18 | 6 | 15 |
| f3(%) | 60 | 76 | 75 | 67 | 78 | 100 | 88 |
4. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, Y.; Zhang, J.; Mu, D. Nonlinear Dynamics of the Small-World Networks-Hopf Bifurcation, Sequence of Period-Doubling Bifurcations and Chaos. J. Phys. Conf. Ser. 2008, 96, 012061. [Google Scholar] [CrossRef]
- Chu, W.; Guan, X.; Cai, Z.; Gao, L. Real-Time Volume Control for Interactive Network Traffic. Comput. Netw. 2013, 57, 1611–1629. [Google Scholar] [CrossRef]
- Wang, J.; Yuan, J.; Li, Q.; Yuan, R. Correlation Dimension Based Nonlinear Analysis of Network Traffics with Different Application Protocols. Chin. Phys. B 2011, 20, 050506. [Google Scholar] [CrossRef]
- Feng, H.; Shu, Y.; Yang, O. Nonlinear Analysis of Wireless LAN Traffic. Nonlinear Anal. Real World Appl. 2009, 10, 1021–1028. [Google Scholar] [CrossRef]
- Nooruzzaman, M.; Koyama, O.; Katsuyama, Y. Congestion Removing Performance of Stackable ROADM in WDM Networks under Dynamic Traffic. Comput. Netw. 2013, 57, 2364–2373. [Google Scholar] [CrossRef]
- Sergiou, C.; Vassiliou, V.; Paphitis, A. Congestion Control in Wireless Sensor Networks through Dynamic Alternative Path Selection. Comput. Netw. 2014, 75, 226–238. [Google Scholar] [CrossRef]
- Chen, B.-S.; Yang, Y.-S.; Lee, B.-K.; Lee, T.-H. Fuzzy Adaptive Predictive Flow Control of ATM Network Traffic. IEEE Trans. Fuzzy Syst. 2003, 11, 568–581. [Google Scholar] [CrossRef]
- Alheraish, A. A Comparison of AR Full Motion Video Traffic Models in B-ISDN. Comput. Electr. Eng. 2005, 31, 1–22. [Google Scholar] [CrossRef]
- Szeto, W.Y.; Ghosh, B.; Basu, B.; O’Mahony, M. Multivariate Traffic Forecasting Technique Using Cell Transmission Model and SARIMA Model. J. Transp. Eng. ASCE 2009, 135, 658–667. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Y.; Lu, H. Seasonal Autoregressive Integrated Moving Average and Support Vector Machine Models Prediction of Short-Term Traffic Flow on Freeways. Transp. Res. Rec. 2011, 2215, 85–92. [Google Scholar] [CrossRef]
- Swift, D.K.; Dagli, C.H. A Study on the Network Traffic of Connexion by Boeing: Modeling with Artificial Neural Networks. Eng. Appl. Artif. Intell. 2008, 21, 1113–1129. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence. Lect. Notes Math. 1981, 898, 361–381. [Google Scholar]
- Kugiumtzis, D. State Space Reconstruction Parameters in the Analysis of Chaotic Time Series. Physica D 1996, 95, 13–28. [Google Scholar] [CrossRef]
- Kim, H.S.; Eykholt, R.J.; Salas, D. Nonlinear Dynamics, Delay Times, and Embedding Windows. Physica D 1999, 127, 48–60. [Google Scholar] [CrossRef]
- David, R. Five Turbulent Problems. Physica D 1983, 7, 40–44. [Google Scholar]
- Boffetta, G.; Paladin, G.; Vulpiani, A. Strong Chaos without the Butterfly Effect in Dynamical Systems with Feedback. J. Phys. A Math. Gen. 1996, 29, 2291–2298. [Google Scholar] [CrossRef]
- Joach, M.H.; Erner, W.L. Lyapunov Exponents from Time Series of Acoustic Chaos. Phys. Rev. A 1989, 39, 2146–2152. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov Exponent from a Time Series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; Deluca, C.J. A Practical Method for Calculating Largest Lyapunov Exponents from Small Data Sets. Physica D 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, J.F.; Cao, C.X. A Prediction of Network Traffic Flow Based on Lyapunov Exponent. J. Chongqing Univ. 2004, 27, 28–30. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, J. Predicting Traffic Flow in Local Area Networks by the Largest Lyapunov Exponent. Entropy 2016, 18, 32. https://doi.org/10.3390/e18010032
Liu Y, Zhang J. Predicting Traffic Flow in Local Area Networks by the Largest Lyapunov Exponent. Entropy. 2016; 18(1):32. https://doi.org/10.3390/e18010032
Chicago/Turabian StyleLiu, Yan, and Jiazhong Zhang. 2016. "Predicting Traffic Flow in Local Area Networks by the Largest Lyapunov Exponent" Entropy 18, no. 1: 32. https://doi.org/10.3390/e18010032
APA StyleLiu, Y., & Zhang, J. (2016). Predicting Traffic Flow in Local Area Networks by the Largest Lyapunov Exponent. Entropy, 18(1), 32. https://doi.org/10.3390/e18010032





