Long Range Dependence Prognostics for Bearing Vibration Intensity Chaotic Time Series
Abstract
:1. Introduction
- Statistical time series modeling approaches.
- Computational intelligence (CI) approaches.
- Prediction methods for chaos time series.
2. Chaotic Characteristics Analysis of Bearing Vibration Intensity Series
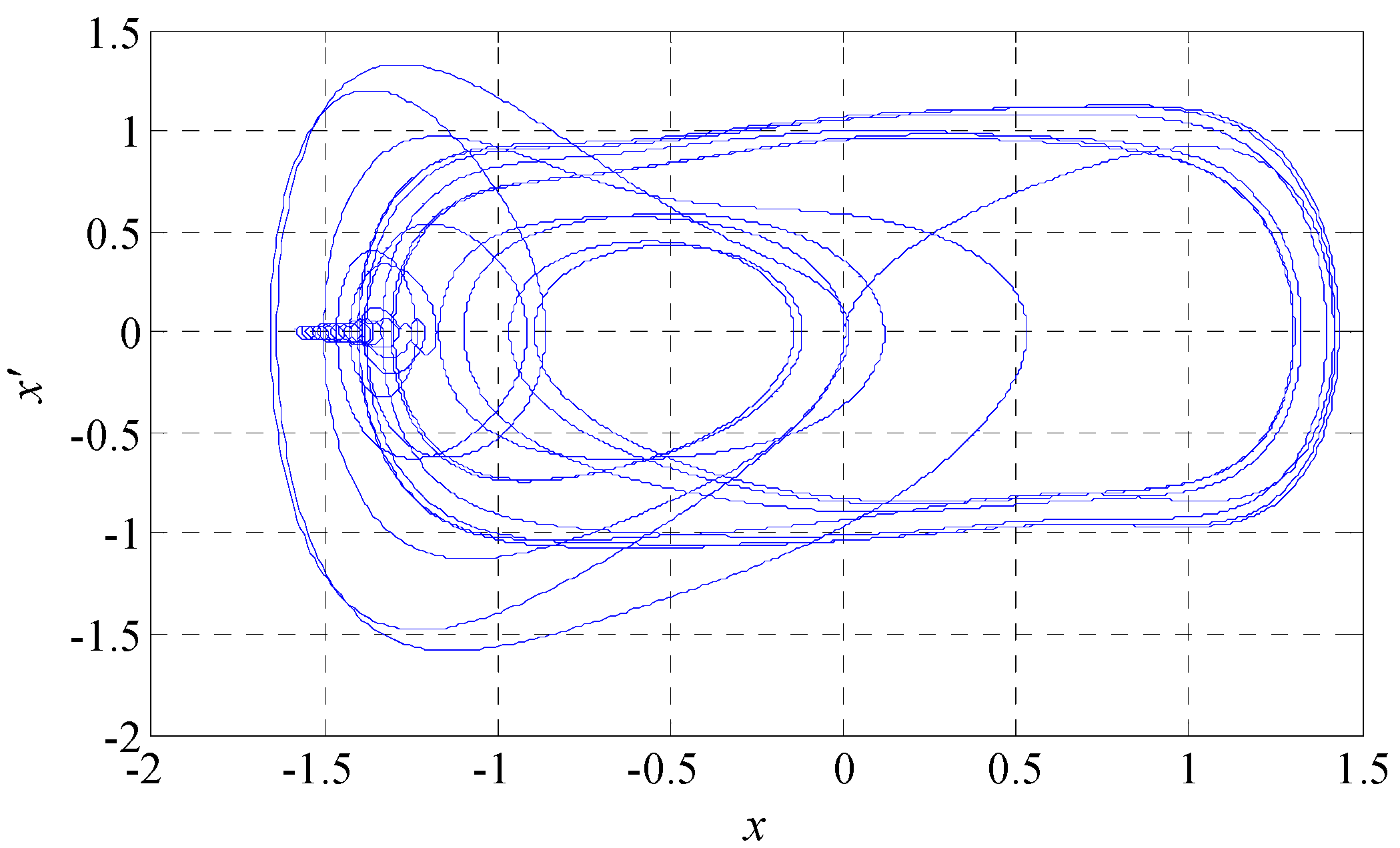
2.1. Phase Space Reconstruction
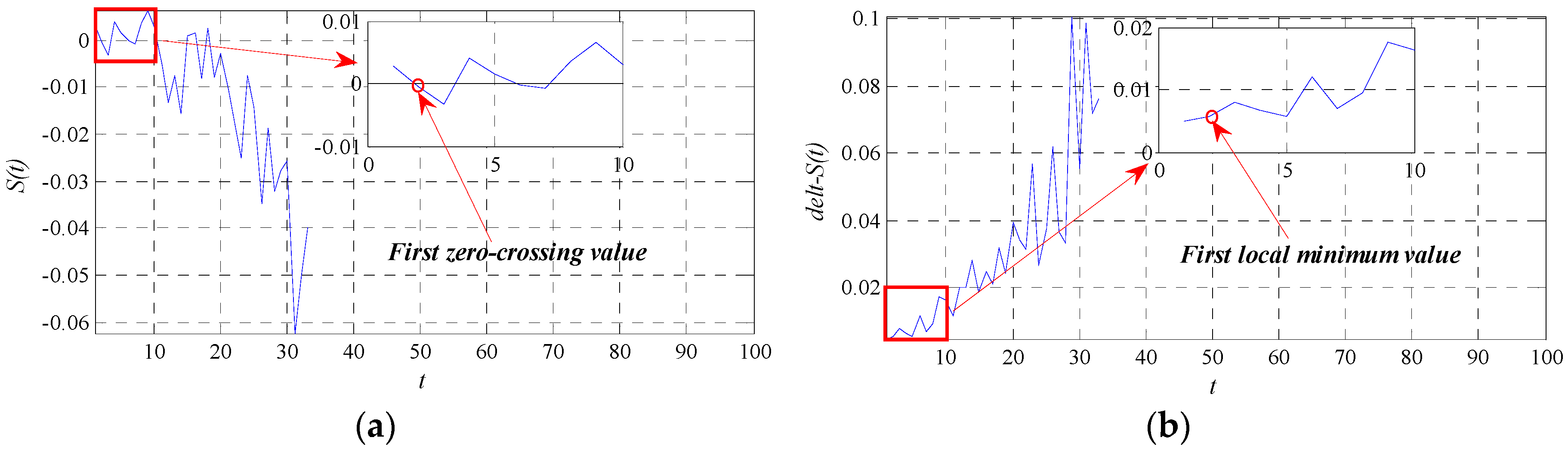
2.2. The Optimal Delay Time τ
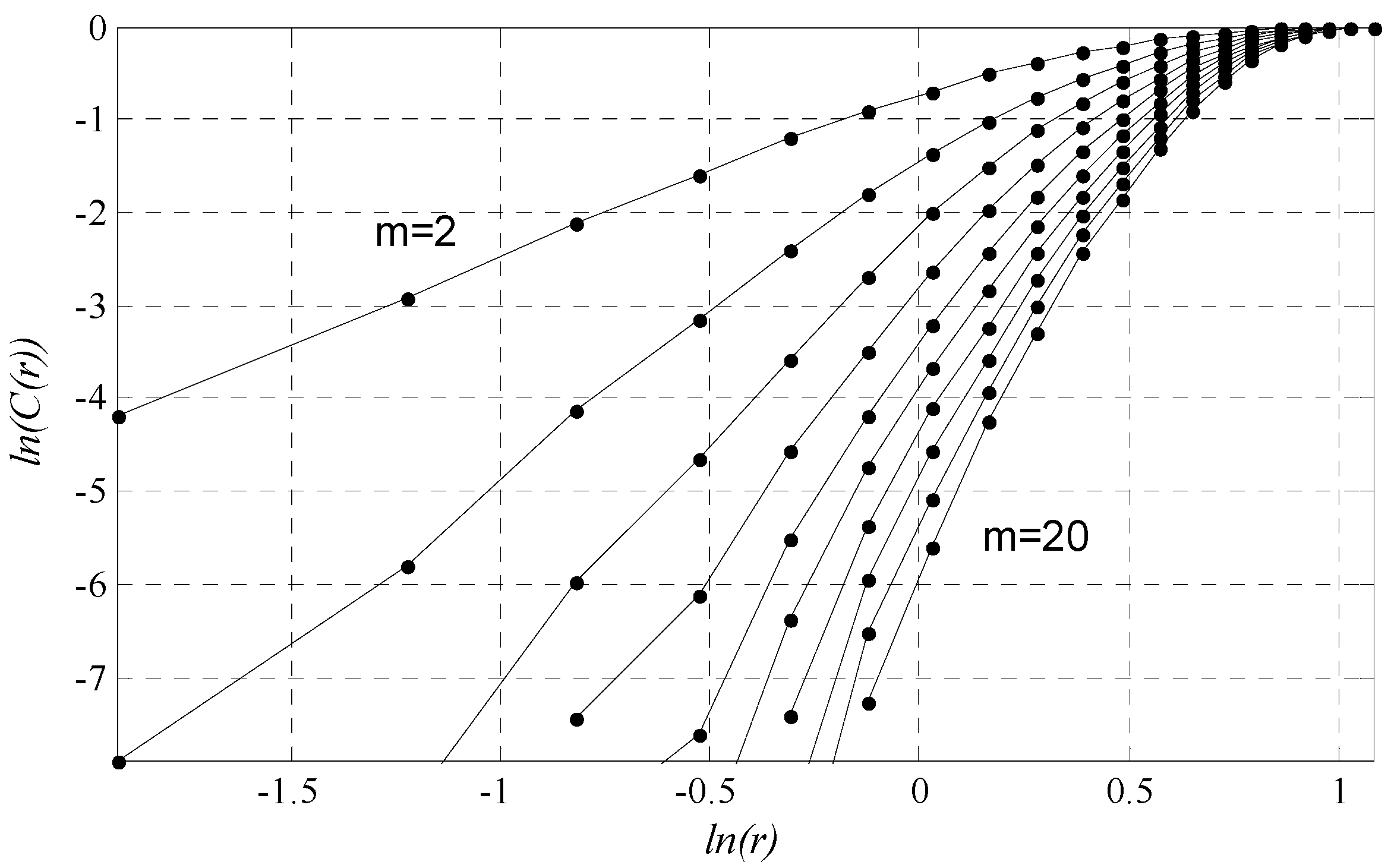
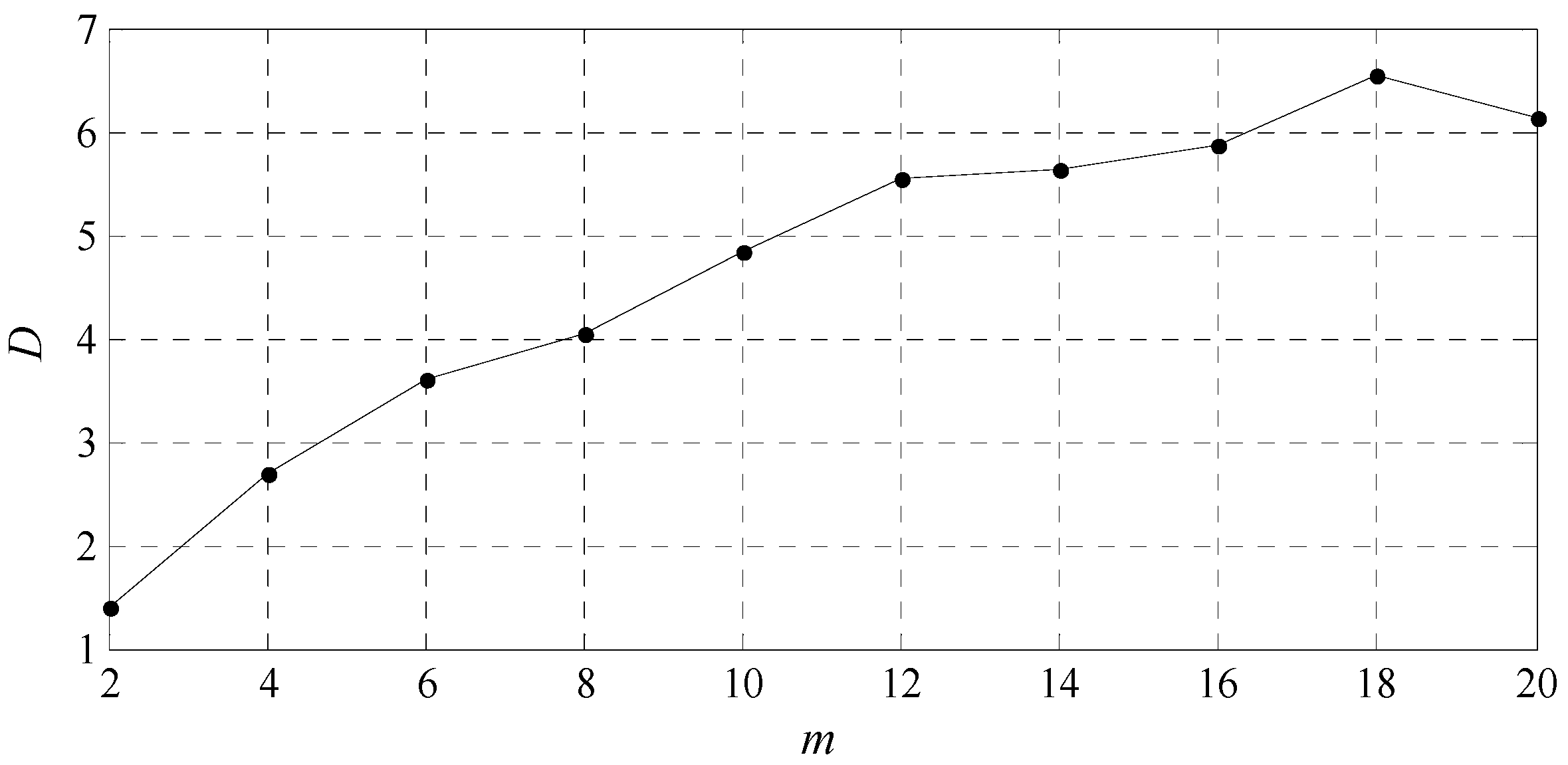
2.3. Optimal Embedding Dimension and Saturated Correlation Dimension
2.4. Largest Lyapunov Exponent (LLE)
3. Prognostic Model of Long Range Dependence
3.1. Theory of Long Range Dependence
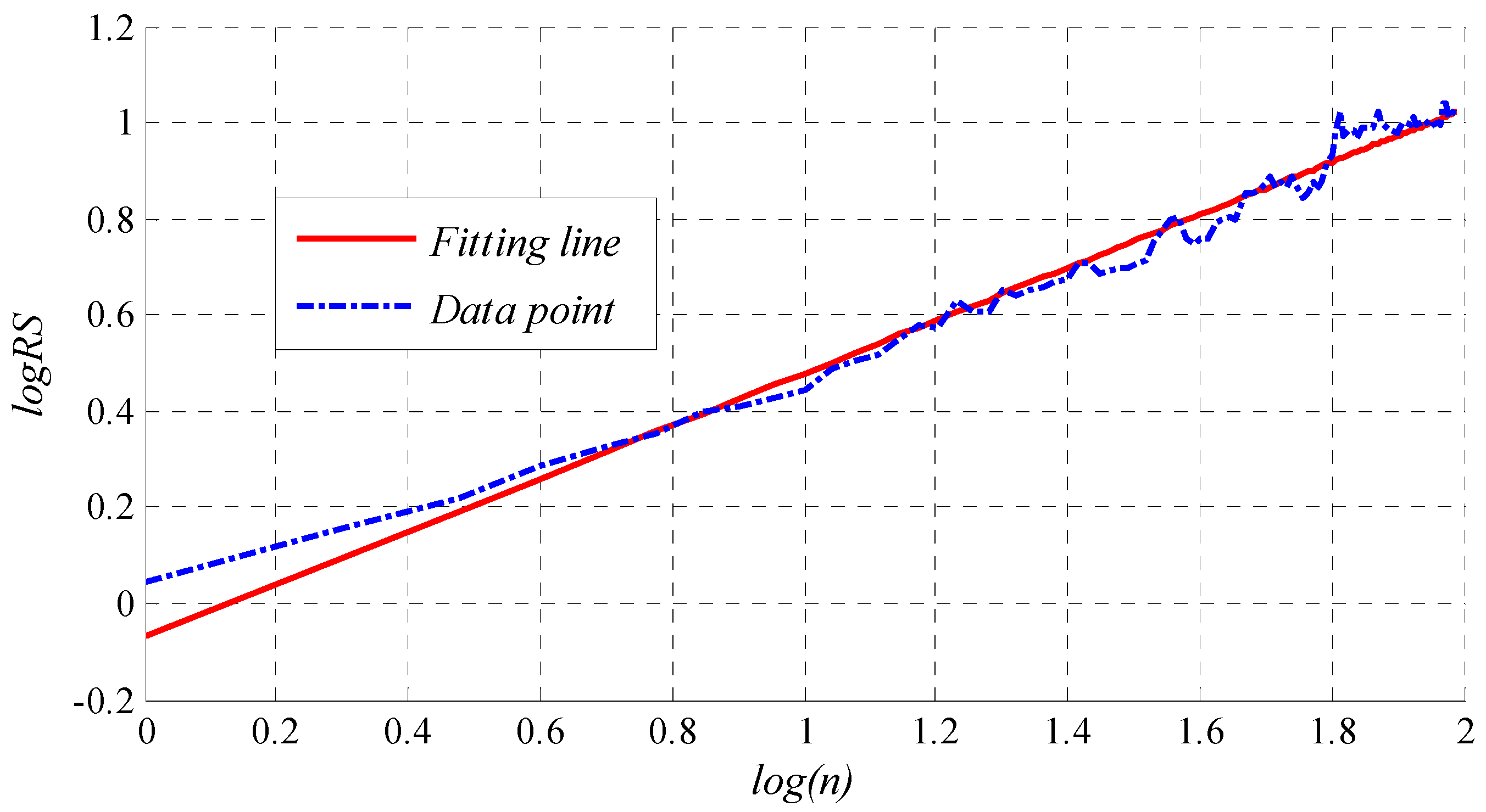
3.2. Hurst with R/S Method
3.3. LRD Prediction Steps
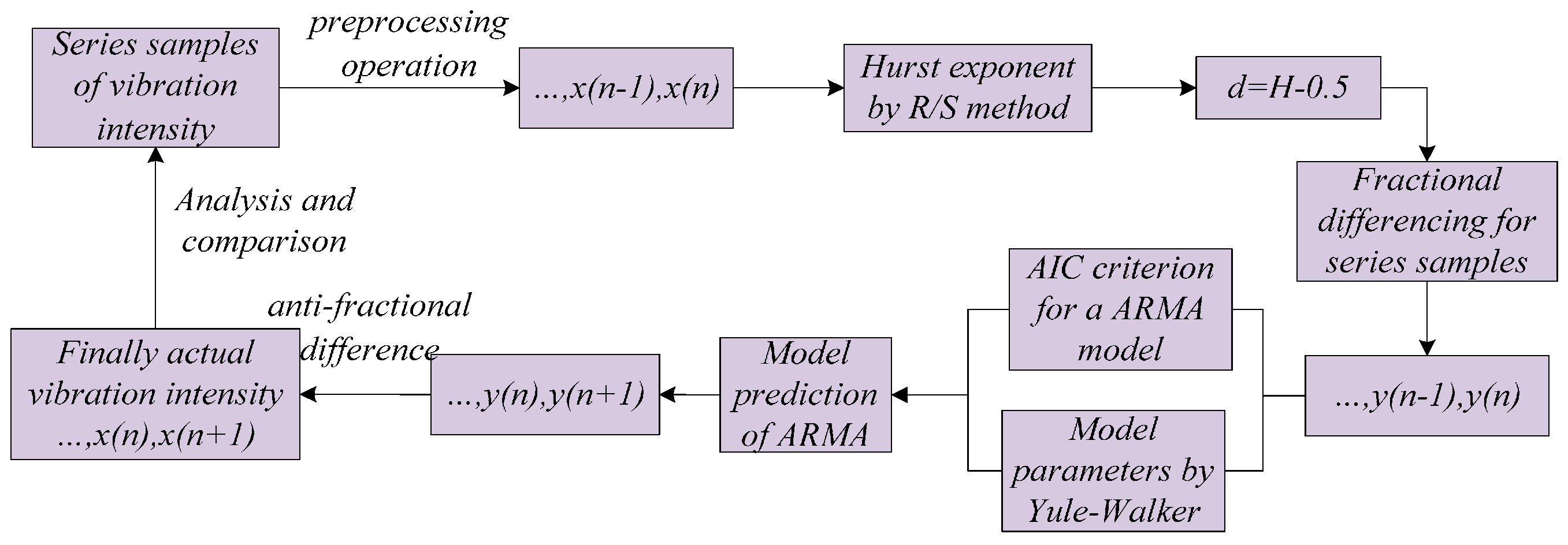
4. Experimental Verification
4.1. Experimental Setup

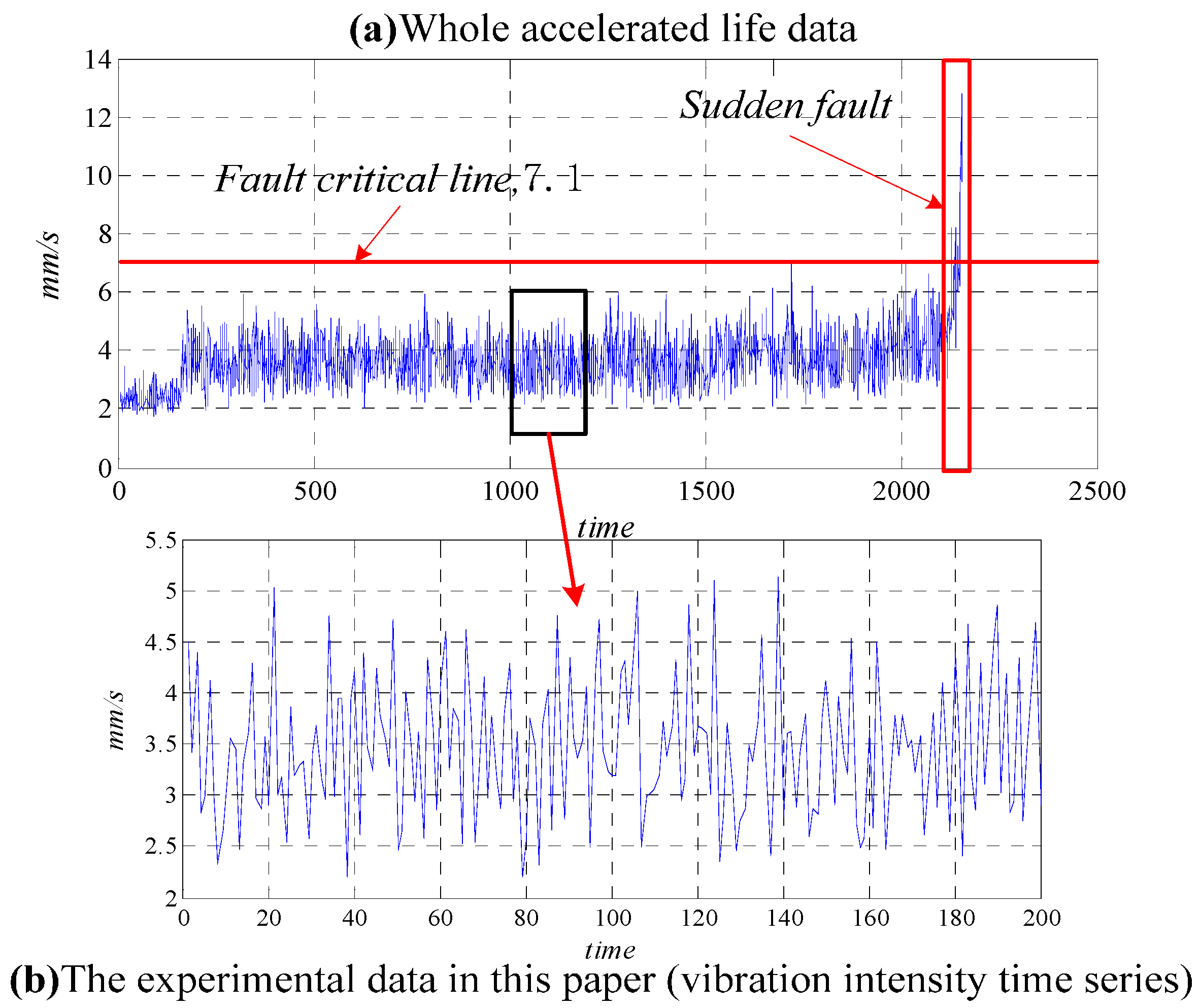
4.2. Chaotic Characteristic Analysis of Bearing Vibration Intensity Time Series
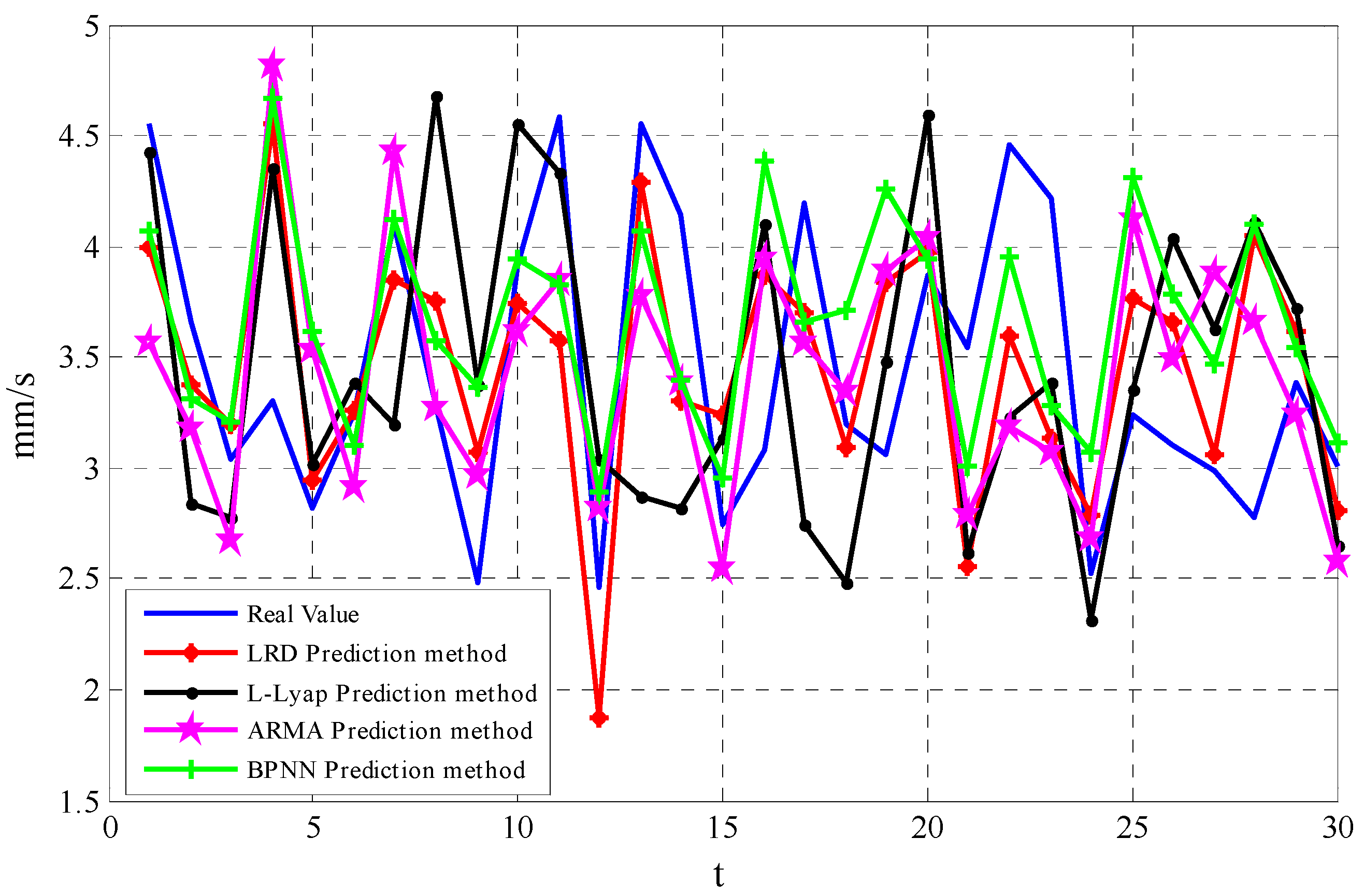
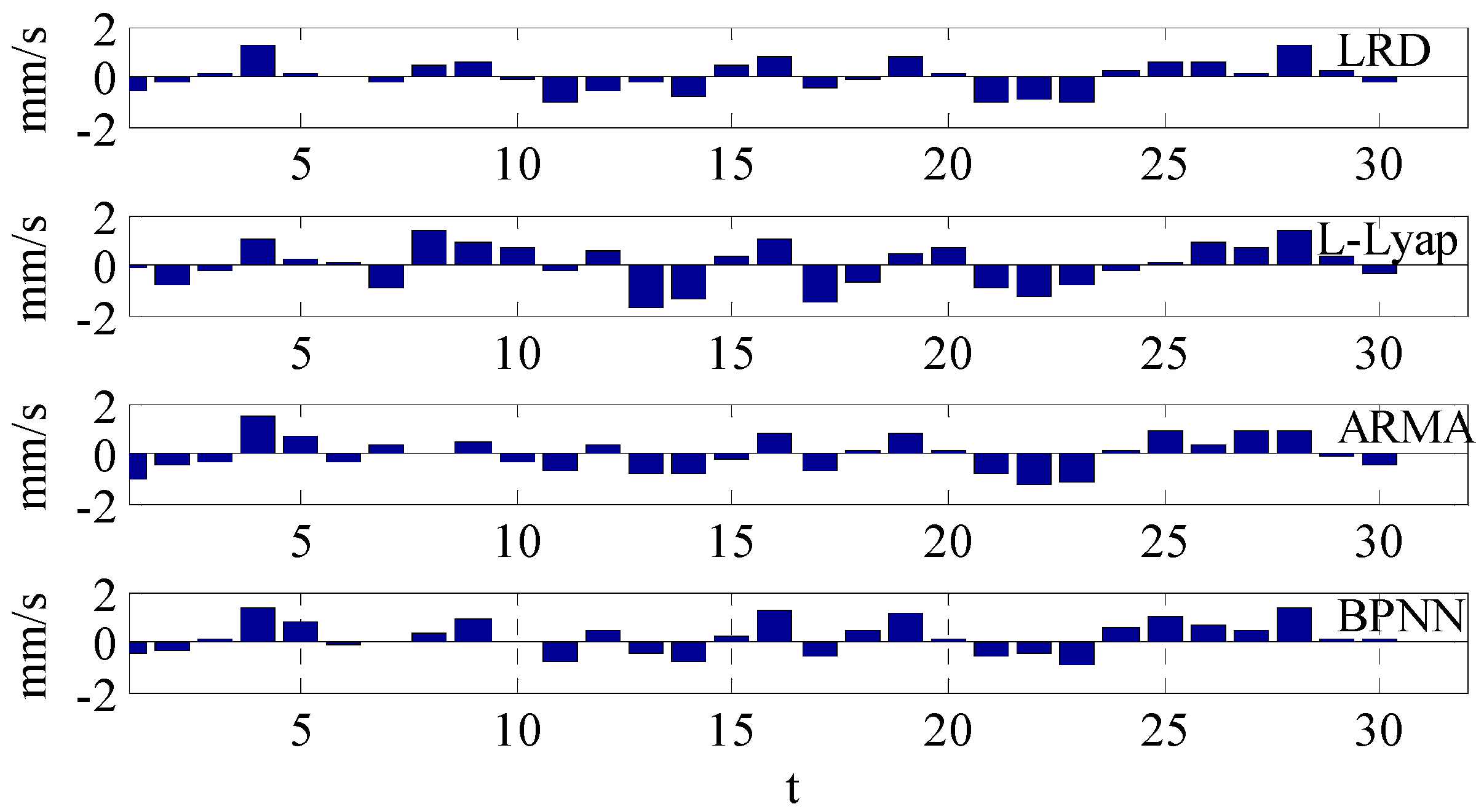
4.3. Prediction Analysis of LRD
| Predict Error Criterions | Computational Formula |
|---|---|
| Mean Absolute Error | |
| Root-Mean-Square Error | |
| Normalized Mean Square Error | |
| Maximum of Absolute Error |
| Prediction Method | MAE | RMSE | NMSE | Max-AE |
|---|---|---|---|---|
| LRD | 0.000592 | 0.0033 | 1.3274 | 1.2703 |
| L-Lyap | 0.0090 | 0.0500 | 1.5462 | 1.6773 |
| ARMA | 0.0241 | 0.1345 | 1.6106 | 1.5077 |
| BPNN | 0.2061 | 1.1484 | 1.8524 | 1.3635 |
5. Conclusions
- The vibration intensity time series have chaotic properties, and the chaotic characteristics of vibration intensity time series can be jointly determined by the largest Lyapunov exponent and phase plane trajectory.
- Experimental results and analysis demonstrate the unique ability of the f-ARIMA model for chaotic time series. The long range dependence prediction method is powerful for problems characterized by chaotic time series, small samples and nonlinearity. The LRD prediction method is better than other prediction methods in prediction accuracy and prediction performance, thus providing a new approach for the running tendency prediction of rotating machinery and some guidance value for engineering practice. In addition, the Hurst exponent can be calculated by the time series self-feature, instead of a subjective integer difference.
- High prediction accuracy is the key and critical to CPHM for improving reliability and reducing overall maintenance costs. The significant economic impact of prediction accuracy or prediction errors in rotating machinery status prediction on the mechanical equipment market and the systematic chaotic and self-similarity properties of different rotating machinery prediction models would be meaningful topics for further research.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| NO | Real | LRD | LRD_AE | LRD_RE | L-Lyap | L-Lyap_AE | L-Lyap_RE | ARMA | ARMA_AE | ARMA_RE | BPNN | BPNN_AE | BPNN_RE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.5522 | 3.9986 | −0.5536 | −0.121612 | 4.427 | −0.1252 | −0.027503 | 3.5635 | −0.9887 | −0.217192 | 4.0736 | −0.4786 | −0.105136 |
| 2 | 3.6649 | 3.3793 | −0.2856 | −0.077928 | 2.8398 | −0.8251 | −0.225136 | 3.1812 | −0.4837 | −0.131982 | 3.3158 | −0.3491 | −0.095255 |
| 3 | 3.036 | 3.199 | 0.163 | 0.0536891 | 2.7735 | −0.2625 | −0.086462 | 2.668 | −0.368 | −0.121212 | 3.2062 | 0.1702 | 0.0560606 |
| 4 | 3.3038 | 4.5551 | 1.2513 | 0.3787457 | 4.3493 | 1.0455 | 0.3164538 | 4.8115 | 1.5077 | 0.4563533 | 4.6673 | 1.3635 | 0.4127066 |
| 5 | 2.8203 | 2.948 | 0.1277 | 0.0452789 | 3.0233 | 0.203 | 0.0719782 | 3.5361 | 0.7158 | 0.2538028 | 3.6186 | 0.7983 | 0.283055 |
| 6 | 3.2525 | 3.2578 | 0.0053 | 0.0016295 | 3.3853 | 0.1328 | 0.0408301 | 2.9159 | −0.3366 | −0.10349 | 3.1038 | −0.1487 | −0.045719 |
| 7 | 4.1008 | 3.8482 | −0.2526 | −0.061598 | 3.2006 | −0.9002 | −0.219518 | 4.4296 | 0.3288 | 0.0801795 | 4.1213 | 0.0205 | 0.004999 |
| 8 | 3.2772 | 3.7583 | 0.4811 | 0.1468021 | 4.6817 | 1.4045 | 0.4285671 | 3.2749 | −0.0023 | −0.000702 | 3.5804 | 0.3032 | 0.092518 |
| 9 | 2.4798 | 3.0703 | 0.5905 | 0.238124 | 3.3767 | 0.8969 | 0.3616824 | 2.9644 | 0.4846 | 0.195419 | 3.3707 | 0.8909 | 0.3592628 |
| 10 | 3.9129 | 3.7449 | −0.168 | −0.042935 | 4.5568 | 0.6439 | 0.1645583 | 3.6133 | −0.2996 | −0.076567 | 3.9402 | 0.0273 | 0.0069769 |
| 11 | 4.5876 | 3.5724 | −1.0152 | −0.221292 | 4.3291 | −0.2585 | −0.056348 | 3.8472 | −0.7404 | −0.161392 | 3.8285 | −0.7591 | −0.165468 |
| 12 | 2.4631 | 1.8725 | −0.5906 | −0.239779 | 3.039 | 0.5759 | 0.2338111 | 2.8213 | 0.3582 | 0.1454265 | 2.8934 | 0.4303 | 0.1746986 |
| 13 | 4.55 | 4.2955 | −0.2545 | −0.055934 | 2.8727 | −1.6773 | −0.368637 | 3.7735 | −0.7765 | −0.170659 | 4.067 | −0.483 | −0.106154 |
| 14 | 4.146 | 3.3061 | −0.8399 | −0.202581 | 2.8231 | −1.3229 | −0.319079 | 3.3848 | −0.7612 | −0.183599 | 3.3941 | −0.7519 | −0.181356 |
| 15 | 2.7487 | 3.2427 | 0.494 | 0.1797213 | 3.1311 | 0.3824 | 0.1391203 | 2.5418 | −0.2069 | −0.075272 | 2.9592 | 0.2105 | 0.0765817 |
| 16 | 3.0865 | 3.8732 | 0.7867 | 0.2548842 | 4.1049 | 1.0184 | 0.329953 | 3.9403 | 0.8538 | 0.276624 | 4.3831 | 1.2966 | 0.4200875 |
| 17 | 4.1998 | 3.7001 | −0.4997 | −0.118982 | 2.7413 | −1.4585 | −0.347278 | 3.5695 | −0.6303 | −0.150079 | 3.6615 | −0.5383 | −0.128173 |
| 18 | 3.1988 | 3.0906 | −0.1082 | −0.033825 | 2.4823 | −0.7165 | −0.22399 | 3.3457 | 0.1469 | 0.0459235 | 3.7081 | 0.5093 | 0.159216 |
| 19 | 3.0569 | 3.8389 | 0.782 | 0.2558147 | 3.4847 | 0.4278 | 0.1399457 | 3.8914 | 0.8345 | 0.272989 | 4.2552 | 1.1983 | 0.3919984 |
| 20 | 3.8719 | 3.9799 | 0.108 | 0.0278933 | 4.5922 | 0.7203 | 0.1860327 | 4.0409 | 0.169 | 0.0436478 | 3.9445 | 0.0726 | 0.0187505 |
| 21 | 3.5429 | 2.5529 | −0.99 | −0.279432 | 2.6148 | −0.9281 | −0.261961 | 2.7855 | −0.7574 | −0.21378 | 3.0093 | −0.5336 | −0.150611 |
| 22 | 4.4554 | 3.5936 | −0.8618 | −0.193428 | 3.2339 | −1.2215 | −0.274162 | 3.1912 | −1.2642 | −0.283746 | 3.9563 | −0.4991 | −0.112021 |
| 23 | 4.2155 | 3.1371 | −1.0784 | −0.255818 | 3.383 | −0.8325 | −0.197485 | 3.0732 | −1.1423 | −0.270976 | 3.2859 | −0.9296 | −0.22052 |
| 24 | 2.521 | 2.788 | 0.267 | 0.1059104 | 2.3158 | −0.2052 | −0.081396 | 2.6854 | 0.1644 | 0.0652122 | 3.0682 | 0.5472 | 0.2170567 |
| 25 | 3.2362 | 3.7682 | 0.532 | 0.1643903 | 3.36 | 0.1238 | 0.0382547 | 4.1212 | 0.885 | 0.2734689 | 4.3122 | 1.076 | 0.3324887 |
| 26 | 3.1059 | 3.6585 | 0.5526 | 0.1779194 | 4.0435 | 0.9376 | 0.3018771 | 3.4948 | 0.3889 | 0.1252133 | 3.7854 | 0.6795 | 0.2187772 |
| 27 | 2.9839 | 3.0617 | 0.0778 | 0.0260733 | 3.6305 | 0.6466 | 0.2166963 | 3.8778 | 0.8939 | 0.2995744 | 3.4673 | 0.4834 | 0.1620027 |
| 28 | 2.7785 | 4.0488 | 1.2703 | 0.4571891 | 4.1086 | 1.3301 | 0.4787115 | 3.6614 | 0.8829 | 0.3177614 | 4.0978 | 1.3193 | 0.4748245 |
| 29 | 3.3918 | 3.6153 | 0.2235 | 0.0658942 | 3.7199 | 0.3281 | 0.0967333 | 3.2349 | −0.1569 | −0.046259 | 3.5432 | 0.1514 | 0.0446371 |
| 30 | 3.0046 | 2.8075 | −0.1971 | −0.065599 | 2.6517 | −0.3529 | −0.117453 | 2.581 | −0.4236 | −0.140984 | 3.1122 | 0.1076 | 0.0358118 |
References
- Hong, S.; Zhou, Z.; Zio, E.; Wang, W. An adaptive method for health trend prediction of rotating bearings. Digit. Signal Process. 2014, 35, 117–123. [Google Scholar] [CrossRef]
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Ali, J.B.; Chebel-Morello, B.; Saidi, L.; Malinowski, S.; Fnaiech, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56–57, 150–172. [Google Scholar]
- García, F.P.; Pedregal, D.J.; Clive, R. Time series methods applied to failure prediction and detection. Reliab. Eng. Syst. Saf. 2010, 95, 698–703. [Google Scholar] [CrossRef]
- Kosasih, B.Y.; Caesarendra, W.; Tieu, K.; Widodo, A.; Moodie, C.A.S.; Tieu, A.K. Degradation trend estimation and prognosis of large low speed slewing bearing lifetime. Appl. Mech. Mater. 2014, 493, 343–348. [Google Scholar] [CrossRef]
- Badu, C.N.; Reddy, B.E. Prediction of selected Indian stock using a partitioning—Interpolation based ARIMA–GARCH model. Appl. Comput. Inf. 2015, 11, 130–143. [Google Scholar]
- Şeker, S.; Ayaz, E.; Türkcan, E. Elman’s recurrent neural network applications to condition monitoring in nuclear power plant and rotating machinery. Eng. Appl. Artif. Intel. 2003, 16, 647–656. [Google Scholar] [CrossRef]
- Malhi, A.; Gao, R.X. Recurrent neural networks for long-term prediction in machine condition monitoring. In Proceedings of the 21st IEEE Instrumentation and Measurement Technology Conference, Como, Italy, 18–20 May 2004; pp. 2048–2053.
- Payganeh, G.H.; Khajavi, M.N.; Ebrahimpour, R.; Babaei, E. Machine fault diagnosis using MLPs and RBF Neural Networks. Appl. Mech. Mater. 2011, 110, 5021–5028. [Google Scholar] [CrossRef]
- Dong, S.; Luo, T. Bearing degradation process prediction based on the PCA and optimized LS-SVM model. Measurement 2013, 46, 3143–3152. [Google Scholar] [CrossRef]
- Kim, H.-E.; Tan, A.C.C.; Mathew, J.; Choi, B.-K. Bearing fault prognosis based on health state probability estimation. Expert Syst. Appl. 2012, 39, 5200–5213. [Google Scholar] [CrossRef]
- Lall, P.; Lowe, R.; Goebel, K. Prognostics health management of electronic systems under mechanical shock and vibration using Kalman filter models and metrics. IEEE Trans. Ind. Electron. 2012, 59, 4301–4314. [Google Scholar] [CrossRef]
- Dai, F.; Liao, G.H. Chaotic time series adaptive prediction based on volterra series. Adv. Mater. Res. 2014, 945–949, 2495–2498. [Google Scholar] [CrossRef]
- Xia, X.T.; Lv, T.M. Dynamic Prediction of Rolling Bearing Friction Torque Using Lyapunov Exponent Method. Appl. Mech. Mater. 2010, 44–47, 1120–1124. [Google Scholar] [CrossRef]
- Selina, S.Y.N.; Cabrera, J.; Tse, P.W.T.; Chen, A.H.; Tsui, K.L. Distance-based analysis of dynamical systems reconstructed from vibrations for bearing diagnostics. Nonlinear Dyn. 2015, 80, 147–165. [Google Scholar]
- Li, M.; Li, J.-Y. On the predictability of long-range dependent series. Math. Probl. Eng. 2010, 2010, 397454. [Google Scholar] [CrossRef]
- Li, M.; Chi, C.-H. A correlation-based computational model for synthesizing long-range dependent data. J. Frankl. Inst. 2004, 340, 503–514. [Google Scholar] [CrossRef]
- Gyires, T. Software Agents Architecture for Controlling Long-Range Dependent Network Traffic. Math. Comput. Model. 2003, 38, 839–848. [Google Scholar] [CrossRef]
- Vivero, O.; Heath, W.P. A regularised estimator for long-range dependent processes. Automatica 2012, 48, 287–296. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, R.; Zhou, A.; Zaveri, N. Fractional order signal processing of electrochemical noises. J. Vib. Control 2008, 14, 1443–1456. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Y.Q. FARIMA with stable innovations model of Great Salt Lake elevation time series. Signal Process. 2011, 91, 553–561. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents form a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Song, W.Q.; Deng, S.; Yang, J.; Cheng, Q. Tool Wear Detection Based on Duffing-Holmes Oscillator. Math. Probl. Eng. 2008, 2008, 510406. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Kim, H.S.; Eykholt, R.; Salas, J.D. Nonlinear dynamics, delay times, and embedding windows. Phys. D Nonlinear Phenom. 1999, 127, 48–60. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Dimensions and entropies of strange attractors from a fluctuating dynamics approach. Phys. D Nonlinear Phenom. 1984, 13, 34–54. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Phys. D Nonlinear Phenom. 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Hauer, B.D.; Maciejko, J.; Davis, J.P. Nonlinear power spectral densities for the harmonic oscillator. Ann. Phys. 2015, 361, 148–183. [Google Scholar] [CrossRef]
- Beran, J. Statistics for Long-Memory Processes, 1st ed.; Chapman & Hall: London, UK, 1994. [Google Scholar]
- Hosking, J.R.M. Fractional differencing. Biometrika 1981, 68, 165–176. [Google Scholar] [CrossRef]
- Kavasseri, R.G.; Seetharaman, K. Day-ahead wind speed forecasting using f-ARIMA models. Renew. Energy 2009, 34, 1388–1393. [Google Scholar] [CrossRef]
- Rizk, A.; Fidler, M. Non-asymptotic end-to-end performance bounds for networks with long range dependent fBm cross traffic. Comput. Netw. 2012, 56, 127–141. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civil. Eng. 1951, 116, 770–808. [Google Scholar]
- Center for Intelligent Maintenance Systems. Available online: http://www.imscenter.net/ (accessed on 3 December 2015).
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet Filter-based Weak Signature Detection Method and its Applicationon Roller Bearing Prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Liu, L.-H.; Ma, J.; Xu, X.-L. The Turbine Machine Fault Prediction Based on Kernel Principal Component Analysis. Adv. Mater. Res. 2011, 383, 4787–4791. [Google Scholar]
- Chen, W.Z.; Wang, B.W.; Hu, X.Y. Acceleration signal processing by numerical integration. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2010, 38, 1–4. (In Chinese) [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Liang, S.Y.; Yang, J.; Li, B. Long Range Dependence Prognostics for Bearing Vibration Intensity Chaotic Time Series. Entropy 2016, 18, 23. https://doi.org/10.3390/e18010023
Li Q, Liang SY, Yang J, Li B. Long Range Dependence Prognostics for Bearing Vibration Intensity Chaotic Time Series. Entropy. 2016; 18(1):23. https://doi.org/10.3390/e18010023
Chicago/Turabian StyleLi, Qing, Steven Y. Liang, Jianguo Yang, and Beizhi Li. 2016. "Long Range Dependence Prognostics for Bearing Vibration Intensity Chaotic Time Series" Entropy 18, no. 1: 23. https://doi.org/10.3390/e18010023







