On the Exact Solution of Wave Equations on Cantor Sets
Abstract
:1. Introduction
2. Preliminaries
Yang-Laplace Transforms (YLT)
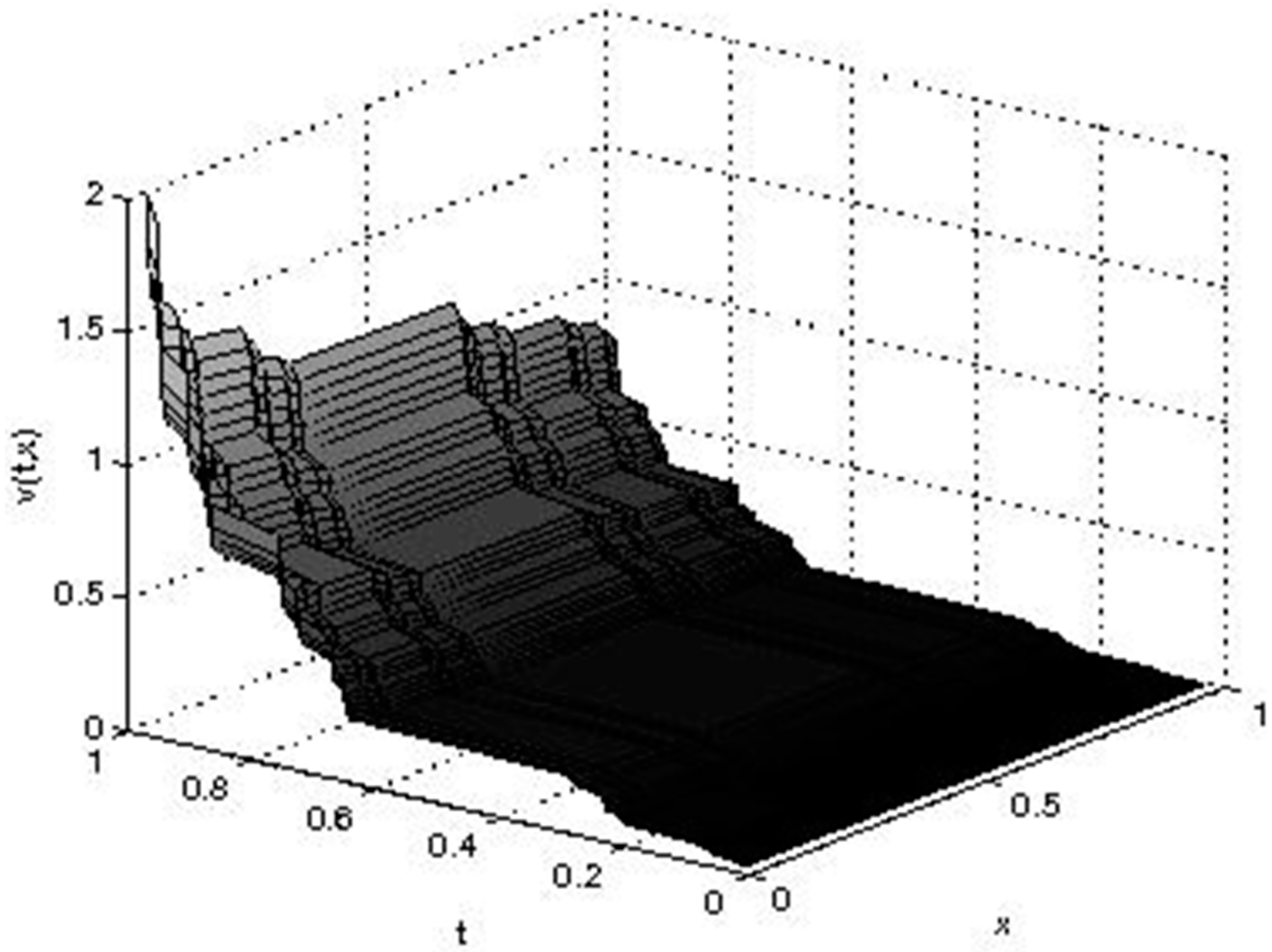
3. Iteration Scheme


4. Interpretation of the Iterative Scheme



5. Conclusions

Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| I(γ) | Local fractional integral |
| δ(γ) | Local fractional variation |
| Eγ | Mittage-Leffler function |
| Ɫγ | Yang-Laplace transform |
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1982. [Google Scholar]
- Adda, F.B.; Cresson, J. About Non-Differentiable Functions. J. Math. Anal. Appl. 2001, 263, 721–737. [Google Scholar] [CrossRef]
- Calcagni, G. Geometry and Field Theory in Multi-Fractional Space Time. J. High Energy Phys. 2012, 1, 1–77. [Google Scholar]
- Zhao, Y.; Baleanu, D.; Cattani, C.; Cheng, D.F.; Yang, X.J. Local Fractional Discrete Wavelet Transform for Solving Signals on Cantor Sets. Math. Prob. Eng. 2013, 2013, 560932:1–560932:6. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Calculus on Fractal Subsets of Real Line—I: Formulation. Fractals 2009, 17, 53–81. [Google Scholar] [CrossRef]
- Yang, A.M.; Li, J.; Srivastava, H.M.; Xie, G.N.; Yang, X.J. Local Fractional Laplace Variational Iteration Method for Solving Linear Partial Differential Equations with Local Fractional Derivative. Discret. Dyn. Nat. Soc. 2014, 2014, 365981:1–365981:8. [Google Scholar] [CrossRef]
- Xu, S.; Ling, X.; Cattani, C.; Xie, G.N.; Yang, X.J.; Zhao, Y. Local Fractional Fourier Series Solutions for Non-Homogeneous Heat Equations Arising in Fractal Heat Flow with Local Fractional Derivative. Adv. Mech. Eng. 2014, 6. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Blumen, A. Fractal Geometry: What Is It, and What Does It Do? Proc. R. Soc. Lond. A 1989, 423. [Google Scholar] [CrossRef]
- Zhang, Y.; Baleanu, D.; Yang, X.J. On a Local Fractional Wave Equation under Fixed Entropy Arising in Fractal Hydrodynamics. Entropy 2014, 16, 6254–6262. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Golmankhaneh, K.; Baleanu, D.; Yang, X.J. Local Fractional Sumudu Transform with Application to IVPs on Cantor Sets. Abs. Appl. Anal. 2014, 2014, 620529:1–620529:7. [Google Scholar] [CrossRef]
- Li, Y.Y.; Zhao, Y.; Xie, G.N.; Baleanu, D.; Yang, X.J.; Zhao, K. Local Fractional Poisson and Laplace Equations with Applications to Electrostatics in Fractal Domain. Adv. Math. Phys. 2014, 2014. [Google Scholar] [CrossRef]
- Christianto, V.; Rahul, B. A Derivation of Proca Equations on Cantor Sets: A Local Fractional Approach. Bull. Math. Sci. Appl. 2014, 3, 75–87. [Google Scholar] [CrossRef]
- Hao, Y.-J.; Srivastava, H.M.; Jafari, H.; Yang, X.J. Helmholtz and Diffusion Equations Associated with Local Fractional Derivative Operators Involving the Cantorian and Cantor-Type Cylindrical Coordinates, Adv. Math. Appl. 2013, 2013, 754248:1–754248:5. [Google Scholar]
- Carpinteri, A.; Sapora, A. Diffusion Problems in Fractal Media Defined on Cantor Sets. Z. Angew. Math. Mech. 2010, 90, 203–210. [Google Scholar] [CrossRef]
- Yang, A.M.; Yang, X.-J.; Li, Z.B. Local Fractional Expansion Method for Solving Wave and Diffusion Equations on Cantor Sets. Abstr. Appl. Anal. 2013, 2013, 351057:1–351057:5. [Google Scholar] [CrossRef]
- Su, W.-H.; Yang, X.J.; Jafari, H.; Baleanu, D. Fractional Complex Transform Method for Wave Equations on Cantor Sets within Local Fractional Differential Operator. Adv. Differ. Equ. 2013, 1, 1–8. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baleanu, D.; Khan, H.; Jafari, H.; Khan, R.A. On the Exact Solution of Wave Equations on Cantor Sets. Entropy 2015, 17, 6229-6237. https://doi.org/10.3390/e17096229
Baleanu D, Khan H, Jafari H, Khan RA. On the Exact Solution of Wave Equations on Cantor Sets. Entropy. 2015; 17(9):6229-6237. https://doi.org/10.3390/e17096229
Chicago/Turabian StyleBaleanu, Dumitru, Hasib Khan, Hossien Jafari, and Rahmat Ali Khan. 2015. "On the Exact Solution of Wave Equations on Cantor Sets" Entropy 17, no. 9: 6229-6237. https://doi.org/10.3390/e17096229






