Analytic Exact Upper Bound for the Lyapunov Dimension of the Shimizu–Morioka System
Abstract
:1. Introduction
2. Lyapunov Dimension
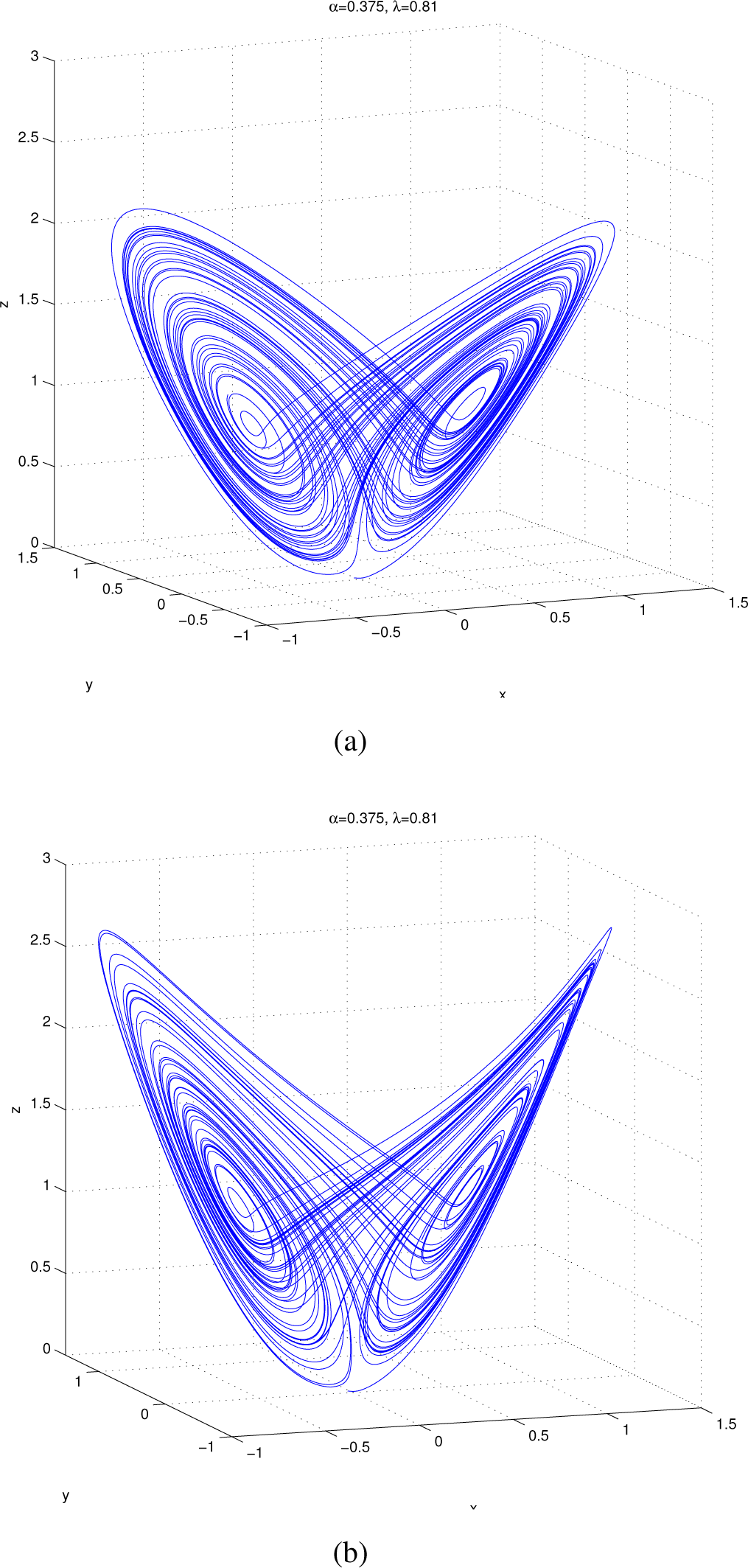
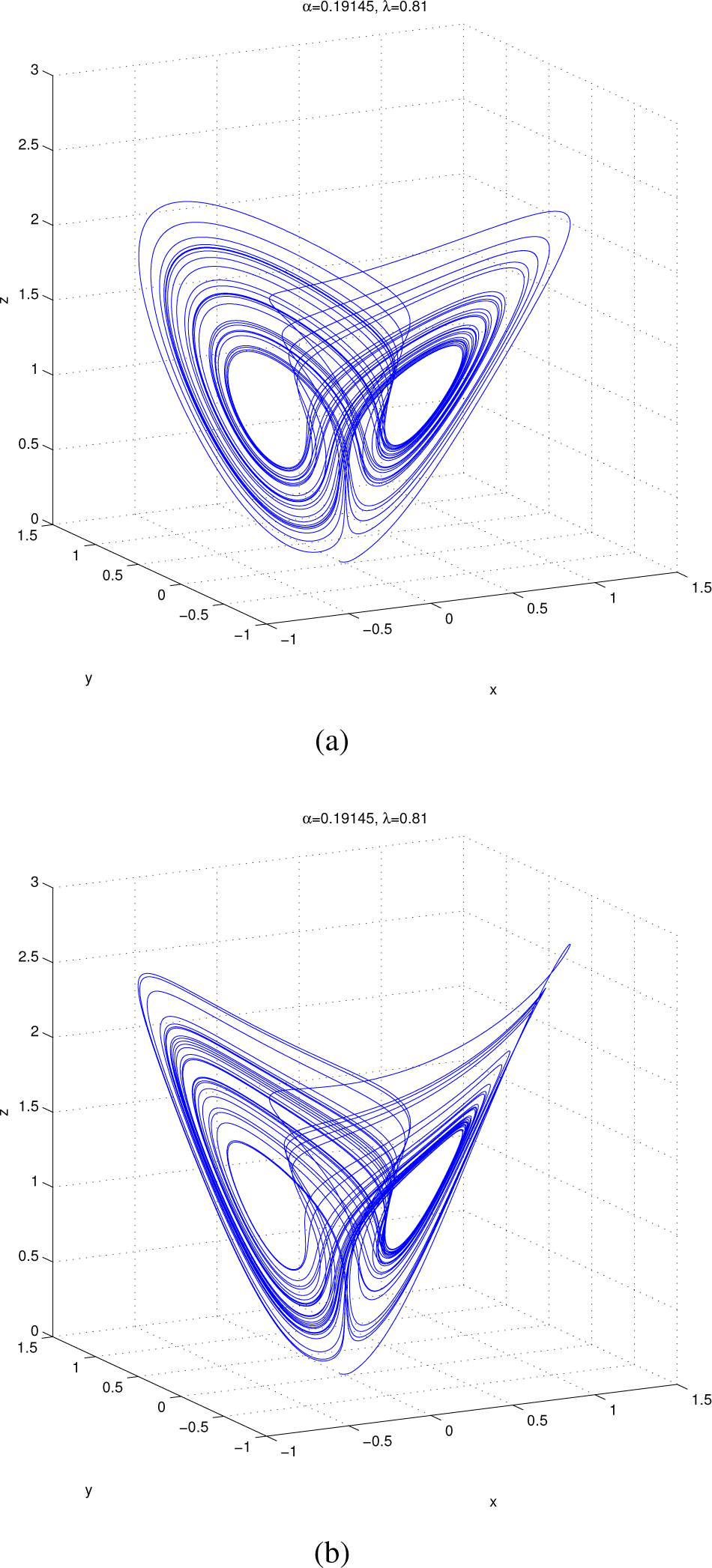
3. Lyapunov Dimension of the Shimizu–Morioka System
4. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lyapunov, A.M. The General Problem of the Stability of Motion; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Oseledec, V.I. Multiplicative Ergodic Theorem: Characteristic Lyapunov Exponents of Dynamical Systems. Trans. Moscow Math. Soc. 1968, 19, 179–210. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V. Time-Varying Linearization and the Perron Effects. Int. J. Bifurcat. Chaos. 2007, 17, 1079–1107. [Google Scholar]
- Kuznetsov, N.V.; Mokaev, T.N.; Vasilyev, P.A. Numerical Justification of Leonov Conjecture on Lyapunov Dimension of Rossler Attractor. Commun. Nonlinear Sci. Numer. Simulat. 2014, 19, 1027–1034. [Google Scholar]
- Kuznetsov, N.V.; Alexeeva, T.; Leonov, G.A. Invariance of Lyapunov Characteristic Exponents, Lyapunov Exponents, and Lyapunov Dimension for Regular and Non-regular Linearizations 2014. arXiv:1410.2016v2.
- Millionschikov, V.M. A Formula for the Entropy of Smooth Dynamical Systems. Differencial’nye Uravenija 1976, 12, 2188–2192. [Google Scholar]
- Pesin, Y. Characteristic Lyapunov Exponents and Smooth Ergodic Theory. Russ. Math. Surv. 1977, 32, 55–114. [Google Scholar]
- Kolmogorov, A. On Entropy per Unit Time as a Metric Invariant of Automorphisms. Dokl. Akad. Nauk SSSR 1959, 124, 754–755. [Google Scholar]
- Sinai, Y. On the Notion of Entropy of Dynamical Systems. Dokl. Akad. Nauk SSSR 1959, 124, 768–771. [Google Scholar]
- Kaplan, J.L.; Yorke, J.A. Chaotic Behavior of Multidimensional Difference Equations. In Functional Differential Equations and Approximations of Fixed Points; Springer: Berlin, Germany, 1979; pp. 204–227. [Google Scholar]
- Douady, A.; Oesterle, J. Dimension de Hausdorff des Attracteurs. CR Acad. Sci. Paris 1980, 290, 1135–1138. [Google Scholar]
- Ledrappier, F. Some Relations between Dimension and Lyapounov Exponents. Commun. Math. Phys. 1981, 81, 229–238. [Google Scholar]
- Pontrjagin, L.; Schnirelmann, L. Sur une Propriété Métrique de la Dimension. Ann. Math. 1932, 156–162. [Google Scholar]
- Ott, E.; Withers, W.; Yorke, J. Is the Dimension of Chaotic Attractors Invariant under Coordinate Changes? J. Stat. Phys. 1984, 36, 687–697. [Google Scholar]
- Dettmann, C.; Frankel, N.; Cornish, N. Chaos and Fractals around Black Holes. Fractals 1995, 3, 161–181. [Google Scholar]
- Hoover, W.; Hoover, C. Why Instantaneous Values of the “Covarian” Lyapunov Exponents Depend upon the Chosen State-Space Scale. Fractals 2014, 20, 5–8. [Google Scholar]
- Sprott, J.; Hoover, W.; Hoover, C. Heat Conduction, and the Lack Thereof, in Time-Reversible Dynamical Systems: Generalized Nosé-Hoover Oscillators with a Temperature Gradient. Phys. Rev. E 2014, 89, 042914. [Google Scholar]
- Gelfert, K.; Motter, A. (Non)Invariance of Dynamical Quantities for Orbit Equivalent Flows. Commun. Math. Phys. 2010, 300, 411–433. [Google Scholar]
- Barreira, L.; Gelfert, K. Dimension Estimates in Smooth Dynamics: A Survey of Recent Results. Ergod. Theor. Dyn. Syst. 2011, 31, 641–671. [Google Scholar]
- Temam, R. Infinite-Dimensional Dynamical Systems in Mechanics and Physics, 2nd ed; Springer: New York, NY, USA, 1997. [Google Scholar]
- Hunt, B. Maximum Local Lyapunov Dimension Bounds the Box Dimension of Chaotic Attractors. Nonlinearity 1996, 9, 845–853. [Google Scholar]
- Shimizu, T.; Morioka, N. On the Bifurcation of a Symmetric Limit Cycle to an Asymmetric One in a Simple Model. Phys. Lett. A 1980, 76, 201–204. [Google Scholar]
- Leonov, G.A. On Estimations of the Hausdorff Dimension of Attractors. Vestnik Leningradskogo Gos. Univ. Ser. 1991, 1, 41–44. [Google Scholar]
- Leonov, G.A.; Boichenko, V.A. Lyapunov’s Direct Method in the Estimation of the Hausdorff Dimension of Attractors. Acta Appl. Math. 1992, 26, 1–60. [Google Scholar]
- Boichenko, V.A.; Leonov, G.A.; Reitmann, V. Dimension Theory for Ordinary Differential Equations; Vieweg Teubner Verlag: Wiesbaden, Germany, 2005. [Google Scholar]
- Leonov, G.A. Strange Attractors and Classical Stability Theory. Nonlinear Dyn. Syst. Theor. 2008, 8, 49–96. [Google Scholar]
- Leonov, G.A. Lyapunov Functions in the Attractors Dimension Theory. J. Appl. Math. Mech. 2012, 76, 129–141. [Google Scholar]
- Leonov, G.; Kuznetsov, N.; Mokaev, T. Homoclinic Orbits, and Self-excited and Hidden Attractors in a Lorenz-Like System Describing Convective Fluid Motion. Eur. Phys. J. Special Topics. 2015, 224, 1421–1458. [Google Scholar]
- Kuznetsov, N.V.; Leonov, G.A.; Vagaitsev, V.I. Analytical-Numerical Method for Attractor Localization of Generalized Chua’s System. IFAC Proc. Vol. 2010, 4, 29–33. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V.I. Localization of Hidden Chua’s Attractors. Phys. Lett. A 2011, 375, 2230–2233. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V.I. Hidden Attractor in Smooth Chua Systems. Physica D 2012, 241, 1482–1486. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V. Hidden Attractors in Dynamical Systems. From Hidden Oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman Problems to Hidden Chaotic Attractors in Chua Circuits. Int. J. Bifurcat. Chaos. 2013, 23, 1330002. [Google Scholar]
- Kuznetsov, N.V.; Kuznetsova, O.A.; Leonov, G.A. Visualization of Four Normal Size Limit Cycles in Two-Dimensional Polynomial Quadratic System. Differ. Equ. Dyn. Syst. 2013, 21, 29–34. [Google Scholar]
- Leonov, G.A.; Bragin, V.O.; Kuznetsov, N.V. Algorithm for Constructing Counterexamples to the Kalman Problem. Dokl. Math. 2010, 82, 540–542. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V. Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems. Dokl. Math. 2011, 84, 475–481. [Google Scholar]
- Bragin, V.O.; Vagaitsev, V.I.; Kuznetsov, N.V.; Leonov, G.A. Algorithms for Finding Hidden Oscillations in Nonlinear Systems. The Aizerman and Kalman Conjectures and Chua’s Circuits. J. Comput. Syst. Sci. Int. 2011, 50, 511–543. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V. On Differences and Similarities in the Analysis of Lorenz, Chen, and Lu Systems. Appl. Math. Comput. 2015, 256, 334–343. [Google Scholar]
- Leonov, G.; Kuznetsov, N.; Korzhemanova, N.; Kusakin, D. Estimation of Lyapunov Dimension for the Chen and Lu Systems 2015. arxiv:1504.04726.
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leonov, G.A.; Alexeeva, T.A.; Kuznetsov, N.V. Analytic Exact Upper Bound for the Lyapunov Dimension of the Shimizu–Morioka System. Entropy 2015, 17, 5101-5116. https://doi.org/10.3390/e17075101
Leonov GA, Alexeeva TA, Kuznetsov NV. Analytic Exact Upper Bound for the Lyapunov Dimension of the Shimizu–Morioka System. Entropy. 2015; 17(7):5101-5116. https://doi.org/10.3390/e17075101
Chicago/Turabian StyleLeonov, Gennady A., Tatyana A. Alexeeva, and Nikolay V. Kuznetsov. 2015. "Analytic Exact Upper Bound for the Lyapunov Dimension of the Shimizu–Morioka System" Entropy 17, no. 7: 5101-5116. https://doi.org/10.3390/e17075101
APA StyleLeonov, G. A., Alexeeva, T. A., & Kuznetsov, N. V. (2015). Analytic Exact Upper Bound for the Lyapunov Dimension of the Shimizu–Morioka System. Entropy, 17(7), 5101-5116. https://doi.org/10.3390/e17075101





