Abstract
We study the entanglement of a pure state of a composite quantum system consisting of several subsystems with d levels each. It can be described by the Rényi–Ingarden–Urbanik entropy Sq of a decomposition of the state in a product basis, minimized over all local unitary transformations. In the case q = 0, this quantity becomes a function of the rank of the tensor representing the state, while in the limit q → ∞, the entropy becomes related to the overlap with the closest separable state and the geometric measure of entanglement. For any bipartite system, the entropy S1 coincides with the standard entanglement entropy. We analyze the distribution of the minimal entropy for random states of three- and four-qubit systems. In the former case, the distribution of the three-tangle is studied and some of its moments are evaluated, while in the latter case, we analyze the distribution of the hyperdeterminant. The behavior of the maximum overlap of a three-qudit system with the closest separable state is also investigated in the asymptotic limit.
1. Introduction
After more than twenty years of intensive research, the entanglement of the pure states of bipartite quantum systems is rather well understood [1,2] for two subsystems of an arbitrary dimension d. In this case, any pure state can be represented in a product basis by a matrix of coefficients of order d, and its standard singular values’ decomposition allows one to reveal entanglement.
On the other hand, in the case of systems composed of n ≥ 3 subsystems, the problem becomes much more complicated, as the state is represented by a tensor of size d and n dimensions. Even though several important results were obtained, especially in the case of three [3–5] and four qubits [6–10], and several measures of entanglement in such systems were proposed [11–14], it is fair to say that the complete understanding of the phenomenon of entanglement in multipartite systems is still missing.
To characterize the entanglement of a quantum state of a bi-partite system, it is natural to analyze the degree of mixing of the reduced density matrix. For instance, making use of von Neumann entropy, one arrives at one of the most often used measures: the entropy of entanglement [15]. It is often convenient to apply for this purpose also the generalized entropy of Rényi [2] or some other kinds of entropy.
The aim of the present work is to propose a possible generalization of this quantity for the case of multipartite systems, for which a pure state is represented by a tensor. Furthermore, we would like to make a connection with the geometric measure of entanglement, which depends on the distance of the state considered to the closest separable state [16–18].
Following the papers of Parker and Rijmen [19] and Bravyi [20], we suggest to analyze the entropy of decomposition of a quantum state in a product basis, sometimes called Ingarden–Urbanik entropy [21], minimized over all local unitaries. This quantity can be generalized in the sense of Rényi. Interestingly, to establish a direct link with the geometric measure of entanglement [16,18], it is sufficient to consider the Rényi–Ingarden–Urbanik (RIU) entropy and to send the Rényi parameter q to infinity.
Even though the approach advocated here is applicable for arbitrary composite quantum systems, for concreteness, we concentrate the majority of this work for the case of three and four qubits. It is demonstrated that there is no a single pure state for which the minimal RIU entropy is the largest for all values of the Rényi parameter q. Investigating the problem for selected values of q, we identify certain pure states, which are conjectured to maximize this particular measure of entanglement.
Furthermore, we make also use of a statistical approach to analyze the distribution of the hyperdeterminant and minimal RIU entropy for random quantum pure states. They are distributed with respect to the unique unitarily-invariant Haar measure on the space of pure quantum states, the complex projective space, ℂPN−1, where the total dimension of the complex Hilbert space is N = dn. Analyzing systems composed of three subsystems of an arbitrary dimension d, we obtain a bounds for the geometric measure of entanglement for generic states of such a system.
This paper is organized as follows. In Section 2, we introduce the RIU entropy for a pure state of a multipartite system, while in Section 3, different techniques of tensor decomposition are reviewed. In Section 4, we present results obtained for three-qubit system, while analogous results for four qubits are presented in Section 5. A more general case of three subsystems consisting of an arbitrary number of levels is discussed in Section 6. Computations of the moments of the distribution of three-tangle and a derivation of the bound for the geometric measure of entanglement are relegated to the Appendix.
2. Minimal Rényi–Ingarden–Urbanik Entropy
Consider a quantum state describing a system consisting of n subsystems, with d levels each,
. Working in an arbitrary product basis, one can represent such a state by an n-index tensor,
The standard normalization condition, ⟨ψ|ψ⟩ = 1, implies that:
It will be convenient to introduce a multi-index μ = (i1, i2,…, in), where µ can be identified with the set {1,…, N = nd}, and to use a shorter notation
. Hence, p(|ψ⟩) = (p1,…pN) represents an N-point probability vector
, which can be characterized by the Rényi entropy
. For q → 1, this quantity reduces to the standard Shannon entropy
, which in the context of the decomposition of the state |ψ⟩, is called the Ingarden–Urbanik entropy [21–23] and written
. In will be convenient to use natural logarithms throughout this paper, written log 2 ≈ 0.693.
The product basis |i1⟩ ⊗ |i2⟩ ⊗…⊗ |in⟩ is determined up to a local unitary transformation, Uloc = V1 ⊗ V2 ⊗…⊗ Vn, where an unitary matrix Vj acts on the j-th subsystem. As the Ingarden–Urbanik entropy of the decomposition depends explicitly on the choice of the product basis, it is natural to analyze the optimal value, minimized over the set of local unitaries [22,23].
We shall study a more general case of the Rényi entropies Sq with Rényi parameter q ≥ 0. For any multipartite state
, we define the minimal Rényi–Ingarden–Urbanik (RIU) entropy,
where the minimum is taken over the entire set of local unitary transformations.
Proposition 1. For any N qudit state,
, its minimal RIU entropy is bounded from above,
, where:
This statement follows directly from the work of Carteret, Higuchi and Sudbery [22], who showed that performing a local unitary transformation Uloc = U1 ⊗…⊗ Un, one can always find a product basis, such that the decomposition Equation (1) contains no more than Rmax terms. A suitable choice of n unitary matrices of size d allows one to bring d(d − 1)/2 elements of the tensor C to zero. Therefore, out of all its dn entries, at least nd(d − 1)/2 can be always set to zero. This fact can be also formulated as the following statement
Proposition 2. For any n qudit state,
, represented by a tensor C as in Equation (1), its tensor rank R is bounded by Rmax = dn − nd(d − 1)/2, where R is the minimal number r of terms in its decomposition involving arbitrary coefficients fν,
Observe that in the case of the Rényi entropy of order zero, q = 0, one has
, where R is the tensor rank of the tensor C(ψ). The quantity log R is known as the Schmidt measure characterizing the entanglement of the multipartite pure state [24,25], while the rank R was used to determine probabilistic conversion of the three-qubit pure state [26]. Since the Rényi entropy is in general a non-increasing function of the parameter q, one gets the general bound:
For instance, in the case of a three-qubit system (n = 3 and d = 2), the bound Equation (4) gives Rmax = 8 − 3 = 5 in agreement with the five-term standard form of a three-qubit pure state by Acin et al. [3].
Besides Case
- q = 0, corresponding to the tensor rank of |ψ⟩, we shall also consider some other particular cases of the definition Equation (3).
- q = 1. The minimal IU entropy determines the minimal information gained by environment after performing a projective von-Neumann measurement of the pure state |ψ⟩ ⟨ψ| in an arbitrary product basis [20].
- q = 2. The minimal decomposition entropy characterizes the maximal purity of the probability vector pµ associated with the outcomes of a projective measurement in a product basis and is accessible in a coincidence experiment with two copies of the multipartite state |ψ⟩. This quantity was used by Parker and Rijmen [19] to analyze multipartite entanglement in the context of coding theory.
- q = ∞. In the limiting case q → ∞, the minimal RIU entropy gives , where the largest component of the vector pµ reads λmax = max |⟨ψ|χsep⟩|2. The maximum is taken over the set of all separable states, |χsep⟩ = Uloc|0⋯0⟩, so λmax is a decreasing function of the Fubini–Study distance to the closest separable state [16,17], , and its function is called the geometric measure of entanglement [18], .
In the case of bipartite systems (n = 2), one can use the standard singular value decomposition of the matrix C to show that the probability vector pµ coincides with the vector of Schmidt coefficients λj determining the Schmidt decomposition [2],
, where
This observation leads to:
Proposition 3. For any bipartite state, |ψ⟩ ∈ d ⊗ d, its minimal RIU entropy coincides with the Rényi entropy of entanglement, so in the case q = 1, one arrives at the standard entropy of entanglement:
3. Tensor Decompositions
Singular value decomposition (SVD) of the matrix containing the expansion coefficients of a bipartite pure state plays a crucial role in evaluating the minimal RIU entropy. However, in the case of multipartite systems and quantum states described by higher order tensors, this decomposition is not directly applicable.
In this section, we consider two generalizations of SVD, the higher order singular value decomposition (HO-SVD) [27] and the parallel factor model (PARAFAC) [28]. Both decompositions were developed in the framework of principal component analysis [29] and have found several applications in signal processing, numerical linear algebra, graph analysis and numerical analysis [30]. Throughout this section, we will consider such schemes to evaluate some bounds for the minimal RIU entropy and the geometric measure of entanglement.
Let us define a tensor C as a multidimensional or n-way array of numbers, so it can be identified with an element of
. Accordingly, a matrix and a vector are a two-way and a one-way tensor, respectively. Note that such a space is linear. Given two tensors A,
, their inner product is inherited from the linear space
and defined as follows:
where the over-bar denotes the complex conjugation. The corresponding induced norm is the Frobenius norm [27,30], written
. It implies the Frobenius distance, d(A, B) := ║A − B║. Note that the coefficients of the state Equation (1) can be arranged in a tensor
, and conversely, a given tensor in such a space defines a certain pure state |ψ⟩ in the Hilbert space
.
3.1. Higher Order Singular Value Decomposition
Let
be an n-way tensor. We define the k-th unfolding C(k) as the matrix of size dk × (dk+1dk+2 ⋯dnd1d2 ⋯dk−1) that contains the tensor element
in the entry (ik, j), with:
The k-mode product of a matrix
with C is defined (element-wise) as:
The higher order singular value decomposition allows one to construct a tensor A, called the co-tensor [30], of the same dimension as C, such that:
where each U(k) acts according to Equation (9), and any two sub-tensors
and
, with p and q fixed, are orthonormal:
The numbers
are called the k-mode singular values of C; they are non-negative and fulfill
for all p < q. Such a decomposition is accomplished by taking each U(k) in Equation (10) as the matrix of left singular vectors of C(n). Note that finding the SVD of the k-th unfolding of the coefficients tensor of Equation (1) is equivalent to diagonalizing the reduced density matrix of the k-th party of the system. Moreover, according to Equation (10), the co-tensor A of C defines a state |ψ⟩HO−SVD that is LUequivalent to Equation (1). In this manner, Liu et al have recently proposed an entanglement classification based on the study of HO-SVD and the local symmetries of the multipartite states [31].
3.2. Parallel Factor Decomposition
The idea of expressing a tensor as a sum of rank-one tensors was applied in several contexts. For instance, in psychometrics, it is known as canonical decomposition (CANDECOMP), while in brain imaging analysis, it is referred as parallel factor decomposition (PARAFAC); see [28] and the references therein. For other applications of this decomposition, see also [30].
The PARAFAC is a decomposition of an n-way tensor
into a sum of rank-one tensors,
where
denotes the k-th column of a matrix of size dℓ × R, with ℓ = 1,…, n and λ is a vector of size R. The symbol ○ represents the dyadic product of vectors [32]. In terms of the components, PARAFAC decomposition reads:
In practice, we are interested in an approximation given by sum of r rank-one tensors:
Usually, a least squares approximation Equation (12) is concerned, in which case one has to minimize the quantity dP = ║C − CPARAFAC║. Since the problem is not linear, usually, we obtain an approximate solution only, accomplished through the alternating least squares (ALS) algorithm. In this work, we use the algorithm provided by Nion and De Lathauwer [33] to compute the PARAFAC decomposition of a three-way complex tensor. In the case of r = 1, the state:
is fully separable. Hence, the quantities dP and λp = |⟨ψ|ψP⟩|2 are bounds for the geometric measure of entanglement EG and the separable state maximum overlap λmax, respectively.
4. Three Qubits
In this section, we analyze pure states of a system consisting of three qubits: n = 3 and d = 2. The exact values of the minimal RIU entropy are found for the states W and GHZ for particular values of the Rényi parameter q. Generic properties of the minimal RIU entropy are also discussed. Furthermore, some moments of the three-tangle τ are computed, and the corresponding distribution is analyzed.
4.1. Minimal Decomposition Entropy
In the case of a three-qubit system, any pure state
can be represented in the five-term decomposition of Acin et al. [3],
Where
, and four coefficients can be chosen to be real. Observe that selecting
, and neglecting others, one obtains the state
, while setting
2, one has
. As the number of terms in these states cannot be reduced by any local unitary transformation their tensor ranks are equal to two and three, respectively, so that
and
. It is possible to write a state |A5⟩ with all coefficients equal,
, for which
. In the same form, we define |A4⟩ = (|000⟩ + |010⟩ + |001⟩ + |111⟩)/2, such that
.
For any general value of the Rényi parameter q, we are not aware of any constructive procedure that gives the exact value of minimal RIU entropy Equation (3). However, for permutation invariant states, we can follow the general scheme of calculating the maximum overlap with the closest separable state. For such states, it was first conjectured and later proven that in order to obtain the maximal overlap, it is enough to take the product state to be a tensor product of the same single-party real state [34–36]. In this spirit, to minimize the RIU entropy for permutation invariant states, the product of local unitary matrices Uloc in Equation (3) will be taken as:
This task can be done easily in some special cases, i.e.,
for any q and
. To evaluate the expression Equation (3) for an arbitrary state, we perform a random walk over the space of unitary matrices. Figure 1 shows the minimal RIU entropy obtained numerically for some particular states and different values of q. In the case of the state |W⟩ and |A5⟩, one can compare the value obtained by this procedure with the analytical results.
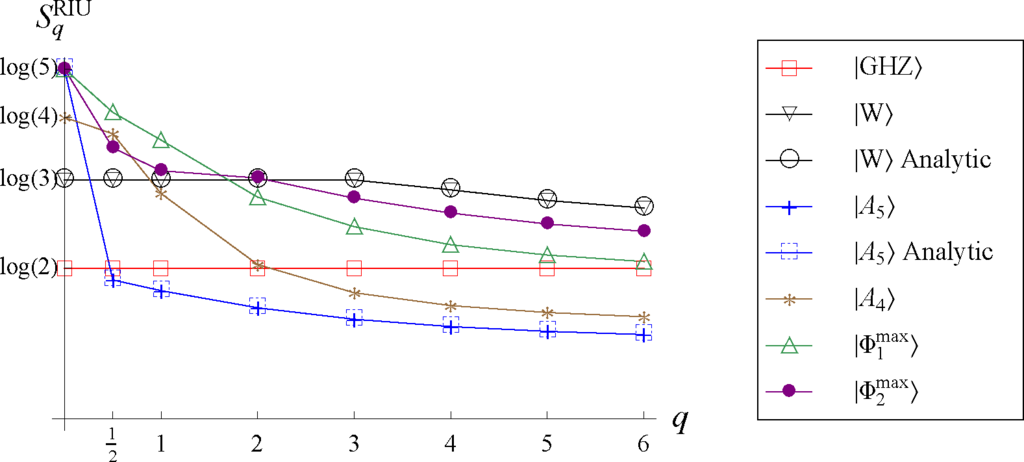
Figure 1.
Minimal Rényi–Ingarden–Urbanik (RIU) entropy obtained numerically for several three-qubit states as a function of the Rényi parameter q. Comparison with analytical results available for states invariant with respect to permutation confirms the accuracy of the numerical procedure.
In the following, we are concerned with typical properties of the minimum value of the RIU entropy. First, we compute the value of the Rényi entropy of a random state; then, the same quantity is evaluated in the corresponding co-tensor, and finally, we compute the
by performing the random walk procedure described above. As we pointed before, we are mainly interested in the cases q = 1, q = 2 and q = 100. The latter value serves as an approximation for the limiting case
. The probability distributions of estimations of the minimal RIU entropy for random states are presented in Figure 2. The mean, second moment and standard deviation for these distributions are reported in Table 1. In the case of q = 1, some analytical results are available [37,38].
where N is the size of the system and Ψ(x) denotes the digamma function and Ψ′(x) its derivative. In our case, we set N = 8 to obtain ⟨S1⟩ = 1.718 and ΔS1 = 0.160, so our numeric calculations are in good agreement with these analytical predictions. We compute the maximum overlap of the state |ψ⟩ with the closest separable state by performing a random walk in the space of unitary matrices; this quantity is denoted as
. The PARAFAC decomposition of |ψ⟩ yields a bound
for this overlap. A comparison between these three distributions is presented in Figure 3.
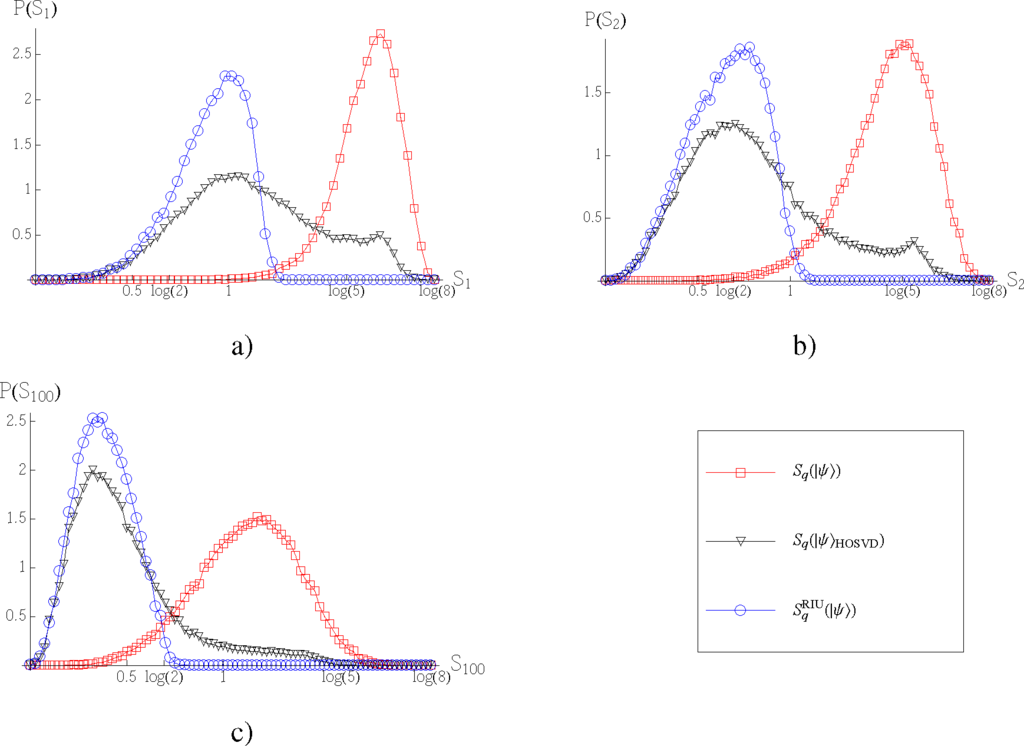
Figure 2.
Distributions of the Rényi entropy of a random probability vector describing a generic three-qubit state (□), the Rényi entropy of the corresponding co-tensor (∇) and the estimation of minimal RIU entropy (○) for (a) q = 1, (b) q = 2 and (c) q = 100.

Table 1.
Mean value, second moment and standard deviation of the Rényi entropy of the probability vector corresponding to a three-qubit random pure state (left), its corresponding co-tensor (center) and the minimal RIU entropy for q = 1, 2, 100.
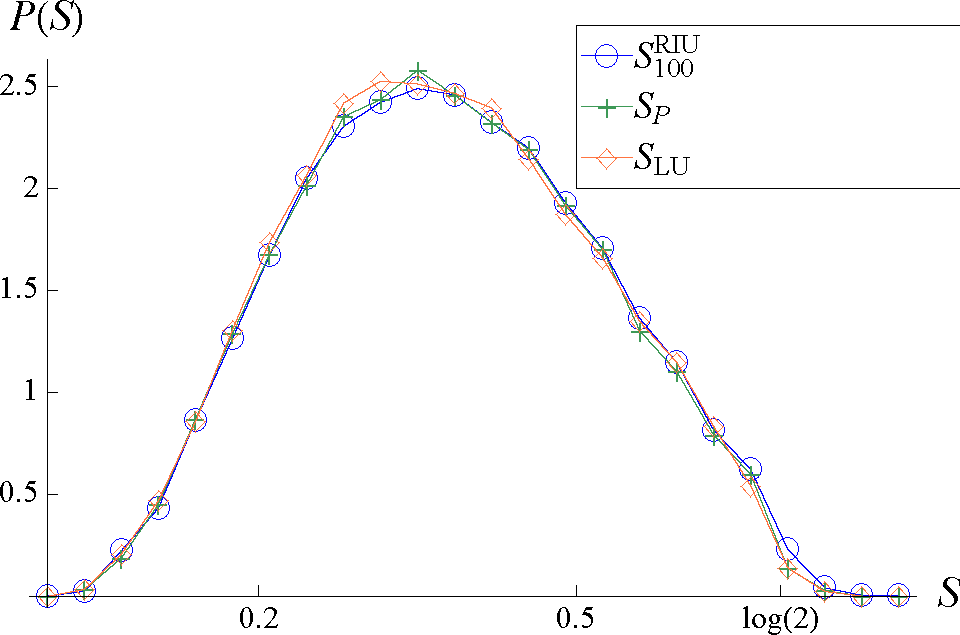
Figure 3.
Comparison between the distributions of
(○),
(+) and
(⋄) for three-qubit random states.
For any value of the Rényi parameter q ≥ 0, one can ask for a state
, for which its minimal entropy
achieves its maximum value. It is known that in the case of three qubits, the maximal entangled state with respect the geometric measure is the state |W⟩ [39,40], and hence, the largest value of the RIU entropy reads
. We found numerically states for which
attain the maximum values. For q = 1, 2, the coefficient vectors in the basis Equation (16) of these maximal states read:
Furthermore, we compute also
for other values of the Rényi parameter q; see Figure
4.2. Distribution of Three-Tangle
The residual entanglement or three-tangle Τ was introduced by Coffman et al. [41]. It quantifies the genuine entanglement of a system of three qubits A, B and C in the following sense. Let
and
denote the concurrences [42] of the density matrices of the pairs of qubits A, B and A, C, respectively. Since the qubits BC can be regarded as a single subsystem, we can ask for the entanglement between A and BC. Such a quantity will be denoted as
, and it is equal to
[41], where
is the reduced density matrix of the qubit A when the partial trace with respect to B and C has been performed. The following inequality holds.
and using it, we define the three-tangle as.
This quantity measures the amount of entanglement between the qubit A and the subsystem BC that is not related to the entanglement in the pairs A, B and A, C. The three-tangle Τ is invariant under the permutation of sub-systems and vanishes on all states that are separable under any cut. The three-tangle for State (1) with n = 3 and d = 2 is given by:
where:
is the Cayley hyperdeterminant of the tensor C. Here,
stands for the Levi–Civita tensor of rank two, and the sum is performed over all indexes. The three-tangle is bounded by zero and one. For the
state, the residual entanglement attains its maximum value. Indeed, the pairwise concurrences
and
vanish and
, so this state is referred to as a genuinely three-partite entangled state.
The hyperdeterminant Det3(C) is a homogeneous polynomial function of degree four, first introduced by Caley [43]. It is invariant under the action of the group
[44]. This notion of invariance plays an important role in the construction of entanglement monotones for pure states of multiqubit systems [45]. Moreover, a classification of multipartite entangled states has been accomplished by analyzing singularities of the hyperdeterminant [46].
Now, we will discuss properties of typical quantum states of a three-qubit system. Kendon et al. [47] studied the distribution of three-tangle for an ensemble of random pure states drawn according to the
Haar measure. By direct integration of Equation (21) with respect to the unitary invariant measure, they obtained the average value
. In Figure 4, we show the probability densities of τ and τ2 evaluated over a sample of 105 random pure states. Moreover, the first six even moments of τ can be calculated by symbolic integration using the Betaintegral (see Appendix A1). The distribution of the three-tangle can be approximated by the Beta distribution Beta(α, β; τ), using the moment method to estimate the parameters
and
. Hence, we get:
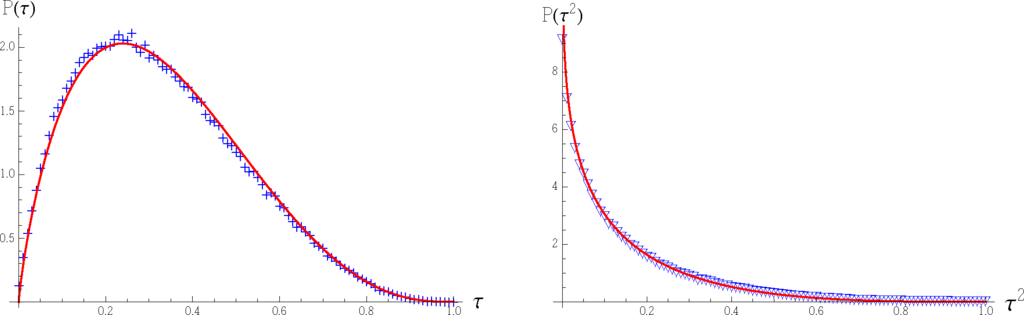
Figure 4.
Distributions of the three-tangle (+) and its square (∇) for three-qubit pure random states. The solid lines are approximations with Beta distributions Equation (23) on the left and Equation (24) on the right.
By virtue of the chain rule, we get an approximated distribution function for τ2:
The above distributions are presented in Figure 4 together with the estimation obtained by numerical simulations. In order to show the accuracy of our approximation, we show in Table 2 a comparison between the first six even moments of the distribution Equation (23) and the moments of P(τ) obtained by symbolic integration.

Table 2.
Comparison of the first six even moments of τ approximated with the Equation (23) (center column) and computed using the symbolic integration package (right column).
5. Four Qubits
In this section, we compute both the minimal RIU entropy and the hyperdeterminant for several exemplary four-qubit states; we also analyze some typical properties of these quantities.
5.1. Minimal Decomposition Entropy
According to Carteret et al. [22], a given state
can be written using twelve terms:
and the other coefficients Ci,,j,k,ℓ are real and non-negative if at most one of the indexes differs from one. The state
is obtained by choosing
. Hence,
. Moreover, we define a state
for which the non-vanishing coefficients in the above expansion are
. In this case,
.
A proper basis for n qubit permutation-invariant states is constituted by the so-called Dicke states:
Note that
and
. In the computations below, we will consider the case of n = 4. The calculation of the minimal RIU entropy for permutation-invariant states can be turned into a one-variable optimization by taking
. We found
, for all q and
; for the other values of q, minimization will be accomplished numerically. On the other hand, the optimal decomposition of the state
is obtained by taking
. Accordingly, it is possible to get a compact formula for its minimal RIU entropy:
Hence, we get
by taking the limit q → 1. On the other hand, when q → ∞, one arrives at
, which is consistent with the well-known result of the overlap of
with the closest separable state [34]. Note that by symmetry,
. In Figure 5, we compare the results obtained in this way with those acquired by performing a random walk over the space of unitary matrices for several values of q.
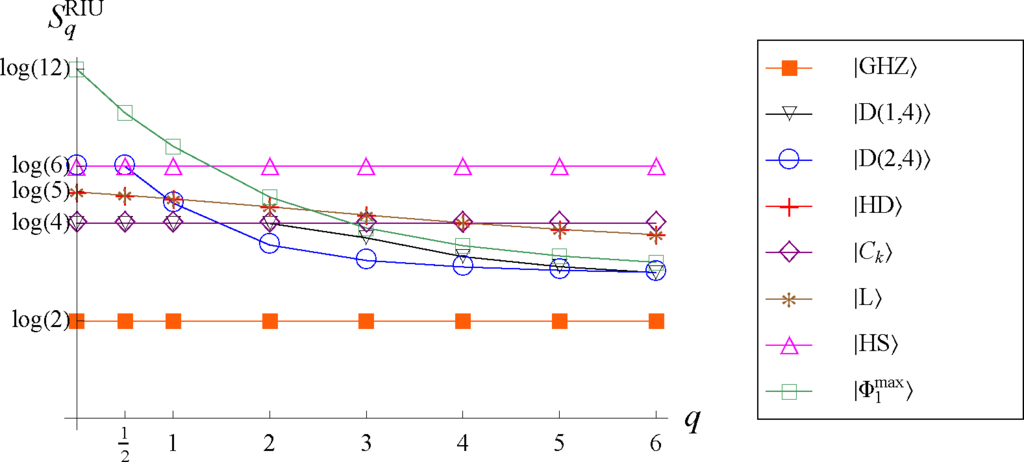
Figure 5.
The minimal RIU entropy
computed for several four-qubit states as a function of the parameter q.
Consider also some other exemplary four-qubit states. The hyperdeterminant state:
maximizes the four-qubit hyperdeterminant [48]. The minimal RIU entropy for the former state can be computed in the same way as for the Dicke state Equation (27), as it is shown [34–36] that the state Equation (28) presents the optimal decomposition minimizing the RIU entropy for any q. Then, we obtain:
In the limit q → ∞, we get
, which is consistent with the maximum overlap with the closest separable states computed according to [34]. On the other hand, the cluster states identified by Gour and Wallach [8]:
are the four-qubit states that maximize the Rényi α-entropy of the partial trace for α ≥ 2. They also found that the state:
maximizes the average Tsallis ≥-entropy of the partial trace for all α > 2. The minimal RIU entropy of the former states is shown in Figure 5 for several values of q. Based on our numerical calculations for the cluster states, we conjecture that
with k = 1,2,3 for any value of the Rényi parameter.
We also consider the four-qubit state found by Higuchi and Sudbery [49]:
where w=exp(2iπ/3), which has maximum average von Neumann entropy of partial traces averaged over all possible three splittings of a four qubit system into two bipartite systems. Numerical values of
are shown in Figure 5.
We are also interested in the typical properties of the minimum of
for four qubits. For an ensemble of 105 random pure states, we compute,
,
and
, taking q = 1,2,100. The corresponding distributions are shown in Figure 6 and in Table 3. In the first case and with q = 1, we can compare our results with those provided by the analytic expression Equation (18), ⟨S1⟩ = 2.381 and ΔS1 = 0.124. To provide an approximation of
, we analyzed the entropy with the Rényi parameter q = 100. In Figure 7, we show the distributions of the minimal RIU entropy
and
, where
max is the maximum overlap with the closest separable state computed through a random walk in the space of unitary matrices.
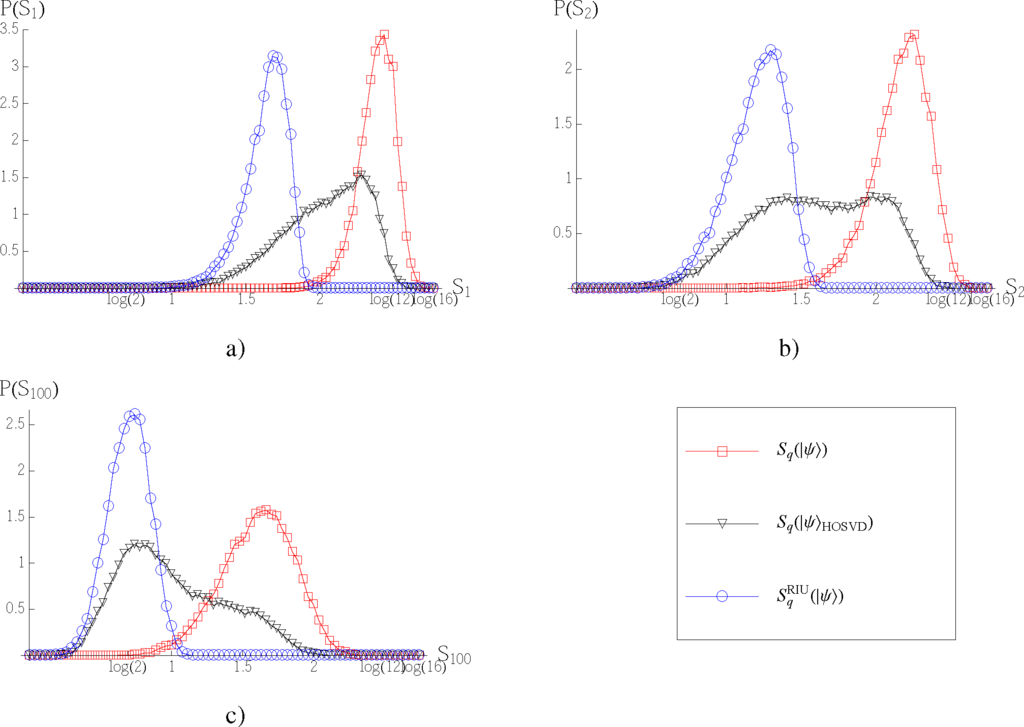
Figure 6.
Distributions of the Rényi entropy of a four-qubit random state probability vector (□), the Rényi entropy of the corresponding co-tensor (∇) and the minimal RIU entropy (○) for (a) q = 1, (b) q = 2 and (c) q = 100.

Table 3.
Mean value, second moment and standard deviation of the Rényi entropy of a four-qubit random pure state (left), its corresponding co-tensor (center) and the minimal of the RIU entropy for q = 1, 2, 100.
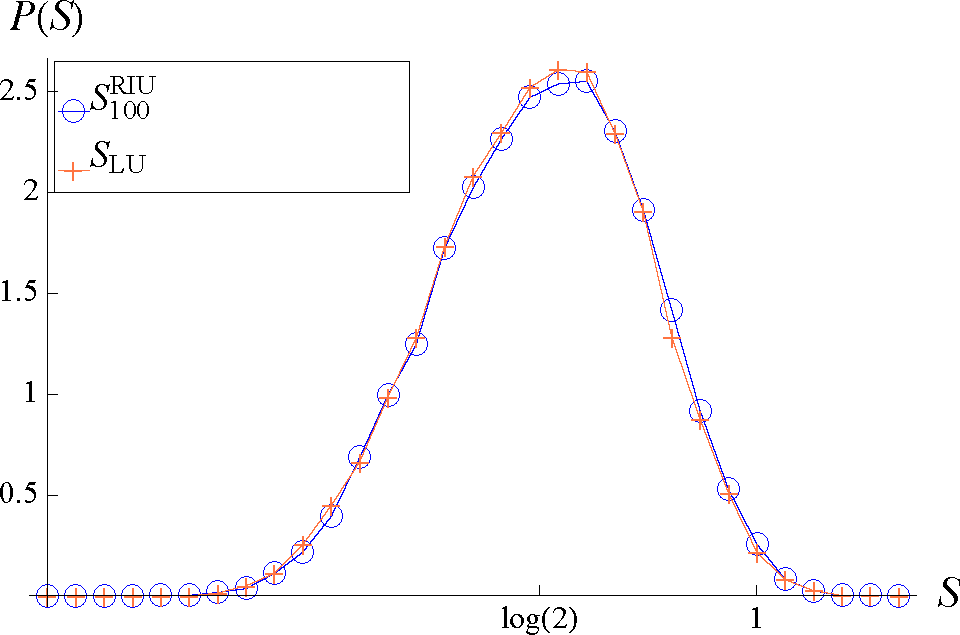
Figure 7.
Comparison between the distributions of
(○) and
(+) for a four-qubit system.
As in the three-qubit case, we are looking for the maximal states of the minimal RIU entropy. For the maximal symmetric state with respect to the geometric measure of entanglement
, the RIU entropy yields
[40]. Moreover, our numerical results allow us to conjecture that
is the largest value of the minimal RIU entropy with q = ∞ among the four-qubit states.
For q = 1, we found numerically a state
for which
is maximal. In the decomposition Equation (25), this state reads:
Further numerical tests support the conjecture that the state |HS⟩, for which
, maximizes the minimal RIU entropy for q ≥ 2.
5.2. Distribution of the Hyperdeterminant |Det4|
In the case of four-qubit states, the hyperdeterminant Det4 is a polynomial of degree 24. It can be constructed following Schläfli’s procedure [46]. In analogy to the three-tangle, we consider the following function of the coefficients tensor C of the state |ψ⟩ ∈ 16,
For a separable four-qubit state, one has T (|ψsep⟩) = 0, but it vanishes also for the states |D(1, 4)⟩, |D(2, 4)⟩, |Ck⟩, |HS⟩ and |GHZ⟩.
Alsina and Latorre found recently [48] that both |HD⟩ and |L⟩ maximize the hyperdeterminant, and they also discussed the relation between these states for which T (|HD⟩) = T (|L⟩) = 1. Furthermore, numerical simulations indicate that they have the same minimal RIU entropy
.
We evaluate the quantity Equation (34) over an ensemble of 107 random pure states. The mean and the standard deviation read ⟨T⟩ = 9.74 × 10−4 and ⟨∆T⟩ = 2.39 × 10−3, respectively, while the corresponding distribution is shown in Figure 8.
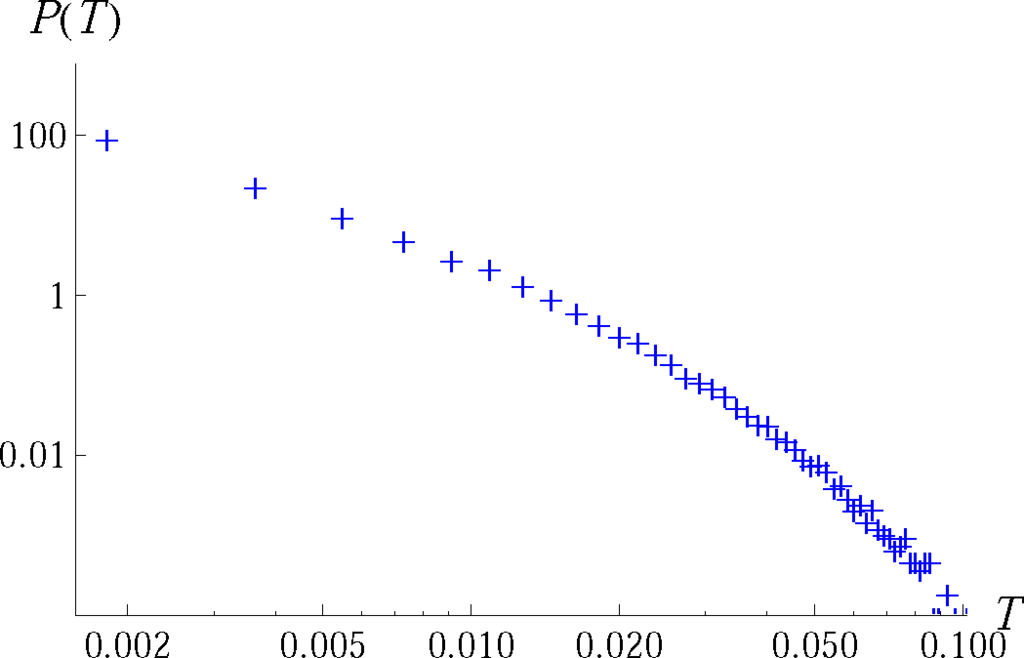
Figure 8.
Distribution of the absolute value of the hyperdeterminant P (T) (+) for four-qubit pure random states in a log-log plot.
6. Three Qudits: Asymptotic Case
Statistical properties of random tensors and their asymptotic limit became a subject of intensive research [50,51]. In this section, we study random tenors of dimension three and arbitrary size, which describe generic states of a system composed of three qudits. We analyze the bounds for the geometric measure of entanglement of such states provided by the tensor decompositions HOSVD and PARAFAC.
Consider a typical state
drawn from the Haar measure. Let λmax and λH denote the largest component of the probability vectors p(|ψ⟩) and p(|ψ⟩HOSVD), respectively, and consider the overlap λP = |⟨ψ|ψP⟩|2, where |ψP⟩ is the state Equation (15). In the cases d = 2, 3, we also evaluate the maximum overlap of |ψ⟩ with the closest separable state by performing a random walk optimization procedure in the space of unitary matrices. Figure 9a shows the average value of four quantities as a function of the size of the quit d computed over an ensemble of 105 random states. The mean value of λmax can be expressed [52] in terms of the harmonic numbers HN,
where N = d3, in our case. Therefore, for a random pure state of three qudits, the average largest overlap to a pure state scales as d−3. Performing decompositions for an ensemble of such random tensors, we find that for large d, the largest overlaps optimized by HOSVD and PARAFAC behave as:
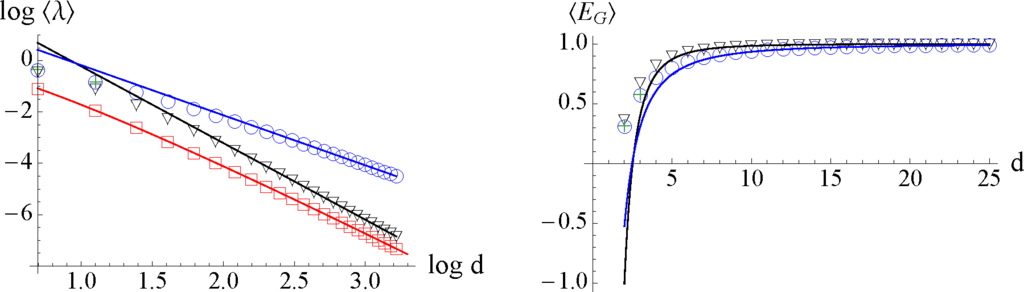
Figure 9.
The mean of the maximum component (left) and the geometric measure of entanglement (right) for random states of a tri-partite system as a function of the qudit size. Bullets correspond to numeric simulations: (□) stands for the greatest tensor element λmax; (∇) the maximum component of the higher order singular value decomposition (HO-SVD) co-tensor λH; (○) stands for the parallel factor model (PARAFAC) overlap λP; and (+) refers to the overlap with the closest separable state maximized by LU. The solid red line (—) is the result Equation (35) with N = d3; the solid lines (—) and (—) are the best linear fits for HOSVD and PARAFAC, respectively.
In both cases, the corresponding bound for the geometric measure of entanglement reads ⟨EG⟩ ∼ 1 − ⟨λk⟩, where k = H, P. Figure 9b shows the geometric measure of entanglement for a three-qudit system as function of the qudit size. Moreover, based on the scaling of ⟨λP⟩, we conjecture that the maximum overlap with respect to the closest separable state for a three-qudit system scales as ⟨λmax⟩ ∼ d−2 for large d.
7. Conclusions
We have analyzed the Rényi–Ingarden–Urbanik entropy of pure states of quantum multipartite systems minimized over all local unitary operations. For separable states, such a quantity is zero irrespective of the value of the Rényi parameter q > 0. In general, it is not easy to get analytical results for a given state and arbitrary value of the Rényi parameter q. In the special case of permutation-invariant states, the problem becomes easier, as minimization in the space of local unitary operators can be turned into an optimization of a one-variable function.
We computed the minimal RIU entropy of several representative three- and four-qubit states for various values of the Rényi parameter. Some particular states, which maximize the minimal RIU entropy for q = 1 and q = 2, were identified. Note that this quantity can be considered as a measure of pure state entanglement in multipartite systems, and for q → ∞, it becomes a function of the geometric measure of entanglement. In the case of three qubits, the latter quantity is maximal for the state |W i, while for four qubits, it achieves the maximum for the state Equation (32) of Higuchi and Sudbery [49]. The minimal RIU entropy can be extended for mixed states using Uhlman’s convex roof construction in analogy to the standard entropy of formation [53]. However, discussions on this matter will be reported elsewhere.
Furthermore, we analyzed the distribution of the minimal RIU entropy for an ensemble of random states for some selected values of the Rényi parameter, q = 1, 2, 100. Our numerical simulations demonstrate the usefulness of the PARAFAC algorithm, which allows one the find the principal component of a tensor representing a multipartite pure state and to estimate its geometric measure of entanglement.
We studied also the distribution of three-tangle for random pure states of a three-qubit system and derived a few even moments of this distribution. Numerical results show that this distribution may be approximated by a Beta distribution. In the case of four qubits, we analyzed the distribution of the absolute value of the hyperdeterminant of a random pure state.
Finally, the behavior of the maximum overlap of a random state of a system consisting of three subsystems of size d and the closest separable states was investigated in the asymptotic limit. Although the size of the largest component of a random state scales as d−3, numerical results obtained by the PARAFAC decomposition of a tensor allow us to conjecture that the maximal overlap scales in this case as d−2. This is consistent with an analytic result based on the Marchenko–Pastur asymptotic distribution of singular values of random matrices, which gives an upper bound d−1.
Appendix
A1. Moments of Three-Tangle τ
In the case of even moments of order 2k of three-tangle τ for a three qubit tensor, it is easy to note that it is a linear combination of moments of rank 8k for a random normalized vector. The moments of normalized vectors distributed uniformly can be calculated with the use of the Beta integral.
Let |ψ⟩ be a random unit vector of size d distributed uniformly on a complex sphere; then, for a vector p of non-negative integers, the following expectation value reads:
One can also note that all moments of random vector |ψ⟩, which are not in the form presented above, are equal to zero. This follows, for example, form Collins– Śniady formula [54] for integrals of monomials over unitary matrices distributed with the Haar measure.
Calculation of the second moment, ⟨τ2⟩ = 8/55, is a simple task, but for higher moments, the number of terms grows so rapidly, that we have used a package for symbolic computations IntU, which yielded the moments presented in Table 2. This package allows for exact calculation of polynomial integrals over the unitary group with respect to the Haar measure [55].
A2. Bound for Geometric Measure of Entanglement for Tripartite States
The law of Marchenko–Pastur describes the asymptotic behavior of singular values of non-Hermitian, rectangular random matrices. Let X be a random matrix X of size N × K with entries given by complex random i.i.d. normal variables with zero mean and variance one. We define Y = XX†/trXX† and for c > 1 consider a random counting measure on a real line, which counts the number of rescaled eigenvalues of Y, which belongs to a given set, i.e.,
For the measure defined above, if N, K → ∞ with the additional assumption K/N → c, there exists a limiting distribution µM → µ given by:
with:
The above theorem gives us the behavior of the largest eigenvalue of a matrix Y, which is
.
In the case when N, K → ∞, but K/N → ∞, the theorem does not give us the limiting distribution, but form the theorem, we will extract the rate of convergence of the largest eigenvalue.
Consider, the case when K = N2, then K/N = N, the direct usage of the Marchenko–Pastur law would give us a behavior of the largest eigenvalue of Y, i.e.,
.
Now, we will try to use the above asymptotics to bound the geometric measure of entanglement for tripartite random states.
Consider a random tensor |ψ⟩ ∈ ℂd ⊗ ℂd ⊗ ℂd = H1 ⊗ H2 ⊗ H3. The geometric measure of entanglement is related to the overlap with the nearest product state, i.e.,
In the above equation, a set sep consist of vectors in the form ϕ1 ⊗ ϕ2 ⊗ ϕ3 for ϕi ∈ i. For distinct i, j, k ∈ {1, 2, 3}, we denote sepi|jk vectors of the form ϕ1 ⊗ ϕ2 for ϕi ∈ i and ϕ2 ∈ j ⊗ k. We have that sep ⊂ sepi|jk, which gives us:
The last maximum above is a square of the largest Schmidt coefficient for vector |ψ⟩.
If we consider the behavior of large random tripartite states, the above inequality, combined with the relations obtained form the Marchenko–Pastur law, we obtain:
Acknowledgments
We are thankful to D. Alsina and J.I. Latorre for fruitful discussions and for sharing their results prior to publication. M.E. is thankful to the Jagiellonian University for kind hospitality and support during his stay in Cracow. We acknowledge support of the Mexican National Council for Science and Technology (Conacyt) (M.E.) and by Grant Numbers DEC-2011/02/A/ST1/00119 (K.Ż.) and DEC-2012/04/S/ST6/00400 (Z.P.), financed by the Polish National Science Center.
Author Contributions
M.E. performed all of the numerical work, while Z.P. and K.Ż. were involved in the analytic calculations. All authors contributed to writing the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar]
- Bengtsson, I.; Życzkowski, K. Geometry of Quantum States. An Introduction to Quantum Entanglement, 1st ed; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Acin, A.; Andrianov, A.; Costa, L.; Jané, E.; Latorre, J.I.; Tarrach, R. Generalized Schmidt decomposition and classffication of three-quantum-bit states. Phys. Rev. Lett. 2000, 85, 1560–1563. [Google Scholar]
- Sudbery, A. On local invariants of pure three-qubit states. J. Phys. A 2001, 34, 643–652. [Google Scholar]
- Williamson, M.S.; Ericsson, M.; Johansson, M.; Sjoqvist, E.; Sudbery, A.; Vedral, V.; Wootters, W.K. Geometric local invariants and pure three-qubit states. Phys. Rev. A 2011, 83, 062308. [Google Scholar]
- Luque, J.G.; Thibon, J.Y. Polynomial invariants of four qubits. Phys. Rev. A 2003, 67, 042303. [Google Scholar]
- Lévay, P. On the geometry of four-qubit invariants. J. Phys. A 2006, 39, 9533–9545. [Google Scholar]
- Gour, G.; Wallach, N.R. All maximally entangled four-qubit states. J. Math. Phys. 2010, 51, 112201. [Google Scholar]
- Viehmann, O.; Eltschka, C.; Siewert, J. Polynomial invariants for discrimination and classification of four-qubit entanglement. Phys. Rev. A 2011, 83, 052330. [Google Scholar]
- Sharma, S.S.; Sharma, N.K. Negativity fonts, multiqubit invariants and four qubit maximally entangled states. Quantum Inf. Proc. 2012, 11, 1695–1714. [Google Scholar]
- Osterloh, A.; Hyllus, P. Estimating multipartite entanglement measures. Phys. Rev. A 2010, 81, 022307. [Google Scholar]
- Hilling, J.J.; Sudbery, A. The geometric measure of multipartite entanglement and the singular values of a hypermatrix. J. Math. Phys. 2010, 51, 072102. [Google Scholar]
- Gühne, O.; Seevinck, M. Separability criteria for genuine multiparticle entanglement. New J. Phys. 2010, 12, 053002. [Google Scholar]
- Rudnicki, Ł.; Horodecki, P.; Życzkowski, K. Collective uncertainty entanglement test. Phys. Rev. Lett. 2011, 107, 150502. [Google Scholar]
- Bennett, C.H.; di Vincenzo, D.P.; Smolin, J.A.; Wootters, W.K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 1996, 54, 3824. [Google Scholar]
- Brody, D.C.; Hughston, L.P. Geometric quantum mechanics. J. Geom. Phys. 2001, 38, 19–53. [Google Scholar]
- Życzkowski, K.; Bentgsson, I. Relativity of Pure States Entanglement. Ann. Phys. 2002, 295, 115–135. [Google Scholar]
- Wei, T.C.; Goldbart, P.M. Geometric measure of entanglement and applications to bipartite and multipartite quantum states. Phys. Rev. A 2003, 68, 042307. [Google Scholar]
- Parker, M.G.; Rijmen, V. The Quantum Entanglement of Binary and Bipolar Sequences, Sequences and Their Applications, SETA’01. In Discrete Mathematics and Theoretical Computer Science Series; Helleseth, T., Kumar, P.V., Yang, K., Eds.; Springer: London, UK, 2001. [Google Scholar]
- Bravyi, S. Entanglement entropy of multipartite pure states. Phys. Rev. A 2003, 67, 012313. [Google Scholar]
- Ingarden, R.S.; Urbanik, K. Quantum informational thermodynamics. Acta Phys. Pol. 1962, 21, 281–304. [Google Scholar]
- Carteret, H.A.; Higuchi, A.; Sudbery, A. Multipartite generalisation of the Schmidt decomposition. J. Math. Phys. 2000, 41, 7932–7939. [Google Scholar]
- Spekkens, R.W.; Sipe, J.E. Non-orthogonal preferred projectors for modal interpretations of quantum mechanics. Found. Phys. 2001, 31, 1403–1430. [Google Scholar]
- Eisert, J.; Briegel, H.J. Schmidt measure as a tool for quantifying multiparticle entanglement. Phys. Rev. A 2001, 64, 022306. [Google Scholar]
- Hein, M.; Eisert, J.; Briegel, H.J. Multiparty entanglement in graph states. Phys. Rev. A 2004, 69, 062311. [Google Scholar]
- Chitambar, E.; Duan, R.; Shi, Y. Tripartite Entanglement Transformations and Tensor Rank. Phys. Rev. Lett. 2008, 101, 140502. [Google Scholar]
- De Lathauwer, L.; de Moor, B.; Vandewalle, J. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 2000, 21, 1253–1278. [Google Scholar]
- Bro, R. PARAFAC. Tutorial and applications. Chemometr. Intell. Lab. Syst. 1997, 38, 149–171. [Google Scholar]
- Jiang, B.; Ma, S.; Zhang, S. Tensor principal component analysis via convex optimization. Math. Program. Ser. A 2015, 150, 423–457. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor Decompositions and Applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar]
- Liu, B.; Li, J.L.; Li, X.; Qiao, C.F. Local unitary classification of arbitrary dimensional multipartite pure states. Phys. Rev. Lett. 2012, 108, 50501. [Google Scholar]
- Enríquez, M.; Rosas-Ortiz, O. The Kronecker product in terms of Hubbard operators and the Clebsch-Gordan decomposition of SU(2) × SU(2). Ann. Phys. 2013, 339, 218–265. [Google Scholar]
- Nion, D.; de Lathauwer, L. An Enhanced Line Search Scheme for Complex-Valued Tensor Decompositions. Application in DS-CDMA. Signal Process. 2008, 88, 749–755. [Google Scholar]
- Hübener, R.; Kleinmann, M.; Wei, T.C.; Gühne, O. Geometric measure of entanglement for symmetric states. Phys. Rev. A 2009, 80, 032324. [Google Scholar]
- Hayashi, M.; Markham, D.; Murao, M.; Owari, M.; Virmani, S. The geometric measure of entanglement for a symmetric pure state with non-negative amplitudes. J. Math. Phys. 2009, 50, 122104. [Google Scholar]
- Wei, T.C.; Severini, S. Matrix permanent and quantum entanglement of permutation invariant states. J. Math. Phys. 2010, 51, 092203. [Google Scholar]
- Slomczyński, W.; Życzkowski, K. Mean dynamical entropy of quantum maps on the sphere diverges in the semiclassical limit. Phys. Rev. Lett. 1998, 80, 1880–1883. [Google Scholar]
- Mirbach, B.; Korsch, H.J. A generalized entropy measuring quantum localization. Ann. Phys. 1998, 265, 80–97. [Google Scholar]
- Chen, L.; Xu, A.; Zhu, H. Computation of the geometric measure of entanglement for pure multiqubit states. Phys. Rev. A 2010, 82, 032301. [Google Scholar]
- Aulbach, M.; Damian, M.; Mio, M. The maximally entangled symmetric state in terms of the geometric measure. New J. Phys. 2010, 12, 073025. [Google Scholar]
- Coffmand, V.; Kundu, J.; Wootters, W.K. Distributed entanglement. Phys. Rev. A 2000, A61, 052306. [Google Scholar]
- Hill, S.; Wootters, W.K. Entanglement of a Pair of Quantum Bits. Phys. Rev. Lett. 1997, 78, 5022–5025. [Google Scholar]
- Cayley, A. On the Theory of Linear Transformations. Camb. Math. J 1845, 4, 193–209. [Google Scholar]
- Gelfand, I.M.; Kapranov, M.M.; Zelevinsky, A.V. Discriminants, Resultants, and Multidimensional Determinants, 1st ed; Birkhauser: Boston, MA, USA, 1994. [Google Scholar]
- Osterloh, A.; Siewert, J. Constructing N-qubit entanglement monotones from antilinear operators. Phys. Rev. A 2005, 72, 012337. [Google Scholar]
- Miyake, A. Classification of multipartite entangled states by multidimensional determinants. Phys. Rev. A 2003, 67, 012108. [Google Scholar]
- Kendon, V.; Nemoto, V.K.; Munro, W. Typical entanglement in multiple-qubit systems. J. Mod. Opt. 2002, 49, 1709–1716. [Google Scholar]
- Alsina, D.; Latorre, J.I. Unpublished Preprint; Barcelona, Spain, 2014.
- Higuchi, A.; Sudbery, A. How entangled can two couples get? Phys. Lett. A 2000, 273, 213–217. [Google Scholar]
- Ambainis, A.; Harrow, A.W.; Hastings, M.B. Random tensor theory: Extending random matrix theory to mixtures of random product states. Commun. Math. Phys. 2012, 310, 25–74. [Google Scholar]
- Gurau, R. Universality for random tensors. Ann. Inst. H. Poincaré Probab. Statist. 2014, 50, 1474–1525. [Google Scholar]
- Adamczak, R.; Latała, R.; Puchała, Z.; Życzkowski, K. Asymptotic entropic uncertainty relations 2014, arXiv, 1412.7065.
- Uhlmann, A. Entropy and optimal decompositions of states relative to a maximal commutative subalgebra. Open Syst. Inf. Dyn. 1998, 5, 209–228. [Google Scholar]
- Collins, B.; Śniady, P. Integration with respect to the haar measure on unitary, orthogonal and symplectic group. Commun. Math. Phys. 2006, 264, 773–795. [Google Scholar]
- Puchała, Z.; Miszczak, J.A. Symbolic integration with respect to the Haar measure on the unitary group in Mathematica 2011, arXiv, 1109.4244.
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).