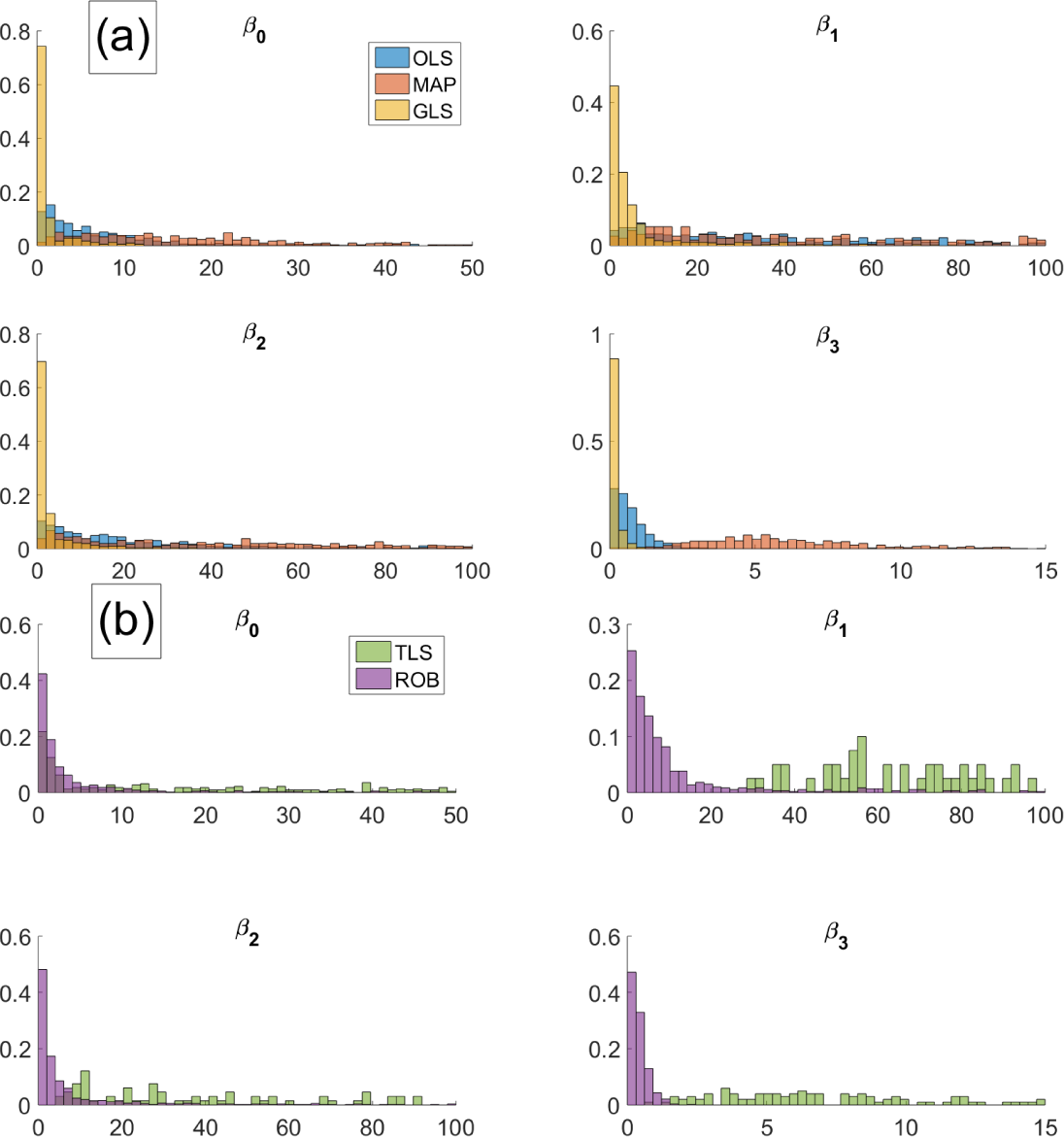
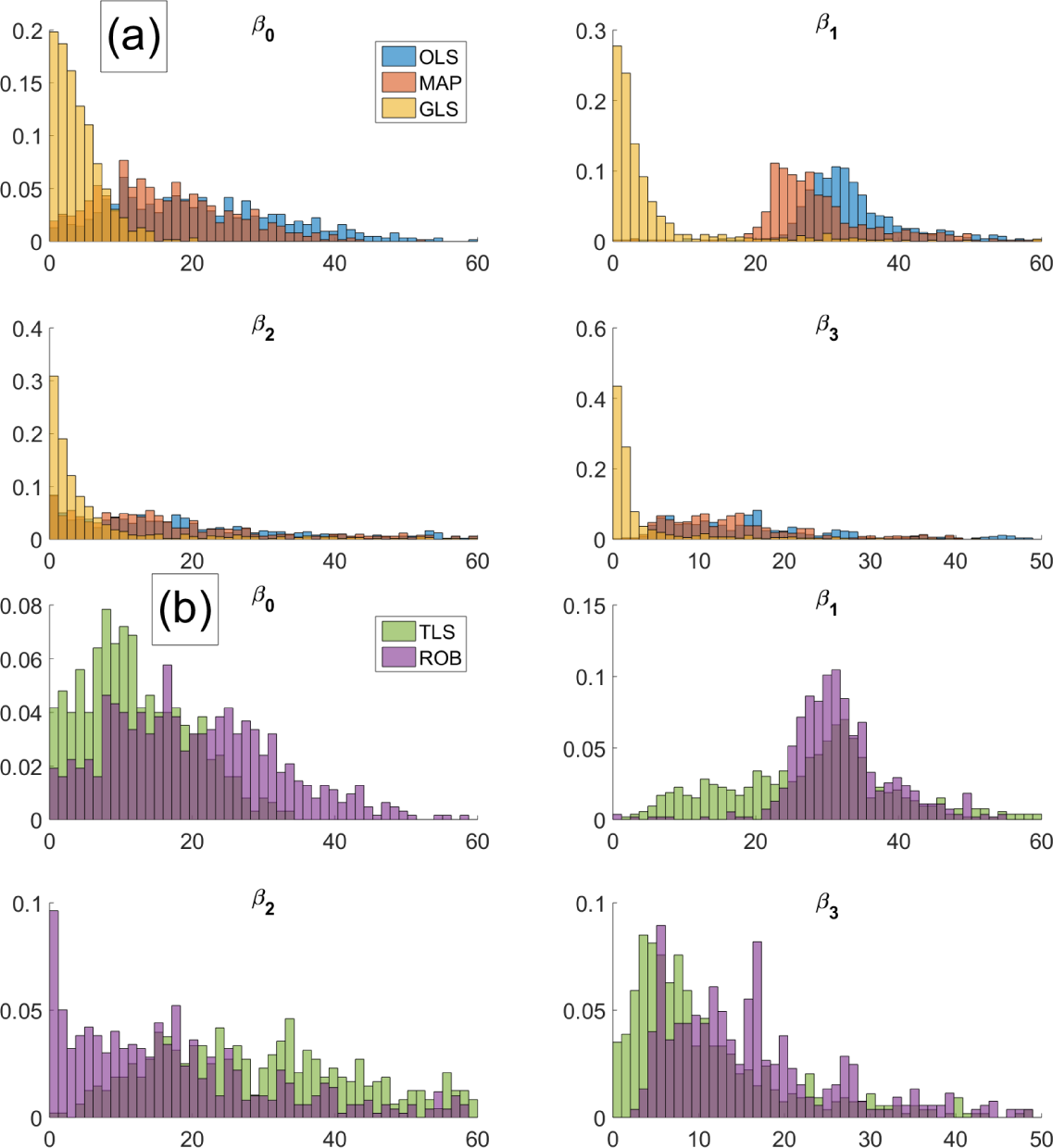
We first concentrate on estimating the slope of a regression line with a single predictor variable. To this end, a dataset was generated consisting of ten points labeled by coordinates ξ
n and η
n (
n = 1, …, 10), with the ξ
n chosen unevenly between zero and 50 and η
n = βξ
n, taking β = 3. Then, Gaussian noise was added to all coordinates according to
Equation (6), with σ
y = 2.0 and σ
x = 0.5, resulting in values
xn for the predictor variable and
yn for the response variable. Finally, one outlier was created by multiplying the value of
yk by a factor distributed uniformly between 1.5 and 2.5, with
k chosen uniformly among the indices 8, 9 and 10.
We next estimated β by means of GLS and compared the estimates with those obtained by OLS, maximum
a posteriori (MAP) using the model in
Equation (7) for the likelihood and an uninformative prior [
30], total least squares (TLS), which is a typical errors-in-variables technique [
31], and a robust method (ROB) based on iteratively reweighted least squares (bisquare weighting) [
32], included in the MATLAB Statistics toolbox [
33]. It should be noted that MAP takes into account the error bars on the predictor variables. In all cases, we assumed knowledge of the values of σ
x and σ
y. In order to get an idea of the variability of the estimates, Monte Carlo sampling of the data-generating distributions was performed, and the estimation was carried out 100 times.
The results are given in
Table 1, mentioning the sample average and standard deviation of the estimates
over the 100 runs for each of the methods. GLS is seen to perform very well and similar to the robust method ROB, but the other techniques yield considerably worse results. The average estimate of σ
obs was 5.43 with a standard deviation of 0.24. On the other hand, the modeled value of the standard deviation in the conditional distribution for
y was
. Hence, GLS succeeds in ignoring the outlier by increasing the estimated variability of the data. Put differently, the effect of the outlier is, in a sense, to increase the overall variability of the data, which GLS takes into account by increasing the observed standard deviation of the data (σ
obs) with respect to the standard deviation predicted by the model (σ
mod).
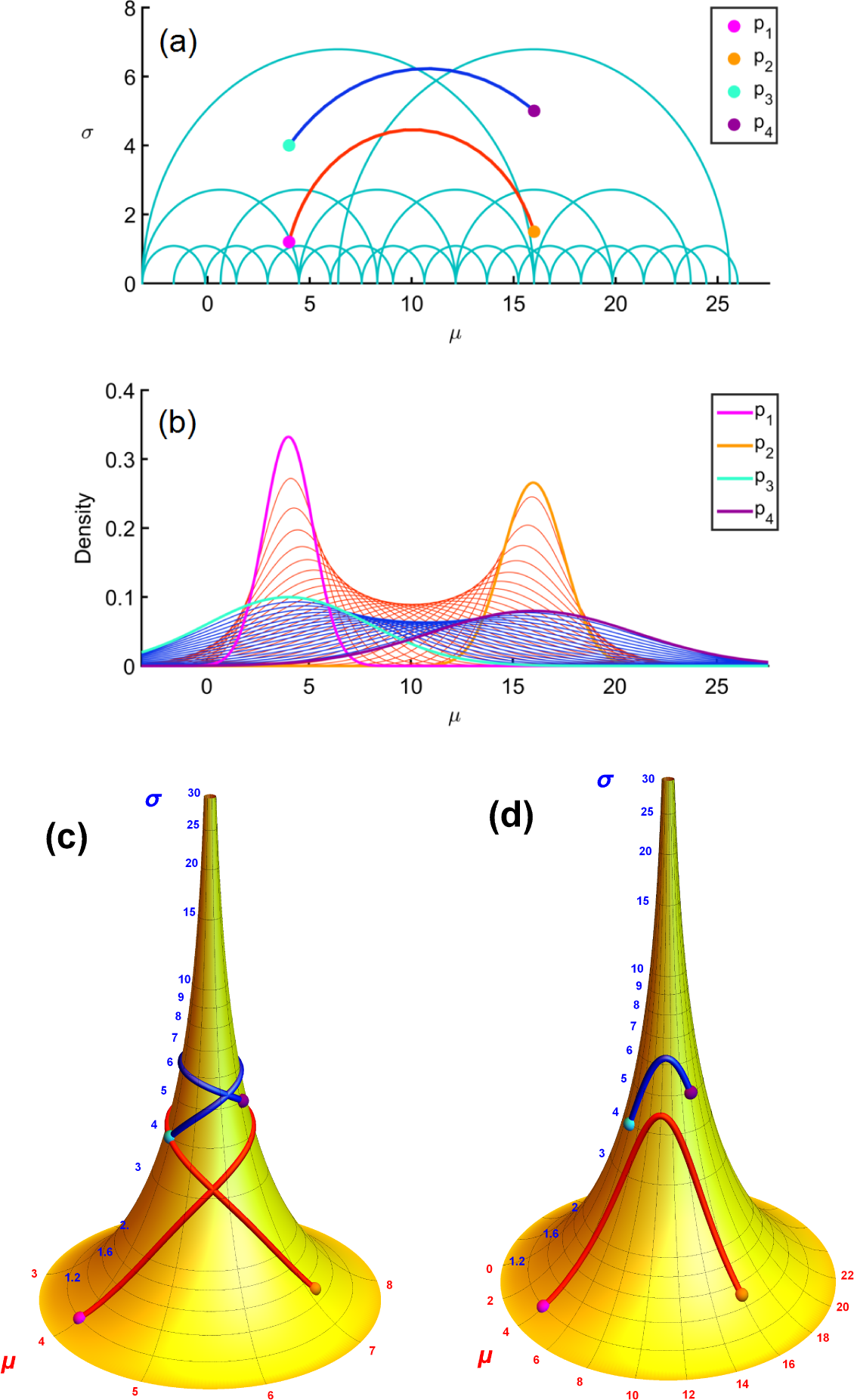
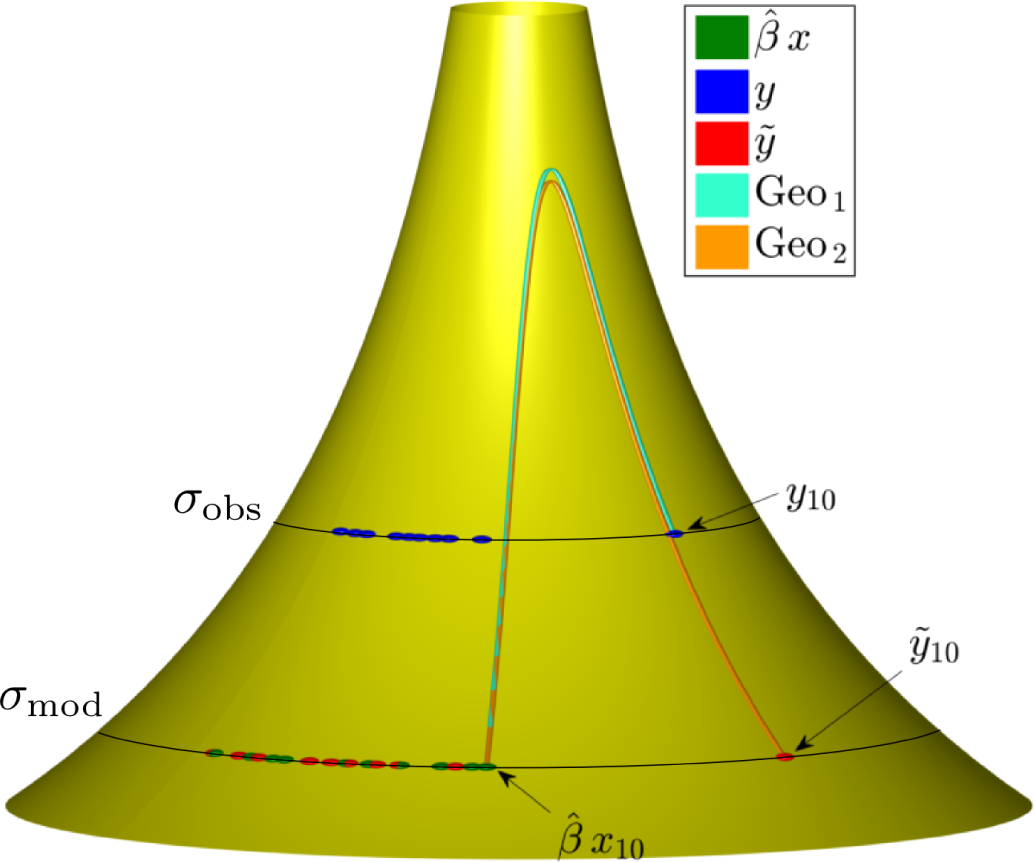
As mentioned before, this result can also be understood in terms of the pseudosphere as a geometrical model for the normal distribution. To see this, we refer to
Figure 2, where several sets of points (distributions) are drawn on a portion of the surface of the pseudosphere for one particular dataset generated as described above. First, the modeled distributions are plotted with their means
(see
Equation (7)) and standard deviations σ
mod = 2.5, using the average estimate
obtained by GLS. These are the green points on the surface, and they lie on a parallel, since they all correspond to Gaussians with the same standard deviation σ
mod. In this particular dataset, the index of the outlier was
k = 10, so the point
is indicated individually. Obviously, according to the model, no outlier is expected, so the modeled distribution corresponding to
k = 10, which is the green point just mentioned, lies close to the other predicted points (distributions). Next, we plot the observed distributions with their means
yn and standard deviations σ
obs (for this dataset estimated at
). These are the blue points, lying at a constant standard deviation σ
obs, which is higher than σ
mod (5.43 > 2.5). The outlier
y10 can clearly be observed, and being an outlier, it lies relatively far away from the rest of the blue points (observed distributions). Now suppose that, like MAP, GLS would not be able to increase σ
obs relative to σ
mod in order to accommodate the outlier. Then, the observed distributions would have the same observed means (the measured values
yn), but they would have the standard deviation predicted by the model. Hence, they would lie on the parallel corresponding to σ
mod, just like the green points. We have plotted these fictitious distributions as the red points at the level of σ
mod, and they are labeled
ỹ. Again, the outlier (labeled
ỹ10) can be seen, but it seems to lie further away from the other red points (the points
ỹn) compared to the actually observed situation,
i.e., the distance from
y10 to the other
yn (blue points). At least this is the case when using (visually) the Euclidean distance in the embedding Euclidean space. We can verify that this is indeed so by using the proper geodesic distance on the surface: overall, the blue points lie closer together (including the outlier) than the red points. Now, in fact, GLS aims at minimizing the distance between each green point (modeled distribution) and its corresponding blue point (observed distribution), so as far as the outlier is concerned, we should really be looking at the geodesic between the point
and the point (
y10, σ
obs). The geodesic (labeled “Geo
1”) between these points is also drawn on the surface, and again, we compare this to the fictitious situation, represented by the geodesic (labeled “Geo
2”) between
and (
ỹ10, σ
mod). Indeed, again, we see that the geodesic Geo
1 is shorter than Geo
2. Therefore, by increasing σ
obs relative to σ
mod, the outlier is not so much an outlier anymore, as measured on the pseudosphere!When calculating the GD, one finds 2.4 for Geo
1 and 2.8 for Geo
2. Therefore, GLS obtains a lower value of the objective function (sum of squared geodesic distances) if it increases σ
obs with respect to σ
mod. Of course, there is a limit to this: GLS cannot continue raising σ
obs indefinitely, trying to mitigate the distorting effect of the outlier, for then, the other points would get a too high observed standard deviation, which is not supported by the data. The image that we see in
Figure 2 is the best compromise that GLS could find. In fact, we note that, in the case we suspect that
y10 could be an outlier, it may very well be worthwhile to introduce two parameters to describe the observed standard deviation: one for the nine points that seem to follow the model and one to take care of the outlier. This would be a very straightforward extension of the method, and we explore this to some extent when using data from the ITPA database below. There, we assign a separate parameter to describe the observed standard deviation of all data coming from a specific tokamak, hence defining an individual parameter for each machine.