Consensus Analysis of Heterogeneous Multi-Agent Systems with Time-Varying Delay

Abstract

This paper studies consensus and H_∞ consensus problems for heterogeneous multi-agent systems composed of first-order and second-order integrator agents. We first rewrite the multi-agent systems into the corresponding reduced-order systems based on the graph theory and the reduced-order transformation. Then, the linear matrix inequality approach is used to consider the consensus of heterogeneous multi-agent systems with time-varying delays in directed networks. As a result, sufficient conditions for consensus and H_∞ consensus of heterogeneous multi-agent systems in terms of linear matrix inequalities are established in the cases of fixed and switching topologies. Finally, numerical simulations are given to illustrate the effectiveness of the theoretical results.

1. Introduction

In recent years, the consensus control of multi-agent systems has attracted much attention, due to its broad applications in communication, system control theory, applied mathematics, design of sensor networks, computer science, and so on. Up to now, many researchers have made great achievements for the consensus problem of multi-agent systems by using the method of graph theory, matrix theory, the frequency-domain analysis method, the Lyapunov direct method, etc. [1–5]. Consensus seeking has been analyzed mainly for first-order multi-agent systems modeled by a single integrator [6–11] and second-order multi-agent systems modeled by double integrators [12–14], respectively.

Most multi-agent systems considered in the literature are homogeneous, that is all of the agents have the same dynamics behavior. However, the dynamics of the agents is quite different because of various restrictions or the common goals with mixed agents in practical systems. Therefore, it is natural to consider heterogeneous multi-agent system. Compared with the first-order and the second-order integrator multi-agent systems, the study of heterogeneous multi-agent systems composed of both first-order and second-order integrator agents seems to be more complicated. So far, there are very few results on the consensus of heterogeneous multi-agent systems, except Zheng and Wang [15–17], where consensus problems of a heterogeneous multi-agent system were studied by applying the graph theory and the Lyapunov direct method.

Furthermore, in many practical applications involving multi-agent systems, the communication delay [18–23], leader-following networks [24–26], discrete-time [27–29], as well as H_∞ consensus problems [30–32] should be considered in the consensus of multi-agent systems. Therefore, in this work, we investigate the consensus and H_∞ consensus problems for heterogeneous multi-agent systems in fixed and switching topologies with a time delay.

Because of the complexity of the heterogeneous multi-agent system with time-delays, many existing methods for the consensus of the first-order and the second-order multi-agent systems become invalid. Therefore, the purpose of this paper is to establish consensus and H_∞ consensus criteria for heterogeneous multi-agent systems by applying the linear matrix inequality technique. We first rewrite the heterogeneous multi-agent system into a reduced-order system by using a reduced-order transformation. Then, by choosing an appropriate Lyapunov functional, sufficient conditions for consensus are derived in the cases of fixed and switching topologies by using the linear matrix inequality method.

The paper is organized as follows. In Section 2, some preliminaries on graph theory, model formulation and the reduced-order transformation of the heterogeneous multi-agent system are given. In Section 3, sufficient conditions in terms of linear matrix inequalities are established for consensus and H_∞ consensus of the heterogeneous multi-agent system with time-varying delay. In Section 4, some simulation results are presented. The conclusion is given in Section 5.

The following notations are used throughout this paper. ${\mathrm{I}}_n=\{1,2,\dots ,n\}$ is an index set. A^T means the transpose of the matrix A. I_n is an n × n-dimensional identity matrix. a_m = (a, a,⋯, a)^T is an m-dimensional column vector with a ∈ ℝ. We say X > Y if X − Y is positive-definite, where X and Y are symmetric matrices of same dimensions. We use an asterisk * to represent a term that is induced by symmetry, and diag{⋯} stands for a block-diagonal matrix. L₂[0, ∞) denotes the space of square-integrable vector functions over [0, ∞).

2. Preliminaries

Throughout this paper, we denote a weighted digraph by $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$, where $\mathcal{V}=\{1,2,\cdots ,n\}$ is the set of nodes with n ≥ 2; node i represents the i-th agent; $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ is the set of edges; an edge of $\mathcal{G}$ is denoted by an order pair (i, j), and $(i,j)\in \mathcal{E}$ if and only if a_ji > 0; $\mathcal{A}=[a_{ij}]$ is an n × n-dimensional weighted adjacency matrix with a_ii = 0. If (i, j) is an edge of $\mathcal{G}$, node i is called the parent of node j. A directed tree is a directed graph, where every node, except one special node without any parent, which is called the root, has exactly one parent, and the root can be connected to any other nodes through paths. The Laplacian matrix L = [l_ij] of digraph $\mathcal{G}$ is defined by $l_{ii}={\displaystyle {\sum }_{j=1}^n{a}_{ij}}$ and l_ij = −a_ij for i ≠ j, i, $j\in {\mathcal{I}}_n$.

Suppose that the heterogeneous multi-agent system consists of both first-order and second-order integrator agents, and the number of first-order integrator agents is m (m < n). Then, the heterogeneous multi-agent system is given as follows:

$$\{\begin{array}{ccc}{\dot{x}}_i=u_i,& i\in {\mathcal{I}}_m,& \\ {\dot{x}}_i=v_i,& {\dot{v}}_i=u_i,& i\in {\mathcal{I}}_n/{\mathcal{I}}_m=\{m+1,m+2,\cdots ,n\},\end{array}$$

(1)

where x_i ∈ ℝ for $i\in {\mathcal{I}}_n$ and v_i ∈ ℝ for $i\in {\mathcal{I}}_n/{\mathcal{I}}_m$ are the state of agent w_i, and u_i ∈ ℝ for $i\in {\mathcal{I}}_n$ is the control input of agent w_i, which is also called a protocol throughout this paper.

Consider the following linear protocol:

$$u_i=\{\begin{array}{l}{\displaystyle \sum _{j=1}^n{a}_{ij}(x_j(t-\tau (t))-x_i}(t-\tau (t)))i\in {\mathcal{I}}_m,\hfill \\ {\displaystyle \sum _{j=1}^n{a}_{ij}(x_j(t-\tau (t))-x_i(t-\tau (t)))-k_i{v}_i(t),i\in {\mathcal{I}}_n/{\mathcal{I}}_m,}\hfill \end{array}$$

(2)

where k_i > 0, $i\in {\mathcal{I}}_n/{\mathcal{I}}_m$, are the feedback gains. The time-delay τ is the piecewise-continuous function satisfying:

• (H1) 0 ≤ τ(t) ≤ h and $\dot{\tau }(t)\le d$ for t ≥ 0, where h > 0 and 0 ≤ d < 1 are constants.
• (H2) 0 ≤ τ(t) ≤ h for t ≥ 0, where h > 0 is a constant.

Denote $x(t){(x_{(1)}^T(t)x_{(2)}^T(t))}^T$ with x₍₁₎(t) = (x₁(t),⋯, x_m(t))^T, x₍₂₎(t) = (x_m+1(t),⋯, x_n(t))^T and v(t) = (v_m+1(t),⋯, v_n(t))^T. Substituting Protocol (2) into System (1), we get the following matrix form of System (1):

$$\{\begin{array}{l}{\dot{x}}_{(1)}(t)=-L_{1}x(t-\tau (t)),\hfill \\ {\dot{x}}_{(2)}(t)=v(t),\hfill \\ \dot{v}(t)=-L_{2}x(t-\tau (t))-Kv(t),\hfill \end{array}$$

(3)

where K = diag{k_m+1, k_m+2,⋯, k_n}, $L={(L_1^T,L_2^T)}^T$ and matrix L₁ and L₂ are m × n-dimensional and (n − m) × n-dimensional, respectively.

We introduce the reduced-order transformation as follows:

$$y_j(t)=x_{j+1}(t)-x_1(t),j\in {\mathcal{I}}_{n-1}.$$

(4)

By the straightforward computation, we get:

$$y_{(1)}(t)=E{x}_{(1)}(t),x(t)=x_1(t)1_n+Fy(t),$$

where E = (−1_m−1 I_m−1) and F = (0_n−1 I_n−1)^T are (m − 1) × m-dimensional and n × (n − 1)-dimensional matrices, respectively, and $y(t)={(y_{(1)}^T(t)y_{(2)}^T(t))}^T$ with y₍₁₎(t) = (y₁(t),⋯, y_m−1(t))^T and y₍₂₎(t) = (y_m(t),⋯, y_n−1(t))^T.

Note that with the fact L1_n = 0, we can obtain from (3) that:

$${\dot{y}}_{(1)}(t)=E{\dot{x}}_{(1)}(t)=-E{L}_{1}Fy(t-\tau (t)).$$

If $i\in {\mathcal{I}}_{n-1}/{\mathcal{I}}_{m-1}$, we have:

$${\dot{y}}_i(t)=v_{i+1}(t)-{\displaystyle \sum _{j=2}^n{a}_{1j}{y}_{j-1}(t-\tau (t))}.$$

Therefore,

$${\dot{y}}_{(2)}(t)=v(t)-{\displaystyle \sum _{j=2}^n{a}_{1j}{y}_{j-1}(t-\tau (t))},$$

and:

$$\dot{v}(t)=-L_{2}Fy(t-\tau (t))--Kv(t).$$

Let z(t) = (y^T(t) v^T (t))^T; we have the following reduce-order system in matrix form:

$$\dot{z}(t)=Bz(t)+Cz(t-\tau (t)),$$

(5)

where:

$$B=\left(\begin{array}{cc}0& 0\\ 0& I_{n-m}\\ 0& -K\end{array}\right),C=\left(\begin{array}{cc}-E{L}_{1}F& 0\\ A& 0\\ -L_{2}F& 0\end{array}\right),$$

A = (a, a,⋯, a)^T is a (n − m) × (n − 1)-dimensional matrix with (n − 1)-dimensional column vector a = (−a₁₂, −a₁₃,⋯, −a_1n)^T.

When the heterogeneous multi-agent system involves disturbance input, we consider the following protocol of the form:

$$u_i=\{\begin{array}{l}{\displaystyle \sum _{j=1}^n{a}_{ij}(x_j(t-\tau (t))-x_i}(t-\tau (t))+w_{ij}(t)),i\in {\mathcal{I}}_m,\\ {\displaystyle \sum _{j=1}^n{a}_{ij}(x_j(t-\tau (t))-x_i}(t-\tau (t))-k_i{v}_i(t)+w_{ij}(t)),i\in {\mathcal{I}}_n/{\mathcal{I}}_m,\end{array}$$

(6)

where w_ij(t) ∈ L₂[0, ∞) are disturbance inputs.

Denote the i-th row of the matrix $\mathcal{A}$ by α_i, Σ₁ = diag{α₁, α₂,⋯, α_m}, Σ₂ = diag{α_m+1,⋯, α_n}, w_i(t) = (w_i1(t),⋯, w_in(t))^T, $w(t)={(w_{(1)}^T(t),w_{(2)}^T(t))}^T$, with $w_{(1)}(t)={(w_1^T(t),\cdots ,w_m^T(t))}^T$ and $w_{(2)}(t)={(w_{m+1}^T(t),\cdots ,w_n^T(t))}^T$.

The matrix form of the heterogeneous multi-agent System (1) with Protocol (6) takes the form:

$$\{\begin{array}{l}{\dot{x}}_{(1)}(t)=-L_{1}x(t-\tau (t))+{\mathrm{\Sigma }}_1{w}_{(1)}(t),\hfill \\ {\dot{x}}_{(2)}(t)=v(t),\hfill \\ \dot{v}(t)=-L_{2}x(t-\tau (t))+{\mathrm{\Sigma }}_2{w}_{(2)}(t)-Kv(t),\hfill \end{array}$$

(7)

By using the reduced-order transformation (4), we can get the following reduce-order system:

$$\dot{z}(t)=Bz(t)+Cz(t-\tau (t))+\tilde{\mathrm{\Sigma }}w(t),$$

(8)

where z(t) is defined above, $\tilde{\mathrm{\Sigma }}=\left(\begin{array}{cc}E{\mathrm{\Sigma }}_1& 0\\ \mathrm{\Lambda }& 0\\ 0& {\mathrm{\Sigma }}_2\end{array}\right)$, Λ = (−a_n−m, 0) with a_n−m=(α₁, α₁,⋯, α₁)^T the (n − m) × m-dimensional matrix.

Definition 1. Say System (3) achieves consensus asymptotically, if for any x(0) = x₀ and v(0) = v₀; we have:

$$\begin{array}{ll}\underset{t\to \infty }{\lim }|x_i(t)-x_j(t)|=0,\hfill & i,j\in {\mathcal{I}}_n,i\ne j,\hfill \\ \underset{t\to \infty }{\lim }{v}_i(t)=0,\hfill & i\in {\mathcal{I}}_n/{\mathcal{I}}_m.\hfill \end{array}$$

Definition 2. Say System (7) achieves H_∞ consensus asymptotically if System (3) achieves consensus asymptotically, and there exists a constant γ > 0, such that:

$${\displaystyle {\int }_0^{\infty }{z}^T(t)z(t)dt\le \gamma {\displaystyle {\int }_0^{\infty }{w}^T(t)w(t)dt}}$$

(9)

holds for all nonzero w ∈ L₂[0, ∞) under zero initial condition, where z(t) = (y^T(t), v^T (t))^T.

3. Main Results

The following two lemmas are required.

Lemma 1. [33] (Schur complement). Let M, P, Q be given matrices, such that Q > 0. Then:

$$\left(\begin{array}{cc}P& M\\ M^T& -Q\end{array}\right)<0\iff P+M{Q}^{-1}{M}^T<0.$$

Lemma 2. [20] For any real differentiable vector function x(t) ∈ Rⁿ and any n × n-dimensional constant matrix W = W^T > 0, the following inequality holds:

$${[x(t)-x(t-\tau (t))]}^{T}W[x(t)-x(t-\tau (t))]\le h{\displaystyle {\int }_{t-\tau (t)}^t{\dot{x}}^T(s)W\dot{x}(s)ds,t\ge 0.}$$

where 0 ≤ τ(t) ≤ h.

Theorem 1. Assume that (H1) holds for given h > 0 and 0 ≤ d < 1. The heterogeneous multi-agent System (3) achieves consensus asymptotically if there exist positive definite matrices P, Q and R of appropriate dimensions, such that:

$$\left(\begin{array}{ccc}{B}^{T}P+PB-Q+R& PC+Q& h{B}^{T}Q\\ *& -Q-(1-d)R& h{C}^{T}Q\\ *& *& -Q\end{array}\right)<0.$$

(10)

Proof. Based on the reduced-order transformation, it is sufficient to show that System (5) is asymptotically stable. By Lemma 1, we see that (10) is equivalent to:

$$\mathrm{\Psi }=\left(\begin{array}{cc}{B}^{T}P+PB-Q+R& PC+Q\\ *& -q-(1-d)R\end{array}\right)+h^2{(B,C)}^{T}Q(B,C)<0.$$

(11)

Take a Lyapunov functional as follows:

$$V(t)=z^T(t)Pz(t)+h{\displaystyle {\int }_{t-h}^t(s-t+h){\dot{z}}^T}(s)Q\dot{z}(s)ds+{\displaystyle {\int }_{t-\tau (t)}^t{z}^T(s)Rz(s)ds.}$$

(12)

Denote η^T (t) = (z^T (t), z^T (t − τ(t))). By (5) and Lemma 2, we have:

$$\begin{array}{l}\dot{V}(t)\le z^T(t)(B^{T}P+PB)z(t)+2z^T(t)PCz(t-\tau (t))\\ +h^2{\eta }^T(t){(B,C)}^{T}Q(B,C)\eta (t)\\ -{[z(t)-z(t-\tau (t))]}^{T}Q[z(t)-z(t-\tau (t))]\\ +z^T(t)Rz(t)-(1-d)z^T(t-\tau (t))Rz(t-\tau (t))\\ ={\eta }^T(t)\mathrm{\Psi }\eta (t).\end{array}$$

By (11), we have that there exists a constant α > 0, such that $\dot{V}(t)\le -\alpha ||z(t)||$. Therefore, the reduced-order System (5) is asymptotically stable, which implies that the heterogeneous multi-agent System (3) achieves consensus asymptotically. □

When nothing is known about the derivative, we use the following Lyapunov functional:

$$V_1(t)=z^T(t)Pz(t)+h{\displaystyle {\int }_{t-h}^t(s-t+h){\dot{z}}^T(s)Q\dot{z}}(s)ds.$$

(13)

Similar to the proof of Theorem 1, we can easily obtain the following corollary.

Corollary 1. Assume that (H2) holds for given h > 0. The heterogeneous multi-agent System (3) achieves consensus asymptotically if there exist positive-definite matrices P and Q of appropriate dimensions, such that:

$$\left(\begin{array}{ccc}{B}^{T}P+PB-Q& PC+Q& h{B}^{T}Q\\ *& -Q& h{C}^{T}Q\\ *& *& -Q\end{array}\right)<0.$$

(14)

Remark 1. For the particular case when τ(t) = 0, we have that System (3) achieves consensus asymptotically, if and only if there exists a positive-definite matrix P ∈ ℝ^{(2n−m−1)×(2n−m−1)}, such that (B + C)^T P + P (B + C) < 0. That is, the (2n − m − 1) × (2n − m − 1)-dimensional matrix (B + C) is Hurwitz.

Remark 2. Similar to the analysis given in [12], the assumption that$\mathcal{G}$ has a spanning tree is only necessary, but not sufficient, for the consensus of System (3). Generally speaking, the consensus of System (3) not only depends on the Laplacian matrix$L(\mathcal{G})$, but also depends on the gain matrix K.

The method used in Theorem 1 can also be applied to the H_∞ consensus problem of the heterogeneous multi-agent System (7).

Theorem 2. Assume that (H1) holds for given h > 0 and 0 ≤ d < 1. If there exist positive definite matrices P, Q and R of appropriate dimensions, constants α > 0 and β > 0, such that:

$$\left(\begin{array}{cccc}\mathrm{\Delta }& PC+Q& P\tilde{\mathrm{\Sigma }}& h{B}^{T}Q\\ *& -Q-(1-d)R& 0& h{C}^{T}Q\\ *& *& -\beta I_n& h{\tilde{\mathrm{\Sigma }}}^{T}Q\\ *& *& *& -Q\end{array}\right)<0,$$

(15)

where Δ = B^T P + P B − Q + R + αI_2n−m−1, then the heterogeneous multi-agent System (7) asymptotically achieves H_∞ consensus with γ = β/α.

Proof. Choose the Lyapunov functional defined by (12). Firstly, (15) implies that (10) holds. By Theorem 1, System (7) with w = 0 achieves consensus asymptotically. Next, we show that (9) holds with γ = β/α for all nonzero w ∈ L₂[0, ∞) under zero initial condition. In fact, similar to the analysis given in Theorem 1, we have:

$$\begin{array}{l}\dot{V}(t)\le z^T(t)(B^{T}P+PB)z(t)+2z^T(t)PCz(t-\tau )\\ +2z^T(t)P\tilde{\mathrm{\Sigma }}w(t)+h^2{\dot{z}}^T(t)Q\dot{z}(t)\\ -{[z(t)-z(t-\tau )]}^{T}Q[z(t)-z(t-\tau )]\\ +z^T(t)Rz(t)-(1-d)z^T(t-\tau (t))Rz(t-\tau (t)),\end{array}$$

which implies that:

$$\dot{V}(t)+\alpha z^T(t)z(t)-\beta w^T(t)w(t)\le {\xi }^T(\tilde{\mathrm{\Omega }}+h^2{\tilde{\mathrm{\Phi }}}^{T}Q\tilde{\mathrm{\Phi }})\xi ,$$

(16)

where ξ = (z^T (t), z^T (t − τ(t)), w^T(t))^T,

$$\{\begin{array}{l}\tilde{\mathrm{\Phi }}=(B,C,\tilde{\mathrm{\Sigma }}),\hfill \\ \tilde{\mathrm{\Omega }}=\left(\begin{array}{ccc}\mathrm{\Delta }& PC+Q& P\tilde{\mathrm{\Sigma }}\\ *& -Q-(1-d)R& 0\\ *& *& -\beta I_n\end{array}\right)\hfill \end{array}.$$

(17)

By (15), (16) and (17), we have that:

$$\dot{V}(t)+\alpha z^T(t)z(t)-\beta w^T(t)w(t)<0,t\ge 0.$$

(18)

Integrating (18) from zero to ∞ under zero initial condition, we get:

$${\displaystyle {\int }_0^{\infty }{z}^T(t)z(t)dt\le \frac{\beta }{\alpha }{\displaystyle {\int }_0^{\infty }{w}^T(t)w(t)dt.}}$$

□

We obtain the following corollary if nothing is known about the derivative of τ(t).

Corollary 2. Assume that (H2) holds for given h > 0. If there exist positive-definite matrices P, Q of appropriate dimensions, constants α > 0 and β > 0, such that:

$$\left(\begin{array}{cccc}\tilde{\mathrm{\Delta }}& PC+Q& P\tilde{\mathrm{\Sigma }}& h{B}^{T}Q\\ *& -Q& 0& h{C}^{T}Q\\ *& *& -\beta I_n& h{\tilde{\mathrm{\Sigma }}}^{T}Q\\ *& *& *& -Q\end{array}\right)<0,$$

(19)

where$\tilde{\mathrm{\Delta }}=B^{T}P+PB-Q+\alpha I_{2n-m-1}$, then the heterogeneous multi-agent System (7) asymptotically achieves H_∞ consensus with γ = β/α.

Remark 3. Unlike most of the consensus analysis for multi-agent systems, it does not require that a_ij ≥ 0 for all i ≠ j in the proofs of Theorems 1, 2 and Corollaries 1, 2. Therefore, even when a_ij < 0 for some i ≠ j, System (7) can also achieve H_∞ consensus asymptotically under appropriate conditions.

We now extend the aforementioned results to the following dynamic protocol with switched topologies:

$$u_i=\{\begin{array}{l}{\displaystyle \sum _{j=1}^n{a}_{ij}^{\sigma (t)}(x_j(t-\tau (t))-x_i(t-\tau (t))),i\in {\mathcal{I}}_m,}\hfill \\ {\displaystyle \sum _{j=1}^n{a}_{ij}^{\sigma (t)}(x_j(t-\tau (t))-x_i(t-\tau (t)))-k_i{v}_i(t),i\in {\mathcal{I}}_n/{\mathcal{I}}_m,}\hfill \end{array}$$

(20)

where t ≥ 0, σ(t) : [0, ∞) → Γ = {1, 2,⋯, p} is a switching signal that determines which subsystem is active at time t; $a_{ij}^k\ge 0$, i, $j\in {\mathcal{I}}_n$, k ∈ Γ, are entries of the weighted adjacency matrix ${\mathcal{A}}_k$. When σ(t) = k ∈ Γ, we denote the involved digraph by ${\mathcal{G}}_k=(\mathcal{V},{\mathcal{E}}_k,{\mathcal{A}}_k)$.

Under the transformation (4), System (1) with Protocol (20) can be described by the following switched system:

$$\dot{z}(t)=B_{k}z(t)+C_{k}z(t-\tau (t)),$$

(21)

where z is defined above, $B_k=\left(\begin{array}{cc}0& 0\\ 0& I_{n-m}\\ 0& -K\end{array}\right),C_k=\left(\begin{array}{cc}-E{L}_1^{k}F& 0\\ A^k& 0\\ -L_1^{k}F& 0\end{array}\right)$,

$$A^k=\left(\begin{array}{cccc}-a_{12}^k& -a_{13}^k& \cdots & -a_{1n}^k\\ -a_{12}^k& -a_{13}^k& \cdots & -a_{1n}^k\\ ⋮& ⋮& \ddots & ⋮\\ -a_{12}^k& -a_{13}^k& \cdots & -a_{1n}^k\end{array}\right),$$

$L_1^k$, $L_2^k$ and A^k are defined as L₁, L₂ and A, respectively. Let the Lyapunov functionals defined by (12) and (13) be the common Lyapunov functional for the switched System (21), respectively. Then, similar to the analysis in Theorem 1 and Corollary 1, we get the following consensus results for the case of switching topology.

Theorem 3. Assume that (H1) holds for given h > 0 and 0 ≤ d < 1. The heterogeneous multi-agent System (1) with Protocol (20) can asymptotically achieve consensus under arbitrary switching if there exist positive-definite matrices P, Q and R of appropriate dimensions, such that:

$$\left(\begin{array}{ccc}{B}_k^{T}P+P{B}_k-Q+R& P{C}_k+Q& h{B}_k^{T}Q\\ *& -Q-(1-d)R& h{C}_k^{T}Q\\ *& *& -Q\end{array}\right)<0,k\in \Gamma .$$

(22)

Corollary 3. Assume that (H2) holds for given h > 0. The heterogeneous multi-agent System (1) with Protocol (20) asymptotically achieves consensus under arbitrary switching if there exist positive definite matrices P and Q of appropriate dimensions, such that:

$$\left(\begin{array}{ccc}{B}_k^{T}P+P{B}_k-Q& P{C}_k+Q& h{B}_k^{T}Q\\ *& -Q& h{C}_k^{T}Q\\ *& *& -Q\end{array}\right)<0,k\in \Gamma .$$

(23)

Consider the following dynamic protocol with disturbance input:

$$u_i=\{\begin{array}{l}{\displaystyle \sum _{j=1}^n{a}_{ij}^{\sigma (t)}(x_j(t-\tau (t))-x_i(t-\tau (t))+w_{ij}(t)),i\in {\mathcal{I}}_m,}\hfill \\ {\displaystyle \sum _{j=1}^n{a}_{ij}^{\sigma (t)}(x_j(t-\tau (t))-x_i(t-\tau (t))-k_i{v}_i(t)+w_{ij}(t)),i\in {\mathcal{I}}_n/{\mathcal{I}}_m,}\hfill \end{array}$$

(24)

Similar to the proof of Theorem 2, we have the following H_∞ consensus results.

Theorem 4. Assume that (H1) holds for given h > 0 and 0 ≤ d < 1. The heterogeneous multi-agent System (1) with Protocol (24) asymptotically achieves H_∞ consensus with γ = β/α under arbitrary switching if there exist positive-definite matrices P, Q, R of appropriate dimensions and constants α > 0, β > 0, such that:

$$\left(\begin{array}{cccc}{\mathrm{\Delta }}_k& P{C}_k+Q& P{\tilde{\mathrm{\Sigma }}}_k& h{B}_k^{T}Q\\ *& -Q-(1-d)R& 0& h{C}_k^{T}Q\\ *& *& -\beta I_n& h{\tilde{\mathrm{\Sigma }}}_k^{T}Q\\ *& *& *& -Q\end{array}\right)<0,k\in \Gamma ,$$

where${\mathrm{\Delta }}_k=B_k^{T}P+P{B}_k-Q+R+\alpha I_{2n-m-1}$, ${\tilde{\mathrm{\Sigma }}}_k$ is defined as$\tilde{\mathrm{\Sigma }}$, B_k and C_k are defined above.

Corollary 4. Assume that (H2) holds for given 0 ≤ d < 1. The heterogeneous multi-agent System (1) with Protocol (24) asymptotically achieves H∞ consensus with γ = β/α under arbitrary switching, if there exist positive-definite matrices P and Q of appropriate dimensions and constants α > 0, β > 0, such that:

$$\left(\begin{array}{cccc}{\tilde{\mathrm{\Delta }}}_k& P{C}_k+Q& P{\tilde{\mathrm{\Sigma }}}_k& h{B}_k^{T}Q\\ *& -Q& 0& h{C}_k^{T}Q\\ *& *& -\beta I_n& h{\tilde{\mathrm{\Sigma }}}_k^{T}Q\\ *& *& *& -Q\end{array}\right)<0,k\in \Gamma ,$$

where${\tilde{\mathrm{\Delta }}}_k=B_k^{T}P+P{B}_k-Q+\alpha I_{2n-m-1}$, ${\tilde{\mathrm{\Sigma }}}_k$ is defined above.

Remark 4. In this paper, by introducing a reduced-order transformation, the consensus of heterogeneous multi-agent systems is transformed into the stability of the corresponding delay systems. Therefore, we can derive some other less conservative LMIcriteria by choosing different Lyapunov functionals and using some improved integral inequalities, such as in [34–36].

4. Numerical Examples

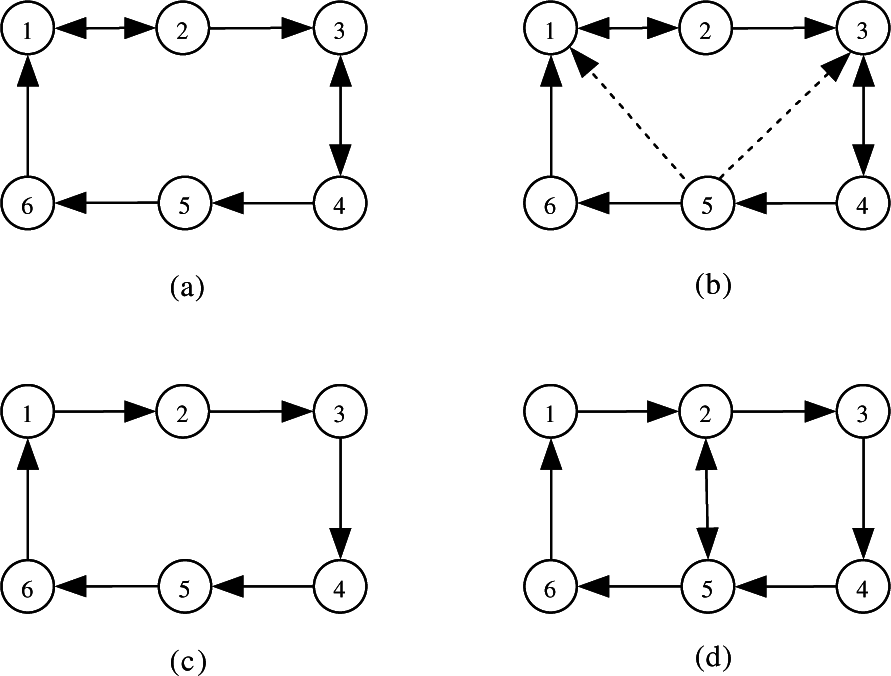
Consider the following four digraphs with six vertices shown in Figure 1, where Vertices 1–4 denote first-order integrators, Vertices 5–6 denote second-order integrators and the weights associated with the edges shown by solid lines and dashed lines are one and −0.5, respectively. For the sake of convenience, we let K = 2I₂.

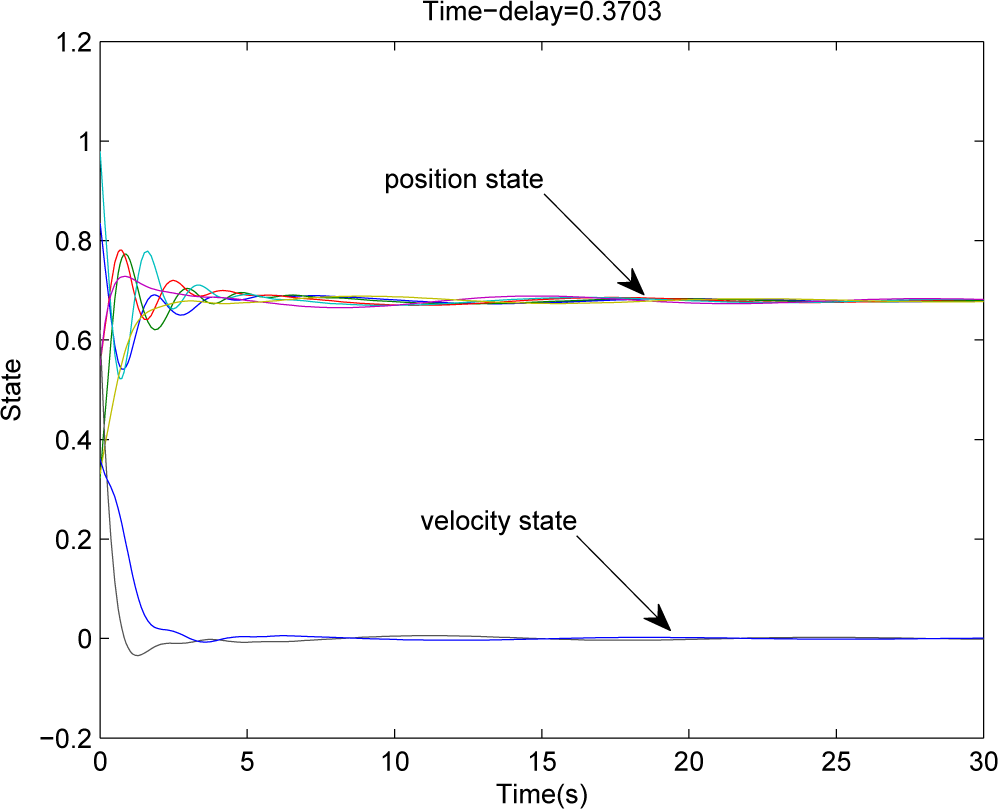
When $\mathcal{G}={\mathcal{G}}_a$, we have that (14) is feasible for given 0 < h ≤ 0.3690. By Corollary 1, System (3) achieves consensus asymptotically. The state trajectory under the stochastic initial condition is shown in Figure 2.

In Remark 3, we show that Corollary 1 can also be applied to the extreme case when parts of weights a_ij are negative. For example, if $\mathcal{G}={\mathcal{G}}_b$, we have that (14) is still feasible for given 0 < h ≤ 0.3703. Therefore, System (3) also achieves consensus asymptotically, even thought there exist negative weights a₅₁ = a₅₃ = −0.5. The corresponding state trajectory under the stochastic initial condition is shown in Figure 3.

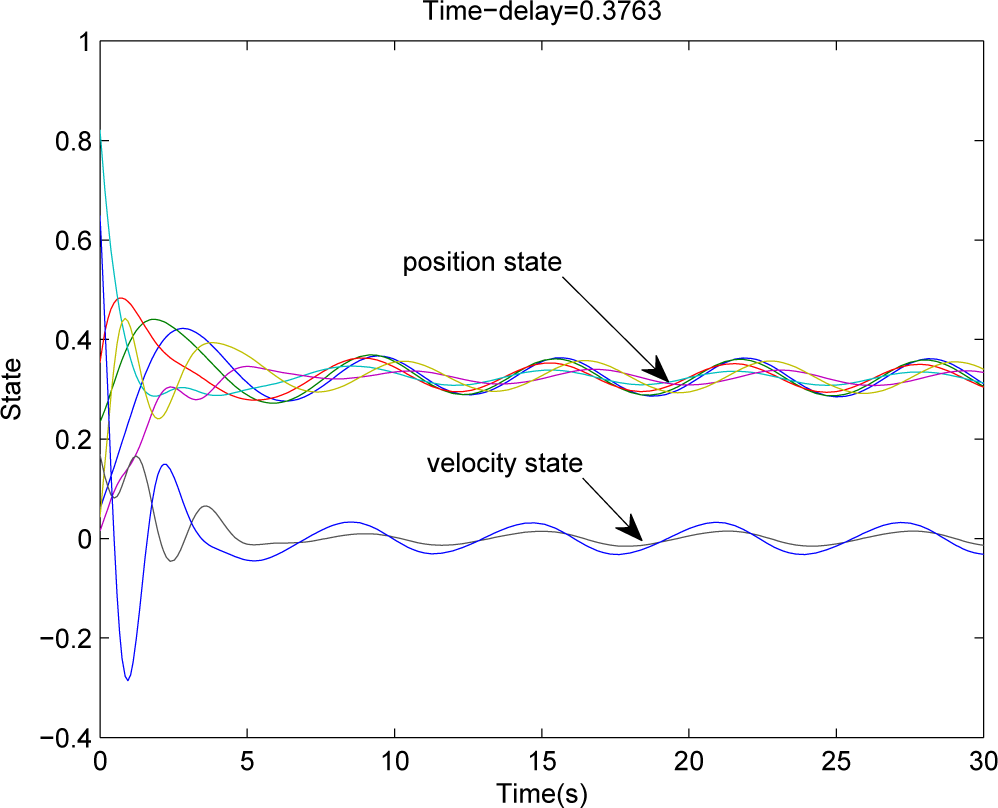
For the case of disturbance input, assume that $\mathcal{G}={\mathcal{G}}_c$ and w_ij(t) = w_j(t) for i, $j\in {\mathcal{I}}_n$. Therefore, ${({\mathrm{\Sigma }}_1^T{\mathrm{\Sigma }}_2^T)}^T=\mathcal{A}$. For given h = 0.3763, we get from (15) that γ = 2.1073. By Corollary 2, we have that System (7) achieves H_∞ consensus with γ = 2.1073. If we let:

$$w(t)=\{\begin{array}{ll}(0.1\sin t)1,\hfill & 0\le t\le 30,\hfill \\ 0.0,\hfill & \text{otherwise},\hfill \end{array}$$

the trajectory of System (7) under a stochastic initial condition is shown in Figure 4.

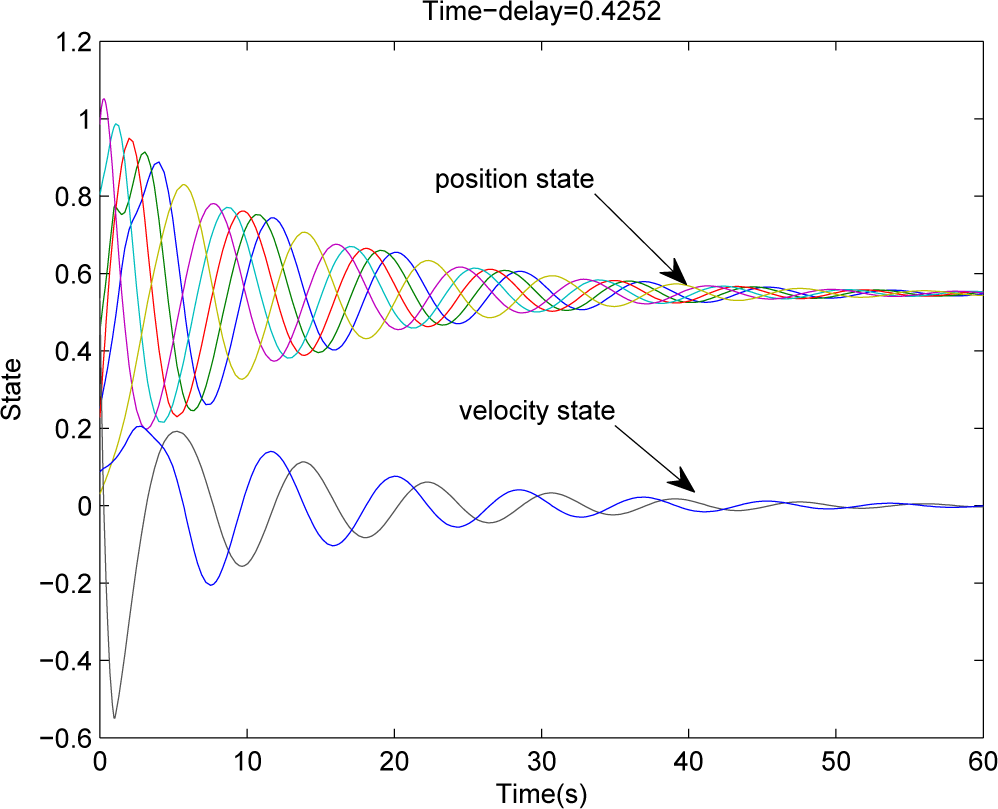
For the case of switching topologies $\{{\mathcal{G}}_c,{\mathcal{G}}_d\}$, we have that (23) is feasible for given 0 < h ≤ 0.4252. By Corollary 3, System (1) with Protocol (20) achieves consensus for 0 < h ≤ 0.4252 under an arbitrary switching signal. The state trajectories of the system are shown in Figure 5, where the initial condition is stochastic, and the switching signal is periodic, which switches every T = 1 second according to ${\mathcal{G}}_c\to {\mathcal{G}}_d\to {\mathcal{G}}_c$.

5. Conclusions

In this paper, by using the linear matrix inequality method, we consider the consensus and H_∞ consensus problems for heterogeneous multi-agent systems with fixed and switching topologies, as well as time-varying delays. By transforming the heterogeneous multi-agent system into a reduced-order system, sufficient conditions for consensus and H_∞ consensus are established in terms of linear matrix inequalities. Finally, simulations are given to illustrate the theoretical results.