Exponential Outer Synchronization between Two Uncertain Time-Varying Complex Networks with Nonlinear Coupling
Abstract
:1. Introduction
2. Problem formulation and preliminaries
3. Theoretical Results
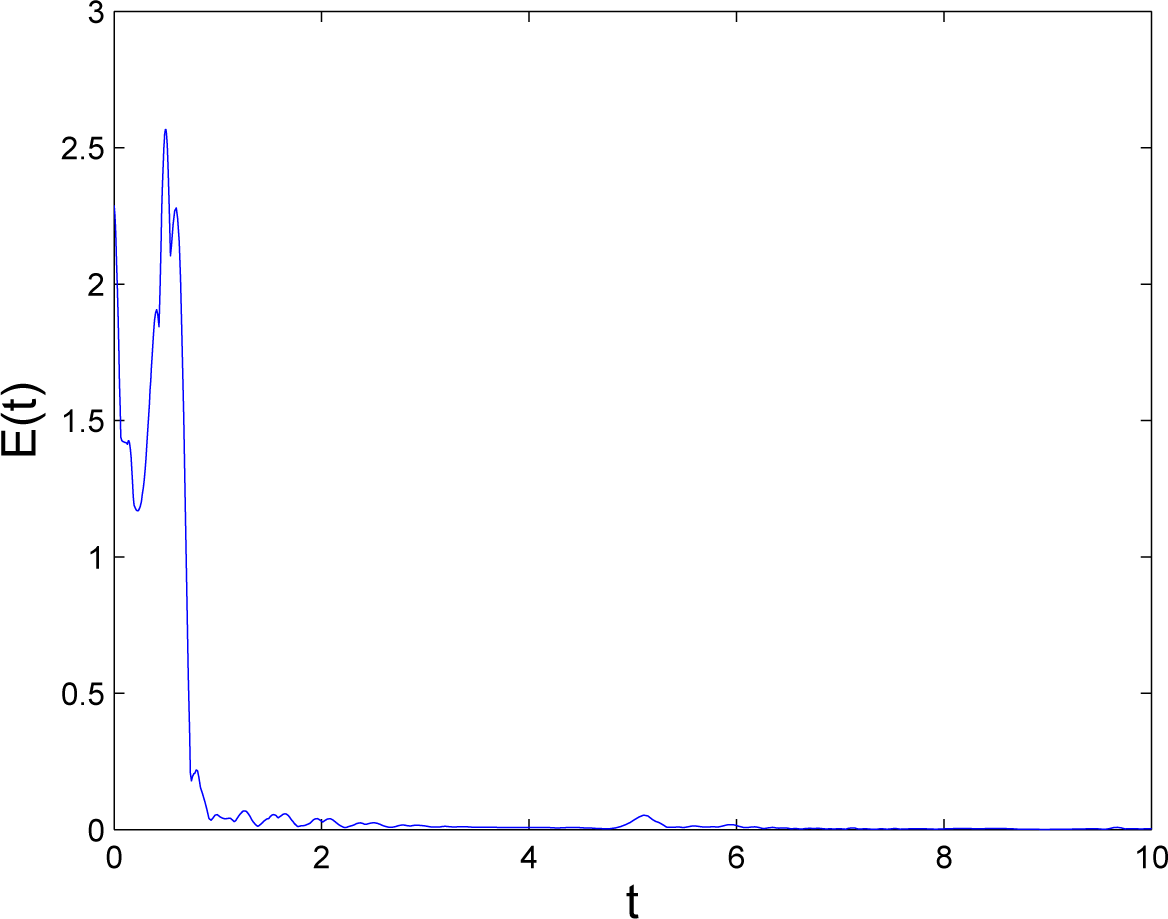
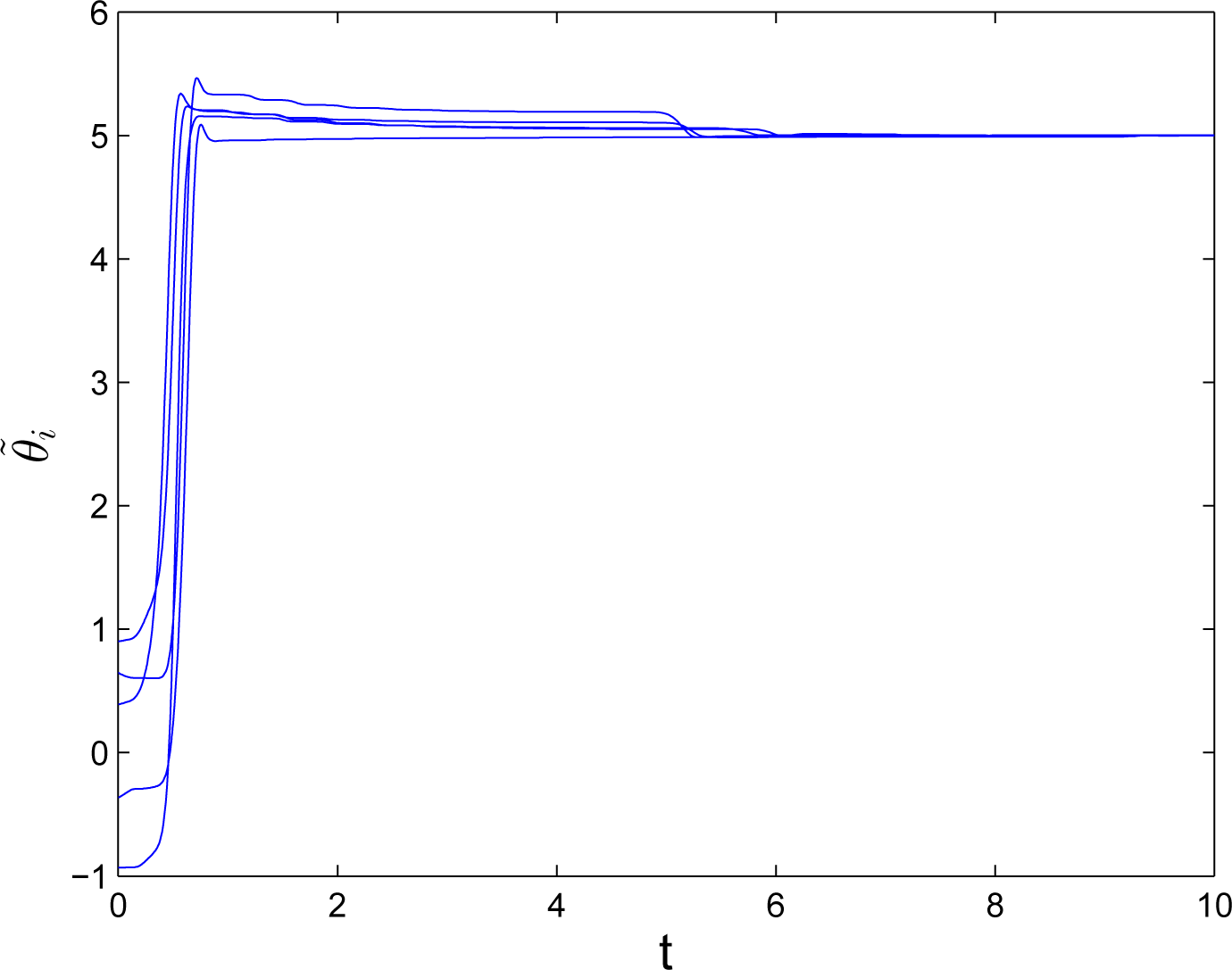
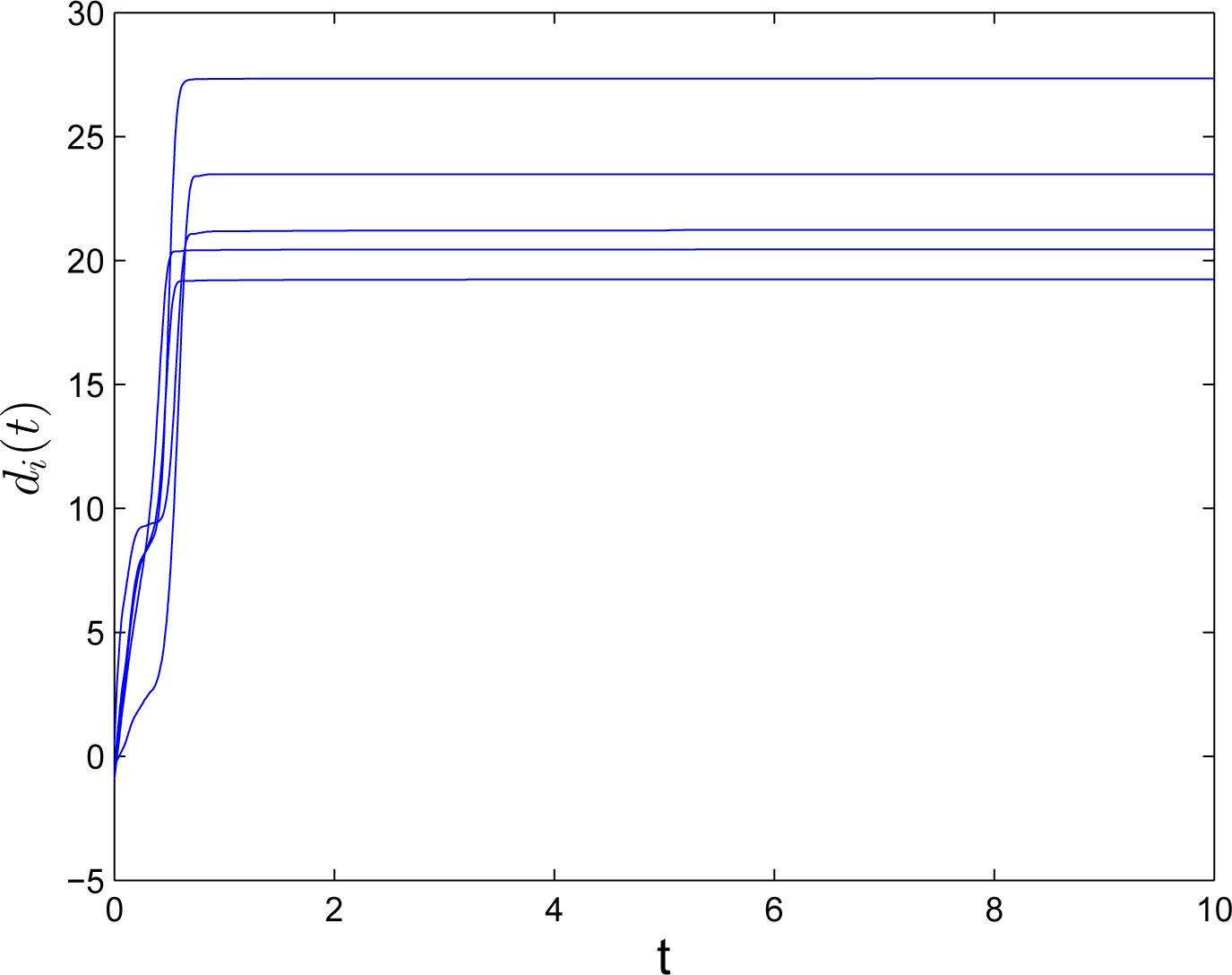
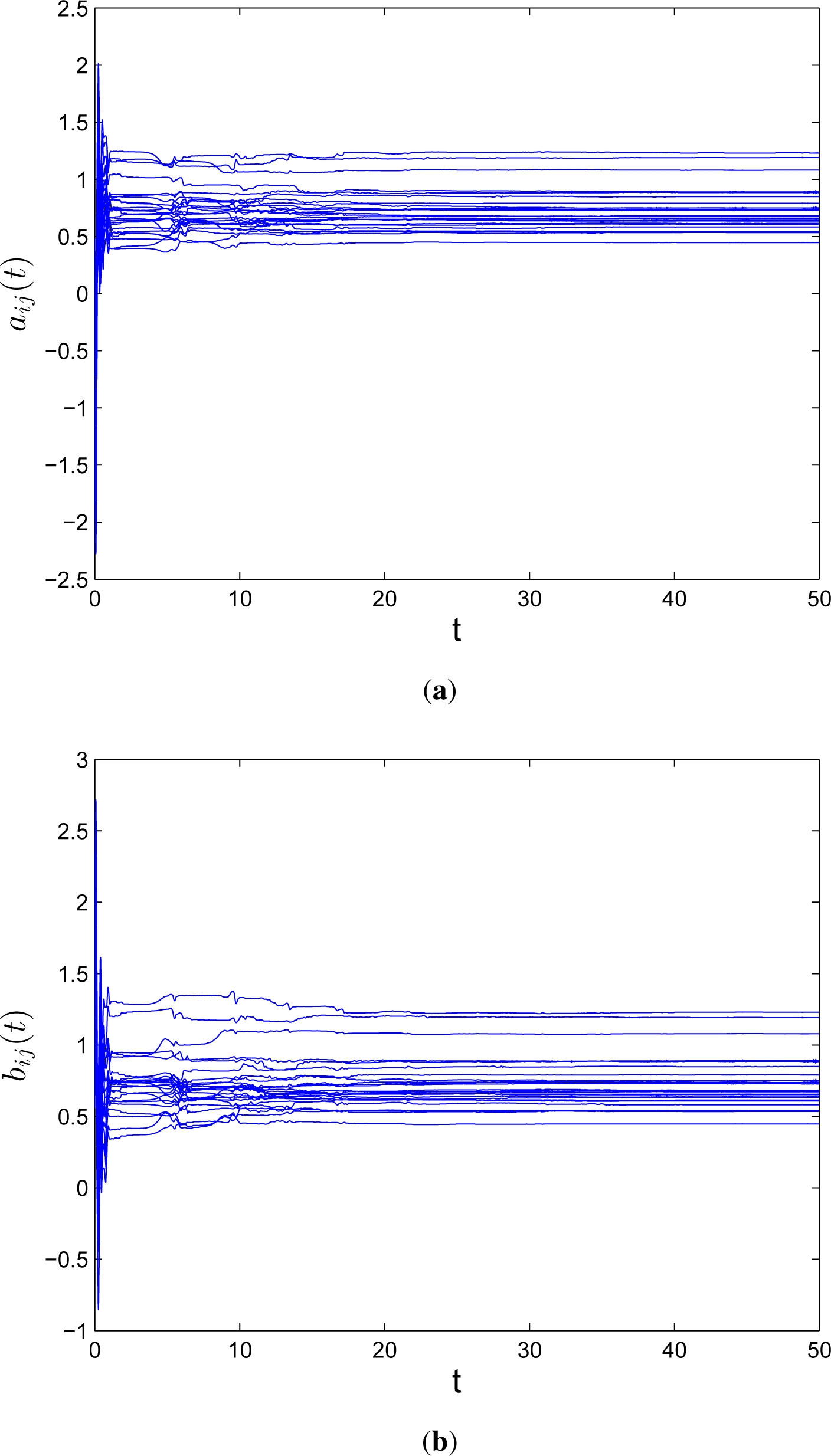
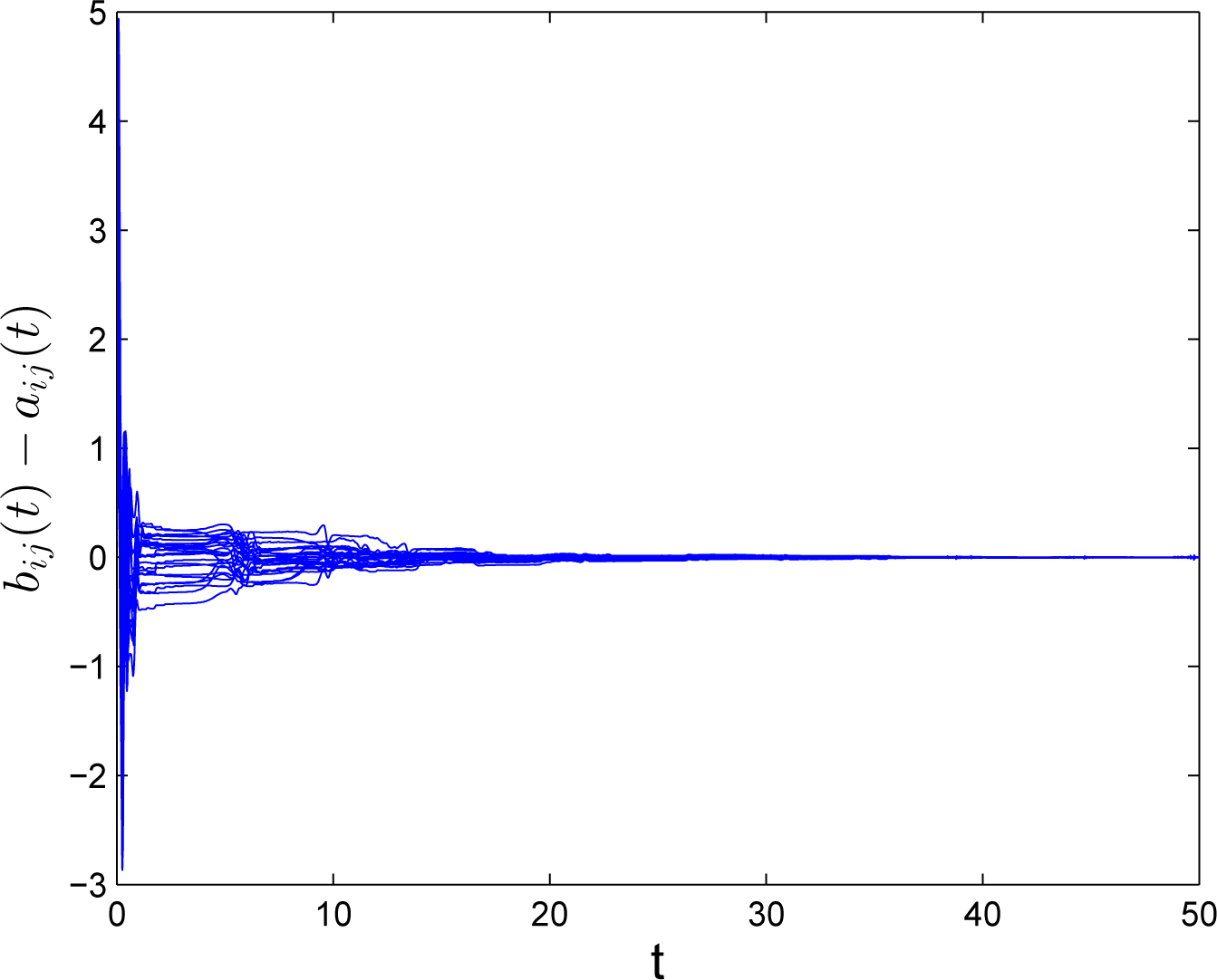
4. Numerical Example
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Watts, D.J.; Strogatz, S.H. Collective dynamics of small-world networks. Nature 1998, 393, 440–442. [Google Scholar]
- Barabási, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.-U. Complex networks: Structure and dynamics. Phys. Rep 2006, 424, 175–308. [Google Scholar]
- Newman, M.E.J. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Sun, W. Random walks on generalized Koch networks. Phys. Scr 2013, 88, 045006. [Google Scholar] [CrossRef]
- Lu, J.; Ho, D.W.C. Local and global synchronization in general complex dynamical networks with delay coupling. Chaos Solitons Fractals 2008, 37, 1497–1510. [Google Scholar]
- Song, Q.; Cao, J.; Liu, F. Synchronization of complex dynamical networks with nonidentical nodes. Phys. Lett. A 2010, 374, 544–551. [Google Scholar]
- Sun, W.; Yang, Y.; Li, C.; Liu, Z. Synchronization inside complex dynamical networks with double time-delays and nonlinear inner-coupling functions. Int. J. Mod. Phys. B 2011, 25, 1531–1541. [Google Scholar]
- Yang, X.; Cao, J. Synchronization of Markovian coupled neural networks with nonidentical node-delays and random coupling strengths. IEEE Trans. Neural Netw. Learn. Syst 2012, 23, 60–71. [Google Scholar]
- Yu, W.; Chen, G.; Lü, J.; Kurths, J. Synchronization via pinning control on general complex networks. SIAM J. Control Optim 2013, 51, 1395–1416. [Google Scholar]
- He, W.; Cao, J. Exponential synchronization of hybrid coupled networks with delayed coupling. IEEE Trans. Neural Netw 2010, 21, 571–583. [Google Scholar]
- Yang, Y.; Cao, J. Exponential synchronization of the complex dynamical networks with a coupling delay and impulsive effects. Nonlinear Anal. Real World Appl 2010, 11, 1650–1659. [Google Scholar]
- Yang, X.; Cao, J.; Lu, J. Stochastic synchronization of complex networks with nonidentical nodes via hybrid adaptive and impulsive control. IEEE Trans. Circuits Syst. I Regul. Pap 2012, 59, 371–384. [Google Scholar]
- Wang, X.; Chen, G. Synchronization in small-world dynamical networks. Int. J. Bifurc. Chaos 2002, 12, 187–192. [Google Scholar]
- Wang, X.; Chen, G. Synchronization in scale free dynamical networks: Robustness and fragility. IEEE Trans. Circuits Syst. I Fundam. Theory Appl 2002, 49, 54–62. [Google Scholar]
- Lu, J.; Cao, J. Adaptive synchronization in tree-like dynamical networks. Nonlinear Anal. Real World Appl 2007, 8, 1252–1260. [Google Scholar]
- Lu, J.; Cao, J. Adaptive synchronization of uncertain dynamical networks with delayed coupling. Nonlinear Dyn 2008, 53, 107–115. [Google Scholar]
- Li, L.; Ho, D.W.C.; Lu, J. A unified approach to practical consensus with quantized data and time delay. IEEE Trans. Circuits Syst. I Regul. Pap 2013, 60, 2668–2678. [Google Scholar]
- Cao, J.; Li, L. Cluster synchronization in an array of hybrid coupled neural networks with delay. Neural Netw 2009, 22, 335–342. [Google Scholar]
- Li, C.; Sun, W.; Kurths, J. Synchronization between two coupled complex networks. Phys. Rev. E 2007, 76, 046204. [Google Scholar] [CrossRef]
- Li, Z.; Xue, X. Outer synchronization of coupled networks using arbitrary coupling strength. Chaos 2010, 20, 023106. [Google Scholar] [CrossRef]
- Tang, H.; Chen, L.; Lu, J.; Tse, C.K. Adaptive synchronization between two complex networks with nonidentical topological structures. Physica A 2008, 387, 5623–5630. [Google Scholar]
- Zheng, S.; Bi, Q.; Cai, G. Adaptive projective synchronization in complex networks with time-varying coupling delay. Phys. Lett. A 2009, 373, 1553–1559. [Google Scholar]
- Wang, G.; Cao, J.; Lu, J. Outer synchronization between two nonidentical networks with circumstance noise. Physica A 2010, 389, 1480–1488. [Google Scholar]
- Wu, X.; Zheng, W.; Zhou, J. Generalized outer synchronization between complex dynamical networks. Chaos 2009, 19, 013109. [Google Scholar] [CrossRef]
- Shang, Y.; Chen, M.; Kurths, J. Generalized synchronization of complex networks. Phys. Rev. E 2009, 80, 027201. [Google Scholar] [CrossRef]
- Wu, Y.; Li, C.; Wu, Y.; Kurths, J. Generalized synchronization between two different complex networks. Commun. Nonlinear Sci. Numer. Simul 2012, 17, 349–355. [Google Scholar]
- Wu, Y.; Li, C.; Yang, A.; Song, L.; Wu, Y. Pinning adaptive anti-synchronization between two general complex dynamical networks with non-delayed and delayed coupling. Appl. Math. Comput 2012, 218, 7445–7452. [Google Scholar]
- Yin, S.; Ding, S.X.; Xie, X.; Luo, H. A review on basic data-driven approaches for industrial process monitoring. IEEE Trans. Ind. Electron 2014, 61, 6418–6428. [Google Scholar]
- Yin, S.; Li, X.; Gao, H.; Kaynak, O. Data-based techniques focused on modern industry: An overview. IEEE Trans. Ind. Electron 2015, 62, 657–667. [Google Scholar]
- Yin, S.; Huang, Z. Performance monitoring for vehicle suspension system via fuzzy positivistic C-means clustering based on accelerometer measurements. IEEE/ASME Trans. Mechatron 2014. [Google Scholar] [CrossRef]
- Yin, S.; Zhu, X.; Kaynak, O. Improved PLS focused on key performance indictor related fault diagnosis. IEEE Trans. Ind. Electron 2015, 62, 1651–1658. [Google Scholar]
- Yin, S.; Wang, G.; Yang, X. Robust PLS approach for KPI-related prediction and diagnosis against outliers and missing data. Int. J. Syst. Sci 2014, 45, 1375–1382. [Google Scholar]
- Liu, H.; Lu, J.; Lü, J.; Hill, D.J. Structure identification of uncertain general complex dynamical networks with time delay. Automatica 2009, 45, 1799–1807. [Google Scholar]
- Xu, Y.; Zhou, W.; Fang, J.; Sun, W.; Pan, L. Topology identification and adaptive synchronization of uncertain complex networks with non-derivative and derivative coupling. J. Frankl. Inst 2010, 347, 1566–1576. [Google Scholar]
- Zhang, Q.; Lu, J. Exponentially adaptive synchronization of an uncertain delayed dynamical network. J. Syst. Sci. Complex 2011, 24, 207–217. [Google Scholar]
- Che, Y.; Li, R.; Han, C.; Wang, J.; Cui, S.; Deng, B.; Wei, X. Adaptive lag synchronization based topology identification scheme of uncertain general complex dynamical networks. Eur. Phys. J. B 2012, 85. [Google Scholar] [CrossRef]
- Sun, W.; Li, S. Generalized outer synchronization between two uncertain dynamical networks. Nonlinear Dyn 2014, 77, 481–489. [Google Scholar]
- Che, Y.; Li, R.; Han, C.; Cui, S.; Wang, J.; Wei, X.; Deng, B. Topology identification of uncertain nonlinearly coupled complex networks with delays based on anticipatory synchronization. Chaos 2013, 23, 013127. [Google Scholar] [CrossRef]
- Wu, X.; Lu, H. Outer synchronization of uncertain general complex delayed networks with adaptive coupling. Neurocomputing 2012, 82, 157–166. [Google Scholar]
- Cheng, C.; Liao, T.; Hwang, C. Exponential synchronization of a class of chaotic neural networks. Chaos Solitons Fractals 2005, 24, 197–206. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 2nd ed; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Hindmarsh, J.L.; Rose, R.M. A model of neuronal bursting using three coupled first order differential equations. Proc. R. Soc. Lond. Ser. B 1984, 221, 87–102. [Google Scholar]
- Shi, X.; Lu, Q. Firing patterns and complete synchronization of coupled Hindmarsh-Rose neurons. Chin. Phys 2005, 14, 77–85. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Liu, L. Exponential Outer Synchronization between Two Uncertain Time-Varying Complex Networks with Nonlinear Coupling. Entropy 2015, 17, 3097-3109. https://doi.org/10.3390/e17053097
Wu Y, Liu L. Exponential Outer Synchronization between Two Uncertain Time-Varying Complex Networks with Nonlinear Coupling. Entropy. 2015; 17(5):3097-3109. https://doi.org/10.3390/e17053097
Chicago/Turabian StyleWu, Yongqing, and Li Liu. 2015. "Exponential Outer Synchronization between Two Uncertain Time-Varying Complex Networks with Nonlinear Coupling" Entropy 17, no. 5: 3097-3109. https://doi.org/10.3390/e17053097
APA StyleWu, Y., & Liu, L. (2015). Exponential Outer Synchronization between Two Uncertain Time-Varying Complex Networks with Nonlinear Coupling. Entropy, 17(5), 3097-3109. https://doi.org/10.3390/e17053097




