1. Introduction
Many systems in practice always involve kinds of constrained signals, such as the bind on the state and control input. Moreover, controllers are to be designed in order to guarantee the stability and some desired performance under the limitations of the system. Several approaches have been put forward to address this problem, such as positive invariance [
1,
2], predictive control [
3] and the polynomial approach [
4]. In addition, it is shown that linear programming is also powerful for solving controller synthesis in presence of bounded state and input, see [
5,
6] and the references therein.
Switched linear systems, which consist of a family of subsystems and a switching signal orchestrates switching among these subsystems, have drawn a lot of attention in recent decades. There are several papers on the stability and stabilization issues of switched linear systems [
7–
12]. In [
7,
8], a sufficient and necessary condition was proposed for the existence of a common quadratic Lyapunov function under arbitrary switching. The multiple Lyapunov function method has been usually pursued in under average dwell time switching [
9,
10]. The switching stabilization problem of switched linear systems has been also studied in [
11,
12]. On the other hand, dynamic systems whose states are always nonnegative are coined as positive systems [
13]. Positive switched systems consist of a family of positive subsystems and a switching law specifying when and how the switching takes place have attracted much attention due to their wide range of applications in network congestion control [
14], formation flying [
15], and medical treatment [
16]. Due to some unpredictable factors, such as the changes of operation environment, the aging of the equipment, it is significant to research the stabilization problem of uncertain systems. Moreover, many real systems can be modeled as systems with interval and polytopic uncertainties.
Recently, stability and stabilization properties for switched positive linear systems have been studied by resorting to the linear copositive Lyapunov function approaches. For arbitrary switching, common linear copositive Lyapunov function is applied in [
17–
20]. Some other results about switched positive linear systems can refer to literature [
21–
26]. The stability and robust stabilization issues by the multiple linear Lyapunov function approach is considered under the dwell time switching in [
21,
22]. The mutually relations among the linear copositive functions, quadratic copositive functions, and the quadratic positive definite functions are gives in [
23]. For systems with exogenous disturbance, the
L1-gain analysis and control synthesis are studied in [
24,
25]. The concept of finite-time stability to switched positive linear systems is extended by reference [
26]. In practice, delay phenomena widely exist in dynamic systems [
27,
28]. Then the concept of stability to switched positive linear systems with delays is shown by [
29]. The constrained control of positive linear systems with multiple delays is investigated in [
30,
31]. The system states to the nonnegative orthant by state feedback with memory and memoryless controller are derived in reference [
32,
33]. The robust stabilization problems under constrained controls for system with interval and polytopic uncertainties are investigated in reference [
34]. For switched positive linear systems with multiple delays, the stability problem both continuous and discrete time systems are solved in [
35]. The controller synthesis for witched positive linear systems with delays is a concern of [
36]; specifically, a nonnegative memoryless controller subject to the nonnegative limitation on the system matrix. Finding a set of controllers in order to lift the limitation provides the motivation for the research presented in this paper.
In this paper, the stabilization problem for switched linear systems with time-varying delay is addressed by using the constrained state feedback controller with memory. The main contributions can be summarized as follows: (i) sufficient conditions are established for the existence of such controller under the sign constraint or nonsymmetrical bounds, which guarantees that the closed-loop systems are positive and asymptotically stable. (ii) the results are extended to the systems with polytopic and interval uncertainties. (iii) the approach we proposed not only can be applied to switched positive linear systems but also be true to general switched linear systems with delay. Thus, it can be interpreted as enforcing the system with delay to be positive by state-feedback with memory. The linear programming method is utilized to solve this controller synthesis issue with bounded controls. The rest of paper is organized as follows. In Section 2, preliminary results are provided. Section 3 addresses the controller synthesis with bounded state and control input. Section 4 solves the constraint controller synthesis for systems with interval uncertainties. The controller synthesis for systems with polytopic uncertainties is studied in Section 5. Numerical examples are shown in Section 6. Section 7 concludes the paper.
Notations: The notations n and m×n denote the n-dimensional Euclidean space and the space of m × n matrices, respectively. hi is the i-th component of vector h ∈ n, and h ⪰ 0 (h ≻ 0) means that hi ≥ 0 (hi > 0). Similarly, aij stands for the i-th row j-th column of matrix A ∈ m×n, A ⪰ 0 (A ≻ 0) implies that aij ≥ 0 (aij > 0) for i = 1, 2, …, m and j = 1, 2, …, n. A is called a Metzler matrix if the off-diagonal entries of A are nonnegative, i.e., aij ≥ 0 for all i ≠ j.
3. Synthesis with Bounded Control
In this section, we consider the stabilization problem for switched linear systems with delay via bounded state feedback controllers with memory under arbitrary switching signal.
3.1. Sign-Restricted Control
This subsection solve stabilization issue of system by nonnegative and negative controls.
Theorem 1. Consider system (1), if there exist matrices H =
diag{
h1,
h2, …,
hn} ≻ 0,
Yp = [
ypij] ⪰ 0 ∈
m×n and Ydp = [
ydpij] ⪰ 0 ∈
m×n for p ∈
such thatthen the closed-loop system (3) is positive and stable by a set of nonnegative controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
under arbitrary switching signal. For p ∈,
Fp and Fdp are given by Proof. Firstly, it follows from
(7) that
ypkj =
fpkjhj, then
By virtue of
(4) together with that
hj ≥ 0, we can obtain that the off-diagonal components of
Ap +
Bp Fp are nonnegative, or
Ap +
BpFp is a Metzler matrix. Similarly we can get
Adp +
Bp Fdp ⪰ 0 from inequality
(5). So the closed-loop system
(3) is positive.
Secondly, consider the element of the system matrices and manipulate them according to the certain way
Note that
(6), we have (
Ap +
Bp Fp +
Adp +
Bp Fdp)
h ≺ 0. Therefore, the closed-loop system
(3) is asymptotically stable via Lemma 2.
Finally, Fp ⪰ 0 and Fdp ⪰ 0 are established from H ≺ 0, Yp ⪰ 0 and Ydp ⪰ 0. Thus, the state feedback controller with memory is nonnegative. □
Remark 1. Observe that linear programming (LP) conditions in Theorem 1 do not impose any restriction on the original system, i.e., Ap is not necessarily a Metzler matrix and Adp is not necessarily positive matrix, so this can be viewed as a controlled positivity problem. Certainly, the results of Theorem 1 can be also applied to switched positive linear systems. Finally, negative results can derived similarly, that is Corollary 1 in the following.
Corollary 1. Consider system (1), if there exist matrices H =
diag{
h1,
h2, …,
hn} ≻ 0,
Yp = [
ypij] ≺ 0
∈ m×n and Ydp = [
ydpij] ≺ 0
∈ m×n for p ∈
such thatthen the closed-loop system (3) is positive and stable by a set of negative controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈
,
Fp and Fdp are given by 3.2. Bounded and Sign-Restricted Controls
The synthesis issue for switched linear systems in present of bounded and sign-restricted controls is solved in this subsection.
Next, we focused on stabilization of switched linear systems by bounded nonnegative control, that is 0 ⪯ u(t) ⪯ ū. For fixed ū ≻ 0, find h ≻ 0 corresponding to bounded control law subject to the resulting closed-loop system is positive and asymptotically stable for 0 ⪯ φ(t) ⪯ h.
Theorem 2. Consider system (1) with nonnegative bounded control, if there exist matrices H = diag{
h1,
h2, …, hn} ≻ 0,
Yp = [
ypij] ⪰ 0 ∈
m×n and Ydp = [
ydpij] ⪰ 0 ∈
m×n p ∈
satisfyingthen the closed-loop system (3) is not only positive but also asymptotically stable by a set of controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈
,
Fp and Fdp can derived byMoreover, define ū = [
ū1,
ū2, …,
ūm]
T, then 0 ⪯
u(
t) ⪯
ū is established for any initial condition satisfying 0 ⪯
x(0) ⪯
h. Proof. We can prove the closed-loop system
(3) is positive and asymptotically stable similar to Theorem 1. Then by Lemma 3, 0 ⪯
x(
t) ⪯
h holds on for any initial condition satisfying 0 ⪯
φ(
t) ⪯
h. Combining with inequality
(17), it is easy to see that the state-feedback control with memory satisfies 0 ⪯
u(
t) ⪯
ū.
In this sequel, consider the controller synthesis of switched linear systems by bounded and negative control. For prescribed ũ ≺ 0, our objective is to find h ≻ 0 corresponding to the bounded control ũ ⪯ u(t) ⪯ 0 subject to the resulting closed-loop system is positive and asymptotically stable for 0 ⪯ φ(t) ⪯ h.
Corollary 2. Consider system (1), if there exist matrices H =
diag{
h1,
h2, …,
hn} ≻ 0,
Yp = [
ypij] ≺ 0 ∈
m×n and Ydp = [
ydpij] ≺ 0 ∈
m×n for p ∈
satisfyingthen the closed-loop system (3) is positive and asymptotically stable under a set of controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈
,
Fp and Fdp can be obtained byMoreover, define ũ = [
ũ1,
ũ2, …,
ũm]
T, then ũ ⪯
u(
t) ⪯ 0
is established for any initial condition satisfying 0 ⪯
x(0) ⪯
h. 3.3. Asymmetrically Bounded Control
This subsection considers the following problem: for prescribed ū1 ≻ 0 and ū2 ≻ 0, the aim is to determine bounded control law −ū1 ⪯ u(t) ⪯ ū2 and vector h ≻ 0 such that the resulting closed-loop system is positive and asymptotically stable for any initial condition 0 ⪯ φ(t) ⪯ h.
Theorem 3. Consider system (1), if there exist matrices H =
diag{
h1,
h2, …,
hn} ≻ 0
and,
,
l ∈ {1, 2}
subject tothen the closed-loop system (3) is not only positive but also asymptotically stable by a set of controllers with memory u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t)).
For p ∈
,
Fp Fdp can be computed as followsFurthermore, let and,
then −
ū1 ⪯
u(
t) ⪯
ū2 sets up for any initial condition fulfilling 0 ⪯
φ(
t) ⪯
h. Proof. It follows the proof of Theorem 1 because that gain matrix Fp can be described as:
, where
and
. □
3.4. Synthesis with State Constraints
This subsection concerned with stabilization problem with state constraints: for given
choose controller with memory together with initial condition 0 ⪯ φ(t) ⪯ h such that 0 ⪯ x ⪯
sets up, the resulting closed-loop system is positive and asymptotically stable.
Theorem 4. Consider system (1), if there exist matrices H = diag{
h1,
h2, …,
hn} ≻ 0,
Yp = [
ypij] ∈
m×n and Ydp = [
ydpij] ∈
m×n for p ∈
such thatthen the closed-loop system (3) is not only positive but also asymptotically stable by a set of controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈
,
Fp and Fdp are given byFurthermore, let,
then holds on for 0 ⪯
φ(
t) ⪯
h. Proof. According to the proof of Theorem 1, it is easy to finish, so it is omitted. □
4. Synthesis with Interval Uncertainties
This section handles the robust stabilization issue via bounded state feedback for systems which are composed of interval uncertain subsystems. In the following, we consider the synthesis via bounded control, that is an extension of the result of Section 3. Assume that the subsystem matrices are unknown and bounded as follows:
4.1. Sign-Restricted Control
An approach for solving the robust stabilization issue of systems with interval uncertainties by nonnegative and negative controls is presented in this subsection.
Theorem 5. Consider system (1), with interval uncertainties, if there exist matrices H =
diag{
h1,
h2, …,
hn} ≻ 0,
Yp = [
ypij] ⪰ 0 ∈
m×n and Ydp = [
ydpij] ⪰ 0 ∈
m×n for p ∈
satisfyingthen the closed-loop system (3) is positive and stable by a set of nonnegative controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈,
Fp and Fdp are given by Proof. From
(36) together with the fact that
Ap+
BpFp ⪰
Ap+
BpFp, then
Ap+
BpFp is a Metzler matrix. Similarly we can get
Adp +
BpFdp ⪰ 0 from inequality
(37). So the closed-loop system is positive. Next, note that
(38), we have that (
Ap +
BpFp +
Adp +
BpFdp)
h ⪯
. Therefore, the closed-loop system
(3) with uncertainties is asymptotically stable by Lemma 2.
Finally, Fp ⪰ 0 and Fdp ⪰ 0 are established from H ≻ 0, Yp ⪰ 0 and Ydp ⪰ 0. Thus, the state feedback controller with memory is nonnegative.□
Corollary 3. Consider system (1) with interval uncertainties, if there exist matrices H = diag{
h1,
h2,
…, hn} ≻ 0,
Yp = [
ypij] ≺ 0 ∈
m×n and Ydp = [
ydpij] ≺ 0 ∈
m×n p ∈
satisfyingthen the closed-loop system (3) is not only positive but also stable by a set of negative controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈
,
Fp and Fdp can be computed as follows 4.2. Bounded and Sign-Restricted Controls
This part considers the controller synthesis issue under sign-restricted and bounded controls for system with interval uncertainties. The aim here is to design the constrained controller such that the closed-loop system is positive and asymptotically stable.
Theorem 6. Consider system (1) with interval uncertainties, if there exist matrices H = diag{
h1,
h2,
…, hn} ≻ 0,
Yp = [
ypij] ⪰ 0 ∈
m×n and Ydp = [
ydpij] ⪰ 0 ∈
m×n p ∈
such thatthen the closed-loop system (3) is not only positive but also asymptotically stable by a set of controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈
,
Fp and Fdp are given byBesides, for fixed ū = [
ū1,
ū2, …,
ūn]
T ≻ 0, 0 ⪯
u(
t) ⪯
ū is established for any initial condition satisfying 0 ⪯
x(0) ⪯
h. Proof. We can obtain the closed-loop system
(3) is positive and asymptotically stable similarly with Theorem 5. Moreover, Combining with inequality
(47), it is easy to see that the state-feedback control with memory satisfy 0 ⪯
u(
t) ⪯
ū. □
Corollary 4. Consider system (1) with interval uncertainties, if there exist matrices H = diag{
h1,
h2,
…, hn} ≻ 0,
Yp = [
ypij] ≺ 0 ∈
m×n and Ydp = [
ydpij] ≺ 0 ∈
m×n p ∈
subject tothen the closed-loop system (3) is not only positive but also asymptotically stable by a set of controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈
,
Fp and Fdp are given byMoreover, choose ũ = [
ũ1,
ũ2,
…, ũm]
T ≺ 0,
then ũ ⪯
u(
t) ⪯ 0
is established for any initial condition satisfying 0 ⪯
x(0) ⪯
h. 4.3. Asymmetrically Bounded Control
The aim in this subsection is to address the following problems: for fixed ū1 ≻ 0 and ū2 ≻ 0, design control law −ū1 ⪯ u(t) ⪯ ū2 such that the resulting closed-loop system is positive and asymptotically stable for any initial condition 0 ⪯ φ(t) ⪯ h.
Theorem 7. Consider system (1) with interval uncertainties, if there exist matrices H = diag{
h1,
h2,
…, hn} ≻ 0,
⪰ 0 ∈
m×n and ⪰ 0 ∈
m×n p ∈
such thatthen the closed-loop system (3) is not only positive but also asymptotically stable by a set of controllers with memory u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t)).
For p ∈,
Fp Fdp are given byFurthermore, take and,
then −
ū1 ⪯
u(
t) ⪯
ū2 sets up for any initial condition fulfilling 0 ⪯
φ(
t) ⪯
h. Proof. It follows the proof of Theorem 5 because that gain matrix Fp can be described as:
, where
and
. □
4.4. Synthesis with State Constraints
This subsection considers synthesis problem for systems with interval uncertainties under state constraints: for fixed
, our aim is to design controller u(k), such that the closed-loop system is asymptotically stable and state is constrained in the box: 0 ⪯ x ⪯
.
Theorem 8. Consider system (1) with interval uncertainties, if there exist matrices H = diag{
h1,
h2,
…, hn} ≻ 0,
Yp = [
ypij] ∈
m×n and Ydp = [
ydpij] ∈
m×n p ∈
subject tothen the closed-loop system (3) is not only positive but also asymptotically stable by a set of controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈,
Fp and Fdp are given byFurthermore, let,
then.
holds for 0 ⪯
φ(
t) ⪯
h. Proof. It is easy to finish based on the proof of Theorem 5, so it is omitted. □
5. Synthesis with Polytopic Uncertainties
In this section, we aim to extend the results in Section 3 to switched linear systems with polytopic uncertainties. Assume that the subsystem matrices belong to the uncertainty set
where
,
and
are given matrices denoting the extreme points of the
p-th subsystem for
s = 1, 2,
…, L, and
L means the total number of extreme points.
5.1. Sign-Restricted Control
In this pat, the objective is to solve the robust stabilization issue of systems with polytopic uncertainties by nonnegative and negative controls.
Theorem 9. Consider system (1) with polytopic uncertainties, if there exist matrices H = diag{
h1,
h2,
…, hn} ≻ 0,
Yp = [
ypij] ⪰ 0 ∈
m×n and Ydp = [
ydpij] ⪰ 0 ∈
m×n p ∈
such thatthen the closed-loop system (3) is not only positive but also stable by a set of nonnegative controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈
,
Fp and Fdp can be derived by Proof. It is straightforward by a convexity argument from Theorem 1. □
Corollary 5. Consider system (1), if there exist matrices H =
diag{
h1,
h2,
…, hn} ≻ 0,
Yp = [
ypij] ≺ 0 ∈
m×n and Ydp = [
ydpij] ≺ 0 ∈
m×n for p ∈
satisfyingthen the closed-loop system (3) is positive and stable by a set of negative controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈
,
Fp and Fdp are given by 5.2. Bounded and Sign-Restricted Controls
This part considers controller synthesis issue under sign-restricted and bounded controls for systems with polytopic uncertainties.
Theorem 10. Consider system (1) with polytopic uncertainties, if there exist matrices H = diag{
h1,
h2,
…, hn} ≻ 0,
Yp = [
ypij] ⪰ 0 ∈
m×n and Ydp = [
ydpij] ⪰ 0 ∈
m×n p ∈
satisfyingthen the closed-loop system (3) is positive and asymptotically stable by a set of controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈,
Fp and Fdp can be obtained byFor defined ū = [
ū1,
ū2,
…, ūm]
T ≻ 0,
0⪯
u(
t) ⪯
ū sets up for any initial condition satisfying 0 ⪯
x(0) ⪯
h. Proof. It is straightforward by a convexity argument from Theorem 2. □
Corollary 6. Consider system (1), polytopic uncertainties, if there exist matrices H =
diag{
h1,
h2,
…, hn} ≻ 0,
Yp = [
ypij] ≺ 0 ∈
m×n and Ydp = [
ydpij] ≺ 0 ∈
m×n for p ∈
such thatthen the closed-loop system (3) is positive and asymptotically stable by a set of controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈
,
Fp and Fdp are given byMoreover, define ũ = [
ũ1,
ũ2,
·…, ũm]
T ≺ 0,
then ũ ⪯
u(
t) ⪯ 0
is established for any initial condition satisfying 0 ⪯
x(0) ⪯
h. 5.3. Asymmetrically Bounded Control
In this part, we focus on the following problem: for prescribed ū1 ≻ 0 and ū2 ≻ 0, the aim is to determine input controller −ū1 ⪯ u(t) ⪯ ū2 such that the resulting closed-loop system is positive and asymptotically stable for any initial condition 0 ⪯ φ(t) ⪯ h.
Theorem 11. Consider system (1) with polytopic uncertainties, if there exist matrices H =
diag{
h1,
h2,
…, hn} ≻ 0,
and l ∈ {1, 2,}
subject tothen the closed-loop system (3) is positive and asymptotically stable under a set of controllers with memory u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t)).
For p ∈
,
Fp Fdp are given byBesides, choose and,
then −
ū1 ⪯
u(
t) ⪯
ū2 sets up for any initial condition fulfilling 0 ⪯
φ(
t) ⪯
h. Proof. It follows the proof of Theorem 3 because the convexity argument. □
5.4. Synthesis with State Constraints
In this subsection, we consider the controller synthesis issue for systems with polytopic uncertainties. Our aim is to determine u(t), such that the closed-loop system is asymptotically stable and the state is constrained in the box:
.
Theorem 12. Consider system (1) with polytopic uncertainties, if there exist matrices H = diag{
h1,
h2,
…, hn} ≻ 0,
Yp = [
ypij] ∈
m×n and Ydp = [
ydpij] ∈
m×n p ∈
such thatthen the closed-loop system (3) is not only positive but also asymptotically stable by a set of controllers u(
t) =
Fσ(t)x(
t) +
Fdσ(t)x(
t −
d(
t))
for arbitrary switching signal. For p ∈
,
Fp and Fdp are given byFurthermore, select,
then holds on for 0 ⪯
φ(
t) ⪯
h. Proof. It is easy to finish according to the proof of Theorem 4, so it is omitted. □
Remark 2. If the matrices Ap, Adp or Bp are known, it is special situation of the results of Section 5. This is based on the fact,
or for ∀1 ≤ s ≤ L. Moreover, it is the general issue when Ap, Adp and Bp are all fixed.
Remark 3. In fact, direct application of Theorem 9 is cumbersome to compute due to the number of vertices might be very large. However, if,
,
for each p ∈
, s ∈ {1, 2, …, L}, thus we can cast the robust stabilization issue of system with polytopic uncertainties as system with interval uncertainties.
Remark 4. The results of time-varying delay can be also applied to the constant delay in this paper.
Remark 5. We use linprog function in Matlab to solve LP and get feasible solutions for LP problems.
6. Numerical Example
In this section, two examples are provided to illustrate the theoretical results.
Example 1. Consider system (1) with the following system matrices It can be seen that all of the system matrices
Ai and
Adi (for
i = 1, 2) are not positive. The objective here is to design a set of constrained state-feedback controllers with memory 0 ⪯
u(
t) ⪯
ū that stabilizes the system and enforces the state to be positive. Take
ū = 100,
d(
t) = 1 + sin(
t). By Theorem 2, we can obtain a set of solutions by LP as
H =
diag{11.6995, 108.0623} and
Then, according to
(18), we can get
By calculating, we have
Note that A1 + B1F1, A2 + B2F2 are Metzler matrices, and Ad1 + B1Fd1, Ad2 + B2Fd2 are positive matrices, thus the closed-loop system is positive.
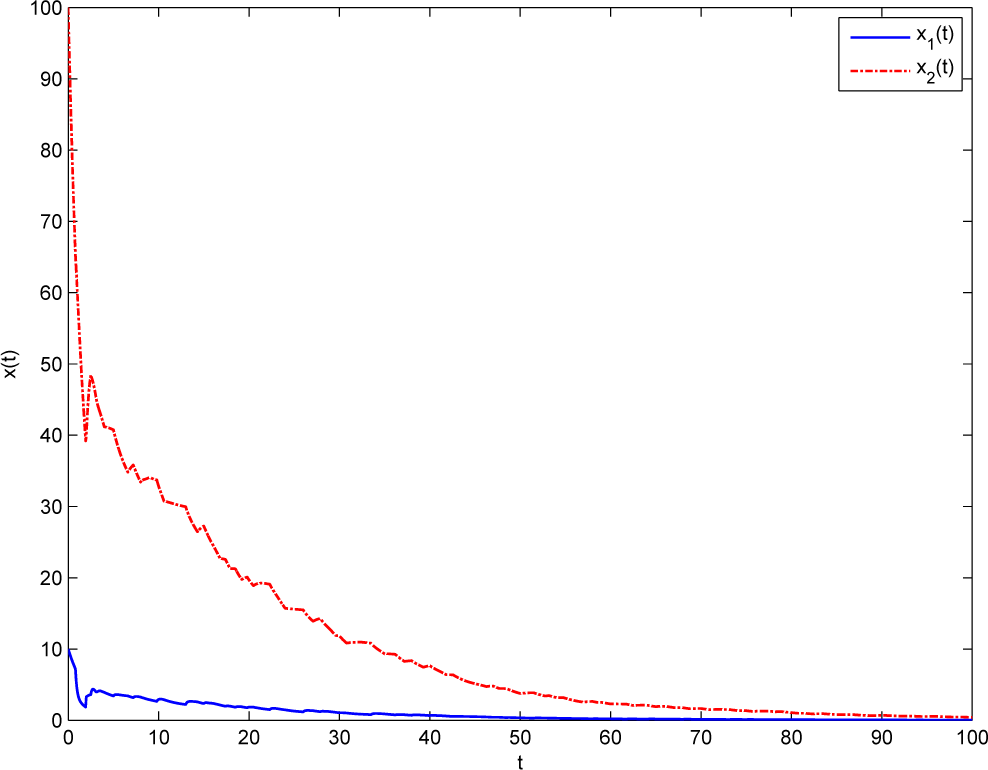
The state evolution with initial conditions
φ(
t) = (10, 100)
⊤ are shown in
Figure 1, it is clear to see that the systems are positive and stable.
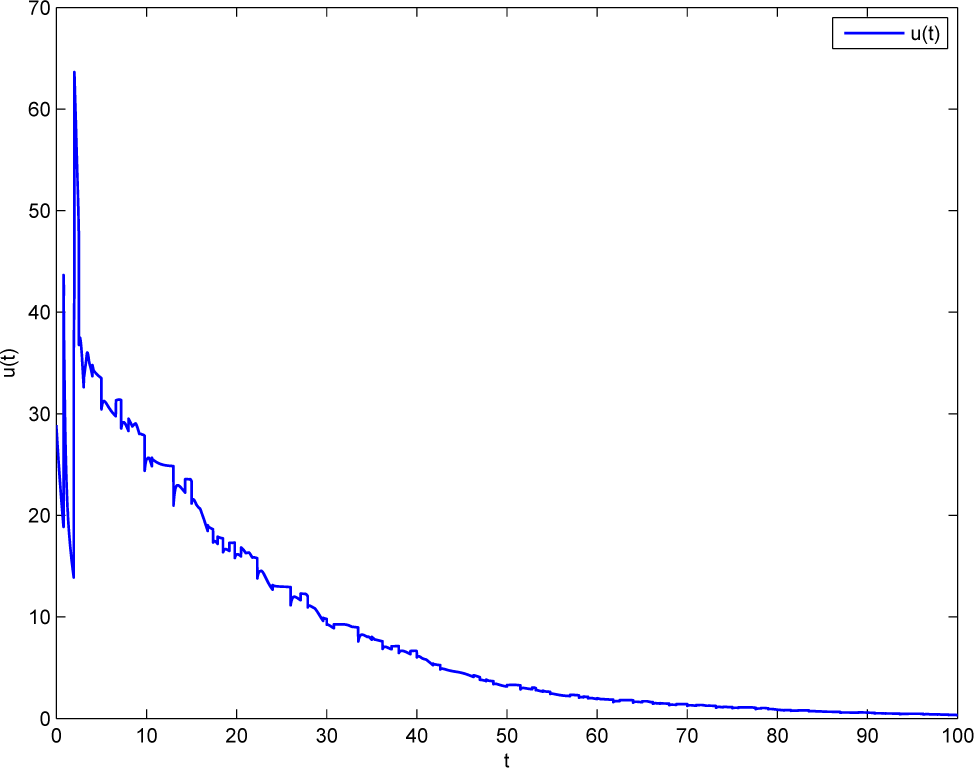
Figure 2 shows that the control input under the switching signal
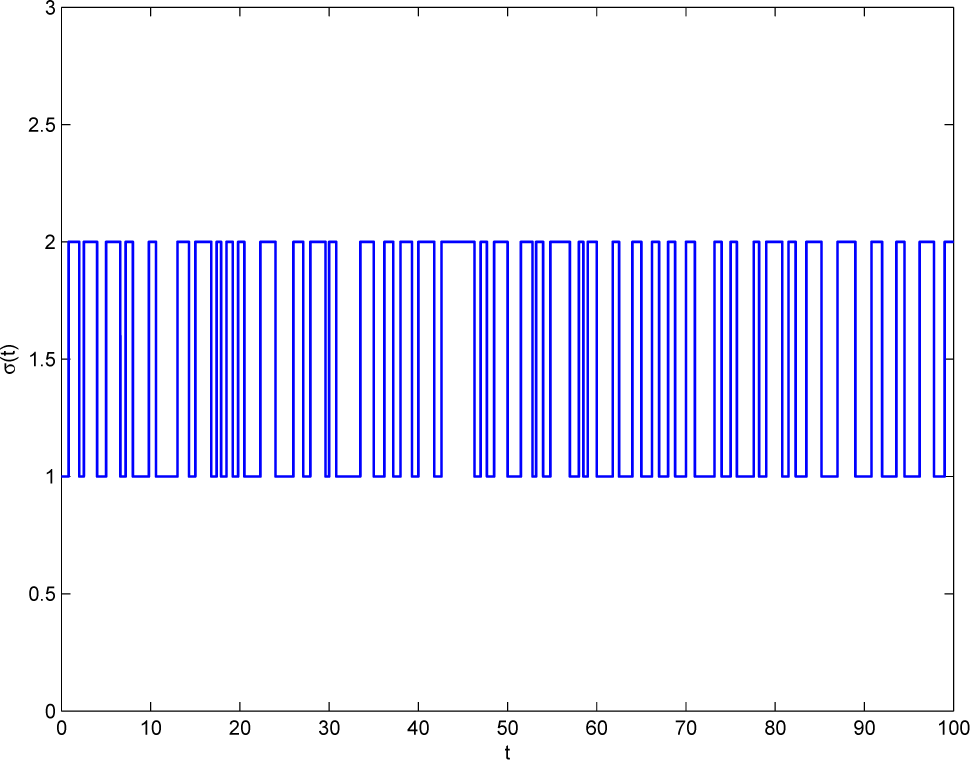
σ(
t). The arbitrary switching signal
σ(
t) is described by
Figure 3.
Example 2. Consider system (1) with the following system matrices It can be seen that the system matrices
Ai is Metzler matrix and
Adi is positive (for
i = 1, 2). The objective here is to design a set of constrained state-feedback controllers with memory 0 ⪯
u(
t) ⪯
ũ that stabilizes the system and enforces the state to be positive. Choose
ũ = [−6, −8]
T,
d(
t) = 0.5. By Corollary 2, we can obtain a set of solutions by LP as
H =
diag{3.4584, 3.7627} and
Then, according to
(23), we can get
By calculating, we have
Note that
A1 +
B1F1,
A2 +
B2F2 are Metzler matrices, and
Ad1 +
B1Fd1,
Ad2 +
B2Fd2 are positive matrices, thus the closed-loop system is positive under this controller.
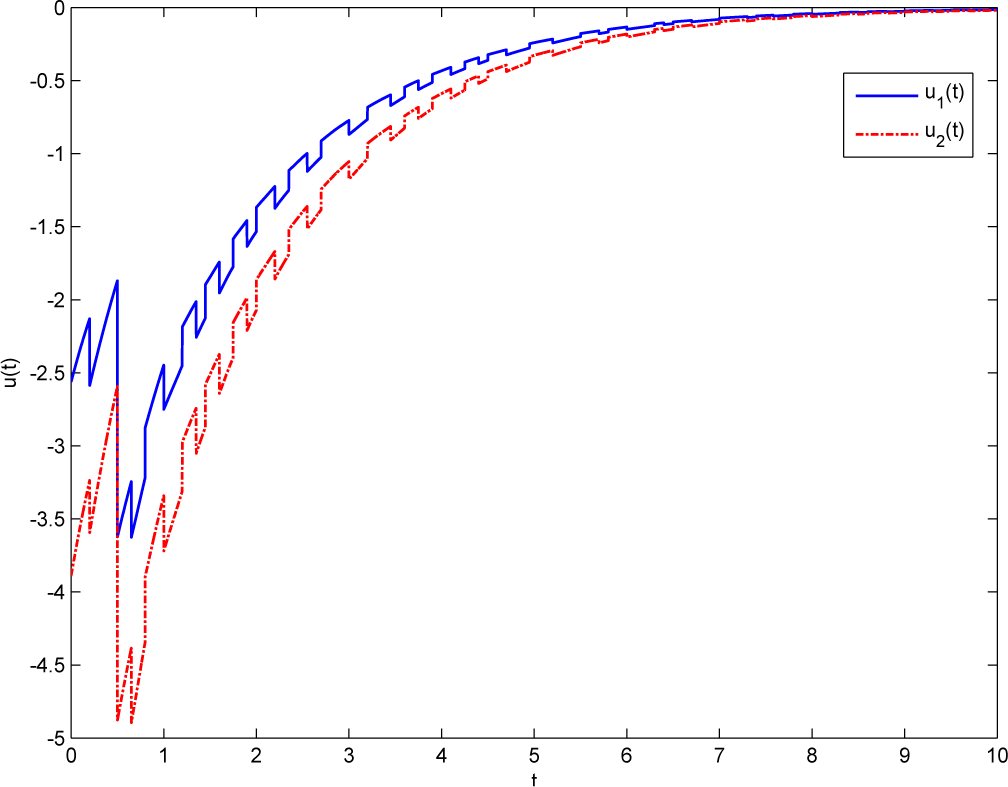
Figure 4 shows the state response under initial conditions
φ(
t) = (3.4, 3.7)
⊤. The control input under the switching signal
σ(
t) is given by
Figure 5.
Figure 6 depicts the arbitrary switching signal
σ(
t).