Generalized Remote Preparation of Arbitrary m-qubit Entangled States via Genuine Entanglements
Abstract
:1. Introduction
2. General RSP Procedure for an Arbitrary m-Qubit Entangled State
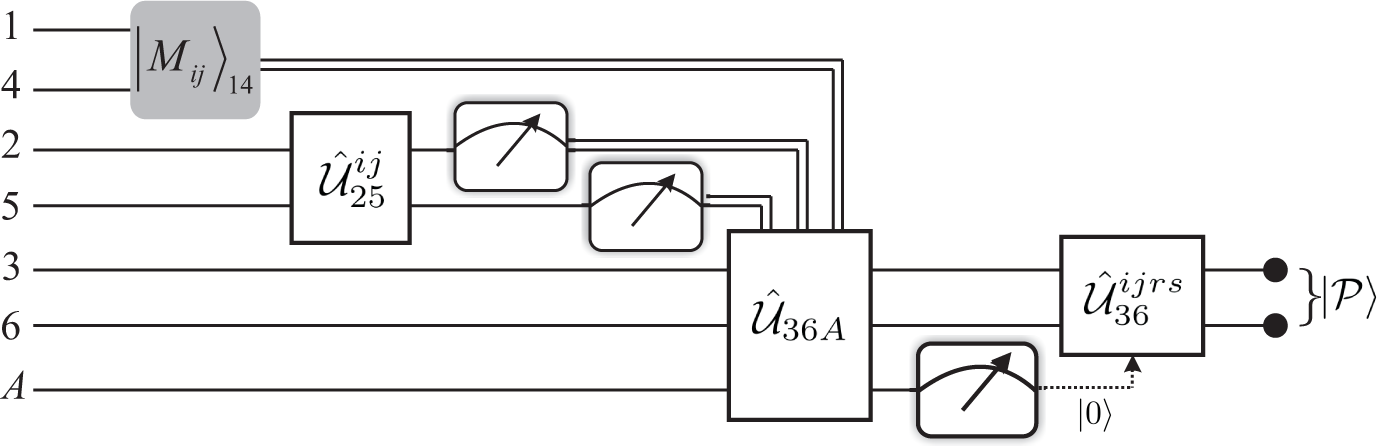
3. RSP for an Arbitrary Two-Qubit Entangled State: An Example
4. Discussion
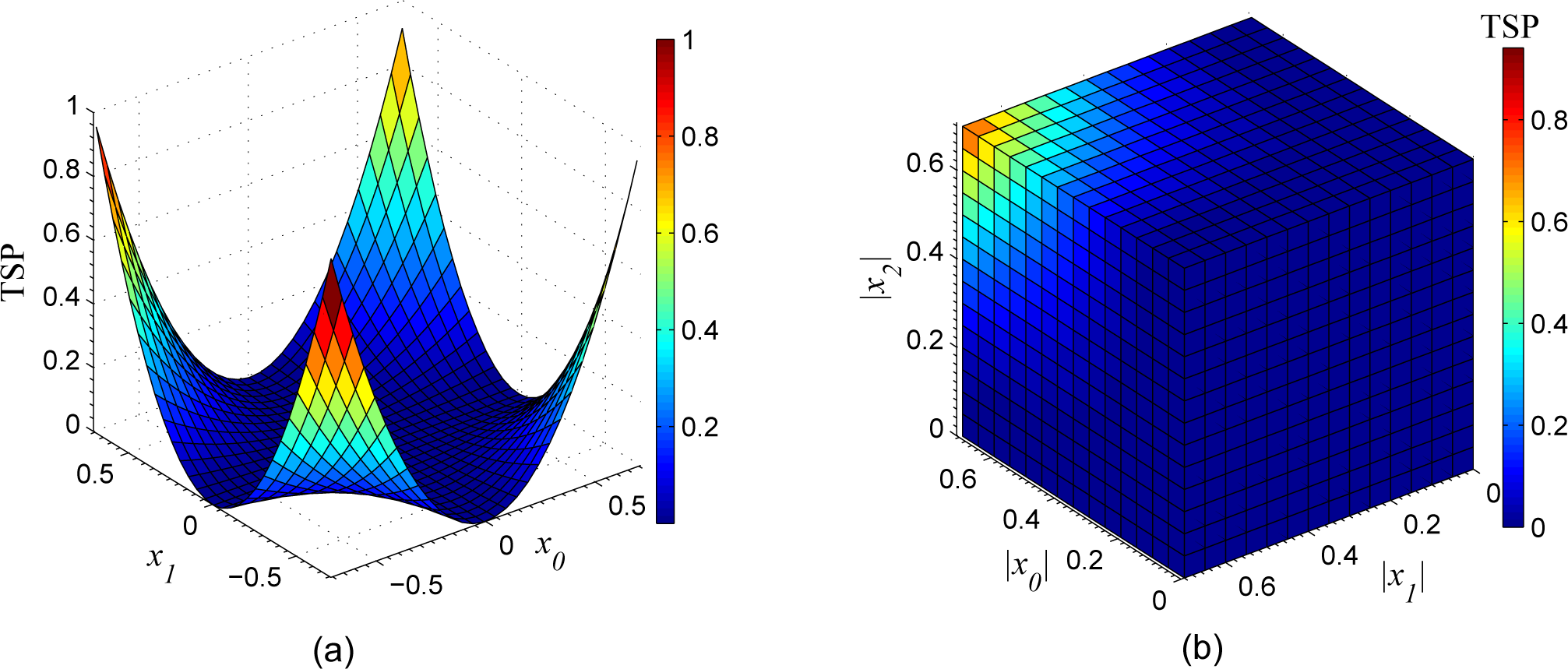
4.1. Total Success Probability and Classical Information Cost
4.2. The Properties of the Current Scheme
5. Summary
Appendix
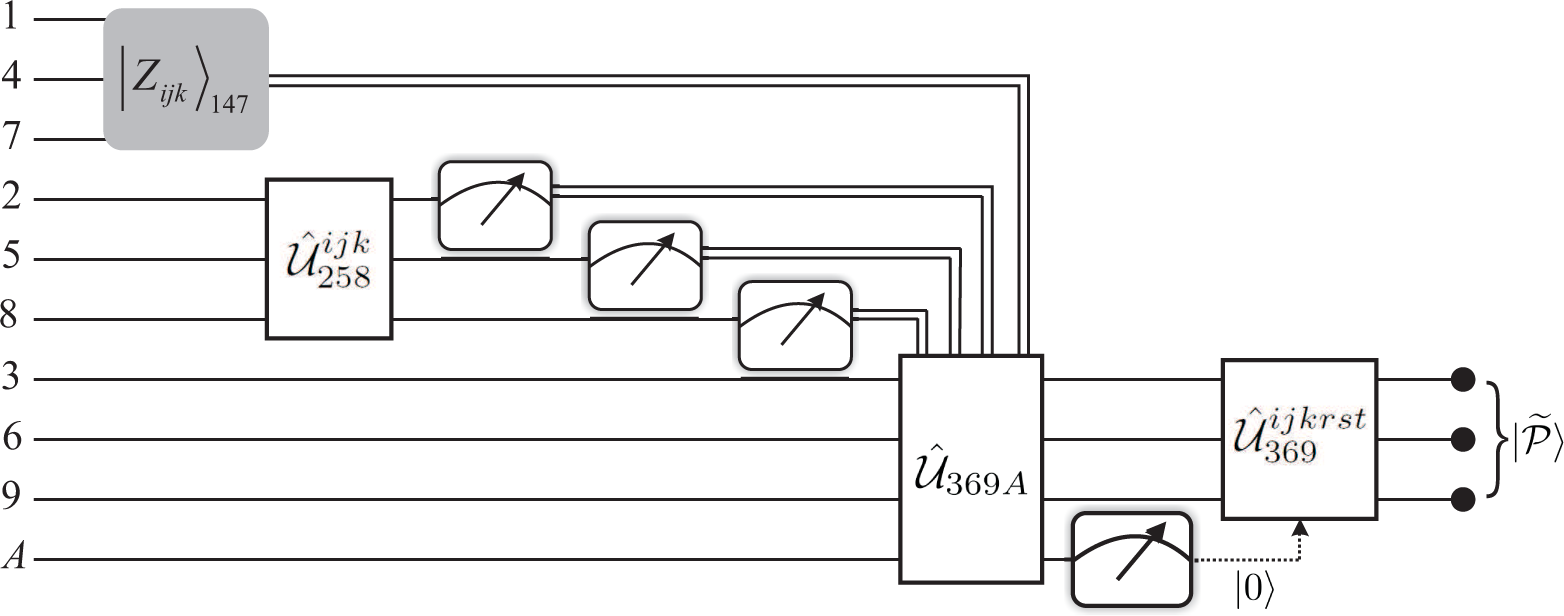
A. General RSP for Three-Qubit Entangled States
B. Three-Qubit Entangled State RSP for (i, j, k, r, s, t) = (0, 0, 1, 0, 0, 1)
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G.; Cŕepeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar]
- Lo, H.K. Classical-communication cost in distributed quantum-information processing: A generalization of quantum communication complexity. Phys. Rev. A 2000, 62, 012313. [Google Scholar]
- Pati, A.K. Minimum classical bit for remote preparation and measurement of a qubit. Phys. Rev. A 2000, 63, 015302. [Google Scholar]
- Bennett, C.H.; DiVincenzo, D.P.; Shor, P.W.; Smolin, J.A.; Terhal, B.M.; Wootters, W.K. Remote state preparation. Phys. Rev. Lett. 2001, 87, 077902. [Google Scholar]
- Hillery, M.; Bužek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829–1834. [Google Scholar]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar]
- Wang, H.F.; Kais, S. Quantum teleportation in one-dimensional quantum dots system. Chem. Phys. Lett. 2006, 421, 338–342. [Google Scholar]
- Kais, S. Entangledment, Electron Correlation, and Density Matrices; Wiley: New York, NY, USA, 2007; Volume 134, pp. 493–535. [Google Scholar]
- Zhu, J.; Kais, S.; Aspuru-Guzik, A.; Rodriques, S.; Brock, B.; Love, P.J. Multipartite quantum entanglement evolution in photosynthetic complexes. J. Chem. Phys. 2012, 137, 074112. [Google Scholar]
- Devetak, I.; Berger, T. Low-entanglement remote state preparation. Phys. Rev. Lett. 2001, 87, 197901. [Google Scholar]
- Leung, D.W.; Shor, P.W. Oblivious remote state preparation. Phys. Rev. Lett. 2003, 90, 127905. [Google Scholar]
- Berry, D.W.; Sanders, B.C. Optimal remote state preparation. Phys. Rev. Lett. 2003, 90, 057901. [Google Scholar]
- Kurucz, Z.; Adam, P.; Janszky, J. General criterion for oblivious remote state preparation. Phys. Rev. A 2006, 73, 062301. [Google Scholar]
- Hayashi, A.; Hashimoto, T.; Horibe, M. Remote state preparation without oblivious conditions. Phys. Rev. A 2003, 67, 052302. [Google Scholar]
- Abeyesinghe, A.; Hayden, P. Generalized remote state preparation: Trading cbits, qubits, and ebits in quantum communication. Phys. Rev. A 2003, 68, 062319. [Google Scholar]
- Ye, M.Y.; Zhang, Y.S.; Guo, G.C. Faithful remote state preparation using finite classical bits and a nonmaximally entangled state. Phys. Rev. A 2004, 69, 022310. [Google Scholar]
- Xia, Y.; Song, J.; Song, H.S. Multiparty remote state preparation. J. Phys. B: At. Mol. Opt. Phys. 2007, 40, 3719–3724. [Google Scholar]
- Nguyen, B.A.; Kim, J. Joint remote state preparation. J. Phys. B: At. Mol. Opt. Phys. 2008, 41, 095501. [Google Scholar]
- Luo, M.X.; Chen, X.B.; Ma, S.Y.; Niu, X.X.; Yang, Y.X. Joint remote preparation of an arbitrary three-qubit state. Opt. Commun 2010, 283, 4796–4801. [Google Scholar]
- Xiao, X.Q.; Liu, J.M.; Zeng, G.H. Joint remote state preparation of arbitrary two- and three-qubit states. J. Phys. B: At. Mol. Opt. Phys. 2011, 44, 075501. [Google Scholar]
- Chen, Q.Q.; Xia, Y.; Nguyen, B.A. Joint remote preparation of an arbitrary three- qubit state via EPR-type pairs. Opt. Commun 2011, 284, 2617–2621. [Google Scholar]
- Nguyen, B.A.; Cao, T.B.; Nung, V.D. Joint remote preparation of four-qubit cluster-type states revisited. J. Phys. B: At. Mol. Opt. Phys. 2011, 44, 135506. [Google Scholar]
- Luo, M.X.; Chen, X.B.; Yang, Y.X.; Niu, X.X. Experimental architecture of joint remote state preparation. Quantum Inf. Process 2012, 11, 751–767. [Google Scholar]
- Zhou, P. Joint remote preparation of an arbitrary m-qudit state with a pure entangled quantum channel via positive operator-valued measurement. J. Phys. A 2012, 45, 215305. [Google Scholar]
- Xia, Y.; Chen, Q.Q.; Nguyen, B.A. Deterministic joint remote preparation of an arbitrary three-qubit state via Einstein-Podolsky-Rosen pairs with a passive receiver. J. Phys. A 2012, 45, 335306. [Google Scholar]
- Zhan, Y.B.; Ma, P.C. Deterministic joint remote preparation of arbitrary two- and three-qubit entangled states. Quantum Inf. Process 2013, 12, 997–1009. [Google Scholar]
- Chen, Q.Q.; Xia, Y.; Nguyen, B.A. Flexible deterministic joint remote state preparation with a passive receiver. Phys. Scr. 2013, 87, 025005. [Google Scholar]
- Hou, K. Joint remote preparation of four-qubit cluster-type states with multiparty. Quantum Inf. Process 2013, 12, 3821–3833. [Google Scholar]
- Jiang, M.; Zhou, L.L.; Chen, X.P.; You, S.H. Deterministic joint remote preparation of general multi-qubit states. Opt. Commun 2013, 301, 39–45. [Google Scholar]
- Peng, J.Y.; Luo, M.X.; Mo, Z.W. Joint remote state preparation of arbitrary two- particle states via GHZ-type states. Quantum Inf. Process 2013, 12, 2325–2342. [Google Scholar]
- Liao, Y.M.; Zhou, P.; Qin, X.C.; He, Y.H. Efficient joint remote preparation of an arbitrary two-qubit state via cluster and cluster-type states. Quantum Inf. Process 2014, 13, 615–627. [Google Scholar]
- Chen, X.B.; Su, Y.; Xu, G.; Sun, Y.; Yang, Y.X. Quantum state secure transmission in network communications. Inf. Sci. 2014, 276, 363–376. [Google Scholar]
- Zhang, Z.H.; Shu, L.; Mo, Z.W.; Zheng, J.; Ma, S.Y.; Luo, M.X. Joint remote state preparation between multi-sender and multi-receiver. Quantum Inf. Process 2014, 13, 1979–2005. [Google Scholar]
- Wang, D.; Ye, L. Multiparty-controlled joint remote state preparation. Quantum Inf. Process 2013, 12, 3223–3237. [Google Scholar]
- Yu, Y.F.; Feng, J.; Zhan, M.S. Preparing remotely two instances of quantum state. Phys. Lett. A 2003, 310, 329–332. [Google Scholar]
- Huang, Y.X.; Zhan, M.S. Remote preparation of multipartite pure state. Phys. Lett. A 2004, 327, 404–408. [Google Scholar]
- Liu, J.M.; Wang, Y.Z. Remote preparation of a two-particle entangled state. Phys. Lett. A 2003, 316, 159–167. [Google Scholar]
- Liu, J.M.; Feng, X.L.; Oh, C.H. Remote preparation of arbitrary two- and three-qubit states. EPL 2009, 87, 30006. [Google Scholar]
- Liu, J.M.; Feng, X.L.; Oh, C.H. Remote preparation of a three-particle state via positive operator-valued measurement. J. Phys. B 2009, 42, 055508. [Google Scholar]
- Wang, D.; Liu, Y.M.; Zhang, Z.J. Remote preparation of a class of three-qubit states. Opt. Commun 2008, 281, 871–875. [Google Scholar]
- Dai, H.Y.; Chen, P.X.; Liang, L.M.; Li, C.Z. Classical communication cost and remote preparation of the four- particle GHZ class state. Phys. Lett. A 2006, 355, 285–288. [Google Scholar]
- Dai, H.Y.; Chen, P.X.; Zhang, M.; Li, C.Z. Remote preparation of an entangled two-qubit state with three parties. Chin. Phys. B 2008, 17, 27–33. [Google Scholar]
- Yan, F.L.; Zhang, G.H. Remote preparation of the two-particle state. Int. J. Quantum Inf 2008, 6, 485–491. [Google Scholar]
- Paris, M.G.A.; Cola, M.; Bonifacio, R. Remote state preparation and teleportation in phase space. J. Opt. B 2003, 5, S360. [Google Scholar]
- Kurucz, Z.; Adam, P.; Kis, Z.; Janszky, J. Continuous variable remote state preparation. Phys. Rev. A 2005, 72, 052315. [Google Scholar]
- Peng, X.H.; Zhu, X.W.; Fang, X.M.; Feng, M.; Liu, M.L.; Gao, K.L. Experimental implementation of remote state preparation by nuclear magnetic resonance. Phys. Lett. A 2003, 306, 271–276. [Google Scholar]
- Xiang, G.Y.; Li, J.; Yu, B.; Guo, G.C. Remote preparation of mixed states via noisy entanglement. Phys. Rev. A 2005, 72, 012315. [Google Scholar]
- Peters, N.A.; Barreiro, J.T.; Goggin, M.E.; Wei, T.C.; Kwiat, P.G. Remote State Preparation: Arbitrary Remote Control of Photon Polarization. Phys. Rev. Lett. 2005, 94, 150502. [Google Scholar]
- Mikami, H.; Kobayashi, T. Remote preparation of qutrit states with biphotons. Phys. Rev. A 2007, 75, 022325. [Google Scholar]
- Jeffrey, E.; Peters, N.A.; Kwiat, P.G. Towards a periodic deterministic source of arbitrary single-photon states. New J. Phys. 2004, 6. [Google Scholar] [CrossRef]
- Liu, W.T.; Wu, W.; Ou, B.Q.; Chen, P.X.; Li, C.Z.; Yuan, J.M. Experimental remote preparation of arbitrary photon polarization states. Phys. Rev. A 2007, 76, 022308. [Google Scholar]
- Wu, W.; Liu, W.T.; Ou, B.Q.; Chen, P.X.; Li, C.Z. Remote state preparation with classically correlated state. Opt. Commun 2008, 281, 1751–1754. [Google Scholar]
- Barreiro, J.T.; Wei, T.C.; Kwiat, P.G. Remote Preparation of Single-Photon "Hybrid" Entangled and Vector-Polarization States. Phys. Rev. Lett. 2010, 105, 030407. [Google Scholar]
- Rådmark, M.; Wieśniak, M.; Zukowski, M.; Bourennane, M. Experimental multilocation remote state preparation. Phys. Rev. A 2013, 88, 032304. [Google Scholar]
- Liu, J.M.; Feng, X.L.; Oh, C.H. Remote preparation of arbitrary two- and three-qubit states. EPL 2009, 87, 30006. [Google Scholar]
- Chen, X.B.; Ma, S.Y.; Su, Y.; Zhang, R.; Yang, Y.X. Controlled remote state preparation of arbitrary two and three qubit states via the Brown state. Quantum Inf. Process 2012, 11, 1653–1667. [Google Scholar]
- Ma, S.Y.; Luo, M.X. Efficient remote preparation of arbitrary two- and three-qubit states via the chi state. Chin. Phys. B 2014, 23, 090308. [Google Scholar]
- Zhan, Y.B. Deterministic remote preparation of arbitrary two- and three-qubit states. EPL 2012, 98, 40005. [Google Scholar]
- Cabello, A. Quantum Key Distribution in the Holevo Limit. Phys. Rev. Lett. 2000, 85, 5635. [Google Scholar]
| ijrs | Ijrs | Ijrs | Ijrs | ||||
|---|---|---|---|---|---|---|---|
| 0000 | I3I6 | 0100 | 1000 | 1100 | |||
| 0001 | 0101 | 1001 | 1101 | ||||
| 0010 | 0110 | 1010 | 1110 | ||||
| 0011 | 0111 | 1011 | 1111 |
| Protocols | Entanglements employed | Quantum operations | CIC | TSP | Γ | |
|---|---|---|---|---|---|---|
| Two-qubit case | [55] | two 2-qubit EPR | one TQPM | 2 | 8.33% | |
| [56] | five-qubit BS | one TQPM and one SQPM | 3 | 12.5% | ||
| [57] | five-qubit χ-state | one TEQPM | 3 | 12.5% | ||
| Our scheme | two 3-qubit GHZ | one TQPM and two SQPM | 4 | 1 | 20% | |
| Three-qubit case | [55] | three 2-qubit EPR | one TEQPM | 3 | 8.33% | |
| [56] | five-qubit BS and EPR | one TEQPM and one SQPM | 4 | 13.64% | ||
| [57] | four-qubit χ-state and GHZ | one FQPM | 4 | 13.64% | ||
| Our scheme | three GHZ | one TEQPM and two SQPM | 6 | 1 | 20% | |
| ijkrst | ijkrst | ijkrst | ijkrst | ||||
|---|---|---|---|---|---|---|---|
| 000000 | I3I6I9 | 010000 | 100000 | 110000 | |||
| 000001 | 010001 | 100001 | 110001 | ||||
| 000010 | 010010 | 100010 | 110010 | ||||
| 000011 | 010011 | 100011 | 110011 | ||||
| 000100 | 010100 | 100100 | 110100 | ||||
| 000101 | 010101 | 100101 | 110101 | ||||
| 000110 | 010110 | 100110 | 110110 | ||||
| 000111 | 010111 | 100111 | 110111 | ||||
| 001000 | 011000 | 101000 | 111000 | ||||
| 001001 | 011001 | 101001 | 111001 | ||||
| 001010 | 011010 | 101010 | 111010 | ||||
| 001011 | 011011 | 101011 | 111011 | ||||
| 001100 | 011100 | 101100 | 111100 | ||||
| 001101 | 011101 | 101101 | 111101 | ||||
| 001110 | 011110 | 101110 | 111110 | ||||
| 001111 | 011111 | 101111 | 111111 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Hoehn, R.D.; Ye, L.; Kais, S. Generalized Remote Preparation of Arbitrary m-qubit Entangled States via Genuine Entanglements. Entropy 2015, 17, 1755-1774. https://doi.org/10.3390/e17041755
Wang D, Hoehn RD, Ye L, Kais S. Generalized Remote Preparation of Arbitrary m-qubit Entangled States via Genuine Entanglements. Entropy. 2015; 17(4):1755-1774. https://doi.org/10.3390/e17041755
Chicago/Turabian StyleWang, Dong, Ross D. Hoehn, Liu Ye, and Sabre Kais. 2015. "Generalized Remote Preparation of Arbitrary m-qubit Entangled States via Genuine Entanglements" Entropy 17, no. 4: 1755-1774. https://doi.org/10.3390/e17041755
APA StyleWang, D., Hoehn, R. D., Ye, L., & Kais, S. (2015). Generalized Remote Preparation of Arbitrary m-qubit Entangled States via Genuine Entanglements. Entropy, 17(4), 1755-1774. https://doi.org/10.3390/e17041755







