1. Introduction
The emerging trend of cooperation among selfish individuals, which seem to prefer defection, has stimulated interest from researchers in the fields of biology and social science. Among all of the forms of games that demonstrate the evolution of cooperation, the prisoners’ dilemma (PD) has drawn continuous attention since it was first formalized by Tucker [
1]. Since then, various mechanisms aiming at helping to incentivize cooperative behavior have been proposed to investigate the PD game [
2–
7].
In the original PD game, each player can choose to be a cooperator (C) or a defector (D) simultaneously. If cooperators face defectors, former players get a payoff T (temptation to defect), while the latter only get payoff S (sucker’s payoff). Mutual cooperation makes both players get the payoff R (reward for mutual cooperation), and mutual defection gives every player the payoff P (punishment for mutual defection). To be considered as a prisoner's dilemma game, the payoffs must satisfy the conditions: T > R > P > S and 2R > (T + S). The condition R > P implies that mutual cooperation yields higher payoff than mutual defection, while T > R and P > S imply that each player will get higher payoff if he or she chooses to be a defector, regardless of what choice the opponent makes in a single round of the game. Besides that, we also require 2R > (T + S), because if the condition did not hold, cooperation would be eliminated, because players would be able to gain more by alternatively exploiting each other rather than cooperating.
Inspired by the idea that voluntary participation in public good games turned out to be a simple, but effective way to prevent the tragedy of the commons [
8], Szabó and Hauert [
9] introduced voluntary participation to the prisoner’s dilemma game and named it the voluntary prisoner’s dilemma (VPD) game in 2002. The VPD game presented by them can be briefly described as follows: “Apart from cooperators and defectors, a third type of strategy, the loner (L), is considered: the risk-averse loners who are unwilling to participate in the game and rather rely on small but fixed earnings.” Then, the payoff matrix of the voluntary prisoner’s dilemma game can be depicted as follows [
9]:
In the VPD game, the parameter R is set to be one and T is set to be b, which satisfy 1 ≤ b ≤ 2. However, slightly different from the traditional PD game, P and S are equal and set to be zero. In addition, the loners will get a fixed payoff σ in any situation with the condition 0 < σ < 1, which can guarantee that loners perform better than two defectors, but are worse off than two cooperators. Obviously, (L, L), (D, L), (L, D) are the Nash equilibriums of the single-shot VPD game; only (L, L) is the unique symmetric Nash equilibrium, but not an evolutionarily-stable strategy (ESS). In the evolutionary VPD game, the three strategies can coexist through cyclic dominance (D invades C invades L invades D), which efficiently prevents the system from getting into a frozen state.
Since then, the VPD game has attracted numerous researchers to extensively research the theory. With exploring the effect of partially random partnership on the measure of cooperation in a society where the pairwise interaction between members is approximated by the VPD game, Szabó and Vukov found that the exploiting strategy (defector) benefits from the increase of randomness in the partnership for the VPD game [
10]. Lei explored the impact of aspiration on the VPD game via a selection parameter ω and discovered that the positive impact of preferential selection is suppressed by the voluntary strategy in prisoner’s dilemma [
11]. Wu
et al. studied the spatial prisoner’s dilemma game with voluntary participation in Newman–Watts small-world networks with the addition of some reasonable variables and drew a conclusion that in the case of a very low temptation to defect, agents are willing to participate in the game and in the typical small-world region, whereas intensive collective oscillations arise in more random regions [
12]. Chen
et al. made simulations for the VPD game on regular lattices and scale-free networks, and the results indicated that system behavior is sensitive to the population structure [
13].
In summary, existing studies have investigated the effect that the value of b (temptation to defect), the value of selection parameter ω, the spatial structure of local interaction and other factors have on the VPD game. However, the inherent cyclic dominance of the strategies (D invades C invades L invades D) results in periodic oscillations in well-mixed populations. Therefore, the difference of evolutionary dynamics, the level of rationality of individuals in the dynamics and the size of a population also will have great influence on the evolutionary equilibrium of the VPD game. Thus, this paper will pay attention to making a comparison between several results of the evolutionary VPD game based on different kinds of deterministic and stochastic evolutionary dynamics.
As previously determined, there are already a variety of deterministic dynamics that have been proposed to study the evolutionary game, such as the replicator dynamic, the Smith dynamic, the Brown-von Neumann-Nash (BNN) dynamic, the best response (BR) dynamic,
etc. [
14,
15]. Among them, the replicator dynamic, which was put forward by Taylor and Jonker in 1978 [
16], is the most widely applied one among all evolutionary dynamics. The Smith dynamic is a dynamic model used by Maynard Smith [
17] to investigate traffic assignment in 1984. The BNN had been considered earlier by Brown and von Neumann when they studied the zero-sum game and proved global convergence to the set of equilibrium in 1950 [
18]. The BR was proposed under the assumption of rational individuals by Gilboa and Matsui in 1991 [
19].
Going forward, if we assume a population of finite size, where the random fluctuations, due to, for instance, sampling effects, have to be taken into account, we can no longer rely on deterministic models. Thus, we must employ the stochastic process rather than ordinary differential equations to investigate the evolutionary game in a finite population consisting of bounded rational individuals.
As a birth-death process, the Moran process is a simple stochastic process employed to investigate evolutionary game dynamics. The selection dynamics of the game with N players can be formulated as a Moran process [
20] with frequency-dependent fitness. The process has two absorbing states,
i = 0 and
i = N,
i.e., if the population has reached either one of these states, then it will stay there forever. Nowak
et al. [
21] found that apart from the payoff matrix, population size also plays an important role in evolutionary game dynamics. In the two-strategy game, there are eight selection scenarios, and the selection scenario can change as a function of population size N. The selection scenarios will converge into one of the three generic selection scenarios of the deterministic replicator dynamics when the population size approaches infinity. Later, Imhof and Nowak [
22] further studied the evolutionary game based on the Wright–Fisher process, which can describe a biological population with discrete generations instead of assuming overlapping generations, as the Moran process does, and obtain the famous 1/3 law in the limit of weak selection. Furthermore, Antal
et al. [
23] focused on stochastic properties of fixation in two strategies games under stochastic evolutionary dynamics and concluded that the time of fixation is identical for both strategies in any particular game. They also discussed the asymptotic behavior of the fixation time and fixation probabilities in the large population size limit. The general conclusion is that if there is at least one pure evolutionarily-stable strategy (ESS) in the infinite population size limit, fixation is fast, while if the ESS is the coexistence of the two strategies, fixation will be slow.
To investigate learning behavior in the evolutionary game, Kandori [
24] firstly introduced the Markov process model to describe the learning dynamics in evolutionary games. Particularly, Tadj and Touzene [
25] proposed the state-dependent quasi birth and death (QBD) process model to describe the learning dynamics for more complicated models, including for games with three strategies.
For games with more than two strategies, the dynamics become much more complex, even in the deterministic model. We will therefore introduce the five classic evolutionary dynamics to study the VPD game, including the replicator dynamic, the Smith dynamic, the BNN dynamic, the BR dynamic and the QBD stochastic dynamics. Furthermore, we will go on to investigate the evolutionary VPD game under the four kinds of classic deterministic dynamics, as well as the QBD stochastic dynamic, in order to discuss the different results arising from these different evolutionary dynamics.
2. Method
Assume an evolutionary VPD game in a population consisting of N individuals; let
xi be the frequency of strategy
i. Thus, the state of the population is given by
. Then,
Fi(
x) is the expected payoff for an individual of strategy
i, and
is the average payoff in the population state
x. Therefore,
In order to investigate the effect of parameter σ on the results of the simulations, we will set three different values of σ, which are 0.2, 0.4 and 0.6, in every respective dynamic, while modeling the dynamics under the same conditions, such as the initial conditions, durations and noise, to make a clear comparison between these dynamics in evolution.
2.1. The Replicator Dynamic for the Evolutionary VPD Game
The replicator dynamic, which was put forward by Taylor and Jonker in 1978 [
16], is the most widely applied among all evolutionary dynamics. The game has been developed to study the dynamics of many complex systems, which even include inhomogeneous communities [
26]. The original equation is denoted by:
Thus, in the VPD game, denote the three strategies D, C, L with 1, 2, 3. Then, we can define the evolutionary VPD game under the replicator dynamic as follows:
The replicator dynamic just requires that players know the payoff of the chosen strategies of the population in that moment well; there is no need to get information about the other strategies. Whether strategy i will be chosen in the next instant or not depends on the frequency rather, than the payoff of it in this instant, which means a certain strategy will not be chosen anymore if it is not adopted in this instant. Consequently, the replicator dynamic indeed is an imitation based on the experiences of players and does not require players to be rational.
2.2. The Smith Dynamic for the Evolutionary VPD Game
The Smith dynamic is a dynamic model used by Maynard Smith to investigate traffic assignment in 1984 [
17]. The equation is:
Here,
. Then, we can define the Smith dynamic in the VPD game as follows:
Under this dynamic, when, and only when, the payoff of an alternative strategy is greater than the current one will players switch to the alternative strategy with an increased positive possibility, which is proportional to the difference between their payoffs. It only requires the knowledge of the payoffs of both alternatives and current strategies, which can be obtained from the players’ own experiences or communication with other players.
2.3. The BNN Dynamic for the Evolutionary VPD Game
The BNN was considered earlier by Brown and von Neumann when they studied the zero-sum game and proved global convergence to the set of equilibrium in 1950 [
18]. It is therefore defined as:
Here,
. Additionally, in 1951, Nash used the BNN dynamic to prove the existence of equilibrium [
27]. The BNN dynamic requires players to be aware of the current strategy’s payoff and the average payoff of all available strategies. To get information about the above, players should be in a higher level of rationality.
2.4. The BR Dynamic for the Evolutionary VPD Game
The BR was proposed by Gilboa and Matsui in 1991 [
19] and is defined as:
That means that players should be rational enough to determine the state of the current population and to respond optimally. Specifically, under the BR dynamic, players should grasp information about the payoffs of all available strategies and then make the best response to the current population state. That means that the players need to be rational agents and have the ability to imitate quickly.
2.5. The QBD Stochastic Dynamic for the Evolutionary VPD Game
In the QBD stochastic dynamic, suppose that the general VPD games are repeatedly played between individuals in a finite population with a size of
N, and a stochastic process can be defined as follows: the state at time
t is a two-dimensional stochastic variable
, where
are the number of players in the population who choose Strategies D and C, while the number of players in the population who choose Strategy L is
. Hence, the profile and the average payoffs of players can be decided by
and
at time
t. Then, the average payoff of a player choosing strategy
i will be
, where
. Therefore,
Next, let us assume
ω1(
t) =
i and
ω2(
t) =
j; then, the individuals in the population will switch from strategy
l to strategy
k (
l,
k =1,2,3;
l ≠
k) with rate:
and
, where
is defined for an arbitrary real function
f.
We can then describe the QBD process for the VPD game, which can be viewed as a two-dimensional Markov process defined on the state space, as follows: the individuals choosing the strategy l in the population will switch to strategy k with rate
, if
, and the transition rate will be 0, if the number of individuals adopting the same strategy in the population reach N, the size of population.
3. Results and Analysis
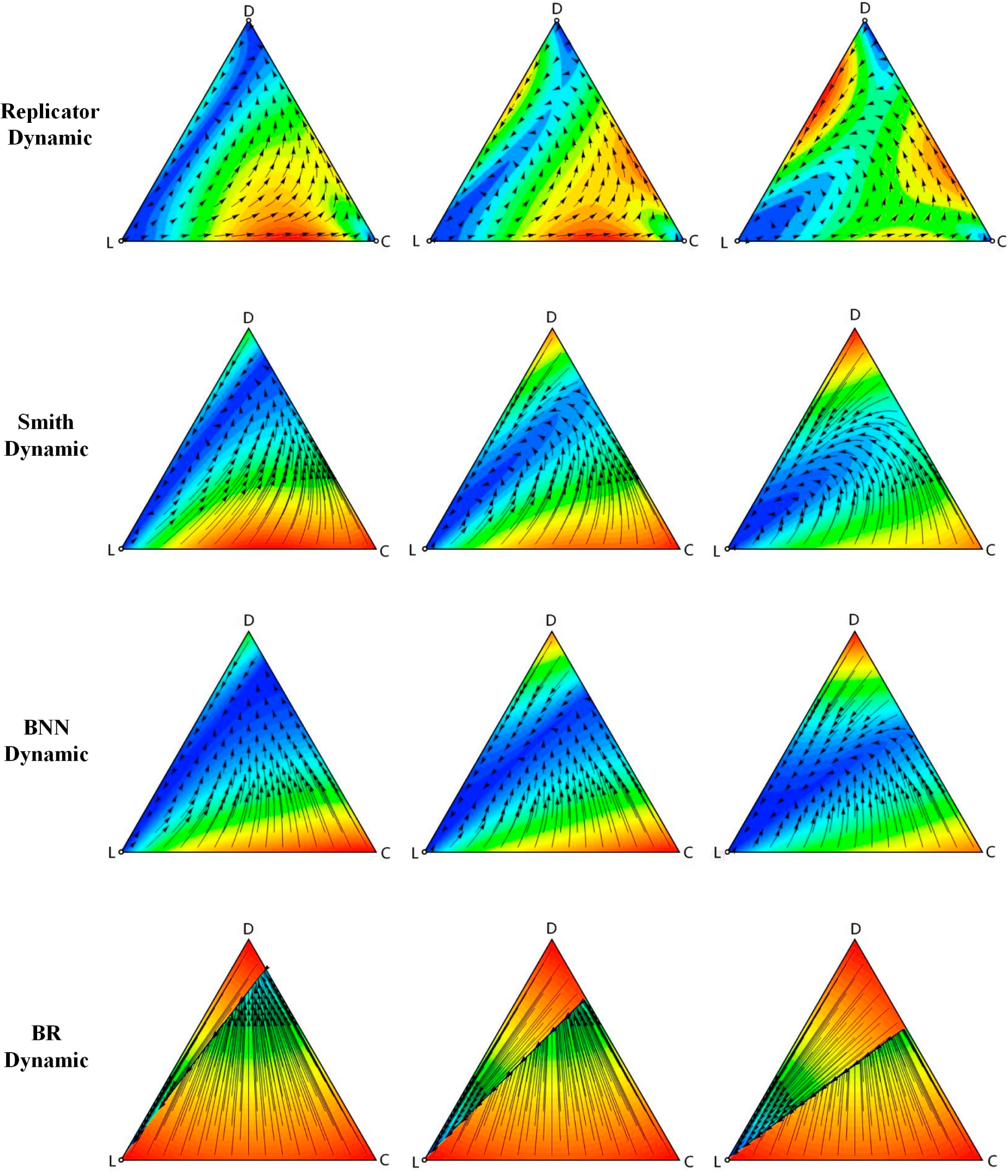
In this section, the simulation results of the four deterministic dynamics and stochastic dynamic were demonstrated. First, the VPD game under different deterministic dynamics was simulated by Dynamo software [
28], and the phase diagrams are mapped out in
Figure 1.
The simulation results showed that there are three unstable rest points under the replicator dynamic. From the solution trajectories with three different σ values, it could be concluded that with larger σ, the points near D move towards L more quickly, and the points near C move towards D slowly.
Figure 1 also shows the simulation results of the Smith dynamic with three different σ. Similar to the simulations of the replicator dynamic, they also have no stable rest points and only have a unique unstable rest point (0, 0, 1), which is the Nash equilibrium of the VPD game. When σ is smaller, such as 0.2 or 0.4, the points near (0, 1, 0) move towards D quickly, while the points near (1, 0, 0) move towards the unstable rest point L slowly. However, as σ increases, all points move towards L. The movement of those points far away from L is faster compared to the other ones.
The characteristics in the BNN dynamic are analogous to those in the Smith dynamic. The simulations have a similarly unstable rest point, which is the Nash equilibrium. The solution trajectories are also analogous. All points of the game in the BNN dynamic have a slower speed of movement than that in the Smith dynamic.
As for the BR dynamic, the properties of the rest points are similar to those in the BNN dynamic and Smith dynamic, while the solution trajectories are obviously different. There seems to exist a split line from (0, 0, 1) to one point on the line between C and D that divides the whole region into two parts. The points above the split line will move along the line, and the points below the split line will move towards it. Comparing the phase diagrams, we can see that when σ increases, the right endpoint of divide will shift down along the C-D line.
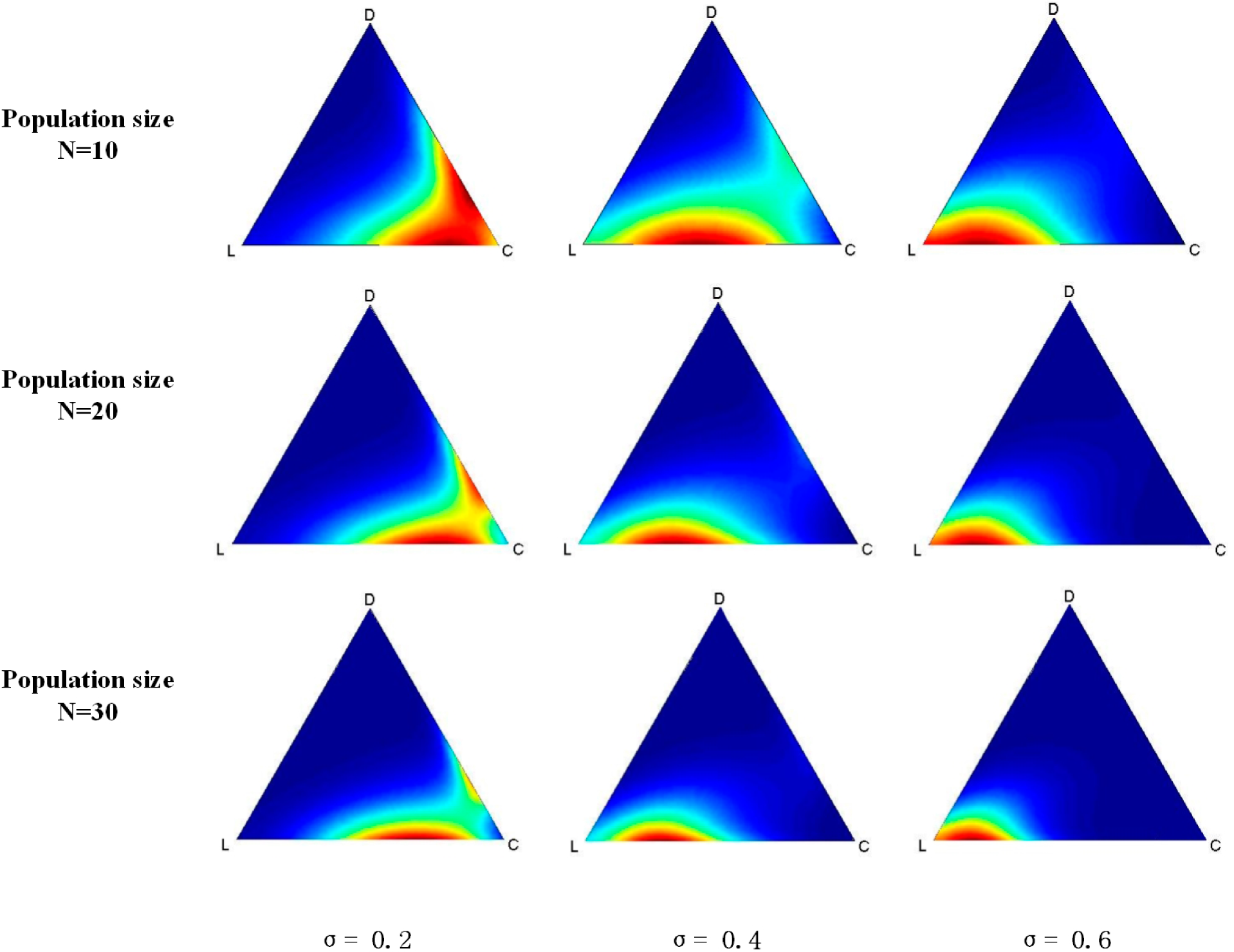
Finally, we simulate the evolutionary VPD game under the QBD process by coding a program and running it on MATLAB 7. The simulation results are shown in
Figure 2. Generally, the red region is where points with a higher probability of being in the stable state move towards L along with the increasing of σ regardless of the size of the population. When σ is 0.2, which represents a low fixed payoff of L, a red region appears at the bottom zone near C, as shown in
Figure 2. The red region will move towards L when σ gets larger.
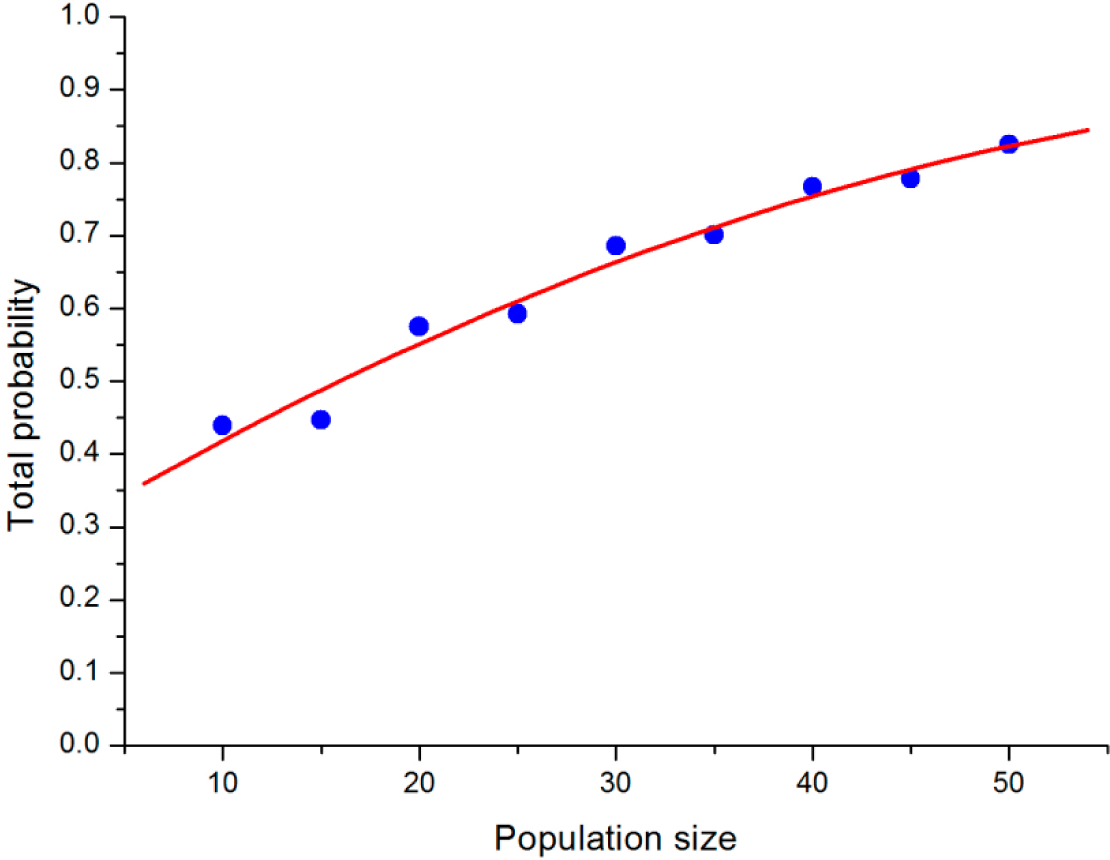
To analyze how the population size will influence the stochastic evolutionary game dynamic, we compared the results under different population sizes, but the same b and σ. After obtaining the limiting distribution of the QBD process for the VPD game with b = 1.5, σ = 0.6, we can define the “main region” of the stable states in the simplex, which contains points in the simplex around L within a radius of 0.3. The total probability of points in the main region represents the concentration trend of the stable state of QBD. From
Figure 3, it is interesting to discover that the total probability of the points in the main region increases along with the increase in population size. When N increases to 50, the total probability of the region climbs to over 0.8. We can infer that the stable states may ultimately converge into the strategy “loner” if the population size is big enough.
4. Conclusions
In this paper, we have investigated the influence of the level of individual rationality and the size of a population on the evolutionary dynamics of the VPD game. Then, the five evolutionary dynamics, such as the replicator dynamic, the Smith dynamic, the BNN dynamic, the BR dynamic and the QBD stochastic process, for the evolutionary VPD game were modeled and simulated.
Simulation results first show that with the increase of σ, the homogenous loner is more likely to be in a stable state in the VPD game regardless of the dynamic. Specifically, under all of the four mentioned deterministic dynamics, L is the rest point of them. Moreover, under stochastic dynamics, the loners have a very high probability to be in a stable state.
Secondly, although the three strategies in the VPD game can coexist by cyclic dominance (D invades C invades L invades D), which efficiently prevents the system from getting into a frozen state, the different speeds of dynamics in the cycle appeared to vary under different evolutionary dynamics. In fact, the speed of the replicator dynamic is the slowest among these four deterministic dynamics, and the speed of the BR dynamic is the highest. This may be attributed to the rationality degree of the individuals in the population, because the individuals in the BR dynamic are supposed to be in complete rationality in the evolution, but the replicator dynamic does not have any rationality assumptions. Therefore, we can conclude that a more rapid evolution will occur in a more rational population.
Finally, when studying the simulation results under the QBD process, we can conclude that as the size of the population increases, the red region in the simplex will be more concentrated, which indicates that the randomness of this model becomes weaker. Thus, we expect that when the size of the population tends to infinity, the limited distribution of the QBD process will be in accordance with the results in the deterministic dynamics.
After Nowak and May originally announced that the spatial structure of populations can induce the emergence of cooperation [
29,
30], many studies explored the spatial prisoner’s dilemma game on a variety of networks, including regular lattices, random regular graphs, random networks with a fixed mean degree distribution, small-world networks and real-world acquaintance networks [
31–
35]. Then, the spatial prisoner’s dilemma game with volunteering was investigated for several random networks by Szabó and Vukov [
10], and the effects of cyclic dominance for other three-strategy games were also investigated on different networks. In fact, not only evolutionary dynamics are strongly affected by population structure, but population structure also will be affected by evolutionary dynamics. Therefore, future research will focus on investigating the co-evolutionary of the population structure and dynamics for the VPD game based on evolutionary set theory or the hyper-network method [
36].