Quantropy

Abstract

There is a well-known analogy between statistical and quantum mechanics. In statistical mechanics, Boltzmann realized that the probability for a system in thermal equilibrium to occupy a given state is proportional to exp(−E/kT ), where E is the energy of that state. In quantum mechanics, Feynman realized that the amplitude for a system to undergo a given history is proportional to exp(−S/iħ), where S is the action of that history. In statistical mechanics, we can recover Boltzmann’s formula by maximizing entropy subject to a constraint on the expected energy. This raises the question: what is the quantum mechanical analogue of entropy? We give a formula for this quantity, which we call “quantropy”. We recover Feynman’s formula from assuming that histories have complex amplitudes, that these amplitudes sum to one and that the amplitudes give a stationary point of quantropy subject to a constraint on the expected action. Alternatively, we can assume the amplitudes sum to one and that they give a stationary point of a quantity that we call “free action”, which is analogous to free energy in statistical mechanics. We compute the quantropy, expected action and free action for a free particle and draw some conclusions from the results.

1. Introduction

There is a famous analogy between statistical mechanics and quantum mechanics. In statistical mechanics, a system can be in any state, but its probability of being in a state with energy E is proportional to exp(−E/T ), where T is the temperature in units where Boltzmann’s constant is one. In quantum mechanics, a system can move along any path, but its amplitude for moving along a path with action S is proportional to exp(−S/iħ), where ħ is Planck’s constant. Therefore, we have an analogy, where making the replacements:

$$\begin{array}{l}E\mapsto S\\ T\mapsto i\mathit{\hslash }\end{array}$$

formally turns the probabilities for states in statistical mechanics into the amplitudes for paths, or “histories”, in quantum mechanics. In statistical mechanics, the strength of thermal fluctuations is governed by T. In quantum mechanics, the strength of quantum fluctuations is governed by ħ.

In statistical mechanics, the probabilities exp(−E/T ) arise naturally from maximizing entropy subject to a constraint on the expected value of energy. Following the analogy, we might guess that the amplitudes exp(−S/iħ) arise from maximizing some quantity subject to a constraint on the expected value of action. This quantity deserves a name, so let us tentatively call it “quantropy”.

In fact, Lisi [5] and Munkhammar [7] have already treated quantum systems as interacting with a “heat bath” of action and sought to derive quantum mechanics from a principle of maximum entropy with amplitudes (or as they prefer to put it, complex probabilities) replacing probabilities. However, seeking to derive amplitudes for paths in quantum mechanics from a maximum principle is not quite correct. Quantum mechanics is rife with complex numbers, and it makes no sense to maximize a complex function. However, a complex function can still have stationary points, where its first derivative vanishes. Therefore, a less naive program is to derive the amplitudes in quantum mechanics from a “principle of stationary quantropy”. We do this for a class of discrete systems and then illustrate the idea with the example of a free particle, discretizing both space and time.

Carrying this out rigorously is not completely trivial. In the simplest case, entropy is defined as a sum involving logarithms. Moving to quantropy, each term in the sum involves a logarithm of a complex number. Making each term well defined requires a choice of branch cut; it is not immediately clear that we can do this and obtain a differentiable function as the result. Additional complications arise when we consider the continuum limit of the free particle. Our treatment handles all these issues.

We begin by reviewing the main variational principles in physics and pointing out the conceptual gap that quantropy fills. In Section 2, we introduce quantropy along with two related quantities: the free action and the expected action. In Section 3, we develop tools for computing all of these quantities. In Section 4, we illustrate our methods with the example of a free particle, and address some of the conceptual questions raised by our results. We conclude by mentioning some open issues in Section 5.

1.1. Statics

Static systems at temperature zero obey the principle of minimum energy. In classical mechanics, energy is often the sum of kinetic and potential energy:

$$E=K+V$$

where the potential energy V depends only on the system’s position, while the kinetic energy K also depends on its velocity. Often, though not always, the kinetic energy has a minimum at velocity zero. In classical mechanics, this lets us minimize energy in a two-step way. First, we minimize K by setting the velocity to zero. Then, we minimize V as a function of position.

While familiar, this is actually somewhat noteworthy. Usually, minimizing the sum of two things involves an interesting tradeoff. In quantum physics, a tradeoff really is required, thanks to the uncertainty principle. We cannot know the position and velocity of a particle simultaneously, so we cannot simultaneously minimize potential and kinetic energy. This makes minimizing their sum much more interesting. However, in classical mechanics, in situations where K has a minimum at velocity zero statics at temperature zero is governed by a principle of minimum potential energy.

The study of static systems at nonzero temperature deserves to be called “thermostatics”, though it is usually called “equilibrium thermodynamics”. In classical or quantum equilibrium thermodynamics at any fixed temperature, a system is governed by the principle of minimum free energy. Instead of our system occupying a single definite state, it will have different probabilities of occupying different states, and these probabilities will be chosen to minimize the free energy:

$$F=\langle E\rangle -\mathit{TS}.$$

Here, 〈E〉 is the expected energy, T is the temperature and S is the entropy. Note that the principle of minimum free energy reduces to the principle of minimum energy when T = 0.

Where does the principle of minimum free energy come from? One answer is that free energy F is the amount of “useful” energy: the expected energy 〈E〉 minus the amount in the form of heat, TS. For some reason, systems in equilibrium minimize this.

Boltzmann and Gibbs gave a deeper answer in terms of entropy. Suppose that our system has some space of states X and that the energy of the state x ∈ X is E(x). Suppose that X is a measure space with some measure dx, and assume that we can describe the equilibrium state using a probability distribution, a function p: X → [0, ∞) with:

$${\displaystyle {\int }_{X}p}(x)\mathit{dx}=1.$$

Then, the entropy is:

$$S=-{\displaystyle {\int }_{X}p(x)\ln p(x)\mathit{dx}}$$

while the expected value of the energy is:

$$\langle E\rangle ={\displaystyle {\int }_{X}E}(x)p(x)\mathit{dx}.$$

Now, suppose our system maximizes entropy subject to a constraint on the expected value of energy. Using the method of Lagrange multipliers, this is the same as maximizing S − β〈E〉, where β is a Lagrange multiplier. When we maximize this, we see the system chooses a Boltzmann distribution:

$$p(x)=\frac{\exp (-\beta E(x))}{{\displaystyle {\int }_X\exp (-\beta E(x))}}.$$

One could call β the “coolness”, since working in units where Boltzmann’s constant equals one is just the reciprocal of the temperature. Therefore, when the temperature is positive, maximizing S − β〈E〉 is the same as minimizing the free energy:

$$F=\langle E\rangle -\mathit{TS}.$$

In summary, every minimum or maximum principle in statics can be seen as a special case or a limiting case of the principle of maximum entropy, as long as we admit that sometimes we need to maximize entropy subject to constraints. This is quite satisfying, because as noted by Jaynes, the principle of maximum entropy is a general principle for reasoning in situations of partial ignorance [4]. Therefore, we have a kind of “logical” explanation for the laws of statics.

1.2. Dynamics

Now, suppose things are changing as time passes, so we are doing dynamics instead of statics. In classical mechanics, we can imagine a system tracing out a path q(t) as time passes from t = t₀ to t = t₁. The action of this path is often the integral of the kinetic minus potential energy:

$$A(q)={\displaystyle {\int }_{t_0}^{t_1}(K(t)-V(t))\mathit{dt}}$$

where K(t) and V (t) depend on the path q. To keep things from getting any more confusing than necessary, we are calling action A instead of the more usual S, since we are already using S for entropy.

The principle of least action says that if we fix the endpoints of this path, that is the points q(t₀) and q(t₁), the system will follow the path that minimizes the action subject to these constraints. This is a powerful idea in classical mechanics. However, in fact, sometimes, the system merely chooses a stationary point of the action. The Euler–Lagrange equations can be derived just from this assumption. Therefore, it is better to speak of the principle of stationary action.

This principle governs classical dynamics. To generalize it to quantum dynamics, Feynman [2] proposed that instead of our system following a single definite path, it can follow any path, with an amplitude a(q) of following the path q. He proposed this formula for the amplitude:

$$a(q)=\frac{\exp (iA(q)/\mathit{\hslash })}{{\displaystyle \int \exp }(iA(q)/\mathit{\hslash })dq}$$

where ħ is Planck’s constant. He showed, in a nonrigorous but convincing way, that when we integrate a(q) over all paths starting at a point x₀ at time t₀ and ending at a point x₁ at time t₁, we obtain a result proportional to the amplitude for a particle to go from the first point to the second. He also gave a heuristic argument showing that as ħ → 0, this prescription reduces to the principle of stationary action.

Unfortunately, the integral over all paths is hard to make rigorous, except in certain special cases. This is a bit of a distraction for our discussion now, so let us talk more abstractly about “histories” instead of paths and consider a system whose possible histories form some space X with a measure dx. We will look at an example later.

Suppose the action of the history x ∈ X is A(x). Then, Feynman’s sum over histories formulation of quantum mechanics says the amplitude of the history x is:

$$a(x)=\frac{\exp (iA(x)/\mathit{\hslash })}{{\displaystyle {\int }_X\exp }(iA(x)/\mathit{\hslash })}.$$

This looks very much like the Boltzmann distribution:

$$p(x)=\frac{\exp (-E(x)/T)}{{\displaystyle {\int }_X\exp }(-E(x)/T)}.$$

Indeed, the only serious difference is that we are taking the exponential of an imaginary quantity instead of a real one. This suggests deriving Feynman’s formula from a stationary principle, just as we can derive the Boltzmann distribution by maximizing entropy subject to a constraint. This is where quantropy enters the picture.

2. Quantropy

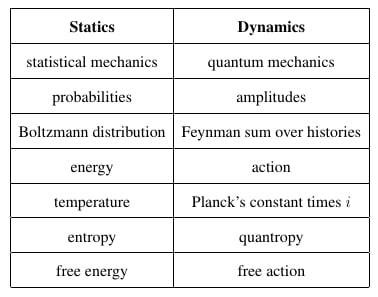
We have described statics and dynamics and a well-known analogy between them. However, we have seen that there are some missing items in the analogy:

Statics	Dynamics
statistical mechanics	quantum mechanics
probabilities	amplitudes
Boltzmann distribution	Feynman sum over histories
energy	action
temperature	Planck’s constant times i
entropy	???
free energy	???

Statics	Dynamics
statistical mechanics	quantum mechanics
probabilities	amplitudes
Boltzmann distribution	Feynman sum over histories
energy	action
temperature	Planck’s constant times i
entropy	???
free energy	???

Our goal now is to fill in the missing entries in this chart. Since the Boltzmann distribution:

$$p(x)=\frac{\exp (-E(x)/T)}{{\displaystyle {\int }_X\exp }(-E(x)/T)\mathit{dx}}$$

comes from the principle of maximum entropy, one might hope Feynman’s sum over histories formulation of quantum mechanics:

$$a(x)=\frac{\exp (iA(x)/\mathit{\hslash })}{{\displaystyle {\int }_X\exp }(iA(x)/\mathit{\hslash })\mathit{dx}}$$

comes from a maximum principle, as well.

Unfortunately Feynman’s sum over histories involves complex numbers, and it does not make sense to maximize a complex function. So, let us try to derive Feynman’s prescription from a principle of stationary quantropy.

Suppose we have a set of histories, X, equipped with a measure dx. Suppose there is a function a: X → ℂ assigning to each history x ∈ X a complex amplitude a(x). We assume these amplitudes are normalized, so that:

$${\displaystyle {\int }_{X}a(x)\mathit{dx}}=1,$$

since that is what Feynman’s normalization actually achieves. We define the “quantropy” of a by:

$$Q=-{\displaystyle {\int }_{X}a(x)}\ln a(x)\mathit{dx}.$$

One might fear this is ill-defined when a(x) = 0, but that is not the worst problem; in the study of entropy, we typically set 0 ln 0 = 0. The more important problem is that the logarithm has different branches: we can add any multiple of 2πi to our logarithm and get another equally good logarithm. To deal with this, let us suppose that as we vary the numbers a(x), they do not go through zero. In the end, a(x) will be defined in terms of the exponential of the action, so it will be nonzero. If we only vary it slightly, it will remain nonzero, so we can choose a specific logarithm ln(a(x)) for each number a(x), which varies smoothly as a function of a(x).

To formalize this, we could treat quantropy as depending not on the amplitudes a(x), but on some function b: X → ℂ, such that exp(b(x)) = a(x). In this approach, we require:

$${\displaystyle {\int }_X{e}^{b(x)}}\mathit{dx}=1,$$

and define the quantropy by:

$$Q=-{\displaystyle {\int }_X{e}^{b(x)}}b(x)\mathit{dx}.$$

Then, the problem of choosing branches for the logarithm does not come up. However, we shall take the informal approach where we express quantropy in terms of amplitudes and choose a specific branch for ln a(x), as described above.

Next, let us seek amplitudes a(x) that give a stationary point of the quantropy Q subject to a constraint on the “expected action”:

$$\langle A\rangle ={\displaystyle {\int }_{X}A(x)a(x)\mathit{dx}.}$$

The term “expected action” is a bit odd, since the numbers a(x) are amplitudes rather than probabilities. While one could try to justify this term from how expected values are computed in Feynman’s formalism, we are mainly using it because 〈A〉 is analogous to the expected value of the energy, 〈E〉, which we saw earlier.

Let us look for a stationary point of Q subject to a constraint on 〈A〉, say 〈A〉 = α. To do this, one would be inclined to use Lagrange multipliers and to look for a stationary point of:

$$Q-\mathrm{\lambda }\langle A\rangle .$$

However, there is another constraint, namely:

$${\displaystyle {\int }_{X}a}(x)\mathit{dx}=1.$$

Therefore, let us write:

$$\langle 1\rangle ={\displaystyle {\int }_{X}a}(x)\mathit{dx}$$

and look for stationary points of Q subject to the constraints:

$$\begin{array}{cc}\langle A\rangle =\alpha ,& \langle 1\rangle =1.\end{array}$$

To do this, the Lagrange multiplier recipe says we should find stationary points of:

$$Q-\mathrm{\lambda }\langle A\rangle -\mu \langle 1\rangle$$

where λ and μ are Lagrange multipliers. The Lagrange multiplier λ is the more interesting one. It is analogous to the “coolness” β = 1/T, so our analogy chart suggests that we should take:

$$\mathrm{\lambda }=1/i\mathit{\hslash }.$$

We shall see that this is correct. When λ becomes large, our system becomes close to classical, so we call λ the “classicality” of our system.

Following the usual Lagrange multiplier recipe, we seek amplitudes for which:

$$\frac{\partial }{\partial a(x)}(Q-\mathrm{\lambda }\langle A\rangle -\mu \langle 1\rangle )=0$$

holds, along with the constraint equations. We begin by computing the derivatives we need:

$$\begin{array}{l}\frac{\partial Q}{\partial a(x)}=-(1+\ln a(x))\hfill \\ \frac{\partial \langle A\rangle }{\partial a(x)}=A(x)\hfill \\ \frac{\partial \langle 1\rangle }{\partial a(x)}=1.\hfill \end{array}$$

Thus, we need:

$$1+\ln a(x)+\mathrm{\lambda }A(x)+\mu =0$$

or:

$$a(x)=\frac{\exp (-\mathrm{\lambda }A(x))}{\exp (\mu +1)}.$$

The constraint:

$${\displaystyle {\int }_{X}a(x)\mathit{dx}=1}$$

then forces us to choose:

$$\exp (\mu +1)={\displaystyle {\int }_X\exp (-\mathrm{\lambda }A(x))\mathit{dx}}$$

so we have:

$$a(x)=\frac{\exp (-\mathrm{\lambda }A(x))}{{\displaystyle {\int }_X\exp (-\mathrm{\lambda }A(x))\mathit{dx}}}.$$

This is precisely Feynman’s sum over histories’ formulation of quantum mechanics if λ = 1/iħ!

Note that the final answer does two equivalent things in one blow:

• It gives a stationary point of quantropy subject to the constraints that the amplitudes sum to 1 and the expected action takes some fixed value.
• It gives a stationary point of the free action:

  $$\langle A\rangle -i\mathit{\hslash }Q$$

  subject to the constraint that the amplitudes sum to 1.

In case the second point is puzzling, note that the “free action” plays the same role in quantum mechanics that the free energy 〈E〉 − TS plays in statistical mechanics. It completes the analogy chart at the beginning of this section. It is widely used in the effective action approach to quantum field theory, though not under the name “free action”: as we shall see, it is simply –iħ times the logarithm of the partition function.

It is also worth noting that when ħ → 0, the free action reduces to the action. Thus, in this limit, the principle of stationary free action reduces to the principle of stationary action in classical dynamics.

3. Computing Quantropy

In thermodynamics, there is a standard way to compute the entropy of a system in equilibrium starting from its partition function. We can use the same techniques to compute quantropy. It is harder to get the integrals to converge in interesting examples. But we can worry about that later, when we do an example.

First, recall how to compute the entropy of a system in equilibrium starting from its partition function. Let X be the set of states of the system. We assume that X is a measure space and that the system is in a mixed state given by some probability distribution p: X → [0, ∞), where, of course:

$${\displaystyle {\int }_{X}p(x)\mathit{dx}=1.}$$

We assume each state x has some energy E(x) ∈ ℝ. Then, the mixed state maximizing the entropy:

$$S=-{\displaystyle {\int }_{X}p}(x)\ln p(x)\mathit{dx}$$

with a constraint on the expected energy:

$$\langle E\rangle ={\displaystyle {\int }_{X}E}(x)p(x)\mathit{dx}$$

is the Boltzmann distribution:

$$p(x)=\frac{e^{-\beta E(x)}}{Z}$$

for some value of the coolness β, where Z is the partition function:

$$Z={\displaystyle {\int }_X{e}^{-\beta E(x)}}\mathit{dx}.$$

To compute the entropy of the Boltzmann distribution, we can thus take the formula for entropy and substitute the Boltzmann distribution for p(x), getting:

$$\begin{array}{l}S={\displaystyle {\int }_{X}p}(x)(\beta E(x)+\ln Z)\mathit{dx}\\ =\beta \langle E\rangle +\ln Z.\end{array}$$

Reshuffling this, we obtain a formula for the free energy:

$$F=\langle E\rangle -\mathit{TS}=-T\ln Z.$$

Of course, we can also write the free energy in terms of the partition function and β:

$$F=-\frac{1}{\beta }\ln Z.$$

We can do the same for the expected energy:

$$\begin{array}{l}\langle E\rangle ={\displaystyle {\int }_{X}E}(x)p(x)\mathit{dx}\\ =\frac{1}{Z}{\displaystyle {\int }_{X}E}(x)e^{-\beta E(x)}\mathit{dx}\\ =-\frac{1}{Z}\frac{dZ}{d\beta }{\displaystyle {\int }_X{e}^{-\beta E(x)}}\mathit{dx}\\ =-\frac{1}{Z}\frac{dZ}{d\beta }\\ =-\frac{d}{d\beta }\ln Z.\end{array}$$

This, in turn, gives:

$$\begin{array}{l}S=\beta \langle E\rangle +\ln Z\\ =-\beta \frac{d\ln Z}{d\beta }+\ln Z.\end{array}$$

In short, if we know the partition function of a system in thermal equilibrium as a function of β, we can easily compute its entropy, expected energy and free energy.

Similarly, if we know the partition function of a quantum system as a function of λ = 1/iħ, we can compute its quantropy, expected action and free action. Let X be the set of histories of some system. We assume that X is a measure space and that the amplitudes for histories are given by a function: a: X → ℂ obeying

$${\displaystyle {\int }_{X}a(x)\mathit{dx}=1.}$$

We also assume each history x has some action A(x) ∈ ℝ. In the last section, we saw that to obtain a stationary point of quantropy:

$$Q=-{\displaystyle {\int }_{X}a(x)}\ln a(x)\mathit{dx}$$

with a constraint on the expected action:

$$\langle A\rangle ={\displaystyle {\int }_{X}A(x)}a(x)\mathit{dx}$$

we must use Feynman’s prescription for the amplitudes:

$$a(x)=\frac{e^{-\mathrm{\lambda }A(x)}}{Z}$$

for some value of the classicality λ = 1/iħ, where Z is the partition function:

$$Z={\displaystyle {\int }_X{e}^{-\mathrm{\lambda }A(x)}}\mathit{dx}.$$

As mentioned, the formula for quantropy here is a bit dangerous, since we are taking the logarithm of the complex-valued function a(x), which requires choosing a branch. Luckily, the ambiguity is greatly reduced when we use Feynman’s prescription for a, because in this case, a(x) is defined in terms of an exponential. Therefore, we can choose this branch of the logarithm:

$$\ln a(x)=\ln \left(\frac{e^{iA(x)/\mathit{\hslash }}}{Z}\right)=\frac{i}{\mathit{\hslash }}A(x)-\ln Z.$$

Once we choose a logarithm for Z, this formula defines ln a(x).

Inserting this formula for ln a(x) into the formula for quantropy, we obtain:

$$Q=-{\displaystyle {\int }_{X}a(x)}\left(\frac{i}{\mathit{\hslash }}A(x)-\ln Z\right)\mathit{dx}$$

We can simplify this a bit, since the integral of a is 1:

$$Q=\frac{1}{i\mathit{\hslash }}\langle A\rangle +\ln Z.$$

We thus obtain:

$$-i\mathit{\hslash }\ln Z=\langle A\rangle -i\mathit{\hslash }Q.$$

This quantity is what we called the “free action” in the previous section. Let us denote it by the letter Φ:

$$\mathrm{\Phi }=-i\mathit{\hslash }\ln Z.$$

In terms of λ, we have:

$$a(x)=\frac{e^{-\mathrm{\lambda }A(x)}}{Z}.$$

Now, we can compute the expected action just as we computed the expected energy in thermodynamics:

$$\begin{array}{l}\langle A\rangle ={\displaystyle {\int }_{X}A(x)}a(x)\mathit{dx}\\ =\frac{1}{Z}{\displaystyle {\int }_{X}A(x)}{e}^{-\mathrm{\lambda }A(x)}\mathit{dx}\\ =-\frac{1}{Z}\frac{d}{d\mathrm{\lambda }}{\displaystyle {\int }_X{e}^{-\mathrm{\lambda }A(x)}\mathit{dx}}\\ =-\frac{1}{Z}\frac{\mathit{dZ}}{d\mathrm{\lambda }}\\ =-\frac{d}{d\mathrm{\lambda }}\ln Z.\end{array}$$

This gives:

$$Q=-\mathrm{\lambda }\frac{d\ln Z}{d\mathrm{\lambda }}+\ln Z.$$

The following chart shows where our analogy stands now.

Statistical Mechanics	Quantum Mechanics
states: x ∈ X	histories: x ∈ X
probabilities: p: X → [0, ∞)	amplitudes: a: X → ℂ
energy: E : X → ℝ	action: A: X → ℝ
temperature: T	Planck’s constant times i: iħ
coolness: β = 1/T	classicality: λ = 1/iħ
partition function: $Z={\int }_X{e}^{-\beta E(x)}\mathit{dx}$	partition function: $Z={\int }_X{e}^{-\mathrm{\lambda }A(x)}\mathit{dx}$
Boltzmann distribution: p(x) = e−βE(x)/Z	Feynman sum over histories: a(x) = e−λA(x)/Z
entropy: $S=-{\displaystyle {\int }_{X}p}(x)\ln p(x)\mathit{dx}$	quantropy: $Q=-{\displaystyle {\int }_{X}a}(x)\ln a(x)\mathit{dx}$
expected energy: 〈E〉 = ∫X p(x)E(x) dx	expected action: 〈A〉 = ∫X a(x)A(x) dx
free energy: F = 〈E〉 − TS	free action: Φ = 〈A〉 − iħQ
$\langle E\rangle =-\frac{d}{d\beta }\ln Z$	$\langle A\rangle =-\frac{d}{d\mathrm{\lambda }}\ln Z$
$F=-\frac{1}{\beta }\ln Z$	$\mathrm{\Phi }=-\frac{1}{\mathrm{\lambda }}\ln Z$
$S=\ln Z-\beta \frac{d}{d\beta }\ln Z$	$Q=\ln Z-\mathrm{\lambda }\frac{d}{d\mathrm{\lambda }}\ln Z$
principle of maximum entropy	principle of stationary quantropy
principle of minimum energy (in T → 0 limit)	principle of stationary action (in ħ → 0 limit)

Statistical Mechanics	Quantum Mechanics
states: x ∈ X	histories: x ∈ X
probabilities: p: X → [0, ∞)	amplitudes: a: X → ℂ
energy: E : X → ℝ	action: A: X → ℝ
temperature: T	Planck’s constant times i: iħ
coolness: β = 1/T	classicality: λ = 1/iħ
partition function: $Z={\int }_X{e}^{-\beta E(x)}\mathit{dx}$	partition function: $Z={\int }_X{e}^{-\mathrm{\lambda }A(x)}\mathit{dx}$
Boltzmann distribution: p(x) = e−βE(x)/Z	Feynman sum over histories: a(x) = e−λA(x)/Z
entropy: $S=-{\displaystyle {\int }_{X}p}(x)\ln p(x)\mathit{dx}$	quantropy: $Q=-{\displaystyle {\int }_{X}a}(x)\ln a(x)\mathit{dx}$
expected energy: 〈E〉 = ∫X p(x)E(x) dx	expected action: 〈A〉 = ∫X a(x)A(x) dx
free energy: F = 〈E〉 − TS	free action: Φ = 〈A〉 − iħQ
$\langle E\rangle =-\frac{d}{d\beta }\ln Z$	$\langle A\rangle =-\frac{d}{d\mathrm{\lambda }}\ln Z$
$F=-\frac{1}{\beta }\ln Z$	$\mathrm{\Phi }=-\frac{1}{\mathrm{\lambda }}\ln Z$
$S=\ln Z-\beta \frac{d}{d\beta }\ln Z$	$Q=\ln Z-\mathrm{\lambda }\frac{d}{d\mathrm{\lambda }}\ln Z$
principle of maximum entropy	principle of stationary quantropy
principle of minimum energy (in T → 0 limit)	principle of stationary action (in ħ → 0 limit)

4. The Quantropy of a Free Particle

Let us illustrate these ideas with an example: a free particle. Suppose we have a free particle on a line tracing out some path as time goes by:

$$q:[0,T]\to \mathrm{ℝ}$$

Then, its action is just the time integral of its kinetic energy:

$$A(q)={\displaystyle {\int }_0^T\frac{mv{(t)}^2}{2}\mathit{dt}.}$$

where $v(t)=\dot{q}(t)$. The partition function is then:

$$Z={\displaystyle \int e^{iA(q)/\mathit{\hslash }}}Dq$$

where we integrate an exponential involving the action over the space of all paths.

Unfortunately, the space of all paths is infinite-dimensional, so Dq is ill-defined: there is no “Lebesgue measure” on an infinite-dimensional vector space. Thus, we start by treating time as discrete, a trick going back to Feynman’s original work [2]. We consider n time intervals of length Δt. We say the position of our particle at the i-th time step is q_i ∈ ℝ, and require that the particle keeps a constant velocity v_i between the (i − 1)-st and i-th time steps:

$$v_i=\frac{q_i-q_{i-1}}{\mathrm{\Delta }t}.$$

Then, the action, defined as an integral, reduces to a finite sum:

$$A(q)={\displaystyle \sum _{i=1}^n\frac{m{v}_i^2}{2}\mathrm{\Delta }t.}$$

We consider histories of the particle where its initial position is q₀ = 0, but its final position q_n is arbitrary. If we do not “nail down” the particle at some particular time in this way, our path integrals will diverge. Therefore, our space of histories is:

$$X={\mathrm{ℝ}}^n$$

and we are ready to apply the formulas in the previous section.

We start with the partition function. Naively, it is:

$$Z={\displaystyle {\int }_X{e}^{-\mathrm{\lambda }A(q)}}Dq$$

where:

$$\mathrm{\lambda }=\frac{1}{i\mathit{\hslash }}.$$

But this means nothing until we define the measure Dq. Since the space of histories is just ℝⁿ with coordinates q₁,…, q_n, an obvious guess for a measure would be:

$$Dq=d{q}_1\cdots d{q}_n.$$

However, the partition function should be dimensionless. The quantity λA(q) and its exponential are dimensionless, so the measure had better be dimensionless, too. However, dq₁ ⋯dq_n has units of lengthⁿ. Therefore, to make the measure dimensionless, we introduce a length scale, Δx, and use the measure:

$$Dq=\frac{1}{{(\mathrm{\Delta }x)}^n}d{q}_1\cdots d{q}_n.$$

It should be emphasized that despite the notation Δx, space is not discretized, just time. This length scale Δx is introduced merely in order to make the measure on the space of histories dimensionless.

Now, let us compute the partition function. For starters, we have:

$$\begin{array}{l}Z={\displaystyle {\int }_X{e}^{-\mathrm{\lambda }A(q)}}Dq\\ =\frac{1}{{(\mathrm{\Delta }x)}^n}{\displaystyle \int e^{-\mathrm{\lambda }m\mathrm{\Delta }t{\sum }_{i=1}^n{v}_i^2/2}}d{q}_1\cdots d{q}_n.\end{array}$$

Since q₀ is fixed, we can express the positions q₁,…, q_n in terms of the velocities v₁,…v_n. Since:

$$d{q}_1\cdots d{q}_n={(\mathrm{\Delta }t)}^{n}d{v}_1\cdots d{v}_n$$

this change of variables gives:

$$Z={\left(\frac{\mathrm{\Delta }t}{\mathrm{\Delta }x}\right)}^n{\displaystyle \int e^{-\mathrm{\lambda }m\mathrm{\Delta }t{\sum }_{i=1}^n{v}_i^2/2}}d{v}_1\cdots d{v}_n.$$

However, this n-tuple integral is really just a product of n integrals over one variable, all of which are equal. Thus, we get some integral to the n-th power:

$$Z={\left(\frac{\mathrm{\Delta }t}{\mathrm{\Delta }x}{\displaystyle {\int }_{-\mathit{\infty }}^{\mathit{\infty }}{e}^{-\mathrm{\lambda }m\mathrm{\Delta }t{v}^2/2}}dv\right)}^n.$$

Now, when α is positive, we have:

$${\displaystyle {\int }_{-\mathit{\infty }}^{\mathit{\infty }}{e}^{-x^2/2\alpha }}\mathit{dx}=\sqrt{2\pi \alpha }$$

but we will apply this formula to compute the partition function, where the constant playing the role of α is imaginary. This makes some mathematicians nervous, because when α is imaginary, the function being integrated is no longer Lebesgue integrable. However, when α is imaginary, we get the same answer if we impose a cutoff and then let it go to infinity:

$$\underset{M\to +\mathit{\infty }}{\lim }{\displaystyle {\int }_{-M}^M{e}^{-x^2/2\alpha }\mathit{dx}=\sqrt{2\pi \alpha }}$$

or damp the oscillations and then let the amount of damping go to zero:

$$\underset{ϵ\downarrow 0}{\lim }{\displaystyle {\int }_{-\mathit{\infty }}^{\mathit{\infty }}{e}^{-x^2/2\alpha -ϵx^2}}\mathit{dx}=\sqrt{2\pi \alpha }.$$

So we shall proceed unabashed and claim:

$$Z={\left(\frac{\mathrm{\Delta }t}{\mathrm{\Delta }x}\sqrt{\frac{2\pi }{\mathrm{\lambda }m\mathrm{\Delta }t}}\right)}^n={\left(\frac{2\pi \mathrm{\Delta }t}{\mathrm{\lambda }m{(\mathrm{\Delta }x)}^2}\right)}^{n/2}.$$

Given this formula for the partition function, we can compute everything we care about: the expected action, free action and quantropy. Let us start with the expected action:

$$\begin{array}{l}\langle A\rangle =-\frac{d}{d\mathrm{\lambda }}\ln Z\\ =-\frac{n}{2}\frac{d}{d\mathrm{\lambda }}\ln \left(\frac{2\pi \mathrm{\Delta }t}{\mathrm{\lambda }m{(\mathrm{\Delta }x)}^2}\right)\\ =\frac{n}{2}\frac{d}{d\mathrm{\lambda }}\left(\ln \mathrm{\lambda }-\ln \left(\frac{2\pi \mathrm{\Delta }t}{m{(\mathrm{\Delta }x)}^2}\right)\right)\\ =\frac{n}{2}\frac{1}{\mathrm{\lambda }}\\ =n\frac{i\mathit{\hslash }}{2}\end{array}$$

This formula says that the expected action of our freely moving quantum particle is proportional to n, the number of time steps. Each time step contributes î/2 to the expected action. The mass of the particle, the time step Δt and the length scale Δx do not matter at all; they disappear when we take the derivative of the logarithm containing them. Indeed, our action could be any function of this sort:

$$\begin{array}{c}A:{\mathrm{ℝ}}^n\to \mathrm{ℝ}\\ A(x)={\displaystyle \sum _{i=1}^n\frac{c_i{x}_1^2}{2}}\end{array}$$

where c_i are positive numbers, and we would still get the same expected action:

$$\langle A\rangle =n\frac{i\mathit{ħ}}{2}$$

Since we can diagonalize any positive definite quadratic form, we can state this fact more generally: whenever the action is a positive definite quadratic form on an n-dimensional vector space of histories, the expected action is n times iħ/2. For example, consider a free particle in three-dimensional Euclidean space, and discretize time into n steps as we have done here. Then the action is a positive definite quadratic form on a 3n-dimensional vector space, so the expected action is 3n times iħ/2.

We can try to interpret this as follows. In the path integral approach to quantum mechanics, a system can trace out any history it wants. If the space of histories is an n-dimensional vector space, it takes n real numbers to determine a specific history. Each number counts as one “decision”. In the situation we have described, where the action is a positive definite quadratic form, each decision contributes iħ/2 to the expected action.

There are some questions worth answering:

• Why is the expected action imaginary? The action A is real. How can its expected value be imaginary? The reason is that we are not taking its expected value with respect to a probability measure, but instead, with respect to a complex-valued measure. Recall that:

  $$\langle A\rangle =\frac{{\displaystyle {\int }_{X}A(x)e^{-\mathrm{\lambda }A(x)}}\mathit{dx}}{{\displaystyle {\int }_X{e}^{-\mathrm{\lambda }A(x)}}\mathit{dx}}.$$
  The action A is real, but λ = 1/iħ is imaginary; so, it is not surprising that this “expected value” is complex-valued.
• Why does the expected action diverge as n → ∞? We have discretized time in our calculation. To take the continuum limit, we must let n → ∞, while simultaneously letting Δt → 0 in such a way that nΔt stays constant. Some quantities will converge when we take this limit, but the expected action will not: it will go to infinity. What does this mean?
  This phenomenon is similar to how the expected length of the path of a particle undergoing Brownian motion is infinite. In fact, the free quantum particle is just a Wick-rotated version of Brownian motion, where we replace time by imaginary time; so, the analogy is fairly close. The action we are considering now is not exactly analogous to the arc length of a path:

  $${\displaystyle {\int }_0^T\left|\frac{dq}{\mathit{dt}}\right|\mathit{dt}}$$

  Instead, it is proportional to this quadratic form:

  $${\displaystyle {\int }_0^T{\left|\frac{dq}{\mathit{dt}}\right|}^2\mathit{dt}.}$$
  However, both of these quantities diverge when we discretize Brownian motion and then take the continuum limit. The reason is that for Brownian motion, with probability 1, the path of the particle is non-differentiable, with Hausdorff dimension > 1 [6]. We cannot apply probability theory to the quantum situation, but we are seeing that the “typical” path of a quantum free particle has infinite expected action in the continuum limit.
• Why does the expected action of the free particle resemble the expected energy of an ideal gas? For a classical ideal gas with n particles in three-dimensional space, the expected energy is:

  $$\langle E\rangle =\frac{3}{2}nT$$

  in units where Boltzmann’s constant is one. For a free quantum particle in three-dimensional space, with time is discretized into n steps, the expected action is:

  $$\langle A\rangle =\frac{3}{2}ni\mathit{\hslash }.$$
  Why are the answers so similar?
  The answers are similar because of the analogy we are discussing. Just as the action of the free particle is a positive definite quadratic form on ℝ ⁿ, so is the energy of the ideal gas. Thus, computing the expected action of the free particle is just like computing the expected energy of the ideal gas, after we make these replacements:

  $$\begin{array}{l}E\mapsto A\\ T\mapsto i\mathit{\hslash }\end{array}$$

The last remark also means that the formulas for the free action and quantropy of a quantum free particle will be analogous to those for the free energy and entropy of a classical ideal gas, except missing the factor of 3 when we consider a particle on a line. For the free particle on a line, we have seen that:

$$\ln Z=\frac{n}{2}\ln \left(\frac{2\pi \mathrm{\Delta }t}{\mathrm{\lambda }m{(\mathrm{\Delta }x)}^2}\right).$$

Setting:

$$K=\frac{2\pi \mathrm{\Delta }t}{m{(\mathrm{\Delta }x)}^2},$$

we can write this more compactly as:

$$\ln Z=\frac{n}{2}(\ln K-\ln \mathrm{\lambda }).$$

We thus obtain the following formula for the free action:

$$\begin{array}{l}\mathrm{\Phi }=-\frac{1}{\mathrm{\lambda }}\ln Z\\ =\frac{1}{\mathrm{\lambda }}\frac{n}{2}(\ln \mathrm{\lambda }-\ln K).\end{array}$$

Note that the ln K term dropped out when we computed the expected action by differentiating ln Z with respect to λ, but it shows up in the free action.

The presence of this ln K term is surprising, since the constant K is not part of the usual theory of a free quantum particle. A completely analogous surprise occurs when computing the partition function of a classical ideal gas. The usual textbook answer involves a term of type ln K, where K is proportional to the volume of the box containing the gas divided by the cube of the thermal de Broglie wavelength of the gas molecules [8]. Curiously, the latter quantity involves Planck’s constant, despite the fact that we we are considering a classical ideal gas! Indeed, we are forced to introduce a quantity with dimensions of action to make the partition function of the gas dimensionless, because the partition function is an integral of a dimensionless quantity over position-momentum pairs, and dpdq has units of action. Nothing within classical mechanics forces us to choose this quantity to be Planck’s constant; any choice will do. Changing our choice only changes the free energy by an additive constant. Nonetheless, introducing Planck’s constant has the advantage of removing this ambiguity in the free energy of the classical ideal gas, in a way that is retroactively justified by quantum mechanics.

Analogous remarks apply to the length scale Δx in our computation of the free action of a quantum particle. We introduced it only to make the partition function dimensionless. It is mysterious, much as Planck’s constant was mysterious when it first forced its way into thermodynamics. We do not have a theory or experiment that chooses a favored value for this constant. All we can say at present is that it appears naturally when we push the analogy between statistical mechanics and quantum mechanics to its logical conclusion, or, a skeptic might say, to its breaking point.

Finally, the quantropy of the free particle on a line is:

$$\begin{array}{l}Q=-\mathrm{\lambda }\frac{d\ln Z}{d\mathrm{\lambda }}+\ln Z\\ =\frac{n}{2}(\ln K-\ln \mathrm{\lambda }+1).\end{array}$$

Again, the answer depends on the constant K: if we do not choose a value for this constant, we only obtain the quantropy up to an additive constant. An analogous problem arises for the entropy of a classical ideal gas: without introducing Planck’s constant, we can only compute this entropy up to an additive constant.

5. Conclusions

There are many questions left to tackle. The biggest is: what is the meaning of quantropy? Unfortunately it seems hard to attack this directly. It may be easier to work out more examples and develop more of an intuition for this concept. There are, however, some related puzzles worth keeping in mind.

As emphasized by Lisi [5], it is rather peculiar that in the path-integral approach to quantum mechanics, we normalize the complex numbers a(x) associated with paths, so that they integrate to 1:

$${\displaystyle {\int }_{X}a(x)\mathit{dx}=1.}$$

It clearly makes sense to normalize probabilities so that they sum to 1. However, starting from the wavefunction of a quantum system, we obtain probabilities only after taking the absolute value of the wavefunction and squaring it. Thus, for wavefunctions, we impose:

$${\displaystyle {\int }_X|\psi (x){|}^2\mathit{dx}=1}$$

rather than:

$${\displaystyle {\int }_X\psi (x)\mathit{dx}=1.}$$

For this reason, Lisi calls the numbers a(x) “complex probabilities” rather than amplitudes. However, the meaning of complex probabilities remains mysterious, and this is tied to the mysterious nature of quantropy. Feynman’s essay on the interpretation of negative probabilities could provide some useful clues [1].

It is also worth keeping in mind another analogy: “coolness as imaginary time”. Here, we treat β as analogous to it/ħ, rather than 1/iħ. This is widely used to convert quantum mechanics problems into statistical mechanics problems by means of Wick rotation, which essentially means studying the unitary group exp(−itH/ħ) by studying the semigroup exp(−βH) and then analytically continuing β to imaginary values. Wick rotation plays an important role in Hawking’s computation of the entropy of a black hole, nicely summarized in his book with Penrose [3]. The precise relation of this other analogy to the one explored here remains unclear and is worth exploring. Note that the quantum Hamiltonian H shows up on both sides of this other analogy.