1. Introduction
Diffusion processes have been a cornerstone of stochastic modeling of time series data, particularly in areas such as finance [
1] and hydrology [
2]. Many extensions to the classic diffusion model have been developed in recent years, addressing such diverse issues as asymmetry, kurtosis, heteroscedasticity and long memory; see, for instance, [
3].
In the simplest case, the increments of a diffusion model are taken as independent Gaussian random variables, making the process a Brownian motion. In this work, by contrast, processes with long memory and non-Gaussian increments are considered.
The proposed model is a generalization of the Gamma-modulated (G-M) diffusion process, in terms of the memory parameter. This model was developed in [
4] to address an asset market problem, extending the ideas of the Black–Scholes paradigm and using Bayesian procedures for model fitting. In that work, the memory parameter was assumed to be known and fixed, with some particular cases, such as the standard Brownian motion and the Student process. The latter one is a generalization of the Student process previously presented in [
5], the marginals of which have a
t-Student distribution with fixed degrees of freedom and a long memory structure.
Here, we enlarge the parameter space considering that the memory parameter is also unknown, provided we have a prior distribution on it.
This extension allows flexibility for the dependence structure of the process, where the Brownian motion and the G-M process become particular cases.
Typically, the trajectories generated by this process exhibit heteroscedasticity, with higher variability at the beginning, which we call “explosion at zero”. In addition, as time increases, the variability decreases at a rate depending on the long memory parameter.
In particular, we will focus on estimation procedures for long-range memory stochastic models from a Bayesian perspective. Other parameters, such as location and dispersion, are also considered.
For the location and scale parameters, we can straightforwardly find natural conjugate prior distributions. However, the same does not occur for the memory parameter, as its marginal likelihood is not workable analytically. This implies that methods used for obtaining a posterior distribution, such as commonly-used likelihood-based solutions, are not suitable for this purpose.
In order to approximate the posterior distribution for the parameters involved, we propose a blended approximate Bayesian computation ABC-MCMC algorithm. This family of ABC algorithms and its very broad set of applications are well reviewed in [
6]. In this work, the MCMC part is built for those components with full conditional posterior distributions that are able to be dealt with, and the ABC is implemented for the memory parameter. Grounded on previous results [
7], for the ABC steps, an appropriate summary statistic was defined, based on the path properties and on the
m-block variances. We obtain, by this proposal, very precise estimates for that parameter.
After generating samples from the posterior, a by-product is the
e-value, an evidence measure for precise hypotheses, such as the Brownian motion and G-M cases. This measure was defined in [
8] and used afterward, for instance, in [
9,
10,
11].
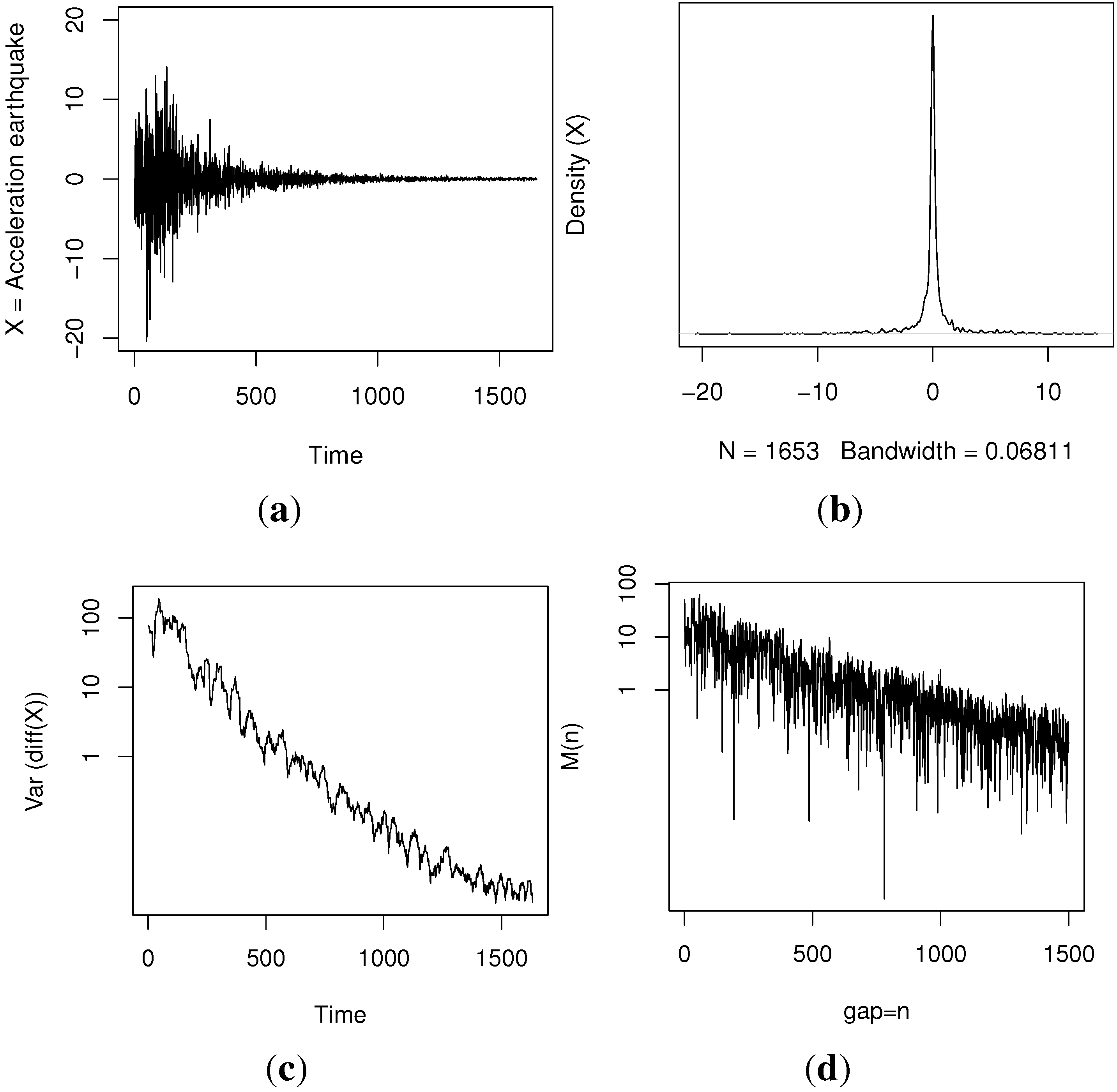
We test and validate our method through simulations and illustrate it with data from the big earthquake that occurred in Chile in 2010.
The definition of the process and some properties are presented in
Section 2. In
Section 3, we describe the ABC-MCMC algorithm. The simulated and real data results are shown in
Section 4, and finally, in
Section 5, we give some final remarks.
2. Generalized Gamma-Modulated Process
Let us consider the standard Brownian motion,
, and a Gamma process,
, as defined in [
4].
A Gamma process is a pure-jump increasing Lévy process with independent and stationary Gamma increments for non-overlapping intervals. For this process, the intensity measure is given by , for any positive x. That is, jumps whose size lies in the interval occur as a Poisson process with intensity . The parameters involved in the intensity measure are a, which controls the rate of jump arrivals, and b, the scaling parameter, which controls the jump sizes.
The marginal distribution of a Gamma process at time t is a Gamma distribution with mean and variance , allowing also the parametrization in terms of the mean, μ, and variance, , per unit time, that is, and .
For the one-dimensional distributions, we have that
in distribution;
,
, where
is the Gamma function;
, for
, and its characteristic function,
, is:
Given times
,
, and given
, the density,
, of the increment
is given by the Gamma density function with mean
and variance
,
In this work, we will consider
.
Given a real value
, we define the generalized Gamma-modulated (G-M) process by:
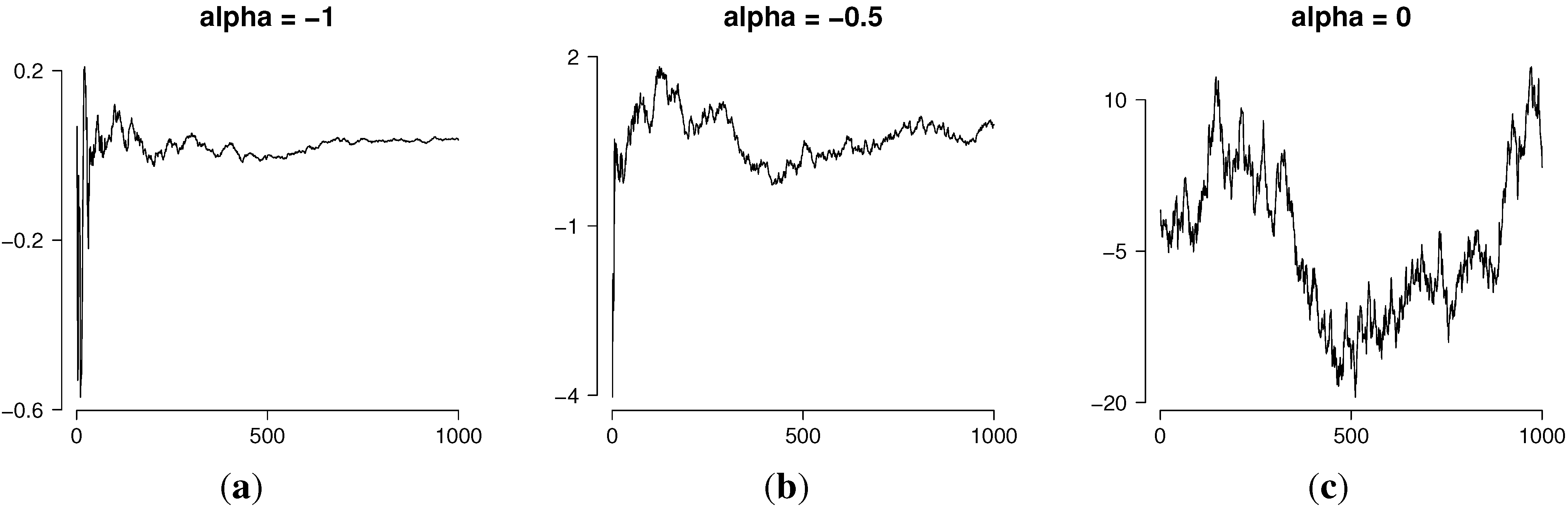
Figure 1 shows typical realizations of the generalized G-M process for different values of the parameter
α. In particular, the value
corresponds to the Brownian motion and
to the Student process studied in [
4].
The next subsections present some useful path characteristics of the process that could lead us to choose this model as an appropriate one for a given problem and to help us make inferences about its parameters, such as the presence of long memory, the variability profile and the variance of the increment process.
Figure 1.
Realizations of the generalized Gamma-modulated (G-M) process for different values of α. (a) ; (b) ; (c) .
Figure 1.
Realizations of the generalized Gamma-modulated (G-M) process for different values of α. (a) ; (b) ; (c) .
2.1. Explosion at Zero
The graphs in
Figure 1a,b, with
, show that the process is highly variable near
, but as
, its variability decreases. We call this path property “explosion at zero” and prove it in the next result.
Proposition 1. Let be the generalized Gamma-modulated process as defined in Equation (1). Then, for all , we have:
Proof. Let us consider
and
. Conditioning in
, we obtain:
with
. The last quantity tends to one as
for
.
Let us consider now the case
,
that tends to zero as
. ☐
2.2. The Increment Process
Let us now consider the increment process, . The next results describe the asymptotic behavior of the variance-covariance structure for these differences and, hence, for the process itself, since has zero expectation.
Proposition 2. For the increment process,
,
Proof. Let us observe that the increment process,
, can be written as
, where:
Working out each term, we obtain:
and:
☐
This property leads us to consider the variance of the observed increment process, , as informative for the parameter α and, therefore, helpful to implement the approximated simulation for its marginal posterior.
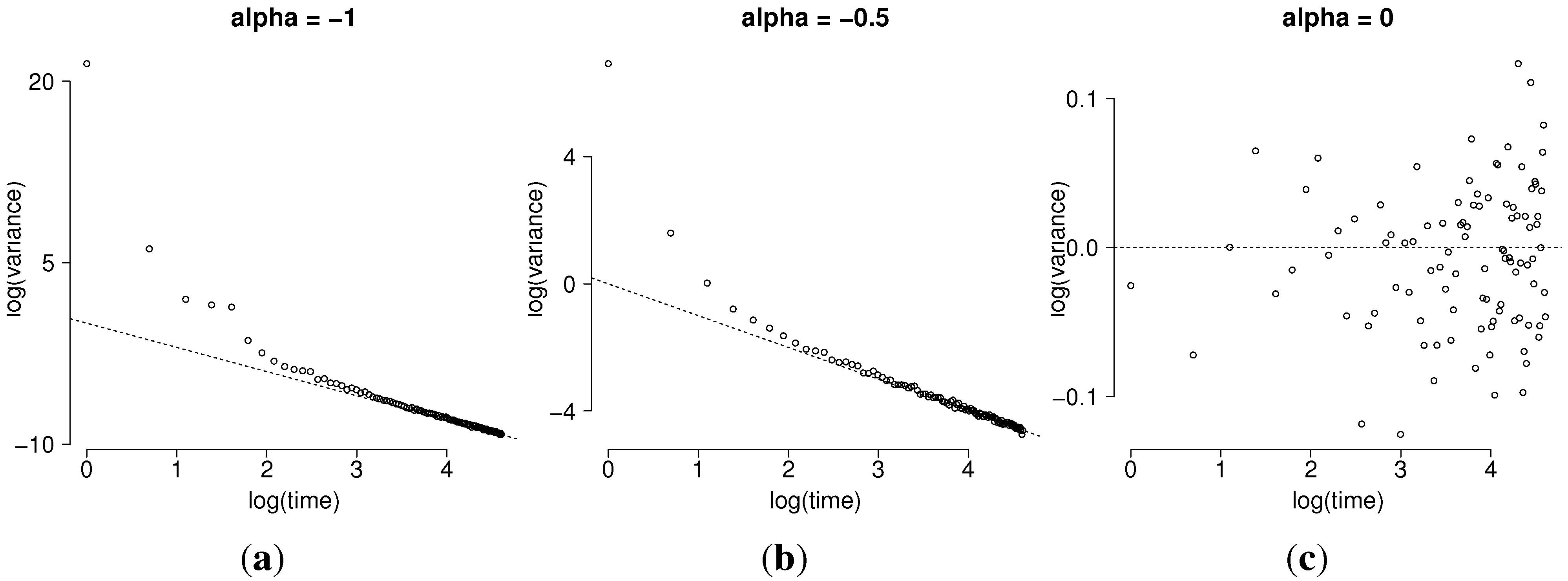
In a data exploratory phase, we could examine the graph of the empirical variances of
from
t to the end of the process, as a function of
t in logarithmic scale. As
t increases, that graph should become linear with slope
.
Figure 2 exhibit this result for some values of
α. Observe that the asymptotic result can be visualized from
, that is from
, for
.
Figure 2.
Sample distribution of , for 1000 simulated trajectories of the generalized G-M process, for different values of α. (a) ; (b) ; (c) .
Figure 2.
Sample distribution of , for 1000 simulated trajectories of the generalized G-M process, for different values of α. (a) ; (b) ; (c) .
Proposition 3. The auto-covariance for lag n of the increment process, denoted by , is of order , if , and it is zero, if , as n increases.
Proof. Let us consider
, because of the explosion at zero. Then:
If
, we can apply the Gautschi inequality [
12], obtaining:
and then:
On the other hand, for , , and therefore, . ☐
In other words, for
, the process has no memory, and we recover the Brownian motion case as already mentioned; for
, the process is called anti-persistent. Recalling the Hurst parameter
H associated with the fractional Brownian motion, the relationship between
H and
α is
; see [
4], for instance.
3. ABC-MCMC Study
When dealing with non-standard posterior distributions, the usual procedure is to use Markov chain Monte Carlo simulation to produce an approximate sample from this posterior. However, when the likelihood function is intractable, MCMC methods cannot be implemented. The class of likelihood-free methods termed, approximate Bayesian computation (ABC), can deal with this problem as long as we are able to simulate from the probabilistic model and a suitable set of summary statistics is available.
The ABC idea was proposed by Pritchard
et al. [
13] and developed further in the last decade. In particular, with respect to the choice of the summary statistics from among diverse options, in [
14], the authors consider a sequential test procedure for deciding whether the inclusion of a new statistic improves the estimation. In [
15], the discussion refers to the choice of informative statistics related to the algorithmic properties.
In our case, in order to perform the ABC algorithm for the memory parameter, α, we have to be able to generate a realization of the target process and we have to know which are the important observable characteristics of the process that lead us to increase our information about α.
Observe that we already know, by Equation (
1), how to simulate from the generalized G-M for each value of the parameter. After obtaining a simulated trajectory, we can compare it then to the observed trajectory through adequate statistics. Intuitively, if they are similar enough, the chosen value of the parameter can be thought of as an appropriate one.
More concretely, suppose that we take the observed increments
from a sample
and that for each
, we generate a realization from a Brownian motion
and a realization from a Gamma process
, obtaining:
For the ease of notation, set
. To compute the proximity between
and
, we will determine the distance between some statistics for each sample. The usual choices for the memory parameter are, among others, the rescaled range
or the rescaled variance
, the periodogram, quadratic variations, aggregated variances, Whittle estimator and functions, as the logarithm, inverse or square root, of these ones [
15,
16]. In [
7], we used those statistics to obtain approximate posterior samples for the memory parameter for fractional self-similar processes.
We tried all of them in this work; however, their performance was not good enough, because of the non-stationarity and the inherent heteroscedasticity of the process. To solve this situation, we considered the slope of the regression of the sampling variance of
m-size blocks on the time, regarding the results in
Section 2.2, and this solution worked much better than the former ones.
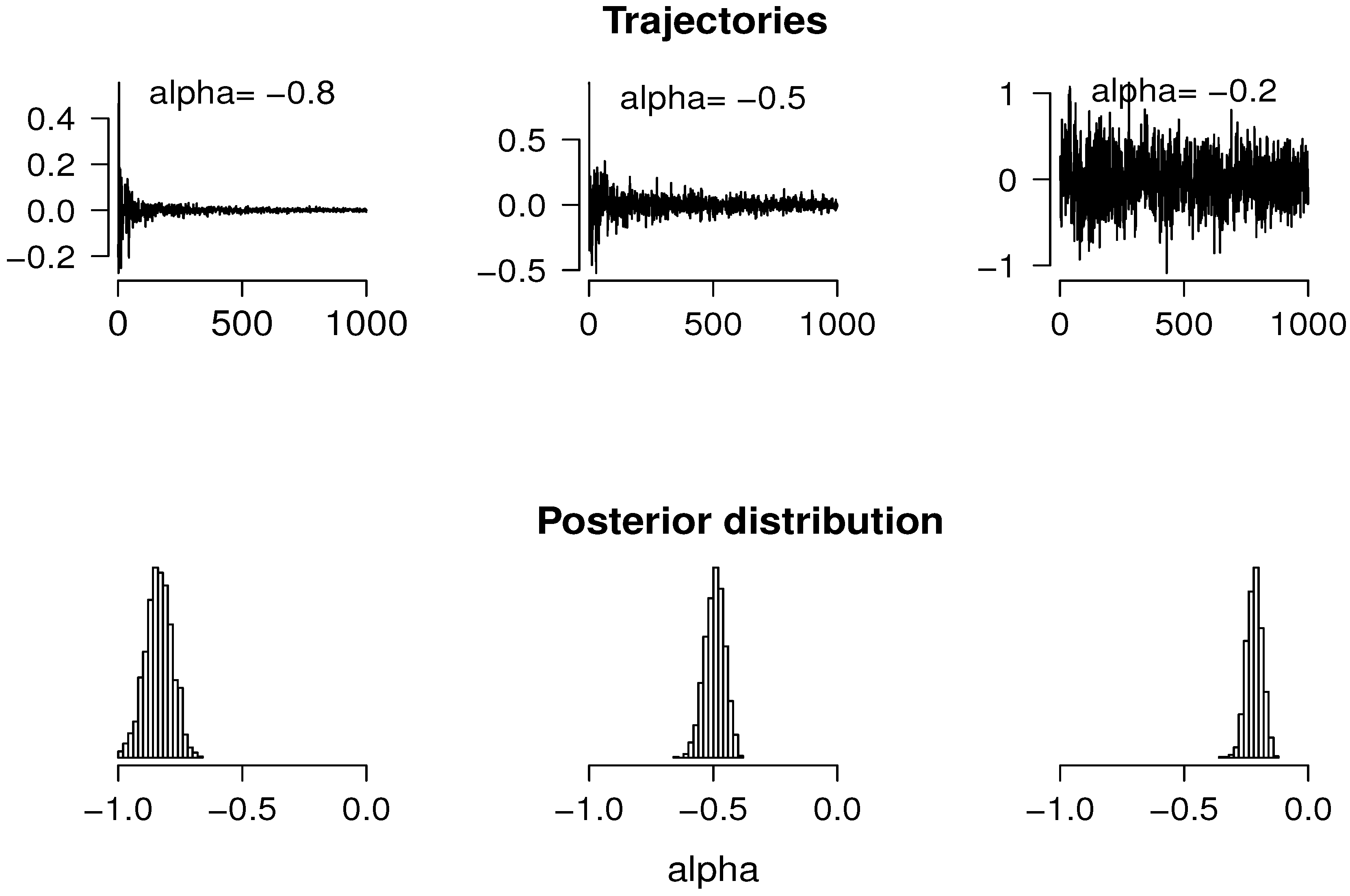
Let denote the following statistic. Giving n observations and an integer , we take consecutive blocks of size m and obtain the sampling variance for each block, , for , where is the integer part of ξ. Those values are used as estimates for the variances at times . In scale, the slope of the regression line obtained through the points , , should be of order of , as time increases. We define as this slope.
The ABC steps for α are then given by the following algorithm.
| Algorithm 1 ABC procedure for α. |
Select α from a prior distribution ; Generate a trajectory for that value α; Given , if , then select α for the sample , otherwise, reject it; Repeat Steps 1–3 until reaching an adequate sample size for the parameter α.
|
The sample obtained in the last step is an approximate sample from the posterior distribution for α, the goodness of which strongly depends on the choice of the statistics and the threshold ε in Step 3.
Note that if
ε is too small, then the rejection rate is high, and the algorithm becomes too slow; on the other hand, if
ε is too big, the algorithm accepts too many values of
α, giving a less precise approximate sample. In general, what is done is to take a small percentile of the simulated distances, that is we select those
α’s giving the closest values to the observed one. In this work, after some trial, we used the first percentile, as proposed by [
17].
Let us consider now the more general model for the increments given by:
for
and
, representing the precision of the fluctuations. As:
, with
,
and
independent of
, for all
, and following the theory associated with the Gamma-modulated process [
4], it is possible to assume a hierarchical representation.
We can rewrite the above model in a multivariate way as:
where, for
,
As a final step, let us assume prior distributions given by:
and prior knowledge for
α,
. Then, given
, auxiliary random effects distributed as:
and an observed trajectory
, the posterior distribution can be computed from:
After straightforward computations and assuming that
, the full conditional posterior distributions for
are:
where:
With this notation, for parameters , we propose the following ABC-MCMC procedure.
| Algorithm 2 ABC-MCMC procedure for . |
Apply the ABC proposal given by Algorithm 1, to obtain a posterior sample for α, ; Sample uniformly from ; Generate a trajectory from the Gamma process; Sample from the conditional posterior ; Repeat Steps 3–4 until the convergence is reached, which can be checked by the usual graphical criterion for , and take their sampling mean; Repeat Steps 2–5, for obtaining a complete posterior sample for .
|
The whole procedure is to then use the ABC algorithm for α and the MCMC scheme for to perform the Bayesian inference of our proposal.
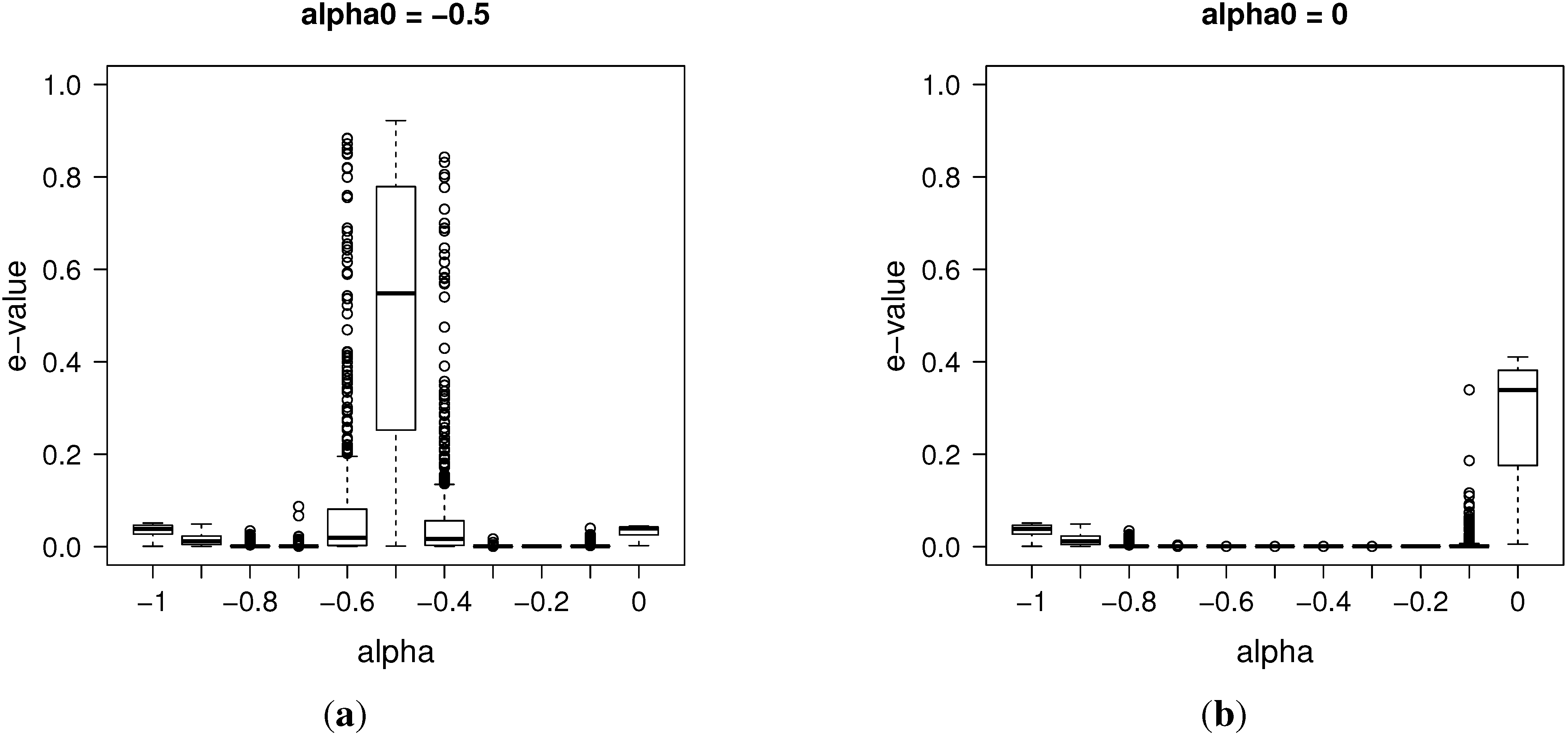
3.1. Posterior Evidence for Sharp Hypotheses
As a by-product of the previous algorithm, we are able to compute approximately the so-called
e-value, an evidence measure defined in [
8] for precise hypothesis testing, which we describe briefly below.
Let us consider a hypothesis of interest
, and define the tangential set
to
as the set:
In other words, the tangential set to considers all points “more probable” than those in , according to the posterior law.
The evidence measure
e-value for the hypothesis
H is defined as:
Therefore, if the tangential set has high posterior probability, the evidence in favor of H is small; if it has low posterior probability, the evidence against H is small. For instance, suppose that we are considering the sharp hypothesis . If the subset has high density, that is it lies near the mode of ), then the e-value must be large, giving high evidence for that sharp hypothesis. Some interesting hypotheses are the precise ones defining the Brownian motion case, when , and the G-M process, when .
In this work, we approximate empirically the integral in the
e-value using the posterior sample obtained by the previous algorithms. As usual, in the Bayesian paradigm, the predictive distribution for the next steps can be computed using this ABC-MCMC sample and the model Equation (
2).
5. Final Remarks
The model proposed here seems to be suitable for the phenomena under study. In particular, interesting properties, including long memory and trajectory behavior, are discussed, on which our inference methodology is grounded.
For the ABC algorithm, we considered at first a minimum entropy criterion for selecting the approximate posterior sample, because that choice had a good performance in estimating the long memory parameter for stationary non-Gaussian processes as, for instance, binary and the Rosenblatt processes [
7]. However, given the trajectory behavior of the G-M process, the most informative statistics we found is the
m-block variance statistic
.
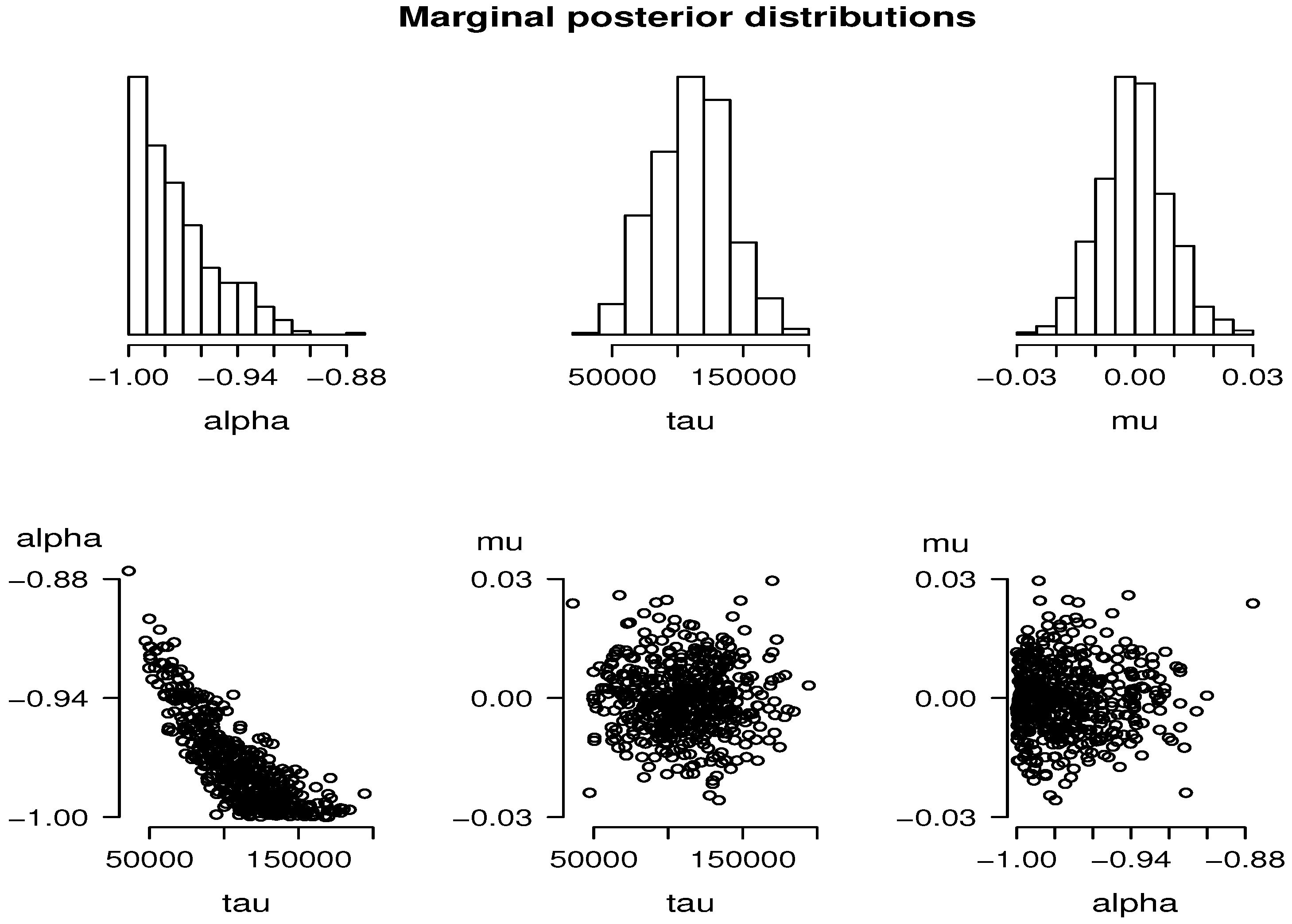
Our results show, firstly, a clear and easy way of implementing the ABC-MCMC algorithms in a standard software. For the real data (), the computational cost was moderate, obtaining a posterior sample of a size of 500 from the ABC-MCMC proposal in one hour.
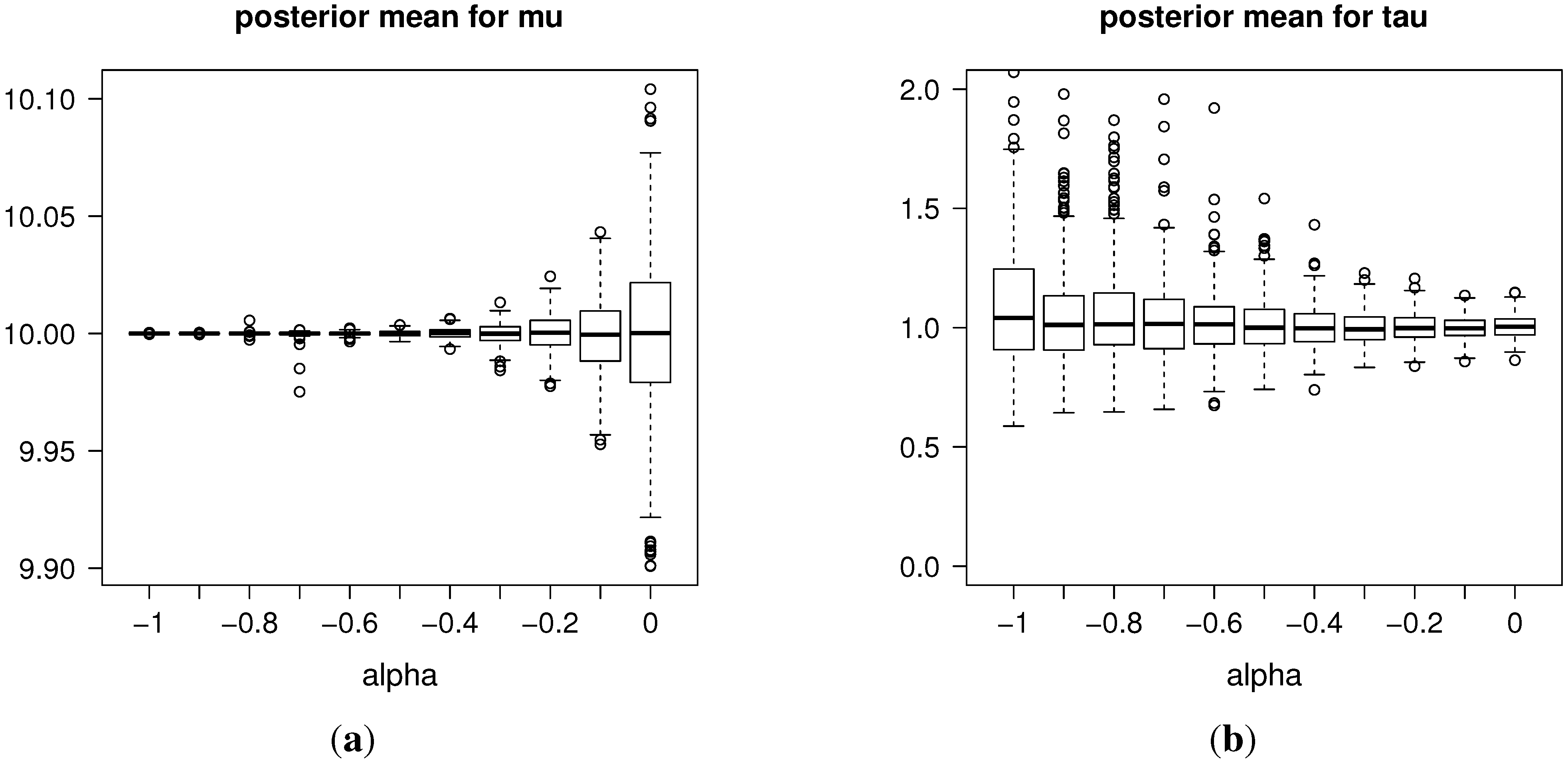
In our simulations, we obtained a very high precision in the estimates given by this procedure. In addition, the estimates for the precision parameter, τ, are affected reasonably by scale changes. For instance, for the rescaled data, , we estimated τ as , approximately.
The chosen parameterization allows for . However, we did not study such a case, since that process diverges as time increases, making the inference procedure harder for α. We recommend then to treat this problem as a separate case.
Finally, we believe that this model has wider applications, mainly for its parsimony and the straightforward interpretation of the parameters. For diagnostic purposes, for example, the predictive series could be used to perceive the increasing fore-shocks before the arrival of a new earthquake.