1. Introduction
Standard thermodynamics is strictly valid only for the homogeneous behavior of large systems, whereas thermal fluctuations often involve small systems. In 1962 Hill introduced the theory of small-system thermodynamics [
1,
2], establishing the fundamental laws that govern finite-size effects in thermodynamics. Although originally developed to describe individual molecules and isolated nanoparticles, this theory is also crucial for treating the heterogeneous distribution of independently relaxing regions that is now known to dominate the primary response of most materials [
3–
8]. The term “nanothermodynamics” was first published in the context of using small-system thermodynamics to treat nanometer-sized fluctuations inside bulk materials [
9,
10]; which is the focus of this brief review.
A key ingredient in nanothermodynamics is the subdivision potential (
E) that must be included in the 1st law of thermodynamics if total energy is to be conserved [
11]. Hill’s
E can be understood by comparison to Gibbs’ chemical potential,
μ.
μ is the change in energy to take a single particle from a bath of particles into the system, whereas
E is the change in energy to take a cluster of
n interacting particles from a bath of clusters into the system, and in general
n interacting particles do not have the same energy as
n isolated particles due to surface terms, length-scale effects, thermal fluctuations,
etc. Thus,
E is needed to systematically treat the nonlinear and non-extensive contributions to energy from a system that contains a heterogeneous distribution of independent regions. Here I describe how the laws of nanothermodynamics guide the development of models and theories that treat independent thermal fluctuations inside bulk samples, and yield improved agreement with the measured response of many materials [
9,
12–
17]. Indeed, these concepts provide a common explanation for several empirical features in the slow response of complex systems including: non-exponential relaxation, non-Arrhenius activation, non-classical critical scaling, and non-homogeneous response. As an introductory example I describe a fundamental mechanism for the non-Nyquist electronic noise found in many materials [
18].
Nature exhibits several types of noise due to thermal fluctuations [
19]. In 1827, Brown first reported sporadic motion of pollen grains in water. In 1905, as the second breakthrough in his
Annus Mirabilis, Einstein explained this “Brownian motion” by assuming random impulses from much smaller particles, which was to provide the first definitive evidence for atoms and molecules. As a function of frequency (
f) Brownian motion exhibits noise with a power spectral density that varies as
S(
f) ∝1/
f2. In 1926 Johnson first measured electronic noise that showed a flat spectral density, S(
f) = const. Nyquist explained this “white” noise by assuming classical thermal fluctuations in the motion of the electrons. Also in 1926 Johnson measured electronic noise with apparent 1/
f frequency dependence. Although there is still no widely accepted explanation for this “1/
f noise,” empirically it is the most common low-frequency behavior. Indeed 1/
f noise is found in metals, semimetals, semiconductors, dielectrics, ferroelectrics, ionic conductors, spin glasses, supercooled liquids, and quantum devices [
20–
23], as well as in music, speech, neural response, and human perception [
24–
27]. Although no single model is likely to explain all these phenomena, I use the laws of nanothermodynamics as a guide to obtain a unified picture for 1/
f noise in many materials. Specifically, the general principle is based on the assumption that particles inside local regions of a bulk sample: conserve total energy by including non-extensive terms in
E (1st law), maintain maximum entropy during equilibrium fluctuations (2nd law), and/or exhibit statistical indistinguishability of identical particles consistent with quantum mechanics, as described in the next section.
2. Nanothermodynamics in Computer Simulations
All simulations presented here utilize the Ising model for binary degrees of freedom (“spins”) on a simple-cubic lattice. The lattice contains a total of
N spins, with exchange interaction (
J) between nearest-neighbor spins, and periodic boundary conditions between outside surfaces of the lattice. Often the lattice is subdivided into smaller regions containing
n <
N spins to study the thermal properties of small systems inside a bulk sample.
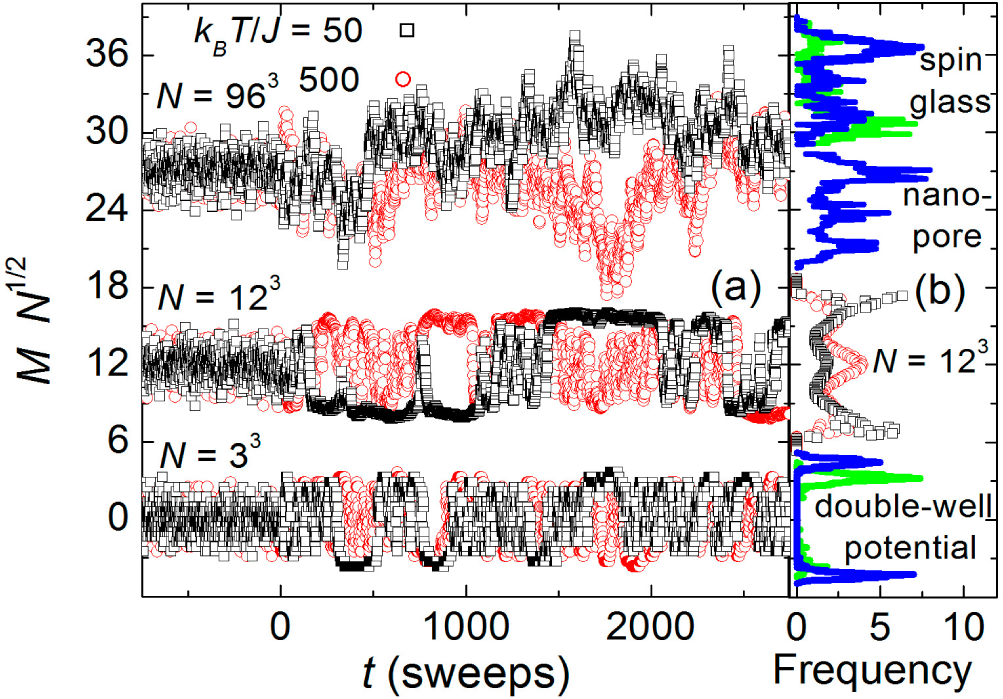
Figure 1a shows the net magnetization as a function of time from simulations of this model. Note the abrupt change in dynamics at time
t = 0: for
t < 0 the spin-flip probability is governed by Boltzmann’s factor alone using the Metropolis algorithm
Equation (1), whereas for
t ≥ 0 there is also a nonlinear correction from nanothermodynamics
Equation (2).
In
Equation (1), Δ
U is the change in interaction energy,
kB is Boltzmann’s constant, and
T is temperature. In
Equation (2)g controls the strength of the nonlinear correction that comes from the alignment entropy using the binomial coefficient for binary degrees of freedom:
, with
its maximum value. When
g = 0 (
t < 0 in
Figure 1a) systems of all size show standard Gaussian fluctuations characteristic of white noise. When
g = 1 (
t ≥ 0) the uppermost set of data (from a large lattice with small regions) shows large wandering on all time scales, indicative of 1/
f noise; while the lower two sets of data (from smaller lattices that contain a single region) exhibit sharp jumps and steps characteristic of non-Gaussian fluctuations. Indeed,
Figure 1b shows that histograms of the simulations exhibit trimodal behavior (symbols), similar to the trimodal behavior found from measurements of 1/
f noise in a spin glass and ionic conduction through a nanopore, shown in the upper part of
Figure 1b (solid lines). In contrast, the bottom pair of lines, from fluctuations in two different sculpted double-well potentials, shows simpler bimodal behavior.
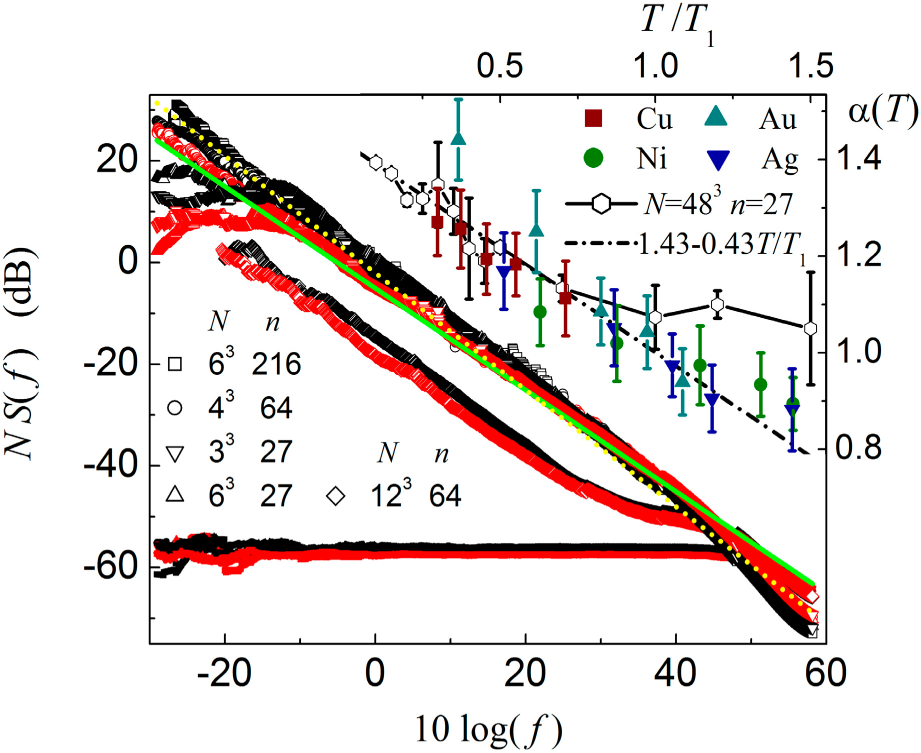
The left side of
Figure 2 shows the Fourier transform from simulations similar to those in
Figure 1a. Simulations using
Equation (1) alone yield white noise that does not depend on
f (lower symbols), whereas adding
Equation (2) yields 1/
f-like noise (symbols along the diagonal). In fact these simulations can be characterized by
S(
f) ∝ 1/f
α(T), with a temperature-dependent spectral-density exponent α(
T) that models the measured behavior from several metals at lower temperatures, as shown in the upper part of
Figure 2. Similar large-amplitude low-frequency noise is found in most substances. Thus,
Equation (2) provides a formula for obtaining measured 1/
f-like noise, including deviations from pure 1/
f-behavior. Moreover, the nonlinear correction is based on fundamental physical laws from nanothermodynamics.
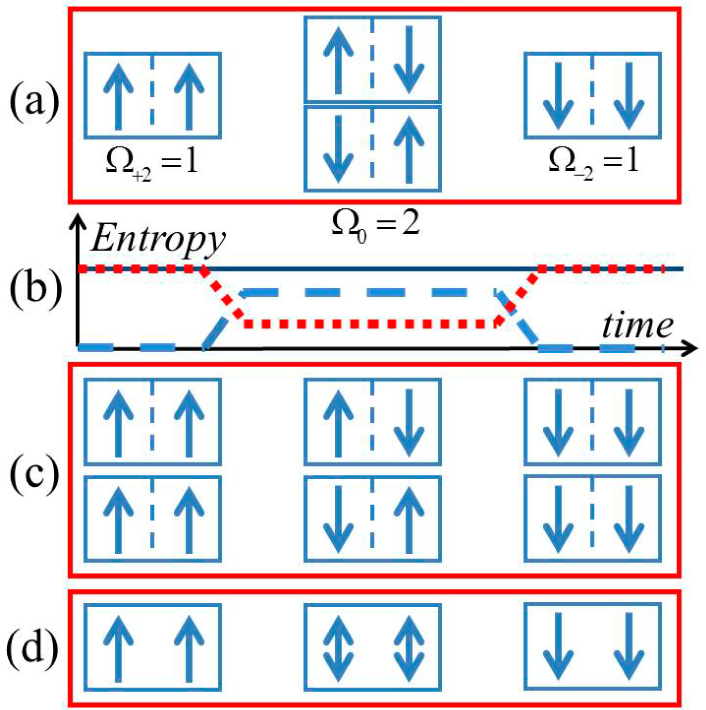
Figure 3 depicts some of the mechanisms that justify the nonlinear correction. Consider two binary degrees of freedom, e.g. two uniaxial spins that can be up or down.
Figure 3a shows that there is one way to have both spins up, one way to have both spins down, and two ways to have no net alignment. The alignment entropy is obtained from Boltzmann’s definition,
S/
kB = ln(Ω), using the multiplicity of each alignment, Ω. The dashed (blue) line in
Figure 3b shows how, during normal thermal fluctuations, this entropy may fluctuate up-and-down between its minimum
S/
kB = 0 and maximum
S/
kB = ln(2) values. Although seeming to violate the second law of thermodynamics, various explanations have been proposed. The 2nd law may be statistical, not absolute, allowing the entropy of isolated small systems to decrease temporarily; but a truly isolated small system cannot be measured. Another explanation is that entropy should be defined using Gibbs ensembles that average over all accessible states, but this inhibits using entropy for time-dependent and out-of-equilibrium behavior. A third possibility is that when the entropy of a local region decreases, the entropy of its bath increases, so that the total entropy remains maximized. Indeed,
Figure 3b shows how the entropy of the bath (dotted line) may balance the entropy of the system (dashed line), so that the combined entropy of the system plus bath is constant (solid line).
This mechanism for the nonlinear correction is a type of entropic force, similar to Boltzmann’s factor [
17]. Boltzmann’s factor favors low-energy states because increasing the energy of the system lowers the entropy of the bath. Similarly, the nonlinear correction favors low-entropy states because increasing the alignment entropy of the system lowers the entropy of the bath. In fact, for the two-spin system the nonlinear correction precisely doubles the average lifetime of each fully aligned state, as shown schematically in
Figure 3c. Thus, each aligned state becomes as likely as both unaligned states. Information theory provides additional insight into this mechanism. If there is no transfer of information between the system and its environment, then the alignment of the system cannot be known and its multiplicity always includes all four states. Again the entropy is constant, but at a higher value
S/
kB = ln(4) due to the lack of information about alignment.
A second mechanism for the nonlinear correction comes from the statistics of indistinguishable particles, as shown schematically in
Figure 3d. To match the probability of each alignment in
Figure 3c, instead of doubling the likelihood of the aligned states, the unaligned state could be a single superposition of up- and down-spins, as expected for identical particles that are subject to the exchange interaction. Indeed, the three net alignments (up, down, and unaligned) form the triplet states of a two-spin system, with the singlet state missing from this simplified picture. Further justification for this interpretation comes from the energy and its fluctuations shown in
Figure 4 (below), where a similar nonlinear correction minimizes the energy of small regions and makes their entropy extensive and additive, consistent with the statistics of indistinguishable particles. Thus, this mechanism for extensive entropy in small regions is similar to the semi-classical ideal gas that resolves Gibbs’ paradox for extensive entropy in large volumes. In other words, the nonlinear correction may be a simplistic way to simulate quantum-like statistics in classical models.
A third way to understand the nonlinear correction is from conservation of energy including Hill’s subdivision potential. Consider a system of
n non-interacting Ising-like spins with magnetic moment
μB in field
B. Each spin can be aligned or anti-aligned with
B, giving energy −
μBB or +
μBB, respectively. The single-particle partition function is
. Because the spins are non-interacting, the partition function for the entire system is
Z = (
Z1)
n, yielding the free energy
A = –
nkBT ln(
Z1). For simplicity let
B → 0, so that
A = –
nkBT ln(2). Again using the binomial coefficient for the exact entropy of the system, the internal energy becomes
If the system is at its average alignment
m = 0, Stirling’s approximation for the factorials when
n is large yields
S0/
kB ≈
n ln(2) and
U0 ≈ 0. However, if total energy is to be conserved during fluctuations, there is a non-extensive contribution to internal energy
Um =
U0 –
Em, where
Em =
kBT (
S0 –
Sm) is Hill’s subdivision potential. In other words, although
U0 ≈ 0 at
m = 0, during thermal fluctuations the change in alignment entropy causes a change in energy, independent of any interaction between particles. Fluctuations in
Em occur because free energy is a thermal average in the canonical ensemble, while energy and entropy may be defined in each microcanonical state. Note that when
m ≠ 0,
Em > 0 lowers the total energy, which favors subdividing a bulk sample into an ensemble of regions that fluctuate independently to increase the fluctuations, as is found in the primary response of most materials. Inserting this
Em as an energy offset in a Boltzmann-like factor yields the nonlinear correction,
Equation (2). Interactions that occur explicitly in
Equation (1) neglect this source of energy, so that
Equation (2) may be necessary to ensure that total energy is strictly conserved in finite-sized systems.
Standard simulations using
Equation (1) alone deviate from nanothermodynamic behavior due to finite-size effects caused by assuming homogeneous systems with uniform correlations. Specifically, when energy fluctuations are averaged over a volume that excludes interacting particles outside the volume, correlations across the interface are neglected. For large homogenous systems the nonlinear correction may give a negligible contribution to conservation of energy:
n → ∞ yields
m → 0, and
Um ≈
U0. However, several experimental techniques have established that the primary response of most materials comes from a heterogeneous distribution of independently-relaxing nanometer-sized regions. Indeed, dynamical heterogeneity on the length scale of nanometers is found in the slow response of liquids, glasses, polymers, and crystals [
3–
8]. In fact, extensive studies of time-dependent specific heat at low temperatures find that the only substance to show no evidence for localized excitations is chemically and isotopically pure NaF crystals [
32]. Furthermore, the technique of nonresonant spectral hole burning (NSHB) establishes that excess energy may be localized in selected degrees of freedom inside a sample for minutes, or even hours [
33,
34], without influencing the energy in neighboring regions. Thus, complexity in the primary response of most substances comes from thermodynamic heterogeneity due to an ensemble of independently relaxing regions, consistent with nanothermodynamics, but different from macroscopic homogeneous behavior needed for standard thermodynamics.
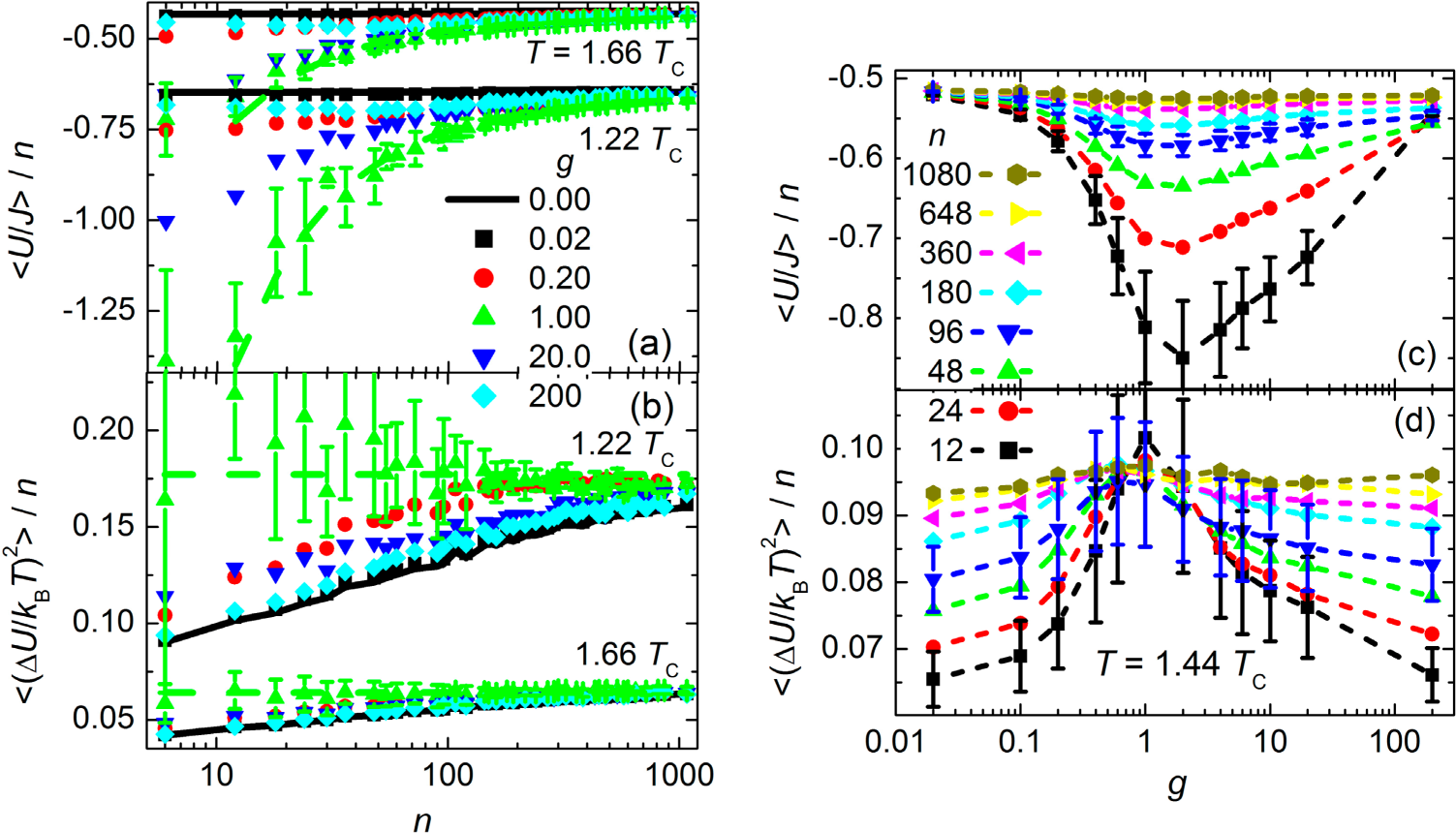
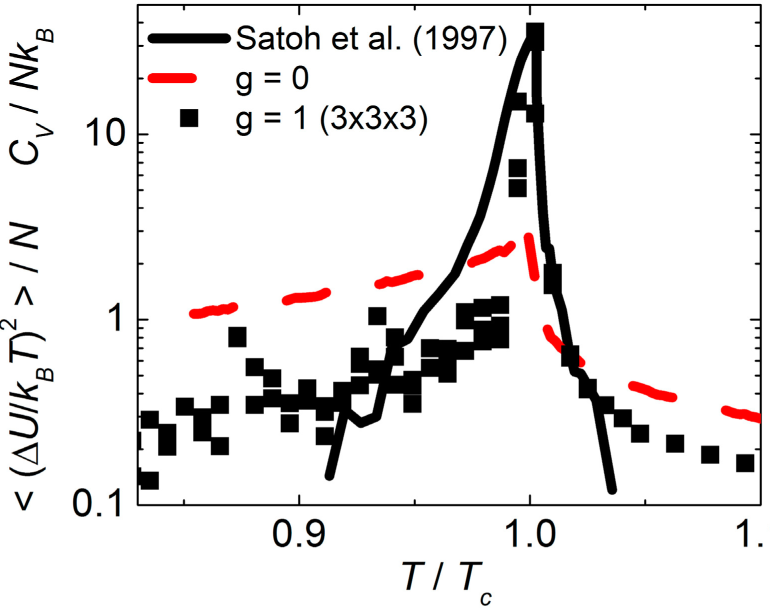
Energy fluctuations in most Monte Carlo simulations exhibit a size dependence [
35] that differs from the expectation for independent small systems that entropy is extensive and additive.
Figure 4 shows the average potential energy density (<
U/
J>/
n) and its fluctuations (<(Δ
U/
kT)
2>/
n) as a function of the number of particles (
n) in local regions of a large lattice. Again the simulations utilize the standard Ising model for binary spins on a simple-cubic lattice with ferromagnetic interaction between nearest-neighbors. The solid (black) lines, from simulations using Boltzmann’s factor alone (
Equation (1)), show constant energy density, whereas the fluctuations in energy density increase with increasing region size. The size dependence of these energy fluctuations yields a size-dependent specific heat, and non-extensive entropy that is incompatible with the laws of nanothermodynamics for an ensemble of independently relaxing regions. The symbols in
Figure 4 show the energy density and its fluctuations for the same Ising model with various strengths (
g) in an approximation of
Equation (2) that yields a quadratic correction to Boltzmann’s factor, with a bypass.
The bypass comes from the Kronecker delta that gives
when Δ
U = 0. A practical reason for this bypass is to accelerate slow relaxation and avoid frozen response. A physical reason is that if Δ
U = 0 spin flips can occur in a microcanonical ensemble, without coupling to the heat bath. Sufficient disorder in a local region may remove the bypass if neighboring states with Δ
U = 0 are not available; consistent with the fact that 1/
f noise generally increases with increasing disorder. Furthermore, most materials exhibit a combination of 1/
f noise at low frequencies and white noise at high frequencies, indicating dynamics without, and with, the bypass, respectively. Indeed, the diamond-shaped symbols in
Figure 2 come from a heterogeneous mixture of
Equation (2) and
. In any case,
Figure 4 shows that increasing
g in
Equation (3) reduces the energy density and increases the energy fluctuations per particle, until
g ≈ 1 where the energy of small regions is minimized and the specific heat is independent of region size. Thus,
g =1 yields behavior that is most consistent with thermodynamic equilibrium: energy that is minimized and fluctuations in energy that yield extensive entropy. Empirical evidence for extensive entropy on the scale of nanometers inside bulk materials comes from measurements of NSHB that show constant specific heat for independently relaxing regions [
36], even for very small regions having
n ~ 10 molecules [
37].
3. Comparison of Computer Simulations with Measurements
The nonlinear correction also improves agreement between computer simulations and the measured response of many materials. The symbols in
Figure 5a show the magnetic susceptibility from single-crystal gadolinium as a function of reduced temperature. At high temperatures the data have a slope of −1.0, consistent with the Curie-Weiss law. As
T →
TC, the red (dashed) line from simulations of the Ising model using Boltzmann’s factor alone shows a slope of −1.24, consistent with the expectation from renormalization group theory for the homogeneous Ising model in the canonical ensemble. However, close inspection of the data reveals that the slope is not constant as
T →
TC. The solid (black) curve in
Figure 5a, which shows improved agreement with the data at all temperatures, comes from simulations of the same Ising model with the nonlinear correction (
Equation (2)) expected for heterogeneous systems obeying nanothermodynamics.
Figure 5b shows the difference between the data (symbols) and simulations of the Ising model without (dashed line), and with (solid line at the origin), the nonlinear correction. Indeed, using
g = 1 with the optimal region size (
n = 27) reduces the standard deviation between the Ising model and the data by an order of magnitude.
Figure 5c shows the effective scaling exponent γ
eff as a function of reduced temperature, from the magnitude of the slope when plotted as in
Figure 5a. The data (symbols) and simulations with nonlinear correction (solid line) show conspicuous features that clearly differ from the monotonic behavior [
38] of simulations using Boltzmann’s factor alone (dashed line). In fact, when measured to within 0.01% of
TC, ultra-high-purity crystals of gadolinium show a sharp maximum with γ
eff > 1.5, and γ
eff → 1 as
T →
TC [
39], consistent with mean-field theory at the transition.
The solid line in
Figure 6 shows the excess specific heat measured in the colossal magneto-resistance material LaMnO
3. The peak identifies the phase transition from a Jahn-Teller distortion that occurs at about 730 K. The dashed line comes from simulations of the Ising model using Boltzmann’s factor alone (
g = 0), while the solid symbols come from the same model with the nonlinear correction (
g = 1) and the optimal region size of
n = 27. Again the nonlinear correction gives significantly better agreement with the measured behavior.
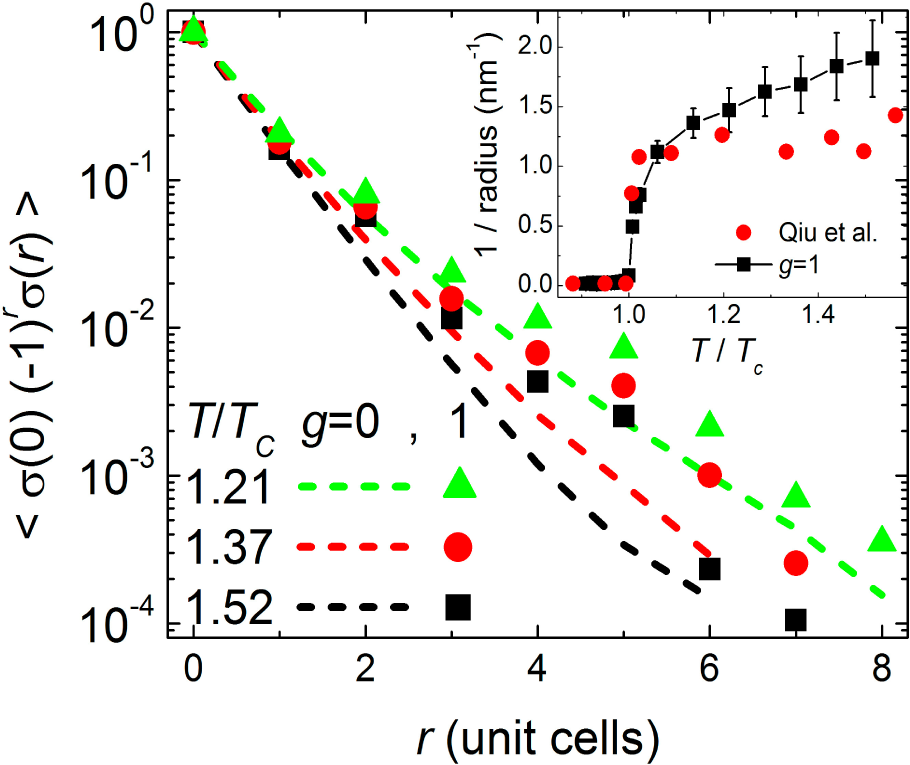
Direct evidence for heterogeneous correlations in crystals of LaMnO
3 comes from neutron scattering [
44,
45]. The upper two lines in
Figure 7 show the pair distribution function (PDF) measured above, and below, the Jahn-Teller transition temperature. The difference between these PDFs (lower curve) shows strong correlations in the positions of neighboring atoms out to a distance of ~1.0 nm, then an abrupt loss in correlation, with a more-gradual loss in correlation beyond this abrupt jump. Strong correlations that persist for three lattice sites are consistent with
n = 3
3 used for the simulations in
Figure 6. The clear non-monotonic loss in correlation is incompatible with the classical Ornstein-Zernicke picture [
46], where the pair-correlation function is predicted to diminish smoothly and homogeneously around every atom. Thus, the classical picture of homogeneous correlations could change on length scales of nanometers, where quantum mechanics may influence the correlations.
Figure 8 shows the pair-correlation function from simulations of the Ising model without (
g = 0, dashed lines) and with (
g = 1, symbols) the nonlinear correction. When
g = 0 there is a smooth loss in correlation, characteristic of the classical picture. When
g = 1 there is stronger correlation over the three contiguous lattice sites within each region, then an abrupt loss in correlation to the neighboring region, consistent with the measured pair distribution function shown in the lower part of
Figure 7. The inset of
Figure 8 shows that linear regression on three adjacent sites in a region, from simulations with
g = 1, yields a correlation length that is similar to the radius of distinct regions determined by neutron scattering.
Additional direct evidence for heterogeneous correlations comes from multi-dimensional NMR [
47,
48]. Measurements and analysis [
37] yield an average size for the independently relaxing regions of 10, 76, and 390 molecules (or monomer units) in glycerol, ortho-terphenyl, and poly (vinyl acetate), respectively. The distribution of relaxation times gives response rates that can vary by several orders of magnitude across nanometer length scales. Nonresonant spectral hole burning measurements indicate that this heterogeneity corresponds to effective local temperatures that also vary between these regions, indicating
thermodynamic heterogeneity. Thus, accurate models and theories of nanometer-sized independently-relaxing regions must obey the laws of nanothermodynamics.
4. Nanocanonical Ensemble, Equilibrium Landau Theory, and Mean-Field Cluster Model
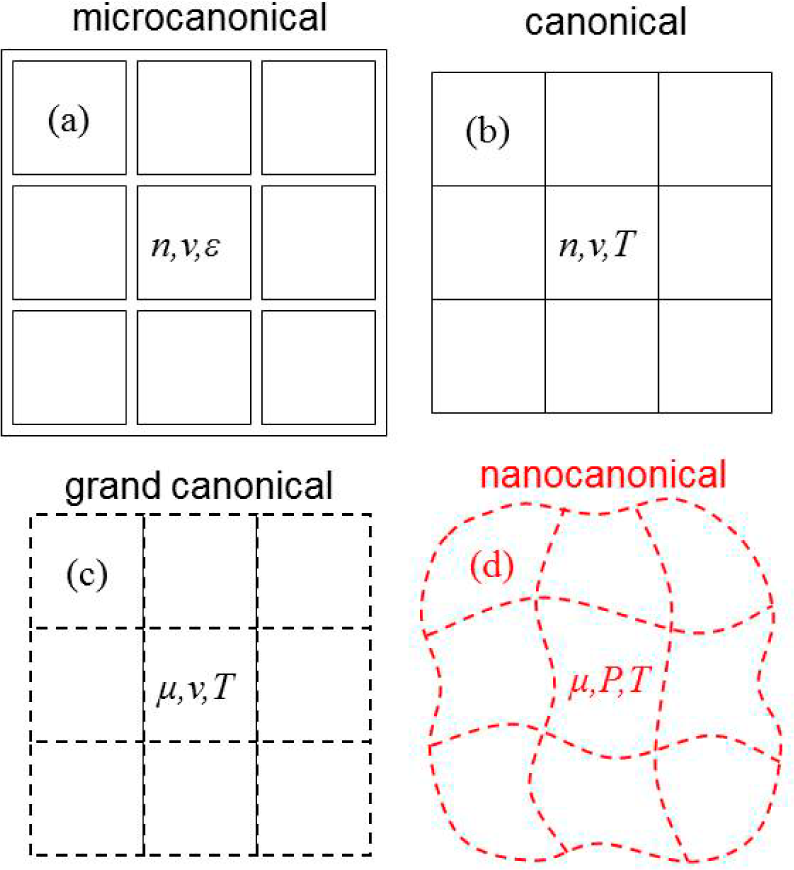
Figure 9 depicts various thermodynamic ensembles for independent fluctuations inside bulk samples.
Figure 9a shows fast fluctuations that do not have time to couple to their environment, so that the internal energy (
ε), volume (
v), and number of particles (
n) of each fluctuation are conserved, yielding the microcanonical ensemble.
Figure 9b shows slower fluctuations that allow heat to pass in and out, so that
ε fluctuates and
T replaces
ε as an environmental variable, yielding the canonical ensemble.
Figure 9c shows fluctuations where particles may join and leave each fluctuation, so that
n fluctuates and
μ replaces
n as an environmental variable, yielding the grand canonical ensemble.
Figure 9d shows completely-open fluctuations where density is conserved as particles join and leave each fluctuation, so that
v fluctuates and pressure (
P) replaces
v as an environmental variable, yielding Hill’s “generalized” ensemble [
2,
49]. This
μ,
P,
T ensemble might also be called “nanocanonical” in accordance with the other ensembles. The nanocanonical ensemble is ill-defined in standard thermodynamics. Indeed, the Gibbs-Duhem equation yields zero free energy for the nanocanonical ensemble, requiring at least one extensive environmental variable to control the size of the systems. For small systems, however, the subdivision potential accommodates non-extensive contributions to energy that allow the small systems to control their own size without external constraints. In fact, NSHB measurements show that some energy may remain localized in slow degrees of freedom for minutes, or even hours. Thus, the most relevant ensembles for independently fluctuating regions inside bulk samples are the microcanonical ensemble for fast fluctuations that do not have time to couple to their environment, and the nanocanonical ensemble for slow fluctuations that must couple fully to their environment without artificial constraints. Furthermore, because different ensembles yield different dynamics, accurate treatment of finite-sized fluctuations requires the correct ensemble.
The nanocanonical ensemble forms the basis of the mean-field cluster model and equilibrium Landau theory for phase transitions. In Landau theory, the symmetry of the system is used to obtain an energy per particle that depends quadratically on the order parameter (e.g., net alignment) of the region ε(m) = –½ε2m2, where ε2 is a constant parameter. When combined with the entropy, approximated to fourth order, the free energy per particle becomes f(m) = ε(m) – TSm/m ≈ f0 + ½ (kBT – ε2) m2 + kBT m4/12, where f0 = –kBT ln(2). For simplicity the integral over all possible energies is extended to m = ±∞, yielding the canonical partition function
. In the usual thermodynamic limit, the system size is assumed to be very large n → ∞, so that the system remains at a minimum in Helmholtz free energy, found from ∂f(m)/∂m = 0. Whereas in the nanocanonical ensemble, region size is also allowed to fluctuate, minimizing the free energy for fluctuations without artificial size constraints. The partition function is
, where n0 is a minimum size for thermal behavior. The mean-field cluster model improves upon the nanocanonical Landau theory by using exact expressions for the alignment entropy of each region Sm, and replacing the integral in Zn by a sum over allowed alignments. In both cases, μ/kBT is adjusted to the constant value that gives best agreement with temperature-dependent data; similar to, but simplified from, an ideal gas where μ/kBT depends logarithmically on temperature.
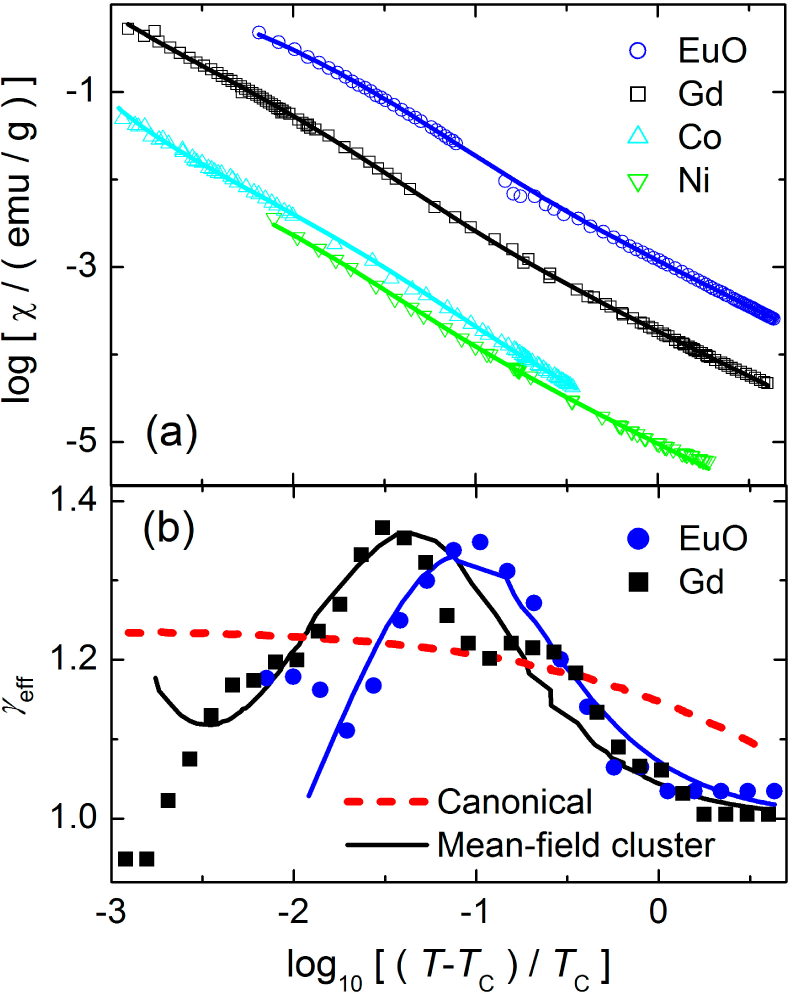
Figure 10 shows paramagnetic susceptibility (
χ) as a function of reduced temperature above the ferromagnetic transition,
T >
TC. The symbols are from measurements on four standard ferromagnetic materials, as given in the legend. The classical mean-field theory (Curie-Weiss law) for homogeneous systems predicts a constant critical-scaling exponent of
γ = 1 in
χ ∝1/(
T −
TC)
γ whereas the data show a steeper slope, especially around (
T –
TC)/
TC ≈ 0.01. Nearer
TC, microscopic models that assume homogeneous correlations via the canonical ensemble predict a constant slope with scaling exponents of γ > 1, whereas close inspection of the data shows temperature-dependent curvature. The solid curves are from the mean-field cluster model, with
μ/
kBT as the constant parameter governing the temperature- dependent shape of the susceptibility. Even in the raw data it is possible to see that the mean-field cluster model for a heterogeneous distribution of independently relaxing regions gives better agreement than homogeneous models.
Figure 10b shows the effective scaling exponent γ
eff as a function of reduced temperature for two sets of data from
Figure 10a. Again these data are clearly incompatible with the Ising model in the canonical ensemble (dashed line). Indeed, more-recent measurements on ultra-pure Gd crystals show that as
T →
TC the critical scaling exponent returns to the classical value γ
eff = 1 [
39], consistent with mean-field theory in the nanocanonical ensemble (solid lines). Thus, the nanocanonical ensemble significantly improves agreement between mean-field models and measured response, similar to how the nonlinear correction from nanothermodynamics improves agreement with computer simulations of the microscopic version of the same model, as shown in
Figures 5 and
6.
The lower two sets of symbols in
Figure 11 show inverse magnetic susceptibility versus temperature from two ferromagnetic materials. The data are some of the same as shown in
Figure 10, but on a linear scale to emphasize the high-temperature regime. At
T > 1.2
TC the data follow a straight line, consistent with the Curie-Weiss law 1/
χ ∝ (
T –
θ), where
θ is the Weiss temperature. Again as
T →
TC there is curvature, consistent with the solid curves from the mean-field cluster model for non-classical critical scaling. The upper two sets of symbols in
Figure 11 show the temperature dependence of the peak-loss frequency
fp, from measurements of dielectric susceptibility of two glass-forming liquids. The data are plotted in a way that yields a straight line if the systems obey the VFT law for super-Arrehenius activation 1/ln(
f0/
fp) ∝ (
T –
TV), where
TV is the Vogel temperature. Similar behavior is characteristic of the WLF formula for scaling of the thermal and dynamic properties of polymers [
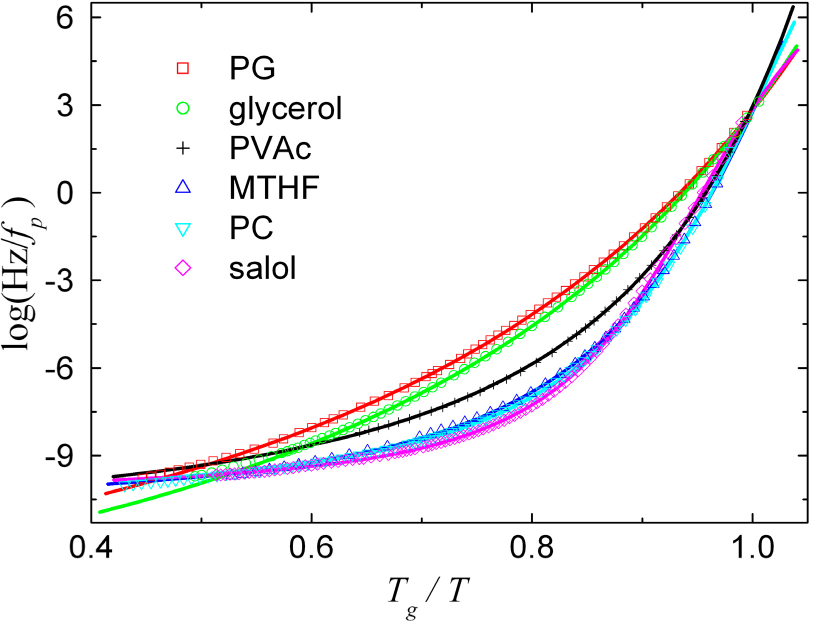
14]. Note the mathematical similarity between the VFT and Curie-Weiss laws, and the qualitatively similar curvature as the critical temperatures are approached. Indeed, VFT-like behavior and measured deviations can also be characterized by the mean-field cluster model, as shown by the solid curves. In glass-forming liquids the underlying phase transition is subtler, due to larger fluctuations in smaller regions that broaden the transition, and dynamical slowing as the transition is approached.
Figure 12 is an Angell plot of 1/
fp from several glass-forming liquids (symbols) that show VFT-like behavior. Again the solid lines show that the VFT law and measured deviations can be characterized by the mean-field cluster model for a phase transition in a nanocanonical distribution of independently relaxing regions.
Nanothermodynamics is needed to obtain the heterogeneous distribution of independently relaxing regions inside bulk samples, found from minimizing the free energy in the nanocanonical ensemble. Of course the size of individual regions is dynamic, fluctuating with time to increase the total entropy. However, in thermal equilibrium the average size and distribution are well defined. Connecting the nanocanonical distribution of region sizes to the equilibrium spectrum of response requires a size-dependent relaxation rate. Good agreement with data is obtained using relaxation rates that vary exponentially with inverse size,
wn =
w∞ exp(
CV/2
nkB). Here
w∞ is the asymptotic relaxation rate for large regions and
CV is the heat capacity for the relaxing degrees of freedom in an average-sized region. The inverse-size dependence in
wn may be related to the 1/
n energy reduction due to the nonlinear correction, as shown by the dashed lines in
Figure 4a. The
CV/
n dependence in
wn signifies the importance of thermal fluctuations: large regions have large heat capacity so that they fluctuate less (per particle) than small regions, reducing the likelihood that large regions will fluctuate between localized states, slowing their relaxation. Indeed, the factors of
N used to match the amplitudes in
Figures 1 and
2 confirm that the mean-squared fluctuations vary inversely proportional to size. The specific form of
wn can be found using a model where fluctuations cause an overlap between discrete energy levels [
5]. In any case, the inverse-size dependence in the relaxation rate yields good agreement with measured spectra of response.
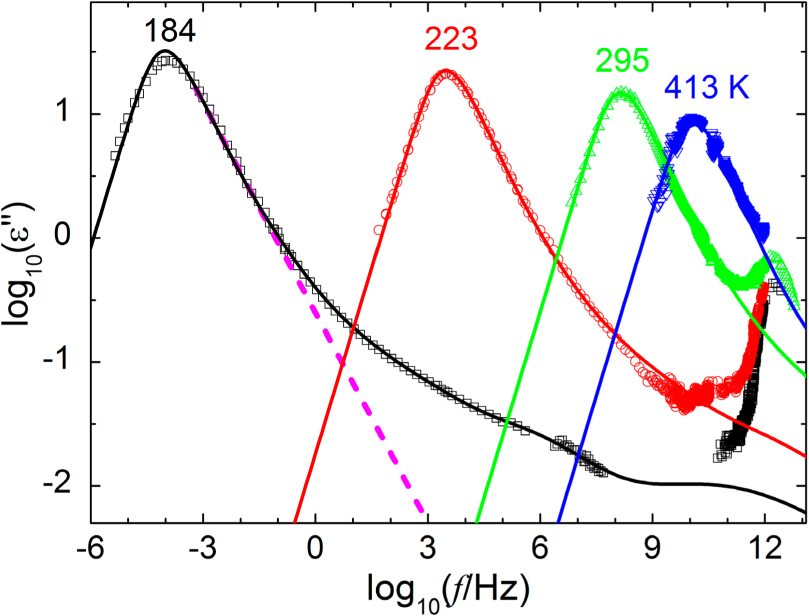
The symbols in
Figure 13 show the frequency-dependent dielectric loss of glycerol at four different temperatures. The solid curves come from
wn, with the distribution of sizes given by thermal equilibrium of the nanocanonical ensemble. The solid curves show good agreement with several observed features. The asymmetric slopes come from the inverse-size dependence in
wn, yielding +1 on the low-frequency side of the peak and –β on the high-frequency side, similar to the KWW law for stretched-exponential relaxation shown by the dashed line. The high-frequency wing comes from small regions, when
CV/
n >
kB. The step-like features that start at the highest frequencies come from integer values of
n = 1, 2, and perhaps 3. For
n > 3 the response from discrete regions merges into a smooth curve. Note that the widths of the dielectric-loss peaks are nearly constant over a wide range of temperatures. This approximate time-temperature superposition is incompatible with a static distribution of activation energies, indicating that the response involves thermal fluctuations that cancel the explicit temperature dependence in the Arrhenius law [
14], consistent with
wn. Also note that
wn predicts that the width and spectrum of response are governed primarily by the specific heat of an average-sized region. Indeed,
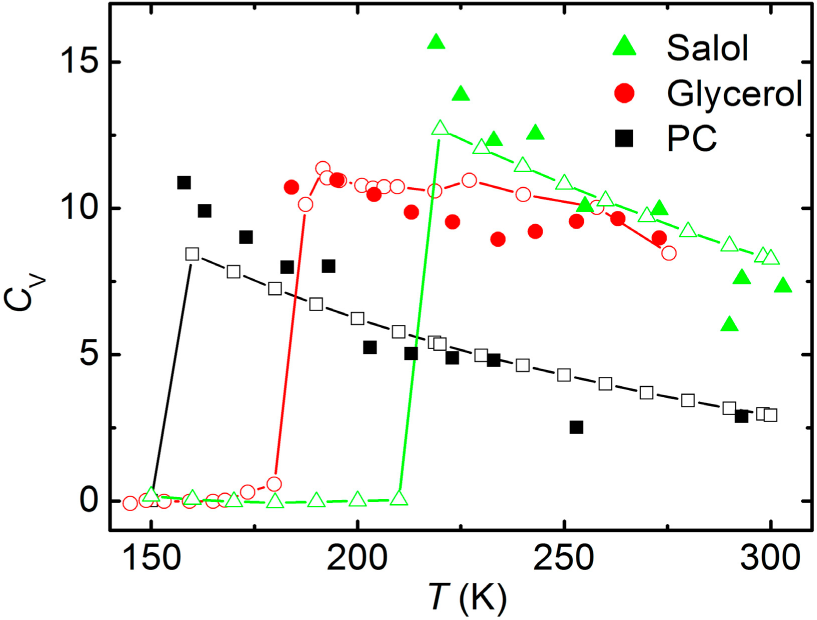
Figure 14 shows that the temperature dependences of
CV deduced from dielectric-loss spectra agree with the values found directly from measurements of excess specific heat.
5. Discussion
Some remarkably universal empirical formulas have been used to characterize the measured response from many materials. The Kohlrausch-Williams-Watts law is used for stretched-exponential relaxation, as shown in
Figure 13. The Vogel-Fulcher law is used for super-Arrhenius activation, as shown in
Figures 11 and
12. Non-classical critical-scaling exponents are used for behavior near phase transitions, as shown in
Figures 5,
10 and
11. Non-Nyquist fluctuations, having a frequency dependence of 1/
fα with α ~ 1, are used for the electronic noise in most materials, as shown in
Figures 1 and
2. In many cases these expressions are convenient mathematical formulas for cataloging the measured response of complex systems, but data of sufficient quality over broad enough range invariably show deviations from these formulas. Many models have been proposed for each of the empirical formulas, so that the deviations may be a decisive way to distinguish between models. Nanothermodynamics provides a common foundation for all of these empirical formulas, including many of the measured deviations. Moreover, nanothermodynamics is necessary to describe the thermal equilibrium of any sample that contains independently fluctuating regions if the fluctuations themselves are to govern the distribution of region sizes.
Of course nanothermodynamics is not a universal theory of everything, there must be a mechanism that allows independently fluctuating regions inside the sample. For example, thermodynamic heterogeneity is not expected for the coherent ground state of superfluids and superconductors. Indeed, non-classical critical scaling from the homogeneous XY model provides extraordinary agreement with measured specific heat near the lambda transition in
4He [
60]. Similarly, simulations using nanothermodynamics differ from Onsager’s solution of the Ising model, because the canonical ensemble in an infinite sample with homogeneous correlations is incompatible with a heterogeneous distribution of independently relaxing regions. Another example is Tsallis entropy that has been used to characterize the properties of various systems [
61]. In fact, some form of non-extensive entropy [
62] is necessary to explain the behavior of Monte Carlo simulations that use Boltzmann’s factor alone, as shown by
g = 0 in
Figure 4 where the energy fluctuations in small regions are non-extensive. Also, the 1/
f characteristics found in most music, markets, and human perception may have a psychological, not physical basis; but perhaps human preferences are influenced by our environment.
Standard models based on homogeneous thermodynamics have been unable to explain several features in the dynamics of complex systems. The deviations may be quite subtle. Indeed, it is difficult to see curvature in the data on a log-log critical-scaling plot, as shown by
Figures 5a and
10a. Nevertheless, other researchers have also recognized that most ferromagnetic materials deviate from standard critical-scaling behavior. In 1989 Collins wrote [
63]: “The critical exponents of iron and nickel are very similar to each other, while those for cobalt are clearly different. There is no theoretical understanding of these results.” Also in 1989 Hohenemser
et al. wrote [
64]: “At the same time our review makes clear that when one restricts the analysis to the best experiments, only a few materials correspond unambiguously to these models, while most do not.” In fact, by plotting the residuals (as in
Figure 5b) there is obvious improvement between measured behavior and the Ising model when treated using concepts from nanothermodynamics. Moreover, the monotonic behavior of standard simulations of the Ising model cannot match the sharp temperature-dependent features in the effective scaling exponent, as shown in
Figures 5c and
10b. In any case, the nanocanonical ensemble must be used if independently-fluctuating regions inside bulk samples are to be included in the thermal equilibrium.