Entropy, Age and Time Operator
Abstract
:1. Introduction
2. Time Operator and Age
3. Lyapunov Functionals and Entropies
- LF1, for all y.
- LF2 The equation has the unique solution .
- LF3 vanishes as .
- LF4 is monotonically decreasing: , if t2 > t1.
4. Age in Terms of Entropy
- Tsallis entropy:
- Kaniadakis entropy:
5. Concluding Remarks
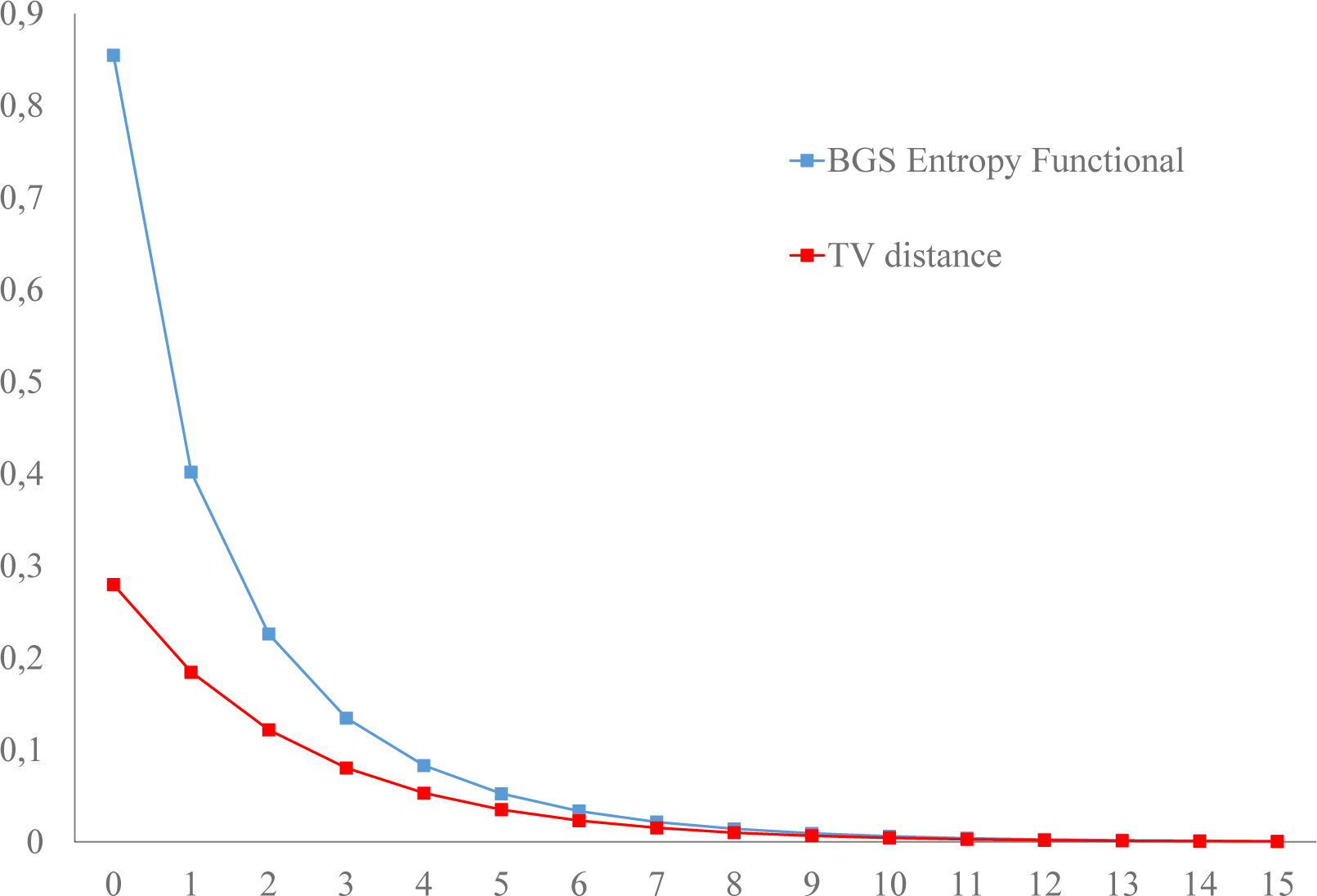
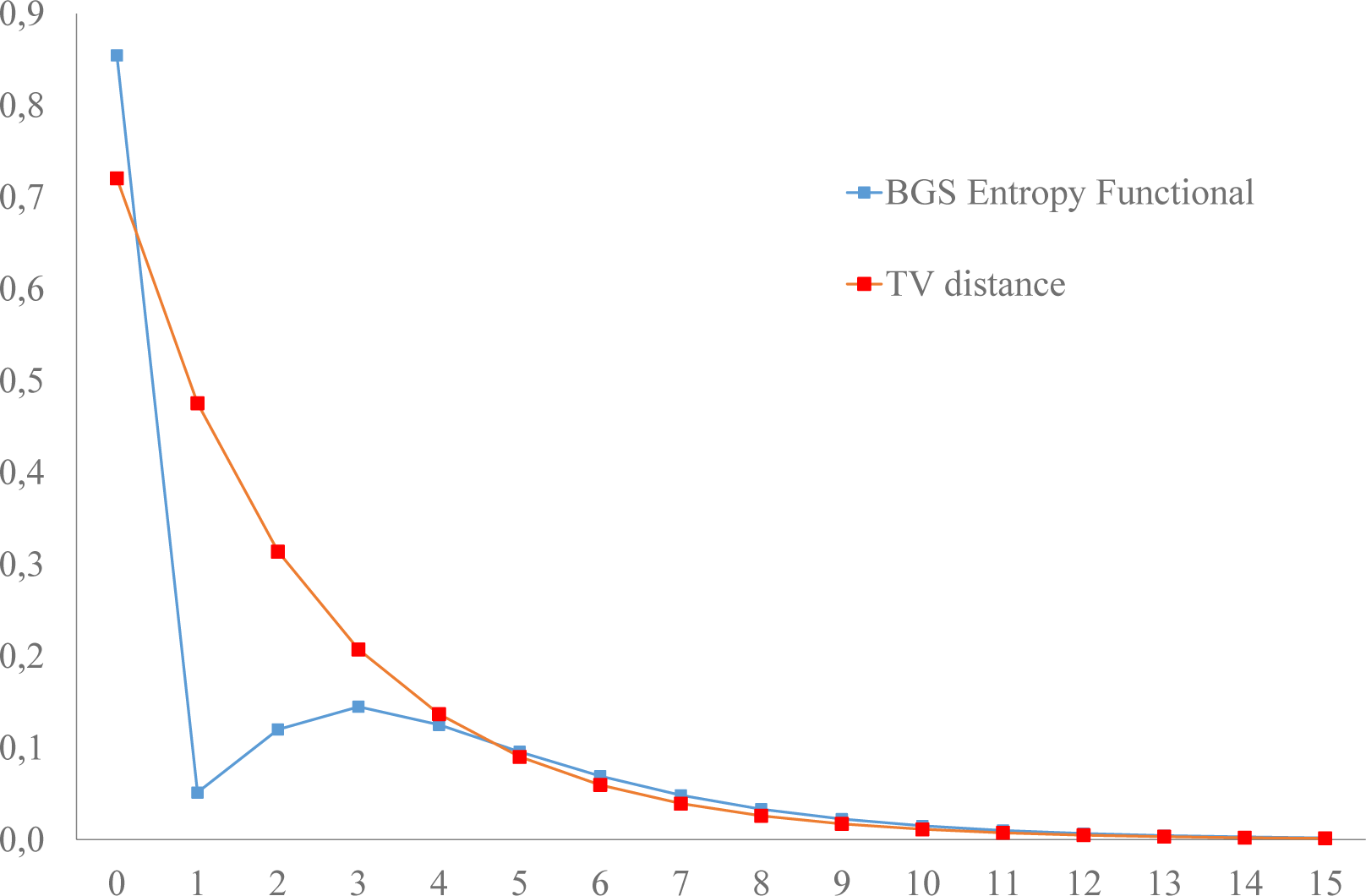
- The Lyapunov functionals defined in terms of norms (total variation and r-norms; Equation (29) in [20] and Equation (14), respectively) evolve monotonically towards equilibrium, respecting the second law of thermodynamics; Figures 1 and 2:
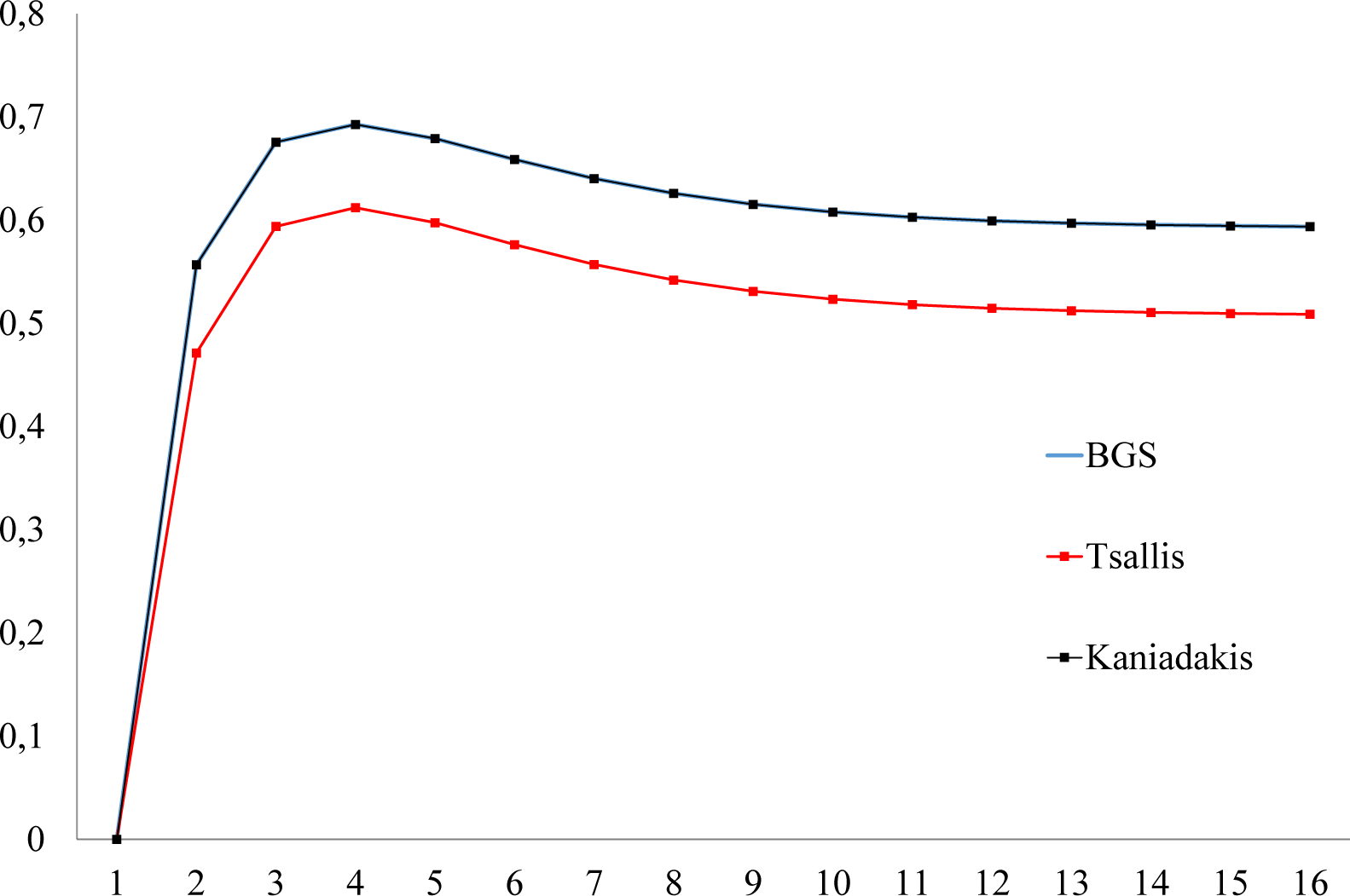
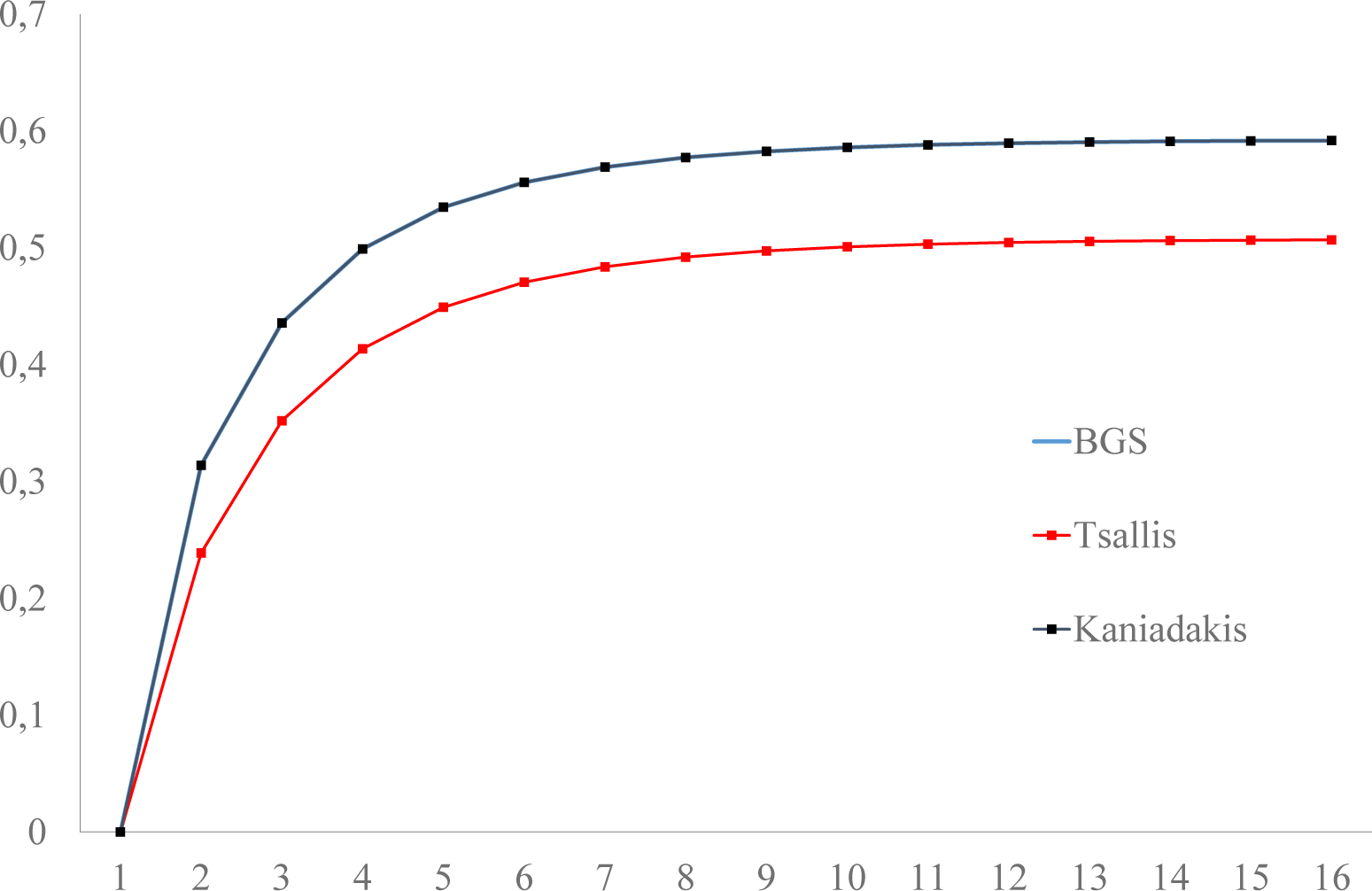
- For the same system, the Lyapunov functionals defined in terms of entropies evolve violating the second law of thermodynamics in three ways (Figure 3): (1) the approach to equilibrium is non-monotonic; (2) the equilibrium distribution is not the maximum entropy distribution; and (3) the initial entropy is lower than the equilibrium entropy, then entropy increases above equilibrium and then decreases monotonically to equilibrium. Monotonicity violations (1) have been reported for non-doubly-stochastic regular Markov chains ([42] (Theorem 5, p. 104); p. 81 in [43]). Examples of evolutions where the maximum entropy is not the equilibrium entropy (2), therefore violating Jaynes [47] maximum entropy principle, have also been reported [48] (pp. 82–83 in [43]). We did not find entropy evolutions with the behavior (3) in Figure 3.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pauli, W. Prinzipien der Quantentheorie 1. In Encyclopedia of Physics; Volume 5, Flugge, S., Ed.; Springer-Verlag: Berlin, Germany, 1958; English Translation: General Principles of Quantum Mechanics; Achuthan, P., Venkatesan, K., Translater; Springer: Berlin, Germany, 1980. [Google Scholar]
- Putnam, C.R. Commutation Properties of Hilbert Space Operators and Related Topic; Springer: Berlin, Germany, 1967. [Google Scholar]
- Misra, B. Nonequilibrium entropy, Lyapounov variables, and ergodic properties of classical systems. Proc. Natl. Acad. Sci. USA 1978, 75, 1627–1631. [Google Scholar]
- Misra, B.; Prigogine, I.; Courbage, M. Lyapunov variable: Entropy and measurements in quantum mechanics. Proc. Natl. Acad. Sci. USA 1979, 76, 4768–4772. [Google Scholar]
- Courbage, M. On necessary and sufficient conditions for the existence of Time and Entropy Operators in Quantum Mechanics. Lett. Math. Phys 1980, 4, 425–432. [Google Scholar]
- Lockhart, C.M.; Misra, B. Irreversebility and measurement in quantum mechanics. Physica A 1986, 136, 47–76. [Google Scholar]
- Antoniou, I.; Suchanecki, Z.; Laura, R.; Tasaki, S. Intrinsic irreversibility of quantum systems with diagonal singularity. Physica A 1997, 241, 737–772. [Google Scholar]
- Courbage, M.; Fathi, S. Decay probability distribution of quantum-mechanical unstable systems and time operator. Physica A 2008, 387, 2205–2224. [Google Scholar]
- Misra, B.; Prigogine, I.; Courbage, M. From deterministic dynamics to probabilistic descriptions. Physica A 1979, 98, 1–26. [Google Scholar]
- Prigogine, I. From Being to Becoming; Freeman: New York, NY, USA, 1980. [Google Scholar]
- Courbage, M.; Misra, B. On the equivalence between Bernoulli dynamical systems and stochastic Markov processes. Physica A 1980, 104, 359–377. [Google Scholar]
- Courbage, M. Intrinsic Irreversibility of Kolmogorov Dynamical Systems. Physica A 1983, 122, 459–482. [Google Scholar]
- Antoniou, I. The Time Operator of the Cusp Map. Chaos Soliton Fractal 2001, 12, 1619–1627. [Google Scholar]
- Gustafson, K.; Misra, B. Canonical Commutation Relations of Quantum Mechanics and Stochastic Regularity. Lett. Math. Phys 1976, 1, 275–280. [Google Scholar]
- Gustafson, K.; Goodrich, R. Kolmogorov systems and Haar systems. Colloq. Math. Soc. Janos Bolyai 1987, 49, 401–416. [Google Scholar]
- Gustafson, K. Lectures on Computational Fluid Dynamics, Mathematical Physic and Linear Algebra; Abe, T., Kuwahara, K., Eds.; World Scientific: Singapore, Singapore, 1997. [Google Scholar]
- Antoniou, I.; Gustafson, K. Wavelets and Stochastic Processes. Math. Comput. Simul 1999, 49, 81–104. [Google Scholar]
- Antoniou, I.; Prigogine, I.; Sadovnichii, V.; Shkarin, S. Time Operator for Diffusion. Chaos Soliton Fractal 2000, 11, 465–477. [Google Scholar]
- Antoniou, I.; Christidis, T. Bergson’s Time and the Time Operator. Mind Matter 2010, 8, 185–202. [Google Scholar]
- Gialampoukidis, I.; Gustafson, K.; Antoniou, I. Time Operator of Markov Chains and Mixing Times. Applications to Financial Data. Physica A 2014, 415, 141–155. [Google Scholar]
- Gialampoukidis, I.; Gustafson, K.; Antoniou, I. Financial Time Operator for random walk markets. Chaos Soliton Fractal 2013, 57, 62–72. [Google Scholar]
- Aldous, D.; Fill, J. Reversible Markov Chains and Random Walks on Graphs, 2002. 14 January 2015.
- Levin, D.A.; Peres, Y.; Wilmer, E.L. Markov Chains and Mixing Times; American Mathematical Society: Providence, RI, USA, 2009. [Google Scholar]
- Aldous, D.; Lovász, L.; Winkler, P. Mixing times for uniformly ergodic Markov chains. Stoch Process. Appl 1997, 71, 165–185. [Google Scholar]
- Levene, M.; Loizou, G. Kemeny’s constant and the random surfer. Am. Math. Mon 2002, 741–745. [Google Scholar]
- Jenamani, M.; Mohapatra, P.K.; Ghose, S. A stochastic model of e-customer behavior. Electron. Commer. R. A 2003, 2, 81–94. [Google Scholar]
- Kirkland, S. Fastest expected time to mixing for a Markov chain on a directed graph. Linear Algebra Appl 2010, 433, 1988–1996. [Google Scholar]
- Crisostomi, E.; Kirkland, S.; Shorten, R. A. Google-like model of road network dynamics and its application to regulation and control. Int. J. Control 2011, 84, 633–651. [Google Scholar]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual Web search engine. Comput. Netw. ISDN 1998, 30, 107–117. [Google Scholar]
- Hamilton, J.D. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 1989, 357–384. [Google Scholar]
- Lockhart, C.M.; Misra, B.; Prigogine, I. Geodesic instability and internal time in relativistic cosmology. Phys. Rev. D 1982, 25, 921. [Google Scholar]
- Kemeny, J.G.; Snell, J.L. (Eds.) Finite Markov Chains; D. Van Nostrand: Princeton, NJ, USA, 1960.
- Howard, R.A. Dynamic Probabilistic Systems; Wiley: New York, NY, USA, 1971; Volume I. [Google Scholar]
- De La Llave, R. Rates of convergence to equilibrium in the Prigogine-Misra-Courbage theory of irreversibility. J. Stat. Phys 1982, 29, 17–31. [Google Scholar]
- Atmanspacher, H. Dynamical Entropy in Dynamical Systems; Springer: Berlin, Germany, 1997. [Google Scholar]
- Mackey, M.C. The dynamic origin of increasing entropy. Rev. Mod. Phys 1989, 61, 981. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys 1988, 52, 479–487. [Google Scholar]
- Kaniadakis, G. Non–linear kinetics underlying generalized statistics. Physica A 2001, 296, 405–425. [Google Scholar]
- Kaniadakis, G. H–theorem and generalized entropies within the framework of nonlinear kinetics. Phys. Lett. A 2001, 288, 283–291. [Google Scholar]
- Kaniadakis, G.; Lissia, M.; Scarfone, A.M. Deformed logarithms and entropies. Physica A 2004, 340, 41–49. [Google Scholar]
- Gorban, A.N. Entropy: The Markov Ordering Approach. Entropy 2010, 12, 1145–1193. [Google Scholar]
- Cover, T.M. Which processes satisfy the second law? In PhysicaL Origins of Time Asymmetry; Halliwell, J.J., Pérez-Mercader, J., Zurek, W.H., Eds.; Cambridge University Press: Cambridge, UK, 1994; pp. 98–107. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Kaniadakis, G. Theoretical foundations and mathematical formalism of the power-law tailed statistical distributions. Entropy 2013, 15, 3983–4010. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics, From Heat Engines to Dissipative Structures; Wiley: Chichester, UK, 1998. [Google Scholar]
- Tsallis, C. The Nonadditive Entropy Sq and Its Applications in Physics and Elsewhere: Some Remarks. Entropy 2011, 13, 1765–1804. [Google Scholar]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Landsberg, P.T. Is equilibrium always an entropy maximum? J. Stat. Phys 1984, 35, 159–169. [Google Scholar]

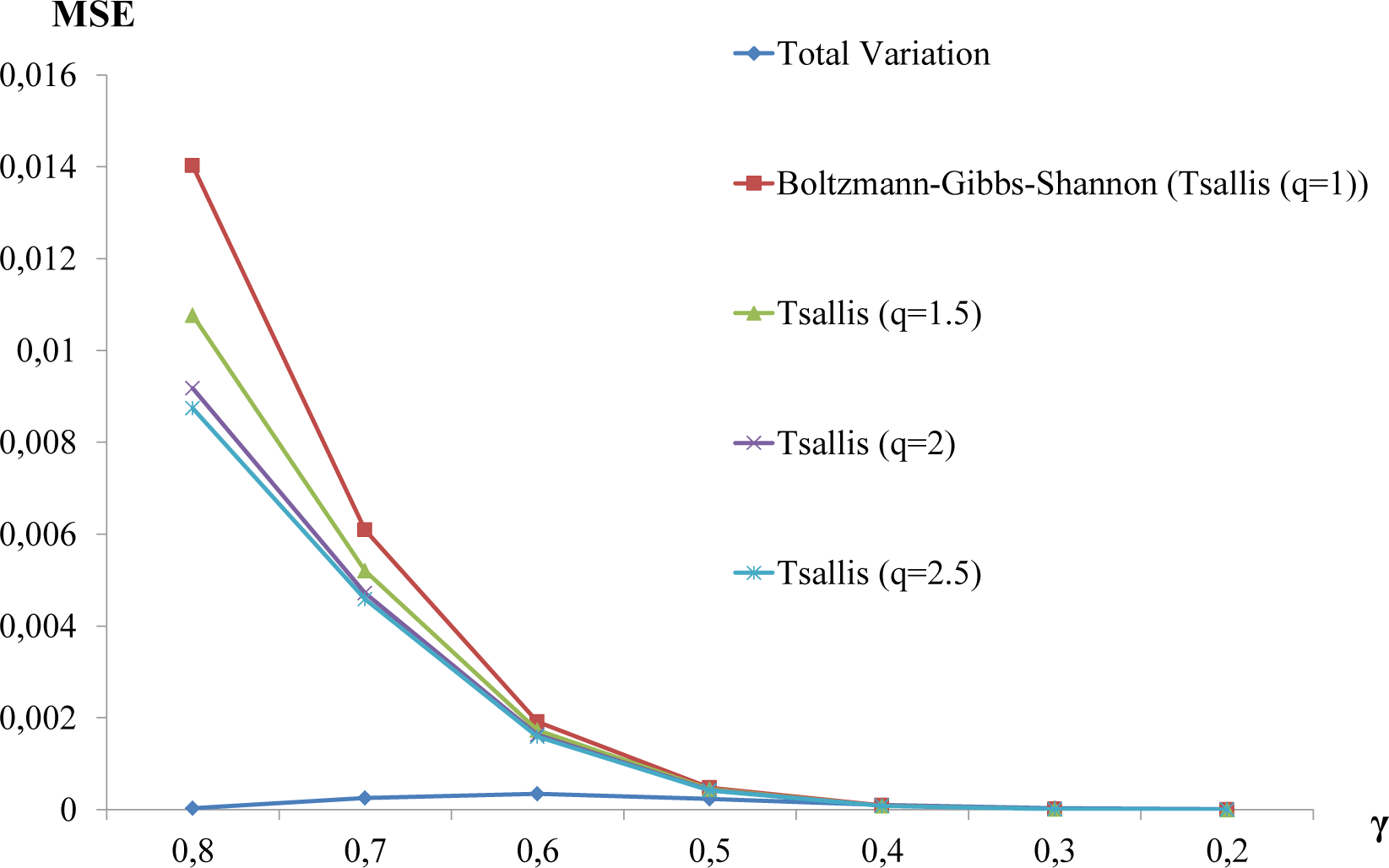

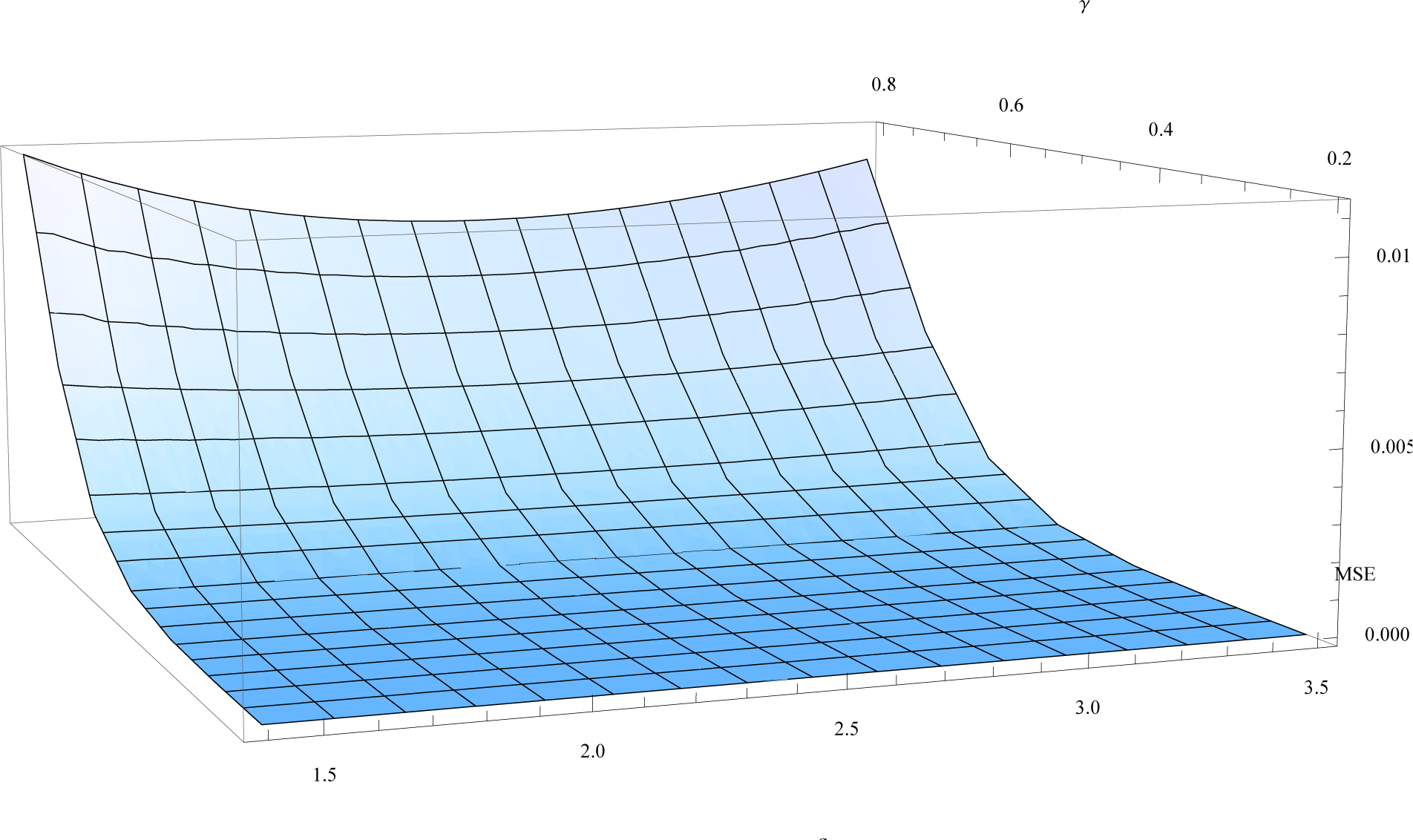
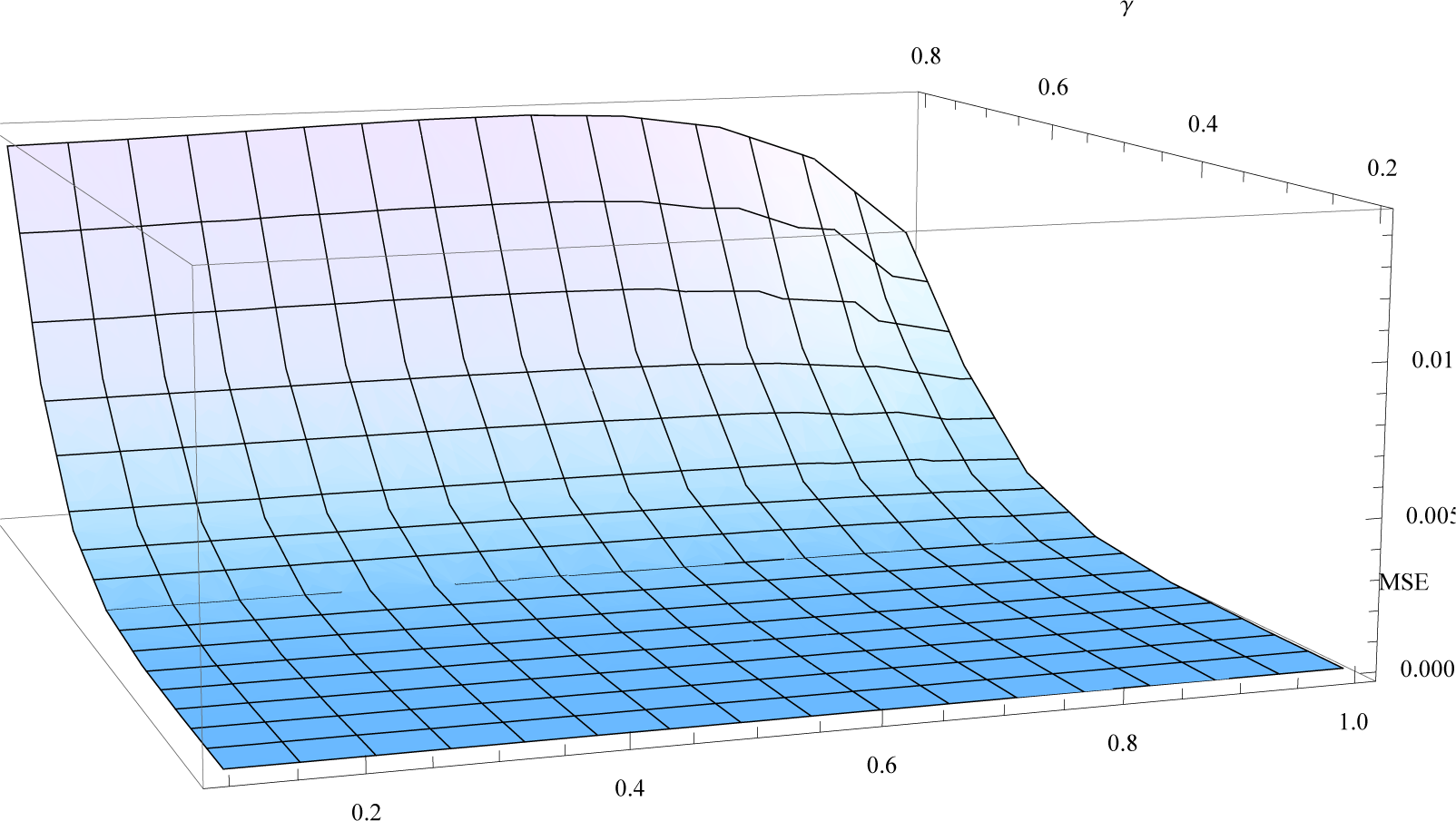

| Rate γ | Pearson Coefficient | Mean Square Error | ||
|---|---|---|---|---|
| 0.8 | 1.975(0.007) | −4.932(0.030) | −1.000 | 0.00002844 |
| 0.7 | 1.047(0.012) | −2.941(0.067) | −0.998 | 0.00025143 |
| 0.6 | 0.600(0.010) | −1.933(0.075) | −0.996 | 0.00034544 |
| 0.5 | 0.350(0.007) | −1.340(0.067) | −0.993 | 0.00023253 |
| 0.4 | 0.198(0.004) | −0.947(0.053) | −0.991 | 0.00010321 |
| 0.3 | 0.102(0.002) | −0.656(0.037) | −0.990 | 0.00003005 |
| 0.2 | 0.043(0.001) | −0.417(0.021) | −0.992 | 0.00000431 |
| 0.1 | 0.100(0.000) | −0.203(0.007) | −0.997 | 0.00000011 |
| Rate γ | Pearson Coefficient | Mean Square Error | ||
|---|---|---|---|---|
| 0.8 | 1.410(0.068) | −2.874(0.269) | −0.979 | 0.01402500 |
| 0.7 | 0.846(0.038) | −2.331(0.228) | −0.978 | 0.00609177 |
| 0.6 | 0.522(0.020) | −1.980(0.176) | −0.981 | 0.00191404 |
| 0.5 | 0.319(0.009) | −1.743(0.127) | −0.987 | 0.00046904 |
| 0.4 | 0.185(0.004) | −1.586(0.085) | −0.993 | 0.00008470 |
| 0.3 | 0.097(0.001) | −1.486(0.051) | −0.997 | 0.00000927 |
| 0.2 | 0.041(0.000) | −1.427(0.023) | −0.999 | 0.00000039 |
| 0.1 | 0.010(0.000) | −1.396(0.006) | −1.000 | 0.00000000 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gialampoukidis, I.; Antoniou, I. Entropy, Age and Time Operator. Entropy 2015, 17, 407-424. https://doi.org/10.3390/e17010407
Gialampoukidis I, Antoniou I. Entropy, Age and Time Operator. Entropy. 2015; 17(1):407-424. https://doi.org/10.3390/e17010407
Chicago/Turabian StyleGialampoukidis, Ilias, and Ioannis Antoniou. 2015. "Entropy, Age and Time Operator" Entropy 17, no. 1: 407-424. https://doi.org/10.3390/e17010407
APA StyleGialampoukidis, I., & Antoniou, I. (2015). Entropy, Age and Time Operator. Entropy, 17(1), 407-424. https://doi.org/10.3390/e17010407





