An Entropy-Based Upper Bound Methodology for Robust Predictive Multi-Mode RCPSP Schedules
Abstract
:1. Introduction
2. Literature Review
2.1. Resource Constrained Project Scheduling Problem
2.1.1. Multi-mode Resource Constrained Project Scheduling Problem
2.1.2. Objectives Solved
2.1.2.1. Time Performance Indicators
2.1.2.2. Financial Indicators
2.1.3. Solution Procedures
2.1.3.1. Exact Procedures
2.1.3.2. Meta-heuristics
2.2. Uncertainty in Project Management
2.2.1. Buffer Time Generation
2.2.2. Entropy as a Measure of Uncertainty
2.3. Robustness
3. Methodology
Repeat until feasible Randomly pick benchmark instance If feasible then Stage I: Generate a schedule with minimized makespan (makespanI) Stage II: Calculate Stage I-schedule’s entropy (makespanII) Stage III: Generate schedule with maximized robustness (makespanIII ≤ makespanII) End End
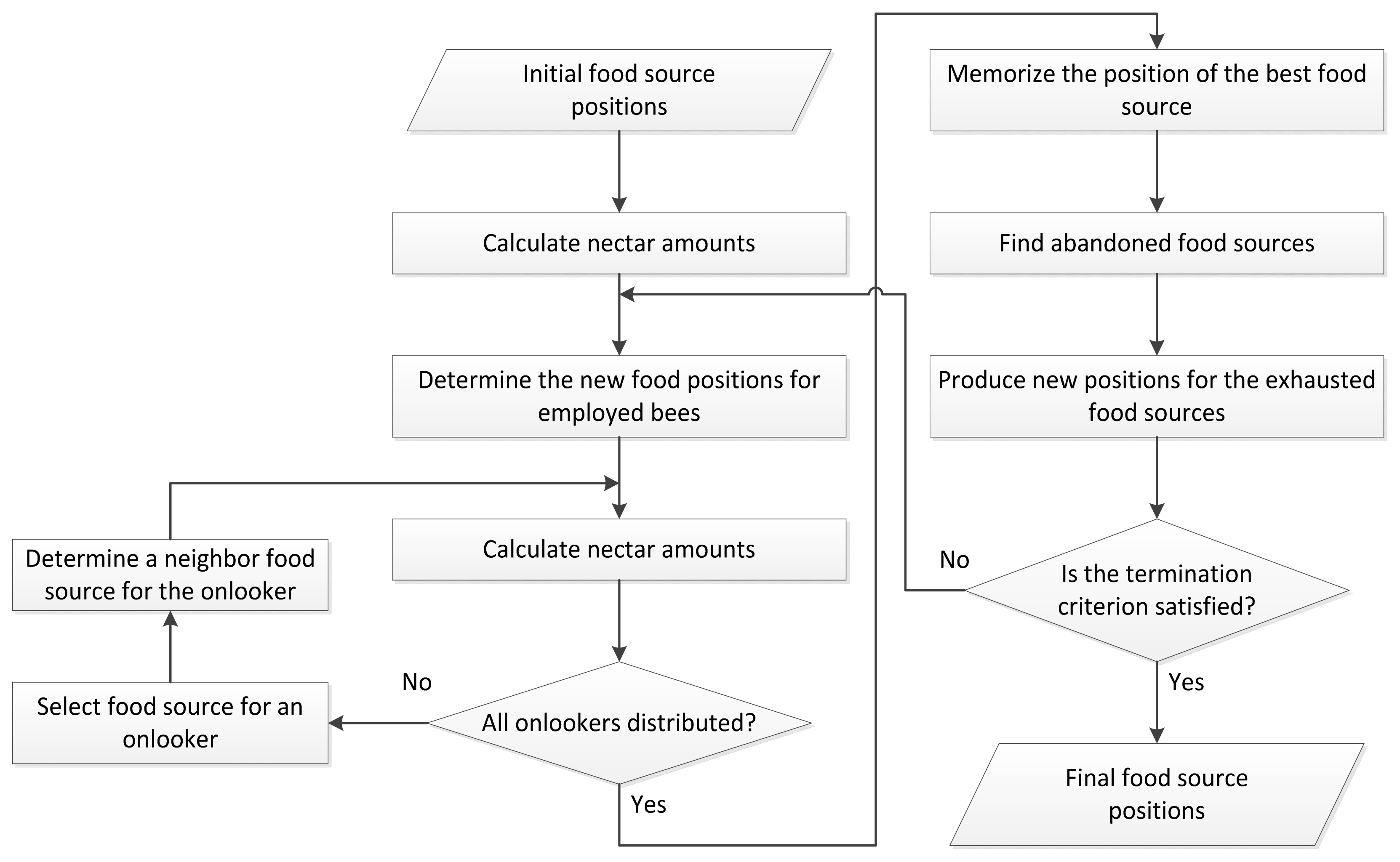
3.1. Artificial Bee Colony
-
The initialization phase: The initial solutions are n-dimensional real vectors generated randomly.
-
The employed bee phase: Each employed bee is associated with a solution and they apply a random modification (local search) on the solution (assigned food source) to find a new solution (new food source). Once the new food source is obtained, it will be evaluated and compared to the previous. If the fitness of the new solution is better than the previous, the bee will forget the old food source and memorize the new one. Otherwise, she will keep applying modifications until the abandonment criterion is reached.
-
The onlooker bee phase: When all employed bees have completed their local search, they share the nectar information of their food source with the onlookers, each of whom will then select a food source in a probabilistic manner. The probability by which an onlooker bee will choose a food source is calculated by:where pi is the probability by which an onlooker chooses a food source i, SN is the total number of food sources, and fi is the fitness value of the food source i. The onlooker bees tend to choose the food sources with better fitness value (higher amount of nectar).
-
The scout bee phase: If the quality of a solution can’t be improved after a predetermined number of trials (abandonment limit), the food source is abandoned, and the corresponding employed bee becomes a scout. This scout will then produce a randomly generated food source.
3.2. Three-Stage Procedure
3.2.1. Stage I—Initial Minimized Makespan Schedule
3.2.1.1. Mode Selection Rules
3.2.1.2. Activity Priority Rules
3.2.1.3. Initial Schedule Generation and Optimization
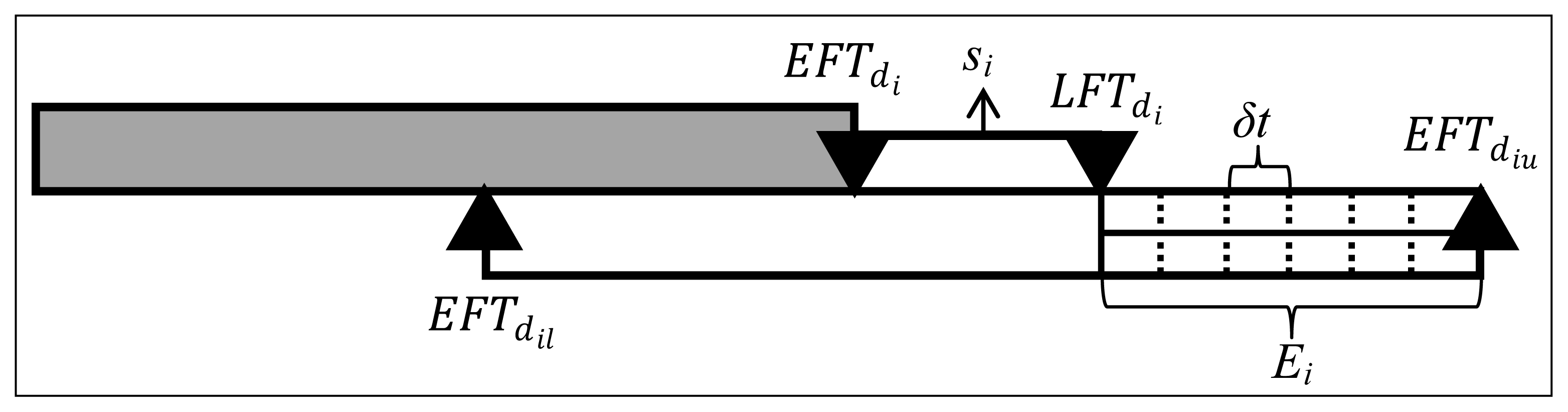
3.3. Stage II—Determining the Schedule’s Entropy
3.4. Stage III—Final Robusted Schedule
-
In the Initialization phase we keep generating schedules, until the initial population is complete. Contrary to the Initialization phase in Stage I in which the initial makespan of the schedule is irrelevant, in Stage III, only the schedules with initial makespan within the range defined previously are considered as part of the initial population, the rest are discarded.
-
The objective function in Stage III maximizes the robustness of the population using Equation (5).
4. Computational Results
4.1. Scope
4.2. Description of the Procedure
4.3. Results
5. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Turner, J.R. The Handbook of Project Based Management; McGraw-Hill: London, UK, 1993. [Google Scholar]
- Turner, J.R. The Handbook of Project Based Management, 2nd ed; McGraw-Hill: London, UK, 1999. [Google Scholar]
- Turner, J.R.; Müller, R. On the nature of the project as a temporary organization. Int. J. Proj. Manag 2003, 21, 1–8. [Google Scholar]
- Blazewicz, J.; Lenstra, J.K.; Kan, A.H.G. Scheduling subject to resource constraints: Classification and complexity. Discret. Appl. Math 1983, 5, 11–24. [Google Scholar]
- Kolisch, R. Project Scheduling under Resource Constraints—Efficient Heuristics for Several Problem Cases; Physica-Verlag: Heidelberg, Germany, 1995. [Google Scholar]
- Elmaghraby, S.E. Activity Networks: Project Planning and Control by Network Models; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Kolisch, R.; Drexl, A. Local search for a non-preemptive multimode resource constrained project scheduling. IIE Trans 1997, 29, 987–999. [Google Scholar]
- Talbot, B. Resource-constrained project scheduling with time resource tradeoffs: The nonpreemptive case. Manag. Sci 1982, 28, 1197–1210. [Google Scholar]
- De Reyck, B.; Demuelemeester, E.L.; Herroelen, W.S. Local search methods for the discrete time/resource trade-off problem in project networks. Nav. Res. Logist. Q 1998, 45, 553–578. [Google Scholar]
- Pollack-Johnson, B.; Liberatore, M.J. Incorporating quality considerations into project time/cost trade-off analysis and decision making. IEEE Trans. Eng. Manag 2006, 53, 31–37. [Google Scholar]
- Ranjbar, M.; De Reyck, B.; Kianfar, F. A hybrid scatter search for the discrete time/resource trade-off problem in project scheduling. Eur. J. Oper. Res 2009, 193, 35–48. [Google Scholar]
- Özdamar, L.; Ulusoy, G.; Bayyigit,, M. A heuristic treatment of tardiness and net present value criteria in resource constrained project scheduling. Int. J. Phys. Distrib. Logist. Manag 1998, 28, 805–824. [Google Scholar]
- Pesch, E. Lower bounds in different problem classes of project schedules with resource constraints. In Project Scheduling: Recent Models, Algorithms and Applications; Weglarz, J., Ed.; Kluwer Academic Publishers: Springer US, New York, NY, USA, 1999; pp. 53–76. [Google Scholar]
- Hartmann, S.; Drexl, A. Project scheduling with multiple modes: A comparison of exact algorithms. Networks 1998, 32, 283–297. [Google Scholar]
- Józefowska, J.; Micka, M.; Rózycki, R.; Waligóra, G. Simulated annealing for multi-mode resource-constrained project scheduling. Ann. Oper. Res 2001, 102, 117–155. [Google Scholar]
- Alcaraz, J.; Maroto, C.; Ruiz, R. Solving the multimode resource constrained project scheduling problem with genetic algorithms. J. Oper. Res. Soc 2003, 54, 614–626. [Google Scholar]
- Bouleimen, K.; Lecocq, H. A new efficient simulated annealing algorithm for the resource-constrained project scheduling problem and its multiple mode version. Eur. J. Oper. Res 2003, 149, 268–281. [Google Scholar]
- Jarboui, B.; Damak, N.; Siarry, P.; Rebai, A. A combinatorial particle swarm optimization for solving multi-mode resource-constrained project scheduling problems. Appl. Math. Comput 2008, 195, 299–308. [Google Scholar]
- Nudtasomboon, N.; Randhawa, S.U. Resource-constrained project scheduling with renewable and non-renewable resources and time-resource tradeoffs. Comput. Ind. Eng 1997, 32, 227–242. [Google Scholar]
- Salewski, F.; Schirmer, A.; Drexl, A. Project scheduling under resource and mode identity constraints: Model, complexity, methods, and application. Eur. J. Oper. Res 1997, 102, 88–110. [Google Scholar]
- Drexl, A.; Nissen, R.; Patterson, J.H.; Salewski, F. Progen/px—An instance generator for resource-constrained project scheduling problems with partially renewable resources and further extensions. Eur. J. Oper. Res 2000, 125, 59–72. [Google Scholar]
- Erenguc, S.S.; Ahn, T.; Conway, D.G. The resource constrained project scheduling problem with multiple crashable modes: An exact solution method. Nav. Res. Logist 2001, 48, 107–127. [Google Scholar]
- Bellenguez, O.; Néron, E. Lower bounds for the multi-skill project scheduling problem with hierarchical levels of skills. Lect. Notes Comput. Sci 2005, 3616, 229–243. [Google Scholar]
- Zhu, G.; Bard, J.F.; Yu, G. A branch-and-cut procedure for the multimode resource-constrained project-scheduling problem. INFORMS J. Comput 2006, 18, 377–390. [Google Scholar]
- Varma, V.A.; Uzsoy, R.; Pekny, J.; Blau, G. Lagrangian heuristics for scheduling new product development projects in the pharmaceutical industry. J. Heuristics 2007, 13, 403–433. [Google Scholar]
- De Reyck, B.; Herroelen, W.S. The multi-mode resource-constrained project scheduling problem with generalized precedence relations. Eur. J. Oper. Res 1999, 119, 538–556. [Google Scholar]
- Heilmann, R. Resource-constrained project scheduling: A heuristic for the multi-mode case. OR Spektrum 2001, 23, 335–357. [Google Scholar]
- Heilmann, R. A branch-and-bound procedure for the multi-mode resource-constrained project scheduling problem with minimum and maximum time lags. Eur. J. Oper. Res 2003, 144, 348–365. [Google Scholar]
- Nonobe, K.; Ibaraki, T. Formulation and tabu search algorithm for the resource constrained project scheduling problem. In Essays and Surveys in Metaheuristics; Ribeiro, C.C., Hensen, P., Eds.; Kluwer Academic Publishers: Norwell, MA, US, 2002; pp. 557–588. [Google Scholar]
- Brucker, P.; Knust, S. Resource-constrained project scheduling and timetabling. In The Practice and Theory of Automated Timetabling III; Burke, E., Erben, W., Eds.; Springer: Berlin/Heidelberg, 2001; Volume 2079, pp. 277–293. [Google Scholar]
- Calhoun, V.D.; Pekar, J.J.; McGinty, V.B.; Adali, T.; Watson, T.D.; Pearlson, G.D. Different activation dynamics in multiple neural systems during simulated driving. Hum. Brain Mapp 2002, 16, 158–167. [Google Scholar]
- Sabzehparvar, M.; Seyed-Hosseini, S.M. A mathematical model for the multi-mode resource-constrained project scheduling problem with mode dependent time lags. J. Supercomput 2008, 44, 257–273. [Google Scholar]
- Barrios, A.; Ballestin, F.; Valls, V. A double genetic algorithm for the MRCPSP/max. Comput. Oper. Res 2011, 38, 33–43. [Google Scholar]
- Tareghian, H.R.; Taheri, S.H. A solution procedure for the discrete time, cost and quality tradeoff problem using electromagnetic scatter search. Appl. Math. Comput 2007, 190, 1136–1145. [Google Scholar]
- Li, H.; Womer, K. Modeling the supply chain configuration problem with resource constraints. Int. J. Proj. Manag 2008, 26, 646–654. [Google Scholar]
- Tiwari, V.; Patterson, J.H.; Mabert, V.A. Scheduling projects with heterogeneous resources to meet time and quality objectives. Eur. J. Oper. Res 2009, 193, 780–790. [Google Scholar]
- Bonfill, A.; Espuña, L.; Puigjaner, L. Proactive approach to address the uncertainty in short-term scheduling. Comput. Chem. Eng 2008, 32, 1689–1706. [Google Scholar]
- Kolisch, R.; Padman, R. An integrated survey of deterministic project scheduling. Omega 2001, 29, 249–272. [Google Scholar]
- Franck, B.; Schwindt, C. Different Resource-constrained Project Scheduling Models with Minimal and Maximal Time-lags; Technical Report WIOR-450; Universität Karlsruhe: Karlsruhe, Germany, 1995. [Google Scholar]
- Vanhoucke, M.; Demeulemeester, E.L.; Herroelen, W.S. An exact procedure for the resource-constrained weighted earliness-tardiness project scheduling problem. Ann. Oper. Res 2001, 102, 179–196. [Google Scholar]
- Neumann, K.; Schwindt, C.; Zimmermann, J. Recent results on resource-constrained project scheduling with time windows: Models, solution methods, and applications. Cent. Eur. J. Oper. Res 2002, 10, 113–148. [Google Scholar]
- Lorenzoni, L.L.; Ahonen, H.; de Alvarenga, A.G. A multi-mode resource-constrained scheduling problem in the context of port operations. Comput. Ind. Eng 2006, 50, 55–65. [Google Scholar]
- Kolisch, R. Integrated scheduling, assembly area- and part-assignment for large-scale, make-to-order assemblies. Int. J. Prod. Econ 2000, 64, 127–141. [Google Scholar]
- Viana, A.; de Sousa, J.P. Using meta-heuristics in multi-objective resource constrained project scheduling. Eur. J. Oper. Res 2000, 120, 359–374. [Google Scholar]
- Ballestin, F.; Valls, V.; Quintanilla, S. Due Dates and RCPSP. In International Series in Operations Research & Management Science; Józefowska, J., Weglarz, J., Eds.; Springer: New York City, US, 2006; Volume 92, pp. 79–104. [Google Scholar]
- Rom, W.O.; Icmeli-Tuckel, O.; Muscatello, J.R. MRP in a job shop environment using a resource constrained project scheduling model. Omega 2002, 30, 275–286. [Google Scholar]
- Nazareth, T.; Verma, S.; Bhattacharya, S.; Bagchi, A. The multiple resource constrained project scheduling problem: A breadth-first approach. Eur. J. Oper. Res 1999, 112, 347–366. [Google Scholar]
- Vanhoucke, M. Scheduling an R&D project with quality-dependent time slots. Lect. Notes Comput. Sci 2006, 3982, 621–630. [Google Scholar]
- Maniezzo, V.; Mingozzi, A. The project scheduling problem with irregular starting time costs. Oper. Res. Lett 1999, 25, 175–182. [Google Scholar]
- Möhring, R.H.; Schulz, A.S.; Stork, F.; Uetz, M. On project scheduling with irregular starting time costs. Oper. Res. Lett 2001, 28, 149–154. [Google Scholar]
- Möhring, R.H.; Schulz, A.S.; Stork, F.; Uetz, M. Solving project scheduling problems by minimum cut computations. Manag. Sci 2003, 49, 330–350. [Google Scholar]
- Achuthan, N.; Hardjawidjaja, A. Project scheduling under time dependent costs—A branch and bound algorithm. Ann. Oper. Res 2001, 108, 55–74. [Google Scholar]
- Dodin, B.; Elimam, A.A. Integrated project scheduling and material planning with variable activity duration and rewards. IIE Trans 2001, 33, 1005–1018. [Google Scholar]
- Nonobe, K.; Ibaraki, T. Chapter 9. A metaheuristic approach to the resource constrained project scheduling with variable activity durations and convex cost functions. In International Series in Operations Research & Management Science; Józefowska, J., Weglarz, J., Eds.; Springer: New York, NY, USA, 2006; Volume 92, pp. 225–248. [Google Scholar]
- Kimms, A. Maximizing the net present value of a project under resource constraints using a Lagrangian relaxation based heuristic with tight upper bounds. Ann. Oper. Res 2001, 102, 221–236. [Google Scholar]
- Vanhoucke, M.; Demeulemeester, E.L.; Herroelen, W.S. On maximizing the net present value of a project under renewable resource constraints. Manag. Sci 2001, 47, 1113–1121. [Google Scholar]
- Mika, M.; Waligóra, G.; Weglvarz, J. Simulated annealing and tabu search for multi-mode resource-constrained project scheduling with positive discounted cash flows and different payment models. Eur. J. Oper. Res 2005, 164, 639–668. [Google Scholar]
- Padman, R.; Zhu, D. Knowledge integration using problem spaces: A study in resource-constrained project scheduling. J. Sched 2006, 9, 133–152. [Google Scholar]
- Icmeli-Tuckel, O.; Rom, W.O. Solving the resource constrained project scheduling problem with optimization subroutine library. Comput. Oper. Res 1996, 23, 801–817. [Google Scholar]
- Ulusoy, G.; Sivrikaya-Şerifoğlu, F.; Şahin, Ş. Four payment models for the multi-mode resource constrained project scheduling problem with discounted cash flows. Ann. Oper. Res 2001, 102, 237–261. [Google Scholar]
- Waligóra, G. Discrete-continuous project scheduling with discounted cash flows—A tabu search approach. Comput. Oper. Res 2008, 35, 2141–2153. [Google Scholar]
- Chen, A.H.L.; Chyu, C.C. Economic optimization of resource-constrained project scheduling: A two-phase meta-heuristic approach. J. Zhejiang Univ. Sci 2010, 11, 481–494. [Google Scholar]
- Icmeli-Tuckel, O.; Erenguc, S.S. A branch and bound procedure for the resource constrained project scheduling problem with discounted cash-flows. Manag. Sci 1996, 42, 1395–1408. [Google Scholar]
- Etgar, R.; Shtub, A.; LeBlanc, L.J. Scheduling projects to maximize net present value—The case of time-dependent, contingent cash flows. Eur. J. Oper. Res 1997, 96, 90–96. [Google Scholar]
- Vanhoucke, M.; Demeulemeester, E.L.; Herroelen, W.S. Maximizing the net present value of a project with linear time-dependent cash flows. Int. J. Prod. Res 2001, 39, 3159–3181. [Google Scholar]
- Vanhoucke, M.; Demeulemeester, E.L.; Herroelen, W.S. Progress payments in project scheduling problems. Eur. J. Oper. Res 2003, 148, 604–620. [Google Scholar]
- Najafi, A.A.; Niaki, S.T.A. A genetic algorithm for resource investment problem with discounted cash flows. Appl. Math. Comput 2006, 183, 1057–1070. [Google Scholar]
- Icmeli-Tuckel, O.; Erenguc, S.S. The resource constrained time/cost tradeoff project scheduling problem with discounted cash flows. J. Oper. Manag 1996, 14, 255–275. [Google Scholar]
- Chiu, H.N.; Tsai, D.M. An efficient search procedure for the resource-constrained multi-project scheduling problem with discounted cash flows. Constr. Manag. Econ 2002, 20, 55–66. [Google Scholar]
- Doersch, R.H.; Patterson, J.H. Scheduling a project to maximize its present value: A zero-one programming approach. Manag. Sci 1977, 23, 882–889. [Google Scholar]
- Sung, C.S.; Lim, S.K. A project activity scheduling problem with net present value measure. Int. J. Prod. Econ 1994, 37, 177–187. [Google Scholar]
- Ulusoy, G.; Cebelli, S. An equitable approach to the payment scheduling problem in project management. Eur. J. Oper. Res 2000, 127, 262–278. [Google Scholar] [Green Version]
- Dayanand, N.; Padman, R. Project contracts and payment schedules: The client’s problem. Manag. Sci 2001, 47, 1654–1667. [Google Scholar]
- Land, A.H.; Doig, A.G. An automatic method of solving discrete programming problems. Econometrica 1960, 28, 497–520. [Google Scholar]
- Mazzola, J.; Neebe, A. Resource-constrained assignment scheduling. Oper. Res 1986, 34, 560–572. [Google Scholar]
- Stinson, J.; Davis, E.; Khumawala, B. Multiple resource-constrained scheduling using branch and bound. AIIE Trans 1978, 10, 252–259. [Google Scholar]
- Christofides, N.; Alvarez-Valdes, R.; Tamarit, J.M. Project scheduling with resource constraints: A branch and bound approach. Eur. J. Oper. Res 1987, 29, 262–273. [Google Scholar]
- Demeulemeester, E.L.; Herroelen, W.S. A Branch-and-Bound procedure for the multiple resource-constrained project scheduling problems. Manag. Sci 1992, 38, 1803–1818. [Google Scholar]
- Demeulemeester, E.L.; Herroelen, W.S. New benchmark results for the resource-constrained project scheduling problem. Manag. Sci 1995, 43, 1485–1492. [Google Scholar]
- Sprecher, A.; Kolisch, R.; Drexl, A. Semi-active, active, and non-delay schedules for the resource-constrained project scheduling problem. Eur. J. Oper. Res 1995, 80, 94–102. [Google Scholar]
- Mingozzi, A.; Maniezzo, V.; Ricciardelli, S.; Bianco, L. An exact algorithm for the resource-constrained project scheduling problem based on a new mathematical formulation. Manag. Sci 1998, 44, 714–729. [Google Scholar]
- Patterson, J.H.; Slowinski, R.; Talbot, F.B.; Weglarz, J. An algorithm for a general class of precedence and resource constrained scheduling problems. In Advances in Project Scheduling; Slowinski, R., Weglarz, J., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1989; pp. 3–28. [Google Scholar]
- Sprecher, A.; Drexl, A. Multi-mode resource-constrained project scheduling by a simple, general and powerful sequencing algorithm. Eur. J. Oper. Res 1998, 107, 431–450. [Google Scholar]
- Sprecher, A.; Hartmann, S.; Drexl, A. An exact algorithm for project scheduling with multiple modes. OR Spektrum 1997, 19, 195–203. [Google Scholar]
- Hartmann, S.A. self-adapting genetic algorithm for project scheduling under resource constraints. Nav. Res. Logist 2002, 49, 433–448. [Google Scholar]
- Zhang, H.; Tam, C.M.; Li, H. Multimode project scheduling based on particle swarm optimization. Comput. Aided Civ. Infrastruct 2006, 21, 90–103. [Google Scholar]
- Damak, N.; Jarboui, B.; Siarry, P.; Loukil, T. Differential evolution for solving multimode resource-constrained project scheduling problems. Comput. Oper. Res 2009, 205, 2653–2659. [Google Scholar]
- Van Petegehm, V.; Vanhoucke, M. An artificial immune system for the multimode resource-constrained project scheduling problem. Lect. Notes Comput. Sci 2009, 5482, 85–96. [Google Scholar]
- De Castro, L.N.; Timmis, J.I. Artificial immune systems: A novel paradigm for pattern recognition. In Artificial Neural Networks in Pattern Recognition; Alonso, L., Corchado, J., Fyfe,, C., Eds.; University of Paisley: Paisley, UK, 2002; pp. 67–84. [Google Scholar]
- Carazo, A.F.; Gómez, T.; Molian, J.; Hernández-Díaz, A.; Guerrero, F.M. Solving a comprehensive model for multi-objective project portfolio selection. Comput. Oper. Res 2010, 37, 630–639. [Google Scholar]
- Wang, L.; Fang, C. An effective estimation of distribution algorithm for the multimode resource constrained project scheduling problem. Comput. Oper. Res 2012, 39, 449–460. [Google Scholar]
- Shi, Y.J.; Chen, W.; Teng, H.F.; Lan, X.P.; Hu, L.C. An efficient hybrid algorithm for resource-constrained project scheduling. Inf. Sci 2010, 180, 1031–1039. [Google Scholar]
- Gao, H. Building Robust Schedules Using Temporal Protection—An Empirical Study of Constraint Based Scheduling under Machine Failure Uncertainty. Master’s Thesis, Department of Industrial Engineering, University of Toronto, Toronto, ON, Canada, 1995. [Google Scholar]
- Davenport, A.J.; Gefflot, C.; Beck, J.C. Slack-based techniques for robust schedules. Proceedings of 6th European Conference on Planning, Toledo, Spain, September 12–14, 2001.
- Mehta, S.V.; Uzsoy, R.M. Predictable scheduling of a job shop subject to breakdowns. IEEE Trans. Robot. Autom 1998, 14, 365–378. [Google Scholar]
- Mehta, S.V.; Uzsoy, R.M. Predictive scheduling of a single machine subject to breakdowns. Int. J. Comput. Integr. Manuf 1999, 12, 15–38. [Google Scholar]
- Herroelen, W.S.; Leus, R. On the merits and pitfalls of critical chain scheduling. J. Oper. Manag 2001, 19, 559–577. [Google Scholar]
- Newbold, R.C. Project Management in the Fast Lane—Applying the Theory of Constraints; The St. Lucie Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- A Guide to Implementing the Theory of Constraints (TOC). Available online: http://www.dbrmfg.co.nz/Projects%20Critical%20Chain.htm accessed on 6 September 2014.
- Van de Vonder, S.; Demeulemeester, E.L.; Herroelen, W.S.; Leus, R. The trade-off between stability and makespan in resource-constrained project scheduling. Int. J. Prod. Res 2006, 44, 215–236. [Google Scholar] [Green Version]
- Leus, R. The Generation of Stable Project Plans. Ph.D. Dissertation, Department of Applied Economics, Katholieke Universiteit Leuven, Leuven, Belgium, 2003. [Google Scholar]
- Leus, R.; Herroelen, W.S. The complexity of machine scheduling for stability with a single disrupted job. Oper. Res. Lett 2005, 33, 151–156. [Google Scholar]
- Van de Vonder, S.; Demeulemeester, E.; Herroelen, W. Proactive heuristic procedures for robust project scheduling: An experimental analysis. Eur. J. Oper. Res 2008, 189, 723–733. [Google Scholar]
- Nazarian, E.; Ko, J. Robust manufacturing line design with controlled moderate robustness in bottleneck buffer time to manage stochastic inter-task times. J. Manuf. Syst 2013, 32, 382–391. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell System Tech J 1948, 27. [Google Scholar]
- Bushuyev, S.; Sochnev, S. Entropy measurement as a project control tool. Int. J. Proj. Manag 1999, 17, 343–350. [Google Scholar]
- Sun, L.; Fu, G.; Wang, M. Application of entropy in design risk management of the large-scale construction project. Proceedings of the 2nd IEEE International Conference on Information Management and Engineering, Chengdu, China, 16–18 April 2010; pp. 116–120.
- Icmeli-Tuckel, O.; Rom, W.O. Analysis of the characteristics of projects in diverse industries. J. Oper. Manag 1998, 16, 43–61. [Google Scholar]
- Icmeli-Tuckel, O.; Rom, W.O. Ensuring quality in resource constrained project scheduling. Eur. J. Oper. Res 1997, 103, 483–496. [Google Scholar]
- Al-Fawzan, M.A.; Haouari, M. A bi-objective model for robust resource-constrained project scheduling. Int. J. Prod. Econ 2005, 96, 175–187. [Google Scholar]
- Kobyalanski, P.; Kutcha, D. A note on the paper by M.A. Al-Fawzan and M. Haouari about A bi-objective model for robust resource-constrained project scheduling. Int. J. Prod. Econ 2007, 107, 496–501. [Google Scholar]
- Chtourou, H.; Haouari, M. A two stage priority rule based algorithm for robust resource constrained project scheduling. Comput. Ind. Eng 2008, 55, 183–194. [Google Scholar]
- Lambrechts, O.; Demeulmeester, E.; Herroelen, W. A tabu search procedure for developing robust predictive project schedules. Int. J. Prod. Econ 2008, 111, 493–508. [Google Scholar]
- Hartmann, S.; Kolisch, R. Experimental evaluation of state-of-the-art heuristics for the resource-constrained project scheduling problem. Eur. J. Oper. Res 2000, 127, 394–407. [Google Scholar]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report TR06; Computing Engineering Department, Erciyes University: Erciyes, Turkey, 2005. [Google Scholar]
- Karaboga, D.; Akay, B. A comparative study of Artificial Bee Colony algorithm. Appl. Math. Comput 2009, 214, 108–132. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim 2007, 39, 459–471. [Google Scholar]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput 2008, 8, 687–697. [Google Scholar]
- Karaboga, D. A new design method based on artificial bee colony algorithm for digital IIR filters. J. Frankl. Inst 2009, 346, 328–348. [Google Scholar]
- Kassabalidis, I.; El-Sharkawi, M.A.; Marks, R.J.; Arabshahi, P.; Gray, A.A. Swarm intelligence for routing in communication networks. Proceedings of the IEEE Global Telecommunication Conference, San Antonio, TX, USA, 25–29 November 2001; 6, pp. 3613–3617.
- Boctor, F.F. Heuristics for Scheduling Projects with Resource Restrictions and Several Resource-Duration Modes. Int. J. Prod. Res 1993, 31, 2547–2558. [Google Scholar]
- Chen, A.H.L.; Chyu, C.C. A memetic algorithm for maximizing net present value in resource-constrained project scheduling problem. Proceedings of the IEEE Congress on Evolutionary Computation, Hong Kong, China, 1–6 June 2008; pp. 2401–2408.
- Brooks, G.H.; White, C.R. An algorithm for finding optimal or near-optimal solutions to the production scheduling problem. J. Ind. Eng 1965, 16, 34–40. [Google Scholar]
- Bedworth, D.D. Industrial Systems: Planning, Analysis, Control; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Whitehouse, G.E.; Brown, J.R. GENRES: An extension of Brook’s algorithm for project scheduling with resource constraints. Comput. Ind. Eng 1979, 3, 261–268. [Google Scholar]
- Demeulemeester, E.L.; Herroelen, W.S. International Series in Operations Research & Management Science: Project Scheduling—A Research Handbook; Kluwer Academic: Boston, MA, USA, 2002; Volume 49. [Google Scholar]
- Alvarez-Valdés, R.; Tamarit, J.M. Heuristic algorithms for resource-constrained project scheduling: A review and empirical analysis. In Advances in Project Scheduling; Slowinski, R., Weglraz, J., Eds.; Elsevier: Amsterdam, The Netherlands, 1989; pp. 113–134. [Google Scholar]
- Elsayed, E.A. Algorithms for project scheduling with resource constraints. Int. J. Prod. Res 1982, 20, 95–103. [Google Scholar]
- Ulusoy, G.; Özdamar, L. Heuristic performance and network/resource characteristics in resource constrained projects scheduling. J. Oper. Res. Soc 1989, 40, 1145–1152. [Google Scholar]
- Davis, E.W.; Patterson, J.H. A comparison of heuristic and optimum solutions in resource constrained project scheduling. Manag. Sci 1975, 21, 944–955. [Google Scholar]
- Brand, J.D.; Meyer, W.L.; Shaffer, L.R. The Resource Scheduling Problem in Construction; Civil Engineering Studies Report No. 5; Department of Civil Engineering, University of Illinois: Urbana, IL, USA, 1964. [Google Scholar]
- The Library PSBLIB. Available online: http://www.om-db.wi.tum.de/psplib/library.html accessed on 2 June 2014.
- Multimode Project Duration Problem MRCPSP/max. Available online: http://www.wiwi.tu-clausthal.de/en/chairs/produktion/research/research-areas/project-generator/%20mrcpspmax accessed on 15 July 2014.

| Priority Rule | Description |
|---|---|
| SFM—Shortest Feasible Mode | Find the feasible mode combination for which the makespan is minimal |
| LRP—Least Resource Proportion | Choose the mode which leads to the smallest value of the criterion, where stands for the requirement of renewable resource type k per period by activity i executed in mode m. Kρ= total number of renewable resource types in the project. |
| LPSRD—Least Product Sum of Resource and Duration | For each activity, choose the execution mode which has the minimum product sum of non-renewable resource usage and its corresponding mode duration, . |
| LTRU—Least Total Resource Usage | Choose the execution mode which requires the least total non-renewable usage, where represents the requirement of non-renewable resource type k per period by activity i executed in mode m. Kv represents the total number of non-renewable resource types in the project. |
| LRS—Least Sum of Non-renewable Resource | Choose the execution mode which requires the least sum of the ratio of the non-renewable consumption to its corresponding resource limitation, . Here, stands for the amount of non-renewable resource type k available per period. |
| Priority Rule | References | Description |
|---|---|---|
| max ACTIM | [123–125] | = CPM – LSTi where CPM stands for the duration of the Critical Path while LST represents the Latest Start Time of activity i. |
| max GCUMRD | [126] | The sum of the renewable resource demand of the activity considered and the renewable resource demands of all its immediate successors. |
| max MTS | [127] | | S̄i | the total number of successors for activity i. |
| max MIS | [127] | | Si | the number of immediate successors for activity i. |
| max ROT | [128] | sum of the ratio of the renewable resource requirement over the resource availability divided by the activity duration for activity i |
| max WRUP | [129] | , a weighted sum of the number of immediate successors and an average resource use over all renewable resource types. |
| min EFT | [130] | EFTi Earliest finish time of activity i. |
| min LFT | [130] | LFTi Latest finish time of activity i. |
| min SLK | [130] | LFTi – EFTi |
| min LNRJ | [126] | | | the total number of activities that are not precedence related with activity i |
| min RSM | [131] | dij = max[0, (EFTi – LSTj)] |
| (a) | |||
|---|---|---|---|
| Stage I ABC Schedule (Optimized Makespan) | |||
| Activity | Start | Duration | Finish |
| 1 | 0 | 0 | 0 |
| 3 | 0 | 2 | 2 |
| 5 | 2 | 7 | 9 |
| 2 | 0 | 2 | 2 |
| 4 | 2 | 2 | 4 |
| 7 | 4 | 4 | 8 |
| 10 | 9 | 3 | 12 |
| 8 | 9 | 6 | 15 |
| 6 | 8 | 2 | 10 |
| 11 | 15 | 3 | 18 |
| 9 | 15 | 2 | 17 |
| 12 | 18 | 0 | 18 |
| (b) | |||
|---|---|---|---|
| Durations Estimation | |||
| Activity | dil | di | diu |
| 1 | 0 | 0 | 0 |
| 3 | 2 | 2 | 8 |
| 5 | 7 | 9 | 10 |
| 2 | 2 | 3 | 5 |
| 4 | 2 | 6 | 7 |
| 7 | 4 | 8 | 9 |
| 10 | 3 | 9 | 9 |
| 8 | 6 | 7 | 7 |
| 6 | 2 | 4 | 10 |
| 11 | 3 | 7 | 8 |
| 9 | 2 | 4 | 10 |
| 12 | 0 | 0 | 0 |
| (c) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Slack, Unfavorable Events and Entropy Calculation | ||||||||
| Activity | EST | EFT | LST | LFT | Slack | EFT diu | Eu | SID |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 2 | 17 | 19 | 17 | 8 | 0 | 0 |
| 5 | 0 | 9 | 0 | 9 | 0 | 10 | 1 | 1 |
| 2 | 0 | 3 | 3 | 6 | 3 | 5 | 0 | 0 |
| 4 | 9 | 15 | 9 | 15 | 0 | 16 | 1 | 1 |
| 7 | 9 | 17 | 14 | 22 | 5 | 18 | 0 | 0 |
| 10 | 3 | 12 | 6 | 15 | 3 | 12 | 0 | 0 |
| 8 | 15 | 22 | 15 | 22 | 0 | 22 | 0 | 0 |
| 6 | 22 | 26 | 22 | 26 | 0 | 32 | 6 | 2 |
| 11 | 15 | 22 | 19 | 26 | 4 | 23 | 0 | 0 |
| 9 | 22 | 26 | 22 | 26 | 0 | 32 | 6 | 2 |
| 12 | 26 | 26 | 26 | 26 | 0 | 26 | 0 | 0 |
| (d) | |||
|---|---|---|---|
| Stage II Entropy Containing Schedule (Upper-bound Makespan) | |||
| Activity | Start | Duration | Finish |
| 1 | 0 | 0 | 0 |
| 3 | 0 | 2 | 2 |
| 5 | 2 | 8 | 10 |
| 2 | 0 | 2 | 2 |
| 4 | 2 | 3 | 6 |
| 7 | 6 | 4 | 10 |
| 10 | 10 | 3 | 14 |
| 8 | 10 | 6 | 16 |
| 6 | 10 | 4 | 13 |
| 11 | 16 | 3 | 19 |
| 9 | 16 | 4 | 19 |
| 12 | 19 | 0 | 19 |
| (a) | ||||
|---|---|---|---|---|
| Stage I ABC Schedule (Lower Bound) | ||||
| Activity | Start | Duration | Finish | RM |
| 1 | 0 | 0 | 0 | 67.25 |
| 3 | 0 | 2 | 2 | 67.25 |
| 5 | 2 | 7 | 9 | 67.25 |
| 2 | 0 | 2 | 2 | 67.25 |
| 4 | 2 | 2 | 4 | 67.25 |
| 7 | 4 | 4 | 8 | 67.25 |
| 10 | 9 | 3 | 12 | 67.25 |
| 8 | 9 | 6 | 15 | 67.25 |
| 6 | 8 | 2 | 10 | 67.25 |
| 11 | 15 | 3 | 18 | 67.25 |
| 9 | 15 | 2 | 17 | 67.25 |
| 12 | 18 | 0 | 18 | 67.25 |
| (b) | ||||
|---|---|---|---|---|
| Stage II Entropy Containing Schedule (Upper Bound) | ||||
| Activity | Start | Duration | Finish | RM |
| 1 | 0 | 0 | 0 | 93.5 |
| 3 | 0 | 2 | 2 | 93.5 |
| 5 | 2 | 8 | 10 | 93.5 |
| 2 | 0 | 2 | 2 | 93.5 |
| 4 | 2 | 3 | 6 | 93.5 |
| 7 | 6 | 4 | 10 | 93.5 |
| 10 | 10 | 3 | 14 | 93.5 |
| 8 | 10 | 6 | 16 | 93.5 |
| 6 | 10 | 4 | 13 | 93.5 |
| 11 | 16 | 3 | 19 | 93.5 |
| 9 | 16 | 4 | 19 | 93.5 |
| 12 | 19 | 0 | 19 | 93.5 |
| (c) | |||||||
|---|---|---|---|---|---|---|---|
| Activity | Start | Duration | Finish | Activity | Start | Duration | Finish |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | 0 | 2 | 2 | 3 | 0 | 2 | 2 |
| 3 | 0 | 2 | 2 | 5 | 2 | 7 | 9 |
| 6 | 2 | 2 | 4 | 2 | 0 | 2 | 2 |
| 5 | 2 | 7 | 9 | 6 | 2 | 2 | 4 |
| 7 | 4 | 4 | 8 | 4 | 4 | 2 | 6 |
| 8 | 9 | 6 | 15 | 7 | 6 | 4 | 10 |
| 9 | 15 | 2 | 17 | 10 | 9 | 3 | 12 |
| 11 | 15 | 3 | 18 | 8 | 10 | 6 | 16 |
| 2 | 8 | 2 | 10 | 11 | 16 | 3 | 19 |
| 10 | 10 | 3 | 13 | 9 | 16 | 2 | 18 |
| 12 | 18 | 0 | 18 | 12 | 19 | 0 | 19 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 2 | 2 | 3 | 0 | 2 | 2 |
| 3 | 0 | 2 | 2 | 2 | 0 | 2 | 2 |
| 5 | 2 | 7 | 9 | 6 | 2 | 2 | 4 |
| 4 | 2 | 2 | 4 | 5 | 2 | 7 | 9 |
| 6 | 4 | 2 | 6 | 4 | 4 | 2 | 6 |
| 7 | 6 | 4 | 10 | 10 | 9 | 3 | 12 |
| 10 | 9 | 3 | 12 | 7 | 6 | 4 | 10 |
| 8 | 10 | 6 | 16 | 8 | 10 | 6 | 16 |
| 9 | 16 | 2 | 18 | 9 | 16 | 2 | 18 |
| 11 | 16 | 3 | 19 | 11 | 16 | 3 | 19 |
| 12 | 19 | 0 | 19 | 12 | 19 | 0 | 19 |
| (d) | ||||
|---|---|---|---|---|
| Stage III Robusted Schedule (FINAL) | ||||
| Activity | Start | Duration | Finish | RM |
| 1 | 0 | 0 | 0 | 93.5 |
| 4 | 0 | 2 | 2 | 93.5 |
| 3 | 0 | 2 | 2 | 93.5 |
| 6 | 2 | 2 | 4 | 93.5 |
| 5 | 2 | 7 | 9 | 93.5 |
| 7 | 4 | 4 | 8 | 93.5 |
| 8 | 9 | 6 | 15 | 93.5 |
| 9 | 15 | 2 | 17 | 93.5 |
| 11 | 15 | 3 | 18 | 93.5 |
| 2 | 8 | 2 | 10 | 93.5 |
| 10 | 10 | 3 | 13 | 93.5 |
| 12 | 18 | 0 | 18 | 93.5 |
| Parameter | Settings (* base level) | ||
|---|---|---|---|
| Population size | 5 | 15 | 30* |
| Abandonment limit | 5* | 10 | 15 |
| MNC | 5 | 10 | 20* |
| δt (relevant time interval) | 1* | 2 | 3 |
| frac | 0.25* | 0.50 | 0.75 |
| Deviation when compared to Optimal Makespan (%) | Deviation when compared to ABC Makespan (%) | |||||
|---|---|---|---|---|---|---|
| ABC Schedule | Entropy Schedule | Robust Schedule | Entropy Schedule | Robust Schedule | ||
| Population Size | 5 | 33.33 | 55.56 | 50.00 | 16.67 | 12.50 |
| 15 | 6.67 | 20.00 | 20.00 | 12.50 | 12.50 | |
| 30 | - | 6.67 | 6.67 | 6.67 | 6.67 | |
| Abandonment Limit | 5 | - | 6.67 | 6.67 | 6.67 | 6.67 |
| 10 | 26.67 | 46.67 | 46.67 | 15.79 | 15.79 | |
| 15 | 31.82 | 45.45 | 31.82 | 10.34 | - | |
| MNC | 5 | 7.69 | 23.08 | 23.08 | 14.29 | 14.29 |
| 10 | 4.55 | 4.55 | 4.55 | - | - | |
| 20 | - | 6.67 | 6.67 | 6.67 | 6.67 | |
| δt (relevant time interval) | 3 | 95.00 | 130.00 | 100.00 | 17.95 | 2.56 |
| 2 | 18.75 | 37.50 | 37.50 | 15.79 | 15.79 | |
| 1 | - | 6.67 | 6.67 | 6.67 | 6.67 | |
| Frac | 0.25 | - | 6.67 | 6.67 | 6.67 | 6.67 |
| 0.5 | 26.67 | 46.67 | 46.67 | 15.79 | 15.79 | |
| 0.75 | 31.82 | 45.45 | 31.82 | 20.00 | - | |
| MNC | 5 | 7.69 | 23.08 | 23.08 | 14.29 | 14.29 |
| 10 | 4.55 | 4.55 | 4.55 | - | - | |
| 20 | - | 6.67 | 6.67 | 6.67 | 6.67 | |
| δt (relevant time interval) | 3 | 95.00 | 130.00 | 100.00 | 17.95 | 2.56 |
| 2 | 18.75 | 37.50 | 37.50 | 15.79 | 15.79 | |
| 1 | - | 6.67 | 6.67 | 6.67 | 6.67 | |
| Frac | 0.25 | - | 6.67 | 6.67 | 6.67 | 6.67 |
| 0.5 | 26.67 | 46.67 | 46.67 | 15.79 | 15.79 | |
| 0.75 | 31.82 | 45.45 | 31.82 | 20.00 | - | |
| No. | Instance | BKO | ABC | ENTROPY | ROBUST | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MS | Dev | RM | MS | Dev | RM | MS | Dev | RM | |||
| 1 | j1020_3 | 21 | 21.00 | - | 44.50 | 21.00 | - | 49.25 | 21.00 | - | 49.25 |
| 2 | j108_3 | 17 | 18.00 | 5.88 | 39.75 | 26.00 | 52.94 | 67.50 | 18.00 | 5.88 | 39.75 |
| 3 | j1063_5 | 12 | 12.00 | - | 20.00 | 15.00 | 25.00 | 105.75 | 12.00 | - | 45.25 |
| 4 | j1046_10 | 20 | 20.00 | - | 64.25 | 24.00 | 20.00 | 101.50 | 20.00 | - | 66.25 |
| 5 | j1037_3 | 29 | 27.00 | (6.90) | 73.00 | 29.00 | - | 80.50 | 26.00 | (10.34) | 75.25 |
| 6 | j1031_6 | 20 | 20.00 | - | 40.00 | 21.00 | 5.00 | 55.50 | 20.00 | - | 61.25 |
| 7 | j104_9 | 21 | 17.00 | (19.05) | 32.50 | 23.00 | 9.52 | 37.00 | 17.00 | (19.05) | 32.50 |
| 8 | j1055_1 | 18 | 18.00 | - | 80.00 | 21.00 | 16.67 | 87.00 | 19.00 | 5.56 | 82.00 |
| 9 | j103_3 | 19 | 18.00 | (5.26) | 39.50 | 19.00 | - | 47.25 | 18.00 | (5.26) | 39.50 |
| 10 | j1016_10 | 26 | 26.00 | - | 39.00 | 27.00 | 3.85 | 42.50 | 26.00 | - | 69.25 |
| 11 | j1020_4 | 17 | 17.00 | - | 28.00 | 17.00 | - | 30.00 | 17.00 | - | 53.75 |
| 12 | j1036_1 | 32 | 32.00 | - | 82.50 | 36.00 | 12.50 | 93.75 | 32.00 | - | 82.50 |
| 13 | j1018_2 | 15 | 15.00 | - | 21.75 | 17.00 | 13.33 | 31.50 | 15.00 | - | 23.25 |
| 14 | j1063_3 | 17 | 17.00 | - | 73.25 | 20.00 | 17.65 | 79.00 | 18.00 | 5.88 | 105.25 |
| 15 | j1060_1 | 13 | 13.00 | - | 21.00 | 15.00 | 15.38 | 62.75 | 13.00 | - | 34.25 |
| 16 | j1029_10 | 28 | 26.00 | (7.14) | 31.00 | 28.00 | - | 33.00 | 27.00 | (3.57) | 59.25 |
| 17 | j1026_2 | 12 | 12.00 | - | 23.50 | 14.00 | 16.67 | 34.00 | 11.00 | (8.33) | 25.50 |
| 18 | j1018_6 | 15 | 15.00 | - | 28.00 | 16.00 | 6.67 | 30.50 | 15.00 | - | 35.00 |
| 19 | j1043_6 | 16 | 16.00 | - | 32.50 | 21.00 | 31.25 | 32.50 | 16.00 | - | 85.75 |
| 20 | j1062_4 | 15 | 15.00 | - | 69.50 | 15.00 | - | 73.50 | 15.00 | - | 85.25 |
| 21 | j107_5 | 24 | 24.00 | - | 39.00 | 26.00 | 8.33 | 44.25 | 25.00 | 4.17 | 41.00 |
| 22 | j1029_10 | 28 | 28.00 | - | 40.50 | 30.00 | 7.14 | 59.75 | 27.00 | (3.57) | 48.50 |
| 23 | j1028_10 | 18 | 18.00 | - | 60.25 | 22.00 | 22.22 | 72.00 | 22.00 | 22.22 | 90.25 |
| 24 | j1014_2 | 19 | 19.00 | - | 41.50 | 21.00 | 10.53 | 79.75 | 19.00 | - | 77.50 |
| 25 | j1010_6 | 18 | 17.00 | (5.56) | 28.75 | 18.00 | - | 32.25 | 14.00 | (22.22) | 42.00 |
| 26 | j1036_5 | 23 | 21.00 | (8.70) | 73.50 | 24.00 | 4.35 | 80.50 | 15.00 | (34.78) | 73.50 |
| 27 | j1044_9 | 17 | 17.00 | - | 62.50 | 21.00 | 23.53 | 66.00 | 17.00 | - | 62.50 |
| 28 | j1023_8 | 18 | 18.00 | - | 40.00 | 20.00 | 11.11 | 46.75 | 18.00 | - | 49.50 |
| 29 | j1018_3 | 17 | 16.00 | (5.88) | 38.00 | 18.00 | 5.88 | 40.00 | 16.00 | (5.88) | 38.00 |
| 30 | j1034_4 | 23 | 23.00 | - | 41.00 | 25.00 | 8.70 | 42.75 | 23.00 | - | 74.75 |
| 31 | j1026_4 | 16 | 16.00 | - | 28.00 | 18.00 | 12.50 | 38.75 | 18.00 | 12.50 | 38.75 |
| 32 | j103_7 | 14 | 14.00 | - | 10.00 | 20.00 | 42.86 | 18.00 | 15.00 | 7.14 | 27.50 |
| 33 | j1063_2 | 17 | 17.00 | - | 71.00 | 22.00 | 29.41 | 163.25 | 17.00 | - | 135.50 |
| 34 | j1042_5 | 20 | 21.00 | 5.00 | 101.00 | 25.00 | 25.00 | 124.50 | 22.00 | 10.00 | 120.25 |
| 35 | j1014_1 | 16 | 17.00 | 6.25 | 43.75 | 19.00 | 18.75 | 54.25 | 17.00 | 6.25 | 90.25 |
| 36 | j1010_9 | 10 | 10.00 | - | 27.00 | 11.00 | 10.00 | 49.75 | 11.00 | 10.00 | 49.75 |
| 37 | j1045_10 | 25 | 26.00 | 4.00 | 120.50 | 27.00 | 8.00 | 127.50 | 27.00 | 8.00 | 141.75 |
| 38 | j1050_4 | 20 | 19.00 | (5.00) | 116.00 | 23.00 | 15.00 | 128.50 | 19.00 | (5.00) | 140.75 |
| 39 | j1051_7 | 21 | 21.00 | - | 81.25 | 23.00 | 9.52 | 86.25 | 21.00 | - | 81.25 |
| 40 | j1060_8 | 13 | 13.00 | - | 40.00 | 14.00 | 7.69 | 101.75 | 13.00 | - | 40.00 |
| Summarized Results for Benchmark Evaluations | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| j10 | j12 | j14 | j16 | j18 | j20 | j30 | mm50 | mm100 | ||
| ABC | Avg. Dev. | (1.06) | 0.41 | 3.43 | 3.36 | 2.12 | 5.78 | 9.61 | 24.72 | 32.94 |
| Std. Dev. | 4.31 | 4.89 | 7.99 | 8.55 | 5.46 | 8.89 | 12.39 | 7.50 | 11.54 | |
| Avg. RM. | 49.68 | 71.93 | 107.51 | 121.25 | 134.01 | 154.83 | 251.03 | 840.56 | 963.99 | |
| Improved BKO’s | 8.00 | 11.00 | 7.00 | 7.00 | 4.00 | 4.00 | - | - | - | |
| p-value | 0.13 | 0.60 | 0.01 | 0.02 | 0.02 | 0.00 | 0.73 | 0.07 | 0.04 | |
| 95% CI. Lower Bound | (2.44) | (1.17) | 0.84 | 0.59 | 0.35 | 2.91 | (3.53) | 10.13 | 18.31 | |
| 95% CI. Upper Bound | 0.32 | 2.00 | 6.02 | 6.13 | 3.89 | 8.66 | 2.50 | 29.20 | 60.59 | |
| ENTROPY | Avg. Dev. | 13.17 | 15.05 | 17.85 | 16.52 | 13.49 | 18.88 | 21.11 | 39.99 | 69.10 |
| Inc. Avg. Dev. (x) | 13.44 | 35.43 | 4.20 | 3.92 | 5.37 | 2.26 | 1.20 | 0.62 | 1.10 | |
| Std. Dev. | 11.60 | 13.76 | 12.49 | 12.62 | 10.35 | 11.74 | 13.57 | 12.30 | 24.28 | |
| Avg. RM. | 65.77 | 95.91 | 124.84 | 153.76 | 167.16 | 195.62 | 293.59 | 1,030.88 | 1,573.40 | |
| Inc. Avg. RM. (%) | 32.40 | 33.34 | 16.12 | 26.81 | 24.73 | 26.35 | 16.96 | 22.64 | 40.32 | |
| p-value | 0.10 | 0.03 | 0.00 | 0.00 | 0.04 | <.0001 | <.0001 | 0.35 | <.0001 | |
| 95% CI. Lower Bound | 9.42 | 10.60 | 13.80 | 12.43 | 10.14 | 15.08 | (1.31) | 30.79 | 53.20 | |
| 95% CI. Upper Bound | 16.93 | 19.51 | 21.89 | 20.61 | 16.84 | 22.68 | 3.78 | 48.78 | 87.06 | |
| ROBUST | Avg. Dev. | (0.51) | 1.24 | 12.94 | 11.61 | 8.33 | 11.08 | 10.96 | 30.37 | 53.66 |
| Inc. Avg. Dev. | (0.52) | 1.99 | 2.77 | 2.46 | 2.93 | 0.92 | 0.14 | 0.23 | 0.63 | |
| Std. Dev. | 9.31 | 7.85 | 9.36 | 11.39 | 7.64 | 8.79 | 12.81 | 9.59 | 18.78 | |
| Avg. RM. | 65.33 | 91.03 | 131.39 | 152.62 | 168.15 | 192.63 | 276.25 | 1,012.07 | 1,363.76 | |
| Inc. Avg. RM. (%) | 31.52 | 26.56 | 22.21 | 25.87 | 25.47 | 24.42 | 10.05 | 20.40 | 31.17 | |
| Improved BKO’s | 7.00 | 11.00 | 1.00 | 1.00 | 1.00 | 1.00 | - | - | - | |
| ROB = ABC or ROB = ENT | 11.00 | 8.00 | 10.00 | 20.00 | 17.00 | 14.00 | 19.00 | 16.00 | 18.00 | |
| p-value | <.0001 | <.0001 | 0.06 | 0.38 | 0.18 | 0.45 | 0.06 | 0.05 | 0.01 | |
| 95% CI. Lower Bound | (3.53) | (1.31) | 9.90 | 7.92 | 5.85 | 8.23 | 9.90 | 29.46 | 41.32 | |
| 95% CI. Upper Bound | 2.50 | 3.78 | 15.97 | 15.30 | 10.80 | 13.93 | 15.97 | 46.59 | 67.61 | |
| MRCPSP/max | |
|---|---|
| H0: | Avg. Dev = 25 |
| H1: | Avg. Dev > 25 |
| MRCPSP/max | |
|---|---|
| H0: | Avg. Dev = 35 |
| H1: | Avg. Dev > 35 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, A.H.-L.; Liang, Y.-C.; Padilla, J.D. An Entropy-Based Upper Bound Methodology for Robust Predictive Multi-Mode RCPSP Schedules. Entropy 2014, 16, 5032-5067. https://doi.org/10.3390/e16095032
Chen AH-L, Liang Y-C, Padilla JD. An Entropy-Based Upper Bound Methodology for Robust Predictive Multi-Mode RCPSP Schedules. Entropy. 2014; 16(9):5032-5067. https://doi.org/10.3390/e16095032
Chicago/Turabian StyleChen, Angela Hsiang-Ling, Yun-Chia Liang, and Jose David Padilla. 2014. "An Entropy-Based Upper Bound Methodology for Robust Predictive Multi-Mode RCPSP Schedules" Entropy 16, no. 9: 5032-5067. https://doi.org/10.3390/e16095032




