Combinatorial Optimization with Information Geometry: The Newton Method
1. Introduction
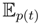 [s(t)] = 0. Because of that, the tangent space at p ∈ V is a vector space of random variables with zero expectation at p. A vector field is a mapping from p to a random variable V (p), such that for all p ∈ , the random variable V(p) is centered at p,
[s(t)] = 0. Because of that, the tangent space at p ∈ V is a vector space of random variables with zero expectation at p. A vector field is a mapping from p to a random variable V (p), such that for all p ∈ , the random variable V(p) is centered at p,
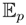 [V(p)] = 0. In other words, each point of the manifold has a different tangent space, and this tangent space can be used as a non-parametric model space of the manifold. In this formalism, a vector field is a mapping from densities to centered random variables, that is, it is what in statistics is called a pivot of the statistical model. To avoid confusion with the product of random variables, we do not use the standard notation for the action of a vector field on a real function. This approach is possibly unusual in differential geometry, but it is fully natural from the statistical point of view, where the Fisher score has a central place. Moreover, this approach scales nicely from the finite state space to the general state space; see the discussion in [9] and the review in [3].
[V(p)] = 0. In other words, each point of the manifold has a different tangent space, and this tangent space can be used as a non-parametric model space of the manifold. In this formalism, a vector field is a mapping from densities to centered random variables, that is, it is what in statistics is called a pivot of the statistical model. To avoid confusion with the product of random variables, we do not use the standard notation for the action of a vector field on a real function. This approach is possibly unusual in differential geometry, but it is fully natural from the statistical point of view, where the Fisher score has a central place. Moreover, this approach scales nicely from the finite state space to the general state space; see the discussion in [9] and the review in [3].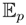 [f] < maxx∈Ω f(x), unless f is constant. We are looking for a sequence pn, n ∈ ℕ, such that
[f] < maxx∈Ω f(x), unless f is constant. We are looking for a sequence pn, n ∈ ℕ, such that
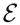 [f] → maxx∈Ω f(x) as n → ∞. The existence of such a sequence is a nontrivial condition for the model . Precisely, the closure of V must contain a density, whose support is contained in the set of maxima {x ∈ Ω|f(x) = max f}. This condition is satisfied by the independence model, V = Span {X1,X2}, where we can write:
[f] → maxx∈Ω f(x) as n → ∞. The existence of such a sequence is a nontrivial condition for the model . Precisely, the closure of V must contain a density, whose support is contained in the set of maxima {x ∈ Ω|f(x) = max f}. This condition is satisfied by the independence model, V = Span {X1,X2}, where we can write:2. Models on a Finite State Space
- Two different exponential families can actually be the same statistical model, as the set of densities in the two exponential families are actually equal. This fact is due to both the arbitrariness of the reference density and the fact that sufficient statistics are actually a vector basis of the vector space generated by the sufficient statistics. In a non-parametric approach, we can refer directly to the vector space of centered log-densities, while the change of reference density is geometrically interpreted as a change of chart. The set of all possible such charts defines a manifold.
- We make a specific interpretation of the tangent bundle as the vector space of Fisher’s scores at each density and use such tangent spaces as the space of coordinates. This produces a different tangent space/space of coordinates at each density, and different tangent spaces are mapped one onto another by a proper parallel transport, which is nothing else than the re-centering of random variables.
- If a basis is chosen, a parametrization is given, and such a parametrization is, in fact, a new chart, whose values are real vectors. In the real parametrization, the natural scalar product in each scores space is given by Fisher’s information matrix.
- Riemannian gradients are defined in the usual way. It is customary in information geometry to call “natural gradient” the real coordinate presentation of the Riemannian gradient. The natural gradient is computed by applying the inverse of the Fisher information matrix to the Euclidean gradient. It seems that there are tree gradients involved, but they all represent the same object when correctly understood.
- The classical notion of expectation parameters for exponential families carries on as another chart on the statistical manifold, which gives rise to a further presentation of a geometrical object.
- While the statistical manifold is unique, there are at least three relevant connections as structures on the vector bundles of the manifold: one relating to the exponential charts, one relating to the expectation charts and one depending on the Riemannian structure.
2.1. Exponential Families As Manifolds
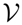 = Span {X1, . . . ,Xm} and define the following exponential family of positive densities p ∈ ℘>:
= Span {X1, . . . ,Xm} and define the following exponential family of positive densities p ∈ ℘>: , then there exist a unique set of parameters θ = θp(q), such that:
, then there exist a unique set of parameters θ = θp(q), such that: is the centering at p, that is,
is the centering at p, that is, is one-to-one on
is one-to-one on
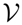 and
and
 Xj, j = 1, . . . ,m, and is a basis of
Xj, j = 1, . . . ,m, and is a basis of

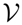 . We view each choice of a specific reference p as providing a chart centered at p on the exponential family
. We view each choice of a specific reference p as providing a chart centered at p on the exponential family
 , namely:
, namely:
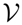 of the log-likelihood.
of the log-likelihood. the inverse of σp, i.e.,
the inverse of σp, i.e.,2.2. Change of Chart
 ; then, we can express p in the chart centered at p̄,
; then, we can express p in the chart centered at p̄, , q = exp (U − kp(U)) p, U ∈
, q = exp (U − kp(U)) p, U ∈

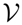 , kp(U) = log (
, kp(U) = log (
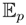 [eU]), in coordinates
, we can write:
[eU]), in coordinates
, we can write: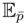 [U] =
[U] =
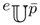 (U) + Ū.
(U) + Ū. , (σp)). This fact has deep consequences that we do not discuss here, e.g., our manifold is an instance of a Hessian manifold [16].
, (σp)). This fact has deep consequences that we do not discuss here, e.g., our manifold is an instance of a Hessian manifold [16].2.3. Tangent Bundle

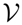 , and it is identified with the tangent space of the manifold at p, Tq
, and it is identified with the tangent space of the manifold at p, Tq  ; see the discussion in [3,9]. Let us check the consistency of this statement with our θ-parametrization.
; see the discussion in [3,9]. Let us check the consistency of this statement with our θ-parametrization. . In the chart centered at q(0), we have from Equation (12):
. In the chart centered at q(0), we have from Equation (12):
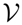 is represented by the coordinates in the base
is represented by the coordinates in the base
 . The tangent bundle T
. The tangent bundle T  as a manifold is defined by the charts (σp, σ̇p) on the domain:
as a manifold is defined by the charts (σp, σ̇p) on the domain: , i.e., V (p),W(p) ∈ Tp
, i.e., V (p),W(p) ∈ Tp  =
=

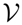 , p ∈
, p ∈
 , we define a Riemannian metric g(V,W)) by:
, we define a Riemannian metric g(V,W)) by:2.4. Gradients
 → ℝ let φp = φ ∘ ep,
, its representation in the chart centered at p:
→ ℝ let φp = φ ∘ ep,
, its representation in the chart centered at p: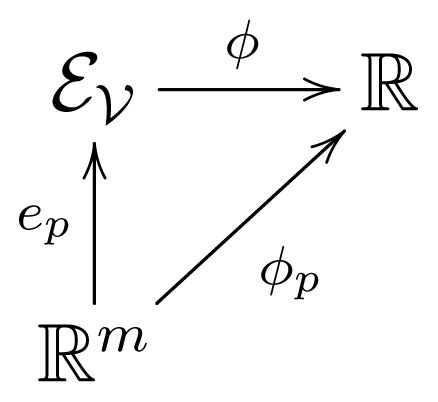
 ; see [15]. It is a standard notion in Riemannian geometry; cf. [4] (p. 46).
; see [15]. It is a standard notion in Riemannian geometry; cf. [4] (p. 46). and θ ∈ ℝm,
and θ ∈ ℝm, , ∇̃φ:
, ∇̃φ:
 → ℝm is defined by:
→ ℝm is defined by: is the vector field ∇φ, such that DYφ = g(∇φ, Y ). Note that the Riemannian gradient takes values in the tangent bundle, while the natural gradient takes values in ℝm. We compute the Riemannian gradient at p as follows. If y = σ̇p(Y (p)),
is the vector field ∇φ, such that DYφ = g(∇φ, Y ). Note that the Riemannian gradient takes values in the tangent bundle, while the natural gradient takes values in ℝm. We compute the Riemannian gradient at p as follows. If y = σ̇p(Y (p)), . Explicitly, we have (see Equation (22)),
. Explicitly, we have (see Equation (22)),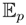 [∇φ(p)
[∇φ(p)
 X].
X].
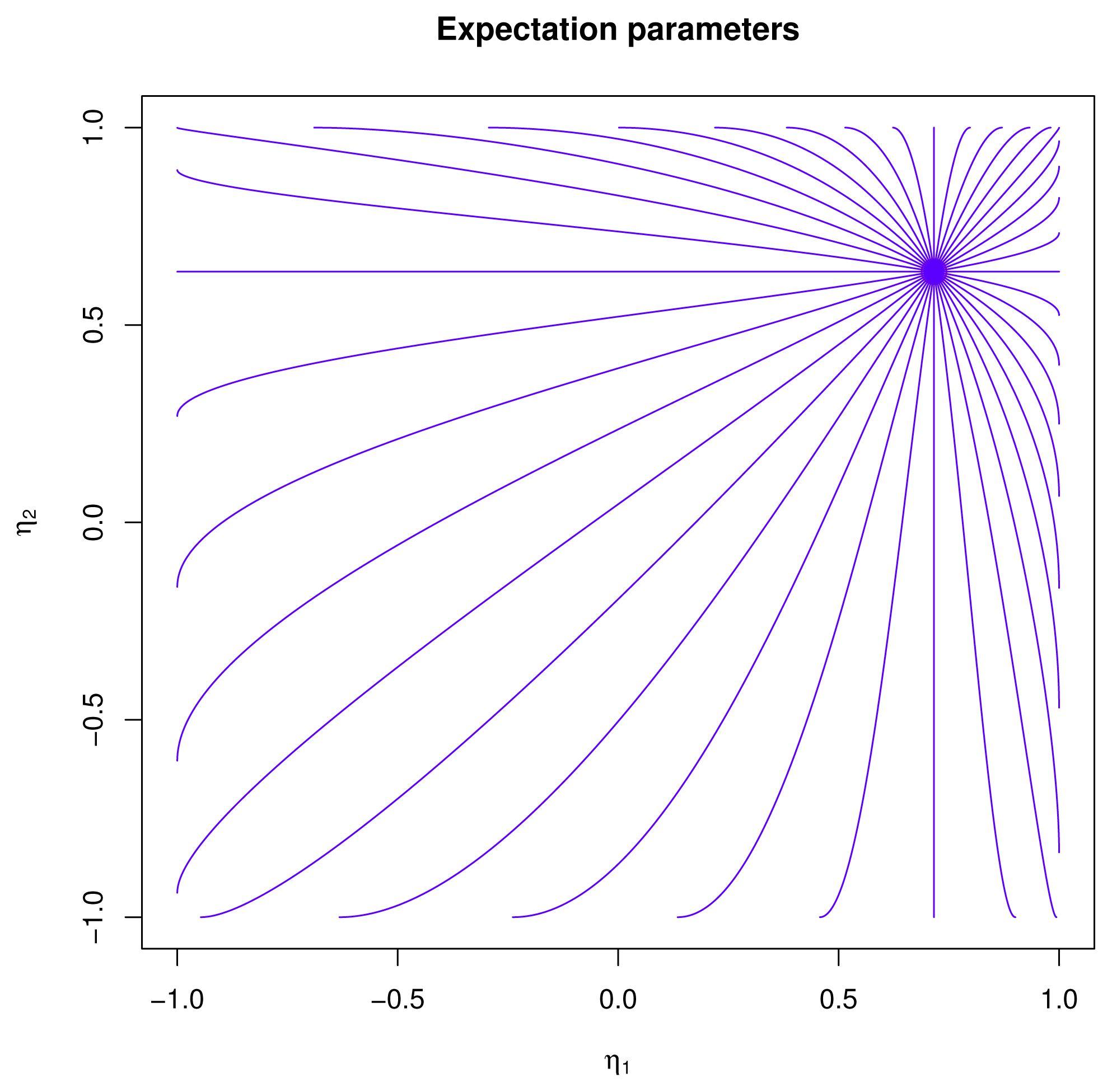
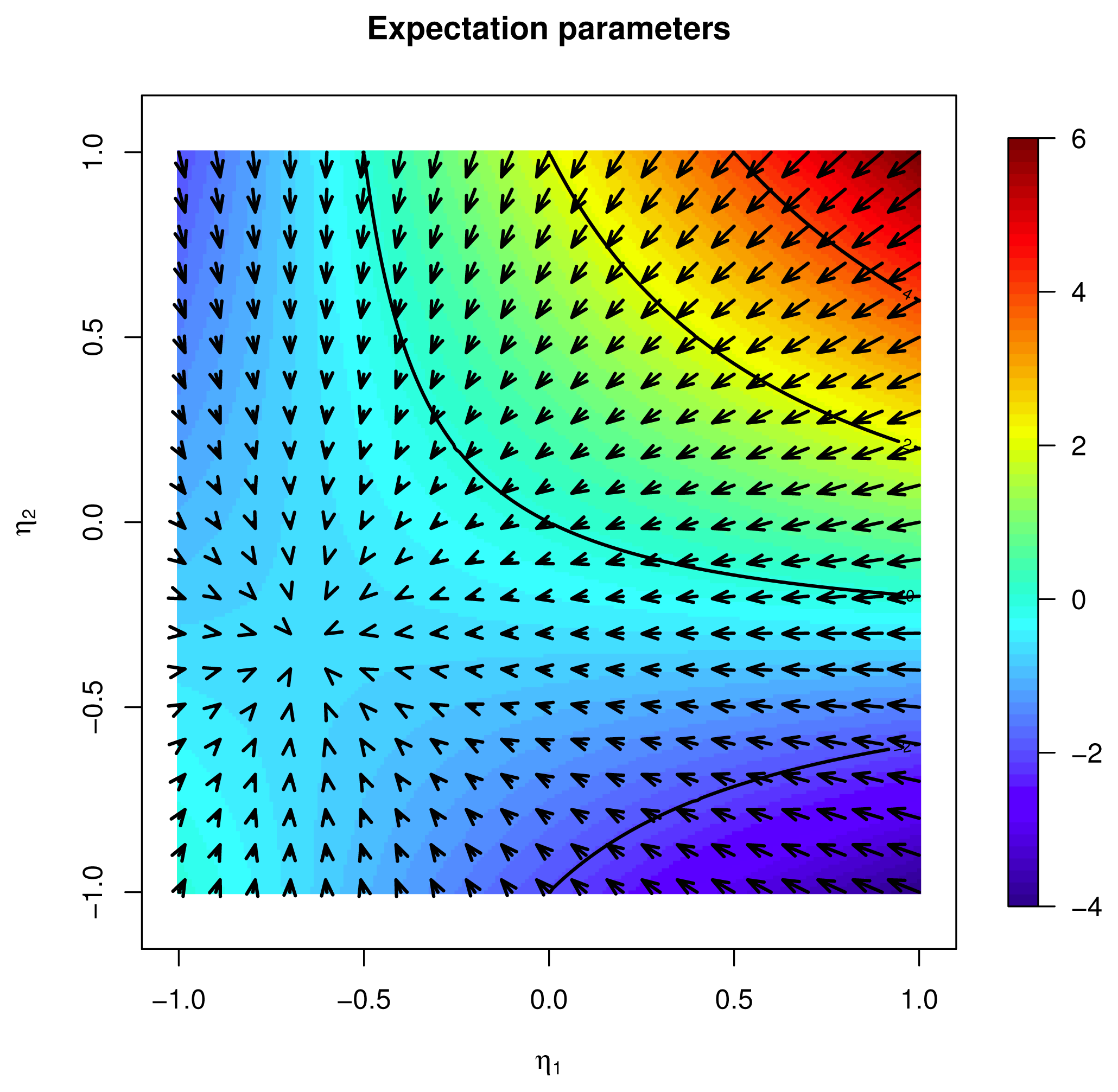
2.4.1. Expectation Parameters
 X; see [1]. The function μp :
X; see [1]. The function μp :
 defined by:
defined by: . The value of the inverse q = Lp(μ) is characterized as the unique q ∈
. The value of the inverse q = Lp(μ) is characterized as the unique q ∈
 , such that μ =
, such that μ =
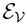 [
[
 X], i.e., the maximum likelihood estimator.
X], i.e., the maximum likelihood estimator.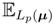 [
[
 X] and μ̄ = μp̄(Lp(μ)) =
X] and μ̄ = μp̄(Lp(μ)) =
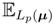 [
[
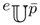 X].
X]. ,
,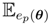 [
[
 X] = ∇φp(θ), hence:
X] = ∇φp(θ), hence:2.4.2. Vector Fields
 and φ:
and φ:
 is a real function, then we define the action of V on φ, ∇V φ, to be the real function:
is a real function, then we define the action of V on φ, ∇V φ, to be the real function: is a family of curves γ(t, p), p ∈
is a family of curves γ(t, p), p ∈
 t ∈ Jp, Jp open real interval containing zero, such that for all p ∈
t ∈ Jp, Jp open real interval containing zero, such that for all p ∈
 and t ∈ Jp,
and t ∈ Jp, .
.2.5. Examples
2.5.1. Expectation
 by F(p) =
by F(p) =
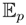 [f]. In the chart centered at p, we have:
[f]. In the chart centered at p, we have:
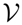 , while ∇̃F(p) in Equation (54) are the coordinates of the projection. Let us consider the family of curves:
, while ∇̃F(p) in Equation (54) are the coordinates of the projection. Let us consider the family of curves: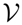 ⊕ ℝ. Then, γ is not, in general, the flow of ∇F, but it is a local approximation, as δγ(0, p) = ∇F(p).
⊕ ℝ. Then, γ is not, in general, the flow of ∇F, but it is a local approximation, as δγ(0, p) = ∇F(p).2.5.2. Binary Independent Variables
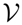 be generated by the coordinate projections = {X1, . . . , Xd}. Note that we use here the coding +1, −1 (from physics) instead of the coding 0, 1, which is more common in combinatorial optimization. The exponential family is
, λ(x) = 2−m for x ∈Ω being the uniform density. The independence of the sufficient statistics Xj under all distributions in
be generated by the coordinate projections = {X1, . . . , Xd}. Note that we use here the coding +1, −1 (from physics) instead of the coding 0, 1, which is more common in combinatorial optimization. The exponential family is
, λ(x) = 2−m for x ∈Ω being the uniform density. The independence of the sufficient statistics Xj under all distributions in
 implies:
implies: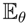 [Xi] −
[Xi] −
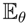 [Xi]
[Xi]
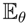 [Xk]2; see [13].
[Xk]2; see [13].2.5.3. Escort Probabilities
 defined by C(a) (p) = ∫ pa dμ. We have:
defined by C(a) (p) = ∫ pa dμ. We have: =
=

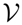 .
. ∋ p ↦ pa/C(a)(a) ∈ ℘>. Let us extend the basis X1, . . . , Xm to a basis X1, . . . , Xn, n ≥ m, whose exponential family is full, i.e., equal to ℘>. The non-parametric coordinate of
in the chart centered at
is the p̄-centering of the random variable:
∋ p ↦ pa/C(a)(a) ∈ ℘>. Let us extend the basis X1, . . . , Xm to a basis X1, . . . , Xn, n ≥ m, whose exponential family is full, i.e., equal to ℘>. The non-parametric coordinate of
in the chart centered at
is the p̄-centering of the random variable: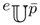 X1, . . . ,
X1, . . . , 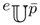 Xn are (aθ1, . . . , aθm, 0, . . . , 0), and the Jacobian of θ ∋ (aθ, 0n−m) is the m × n matrix [aIm|0m×(n −m)].
Xn are (aθ1, . . . , aθm, 0, . . . , 0), and the Jacobian of θ ∋ (aθ, 0n−m) is the m × n matrix [aIm|0m×(n −m)].2.5.4. Polarization Measure
 , define:
, define:3. Second Order Calculus
3.1. Metric Derivative (Levi–Civita connection)
 be vector fields, that is, V (p), W(p) ∈ Tp
be vector fields, that is, V (p), W(p) ∈ Tp  =
=

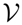 , p ∈
, p ∈
 . Consider the real function R = g(V,W) :
. Consider the real function R = g(V,W) :
 → ℝ, whose value at p ∈
→ ℝ, whose value at p ∈
 is R(p) = gp(V (p), W(p)) =
is R(p) = gp(V (p), W(p)) =
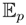 [V (p)W(p)]. Assuming smoothness, we want to compute the derivative of R along the vector field Y :
[V (p)W(p)]. Assuming smoothness, we want to compute the derivative of R along the vector field Y :
 , that is, (DY R)(p) = dRp(0)α, with α = σ̇p(Y (p)). The expression of R in the chart centered at p is, according to Equation (27),
, that is, (DY R)(p) = dRp(0)α, with α = σ̇p(Y (p)). The expression of R in the chart centered at p is, according to Equation (27),Proposition 1
 , whose value at q = ep(θ) has coordinates centered at p given by:
, whose value at q = ep(θ) has coordinates centered at p given by: , we have:
, we have:
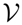 .
.3.2. Acceleration
 . Then, the velocity
is a vector field V (p(t)) = δp(t), defined on the support p(I) of the curve. As the curve is the flow of the velocity field, we can compute the metric derivative of the velocity along the the velocity itself Dδpδp from Equation (91) with V (p(0)) = δp(0); we can use Equation (91) to get:
. Then, the velocity
is a vector field V (p(t)) = δp(t), defined on the support p(I) of the curve. As the curve is the flow of the velocity field, we can compute the metric derivative of the velocity along the the velocity itself Dδpδp from Equation (91) with V (p(0)) = δp(0); we can use Equation (91) to get: →
→
 defined by:
defined by:3.2.1. Example: Binary Independent 2.5.2 Continued
 →
→
 . If (p, U) ∈ T
. If (p, U) ∈ T  , that is, p ∈
, that is, p ∈
 and U ∈ Tp
and U ∈ Tp  , then σλ(p) = θ(0) and U = ∑uj
, then σλ(p) = θ(0) and U = ∑uj  Xj, σ̇λ(U) = u. If:
Xj, σ̇λ(U) = u. If:3.3. Riemannian Hessian
 → ℝ with Riemannian gradient ∇φ(p) = ∑i(∇̃φ)i(p)
→ ℝ with Riemannian gradient ∇φ(p) = ∑i(∇̃φ)i(p)
 Xi,
. The Riemannian Hessian of φ is the metric derivative of the gradient ∇φ along the vector field Y, that is, HessY φ = DY∇φ; see [6] (Ch. 6, Ex. 11), [4] (§5.5). in the following, we denote by the symbol Hess, without a subscript, the ordinary Hessian matrix.
Xi,
. The Riemannian Hessian of φ is the metric derivative of the gradient ∇φ along the vector field Y, that is, HessY φ = DY∇φ; see [6] (Ch. 6, Ex. 11), [4] (§5.5). in the following, we denote by the symbol Hess, without a subscript, the ordinary Hessian matrix. for all vector fields X. We have from Equation (126), with α = σ̇p(Y (p)) and β = σ̇p(X(p)),
for all vector fields X. We have from Equation (126), with α = σ̇p(Y (p)) and β = σ̇p(X(p)), ; see the comments in [4] (Prop. 5.5.2-3). Note that the Riemannian Hessian is positive definite if:
; see the comments in [4] (Prop. 5.5.2-3). Note that the Riemannian Hessian is positive definite if:4. Application to Combinatorial Optimization
4.1. Hessian of a Relaxed Function
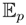 [f], p ∈ ℘>. Define F(p) to be the projection of f, as an element of L2(p), onto Tp
[f], p ∈ ℘>. Define F(p) to be the projection of f, as an element of L2(p), onto Tp  =
=

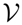 , i.e., F(p) is the element of
, i.e., F(p) is the element of

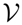 , such that:
, such that: , we have F(p) = ∑if̂p,i
, we have F(p) = ∑if̂p,i  Xi and:
Xi and: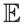 . [f] :
. [f] :
 . We have φp(θ) =
. We have φp(θ) =
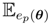 [f], and from the properties of exponential families, the Euclidean gradient is ∇φp(0) = Covp (f, X). It follows that the natural gradient is:
[f], and from the properties of exponential families, the Euclidean gradient is ∇φp(0) = Covp (f, X). It follows that the natural gradient is:4.1.1. Example: Binary Independent 2.5.2 and 3.2.1 Continued
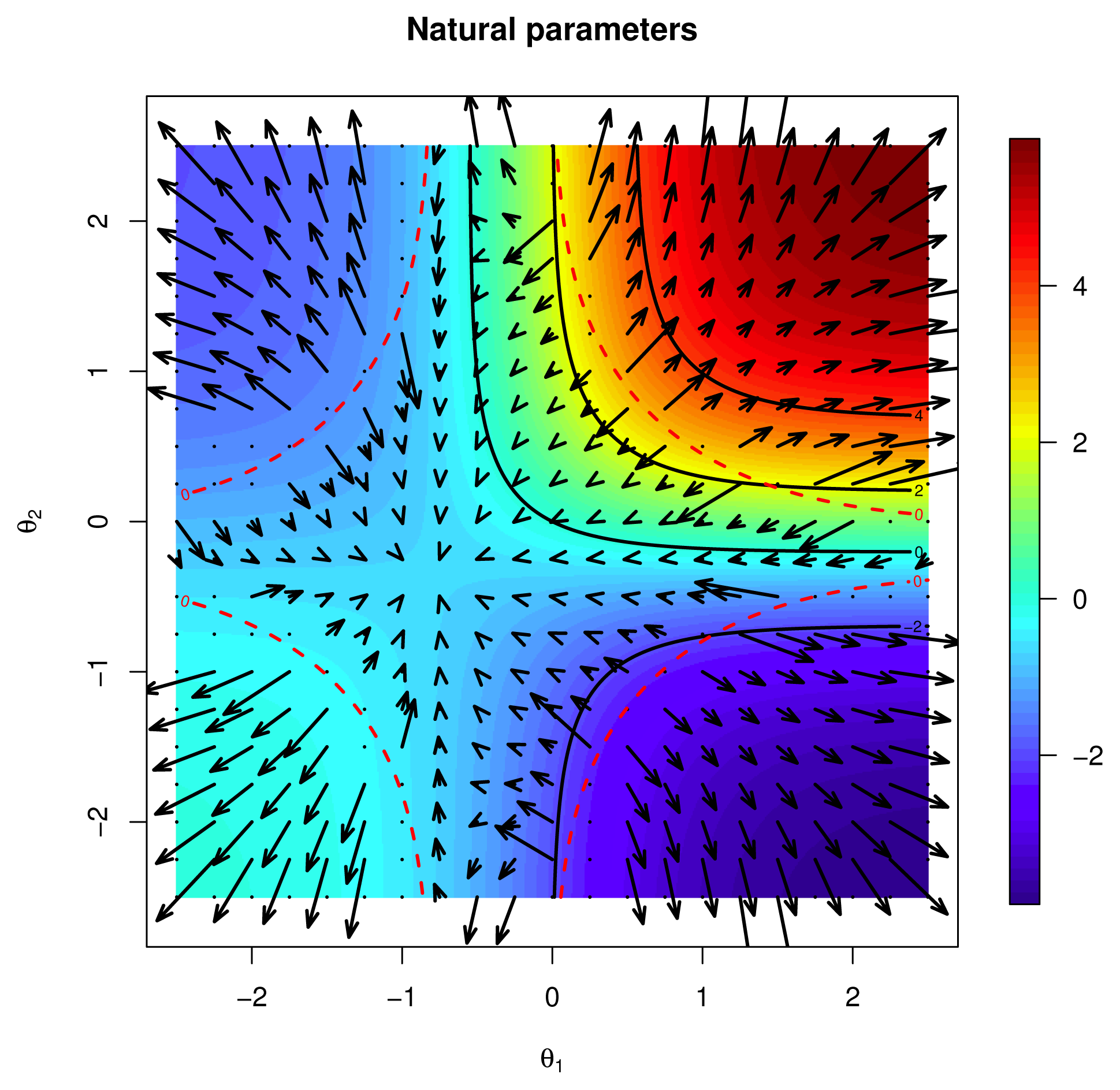
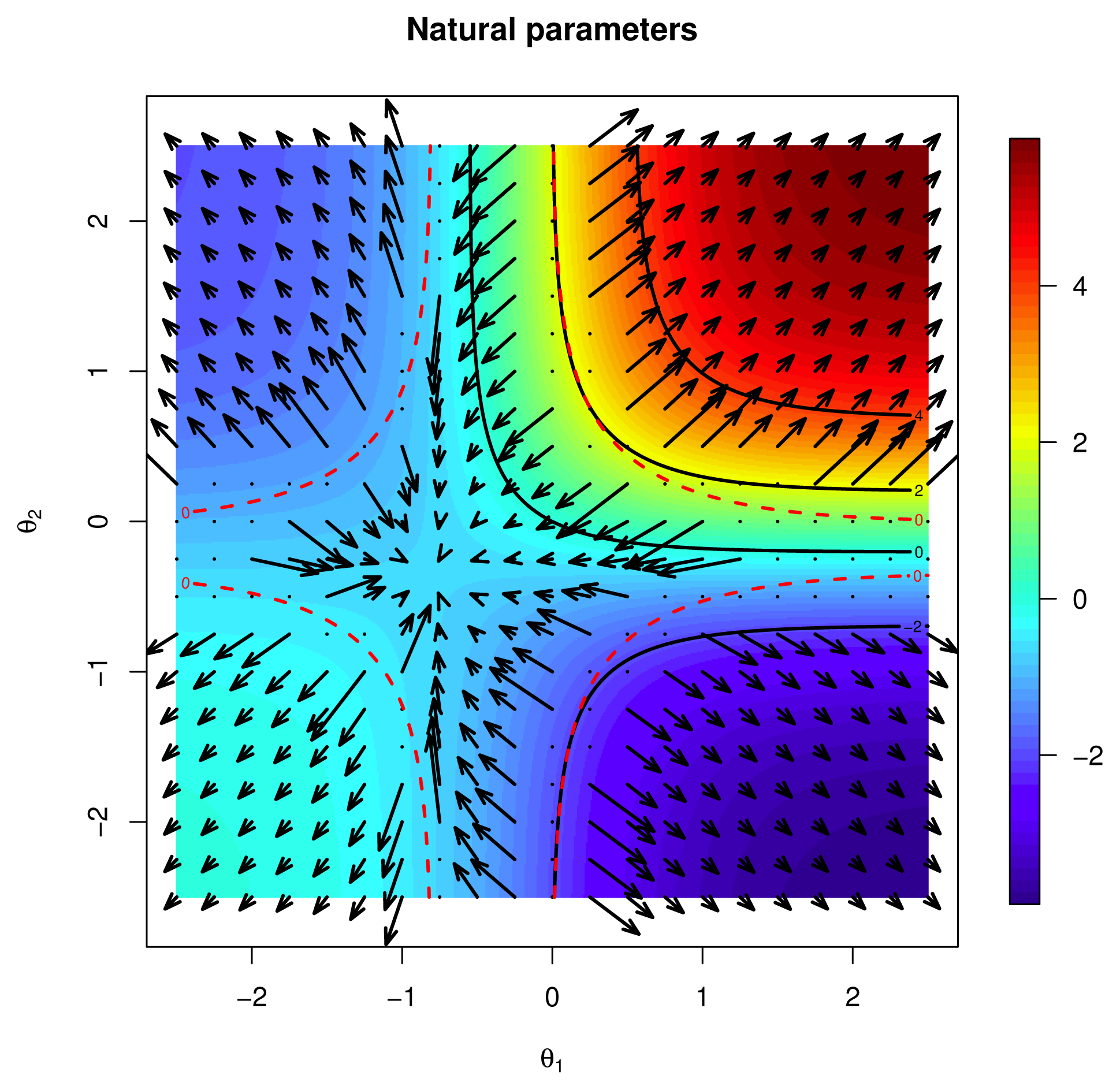
4.2. Newton Method
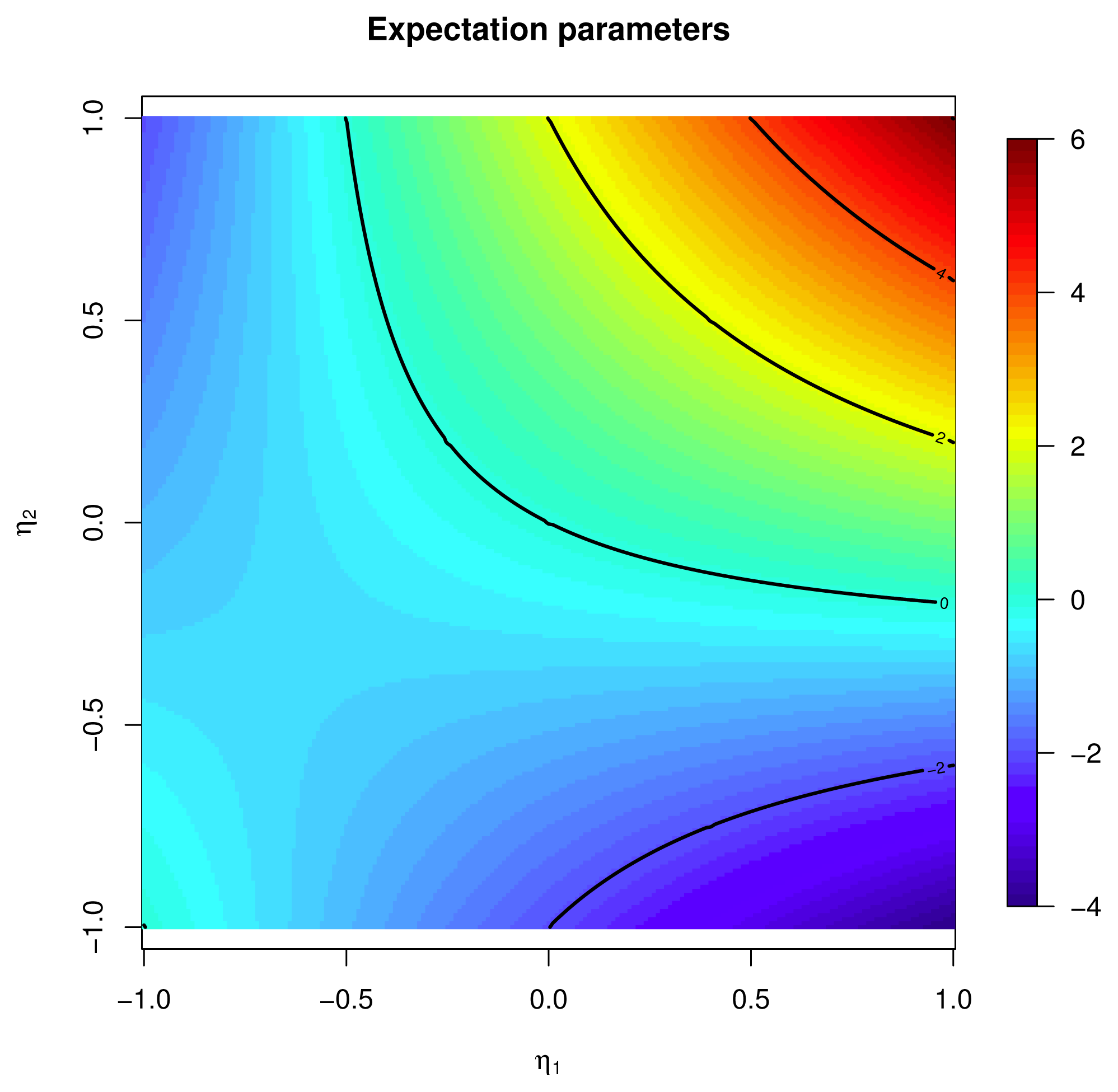
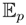 [f], p ∈
[f], p ∈
 , that is, a critical point of the vector field p ↦ ∇F(p), ∇F(p̂) = 0. Here, we follow [4] (Ch. 5–6), and in particular Algorithm 5 on Page 113.
, that is, a critical point of the vector field p ↦ ∇F(p), ∇F(p̂) = 0. Here, we follow [4] (Ch. 5–6), and in particular Algorithm 5 on Page 113. connecting p = p(0) to p̂ = p(1) that:
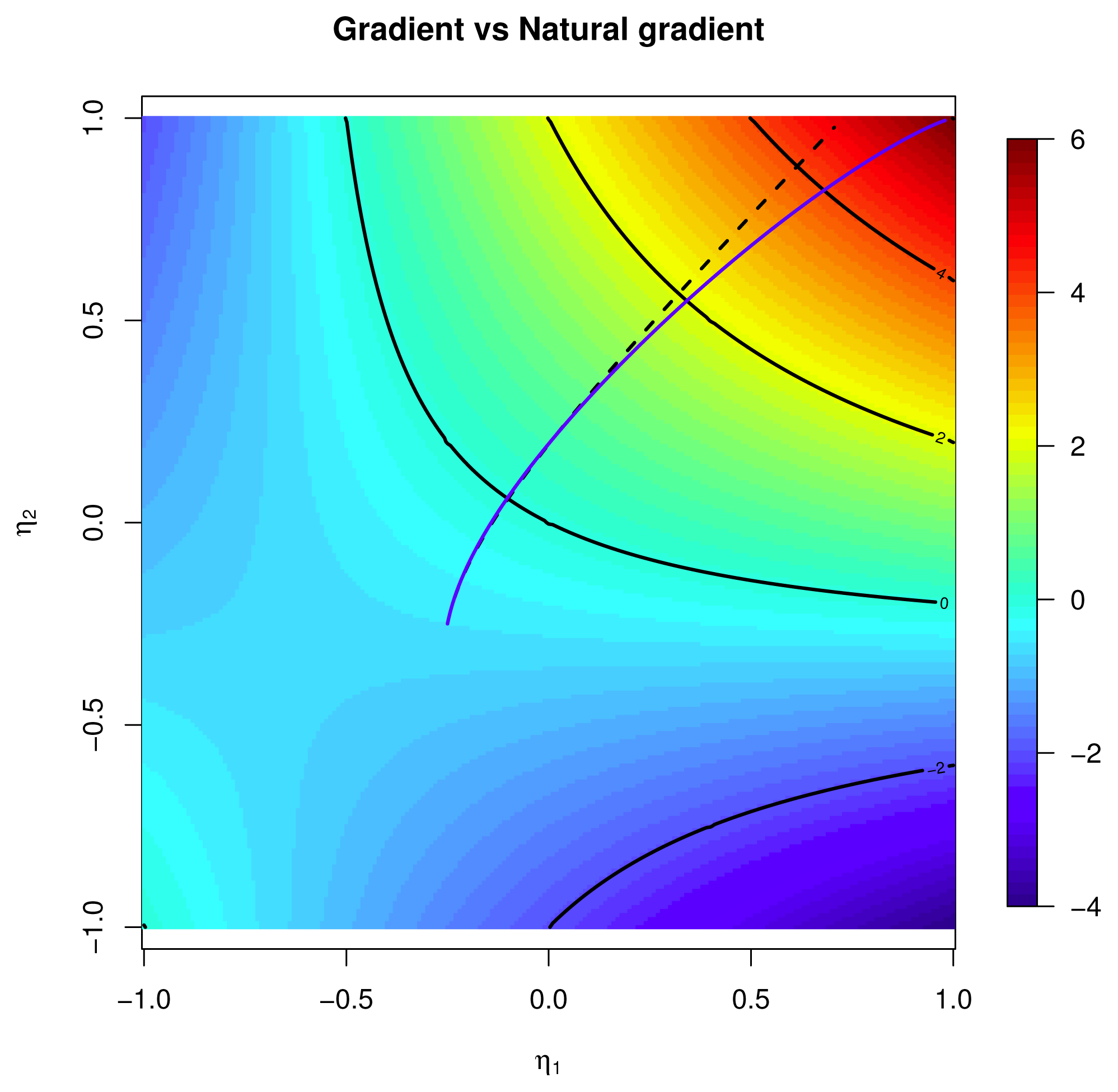
connecting p = p(0) to p̂ = p(1) that:4.3. Example: Binary Independent
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brown, L.D. Fundamentals of Statistical Exponential Families with Applications in Statistical Decision Theory; Number 9 in IMS Lecture Notes. Monograph Series; Institute of Mathematical Statistics: Hayward, CA, USA, 1986; p. 283. [Google Scholar]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; American Mathematical Society: Providence, RI, USA, 2000; p. 206. [Google Scholar]
- Pistone, G. Nonparametric Information Geometry. In Geometric Science of Information; Proceedings of the First International Conference, GSI 2013, Paris, France, 28–30 August 2013, Nielsen, F., Barbaresco, F., Eds.; Lecture Notes in Computer Science, Volume 8085; Springer: Berlin/Heidelberg, Germany, 2013; pp. 5–36. [Google Scholar]
- Absil, P.A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds; Princeton University Press: Princeton, NJ, USA, 2008; p. xvi+224. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 2006; p. xxii+664. [Google Scholar]
- Do Carmo, M.P. Riemannian geometry; Mathematics: Theory & Applications; Birkhäuser Boston Inc.: Boston, MA, USA, 1992; p. xiv+300. [Google Scholar]
- Abraham, R.; Marsden, J.E.; Ratiu, T. Manifolds, Tensor Analysis, and Applications, 2nd ed; Applied Mathematical Sciences, Volume 75; Springer: New York, NY, USA, 1988; p. x+654. [Google Scholar]
- Lang, S. Differential and Riemannian Manifolds, 3rd ed.; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1995; p. xiv+364. [Google Scholar]
- Pistone, G. Algebraic varieties vs. differentiable manifolds in statistical models. In Algebraic and Geometric Methods in Statistics; Gibilisco, P., Riccomagno, E., Rogantin, M.P., Wynn, H.P., Eds.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Malagò, L.; Matteucci, M.; Dal Seno, B. An information geometry perspective on estimation of distribution algorithms: Boundary analysis. Proceedings of the 2008 GECCO Conference Companion On Genetic and Evolutionary Computation (GECCO ’08); ACM: New York, NY, USA, 2008; pp. 2081–2088. [Google Scholar]
- Malagò, L.; Matteucci, M.; Pistone, G. Stochastic Relaxation as a Unifying Approach in 0/1 Programming. Proceedings of the NIPS 2009 Workshop on Discrete Optimization in Machine Learning: Submodularity, Sparsity & Polyhedra (DISCML), Whistler Resort & Spa, BC, Canada, 11–12 December 2009.
- Malagò, L.; Matteucci, M.; Pistone, G. Stochastic Natural Gradient Descent by Estimation of Empirical Covariances. Proceedings of the IEEE Congress on Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; pp. 949–956.
- Malagò, L.; Matteucci, M.; Pistone, G. Towards the geometry of estimation of distribution algorithms based on the exponential family. Proceedings of the 11th Workshop on Foundations of Genetic Algorithms (FOGA ’11), Schwarzenberg, Austria, 5–8 January 2011; ACM: New York, NY, USA, 2011; pp. 230–242. [Google Scholar]
- Malagò, L.; Matteucci, M.; Pistone, G. Natural gradient, fitness modelling and model selection: A unifying perspective. Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Cancun, Mexico, 20–23 June 2013; pp. 486–493.
- Amari, S.I. Natural gradient works efficiently in learning. Neural Comput 1998, 10, 251–276. [Google Scholar]
- Shima, H. The Geometry of Hessian Structures; Scientific Publishing Co Pte. Ltd. World: Hackensack, NJ, USA, 2007; p. xiv+246. [Google Scholar]
- Malagò, L. On the Geometry of Optimization Based on the Exponential Family Relaxation. Ph.D. Thesis, Politecnico di Milano, Milano, Italy, 2012. [Google Scholar]
- Gallavotti, G. Statistical Mechanics: A Short Treatise; Texts and Monographs in Physics; Springer: Berlin, Germany, 1999; p. xiv+339. [Google Scholar]
- Naudts, J. Generalised exponential families and associated entropy functions. Entropy 2008, 10, 131–149. [Google Scholar]
- Esteban, J.; Ray, D. On the Measurement of Polarization. Econometrica 1994, 62, 819–851. [Google Scholar]
- Montalvo, J.; Reynal-Querol, M. Ethnic polarization, potential conflict, and civil wars. Am. Econ. Rev 2005, 796–816. [Google Scholar]
- Stein, W.; et al. Sage Mathematics Software (Version 6.0); The Sage Development Team, 2013. Available online: http://www.sagemath.org (accessed on 27 March 2014).


© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Malagò, L.; Pistone, G. Combinatorial Optimization with Information Geometry: The Newton Method. Entropy 2014, 16, 4260-4289. https://doi.org/10.3390/e16084260
Malagò L, Pistone G. Combinatorial Optimization with Information Geometry: The Newton Method. Entropy. 2014; 16(8):4260-4289. https://doi.org/10.3390/e16084260
Chicago/Turabian StyleMalagò, Luigi, and Giovanni Pistone. 2014. "Combinatorial Optimization with Information Geometry: The Newton Method" Entropy 16, no. 8: 4260-4289. https://doi.org/10.3390/e16084260



