Entropy vs. Majorization: What Determines Complexity?

Abstract

The evolution of a microcanonical statistical ensemble of states of isolated systems from order to disorder as determined by increasing entropy, is compared to an alternative evolution that is determined by mixing character. The fact that the partitions of an integer N are in one-to-one correspondence with macrostates for N distinguishable objects is noted. Orders for integer partitions are given, including the original order by Young and the Boltzmann order by entropy. Mixing character (represented by Young diagrams) is seen to be a partially ordered quality rather than a quantity (See Ruch, 1975). The majorization partial order is reviewed as is its Hasse diagram representation known as the Young Diagram Lattice (YDL).Two lattices that show allowed transitions between macrostates are obtained from the YDL: we term these the mixing lattice and the diversity lattice. We study the dynamics (time evolution) on the two lattices, namely the sequence of steps on the lattices (i.e., the path or trajectory) that leads from low entropy, less mixed states to high entropy, highly mixed states. These paths are sequences of macrostates with monotonically increasing entropy. The distributions of path lengths on the two lattices are obtained via Monte Carlo methods, and surprisingly both distributions appear Gaussian. However, the width of the path length distribution for diversity is the square root of the mixing case, suggesting a qualitative difference in their temporal evolution. Another surprising result is that some macrostates occur in many paths while others do not. The evolution at low entropy and at high entropy is quite simple, but at intermediate entropies, the number of possible evolutionary paths is extremely large (due to the extensive branching of the lattices). A quantitative complexity measure associated with incomparability of macrostates in the mixing partial order is proposed, complementing Kolmogorov complexity and Shannon entropy.

“We’d been talking about storytelling, how there could be many versions of the same story, many ways of telling, and how each version was a kind of manifestation, as if the story itself was a living, evolving entity, a god capable of many guises.”

Vaddey Ratner, In the Shadow of the Banyan [1]

1. Introduction

The evolution from order to disorder involves at least three readily recognizable stages. System complexions near complete order are simple, but as the system ages the simple complexions evolve into intricate structures. This process ceases at equilibrium when the disorder is maximized. For example, the collections of cells making up individual organisms evolve from rudimentary forms to mature individuals, but then age until death. Physical systems such as gases and electro-mechanical devices as well as social structures and ecosystems apparently follow a similar evolutionary template. Appeal to the second law of thermodynamics, namely that the entropy of a system must increase until the system reaches equilibrium, is often invoked as a qualitative explanation of this universal phenomenon. Here we move the dialogue beyond the entropy argument alone, with a simple model that quantifies the evolution of generic systems to equilibrium. Our approach relies on elementary ideas founded in statistical physics and thermodynamics.

Central to the approach is the concept of macrostates and microstates of complex systems. A macrostate is described by a few, preferably observable, variables. Microstates, on the other hand, deal with the specific details making up the system. For example the same temperature and pressure of 22.4 L of gas can be produced by an enormous number of combinations of positions and momenta of the approximately 6 × 10²³ molecules in the container. As a second example, a computer screen will look exactly the same if a character is entered in an application and then deleted. However, the internal configuration of the computer has changed. The internal clock has advanced, background housekeeping programs run nearly continuously, the mailer may be refreshed, etc. These details, however, do not impact the macrostate depicted on the screen.

In order to connect statistical physics characterizations of entropy with the evolution of a system, it is customary to use the Boltzmann entropy. It was originally introduced in statistical mechanics to describe the macrostate of a gas by its characterization in a six dimensional position—momentum phase space for each of the molecules. Since then it has become the default disorder measure in disciplines as diverse as information theory (Shannon entropy), economics, and ecology. Arguably, it is the most widely used formula in science and technology.

The Boltzmann entropy is given by [2,3]

$$\frac{S}{k}=\text{log}\Omega =\text{log}\left(\frac{N!}{{\Pi }_{i=1}^N{\lambda }_i!}\right)$$

(1)

where k is the Boltzmann constant, N is the total number of distinguishable objects in the system, and λ_i are the number of objects in cell i. The term in parentheses on the right hand side of Equation (1) is simply the number of ways (i.e., permutations) the N distinguishable objects can be distributed in the λ_i cells, and is equal to the number of microstates, Ω, capable of producing the macrostate with entropy S. Inspection of Equation (1) shows that if all the objects are in one cell then the entropy is 0, and if they are equally distributed so that each cell has only one object then the system entropy achieves its maximum value of log N!. We contend that both of these states are conceptually simple. The Boltzmann entropy defines irreversibility in isolated systems.

For non-isolated systems, entropy is still a well-established thermodynamic quantity, though its change alone does not determine irreversibility. It is generally not directly measured experimentally. Nevertheless, statistical interpretations of entropy prove useful in a qualitative sense because increasing entropy is one of two factors determining spontaneity of chemical reactions at constant temperature and pressure (the other factor being enthalpy, which when combined with entropy gives the Gibbs free energy). Thus, for non-isolated systems, chemists often invoke heuristic arguments based on statistical disorder. However, for isolated systems near equilibrium, the second law states that entropy quantitatively determines whether or not a chemical or physical process can occur spontaneously. Following Ruch [4], we show that if an isolated system is far from equilibrium, there are many sequences of macrostates that lead to equilibrium, all of which are consistent with a monotonic increase in their Boltzmann entropy. In other words, while the entropy of an isolated system must increase as it evolves toward equilibrium, this can be accomplished in many ways. In this paper we will explore two types of sequences of macrostates that lead to equilibrium, both based on fundamental criteria for the simplest transition from one (more ordered) state to the next (less ordered) state. While these approaches to equilibrium do not in any way violate the second law of thermodynamics, they do not require that entropy uniquely determines the transition from a lower to a higher entropy macrostate. Indeed we find that every individual sequence involves a comparatively small number of macrostates—though, of course, an infinite ensemble of all sequences contains all macrostates.

The paper begins with two sections defining Young diagrams (which uniquely characterize the macrostates) and defining a partial order relation for these diagrams. A unique Boltzmann entropy for each macrostate is easily defined by Equation (1). In Section 4 we give results for the distribution of sequence lengths for ensembles of paths from low to high entropy via Monte Carlo simulation. Two evolutions for the macrostates (diversity and mixing) are studied and both exhibit monotonically increasing Boltzmann entropy. Our arguments will be couched in terms of the lattice of Young diagrams (well known as the Young Diagram Lattice) that describes the partial order of integer partitions according to dominance or majorization [5].

The dynamics on the lattices is studied in Section 5, and using the usual master equation arguments, may be related to the time required to reach equilibrium depending upon the assumed criterion for transitions between macrostates. In Section 6, we discuss some curious properties of the macrostates and their probabilities of occurrence. Finally, Section 7 discusses the results from the perspective of irreversibility and proposes a general relationship between entropy, complexity, and the incomparability of macrostates.

2. Mixing: The Young Diagram and Partitions of Integers

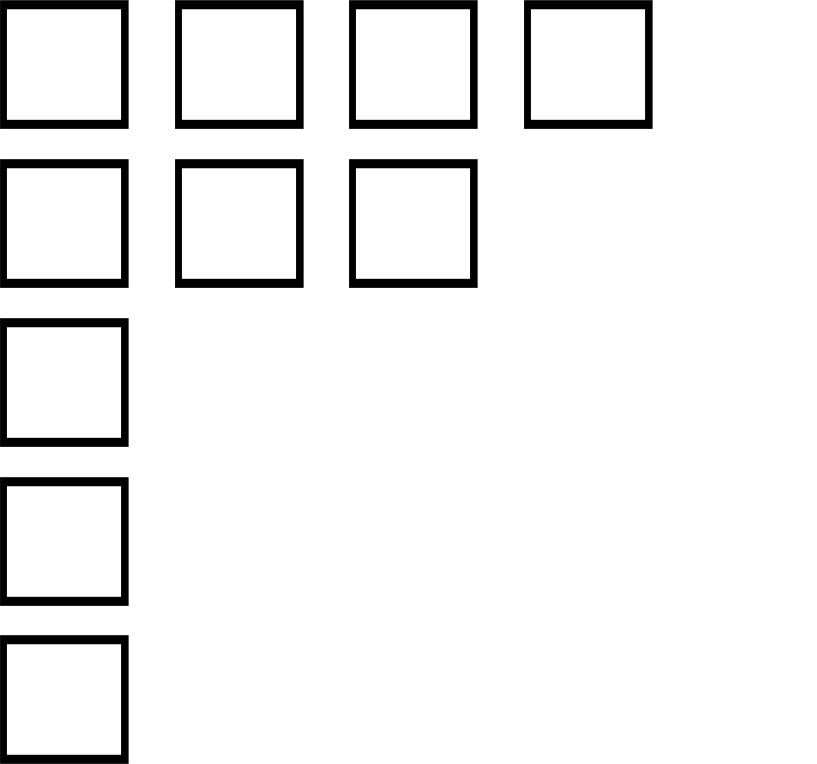
In 1900, Cambridge University mathematician Alfred Young introduced the Young Diagram (YD) [6]. It consisted of a finite collection of boxes arranged in left justified rows such that, proceeding from the top to the bottom of the diagram, successive rows have equal or fewer boxes. Figure 1 shows a YD with 10 boxes (where we have introduced the notation [4,3,1,1,1] for the diagram). (Note on notation: (a) the partition [5] represents the partition of 5 into [5,0,0,0,0]; (b) the partitions [3,1,1] and [1,1,1,1,1] can be written as [3, 1²] and [1⁵]). By construction, the Young diagrams are in one to one correspondence with the partitions of integers. The number of partitions, P (N), grows rapidly with N. For example, there are 9,253,082,936,723,602 partitions for N = 300 and more than 10³¹ for N = 1000. Hardy and Ramanujan [7] obtained an asymptotic formula for the number of partitions of the integer N:

$$P(N)~1/(4N\sqrt{3})\text{exp}\sqrt{2N/3}$$

(2)

While there is an entropy associated with every partition (obtained from Equation (1)), the Young diagram itself gives a more complete description of the macrostate.

3. Orders and Partial Orders for Young Diagrams

Foragiven N, the set of partitions can be ordered by various means, but partitions also can be partially ordered. Here we consider briefly two unique orders, and a partial order.

Young’s original order is as follows [6]. Reading from the top down, the first horizontal line in one diagram that is longer than the corresponding line in the second diagram makes the first diagram the larger. While this provides a unique order to the set of Young diagrams (and partitions), there seems to have been little use for this order in thermodynamics or statistical mechanics.

Recognizing that the partitions of integers are in one-to-one correspondence with macrostates in the microcanonical ensemble, a second example of an ordering of Young diagrams is by entropy. Let [λ₁, λ₂, λ₃, ..., λ_N] (λ_i defined as in Equation (1)) be a partition, then for an isolated system the Boltzmann entropy is given by Equation (1). The Boltzmann entropy provides an order for YDs i.e., the diagrams are ordered according to increasing entropy with partition [N] having entropy 0 and [1^N] having entropy N!.

To define the partial order, we introduce the concept of majorization or dominance. Let λ =[λ₁, λ₂, ..., λ_N] where λ_i is the number of objects of type i (or class i) be a partition of N.

In general we can take λ_i ≥ λ_j if i < j. The criterion of majorization (or dominance) is that a partition λ majorizes another partition μ if

$$\sum _{i=1}^m{\lambda }_i\ge \sum _{i=1}^m{\mu }_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall m=1\hspace{0.17em}\hspace{0.17em}\text{to}\hspace{0.17em}N$$

(3)

and we say that λ majorizes μ, symbolized by λ ≽ μ.

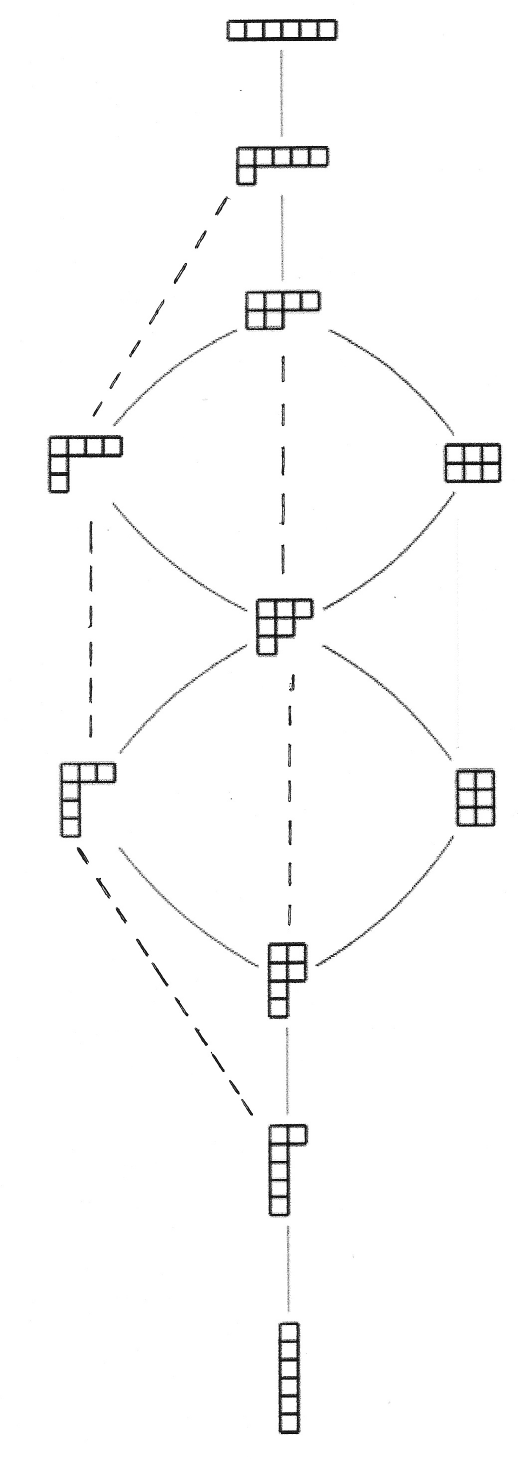
The majorization partial order can be represented by its Hasse Diagram in which the nodes are labeled by YD’s representing the mixing character of the macrostates. A macrostate Φ is connected to macrostate Ψ if and only if the Young diagram for Φ can be obtained from that for Ψ by moving one box to nearest shorter row. The Hasse diagram for N = 6 is shown by the solid lines in Figure 2. We will refer to this as the mixing lattice.

Now we define a second lattice, which we term the diversity lattice. In the diversity lattice, macrostate Φ can immediately succeed macrostate Ψ if the Young diagram for Φ can be obtained by moving one box in Ψ’s diagram to any shorter row (preceded only by rows longer than its original length). It is easily seen that both lattices only connect macrostates with increasing entropy. The diversity lattice includes both the dotted and solid lines in Figure 2. Note that there are many more node connections in the diversity lattice than in the mixing lattice.

The majorization partial order has a long history in number theory. In 1974, Ruch [4] proved that the majorization partial order describes the general process of mixing. Recent attention has been drawn to mixing with regard to quantum entanglement [8] and to molecular genetics as well [9]. The fundamental insight in Ruch’s paper is that mixing character has no numerical value; rather, it can only be represented by a diagram that represents the macrostate (i.e., the Young diagram). Even more generally, Ruch suggested that evolution in general proceeds according to increasing mixing character (as determined by the majorization partial order). This is a stronger requirement than increase of entropy alone, though entirely consistent with thermodynamic principles. As Ruch pointed out, evolution toward equilibrium is not necessarily determined by a single function such as entropy, but rather may be determined by a “quality”—the mixing character—which is partially ordered by majorization.

4. Paths to Equilibrium

We define a path (or chain) as a sequence of Young diagrams that proceeds from the most ordered partition [N] to the least ordered [1^N] in accord with the ordering rule assumed for the diagrams. For any unambiguous order (not a partial order), there is only a single path; and that contains (goes through) each diagram in sequence. The length of this path is thus simply the total number of diagrams given asymptotically in Equation (2).

For partially ordered macrostates, however, it is important to note that, while the macrostates still proceed from lower to higher entropy, they must also proceed in accordance with the rule for allowed transitions between macrostates, depicted in the mixing and diversity lattices. In both cases, the paths occur on a lattice and can be studied via Monte Carlo techniques similar to random growth models on tessellations or directed random walks on lattices [10]. For an isolated system, the macrostate [1^N] represents equilibrium. Thus, paths on the lattices are related to evolution from [N] to [1^N].

In this section we explore paths on both the diversity and mixing lattices. For low N, (N ≤ 10), the paths can be found by inspection. However, since the number of nodes in the lattice increases exponentially with $\sqrt{N}$ for large N, one must resort to statistical sampling. Assuming an equal transition probability between any two macrostates (nodes) connected by a single edge in the lattice, an algorithm for evolution on the lattice may be obtained as follows. Assume that partition i = [i₁, i₂, i₃, ..., i_N] majorizes several partitions j₁, j₂, j₃, ..., j_m and is connected to each by a single edge; then one simply selects one of the j partitions at random (choosing a random number 1 ≤ r ≤ m) and then proceeds until reaching equilibrium. For example, consider the lattices in Figure 2. On the mixing lattice, partition [3, 2, 1] is connected to and majorizes [3, 1, 1, 1] and [2, 2, 2]. In this case m =2 and the Monte Carlo method chooses r =1 or 2 to select the next partition. On the diversity lattice [3, 2, 1] is also connected to [2, 2, 1, 1] (see the dotted line in the figure) and also majorizes it. Thus in this case, m =3 and the Monte Carlo method chooses r =1, 2 or 3 to select which partition occurs next in the path.

We have obtained the distribution of path lengths on the diversity and mixing lattices. The distributions are shown in Figure 3 for N = 200 with a sample size of 10 million paths. Both have a Gaussian shape

$$f(x)=a{e}^{-\frac{{(x-b)}^2}{2c^2}}$$

(4)

For N = 200 there are over 3.9×10¹² partitions so the sample size is “small”. Nevertheless, we found that the distribution appears well converged after 10 million paths are sampled.

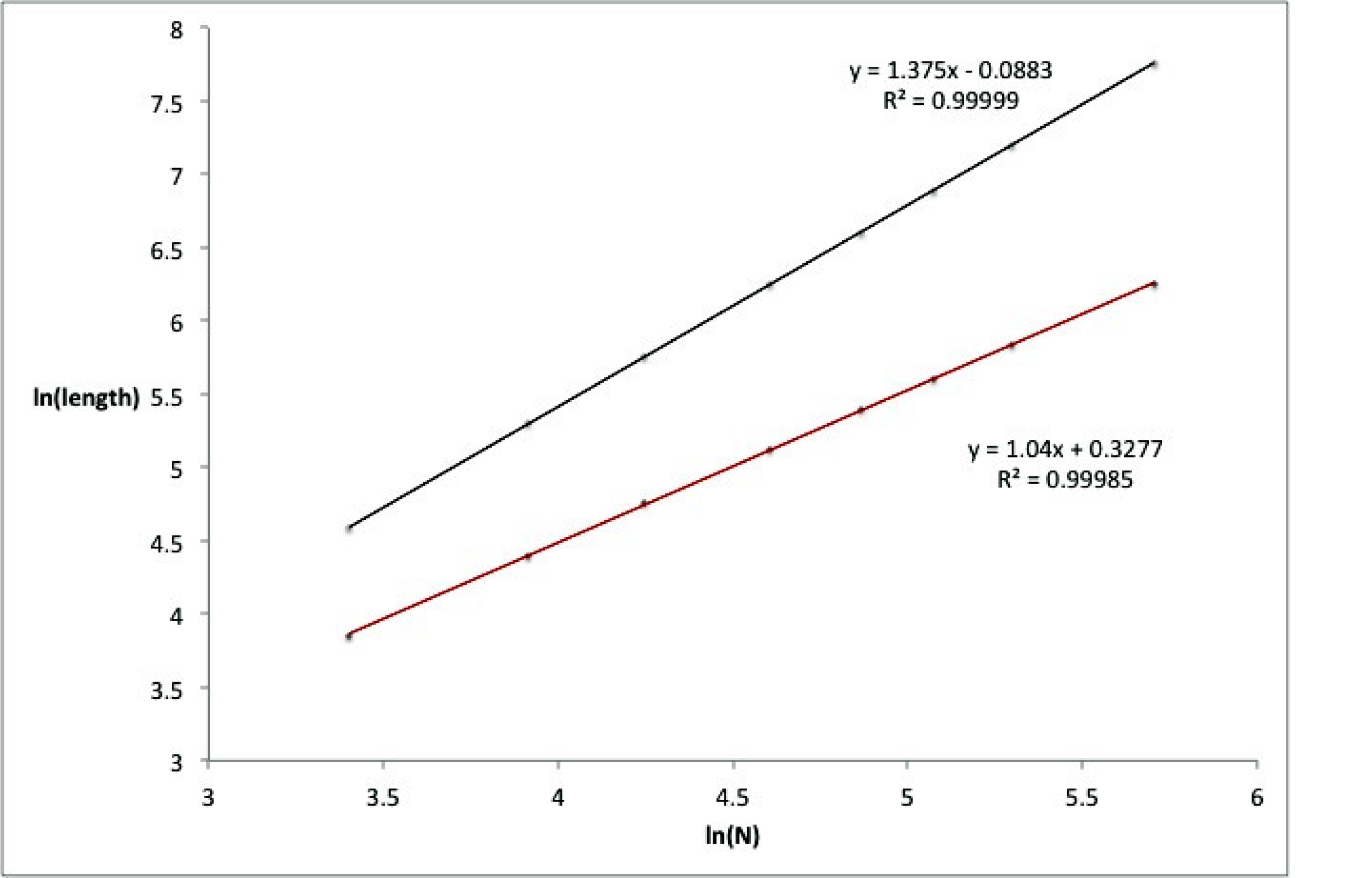
If we assume that the average path length l varies as N^δ, Figure 4 shows a log-log plot yielding δ_diversity ∼ 1 and δ_mixing ∼ 1.375.

In summary, the path lengths vary with N as follows:

$$\begin{array}{ll}l~e^{\sqrt{N}}\hfill & (\text{entropy}\hspace{0.17em}\text{order})\hfill \\ ~N^{1.375}\hfill & (\text{mixing})\hfill \\ ~N\hfill & (\text{diversity})\hfill \end{array}$$

(5)

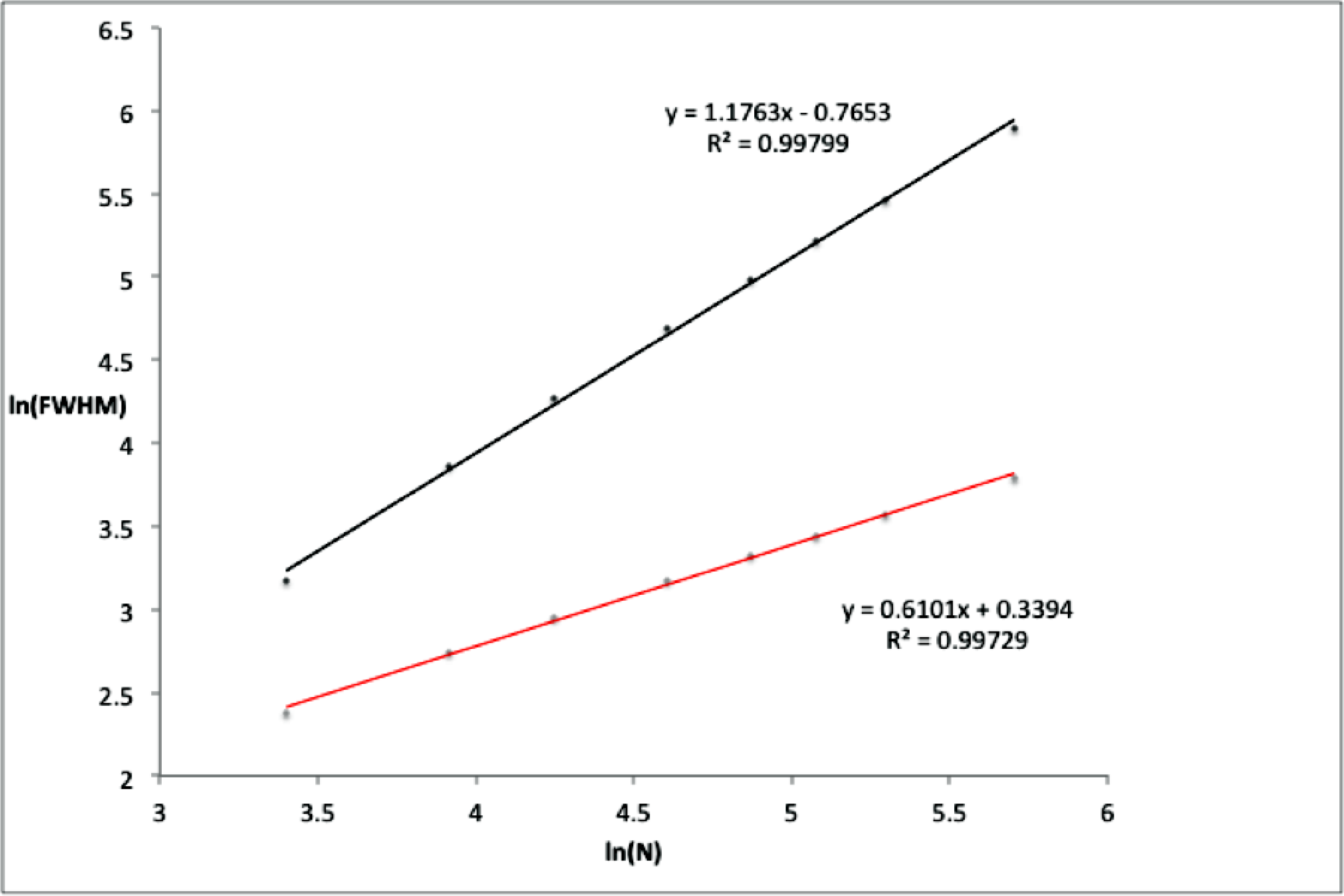
Next we consider the distribution widths. While both the diversity and mixing path distributions appear Gaussian, they have different average path lengths and different distribution widths. If we again assume a power law for the increase of the widths with N we have full width at half maximum (FWHM) ∼N^γ then a plot of the ln FWHM vs. ln N of the distributions should be linear with slope γ. The plots for both distributions are given in Figure 5.

From the figure we see that γ_mixing ∼ 1.18 and γ_diversity ∼ 0.61 or

$${\gamma }_{\mathit{diversity}}~\frac{1}{2}{\gamma }_{\mathit{mixing}}$$

(6)

It is evident from Figure 2 that the number of allowed transitions between partitions is much larger for the diversity lattice than the mixing lattice, hence path lengths are shorter, and the distribution is narrower for the diversity lattice. This occurs because the added paths available on the diversity lattice are generally much shorter, leading to an overall decrease in average path length. The effect of this may be profound because system properties are determined by ensemble averages, which in turn may be averages over the properties of the macrostates as weighted by their probability of occurrence. Thus, there are far more macrostates that contribute to ensemble averages in the mixing lattice as compared with the diversity case. For large N, this will be particularly significant.

We note that the average path length on the mixing lattice is a power law very close to 4/3. Four thirds power laws have been identified in empirical studies in a variety of disciplines. These include allometric relations in biology and ecosystems [11–17] and the growth of Koch curves. It seems then that the mixing lattice paradigm might provide a theoretical basis for this behavior. We will explore this idea further in future work.

In the next section we discuss the evolution from order to disorder in the context of Ruch’s General Thermodynamic Principle.

5. Paths and Time

We now consider various means that an isolated system far from equilibrium might evolve toward equilibrium. Since the states are entropically ordered, entropy alone cannot rule out processes that pass through all or most of the partitions (since every step could correspond to a minimum increase of entropy at each step). Thus, in principle, paths of exponentially increasing length as a function of N are possible.

The increase in entropy is often argued to provide an arrow of time. Now as we have already noted, paths on both the diversity and mixing lattices also pass through states of monotonically increasing entropy. However, for partial orders with “incomparable” diagrams (in our case those incomparable under majorization), a single path on the lattice clearly can go through only one of the incomparable states/partitions/diagrams. Nevertheless, every path on both the diversity and mixing lattices still corresponds to a sequence of states of monotonically increasing entropy. This led Ruch to propose his Principle of Increasing Mixing Character

“The time development of a statistical (Gibbs-) ensemble of isolated systems (microcanonical ensemble) proceeds in such a way that the mixing character increases.”

We explore the consequences of this principle by considering the path length distributions in Section 4 with the assumption that each transition between states in the lattice connected by a single edge occurs with unit time [10]. Thus, for both lattices, ensembles of systems evolve from low to high entropy with a Gaussian distribution of steps to equilibrium. However, the average “relaxation time” from complete order to equilibrium is much longer for the mixing lattice than for the diversity lattice. From the results in Section 4

$$[\mathit{relaxation}(\mathit{mixing})]~{[\mathit{relaxation}(\mathit{diversity})]}^{1.375}$$

(7)

It is also evident from Equation (7) that for large N, the time to reach equilibrium assuming entropic ordering (where every macrostate must be visited and the length is simply the partition number) is exponentially longer than the evolution time for either diversity or mixing.

The distribution’s full width at half maximum provides an estimate of the “band width” of relaxation times so that

$$[\mathit{band}\hspace{0.17em}\mathit{width}\hspace{0.17em}(\mathit{diversity})]~\sqrt{[\mathit{band}\hspace{0.17em}\mathit{width}\hspace{0.17em}(\mathit{mixing})]}$$

(8)

In other words, systems obeying mixing lattice evolution will have average mixing lifetimes that are the square of mixing lifetimes for systems obeying diversity lattice evolutions. Attard [18,19] proposed the concept of second entropy to introduce time specifically. His work developed a variational principle, based on maximizing the so-called transition entropy, which is “the number of molecular configurations associated with a transition between macrostates in a specified time”. While different from (and more general than) our assumption of unit time per transitions on the lattice, his work recognizes the need to explicitly consider the number of molecular configurations associated with macrostate transitions.

6. Properties of the Nodes and Paths

The most striking difference between an order and a partial order is that the latter has nodes that are not comparable. In the Hasse diagram for a partial order, incomparable nodes are those that cannot occur in the same path. It seems natural, then, to define an incomparability number for a node as the total number of nodes with which it cannot be compared according to the partial ordering rule. Both the diversity and mixing lattices satisfy the majorization criteria—hence the incomparability numbers for the nodes is the same in each. Thus if two nodes are incomparable with regard to mixing, they are also incomparable with regard to diversity. This property could be responsible for the common Gaussian shapes for the path distributions. Seitz proposed that incomparability is related to the complexity of the mixing character [20]. This will be discussed further in Section 7.

A second property is conjectured for nodes—namely if the entropy of two nodes has the same value, those nodes are incomparable. For example the partitions of N = 10[4, 3, 1, 1, 1] and [3, 3, 2, 2] have the same entropy in Equation (1). We have verified the conjecture for N ≤ 10. Note, however, that iso-entropic nodes can have different incomparability numbers. We have not investigated the implications of this fact.

Next, we briefly consider the frequency with which nodes are visited in the Monte Carlo procedure.

Table 1. Visit Frequency to Partitions (20 million paths sampled).

N	Partition	Mixing Visits	Diversity Visits
36	[8, 7, 7, 5, all]	1,547,988	57
36	[6, 6, 6, 6, all]	415	0
10	[4, 3, 3]	2,499,401	312,338
10	[4, 4, 1, 1]	7,500,069	682,480
10	[5, 2, 1, 1, 1]	7,502,520	10,074,654
10	[4, 2, 2, 2]	4,169,246	880,079
10	[3, 3, 3, 1]	4,163,456	2,285,122
10	[4, 3, 2, 1]	12,497,480	2,063,059

shows the visit frequency for selected nodes for N = 10 and N = 36. First for N = 36, one sees that practically no paths go through macrostates with partitions that begin with [6, 6, 6, 6, ...] for both mixing and diversity lattices. However, there is a significant difference between paths through macrostates corresponding to partitions beginning with [8, 7, 7, 5...]; 7.75% visit one of those partitions on the mixing lattice but they are almost never visited on the diversity lattice. In the diversity lattice, there are far more short paths than long paths, which for larger N becomes the dominant feature determining the path length distribution. In fact, since every path in the mixing lattice is also a path in the diversity lattice, a careful examination of Figure 3 shows that the mixing paths, though possible, essentially never occur in the diversity distribution for large N.

The results in Table 1 for N = 10 further illustrate the complex relationship between diversity and mixing paths to equilibrium—in mixing evolution 32.5% of the paths pass through [4, 4, 1, 1] and [5, 2, 1, 1, 1], while for the diversity evolution only 3.4% go through [4, 4, 1, 1], and half go through [5, 2, 1, 1, 1]. The paths along the right hand side of the lattice (for the N = 10 mixing lattice see Ruch 1974) then provide an express route to equilibrium on the diversity lattice, many steps of which are prohibited on the mixing lattice.

7. Discussion: Irreversibility, Entropy, Mixing and Complexity

Several alternative paths leading from completely ordered macrostates with zero entropy to the equilibrium macrostate with maximum entropy have been presented and were shown to predict three different dynamics for the evolution of isolated thermodynamic systems. Two of the evolutions studied occurred on lattices where the macrostates are partially ordered according to majorization or dominance, though both still satisfied the requirement that every spontaneous transition must lead to an increase in entropy. As a function of particle number N, the evolution based on entropy alone allowed exponential steps to equilibrium, the evolution based on mixing showed an increase in steps to equilibrium scaling as N^1.375, and a third evolution (which allows for a more rapid increase in diversity) showed a linear increase in steps to equilibrium. Next we discuss these results in the context of previous observations regarding irreversibility with an emphasis on the mixing partial order for macrostates.

In his paper, The Many Faces of Irreversibility, Denbigh [21] observed that “What appears to be the common feature of irreversibility is the fanning out of trajectories, new entities or new states, in the temporal direction towards the future”. Our Monte Carlo simulations illustrated this feature on the two lattices obtained by application of the diversity and mixing rules for transitions between nodes in the YDL. The majorization partial order depicted in the YDL, in turn, was proved by Ruch [4]to represent the general property of “mixedness” of macrostates in the microcanonical ensemble. Our work focused primarily on the distribution of lengths of the trajectories leading temporally from complete order to disorder, and couched much of the discussion in the context of Boltzmann entropy. Indeed, we found that all of the allowed trajectories followed paths of monotonically increasing entropy, and hence the assumption that irreversible trajectories are defined by increase in mixing character is fully consistent with the usual thermodynamic view of increasing entropy. While it is true that there are other functions that increase monotonically along the trajectories (see Ruch’s definition of column partitions and corresponding column entropy [4]), such functions were not discussed. Grad [22] in his seminal paper “The Many Faces of Entropy” discussed this general idea in some mathematical detail.

Denbigh [21] also suggested that there are three distinct forms for the “divergent quality” of the trajectories: (a) a branching towards a greater number of distinct kinds of entities; (b) a divergence from each other of particle trajectories or of sections of wave fronts; and (c) a spreading over an increased number of states of the same entities.

To connect this to our work here, we consider two complementary, yet very different, definitions for entities along a path. The first defines the entity of a macrostate as the set of macrostates that occur along the path that preceded the macrostate—i.e., the set of macrostates on the path leading up to the macrostate (its history). Thus, a given macrostate will have many possible histories depending upon the path taken to reach it. When viewed in this manner, Denbigh’s first form for “divergent quality” describes the diversity of trajectories that occur on the lattice as one proceeds from low to high mixing or entropy, and the second form is related to the fact that the odds that any two paths will be the same is vanishingly small for large N. We note that this divergence seems to generally occur in nature. For example, there is enormous diversity among human beings that is based on an individual’s detailed history and genetic diversity.

To understand Denbigh’s third form for divergent quality we describe a different type of entity associated with a macrostate Ψ. This entity is the set of macrostates to which Ψ is incomparable. Now proceeding from complete order along a path, the number of states incomparable with the macrostates Ψ generally increases, until one reaches the middle of the lattice. This behavior illustrates Denbigh’s third form of divergent quality. By definition of incomparability, the members of the set of macrostates incomparable with macrostate Ψ are those that could not occur on any trajectory containing Ψ. The order of the set I_Ψ we term the incomparability of macrostate, and denote it I_ψ. In some sense, these sets represent “roads not taken”, and it complements the history. Next, evolution from the middle (most complex) portion of the diagram to equilibrium continues through macrostates, but this time the incomparability generally decreases as one approaches equilibrium. Hence a new property of the macrostates has emerged, namely the extent of their incomparability with other macrostates. The incomparability is small for low and high entropies, but quite high at intermediate entropy/mixing character. We conjecture that this property, measured by I_Ψ, may be viewed as a complexity function for macrostates. We further conjecture that this complexity will approximate a convex function of the entropy, S_Ψ, of Ψ. (Note, if macrostates Φ and Ψ are incomparable, it does not follow that I_Φ = I_Ψ. This is because Ψ being incomparable with states Φ and Θ does not necessarily imply that states Φ and Θ are also incomparable. In mathematical order theory, sets of macrostates that are mutually incomparable to one another are antichains. A subtle point is that the order of maximal antichains is less than or equal to the incomparability number.) A similar relationship between incomparability and complexity has been suggested previously [20]. Our complexity here is also consistent with others. (See for example Γ₁₁ in Shiner et al. [23]; Huberman&Hogg [24] and the complexity discussion on the Scholarpedia website.

Examples of system evolution from simple ordered states to complex ones abound. Organizations, cities, organisms, ecosystems, companies and civilizations, all typically begin with a simple, fairly uniform environment. Generally, there is energy input so that entropy increase and energy combine constructively to increase size and diversity that leads to, for example, political parties, New York City, human beings, rain forests, Exxon and Rome. Yet, in each case, there appears to come a point where further growth and complexity becomes increasingly hard to come by, despite the fact that energy input has not ceased. It seems that, absent an ever increasing energy input, decay inevitably sets in, growth ceases, and systems return to simple, but this time, disordered states. All of this, of course, is why entropy is invoked as the arrow of time. In our model system, these observations correspond to the evolution of incomparability of the macrostates that are present.

From Norway to Italy and from France to Greece, one finds (in the European context) popular prints in which a tiered bridge represents the Scale of Life or Stages of life. In Figure 6, we see a simple baby, not very different from other babies, beginning life. As children, differences become more apparent and there is an increase of incomparability among them, which continues to increase until middle age. At that stage of life, people are often labeled as: lawyers, doctors, mechanics, mothers, computer programmers, bowlers, football players, etc. It is then when they are most incomparable with one another. However, as people age and retire, even though their histories continue to diverge, their incomparability with one another seems to decrease, until at extremely old age and death, we again find a high degree of comparability. We regard incomparability as a fundamental characteristic of macrostates, which emerges only when one considers these states as being partially ordered [25]. More generally, attention to partial orders that are present in complex systems has enormous potential for future advances in many fields.

Finally, we list several challenges that arise as the result of the view taken here that mixing character is the fundamental property of macrostates in the microcanonical ensemble that determines spontaneity in isolated systems. First, we found in Section 6 that the frequencies with which macrostates occur in an ensemble of trajectories are drastically different. Some macrostates occur in a vanishingly small number of trajectories, while others occur with much higher frequency. Thus it is important to characterize the relationship of the macrostate’s mixing character to its occurrence frequency. Second, it is interesting that the union of entities defined by the sets of macrostates incomparable with those visited on any trajectory must contain every macrostate. This is a topic of ongoing research. Also, our assumption of equal transition probabilities between macrostates on the lattices, while consistent with common practice, is ad-hoc. Introduction of a transition probability based on the difference of the Boltzmann entropies of the neighboring macrostates (or other criteria) might lead to intermediate cases between mixing and diversity (i.e., the transitions may be weighted according to the entropy change during the transition or other factors). Finally, the complexity measure proposed here should be studied further to clarify the conjectures above and to explore in more detail the relationship to other complexity measures.