1. Introduction
Let
Y be a random variable with a continuous distribution function (cdf)
G(
y) and a probability density function (pdf)
g(
y). The differential entropy
H(
Y) of the random variable is defined by Cover and Thomas [
1] to be:
The cdf and pdf of the random variable
Y having the Rayleigh distribution are given by:
and:
Let
Z =
Y/
σ; then
Z has a standard form of the Rayleigh distribution with the cdf written as:
For the pdf
(2), the entropy simplifies to:
where
γ is the Euler–Mascheroni constant.
The estimation of the parameters of the censored samples has been investigated by many authors, such as Harter and Moore [
2], Dyer and Whisenand [
3], Balakrishnan [
4], Fern
ández [
5] and Kim and Han [
6]. Hater and Moore [
2] derived an explicit form of the maximum likelihood estimators (MLEs) of the scale parameter
σ based on Type II censored data. Dyer and Whisenand [
3] considered the best linear unbiased estimator of
σ based on Type II censored data. Balakrishnan [
4] considered an approximate MLE of
σ based on the doubly generalized Type II censored data. Fern
ández [
5] considered a Bayes estimation of
σ based on the doubly-generalized Type II censored data. Recently, Kim and Han [
6] considered a Bayes estimation of
σ based on the multiply Type II censored data.
In this paper, we derive the estimators for the entropy function of the Rayleigh distribution with an unknown scale parameter under doubly-generalized Type II hybrid censoring. We also compare the proposed estimators in the sense of the root mean squared error (RMSE) for various censored samples.
The rest of this paper is organized as follows. In Section 2, we introduce a doubly generalized Type II hybrid censoring scheme. In Section 3, we describe the computation of the entropy function with MLE and approximate the MLE and Bayes estimator of the unknown scale parameter in the Rayleigh distribution under doubly generalized Type II hybrid censored samples. A real data set has been analyzed in Section 4. In Section 5, the description of different estimators that are compared by performing the Monte Carlo simulation is presented, and Section 6 concludes.
2. Doubly-Generalized Type II Hybrid Censoring Scheme
Consider a life testing experiment in which
n units are tested. Epstein [
7] introduced a hybrid censoring scheme in which the test is terminated at a random time
, where
r ∈ {1, 2,
···,
n},
T ∈ (0,
∞) are pre-fixed and
Yr:n denote the
r-th ordered failure time when the sample size is
n. Next, Childs
et al. [
8] introduced a Type I hybrid censoring scheme and a Type II hybrid censoring scheme. The disadvantage of the Type I hybrid censoring scheme is that there is a possibility that very few failures may occur before time
T. However, the Type II hybrid censoring scheme can guarantee a pre-fixed number of failures. In this case, the termination point is
, where
r ∈ {1, 2,
···,
n} and
T ∈ (0,
∞) are pre-fixed. Though the Type II hybrid censored scheme guarantees a pre-fixed number of failures, it might take a long time to observe
r failures. In order to provide a guarantee in terms of the number of failures observed, as well as the time to complete the test, Chandrasekar
et al. [
9] introduced a generalized Type II hybrid censoring scheme.
Lee
et al. [
10] introduced a doubly generalized Type II hybrid censoring scheme that can be described as follows. Fix 1 ≤
r ≤
n and
T1,
T2,
T3 ∈ (0,
∞), such that
T1 <
T2 <
T3. If the
l-th failure occurs before time
T1, start the experiment at
T1; if the
l-th failure occurs after time
T1, start at
Yl:n. If the
r-th failure occurs before time
T2, terminate the experiment at
T2; if the
r-th failure occurs between
T2 and
T3, terminate at
Yr:n; and in other cases, terminate the test at
T3. Therefore,
T1 represents the time at which the researcher starts the observation in the experiment.
T2 represents the least time for which the researcher conducts the experiment.
T3 represents the longest time for which the researcher allows the experiment to continue. For known
r,
l,
T1,
T2,
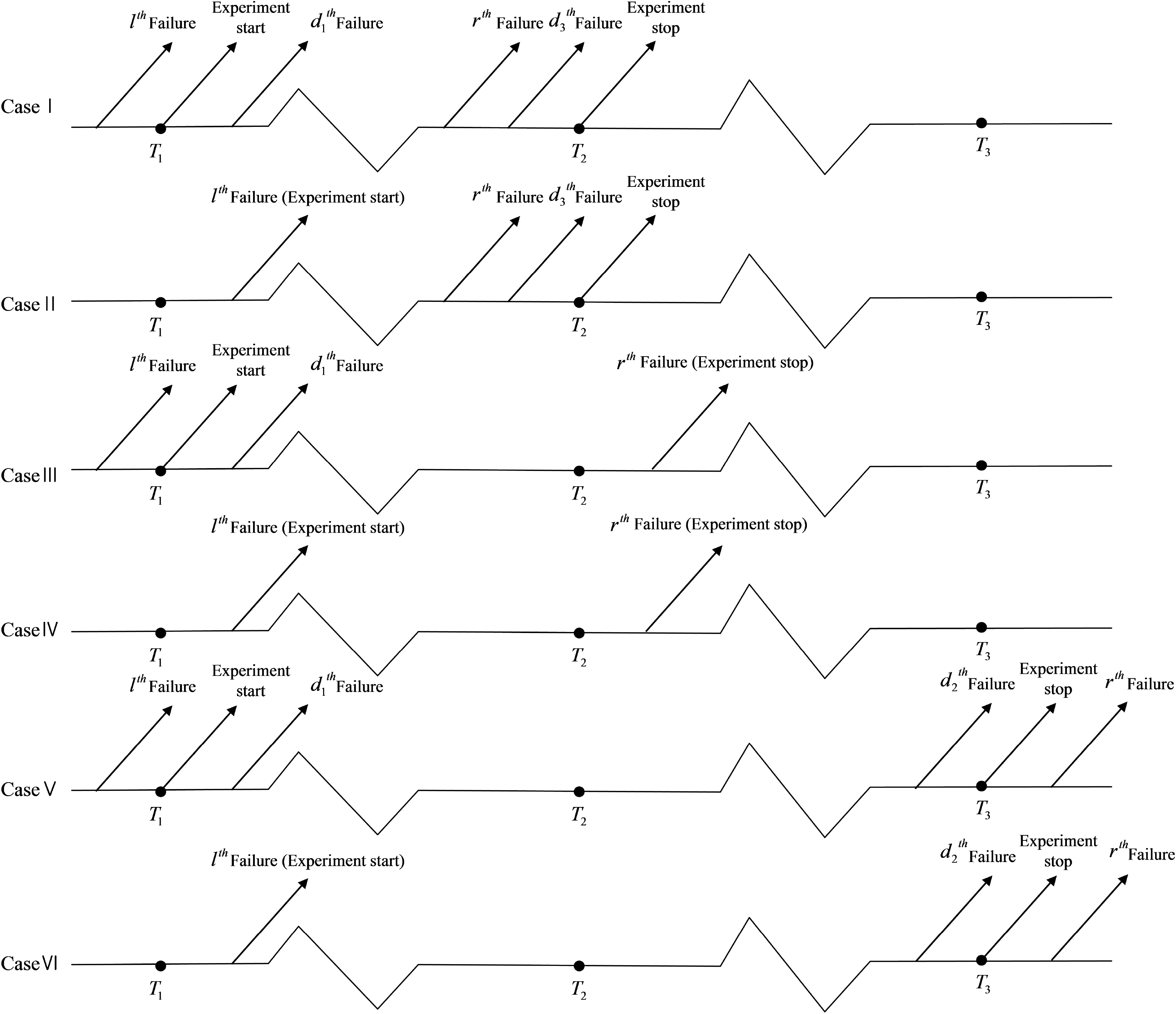
T3, we can observe the following six cases of observations.
Case I : y1 < ··· <yl:n < ··· <yd1−1:n <T1 <yd1:n < ··· <yr:n <yd3:n <T2 < ··· <yd3+1:n, if yl:n <T1 and yr:n <T2.
Case II : y1 < ··· <T1 < ··· <yl:n < ··· <yr:n < ··· <yd3:n <T2 <yd3+1:n, if yl:n >T1 and yr:n <T2.
Case III : y1 < ··· <yl:n < ··· <yd1−1:n <T1 <yd1:n < ··· <T2 < ··· <yr:n, if yl:n <T1 and yr:n >T2.
Case IV : y1 < ··· <T1 < ··· <yl:n < ··· <T2 < ··· <yr:n, if yl:n >T1 and yr:n >T2.
Case V : y1 < ··· <yl:n < ··· <yd1−1:n <T1 <yd1:n < ··· <yd2:n <T3 <yd2+1 < ··· <yr:n, if yl:n <T1 and yr:n >T3.
Case VI : y1 < ··· <T1 < ··· <yl:n < ··· <yd2:n <T3 <yd2+1:n < ··· <yr:n, if yl:n >T1 and yr:n >T3.
Note that, in Case I, Case III and Case V, we do not observe
yd1−1:n, but
yd1−1:n <
T1 <
yd1:n means that the
d1-th failure took place after
T1, and no failure took place between
yd1:n and
T1. In Case I and Case II, we do not observe
yd3+1:n, but
yd3:n <
T2 <
yd3+1:n means that the
d3-th failure took place before
T2 and no failure took place between
yd3:n and
T2. In Case V and Case VI, we do not observe
yd2+1:n, but
yd2:n <
T3 <
yd2+1:n means that the
d2-th failure took place before
T3, and no failure took place between
yd2:n and
T3. A doubly-generalized Type II hybrid censoring scheme is presented in
Figure 1.
4. Illustrative Example
Leiblen and Zelen [
15] performed life tests and determined the number of revolutions to failure for 23 ball bearings. The data are doubly generalized Type II hybrid censored data: 23 components were tested. The observed failure times are as follows: 0.1788, 0.2852, 0.3300, 0.4152, 0.4212, 0.4560, 0.4848, 0.5186, 0.5196, 0.5412, 0.5556, 0.6780, 0.6864, 0.6864, 0.6888, 0.8412, 0.9312, 0.9864, 1.0512, 1.0584, 1.2792, 1.2804, 1.7340.
In this example, we assume that the underlying distribution of this data is the Rayleigh distribution based on the doubly generalized Type II hybrid censoring scheme. We take Case I (
T1=0.32,
T2=0.7,
T1=1.2,
l=1 and
r=17), Case II (
T1=0.32,
T2=0.7,
T1=1.2,
l=4 and
r=20), Case III (
T1=0.32,
T2=0.7,
T1=1.2,
l=7 and
r=23), Case IV (
T1=0.64,
T2=0.7,
T1=1.5,
l=1 and
r=17), Case V (
T1=0.64,
T2=0.7,
T1=1.5,
l=3 and
r=20) and Case VI (
T1=0.64,
T2=0.7,
T1=1.5,
l=7 and
r=23). For the Bayesian inference, the prior parameters are chosen (
α,
β)=(2.0, 2.0) and
c = 3. The Bayes estimator based on the natural conjugate prior and non-informative prior is obtained. Furthermore, the Bayes estimator based on the balanced loss function with
w = 0.3, 0.5 and 0.7 is obtained.
Table 1 presents estimation of entropy of doubly generalized Type II censoring schemes.
5. Results and Discussion
To compare the performance of the proposed estimators, we simulated the RMSE, bias and Kullback–Leibler divergence of all proposed estimators, by employing the Monte Carlo simulation method. We have used three different doubly generalized Type II hybrid censored sampling schemes, namely: Scheme I:
T1=0.3,
T1=1.7 and
T1=2.0; Scheme II:
T1=0.6,
T1=1.7 and
T1=2.0; and Scheme III:
T1=0.3,
T1=1.7 and
T1=2.3. The doubly generalized Type II hybrid censored samples are generated from the Rayleigh distribution with
σ = 1. Using these samples, the RMSE, bias and Kullback–Leibler divergence of entropy estimators are simulated by the Monte Carlo method based on 10,000 runs for the sample size
n = 10, 20, 40 and 100. The prior parameters are chosen (
α,
β) = (2.0, 2.0) and
c = 3. The Bayes estimator based on the natural conjugate prior and non-informative prior is obtained. Furthermore, the Bayes estimator based on the balanced loss function with
w = 0.3, 0.5 and 0.7 is obtained. The simulation results are presented in
Table S1 ∼ Table S10, respectively.
From
Table S1 ∼ Table S10, the following general observations can be made. The RMSEs and Kullback–Leibler divergence decrease as sample size
n increases. For a fixed sample size, the RMSEs and Kullback–Leibler divergence decrease generally as the number of censored samples decreases. For fixed sample and censored samples size, the RMSEs and Kullback–Leibler divergence decrease generally as the times
T2 and
T3 increases. It is also observed that the left censoring scheme has smaller RMSEs and Kullback–Leibler divergence than the corresponding estimators for right and doubly generalized censoring schemes. For Scheme I and the left censoring case, we presented these in
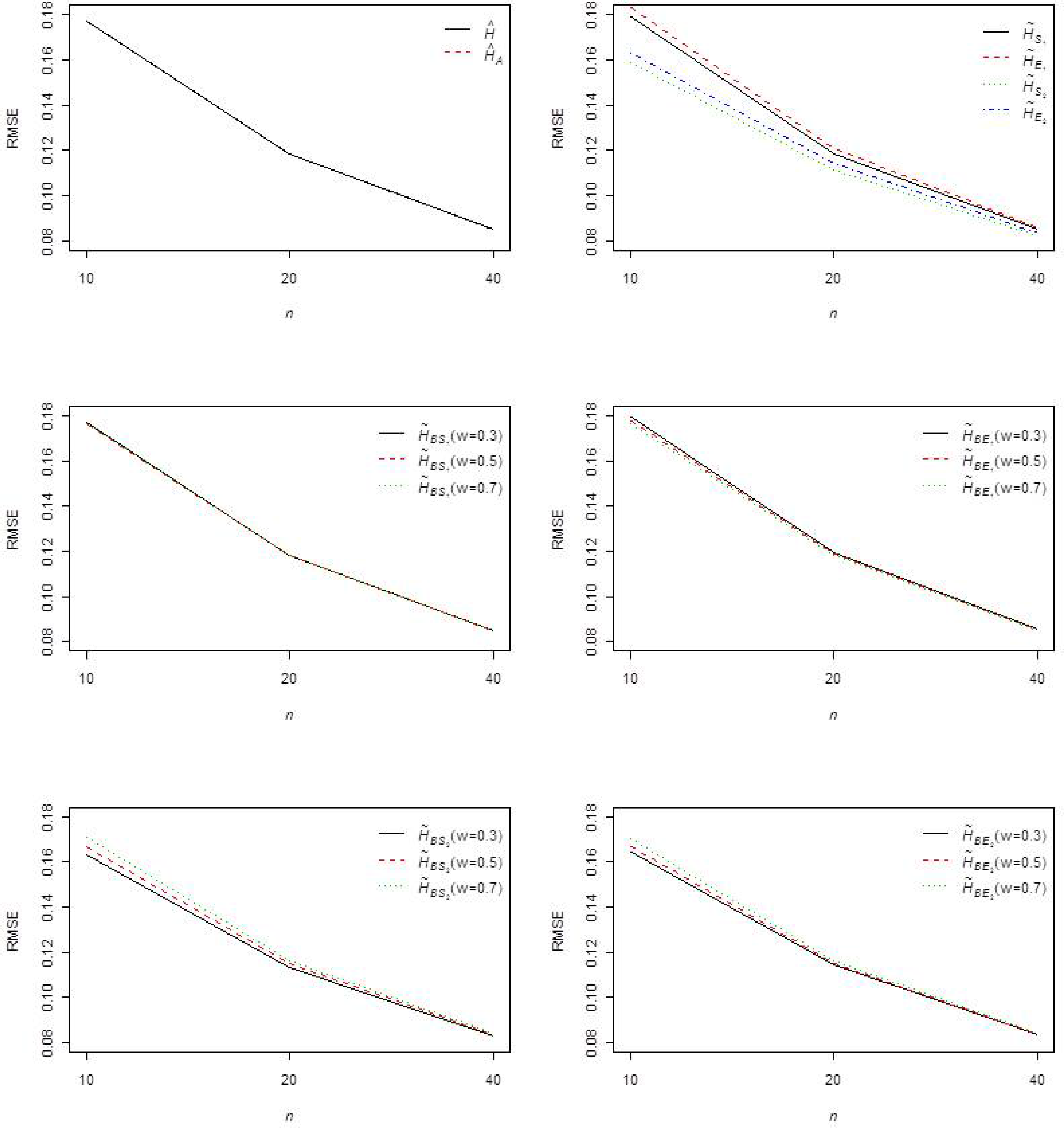
Figure 2.
In
Table S1, the average RMSEs and biases of the entropy estimator with MLE and approximate MLE are presented for various choices of
n,
l,
r and censoring schemes. In general, we observed that MLE and approximate MLE behave quite similarly in terms of RMSE. From
Table S2 ∼ Table S3, average RMSEs and the bias of the entropy estimator with Bayes estimators based on non-informative prior are presented for various choices of
n,
l,
r and censoring schemes. In general, we observed that entropy estimator with Bayes estimator under the squared error loss function is superior to the respective entropy estimator with Bayes estimator under the general entropy loss function in terms of bias and RMSE. For estimating the entropy, the choice
w = 0.7 seems to be a reasonable choice under balanced-square error loss and balanced-entropy loss function. From
Table S4 ∼ Table S5, average RMSEs and the biases of the entropy estimator with the Bayes estimator based on the natural conjugate prior are presented for various choices of
n,
l,
r and censoring schemes. In general, we observed that entropy estimator with the Bayes estimator under the squared error loss function is superior to the respective entropy estimator with the Bayes estimator under the general entropy loss function in terms of bias and RMSE. For estimating the entropy, the choice
w = 0.3 seems to be a reasonable choice under balanced-square error loss and the balanced-entropy loss function.
In
Table S6, the average Kullback–Leibler divergences of the entropy estimator with MLE and approximate MLE are presented for various choices of
n,
l,
r and censoring schemes. In general, we observed that MLE is superior to the respective approximate MLE in terms of Kullback–Leibler divergence. From
Table S7 ∼ Table S8, average Kullback–Leibler divergences of the entropy estimator with the Bayes estimator based on the non-informative prior are presented for various choices of
n,
l,
r and censoring schemes. In general, we observed that the entropy estimator with the Bayes estimator under the squared error loss function is superior to the respective entropy estimator with the Bayes estimator under the general entropy loss function in terms of Kullback–Leibler divergence. For estimating the entropy, the choice
w = 0.7 seems to be a reasonable choice under balanced square error loss and the balanced entropy loss function. From
Table S9 ∼ Table S10, average Kullback–Leibler divergences of the entropy estimator with the Bayes estimator based on the natural conjugate prior are presented for various choices of
n,
l,
r and censoring schemes. In general, we observed that the entropy estimator with the Bayes estimator under the squared error loss function is superior to the respective entropy estimator with the Bayes estimator under the general entropy loss function in terms of the Kullback–Leibler divergence. For estimating the entropy, the choice
w = 0.3 seems to be a reasonable choice under the balanced-square error loss and the balanced-entropy loss function. Overall, the Bayes estimator using the squared error loss function based on the natural conjugate prior provide better estimates compared with other estimates.
6. Conclusions
In many life testing experiments, the experimenter may not observe the lifetimes of all inspected units in the life test. Censored data arises in these situations wherein the experimenter does not obtain complete information for all of the units under study. Different types of censoring arise based on how the data are collected from the life testing experiment. In order to provide a guarantee in terms of the number of failures observed, as well as the time to complete the test, Chandrasekar
et al. [
9] introduced a generalized Type II hybrid censoring scheme. Lee
et al. [
10] introduced a doubly generalized Type II hybrid censoring scheme, which can handle both right-censoring and left-censoring.
In this paper, we discussed entropy estimators for the Rayleigh distribution based on doubly-generalized Type II hybrid censored samples. The paper derived entropy estimators by using the MLE, approximate MLE and Bayes estimators of the σ in the Rayleigh distribution based on doubly generalized Type II hybrid censored samples and compared them in terms of their RMSE, bias and Kullback–Leibler divergence. Bayesian estimates using the non-informative and natural conjugate prior are obtained under three types of loss function, and it is observed that the Bayes estimate with respect to the natural conjugate prior under the squared error loss function works quite well in this case. Although we focused on the entropy estimate of the Rayleigh distribution in this article, the proposed estimation can be easily extended to other distributions. Particularly, the Bayes estimation can be applied to any other distributions. In contrast, an approximate MLE cannot be simply applied to the distributions with a shape parameter. Estimation on entropy parameters from other distributions is of potential interest in future research.