Using Permutation Entropy to Measure the Changes in EEG Signals During Absence Seizures
Abstract
:1. Introduction
2. Materials and Methods
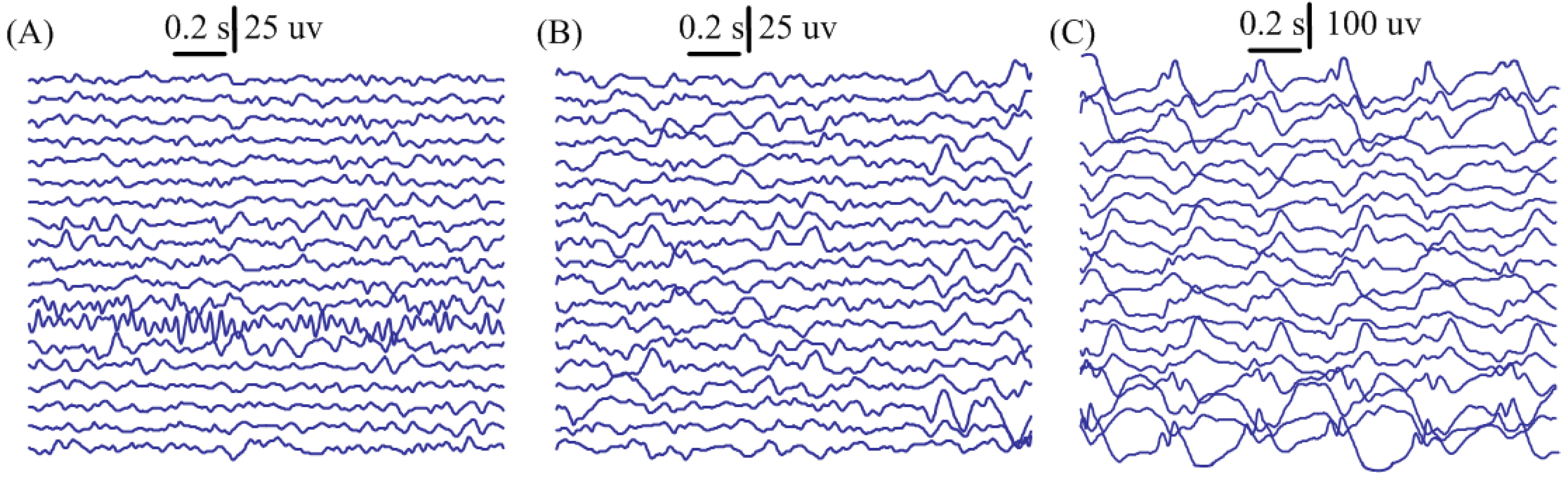
2.1. EEG Recordings
2.2. Permutation Entropy

2.3. Statistical Analysis
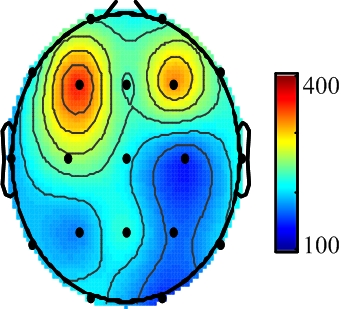
3. Results



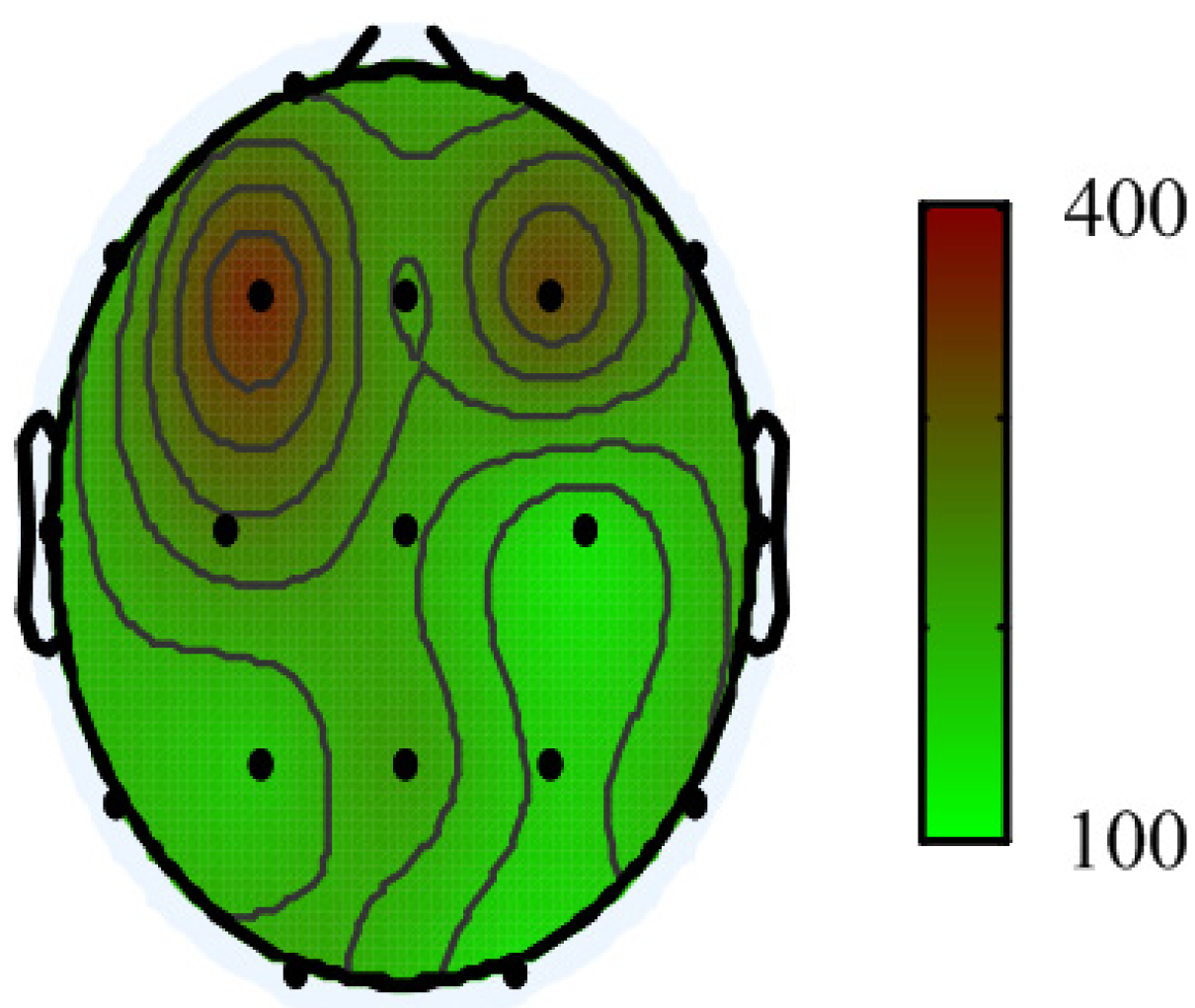
| ANOVA Source of Variation | Sums of Squares | Degrees of Freedom | Mean Square | F-Statistic |
|---|---|---|---|---|
| Between Samples | 5.497 | 2 | 2.7485 | 352.4 p < 0.01 |
| Error | 1.535 | 198 | 0.0078 | |
| Subject | 1.443 | 99 | ||
| Total | 8.475 | 299 |
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Litt, B.; Echauz, J. Prediction of epileptic seizures. Lancet Neurol. 2002, 1, 22–30. [Google Scholar] [CrossRef]
- Engel, J., Jr.; International League Against Epilepsy (ILAE). A proposed diagnostic scheme for people with epileptic seizures and with epilepsy: Report of the ilae task force on classification and terminology. Epilepsia 2001, 42, 796–803. [Google Scholar] [CrossRef]
- Anderson, W.S.; Azhar, F.; Kudela, P.; Bergey, G.K.; Franaszczuk, P.J. Epileptic seizures from abnormal networks: Why some seizures defy predictability. Epilepsy Res. 2012, 99, 202–213. [Google Scholar] [CrossRef]
- Meeren, H.K.; Pijn, J.P.; van Luijtelaar, E.L.; Coenen, A.M.; Lopes da Silva, F.H. Cortical focus drives widespread corticothalamic networks during spontaneous absence seizures in rats. J. Neurosci. 2002, 22, 1480–1495. [Google Scholar]
- Mormann, F.; Andrzejak, R.G.; Elger, C.E.; Lehnertz, K. Seizure prediction: The long and winding road. Brain 2007, 130, 314–333. [Google Scholar] [CrossRef]
- Crunelli, V.; Cope, D.W.; Terry, J.R. Transition to absence seizures and the role of gaba(a) receptors. Epilepsy Res. 2011, 97, 283–289. [Google Scholar] [CrossRef]
- Stacey, W.C.; Litt, B. Technology insight: Neuroengineering and epilepsy-designing devices for seizure control. Nat. Clin. Pract. Neurol. 2008, 4, 190–201. [Google Scholar]
- Stam, C.J. Nonlinear dynamical analysis of EEG and MEG: Review of an emerging field. Clin. Neurophysiol. 2005, 116, 2266–2301. [Google Scholar] [CrossRef]
- Kurth, S.; Achermann, P.; Rusterholz, T.; LeBourgeois, M. Development of brain EEG connectivity across early childhood: Does sleep play a role? Brain Sci. 2013, 3, 1445–1460. [Google Scholar] [CrossRef]
- Herman, S.T.; Takeoka, M.; Hughes, J.R.; Drislane, F.W. Electroencephalography in clinical epilepsy research. Epilepsy Behav. 2011, 22, 126–133. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Lin, C.-C.; Tsai, J.-J.; Sun, Y.-N. Model-based spike detection of epileptic EEG data. Sensors 2013, 13, 12536–12547. [Google Scholar] [CrossRef]
- Rogowski, Z.; Gath, I.; Bental, E. On the prediction of epileptic seizures. Biol. Cybern. 1981, 42, 9–15. [Google Scholar] [CrossRef]
- Iasemidis, L.D.; Sackellares, J.C.; Zaveri, H.P.; Williams, W.J. Phase space topography and the lyapunov exponent of electrocorticograms in partial seizures. Brain Topogr. 1990, 2, 187–201. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef]
- Navarro, V.; Martinerie, J.; le van Quyen, M.; Clemenceau, S.; Adam, C.; Baulac, M.; Varela, F. Seizure anticipation in human neocortical partial epilepsy. Brain 2002, 125, 640–655. [Google Scholar] [CrossRef]
- Niknazar, M.; Mousavi, S.R.; Motaghi, S.; Dehghani, A.; Vosoughi Vahdat, B.; Shamsollahi, M.B.; Sayyah, M.; Noorbakhsh, S.M. A unified approach for detection of induced epileptic seizures in rats using ecog signals. Epilepsy Behav. 2013, 27, 355–364. [Google Scholar] [CrossRef]
- Gao, J.; Hu, J.; Tung, W.-W. Entropy measures for biological signal analyses. Nonlinear Dyn. 2011, 68, 431–444. [Google Scholar]
- Morabito, F.C.; Labate, D.; la Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate multi-scale permutation entropy for complexity analysis of alzheimer’s disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Huang, J.-R.; Fan, S.-Z.; Abbod, M.; Jen, K.-K.; Wu, J.-F.; Shieh, J.-S. Application of multivariate empirical mode decomposition and sample entropy in EEG signals via artificial neural networks for interpreting depth of anesthesia. Entropy 2013, 15, 3325–3339. [Google Scholar] [CrossRef]
- Buzsáki, G. Rhythms of the Brain; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Sleigh, J.W.; Steyn-Ross, D.A.; Steyn-Ross, M.L.; Grant, C.; Ludbrook, G. Cortical entropy changes with general anaesthesia: Theory and experiment. Physiol. Meas. 2004, 25, 921–934. [Google Scholar] [CrossRef]
- Van Drongelen, W.; Nayak, S.; Frim, D.M.; Kohrman, M.H.; Towle, V.L.; Lee, H.C.; McGee, A.B.; Chico, M.S.; Hecox, K.E. Seizure anticipation in pediatric epilepsy: Use of kolmogorov entropy. Pediatr. Neurol. 2003, 29, 207–213. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar]
- Wei, Q.; Liu, Q.; Fan, S.-Z.; Lu, C.-W.; Lin, T.-Y.; Abbod, M.; Shieh, J.-S. Analysis of EEG via multivariate empirical mode decomposition for depth of anesthesia based on sample entropy. Entropy 2013, 15, 3458–3470. [Google Scholar] [CrossRef]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Cao, Y.; Tung, W.W.; Gao, J.B.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 2004, 70, 046217. [Google Scholar] [CrossRef]
- Nicolaou, N.; Georgiou, J. Detection of epileptic electroencephalogram based on permutation entropy and support vector machines. Expert Syst. Appl. 2012, 39, 202–209. [Google Scholar] [CrossRef]
- Bruzzo, A.A.; Gesierich, B.; Santi, M.; Tassinari, C.A.; Birbaumer, N.; Rubboli, G. Permutation entropy to detect vigilance changes and preictal states from scalp EEG in epileptic patients. A preliminary study. Neurol. Sci. 2008, 29, 3–9. [Google Scholar] [CrossRef]
- Li, X.; Ouyang, G.; Richards, D.A. Predictability analysis of absence seizures with permutation entropy. Epilepsy Res. 2007, 77, 70–74. [Google Scholar] [CrossRef]
- Mammone, N.; Labate, D.; Lay-Ekuakille, A.; Morabito, F.C. Analysis of absence seizure generation using EEG spatial-temporal regularity measures. Int. J. Neural Syst. 2012, 22, 1250024. [Google Scholar] [CrossRef]
- Ferlazzo, E.; Mammone, N.; Cianci, V.; Gasparini, S.; Gambardella, A.; Labate, A.; Latella, M.A.; Sofia, V.; Elia, M.; Morabito, F.C.; et al. Permutation entropy of scalp EEG: A tool to investigate epilepsies: Suggestions from absence epilepsies. Clin. Neurophysiol. 2014, 125, 13–20. [Google Scholar] [CrossRef]
- Gorji, A.; Mittag, C.; Shahabi, P.; Seidenbecher, T.; Pape, H.C. Seizure-related activity of intralaminar thalamic neurons in a genetic model of absence epilepsy. Neurobiol. Dis. 2011, 43, 266–274. [Google Scholar] [CrossRef]
- Cavanna, A.E.; Monaco, F. Brain mechanisms of altered conscious states during epileptic seizures. Nat. Rev. Neurol. 2009, 5, 267–276. [Google Scholar] [CrossRef]
- Bai, X.; Vestal, M.; Berman, R.; Negishi, M.; Spann, M.; Vega, C.; Desalvo, M.; Novotny, E.J.; Constable, R.T.; Blumenfeld, H. Dynamic time course of typical childhood absence seizures: EEG, behavior, and functional magnetic resonance imaging. J. Neurosci. 2010, 30, 5884–5893. [Google Scholar] [CrossRef]
- Killory, B.D.; Bai, X.; Negishi, M.; Vega, C.; Spann, M.N.; Vestal, M.; Guo, J.; Berman, R.; Danielson, N.; Trejo, J.; et al. Impaired attention and network connectivity in childhood absence epilepsy. NeuroImage 2011, 56, 2209–2217. [Google Scholar] [CrossRef]
- Blumenfeld, H. Impaired consciousness in epilepsy. Lancet Neurol. 2012, 11, 814–826. [Google Scholar] [CrossRef]
- Rosso, O.A.; Mendes, A.; Rostas, J.A.; Hunter, M.; Moscato, P. Distinguishing childhood absence epilepsy patients from controls by the analysis of their background brain electrical activity. J. Neurosci. Methods 2009, 177, 461–468. [Google Scholar] [CrossRef]
- Ouyang, G.; Li, X.; Dang, C.; Richards, D.A. Using recurrence plot for determinism analysis of EEG recordings in genetic absence epilepsy rats. Clin. Neurophysiol. 2008, 119, 1747–1755. [Google Scholar] [CrossRef]
- Ouyang, G.; Li, J.; Liu, X.; Li, X. Dynamic characteristics of absence EEG recordings with multiscale permutation entropy analysis. Epilepsy Res. 2013, 104, 246–252. [Google Scholar] [CrossRef]
- Sitnikova, E. Thalamo-cortical mechanisms of sleep spindles and spike-wave discharges in rat model of absence epilepsy (a review). Epilepsy Res. 2010, 89, 17–26. [Google Scholar]
- Sitnikova, E.; van Luijtelaar, G. Electroencephalographic precursors of spike-wave discharges in a genetic rat model of absence epilepsy: Power spectrum and coherence EEG analyses. Epilepsy Res. 2009, 84, 159–171. [Google Scholar] [CrossRef]
- Amor, F.; Baillet, S.; Navarro, V.; Adam, C.; Martinerie, J.; Quyen Mle, V. Cortical local and long-range synchronization interplay in human absence seizure initiation. NeuroImage 2009, 45, 950–962. [Google Scholar] [CrossRef]
- Sadleir, L.G.; Farrell, K.; Smith, S.; Connolly, M.B.; Scheffer, I.E. Electroclinical features of absence seizures in sleep. Epilepsy Res. 2011, 93, 216–220. [Google Scholar] [CrossRef]
- Ouyang, G.; Dang, C.; Richards, D.A.; Li, X. Ordinal pattern based similarity analysis for EEG recordings. Clin. Neurophysiol. 2010, 121, 694–703. [Google Scholar] [CrossRef]
- Ouyang, G.; Li, X.; Dang, C.; Richards, D.A. Deterministic dynamics of neural activity during absence seizures in rats. Phys. Rev. E 2009, 79, 041146. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.A.; Martin, M.T.; Plastino, A.; Fuentes, M.A. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102. [Google Scholar] [CrossRef]
- Li, X.; Ouyang, G. Estimating coupling direction between neuronal populations with permutation conditional mutual information. NeuroImage 2010, 52, 497–507. [Google Scholar]
- Burioka, N.; Cornelissen, G.; Maegaki, Y.; Halberg, F.; Kaplan, D.T.; Miyata, M.; Fukuoka, Y.; Endo, M.; Suyama, H.; Tomita, Y.; et al. Approximate entropy of the electroencephalogram in healthy awake subjects and absence epilepsy patients. Clin. EEG Neurosci. 2005, 36, 188–193. [Google Scholar]
- Steriade, M.; McCormick, D.A.; Sejnowski, T.J. Thalamocortical oscillations in the sleeping and aroused brain. Science 1993, 262, 679–685. [Google Scholar]
- Futatsugi, Y.; Riviello, J.J., Jr. Mechanisms of generalized absence epilepsy. Brain Dev. 1998, 20, 75–79. [Google Scholar] [CrossRef]
- Polack, P.O.; Guillemain, I.; Hu, E.; Deransart, C.; Depaulis, A.; Charpier, S. Deep layer somatosensory cortical neurons initiate spike-and-wave discharges in a genetic model of absence seizures. J. Neurosci. 2007, 27, 6590–6599. [Google Scholar] [CrossRef]
- Meeren, H.; van Luijtelaar, G.; Lopes da Silva, F.; Coenen, A. Evolving concepts on the pathophysiology of absence seizures: The cortical focus theory. Arch. Neurol. 2005, 62, 371–376. [Google Scholar] [CrossRef]
- Holmes, M.D.; Brown, M.; Tucker, D.M. Are “generalized” seizures truly generalized? Evidence of localized mesial frontal and frontopolar discharges in absence. Epilepsia 2004, 45, 1568–1579. [Google Scholar] [CrossRef]
- Rosso, O.A.; Mendes, A.; Berretta, R.; Rostas, J.A.; Hunter, M.; Moscato, P. Distinguishing childhood absence epilepsy patients from controls by the analysis of their background brain electrical activity (ii): A combinatorial optimization approach for electrode selection. J. Neurosci. Methods 2009, 181, 257–267. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, J.; Yan, J.; Liu, X.; Ouyang, G. Using Permutation Entropy to Measure the Changes in EEG Signals During Absence Seizures. Entropy 2014, 16, 3049-3061. https://doi.org/10.3390/e16063049
Li J, Yan J, Liu X, Ouyang G. Using Permutation Entropy to Measure the Changes in EEG Signals During Absence Seizures. Entropy. 2014; 16(6):3049-3061. https://doi.org/10.3390/e16063049
Chicago/Turabian StyleLi, Jing, Jiaqing Yan, Xianzeng Liu, and Gaoxiang Ouyang. 2014. "Using Permutation Entropy to Measure the Changes in EEG Signals During Absence Seizures" Entropy 16, no. 6: 3049-3061. https://doi.org/10.3390/e16063049