Asymptotically Constant-Risk Predictive Densities When the Distributions of Data and Target Variables Are Different
Abstract
: We investigate the asymptotic construction of constant-risk Bayesian predictive densities under the Kullback–Leibler risk when the distributions of data and target variables are different and have a common unknown parameter. It is known that the Kullback–Leibler risk is asymptotically equal to a trace of the product of two matrices: the inverse of the Fisher information matrix for the data and the Fisher information matrix for the target variables. We assume that the trace has a unique maximum point with respect to the parameter. We construct asymptotically constant-risk Bayesian predictive densities using a prior depending on the sample size. Further, we apply the theory to the subminimax estimator problem and the prediction based on the binary regression model.1. Introduction
Let be independent N data distributed according to a probability density, p(x|θ), that belongs to a d-dimensional parametric model, {p(x|θ) : θ ∈ Θ}, where is an unknown d-dimensional parameter and Θ is the parameter space. Let y be a target variable distributed according to a probability density, q(y|θ), that belongs to a d-dimensional parametric model, {q(y|θ) : θ ∈ Θ } with the same parameter, θ. Here, we assume that the distributions of the data and the target variables, p(x|θ) and q(y|θ), are different. For simplicity, we assume that the data and the target variables are independent, given by θ.
We construct predictive densities for target variables based on the data. We measure the performance of the predictive density, , by the Kullback–Leibler divergence, , from the true density, q(y|θ), to the predictive density, :
Then, the risk function, , of the predictive density, , is given by:
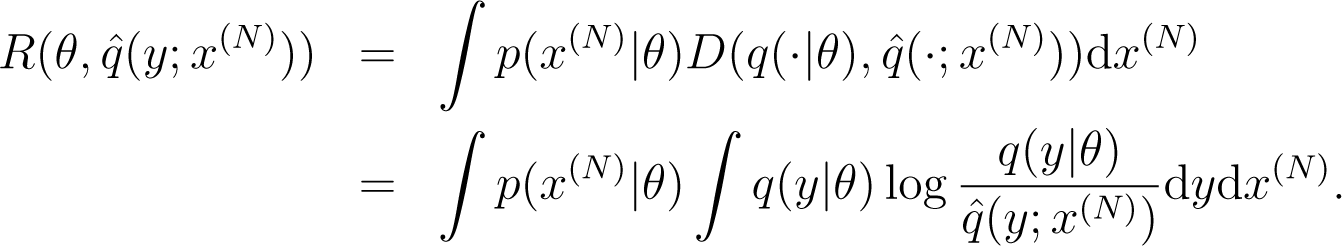
For the construction of predictive densities, we consider the Bayesian predictive density defined by:
where π(θ; N) is a prior density for θ, possibly depending on the sample size, N. Aitchison [1] showed that, for a given prior density, π(θ; N), the Bayesian predictive density, , is a Bayes solution under the Kullback–Leibler risk. Based on the asymptotics as the sample size goes to infinity, Komaki [2] and Hartigan [3] showed its superiority over any plug-in predictive density, , with any estimator, . However, there remains a problem of prior selection for constructing better Bayesian predictive densities. Thus, a prior, π(θ; N), must be chosen based on an optimality criterion for actual applications.
Among various criteria, we focus on a criterion of constructing minimax predictive densities under the Kullback–Leibler risk. For simplicity, we refer to the priors generating minimax predictive densities as minimax priors. Minimax priors have been previously studied in various predictive settings; see [4–8]. When the simultaneous distributions of the target variables and the data belong to the submodel of the multinomial distributions, Komaki [7] shows that minimax priors are given as latent information priors maximizing the conditional mutual information between target variables and the parameter given the data. However, the explicit forms of latent information priors are difficult to obtain, and we need asymptotic methods, because they require the maximization on the space of the probability measures on Θ.
Except for [7], these studies on minimax priors are based on the assumption that the distributions, p(x|θ) and q(y|θ), are identical. Let us consider the prediction based on the logistic regression model where the covariates of the data and the target variables are not identical. In this predictive setting, the assumption that the distributions, p(x|θ) and q(y|θ), are identical is no longer valid.
We focus on the minimax priors in predictions where the distributions, p(x|θ) and q(y|θ), are different and have a common unknown parameter. Such a predictive setting has traditionally been considered in statistical prediction and experiment design. It has recently been studied in statistical learning theory; for example, see [9]. Predictive densities where the distributions, p(x|θ) and q(y|θ), are different and have a common unknown parameter are studied by [10–13].
Let be the (i, j)-component of the Fisher information matrix of the distribution, p(x|θ), and let be the (i, j)-component of the Fisher information matrix of the distribution, q(y|θ). Let gX,ij(θ) and gY,ij(θ) denote the (i, j)-components of their inverse matrices. We adopt Einstein’s summation convention: if the same indices appear twice in any one term, it implies summation over that index from one to d. For the asymptotics below, we assume that the prior densities, π(θ; N), are smooth.
On the asymptotics as the sample size N goes to infinity, we construct the asymptotically constant-risk prior, π(θ; N), in the sense that the asymptotic risk:
is constant up to O(N−2). Since the proper prior with the constant risk is a minimax prior for any finite sample size, the asymptotically constant-risk prior relates to the minimax prior; in Section 4, we verify that the asymptotically constant-risk prior agrees with the exact minimax prior in binomial examples.
When we use the prior, π(θ), independent of the sample size, N, it is known that the N−1-order term, , of the Kullback–Leibler risk is equal to the trace, . If the trace does not depend on the parameter, θ, the construction of the asymptotically constant-risk prior is parallel to [6]; see also [13].
However, we consider the settings where there exists a unique maximum point of the trace, ; for example, these settings appear in predictions based on the binary regression model, where the covariates of the data and the target variables are not identical. In the settings, there do not exist asymptotically constant-risk priors among the priors independent of the sample size, N. The reason is as follows: we consider the prior, π(θ), independent of the sample size, N. Then, the Kullback–Leibler risk of the Bayesian predictive density is expanded as:
Since, in our settings, the first-order term, , is not constant, the prior independent of the sample size, N, is not an asymptotically constant-risk prior.
When there exists a unique maximum point of the trace, , we construct the asymptotically constant-risk prior, π(θ; N), up to O(N−2), by making the prior dependent on the sample size, N, as:
where f(θ) and h(θ) are the scalar functions of θ independent of N and |gX(θ)| denotes the determinant of the Fisher information matrix, gX(θ).
The key idea is that, if the specified parameter point has more undue risk than the other parameter points, then the more prior weights should be concentrated on that point.
Further, we clarify the subminimax estimator problem based on the mean squared error from the viewpoint of the prediction where the distributions of data and target variables are different and have a common unknown parameter. We obtain the improvement achieved by the minimax estimator over the subminimax estimators up to O(N−2). The subminimax estimator problem [14,15] is the problem that, at first glance, there seems to exist asymptotically dominating estimators of the minimax estimator. However, any relationship between such subminimax estimator problems and predictions have not been investigated, and further, in general, the improvement by the minimax estimator over the subminimax estimators has not been investigated.
2. Information Geometrical Notations
In this section, we prepare the information geometrical notations; see [16] for details. We abbreviate ∂/∂θi to ∂i, where the indices, i, j, k,…, run from one to d. Similarly, we abbreviate ∂2/∂θi∂θj, ∂3/∂θi∂θj∂θk and ∂4/∂θi∂θj∂θk∂θl to ∂ij, ∂ijk and ∂ijkl, respectively. We denote the expectations of the random variables, X, Y and X(N), by EX[·], EY [·] and EX(N) [·], respectively. We denote their probability densities by p(x|θ), q(y|θ) and p(x(N)|θ), respectively.
We define the predictive metric proposed by Komaki [13] as:
When the parameter is one-dimensional, gθθ(θ) denotes Fisher information and gθθ(θ) denotes its inverse. Let and be the quantities given by:
and:
Using these quantities, the e-connection and m-connection coefficients with respect to the parameter, θ, for the model, {p(x|θ) : θ ∈ Θ}, are given by:
and:
respectively.
The (0, 3)-tensor, , is defined by:
The tensor, , also produces a (0, 1)-tensor:
In the same manner, the information geometrical quantities, and , are defined for the model, {q(y|θ) : θ ∈ Θ}.
Let be a (1, 2)-tensor defined by:
For a derivative, , of the scalar function, υ(θ), the e-covariant derivative is given by:
3. Asymptotically Constant-Risk Priors When the Distributions of Data and Target Variables Are Different
In this section, we consider the settings where the trace, , has a unique maximum point. We construct the asymptotically constant-risk prior under the Kullback–Leibler risk in the sense that the asymptotic risk up to O(N−2) is constant. We find asymptotically constant-risk priors up to O(N−2) in two steps: first, expand the Kullback–Leibler risks of Bayesian predictive densities; second, find the prior having an asymptotically constant risk using this expansion.
From now on, we assume the following two conditions for the prior, π(θ; N):
(C1) The prior, π(θ; N), has the form:
where f(θ) and h(θ) are smooth scalar functions of θ independent of N.
(C2) The unique maximum point of the scalar function, f(θ), is equal to the unique maximum point of the trace, .
Based on Conditions (C1) and (C2), we expand the Kullback–Leibler risk of a Bayesian predictive density up to O(N−2).
Theorem 1. The Kullback–Leibler risk of a Bayesian predictive density based on the prior, π(θ; N), satisfying Condition (C1), is expanded as:
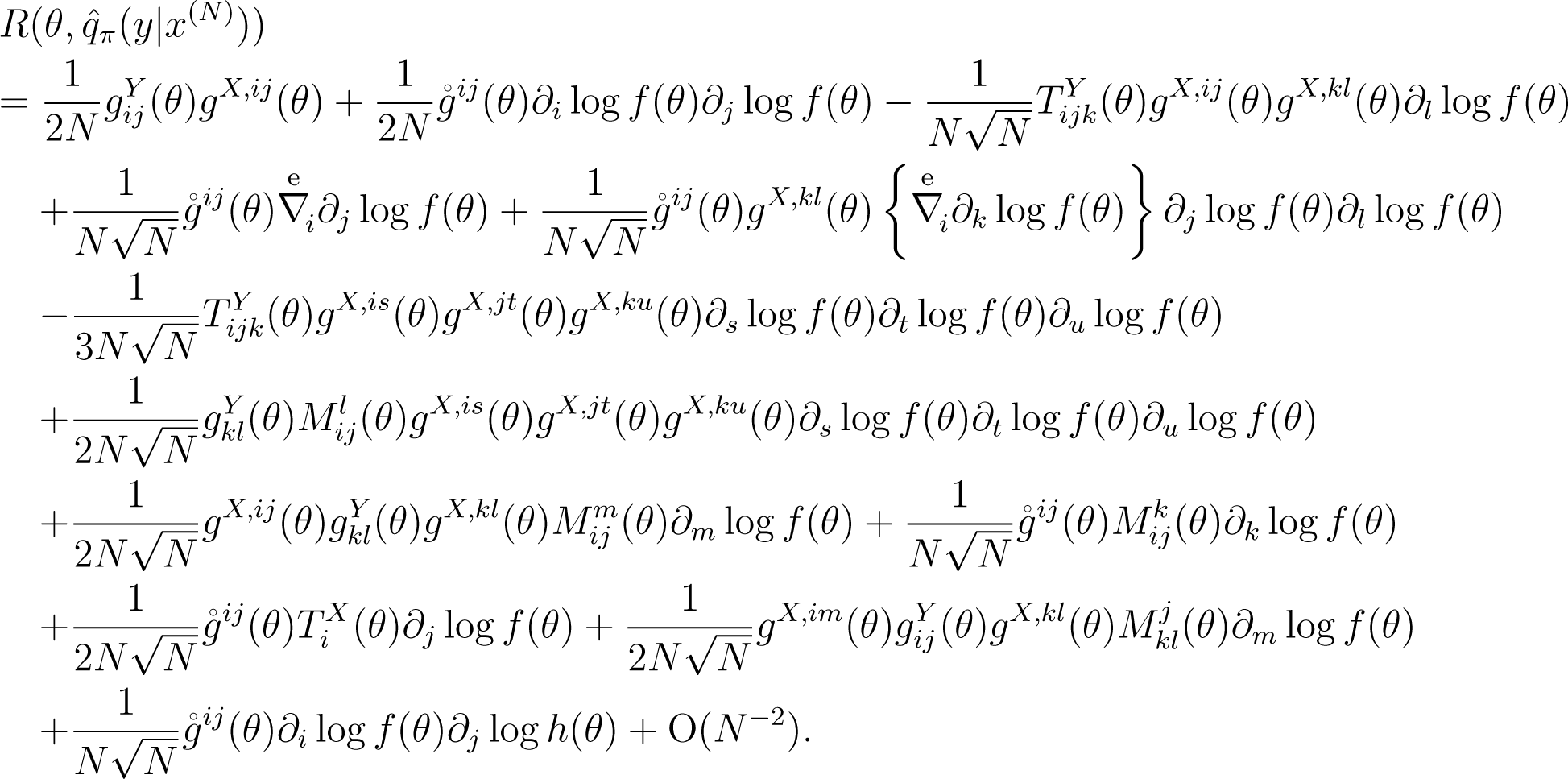
The proof is given in the Appendix. The first term in (1) represents that the precision of the estimation is determined by the geometric quantity of the data, gX;ij(θ), and the metric of the parameter is determined by the geometric quantity of the target variables, . Note that each term in (1) is invariant under the reparametrization.
Remark 1. For the subsequent theorem, it is important that at the point, θf, maximizing the scalar function, is given by:
The N−3/2-order term of this risk is common whenever we use the same scalar function, log f(θ). This term is negative because of the definition of the point, θf. Under Condition (C2), θf is equal to the unique maximum point, θmax, of the trace, .
Based on (1) and (2), we construct asymptotically constant-risk priors using the solutions of the partial differential equations.
Theorem 2. Suppose that the scalar functions, and, satisfy the following conditions:
(A1) is the solution of the Eikonal equation given by:
where θmax is the unique maximum point of the scalar function, .
(A2) is the solution of the first-order linear partial equation given by:
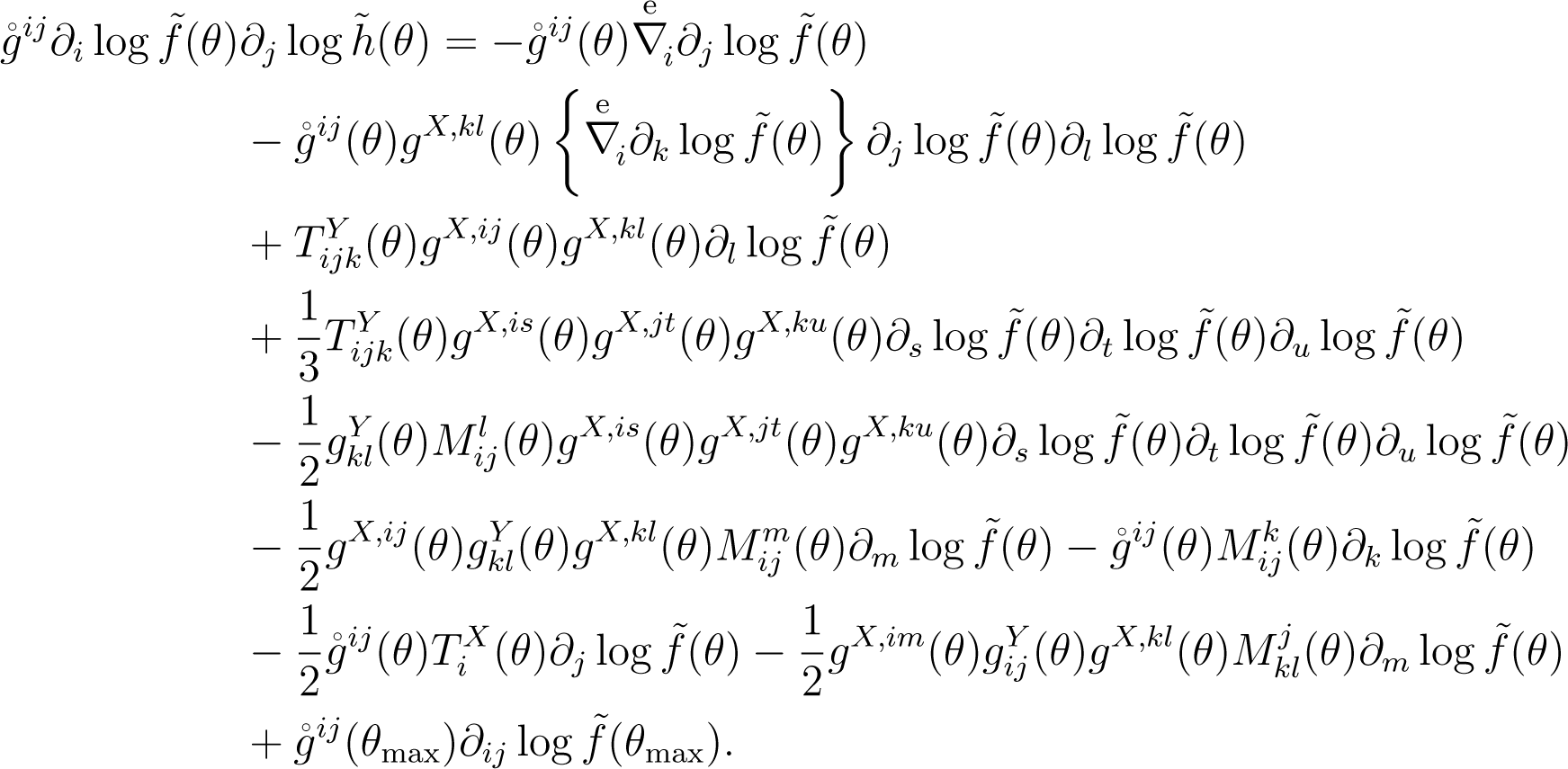
Let π(θ; N) be the prior that is constructed as:
Further, suppose that satisfies Condition (C2).
Then, the Bayesian predictive density based on the prior, π(θ; N), has the asymptotically smallest constant risk up to O(N−2) among all priors with the form (C1).
Proof. First, we consider the prior, φ(θ; N), constructed as:
From Theorem 1, the Kullback–Leibler risk, , based on the prior, φ(θ; N), is given by:
This is constant up to o(N−1).
Suppose that there exists another prior, φ(θ; N), constructed as:
and the Bayesian predictive density based on the prior, φ(θ; N), has the asymptotically constant risk:
From Theorem 1, the prior φ(θ; N) must satisfy the equation:
The left-hand side of the above equation is non-negative, because the matrix, , is positive-definite. Hence, the infimum of the constant, k, is equal to . From (5), the N−1-order term of the risk based on the prior, ϕ(θ; N), achieves the infimum, . Thus, the Bayesian predictive density based on the prior, ϕ(θ; N), has the asymptotically smallest constant risk up to o(N−1).
Second, we consider the prior, π(θ; N), constructed as:
The above argument ensures that the prior, π(θ; N), has the asymptotically smallest constant risk up to o(N−1). Thus, we only have to check if the N−3/2-order term of the risk is the smallest constant. From (2), the N−3/2-order term of the risk at the point, θmax, is unchanged by the choice of the scalar function, log h(θ). In other words, the constant N−3/2-order term must agree with the quantity, . From Theorem 1, if we choose the prior, π(θ; N), the N−3/2-order term of the risk is the smallest constant, and it agrees with the quantity, . Thus, the prior, π(θ; N), has the asymptotically smallest constant risk up to O(N−2). □
Remark 2. In Theorem 2, we choose, satisfying Condition (C2) among the solutions of (A1). We consider the model with a one-dimensional parameter, θ. There are four possibilities to the solutions of (A1):
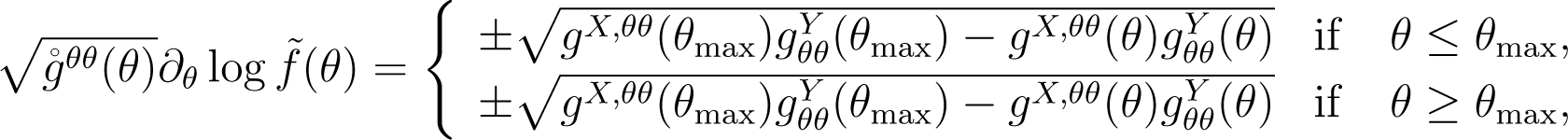
where the double-sign corresponds. From the concavity around θmax as suggested by (C2), we choose as the solution of the following equation:
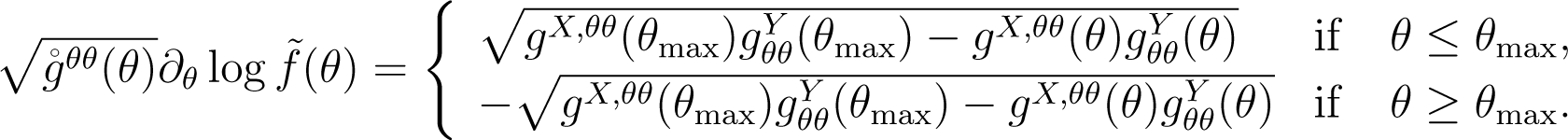
Integrating both sides of Equation (6), the unique function, , is obtained.
Remark 3. Compare the Kullback–Leibler risk based on the asymptotically constant-risk prior, π(θ; N), with that based on the prior, λ(θ), independent of the sample size, N. From Theorem 1 and Theorem 2, the Kullback–Leibler risk based on the asymptotically constant-risk prior, π(θ; N), is given as:
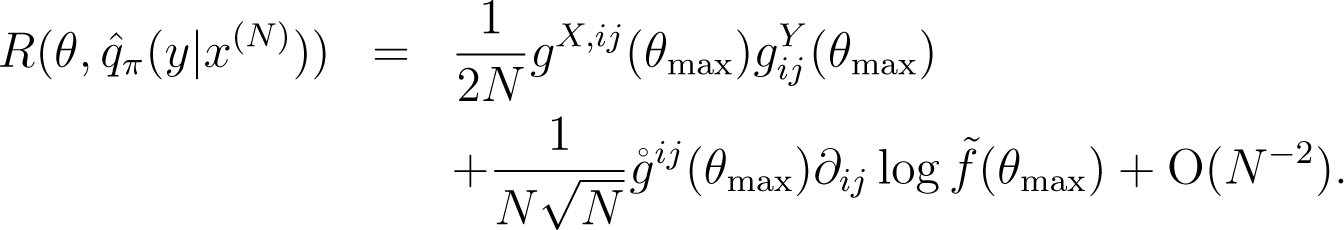
In contrast, the Kullback–Leibler risk based on the prior, λ(θ), is given as:
The N−1-order term in (8) is under the N−1-order term in (7); although the N−3/2-order term in (8) does not exist, the N−3/2-order term in (7) is negative. Thus, the maximum of the risk based on the asymptotically constant-risk prior, π(θ; N), is smaller than that of the risk based on the prior, λ(θ). This result is consistent with the minimaxity of selecting the prior that constructs the predictive density with the smallest maximum of the risk.
4. Subminimax Estimator Problem Based on the Mean Squared Error
In this section, we refer to the subminimax estimator problem based on the mean squared error, from the viewpoint of the prediction where the distributions of data and target variables are different and have a common unknown parameter. First, we give a brief review of subminimax estimator problem through the binomial example.
Example. Let us consider the binomial estimation based on the mean squared error, . For any finite sample size, N, the Bayes estimator, , based on the Beta prior, , is minimax under the mean squared error. The mean squared error of the minimax Bayes estimator, , is given by:
In contrast, the mean squared error of the maximum likelihood estimator, , is given by:
We compare the two estimators, and. In the comparison of the N−1-order terms of the mean squared errors, it seems that the maximum likelihood estimator, , dominates the minimax Bayes estimator, . In other words, the N−1-order term of is not greater than that of for every θ ∈ Θ, and the equality holds when θ = 1/2. This seeming paradox is known as the subminimax estimator problem; see [14,17,18] for details. See also [15] for the conditions that such problems do not occur in estimation.
However, this paradox does not mean the inferiority of the minimax Bayes estimator. This is because, although the mean squared error of the minimax Bayes estimator, , has the negative N−3/2-order term, the mean squared error of the maximum likelihood estimator, , does not have the N−3/2-order term. Hence, in comparison to the mean squared errors up to O(N−2), the maximum of the mean squared error, , is below the maximum of the mean squared error, .
Next, we construct the asymptotically constant-risk prior in the estimation based on the mean squared error when the subminimax estimator problem occurs, from the viewpoint of the prediction. We consider the priors, π(θ; N), satisfying (C1). From Lemma 5 in the Appendix, the mean squared error of the Bayes estimator, , is equal to the Kullback–Leibler risk of the -plugin predictive density, , by assuming that the target variable, y, is a d-dimensional Gaussian random variable with the mean vector, θ, and unit variance. Note that , and for . Thus, if has a unique maximum point, we obtain the asymptotically constant-risk prior, π(θ; N), up to O(N−2) from Lemma 4 in the Appendix and Theorem 2.
Finally, we compare the mean squared error of the asymptotically constant-risk Bayes estimator, , with that of the maximum likelihood estimator, . The mean squared error of the asymptotically constant-risk Bayes estimator, , is given as:
In contrast, the mean squared error of the maximum likelihood estimator, , is given as:
Thus, the maximum of the mean squared error of the asymptotically constant-risk Bayes estimator is smaller than that of estimators by the improvement of order N−3/2 in proportion to the Hessian of the scalar function, at θmax. In the prediction where the trace, , has a unique maximum point, the same improvement holds (Remark 3).
Example revisited. Using the above results, we consider the binomial estimation based on the mean squared error from the viewpoint of the prediction. The geometrical quantities to be used are given by:
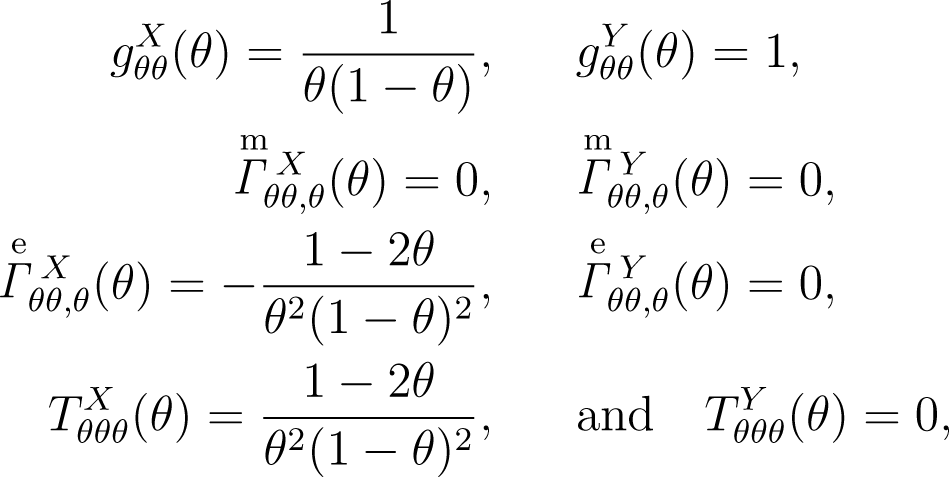
respectively. and vanish, the asymptotically constant-risk prior in the estimation is identical to the asymptotically constant-risk prior in the prediction; compare Theorem 1 with the expansion of in Lemma 4 in the Appendix.
In this example, Equation (3) is given by:
and the solution, , is (1/2) log{θ(1 − θ)}. Here, the second-order derivative of the function, , is given by:
From this, Equation (4) is given by:
and the solution, , is (1/2) log{θ(1 − θ)}. Hence, the asymptotically constant-risk prior, π (θ; N), is a Beta prior with the parameters, and. Note that the asymptotically constant-risk prior coincides with the exact minimax prior. Since gX,θθ(θmax) = 1/2 and, the mean squared error of the asymptotically constant-risk Bayes estimator, , agrees with (9) up to O(N−2).
5. Application to the Prediction of the Binary Regression Model under the Covariate Shift
In this section, we construct asymptotically constant-risk priors in the prediction based on the binary regression model under the covariate shift; see [10].
We consider that we predict a binary response variable, y, based on the binary response variables, x(N). We assume that the target variable, y, and the data, x(N), follow the logistic regression models with the same parameter, β, given by:
and:
where Πx is the success probability of the data and Πy is the success probability of the target variable. Let α and denote known constant terms, and let β denote the common unknown parameter. Further, we assume that the covariates, z and , are different.
Using the parameter θ = Πx, we convert this predictive setting to binomial prediction where the data, x, and the target variable, y, are distributed according to:
and:
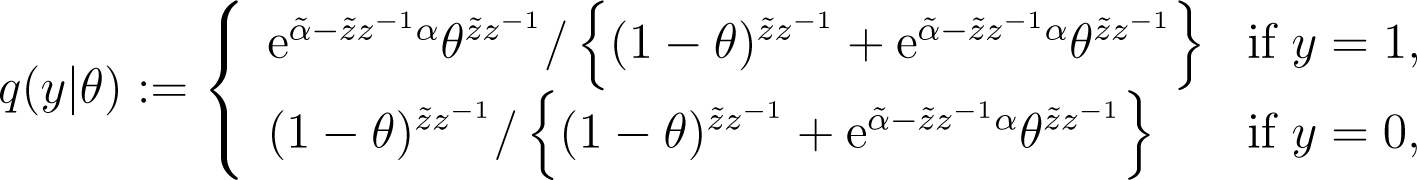
respectively. We obtain two Fisher information for x and y as:
and:
respectively.
For simplicity, we consider the setting where z = 1, and . The geometrical quantities for the model, {p(x|θ) : θ ∈ Θ}, are given by:
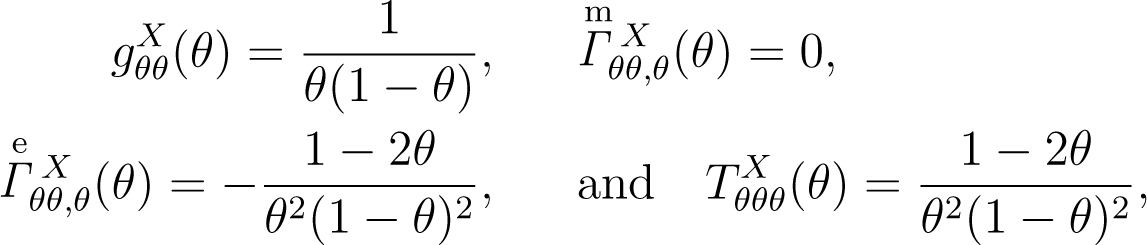
respectively. In the same manner, the geometrical quantities for the model, {q(y|θ) : θ ∈ Θ}, are given by:
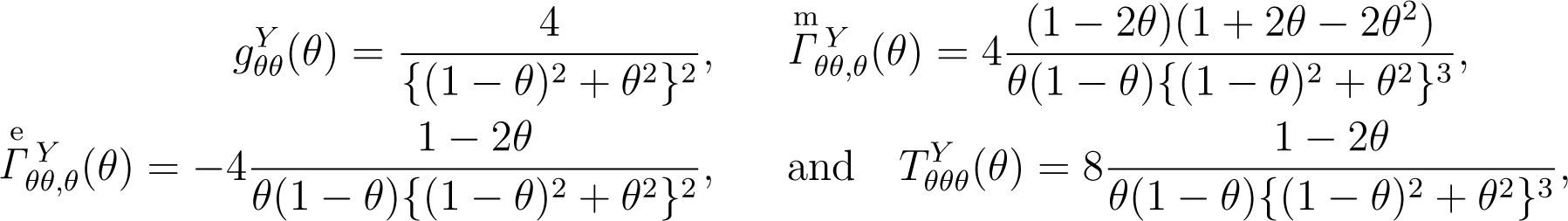
respectively.
Using these quantities, Equation (3) is given by:
By noting that the maximum point of is 1/2, the solution, , of this equation is given by:
Using this solution, we obtain the solution of Equation (4) given by:
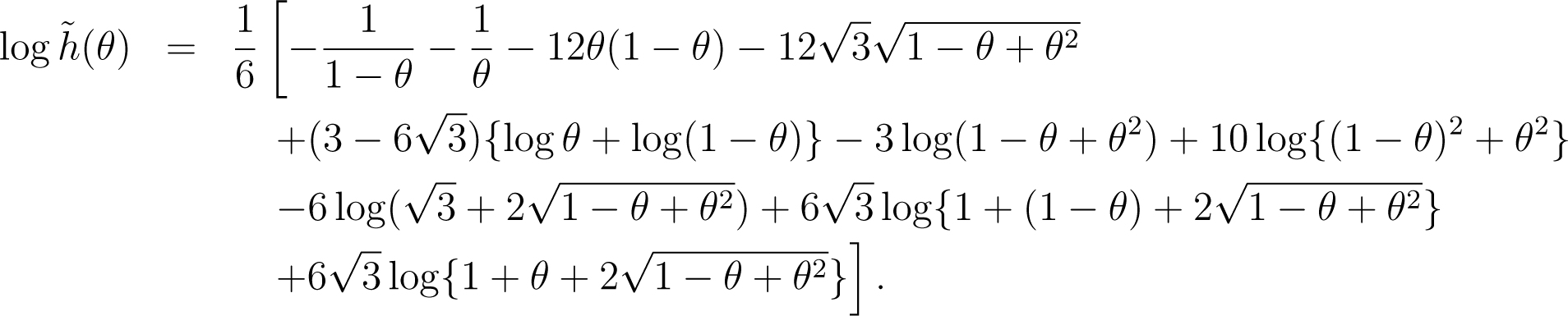
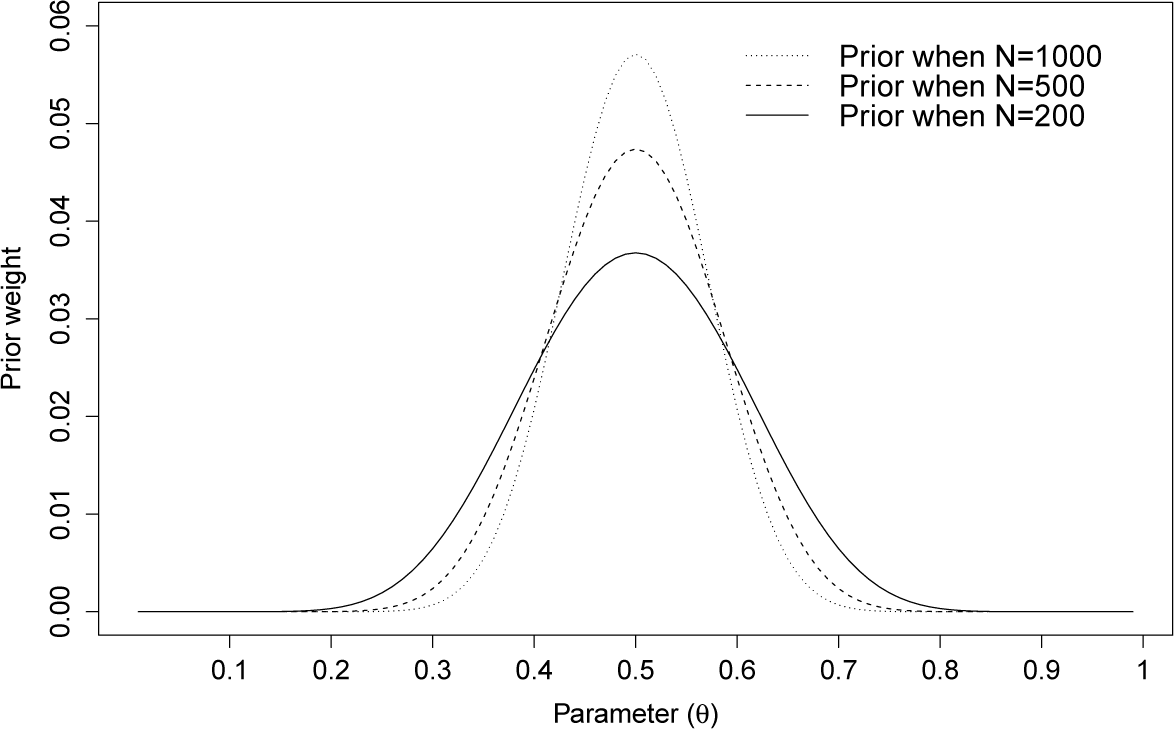
The asymptotically constant-risk priors for the different sample sizes are shown in Figure 1. The prior weight is found to be more concentrated to 1/2 as the sample size, N, grows.
In this example, we obtain the Kullback–Leibler risk of the Bayesian predictive density based on the asymptotically constant-risk prior, π(θ; N), as:
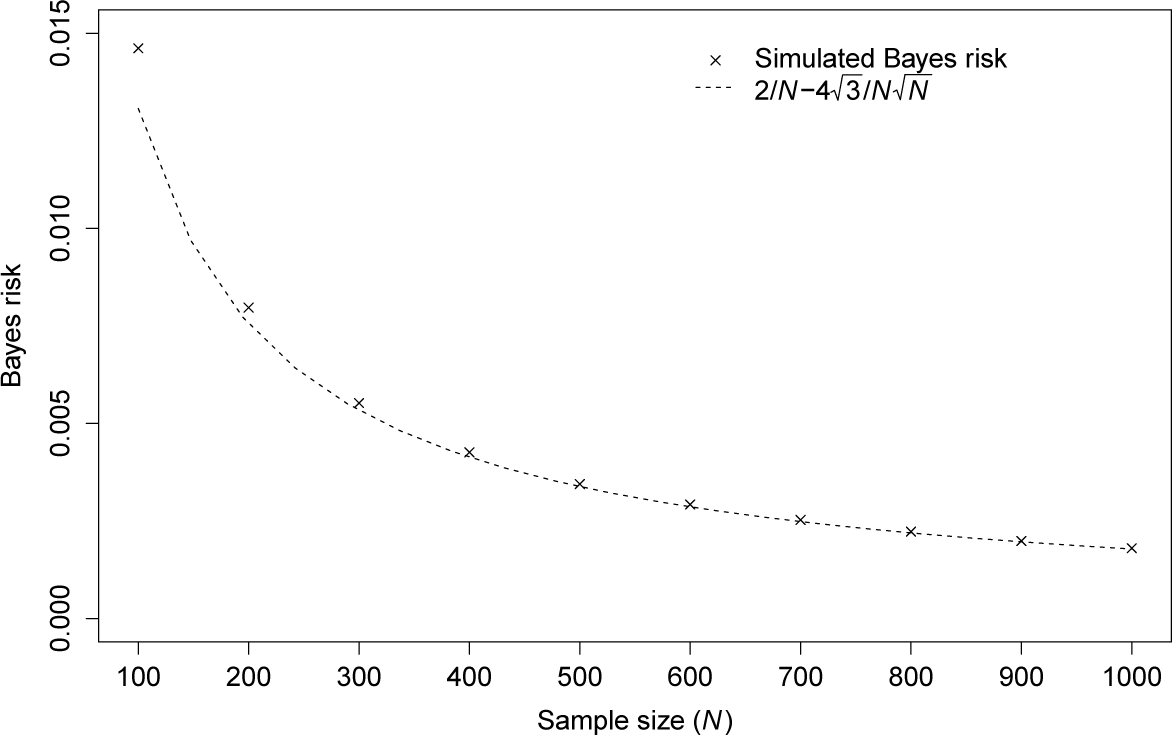
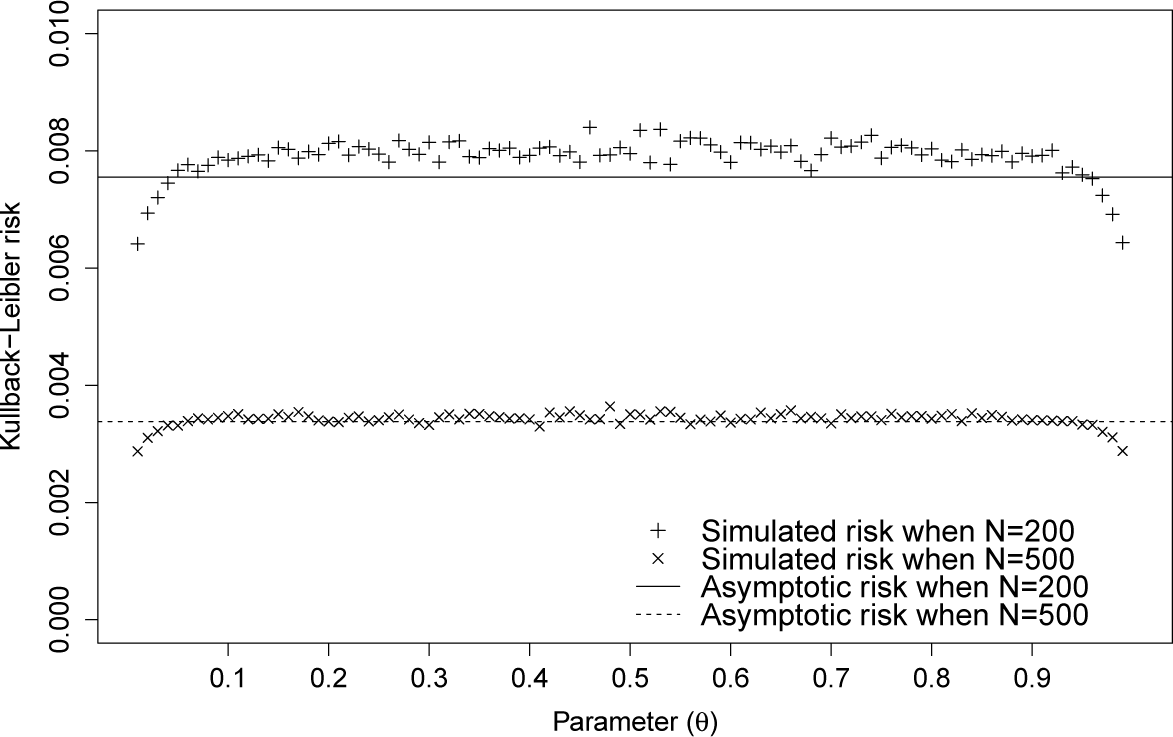
We compare this value with the Bayes risk calculated using the Monte Carlo simulation; see Figure 2. As the sample size, N, grows, the difference appears negligible. Further, we compare this value with the risk itself calculated by the Monte Carlo simulation; see Figure 3. As the sample size, N, grows, the risk becomes more constant.
6. Discussion and Conclusions
We have considered the setting where the quantity, —the trace of the product of the inverse Fisher information matrix, gX,ij(θ), and the Fisher information matrix, —has a unique maximum point, and we have investigated the asymptotically constant-risk prior in the sense that the asymptotic risk is constant up to O(N−2).
In Section 3, we have considered the prior depending on the sample size, N, and constructed the asymptotically constant-risk prior using Equations (3) and (4). In Section 4, we have clarified the relationship between the subminimax estimator problem based on the mean squared error and the prediction where the distributions of data and target variables are different. In Section 5, we have constructed the asymptotically constant-risk prior in the prediction based on the logistic regression model under the covariate shift.
We have assumed that the trace, , is finite. However, the trace may diverge in the non-compact parameter space; for example, it diverges under the predictive setting, where the distribution, q(y|θ), of the target variable is the Poisson distribution and the data distribution, p(x|θ), is the exponential distribution, with Θ equivalent to ℝ. Therefore, for our future work, in such a setting, we should adopt criteria other than minimaxity.
Acknowledgments
The authors thank the referees for their helpful comments. This research was partially supported by a Grant-in-Aid for Scientific Research (23650144, 26280005).
Author Contributions
Both authors contributed to the research and writing of this paper. Both authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
We prove Theorem 1. First, we introduce some lemmas for the proof. For the expansion, we follow the following six steps (the first five steps are arranged in the form of lemmas): the first is to expand the MAPestimator; the second is to calculate their bias and mean squared error; the third is to expand the Kullback–Leibler risk using -plugin predictive density, ; the fourth is to expand the Bayesian predictive density based on the prior π(θ; N); the fifth is to expand the Bayesian estimator minimizing the Bayes risk; and the last is to prove Theorem 1 using these lemmas.
We use some additional notations for the expansion. Let be the maximum point of the scalar function log p(x(N)|θ) + log{π(θ; N)/|gX(θ)|1/2}. Let l(θ|x(N)) denote the log likelihood of the data, x(N). Let lij (θ|x(N)), lijk (θ|x(N)) and lijkl(θ|x(N)) be the derivatives of order 2, 3 and 4 of the log likelihood, l(θ|x(N)). Let Hij(θ|x(N)) denote the quantity, . Let and denote and , respectively. In addition, the brackets (·) denotes the symmetrization: for any two tensors, aij and bij, ai(jbk)l denotes ai(jbk)l = (aijbkl+aikbjl)/2.
Lemma 3. Let be the maximum point of log p(x(N)|θ) + log{π(θ; N)/|gX(θ)|1/2}. Then, the i-th component of this estimator and is expanded as follows:
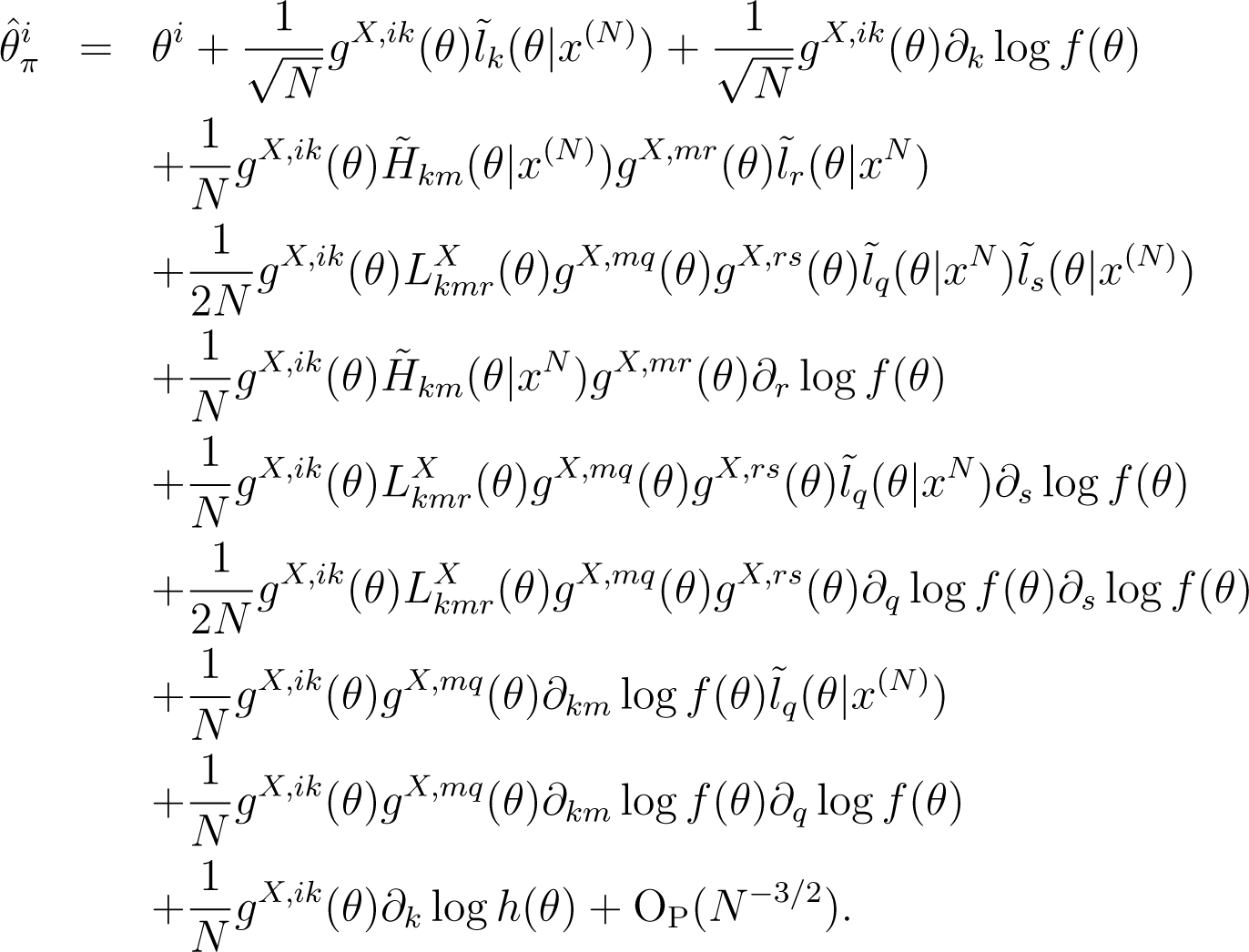
Proof. By the definition of and , we get the equation given by:
From our assumption that prior π(θ; N) has the form given by:
we rewrite this equation as:
By applying Taylor expansion around θ to this new equation, we derive the following expansion:
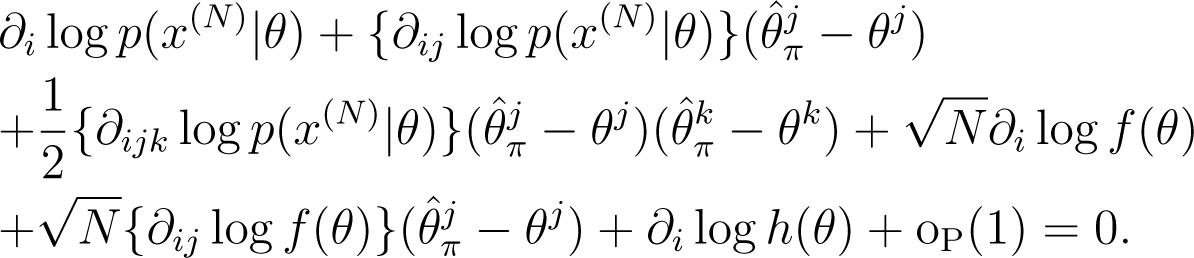
From the law of large numbers and the central limit theorem, we rewrite the above expansion as:
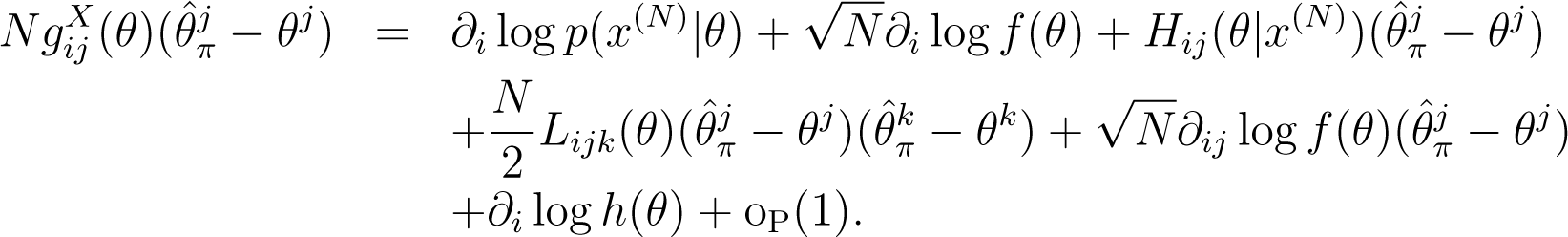
By substituting the deviation, , recursively into Expansion (11), we obtain Expansion (10). □
Lemma 4. Let be the maximum point of log p(x(N)|θ) + log{π(θ; N)/|gX(θ)|1/2}. Then, the i-th component of the bias of the estimator, , is given by:
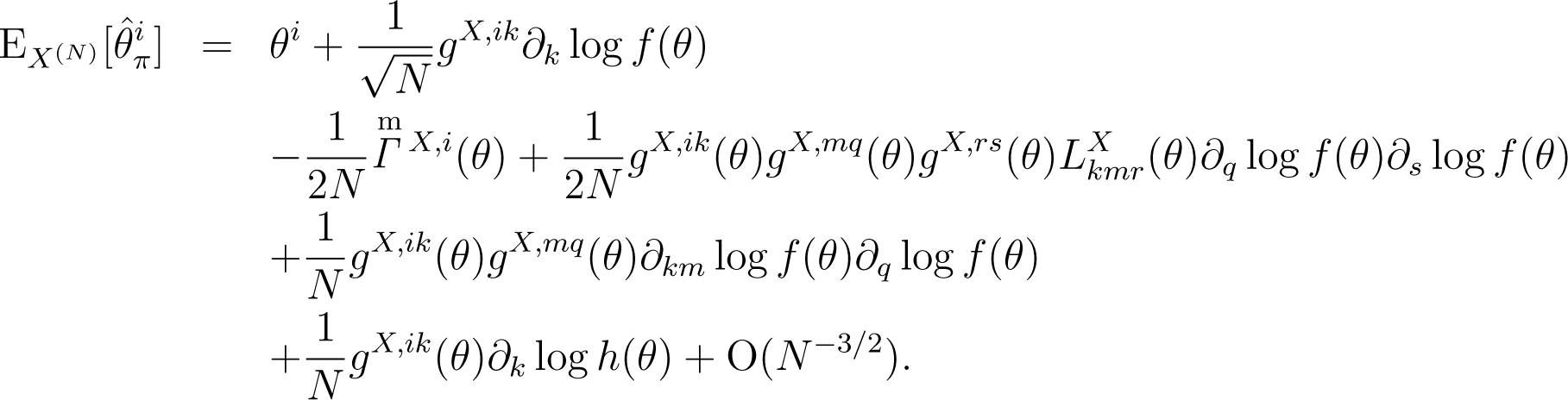
The (i, j)-component of the mean squared error of is given by:
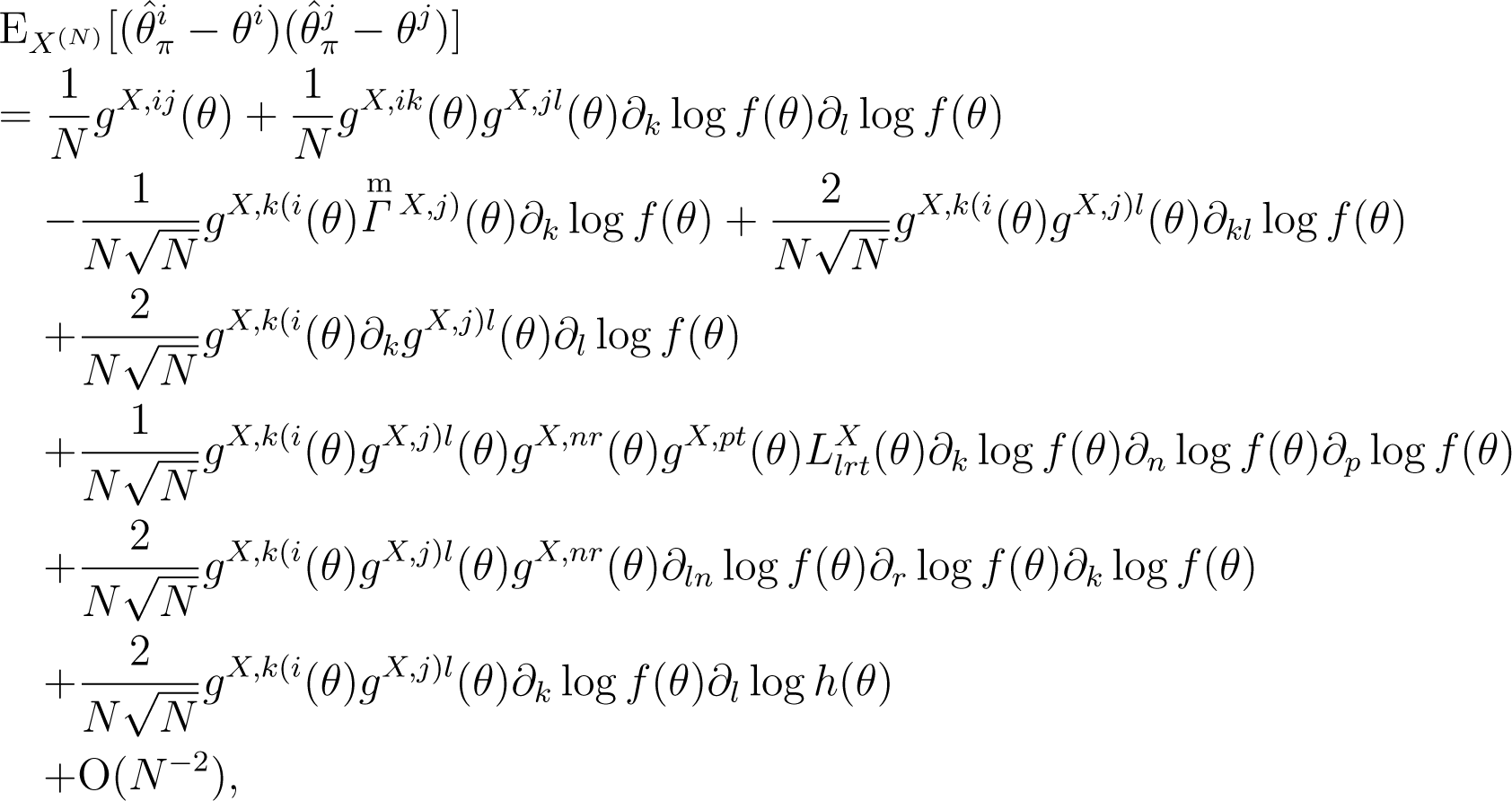
where denotes and denotes. The (i, j, k)-component of the mean of the third power of the deviation, is given by:
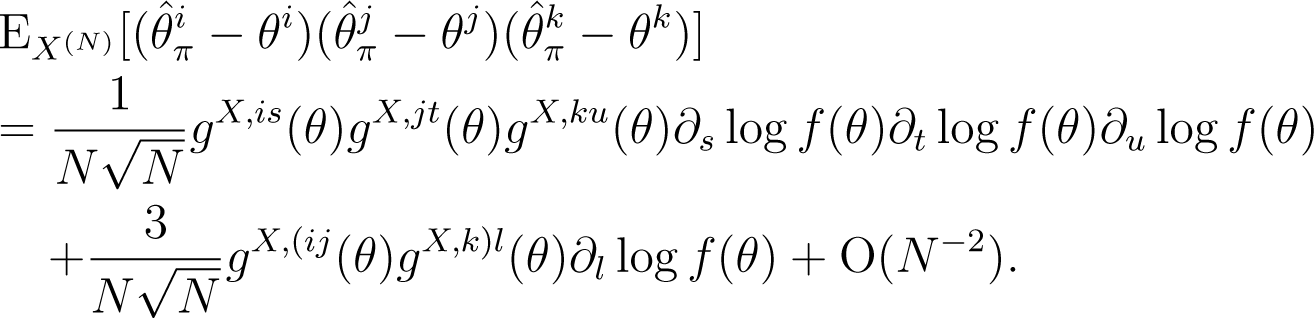
Proof. First, using Lemma 3, we determine the i-th component of the bias of given by:
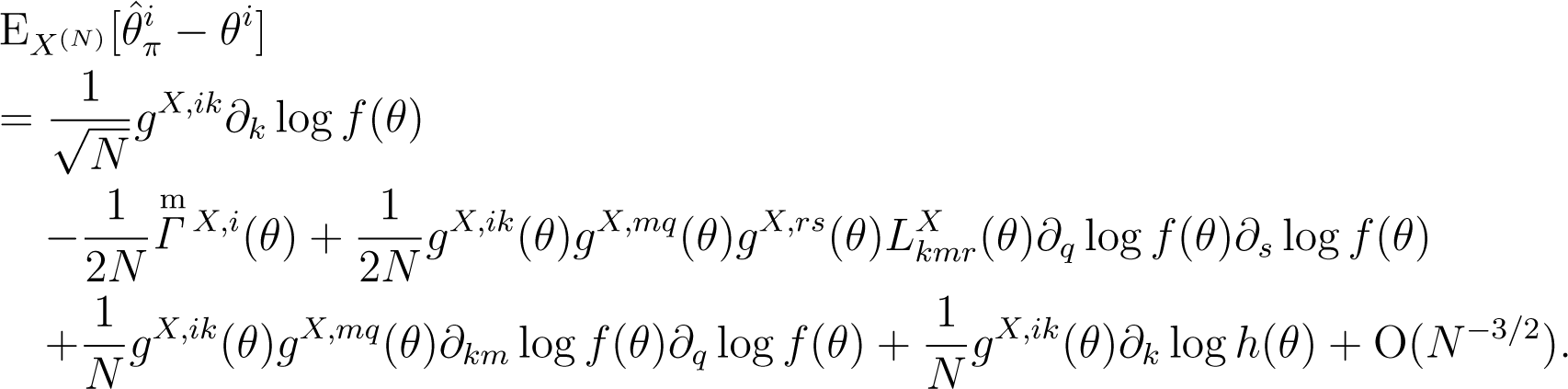
Second, consider the following relationship:
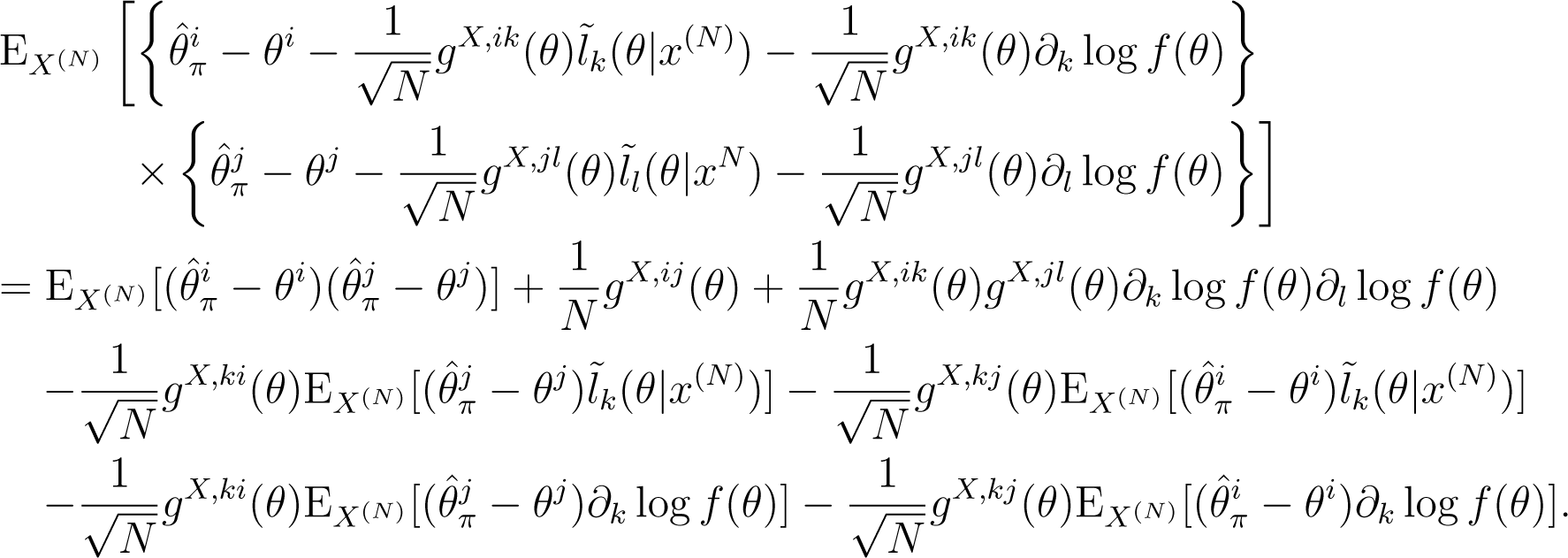
By differentiating the j-th component of the bias, , we obtain the equation given by:
where denotes the delta function: if the upper and the lower indices agree, then the value of this function is one and otherwise zero. Equation (16) has been used by [2,16,19]. By substituting Equations (16) and (12) into Relationship (15), we obtain the (i, j)-component of the mean squared error of given by:
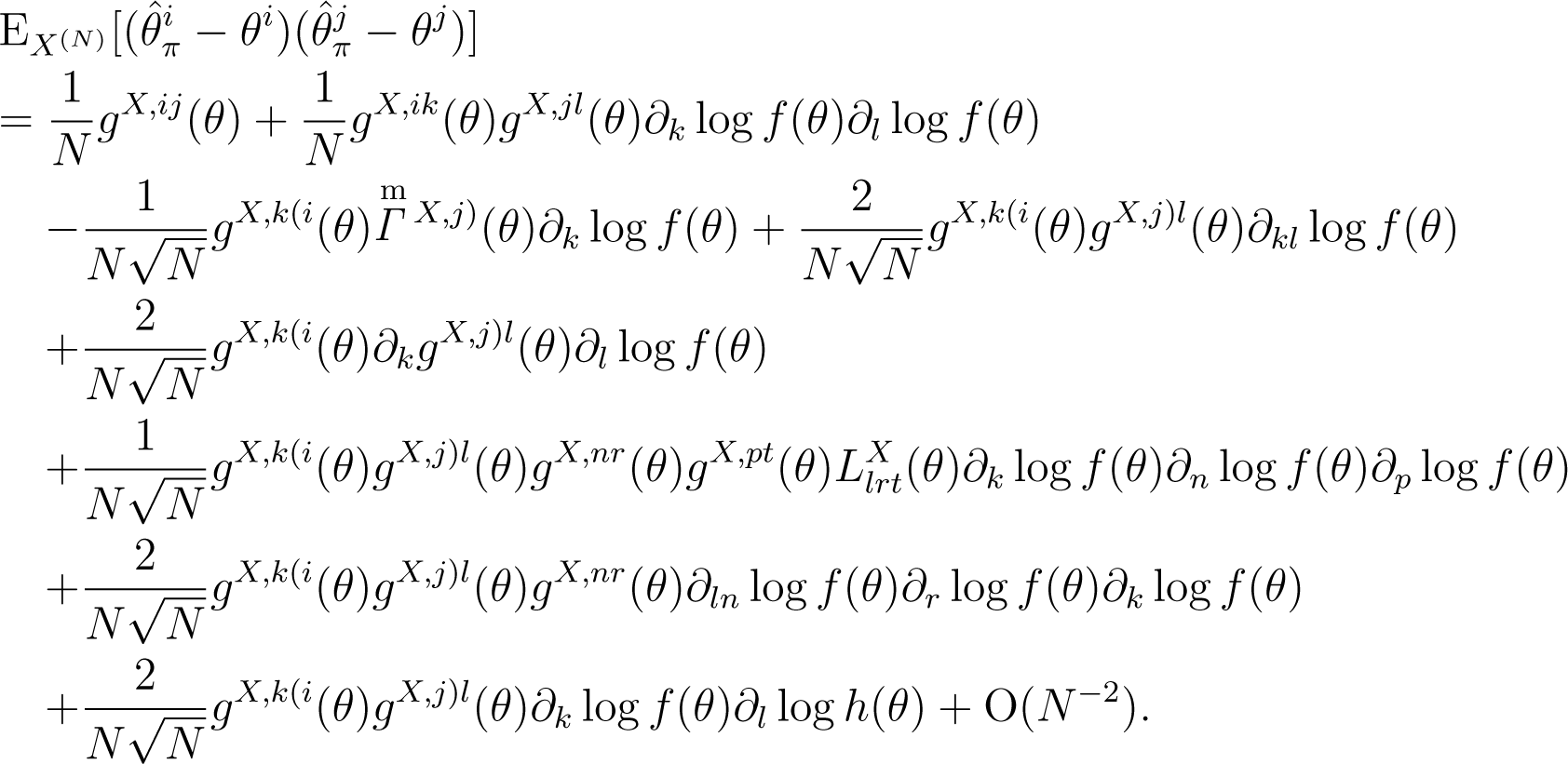
Finally, by taking the expectation of the third power of the deviation, , we obtain the following expansion:
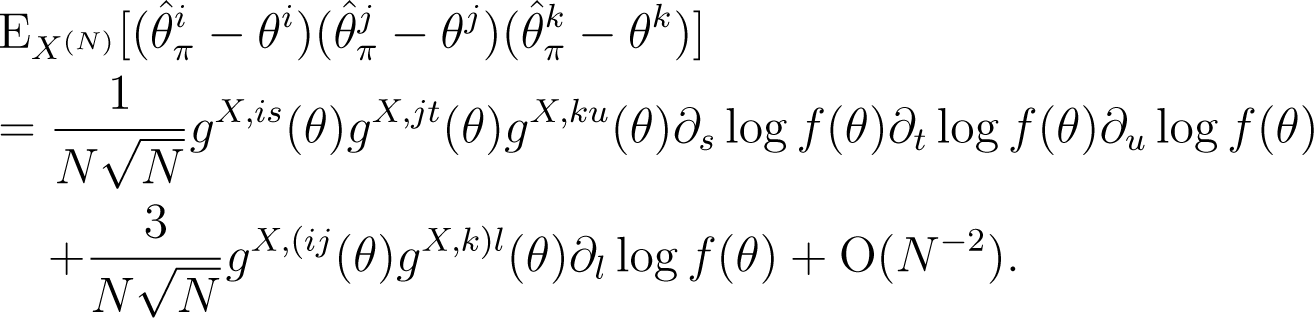
□
Lemma 5. Let be the maximum point of log p(x(N)|θ) + log{π(θ; N)/|gX(θ)|1/2}. The Kullback–Leibler risk of the plug-in predictive density, , with the estimator, , is expanded as follows:
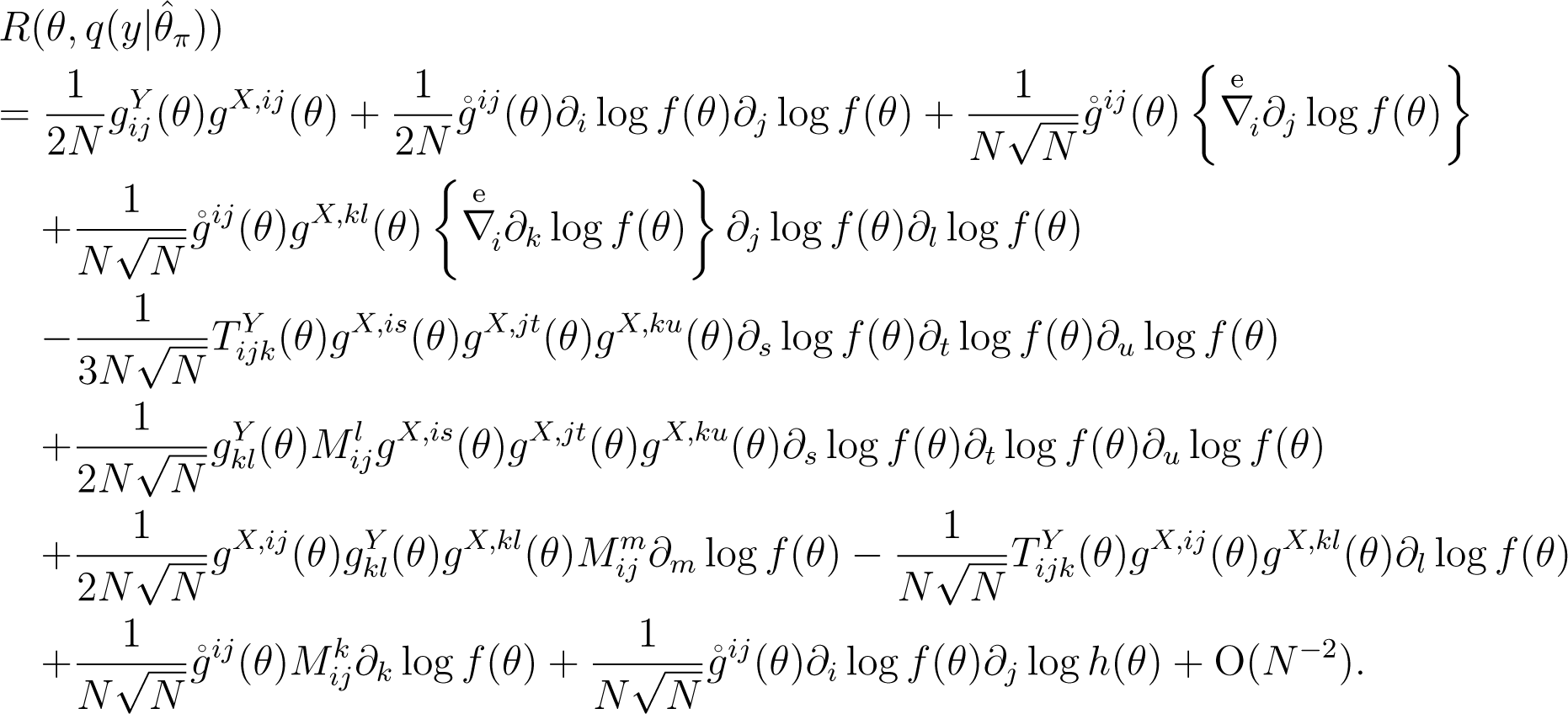
Proof. By applying the Taylor expansion, the Kullback–Leibler risk, , is expanded as:
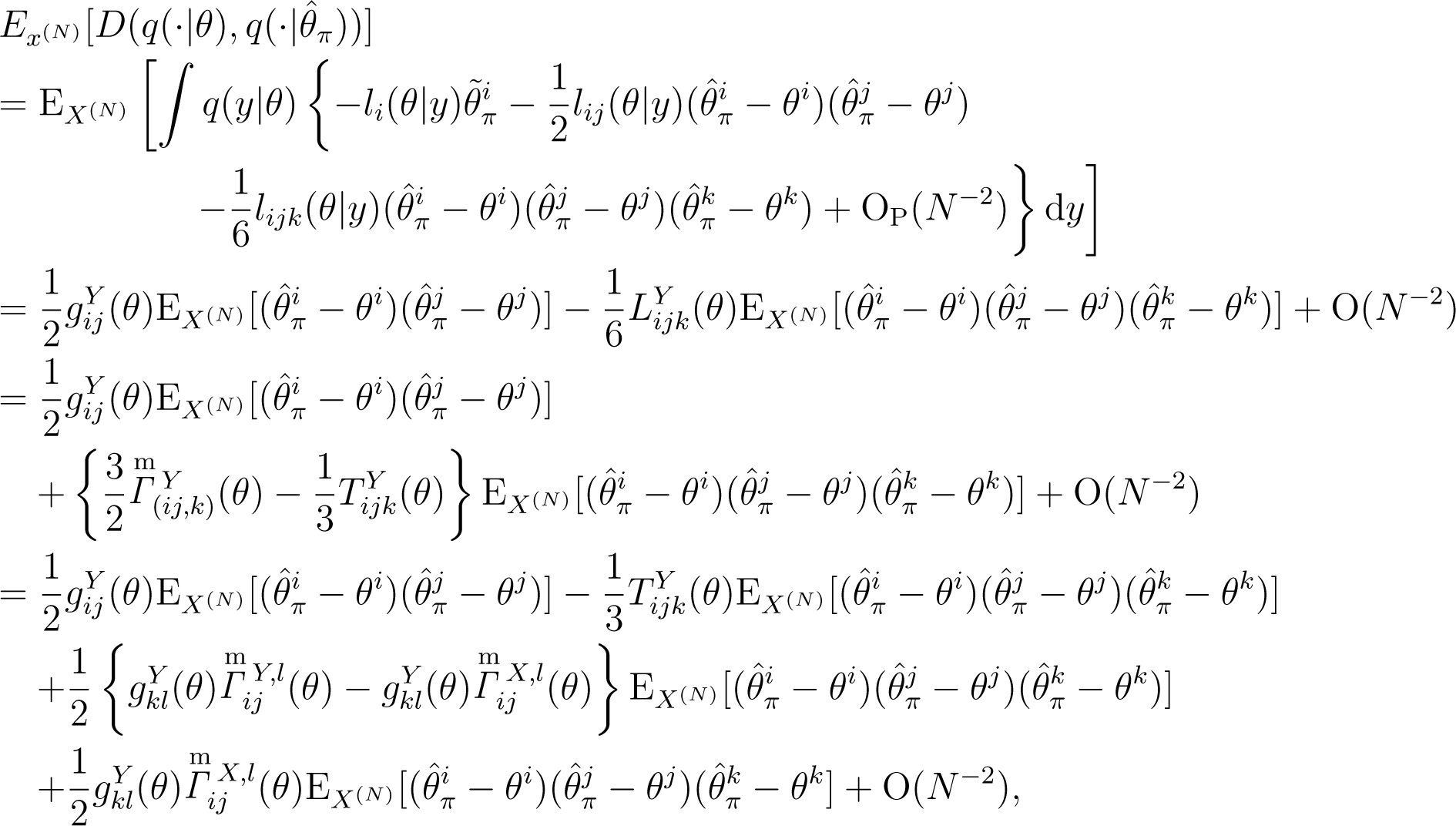
where denotes .
By the definition of the predictive metric, , by Expansions (13) and (14) and by the relationship , the last two terms of the above expansion (18) are expanded as:
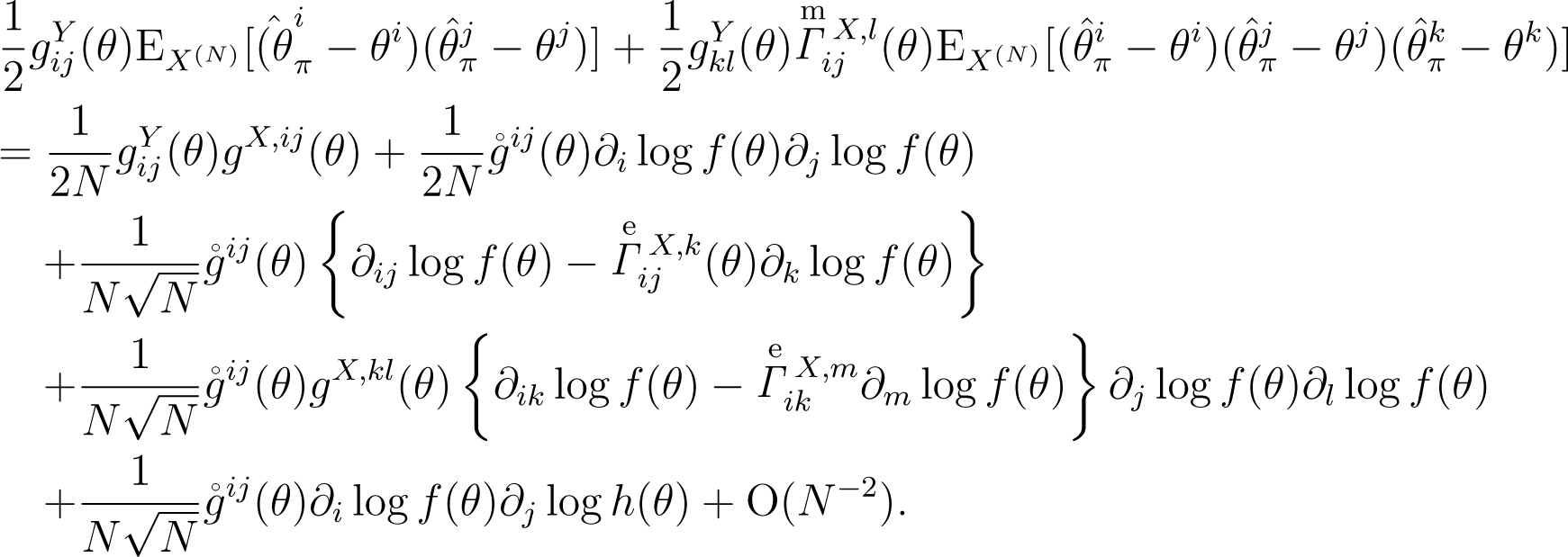
By substituting Expansion (19) into Expansion (18), Expansion (17) is obtained. □
Note that Expansion (17) is invariant up to O(N−2) under the reparametrization, so that each term of this expansion is a scalar function of θ.
Lemma 6. Let be the maximum point of. The Bayesian predictive density based on the prior, π(θ; N), is expanded as:
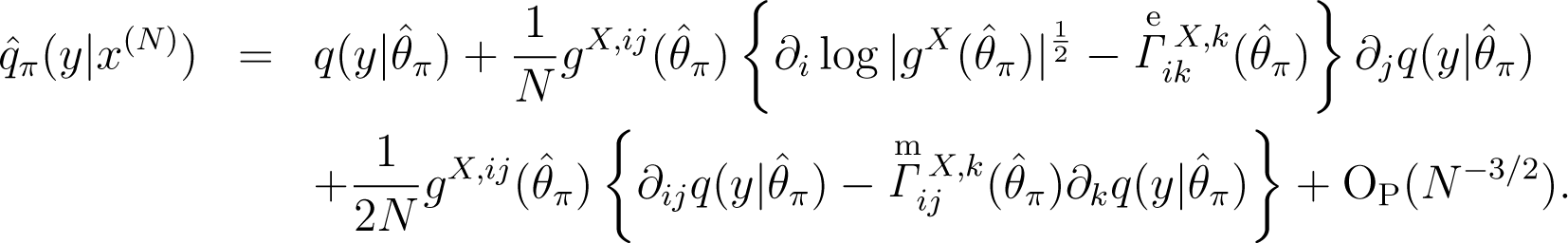
Proof. Let denote . First, using a Taylor expansion twice, we expand the posterior density, π(θ|x(N)), as:
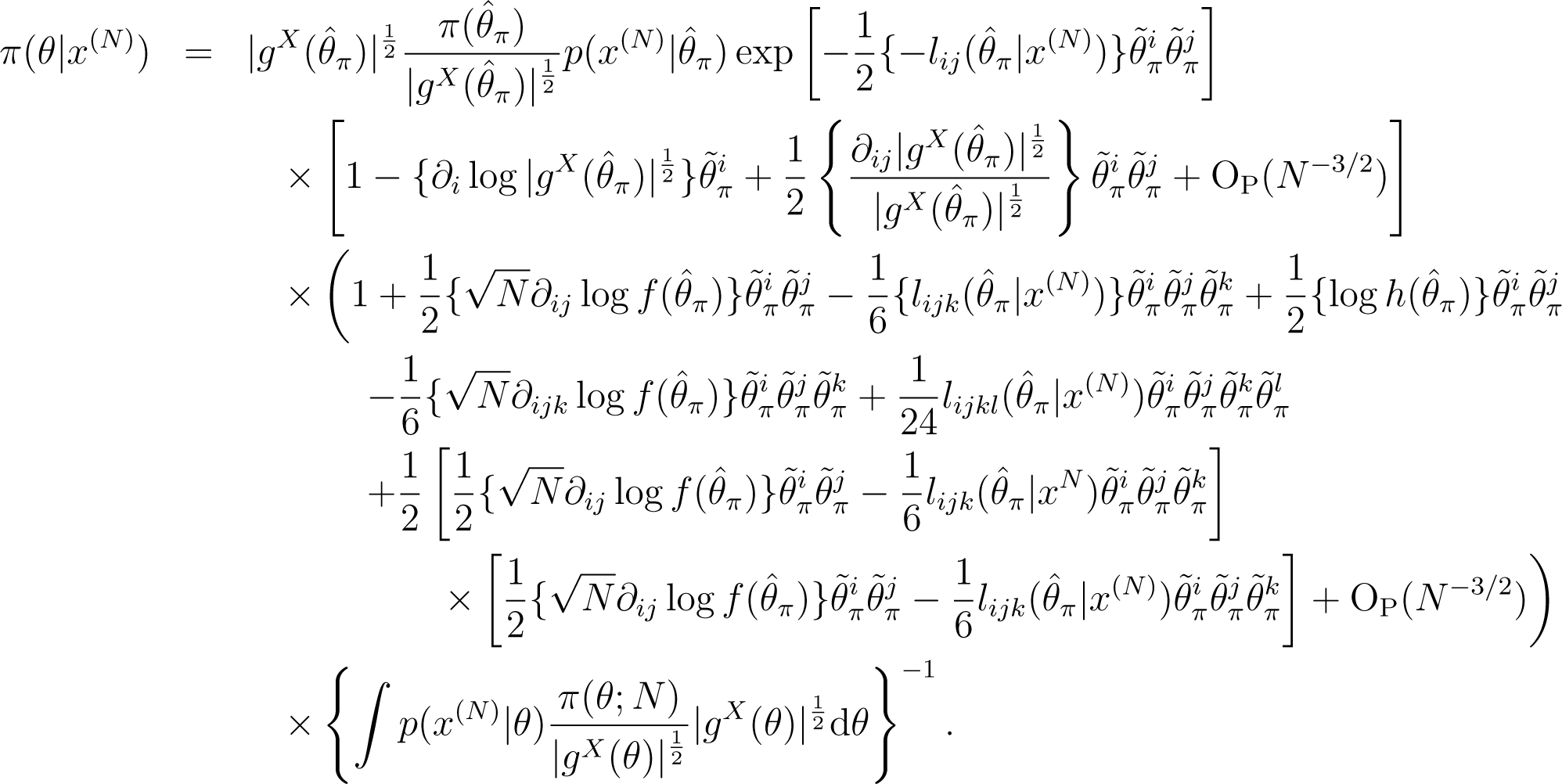
We denote the N−1/2-order, N−1-order and N−3/2-order terms by , and , respectively. Then, this expansion is rewritten as:
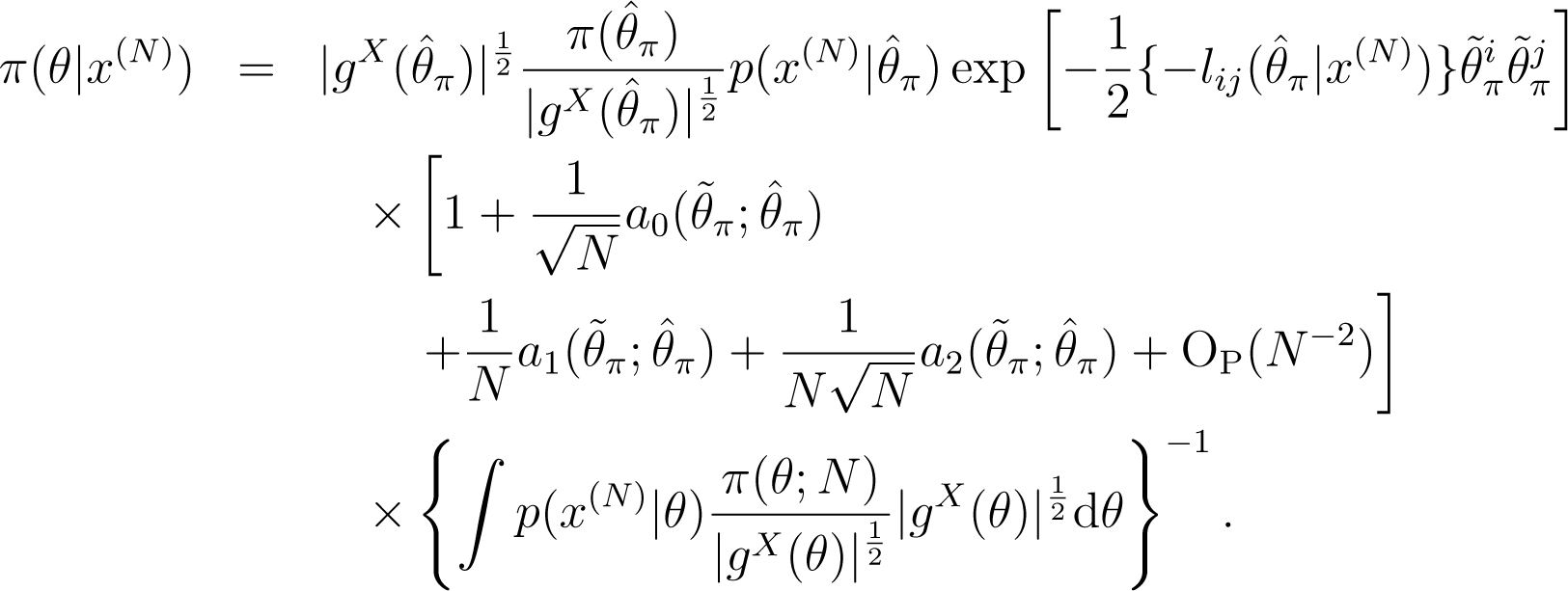
To make the expansion easier to see, the following notations are used. Let be the probability density function of the d-dimensional normal distribution with the precision matrix whose (i, j)-component is . Let be a d-dimensional random vector distributed according to the normal density, The notations, , , and, denote the expectations of, , , and ηiηj, respectively.
Using the above notations, we get the following posterior expansion:
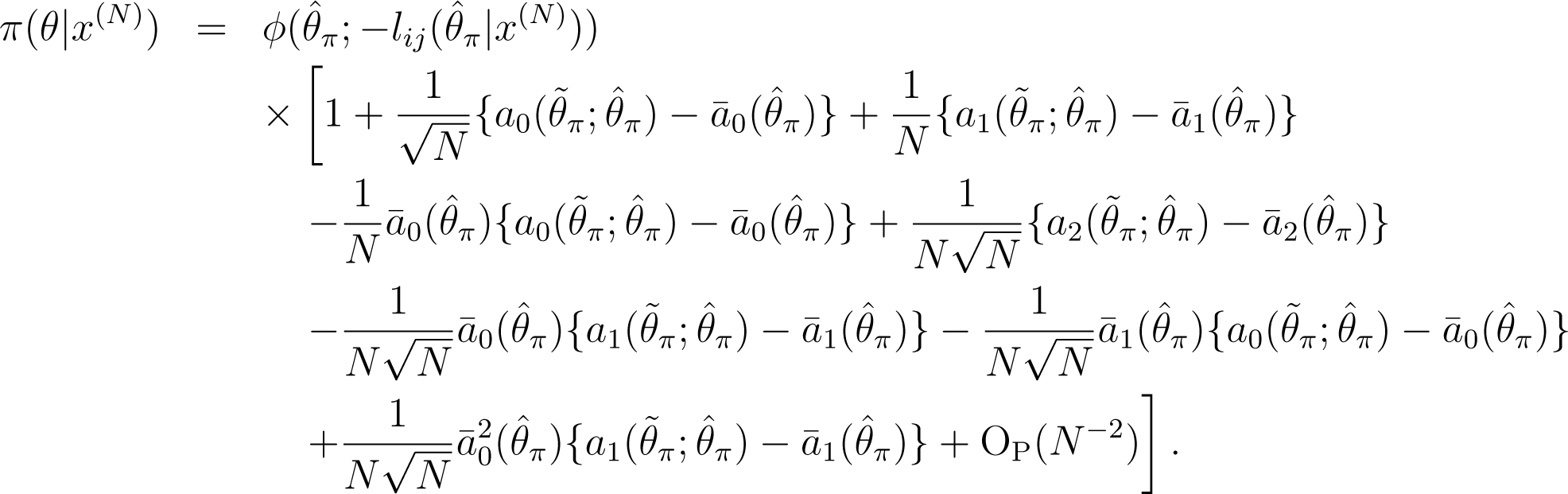
Second, using (21), the Bayesian predictive density, , based on the prior, π(θ; N), is expanded as:
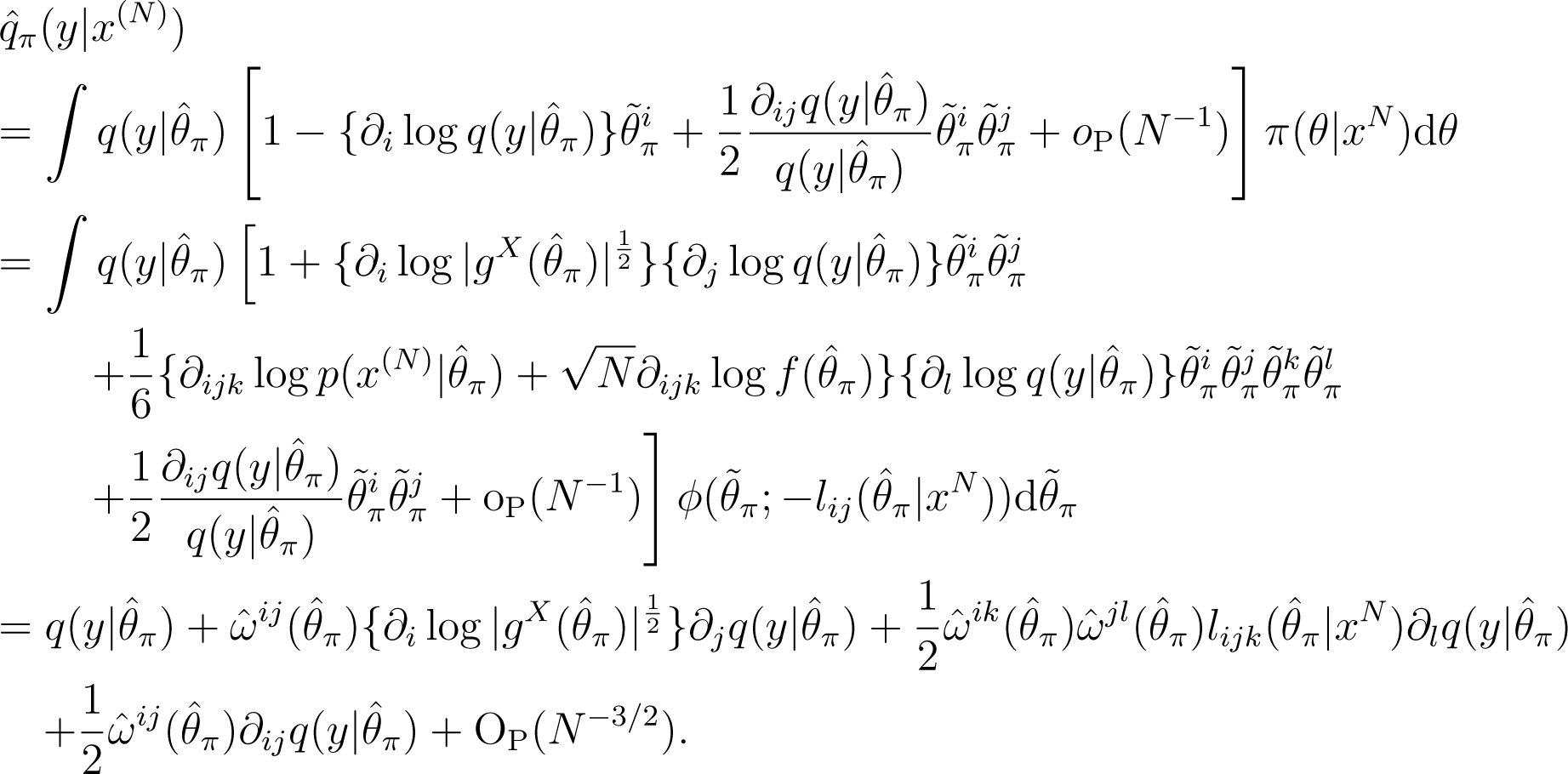
Here, the following two equations hold:
By combining Equation (23) with the Sherman–Morrison–Woodbury formula, the following expansion is obtained:
By substituting Equations (23), (24) and (25) into Expansion (22), Expansion (20) is obtained. □
Note that the integration of Expansion (20) is one up to OP(N−2). Further, Expansion (20) is similar to the expansion in [2]. However, the estimator that is the center of the expansion is different, because of the dependence of the prior on the sample size.
Lemma 7. The Bayesian estimator, , minimizing the Bayes risk, among plug-in predictive densities is given by:
Proof. The Bayes risk, , is decomposed as:
The first term of this decomposition is not dependent on. . From Fubini’s theorem and Lemma 6, the proof is completed. □
Using these lemmas, we prove Theorem 1. First, we find that the Kullback–Leibler risk of the plug-in predictive density with the estimator, , defined in Lemma 7, is given by:
Using Expansion (27) and Lemma 5, we expand the Kullback–Leibler risk, . Here, the risk, , is equal to the risk, , up to O(N−2), because we expand the Bayesian predictive density, as:
Thus, we obtain Expansion (1).
References
- Aitchison, J. Goodness of prediction fit. Biometrika 1975, 62, 547–554. [Google Scholar]
- Komaki, F. On asymptotic properties of predictive distributions. Biometrika 1996, 83, 299–313. [Google Scholar]
- Hartigan, J. The maximum likelihood prior. Ann. Stat 1998, 26, 2083–2103. [Google Scholar]
- Bernardo, J. Reference posterior distributions for Bayesian inference. J. R. Stat. Soc. B 1979, 41, 113–147. [Google Scholar]
- Clarke, B.; Barron, A. Jeffreys prior is asymptotically least favorable under entropy risk. J. Stat. Plan. Inference 1994, 41, 37–60. [Google Scholar]
- Aslan, M. Asymptotically minimax Bayes predictive densities. Ann. Stat 2006, 34, 2921–2938. [Google Scholar]
- Komaki, F. Bayesian predictive densities based on latent information priors. J. Stat. Plan. Inference 2011, 141, 3705–3715. [Google Scholar]
- Komaki, F. Asymptotically minimax Bayesian predictive densities for multinomial models. Electron. J. Stat 2012, 6, 934–957. [Google Scholar]
- Kanamori, T.; Shimodaira, H. Active learning algorithm using the maximum weighted log-likelihood estimator. J. Stat. Plan. Inference 2003, 116, 149–162. [Google Scholar]
- Shimodaira, H. Improving predictive inference under covariate shift by weighting the log-likelihood function. J. Stat. Plan. Inference 2000, 90, 227–244. [Google Scholar]
- Fushiki, T.; Komaki, F.; Aihara, K. On parametric bootstrapping and Bayesian prediction. Scand. J. Stat 2004, 31, 403–416. [Google Scholar]
- Suzuki, T.; Komaki, F. On prior selection and covariate shift of β-Bayesian prediction under α-divergence risk. Commun. Stat. Theory 2010, 39, 1655–1673. [Google Scholar]
- Komaki, F. Asymptotic properties of Bayesian predictive densities when the distributions of data and target variables are different. Bayesian Anal 2014. submitted for publication. [Google Scholar]
- Hodges, J.L.; Lehmann, E.L. Some problems in minimax point estimation. Ann. Math. Stat 1950, 21, 182–197. [Google Scholar]
- Ghosh, M.N. Uniform approximation of minimax point estimates. Ann. Math. Stat 1964, 35, 1031–1047. [Google Scholar]
- Amari, S. Differential-Geometrical Methods in Statistics; Springer: New York, NY, USA, 1985. [Google Scholar]
- Robbins, H. Asymptotically Subminimax solutions of Compound Statistical Decision Problems, Proceedings of the Second Berkley Symposium Mathematical Statistics and Probability, Berkeley, CA, USA, 31 July–12 August 1950; University of California Press: Oakland, CA, USA, 1950; pp. 131–148.
- Frank, P.; Kiefer, J. Almost subminimax and biased minimax procedures. Ann. Math. Stat 1951, 22, 465–468. [Google Scholar]
- Efron, B. Defining curvature of a statistical problem (with applications to second order efficiency). Ann. Stat 1975, 3, 189–1372. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yano, K.; Komaki, F. Asymptotically Constant-Risk Predictive Densities When the Distributions of Data and Target Variables Are Different. Entropy 2014, 16, 3026-3048. https://doi.org/10.3390/e16063026
Yano K, Komaki F. Asymptotically Constant-Risk Predictive Densities When the Distributions of Data and Target Variables Are Different. Entropy. 2014; 16(6):3026-3048. https://doi.org/10.3390/e16063026
Chicago/Turabian StyleYano, Keisuke, and Fumiyasu Komaki. 2014. "Asymptotically Constant-Risk Predictive Densities When the Distributions of Data and Target Variables Are Different" Entropy 16, no. 6: 3026-3048. https://doi.org/10.3390/e16063026



