Tsallis Wavelet Entropy and Its Application in Power Signal Analysis
Abstract
:1. Introduction
2. SWEE and Its Theoretical Defects
2.1. The Definition of SWEE
2.2. The Theoretical Defects of SWEE
3. Research on Issue in SWEE
3.1. Energy Leakage and Wavelet Aliasing
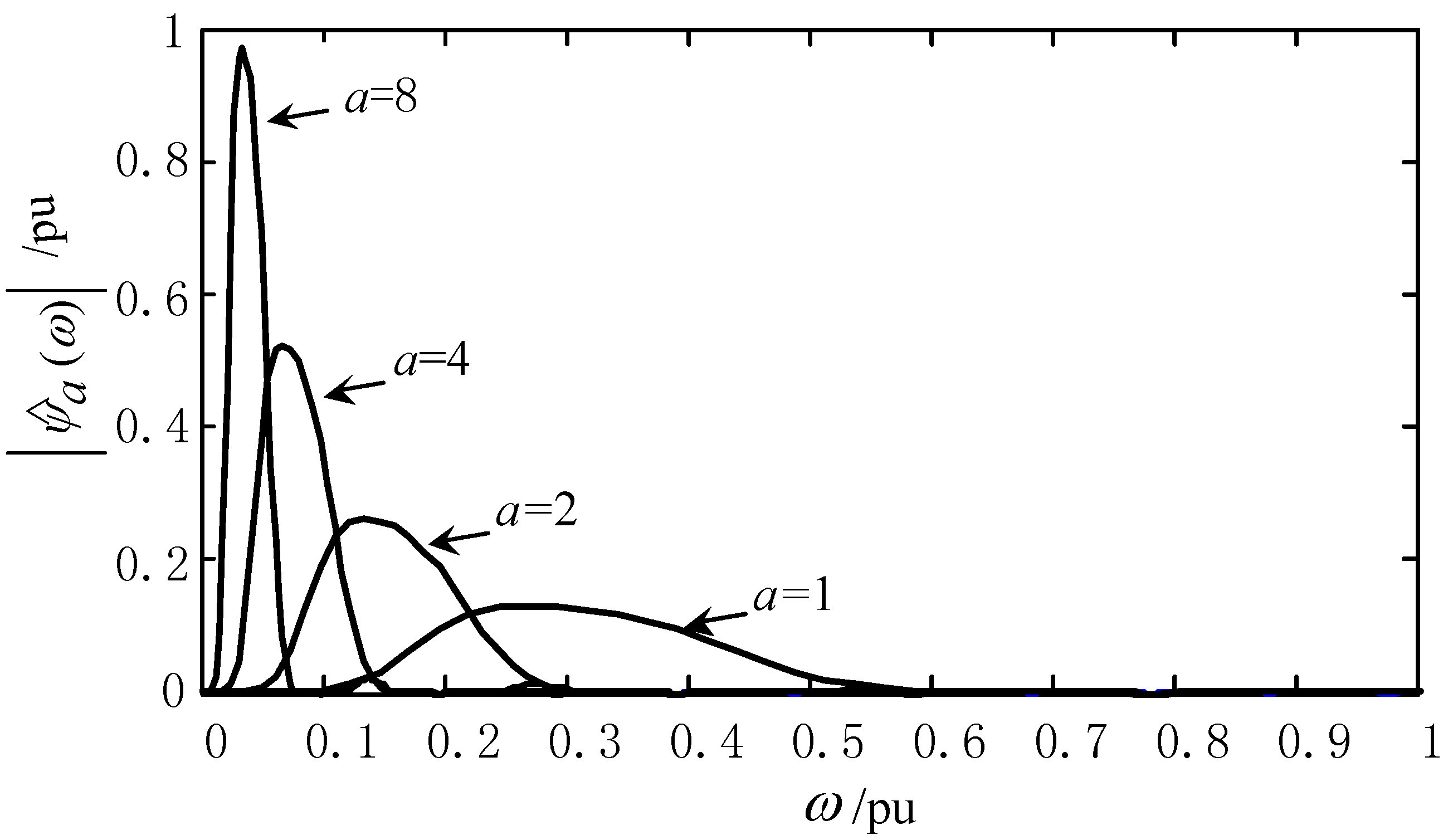
3.2. The Negative Effect of Wavelet Aliasing on SWEE
- (1)
- As ,
- (2)
- As ,
- (a)
- if , with increasing value of , it is found that , is greater than , which means that is greater than .
- (b)
- if , with increasing value of , it is found that , is greater than , which means that is less than .
4. Tsallis Wavelet Energy Entropy—The Development of SWEE
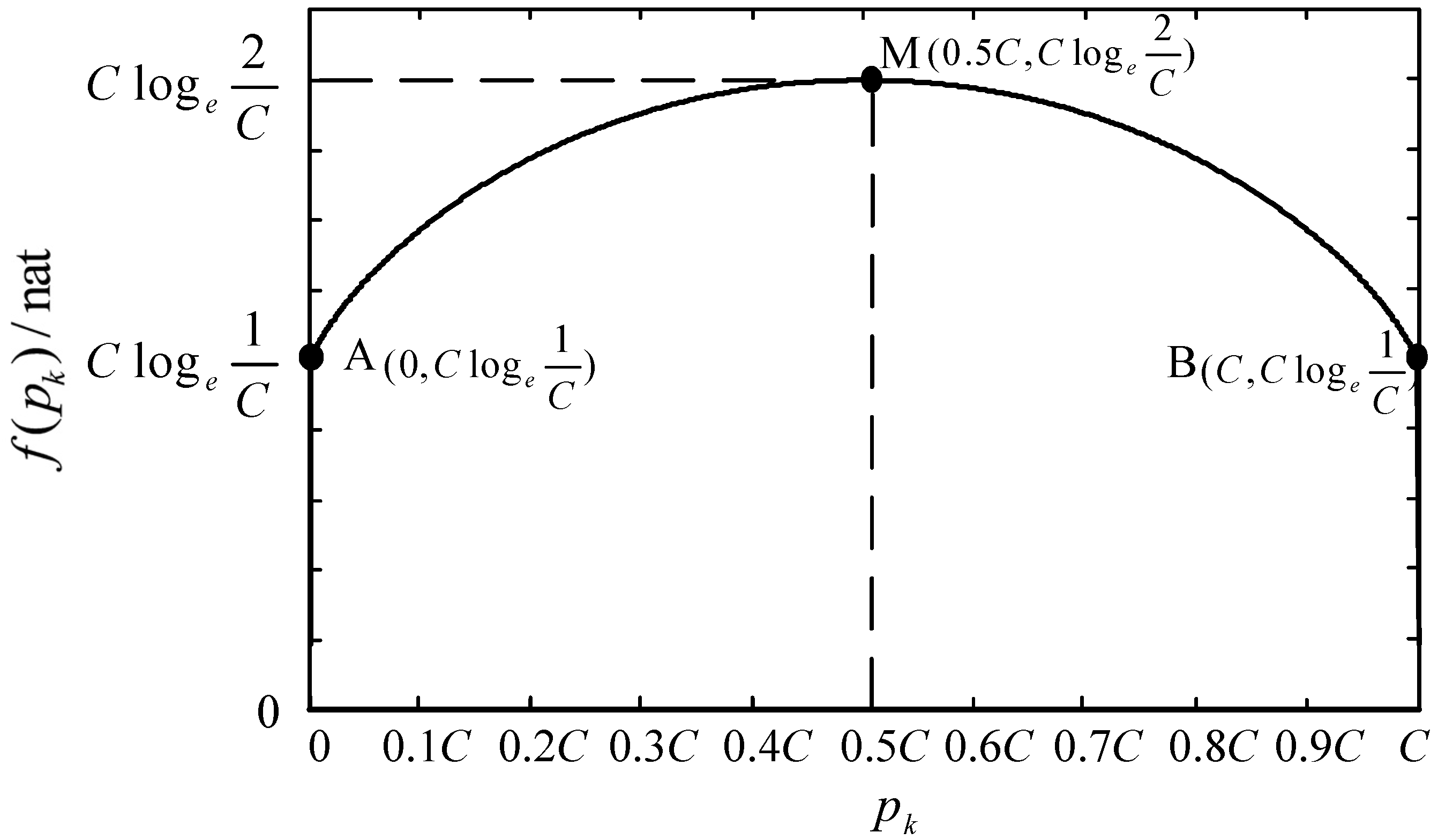
4.1. Tsallis Entropy
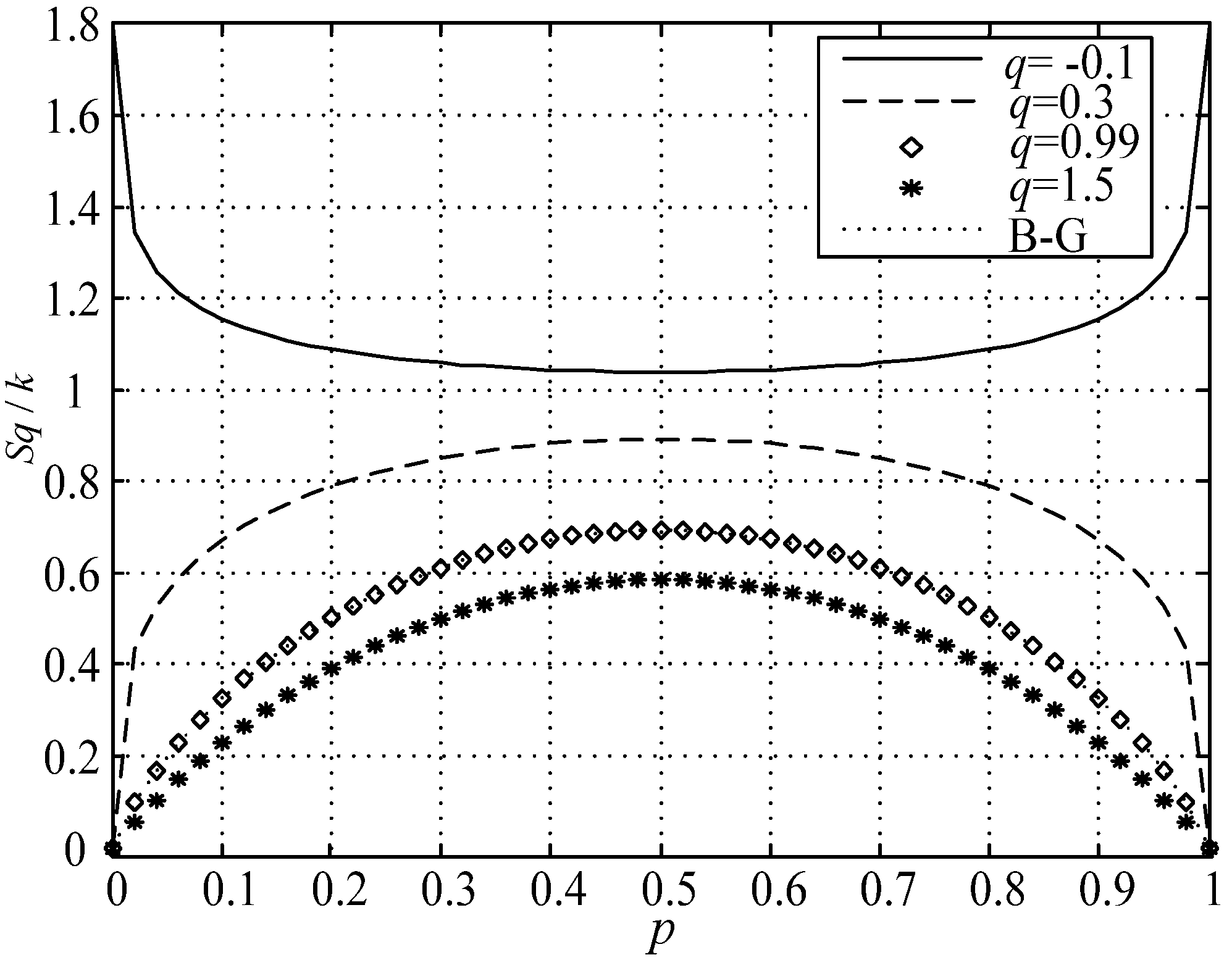
4.2. The Definition of TWEE
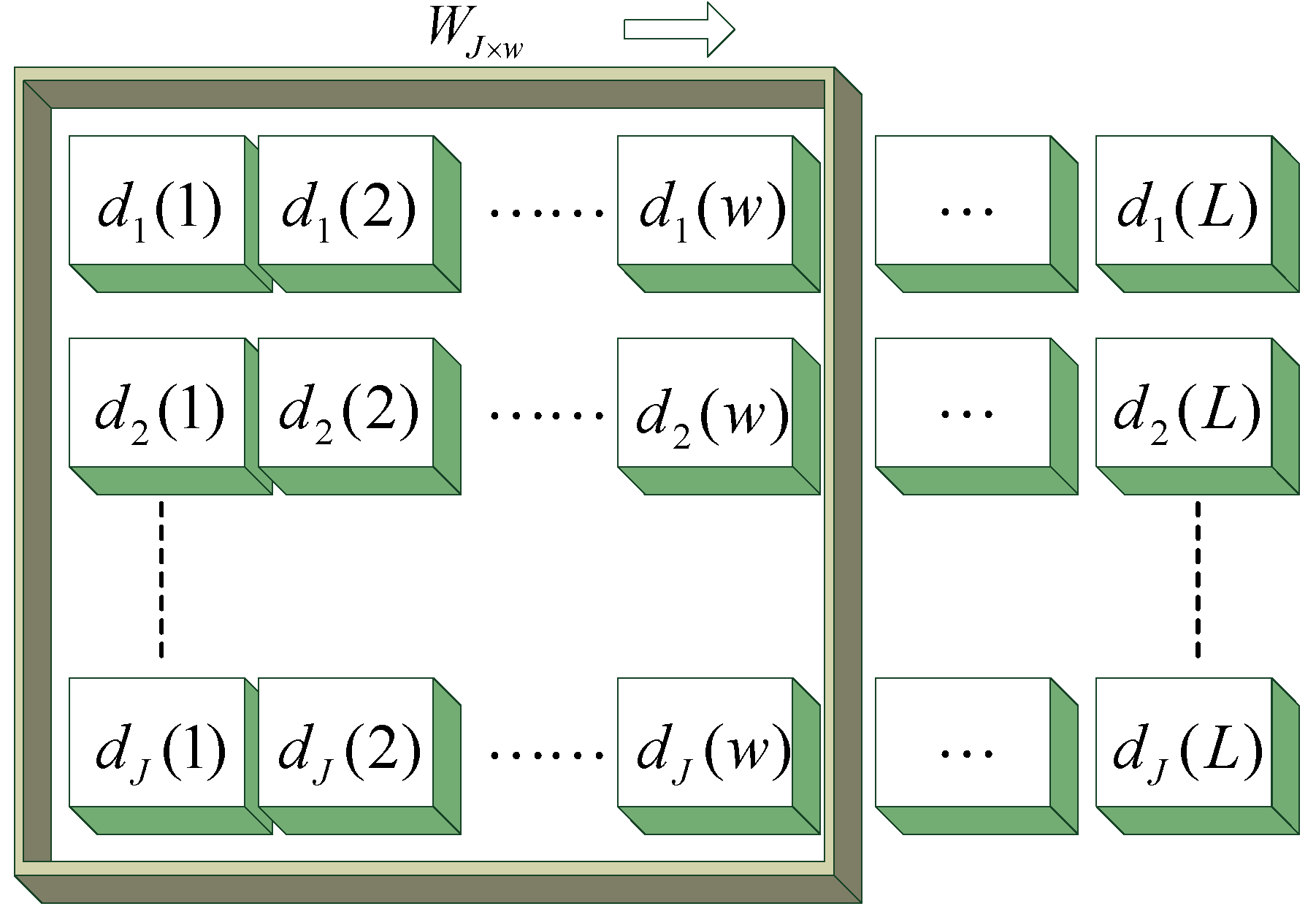
4.3. The Inhibition on Wavelet Aliasing Using TWEE
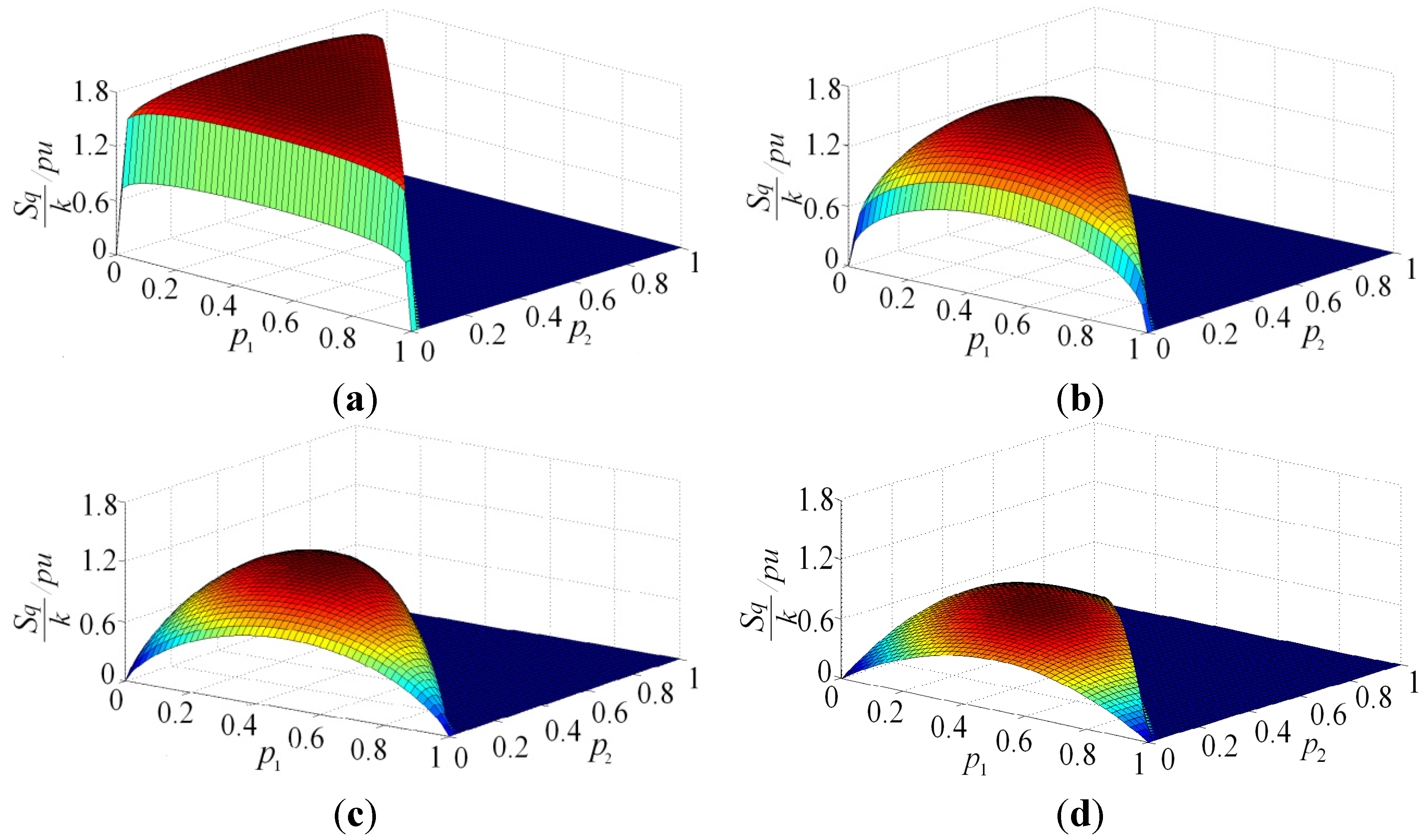

5. TWEE’s Application in Signal Analysis in Power System
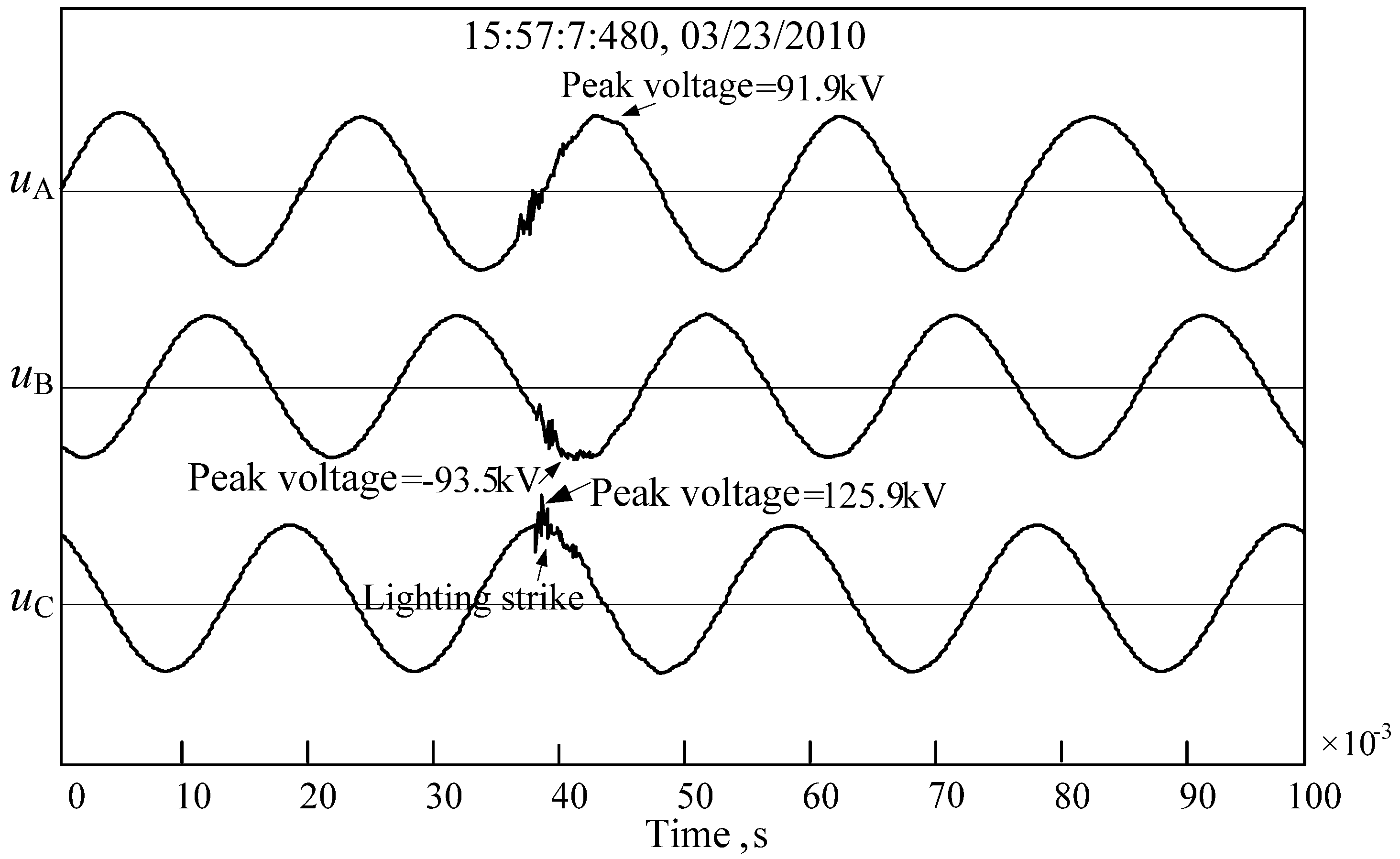
5.1. Original Transient Power Signal
- Fault line: the 110 kV Jiaji transmission line in Guangdong.
- Fault type: lightning strike interference.
- Recording site: the 110 kV side of main transformer of 220 kV Jiahe substation.
- Occurrence time: 15:57:7:480, 23 March 2010.
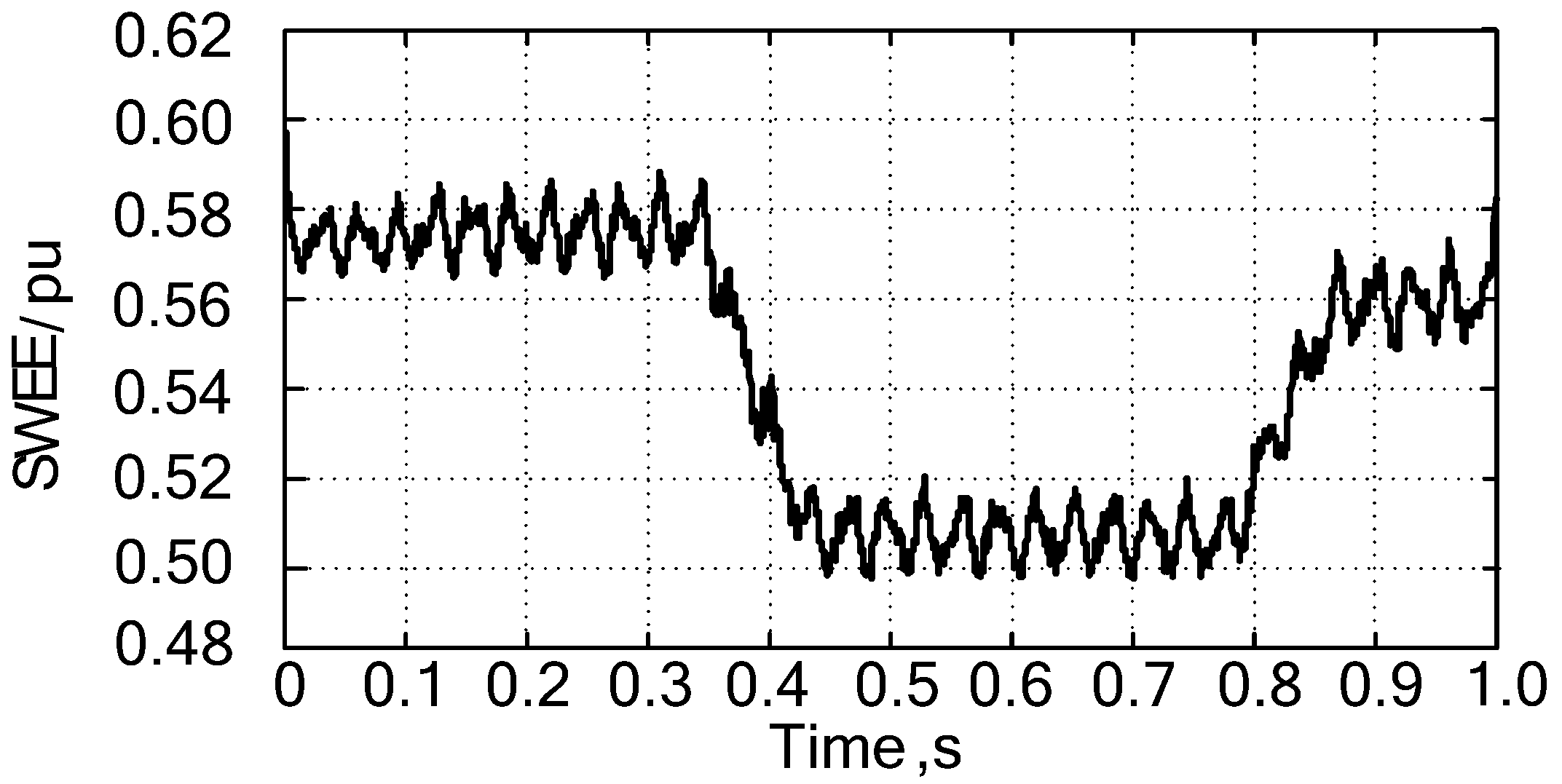
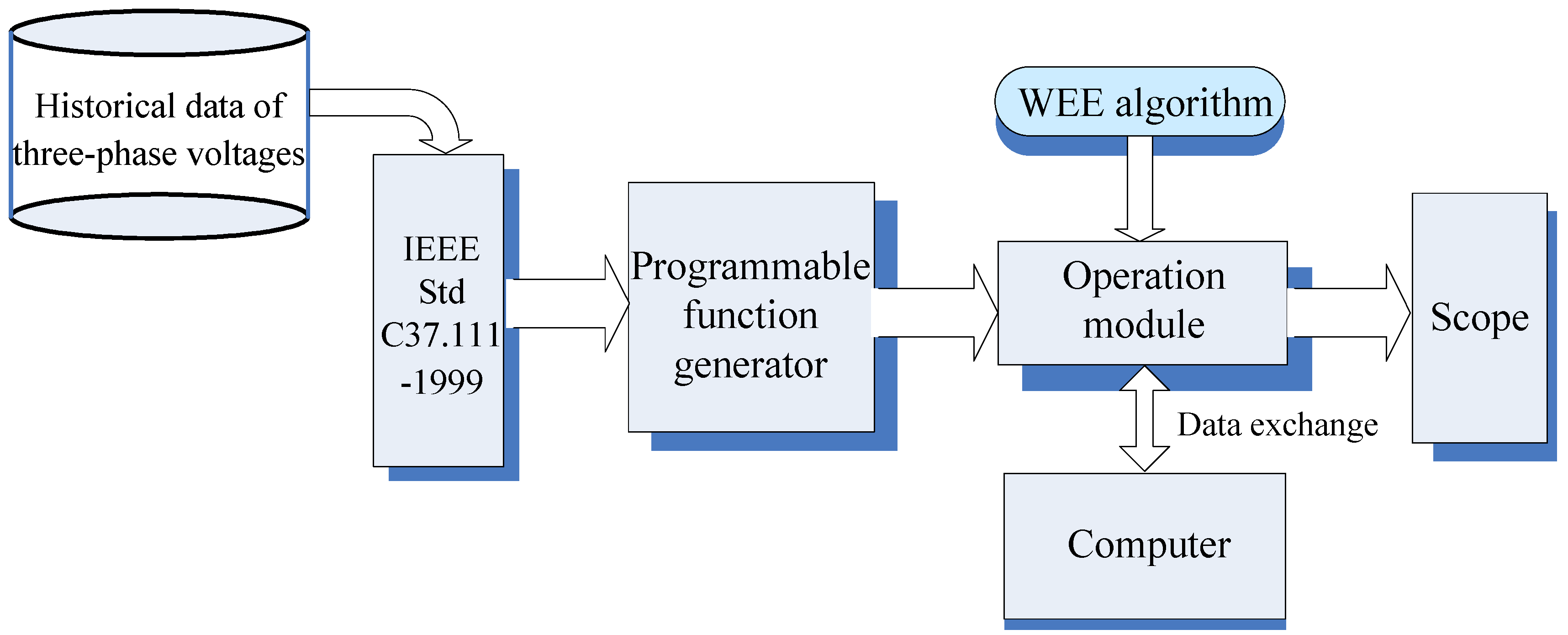
5.2. The Results of Feature Extraction Using Two WEE Algorithm
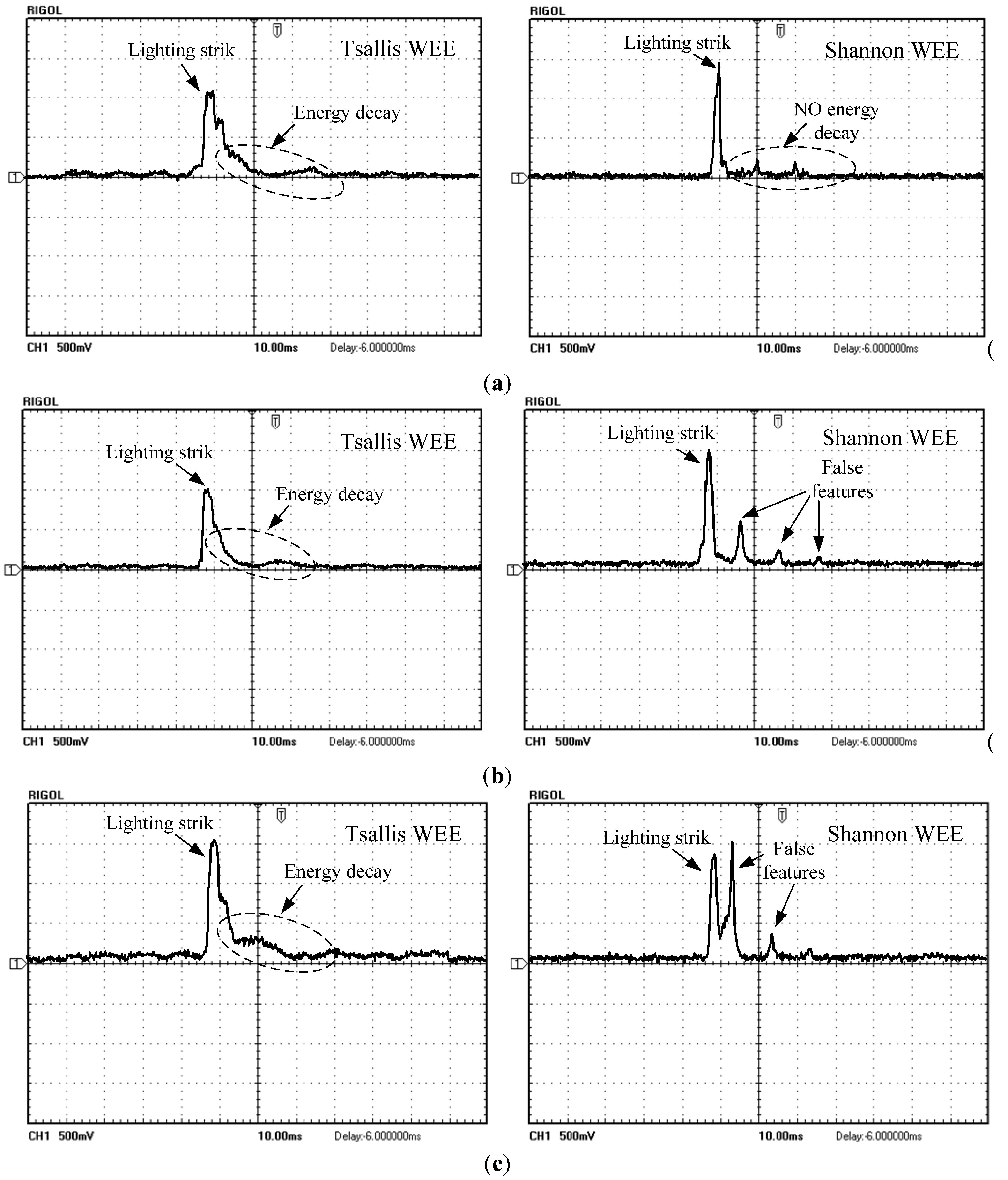
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Quiroga, R.Q.; Rosso, O.A.; Basar, E.; Schürmann, M. Wavelet entropy in event-related potentials: A new method shows ordering of EEG oscillations. Biol. Cybern. 2001, 84, 291–299. [Google Scholar]
- AlNashash, H.A.; Thakor, N.V. Monitoring of global cerebral ischemia using wavelet entropy rate of change. IEEE Trans. Biomed. Eng. 2005, 52, 2119–2122. [Google Scholar]
- Cek, M.E.; Ozgoren, M.; Savaci, F.A. Continuous time wavelet entropy of auditory evoked potentials. Comput. Biol. Med. 2010, 40, 90–96. [Google Scholar] [CrossRef] [PubMed]
- Brunsell, N.A. A multiscale information theory approach to assess spatial-temporal variability of daily precipitation. J. Hydrol. 2010, 385, 165–172. [Google Scholar] [CrossRef]
- Chou, C.M. Wavelet-based multi-scale entropy analysis of complex rainfall time series. Entropy 2011, 13, 241–253. [Google Scholar] [CrossRef]
- Sang, Y.-F.; Wang, Z.-G.; Li, Z.-L. Discrete wavelet entropy aided detection of abrupt change: A case study in the Haihe river basin, China. Entropy 2012, 14, 1274–1284. [Google Scholar] [CrossRef]
- Zarjam, P.; Epps, J.; Chen, F.; Lovell, N.H. Estimating cognitive workload using wavelet entropy-based features during an arithmetic task. Comput. Biol. Med. 2013, 43, 2186–2195. [Google Scholar]
- Yu, B.; Liu, D.; Zhang, T. Fault diagnosis for micro-Gas turbine engine sensors via wavelet entropy. Sensors 2011, 11, 9928–9941. [Google Scholar] [CrossRef] [PubMed]
- He, Z.Y.; Cai, Y.M.; Qian, Q.Q. A study of wavelet entropy theory and its application in electric power system fault detection. Proc. Chin. Soc. Electr. Eng. 2005, 25, 38–43. [Google Scholar]
- He, Z.Y.; Chen, X.Q.; Luo, G.M. Wavelet entropy measure definition and its application for transmission line fault detection and identification. In Proceedings of the International Conference on Power System Technology, Chongqing, China, 22–26 October 2006.
- Hnizdo, V.; Gilson, M.K. Thermodynamic and differential entropy under a change of variables. Entropy 2010, 12, 578–590. [Google Scholar] [CrossRef]
- Baez, J.C.; Fritz, T.; Leinster, T. A characterization of entropy in terms of information loss. Entropy 2011, 13, 1945–1957. [Google Scholar] [CrossRef]
- Wang, A. Nonextensive Statistics and Incomplete Information. Eur. Phys. J. B 2002, 26, 357–368. [Google Scholar]
- Tsallis, C. Possible Generalization of Boltzmann-Gibbs Statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar]
- Huang, Z.F.; Ou, C.J.; Chen, J.C. Incomplete nonextensive statistics and the zeroth law of thermodynamics. Chin. Phys. B 2013, 22, 040501:1–040501:4. [Google Scholar]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Phys. A 1998, 261, 534–554. [Google Scholar]
- Martins, A.; Aguiar, P.; Figueiredo, M. Tsallis Kernels on Measures. In Proceedings of the IEEE Information Theory Workshop, Porto, Portugal, 5–9 May 2008.
- Sneddon, R. The Tsallis entropy of natural information. Phys. A 2007, 386, 101–118. [Google Scholar]
- Heidler, F.; Cvetic, J.M.; Stanic, B.V. Calculation of lightning current parameters. IEEE Trans. Power Deliv. 1999, 14, 399–404. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, J.; Li, G. Tsallis Wavelet Entropy and Its Application in Power Signal Analysis. Entropy 2014, 16, 3009-3025. https://doi.org/10.3390/e16063009
Chen J, Li G. Tsallis Wavelet Entropy and Its Application in Power Signal Analysis. Entropy. 2014; 16(6):3009-3025. https://doi.org/10.3390/e16063009
Chicago/Turabian StyleChen, Jikai, and Guoqing Li. 2014. "Tsallis Wavelet Entropy and Its Application in Power Signal Analysis" Entropy 16, no. 6: 3009-3025. https://doi.org/10.3390/e16063009
APA StyleChen, J., & Li, G. (2014). Tsallis Wavelet Entropy and Its Application in Power Signal Analysis. Entropy, 16(6), 3009-3025. https://doi.org/10.3390/e16063009



