Matrix Algebraic Properties of the Fisher Information Matrix of Stationary Processes
Abstract
: In this survey paper, a summary of results which are to be found in a series of papers, is presented. The subject of interest is focused on matrix algebraic properties of the Fisher information matrix (FIM) of stationary processes. The FIM is an ingredient of the Cramér-Rao inequality, and belongs to the basics of asymptotic estimation theory in mathematical statistics. The FIM is interconnected with the Sylvester, Bezout and tensor Sylvester matrices. Through these interconnections it is shown that the FIM of scalar and multiple stationary processes fulfill the resultant matrix property. A statistical distance measure involving entries of the FIM is presented. In quantum information, a different statistical distance measure is set forth. It is related to the Fisher information but where the information about one parameter in a particular measurement procedure is considered. The FIM of scalar stationary processes is also interconnected to the solutions of appropriate Stein equations, conditions for the FIM to verify certain Stein equations are formulated. The presence of Vandermonde matrices is also emphasized.MSC Classification: 15A23, 15A24, 15B99, 60G10, 62B10, 62M20.1. Introduction
In this survey paper, a summary of results derived and described in a series of papers, is presented. It concerns some matrix algebraic properties of the Fisher information matrix (abbreviated as FIM) of stationary processes. An essential property emphasized in this paper concerns the matrix resultant property of the FIM of stationary processes. To be more explicit, consider the coefficients of two monic polynomials p(z) and q(z) of finite degree, as the entries of a matrix such that the matrix becomes singular if and only if the polynomials p(z) and q(z) have at least one common root. Such a matrix is called a resultant matrix and its determinant is called the resultant. The Sylvester, Bezout and tensor Sylvester matrices have such a property and are extensively studied in the literature, see e.g., [1–3]. The FIM associated with various stationary processes will be expressed by these matrices. The derived interconnections are obtained by developing the necessary factorizations of the FIM in terms of the Sylvester, Bezout and tensor Sylvester matrices. These factored forms of the FIM enable us to show that the FIM of scalar and multiple stationary processes fulfill the resultant matrix property. Consequently, the singularity conditions of the appropriate Fisher information matrices and Sylvester, Bezout and tensor Sylvester matrices coincide, these results are described in [4–6].
A statistical distance measure involving entries of the FIM is presented and is based on [7]. In quantum information, a statistical distance measure is set forth, see [8–10], and is related to the Fisher information but where the information about one parameter in a particular measurement procedure is considered. This leads to a challenging question that can be presented as, can the existing distance measure in quantum information be developed at the matrix level?
The matrix Stein equation, see e.g., [11], is associated with the Fisher information matrices of scalar stationary processes through the solutions of the appropriate Stein equations. Conditions for the Fisher information matrices or associated matrices to verify certain Stein equations are formulated and proved in this paper. The presence of Vandermonde matrices is also emphasized. The general and more detailed results are set forth in [12] and [13]. In this survey paper it is shown that the FIM of linear stationary processes form a class of structured matrices. Note that in [14], the authors emphasize that statistical problems related to stationary processes have been treated successfully with the aid of Toeplitz forms. This paper is organized as follows. The various stationary processes, considered in this paper, are presented in Section 2, the Fisher information matrices of the stationary processes are displayed in Section 3. Section 3 sets forth the interconnections between the Fisher information matrices and the Sylvester, Bezout, tensor Sylvester matrices, and solutions to Stein equations. A statistical distance measure is expressed in terms of entries of a FIM.
2. The Linear Stationary Processes
In this section we display the class of linear stationary processes whose corresponding Fisher information matrix shall be investigated in a matrix algebraic context. But first some basic definitions are set forth, see e.g., [15].
If a random variable X is indexed to time, usually denoted by t, the observations {Xt, t ∈



Definition 2.1
A stochastic process is a family of random variables {Xt, t ∈

Definition 2.2
The Autocovariance function. If {Xt, t ∈





Definition 2.3
Stationarity. The time series {Xt, t ∈ ℤ}, with the index set ℤ ={0,±}1,±}2, . . .}, is said to be stationary if
- (i)
|Xt|2 < ∞
- (ii)
(Xt) = m for all t ∈ ℤ, m is the constant average or mean
- (iii)
γX (r, s) = γX (r + t, s + t) for all r, s, t ∈ ℤ,
From Definition 2.3 can be concluded that the joint probability distributions of the random variables {X1, X2, . . . Xtn} and {X1+k, X2+k, . . . Xtn+k} are the same for arbitrary times t1, t2, . . . , tn for all n and all lags or leads k = 0, ±}1, ±}2, . . .. The probability distribution of observations of a stationary process is invariant with respect to shifts in time. In the next section the linear stationary processes that will be considered throughout this paper are presented.
2.1. The Vector ARMAX or VARMAX Process
We display one of the most general linear stationary process called the multivariate autoregressive, moving average and exogenous process, the VARMAX process. To be more specific, consider the vector difference equation representation of a linear system {y(t), t ∈ ℤ}, of order (p, r, q),
where y(t) are the observable outputs, x(t) the observable inputs and ɛ(t) the unobservable errors, all are n-dimensional. The acronym VARMAX stands for vector autoregressive-moving average with exogenous variables. The left side of (1) is the autoregressive part the second term on the right is the moving average part and x(t) is exogenous. If x(t) does not occur the system is said to be (V)ARMA. Next to exogenous, the input x(t) is also named the control variable, depending on the field of application, in econometrics and time series analysis, e.g., [15], and in signal processing and control, e.g., [16,17]. The matrix coefficients, Aj ∈ ℝn×n, Cj ∈ ℝn×n, and Bj ∈ ℝn×n are the associate parameter matrices. We have the property A0 ≡ B0 ≡ C0 ≡ In.
Equation (1) can compactly be written as
where
we use z to denote the backward shift operator, for example z xt = xt−1. The matrix polynomials A(z), B(z) and C(z) are the associated autoregressive, moving average matrix polynomials, and the exogenous matrix polynomial respectively of order p, q and r respectively. Hence the process described by Equation (2) is denoted as a VARMAX(p, r, q) process. Here z ∈ ℂ with a duplicate use of z as an operator and as a complex variable, which is usual in the signal processing and time series literature, e.g., [15,16,18]. The assumptions Det(A(z)) ≠ 0, such that |z| ≤ 1 and Det(B(z)) ≠ 0, such that |z| < 1 for all z ∈ ℂ, is imposed so that the VARMAX(p, r, q) process (2) has exactly one stationary solution and the condition Det(B(z)) ≠ 0 implies the invertibility condition, see e.g., [15] for more details. Under these assumptions, the eigenvalues of the matrix polynomials A(z) and B(z) lie outside the unit circle. The eigenvalues of a matrix polynomial Y (z) are the roots of the equation Det(Y (z)) = 0, Det(X) is the determinant of X. The VARMAX(p, r, q) stationary process (2) is thoroughly discussed in [15,18,19].
The error {ɛ(t), t ∈ ℤ} is a collection of uncorrelated zero mean n-dimensional random variables each having positive definite covariance matrix ∑ and we assume, for all s, t,
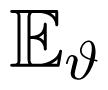
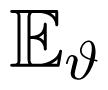
The vec operator transforms a matrix into a vector by stacking the columns of the matrix one underneath the other according to vec , see e.g., [2,20]. A different choice is set forth, when the parameter matrix ϑ ∈ ℝn×n(p+q+r) is of the form
Representation (5) of the parameter matrix has been used in [21]. The estimation of the matrices A1, A2,. . ., Ap, C1, C2,. . ., Cr, B1, B2, . . ., Bq and ∑ has received considerable attention in the time series and statistical signal processing literature, see e.g., [15,17,19]. In [19], the authors study the asymptotic properties of maximum likelihood estimates of the coefficients of VARMAX(p, r, q) processes, stored in a (ℓ × 1) vector ϑ, where ℓ = n2(p + q + r).
Before describing the control-exogenous variable x(t) used in this survey paper, we shall present the different special cases of the model described in Equations (1) and (2).
2.2. The Vector ARMA or VARMA Process
When the process (2) does not contain the control process x(t) it yields
which is a vector autoregressive and moving average process, VARMA(p, q) process, see e.g., [15]. The matrix ϑ represents now all the VARMA parameters, with the total number of parameters being n2(p+q). The VARMA(p, q) version of the parameter vector ϑ defined in (3) is then given by
A VARMA process equivalent to the parameter matrix (4) is then the n × n(p + q) parameter matrix
A description of the input variable x(t), in Equation (2) follows. Generally, one can assume either that x(t) is non stochastic or that x(t) is stochastic. In the latter case, we assume
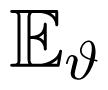
where α(z) and β(z) are the autoregressive and moving average polynomials of appropriate degree and {η(t), t ∈ ℤ} is a collection of uncorrelated zero mean n-dimensional random variables each having positive definite covariance matrix Ω. The spectral density of the VARMA process x(t) is Rx(·)/2π and for a definition, see e.g., [15,16], to obtain
where i is the imaginary unit with the property i2 = −1, ω is the frequency, the spectral density Rx(eiω) is Hermitian, and we further have, Rx(eiω) ≥ 0 and . As mentioned above, the basic assumption, x(t) and ɛ(t) are independent or at least uncorrelated processes, which corresponds geometrically with orthogonal processes, holds and X* is the complex conjugate transpose of matrix X.
2.3. The ARMAX and ARMA Processes
The scalar equivalent to the VARMAX(p, r, q) and VARMA(p, q) processes, given by Equations (2) and (6) respectively, shall now be displayed, to obtain for the ARMAX(p, r, q) process
and for the ARMA(p, q) process
popularized in, among others, the Box-Jenkins type of time series analysis, see e.g., [15]. Where a(z), b(z) and c(z) are respectively the scalar autoregressive, moving average polynomials and exogenous polynomial, with corresponding scalar coefficients aj, bj and cj,
Note that as in the multiple case, a0 = b0 = 1. The parameter vector, ϑ, for the processes, Equations (11) and (12) is then
and
respectively.
In the next section the matrix algebraic properties of the Fisher information matrix of the stationary processes (2), (6), (11) and (12) will be verified. Interconnections with various known structured matrices like the Sylvester resultant matrix, the Bezout matrix and Vandermonde matrix are set forth. The Fisher information matrix of the various stationary processes is also expressed in terms of the unique solutions to the appropriate Stein equations.
3. Structured Matrix Properties of the Asymptotic Fisher Information Matrix of Stationary Processes
The Fisher information is an ingredient of the Cramér-Rao inequality, also called by some the Cauchy-Schwarz inequality in mathematical statistics, and belongs to the basics of asymptotic estimation theory in mathematical statistics. The Cramér-Rao theorem [24] is therefore considered. When assuming that the estimators of ϑ, defined in the previuos sections, are asymptotically unbiased, the inverse of the asymptotic information matrix yields the Cramér-Rao bound, and provided that the estimators are asymptotically efficient, the asymptotic covariance matrix then verifies the inequality
here (ϑ̂) is the FIM, Cov (ϑ̂) is the covariance of ϑ̂, the unbiased estimator of ϑ, for a detailed fundamental statistical analysis, see [25,26]. The FIM equals the Cramér-Rao lower bound, and the subject of the FIM is also of interest in the control theory and signal processing literature, see e.g., [27]. Its quantum analog was introduced immediately after the foundation of mathematical quantum estimation theory in the 1960’s, see [28,29] for a rigorous exposition of the subject. More specifically, the Fisher information is also emphasized in the context of quantum information theory, see e.g., [30,31]. It is clear that the Cramér-Rao inequality takes a lot of attention because it is located on the highly exciting boundary of statistics, information and quantum theory and more recently matrix theory. In the next sections, the Fisher information matrices of linear stationary processes will be presented and its role as a new class of structured matrices will be the subject of study.
When time series models are the subject, using Equation (2) for all t ∈ ℤ to determine the residual ɛ(t) or ɛt(ϑ), to emphasize the dependency on the parameter vector ϑ, and assuming that x(t) is stochastic and that (y(t), x(t)) is a Gaussian stationary process, the asymptotic FIM (ϑ) is defined by the following (ℓ × ℓ) matrix which does not depend on t
where the (v × ℓ) matrix ∂(·)/∂ϑ T, the derivative with respect to ϑ T, for any (v × 1) column vector (·) and ℓ is the total number of parameters. The derivative with respect to ϑ T is used for obtaining the appropriate dimensions. Equality (16) is used for computing the FIM of the various time series processes presented in the previous sections and appropriate definitions of the derivatives are used, especially for the multivariate processes (2) and (6), see [21,22].
3.1. The Fisher Information Matrix of an ARMA(p, q) Process
In this section, the focus is on the FIM of the ARMA process (12). When ϑ is given in Equation (15), the derivatives in Equation (16) are at the scalar level
when combined for all j and k, the FIM of the ARMA process (12) with the variance of the noise process ɛt(ϑ) equal to one, yields the block decomposition, see [32]
The expressions of the different blocks of the matrix (ϑ) are
where the integration above and everywhere below is counterclockwise around the unit circle. The reciprocal monic polynomials â(z) and b̂(z) are defined as â(z) = zpa(z−1) and b̂ (z) = zqb(z−1) and ϑ =(a1, . . . , ap, b1, . . . , bq) T introduced in (15). For each positive integer k we have uk(z) = (1, z, z2, . . . , zk−1) T and vk(z) = zk−1uk(z−1). Considering the stability condition of the ARMA(p, q) process implies that all the roots of the monic polynomials a(z) and b(z) lie outside the unit circle. Consequently, the roots of the polynomials â(z) and b̂(z) lie within the unit circle and will be used as the poles for computing the integrals (18)–(21) when Cauchy’s residue theorem is applied. Notice that the FIM (ϑ) is symmetric block Toeplitz so that and the integrands in (18)–(21) are Hermitian. The computation of the integral expressions, (18)–(21) is easily implementable by using the standard residue theorem. The algorithms displayed in [33] and [22] are suited for numerical computations of among others the FIM of an ARMA(p, q) process.
3.2. The Sylvester Resultant Matrix - The Fisher Information Matrix
The resultant property of a matrix is considered, in order to show that the FIM (ϑ) has the matrix resultant property implies to show that the matrix (ϑ) becomes singular if and only if the appropriate scalar monic polynomials â(z) and b̂(z) have at least one common zero. To illustrate the subject, the following known property of two polynomials is set forth. The greatest common divisor (frequently abbreviated as GCD) of two polynomials is a polynomial, of the highest possible degree, that is a factor of both the two original polynomials, the roots of the GCD of two polynomials are the common roots of the two polynomials. Consider the coefficients of two monic polynomials p(z) and q(z) of finite degree, as the entries of a matrix such that the matrix becomes singular if and only if the polynomials p(z) and q(z) have at least one common root. Such a matrix is called a resultant matrix and its determinant is called the resultant. Therefore we present the known (p + q) × (p + q) Sylvester resultant matrix of the polynomials a and b, see e.g., [2], to obtain
Consider the q ×(p+q) and p×(p+q) upper and lower submatrices
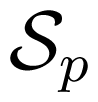
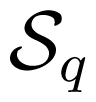
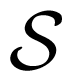
The matrix
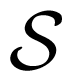
and
where (a, b) is the resultant of â(z) and b̂(z), and is equal to Det
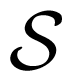
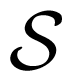
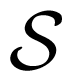
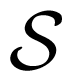
where ν(a, b) is the number of common roots of the polynomials â(z) and b̂(z), with counting multiplicities, see e.g., [3]. The dimension of a subspace


In order to prove that the FIM (ϑ) fulfills the resultant matrix property, the following factorization is derived, Lemma 2.1 in [5],
where the matrix ℘(ϑ) ∈ ℝ(p+q)×(p+q) admits the form
It is proved in [5] that the symmetric matrix ℘(ϑ) fulfills the property, ℘(ϑ) ≻ O. The factorization (27) allows us to show the matrix resultant property of the FIM, Corollary 2.2 in [5] states.
The FIM of an ARMA(p, q) process with polynomials a(z) and b(z) of order p, q respectively becomes singular if and only if the polynomials â(z) and b̂(z) have at least one common root. From Corollary 2.2 in [5] can be concluded, the FIM of an ARMA(p, q) process and the Sylvester resultant matrix
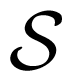
Lemma 3.1
Assume that the polynomials â(z) and b̂(z) have ν(a, b) common roots, counting multiplicities. The factorization (27) of the FIM and the property (26) enable us to prove the equality
Proof
The matrix ℘(ϑ) ∈ ℝ(p+q)×(p+q), given in (27), fulfills the property of positive definiteness, as proved in [5]. This implies that a Cholesky decomposition can be applied to ℘(ϑ), see [35] for more details, to obtain ℘(ϑ) =LT(ϑ)L(ϑ), where L(ϑ) is a ℝ(p+q)×(p+q) upper triangular matrix that is unique if its diagonal elements are all positive. Consequently, all its eigenvalues are then positive so that the matrix L(ϑ) is also positive definite. Factorization of (27) now admits the representation
and taking the property, if A is an m× n matrix, then Ker (A) = Ker (ATA), into account, yields when applied to (30)
Assume the vector u ∈ Ker L(ϑ)





We will now consider the Rank-Nullity Theorem, see e.g., [1], if A is an m × n matrix, then
and the property dim (Im A) = dim (Im AT). When applied to the (p + q) × (p + q) matrix
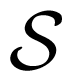
which completes the proof.
Notice that the dimension of the null space of matrix A is called the nullity of A and the dimension of the image of matrix A, dim (Im A), is termed the rank of matrix A. An alternative proof to the one developed in Corollary 2.2 in [5], is given in a corollary to Lemma 3.1, reconfirming the resultant matrix property of the FIM (ϑ).
Corollary 3.2
The FIM (ϑ) of an ARMA(p, q) process becomes singular if and only if the autoregressive and moving average polynomials â(z) and b̂(z) have at least one common root.
Proof
By virtue of the equality (31) combining with the property Det

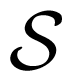
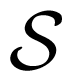





3.3. The Statistical Distance Measure and the Fisher Information Matrix
In [7] statistical distance measures are studied. Most multivariate statistical techniques are based upon the concept of distance. For that purpose a statistical distance measure is considered that is a normalized Euclidean distance measure with entries of the FIM as weighting coefficients. The measurements x1, x2,. . . , xn are subject to random fluctuations of different magnitudes and have therefore different variabilities. It is then important to consider a distance that takes the variability of these variables or measurements into account when determining its distance from a fix point. A rotation of the coordinate system through a chosen angle while keeping the scatter of points given by the data fixed, is also applied, see [7] for more details. It is shown that when the FIM is positive definite, the appropriate statistical distance measure is a metric. In case of a singular FIM of an ARMA stationary process, the metric property depends on the rotation angle. The statistical distance measure, is based on m parameters unlike a statistical distance measure introduced in quantum information, see e.g., [8,9], that is also related to the Fisher information but where the information about one parameter in a particular measurement procedure is considered.
The straight-line or Euclidean distance between the stochastic vector and fixed vector where x, y ∈ ℝn, is given by
where the metric d(x, y):= ||x−y|| is induced by the standard Euclidean norm || · || on ℝn, see e.g., [2] for the metric conditions.
The observations x1, x2, . . . , xn are used to compute maximum likelihood estimated of the parameters ϑ1, ϑ2, . . . , ϑm and where m < n. These estimated parameters are random variables, see e.g., [15]. The distance of the estimated vector ϑ ∈ ℝm, given in (15), is studied. Entries of the FIM are inserted in the distance measure as weighting coefficients. The linear transformation
is applied, where i(φ) ∈ ℝm×n is the Givens rotation matrix with rotation angle φ, with 0 ≤ φ ≤ 2π and i ∈ {1, . . . , m − 1}, see e.g., [36], and is given by
The following matrix decomposition is applied in order to obtain a transformed FIM
where φ(ϑ) and (ϑ) are respectively the transformed and untransformed Fisher information matrices. It is straightforward to conclude that by virtue of (35), the transformed and untransformed Fisher information matrices φ(ϑ) and (ϑ), are similar since the rotation matrix i(φ) is orthogonal. Two matrices A and B are similar if there exists an invertible matrix X such that the equality AX = XB holds. As can be seen, the Givens matrix i(φ) involves only two coordinates that are affected by the rotation angle φ whereas the other directions, which correspond to eigenvalues of one, are unaffected by the rotation matrix.
By virtue of (35) can be concluded that a positive definite FIM, (ϑ) ≻ 0, implies a positive definite transformed FIM, φ(ϑ) ≻ 0. Consequently, the elements on the main diagonal of (ϑ), f1,1, f2,2, . . . , fm,m, as well as the elements on the main diagonal of φ(ϑ), f̃1,1, f̃2,2, . . . , f̃m,m are all positive. However, the elements on the main diagonal of a singular FIM of a stationary ARMA process are also positive.
As developed in [7], combining (33) and (35) yields the distance measure of the estimated parameters ϑ1, ϑ2, . . . , ϑm accordingly, to obtain
where
and fj,l are entries of the FIM (ϑ) whereas f̃i,i(φ) and f̃i+1,i+1(φ) are the transformed components since the rotation affects only the entries, i and i+1, as can be seen in matrix i(φ). In [7], the existence of the following inequalities is proved
this guaratees the metric property of (36). When the FIM of an ARMA(p, q) process is the case, a combination of (27) and (35) for the ARMA(p, q) parameters, given in (15) yields for the transformed FIM,
where ℘(ϑ) is given by (28) and the transformed Sylvester resultant matrix is of the form
Proposition 3.5 in [7], proves that the transformed FIM φ(ϑ) and the transformed Sylvester matrix
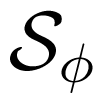
Proposition 3.3
The properties
hold true.
Proof
By virtue of the equalities (39), (40) and the orthogonality property of the rotation matrix i(φ) which implies that Ker i(φ) = {0} combined with the same approach as in Lemma 3.1 completes the proof.
A straightforward conclusion from Proposition 3.3 is then
In the next section a distance measure introduced in quantum information is discussed.
Statistical Distance Measure - Fisher Information and Quantum Information
In quantum information, the Fisher information, the information about a parameter θ in a particular measurement procedure, is expressed in terms of the statistical distance s, see [8–10]. The statistical distance used is defined as a measure to distinguish two probability distributions on the basis of measurement outcomes, see [37]. The Fisher information and the statistical distance are statistical quantities, and generally refer to many measurements as it is the case in this survey. However, in the quantum information theory and quantum statistics context, the problem set up is presented as follows. There may or may not be a small phase change θ, and the question is whether it is there. In that case you can design quantum experiments that will tell you the answer unambiguously in a single measurement. The equality derived is of the form
the Fisher information is the square of the derivative of the statistical distance s with respect to θ. Contrary to (36), where the square of the statistical distance measure is expressed in terms of entries of a FIM (ϑ) which is based on information about m parameters estimated from n measurements, for m < n. A challenging question could therefore be formulated as follows, can a generalization of equality (41) be developed in a quantum information context but at the matrix level ? To be more specific, many observations or measurements that lead to more than one parameter such that the corresponding Fisher information matrix is interconnected to an appropriate statistical distance matrix, a matrix where entries are scalar distance measures. This question could equally be a challenge to algebraic matrix theory and to quantum information.
3.4. The Bezoutian - The Fisher Information Matrix
In this section an additional resultant matrix is presented, it concerns the Bezout matrix or Bezoutian. The notation of Lancaster and Tismenetsky [2] shall be used and the results presented are extracted from [38]. Assume the polynomials a and b given by and , cfr. (13) but where p = q = n, and we further assume a0 = b0 = 1. The Bezout matrix B(a, b) of the polynomials a and b is defined by the relation
This matrix is often referred as the Bezoutian. We will display a decomposition of the Bezout matrix B(a, b) developed in [38]. For that purpose the matrix Uφ and its inverse Tφ are presented, where φ is a given complex number, to obtain
Let (1 − α1z) and (1 − β1z) be a factor of a(z) and b(z) respectively and α1 and β1 are zeros of â(z) and b̂(z). Consider the factored form of the nth order polynomials a(z) and b(z) of the form a(z) = (1 − α1z)a−1(z) and b(z) = (1 − β1z)b−1(z) respectively. Proceeding this way, for α2, . . . , αn yields the recursion a−(k−1)(z) = (1 − αkz)a−k(z), equivalently for the polynomials b−k(z) and a0(z) = a(z) and b0(z) = b(z). Proposition 3.1 in [38] is presented.
The following non-symmetric decomposition of the Bezoutian is derived, considering the notations above
with aα1 such that similarly for bβ1. Iteration gives the following expansion for the Bezout matrix
where is the first unit standard basis column vector in ℝn, by ej we denote the jth coordinate vector, ej = (0, . . . , 1, . . . , 0) T, with all its components equal to 0 except the jth component which equals 1. The following corollarys to Proposition 3.1 in [38] are now presented.
Corollary 3.2 in [38] states. Let φ be a common zero of the polynomials â(z) and b̂(z). Then a(z) = (1 − φz)a−1(z) and b(z) = (1 − φz)b−1(z) and
This a direct consequence of (42) and from which can be concluded that the Bezoutian B(a, b) is non-singular if and only if the polynomials a(z) and b(z) have no common factors. A similar conclusion is drawn for the FIM in (27) so that matrices (ϑ) and B(a, b) have the same singularity property.
Related to Corollary 3.2 in[38], this is where we give a description of the kernel or nullspace of the Bezout matrix.
Corollary 3.3 in [38] is now presented. Let φ1, . . ., φm be all the common zeros of the polynomials â(z) and b̂(z), with multiplicities n1, . . . , nm. Let ℓ be the last unit standard basis column vector in ℝn and put
for k = 1, . . . , m and j = 1, . . . , nk and by J we denote the forward n × n shift matrix, Jij = 1 if i = j + 1. Consequently, the subspace Ker B(a, b) is the linear span of the vectors .
An alternative representation to (27) but involving the Bezoutian B(b, a) and derived in Proposition 5.1 in [38] is of the form
where
and
The matrix S(â) is the symmetrizer of the polynomial â(z), in this paper a0 = 1, see [2] and P is a permutation matrix. In [38] it is shown that the matrix Q(ϑ) is the unique solution to an appropriate Stein equation and is strictly positive definite. However, in the next section an explicit form of the Stein solution Q(ϑ) is developed. Some comments concerning the property summarized in Corollary 5.2 in [38] follow.
The matrix (ϑ) is non-singular if and only if the polynomials a(z) and b(z) have no common factors. The proof is straightforward since the matrix Q(ϑ) is non-singular which implies that the matrix (ϑ) is only non-singular when the Bezoutian B(b, a) is non-singular and this is fulfilled if and only if the polynomials a(z) and b(z) have no common factors.
The matrix (b, a) is non-singular if a0 ≠ 0 and b0 ≠ 0, which is the case since we have a0 = b0 = 1. From (43) can be concluded that the FIM (ϑ) is non-singular only when the matrix (ϑ) is non-singular or by virtue of (44) when the Bezoutian B(b, a) is non-singular. Consequently, the singularity conditions of the Bezoutian B(b, a), the FIM (ϑ) and the Sylvester resultant matrix
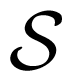
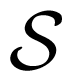
3.5. The Stein Equation - The Fisher Information Matrix of an ARMA(p, q) Process
In [12], a link between the FIM of an ARMA process and an appropriate solution of a Stein equation is set forth. In this survey paper we shall present some of the results and confront some results displayed in the previous sections. However, alternative proofs will be given to some results obtained in [12,38].
The Stein matrix equation is now set forth. Let A ∈ ℂm×m, B ∈ ℂn×n and Γ ∈ ℂn×m and consider the Stein equation
It has a unique solution if and only if λμ ≠ 1 for any λ ∈ σ(A) and μ ∈ σ(B), the spectrum of D is σ(D) = {λ ∈ ℂ: det(λIm − D) = 0}, the set of eigenvalues of D. The unique solution will be given in the next theorem [11].
Theorem 3.4
Let A and B be, such that there is a single closed contour C with σ(B) inside C and for each non-zero w ∈ σ(A), w−1 is outside C. Then for an arbitrary Γ the Stein Equation (45) has a unique solution S
In this section an interconnection between the representation (27) of the FIM (ϑ) and an appropriate solution to a Stein equation of the form (45) as developed in [12] is set forth. The distinct roots of the polynomials â(z) and b̂(z) are denoted by α1, α2, . . . , αp and β1, β2, . . . , βq respectively such that the non-singularity of the FIM (ϑ) is guaranteed. The following representation of the integral expression (28) is given when Cauchy’s residue theorem is applied, equation (4.8) in [12]
where
, i = 1, ..., p and j = 1, ..., q
and
the polynomial p(·; β) is defined accordingly,
and

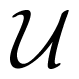

It is clear that the (p + q) × (p + q) Vandermonde matrices Vαβ and V̂αβ are nonsingular when αi ≠ αj, βk ≠ βh and αi ≠ βk for all i, j = 1, . . . , p and k, h = 1, . . . , q. A rigorous systematic evaluation of the Vandermonde determinants DetVαβ and DetV̂αβ, yields
where
Since and given the configuration of the permutation matrix, P, this leads to the equalities and DetP = (−1)(p+q)(p+q−1)/2 so that
We shall now introduce an appropriate Stein equation of the form (45) such that an interconnection with ℘(ϑ) in (47) can be verified. Therefore the following (p + q)× (p + q) companion matrix is introduced,
where the entries gi are given by and ĝ(ϑ) is the vector ĝ(ϑ) = (gp+q(ϑ), gp+q−1(ϑ), . . . , g1(ϑ)) T. Likewise is the vector g(z, ϑ) = a(z)b(z) and g(ϑ) = (g1(ϑ), g1(ϑ), . . . , gp+q(ϑ)) T, for investigating the properties of a companion matrix see e.g., [36], [2]. Since all the roots of the polynomials â(z) and b̂(z) are distinct and lie within the unit circle implies that the products αiβj ≠ 1, αiαj ≠ 1 and βiβj ≠ 1 hold for all i = 1, 2, . . . , p and j = 1, 2, . . . , q. Consequently, the uniqueness condition of the solution of an appropriate Stein equation is verified. The following Stein equation and its solution, according to (45) and (46), are now presented
where the closed contour is now the unit circle |z| = 1 and the matrix Γ is of size (p + q)× (p + q). A more explicit expression of the solution S is of the form
where adj(X) = X−1 Det(X), the adjoint of matrix X. When Cauchy’s residue theorem is applied to the solution S in (49), the following factored form of S is derived, equation (4.9) in [12]
where
and

and the operator ⊗ is the tensor (Kronecker) product of two matrices, see e.g., [2], [20].
Combining (47) and (50) and taking the assumption, αi ≠ αj, βk ≠ βh and αi ≠ βk, into account implies that the inverse of the (p + q)× (p + q) Vandermonde matrices Vαβ and V̂αβ exist, as Lemma 4.2 [12] states.
The following equality holds true
or
Consequently, under the condition αi ≠ αj, βk ≠ βh and αi ≠ βk, and by virtue of (27) and (51), an interconnection involving the FIM (ϑ), a solution to an appropriate Stein equation S, the Sylvester matrix
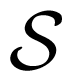
We will formulate a Stein equation when the matrix ,
where ep+q is the last standard basis column vector in ℝp+q, is the i-th unit standard basis column vector in ℝm, with all its components equal to 0 except the i-th component which equals 1. The next lemma is formulated.
Lemma 3.5
The symmetric matrix ℘(ϑ) defined in (28) fulfills the Stein Equation (52).
Proof
The unique solution of (52) is according to (46)
more explictely written,
Using the property of the companion matrix
Consequently, the solution S to the Stein Equation (52) coincides with the matrix ℘(ϑ) defined in (28).
The Stein equation that is verified by the FIM (ϑ) will be considered. For that purpose we display the following p × p and q × q companion matrices
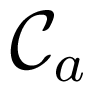
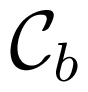
respectively. Introduce the (p + q) × (p + q) matrix and the (p + q) × 1 vector , where and are the first standard basis column vectors in ℝp and ℝq respectively. Consider the Stein equation
followed by the theorem.
Theorem 3.6
The Fisher information matrix (ϑ) (17) coincides with the solution to the Stein equation (53).
Proof
The eigenvalues of the companion matrices
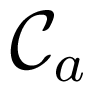
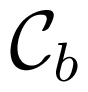
developing this integral expression in a more explicit form yields
Considering the form of the companion matrices
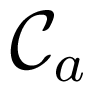
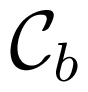
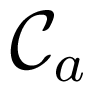
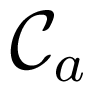
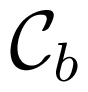
Representation (54) is such that in order to obtain an equivalent representation to the FIM (ϑ) in (17), the transpose of the solution to the Stein Equation (53) is therefore required, to obtain
or
The symmetry property of the FIM (ϑ), leads to S = (ϑ). From the representation (55) can be concluded that the solution S of the Stein Equation (53) coincides with the symmetric block Toeplitz FIM ( ϑ) given in (17). This completes the proof.
It is straightforward to verify that the submatrix (1,2) in (55) is the complex conjugate transpose of the submatrix (2,1), whereas each submatrix on the main diagonal is Hermitian, consequently, the integrand is Hermitian. This implies that when the standard residue theorem is applied, it yields ( ϑ) = T (ϑ).
An Illustrative Example of Theorem 3.6
To illustrate Theorem 3.6, the case of an ARMA(2, 2) process is considered. We will use the representation (17) for computing the FIM (ϑ) of an ARMA(2, 2) process. The autoregressive and moving average polynomials are of degree two or p = q = 2 and the ARMA(2, 2) process is described by,
where y(t) is the stationary process driven by white noise ɛ(t), a(z) = (1 + a1z + a2z2) and b(z) = (1+b1z + b2z2) and the parameter vector is ϑ = (a1, a2, b1, b2)T. The condition, the zeros of the polynomials
are in absolute value smaller than one, is imposed. The FIM (ϑ) of the ARMA(2, 2) process (56) is of the form
where
The submatrices aa(ϑ) and bb(ϑ) are symmetric and Toeplitz whereas ab(ϑ) is Toeplitz. One can assert that without any loss of generality, the property, symmetric block Toeplitz, holds for the class of Fisher information matrices of stationary ARMA(p, q) processes, where p and q are arbitrary, finite integers that represent the degrees of the autoregressive and moving average polynomials, respectively. The appropriate companion matrices
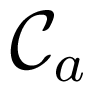
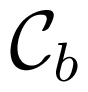
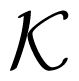
where . It can be verified that the Stein equation
holds true, when (ϑ) is of the form (57) and the matrices
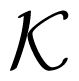
3.5.1. Some Additional Results
In Proposition 5.1 in [38], the matrix Q(ϑ) in (44) fulfills the Stein Equation (59) and the property Q(ϑ) ≻ 0 is proved. It states that when , where e1 is the first unit standard basis column vector in ℝn and en is the last or n-th unit standard basis column vector in ℝn, the following Stein equation admits the form
where
A corollary to Proposition 5.1, [38] will be set forth, the involvement of various Vandermonde matrices in the explicit solution to equation (59) is confirmed. For that purpose the following Vandermonde matrices are displayed,
where V̂β and Vβ have the same configuration as V̂α and Vα respectively. A corollary to Proposition 5.1 in [38] is now formulated.
Corollary 3.7
An explicit expression of the solution to the Stein equation (59) is of the form
where the n × n and 2n × 2n diagonal matrices 
Proof
The condition of a unique solution of the Stein Equation (59) is guaranteed since the eigenvalues of the companions matrices
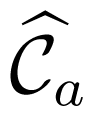
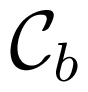
in order to proceed successfully, the following matrix property is displayed, to obtain
When applied to the Equation (62), it yields
Considering that the last column vector of the matrices adj(zIp −
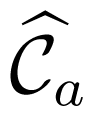
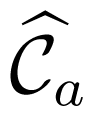
Applying the standard residue theorem leads for the respective submatrices
where the n × n diagonal matrices are
and the 2n × 2n diagonal matrices are
It is clear that the first and third matrices in Q11(ϑ), Q12(ϑ), Q21(ϑ) and Q22(ϑ) are the appropriate Vandermonde matrices displayed in (60), it can be concluded that the representation (61) is verified. This completes the proof.
In this section an explicit form of the solution Q(ϑ), expressed in terms of various Vandermonde matrices, is displayed. Also, an interconnection between the Fisher information (ϑ) and appropriate solutions to Stein equations and related matrices is presented. Proofs are given when the Stein equations are verified by the FIM (ϑ) and the associated matrix ℘(ϑ). These are alternative to the proofs developed in [38]. The presence of various forms of Vandermonde matrices is also emphasized. In the next section some matrix properties of the FIM (ϑ) of an ARMAX process is presented.
3.6. The Fisher Information Matrix of an ARMAX(p, r, q) Process
The FIM of the ARMAX process (11) is set forth according to [4]. The derivatives in the corresponding representation (16) are
where j = 1, . . . , p, l = 1, . . . , r and k = 1, . . . , q. Combining all j, l and k yields the (p + r + q) × (p + r + q) FIM
where the submatrices of
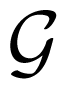
where Rx(z) is the spectral density of the process x(t) and is defined in (10). Let K(z) = a(z)a(z−1)b(z)b(z−1), combining all the expressions in (63) leads to the following representation of
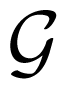
where (X)* is the complex conjugate transpose of the matrix X ∈ ℂm×n. Like in (23) we set forth
here
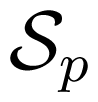
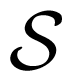
The representation (64) can be expressed by the appropriate block representations of the Sylvester resultant matrices, to obtain
where the matrix ℘(ϑ) is given in (28) and the matrix
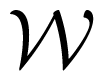
It is shown in [4] that
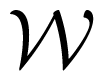
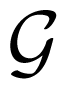
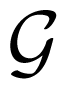
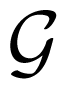
3.7. The Stein Equation - The Fisher Information Matrix of an ARMAX(p, r, q) Process
In Lemma 3.5 it is proved that the matrix ℘(ϑ) (28) fulfills the Stein Equation (52). We will now consider the conditions under which the matrix
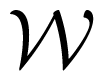
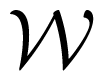
We consider a companion matrix of the form (48) and with size p + q + ℓ, it is denoted by



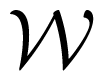
We will formulate a Stein equation when the matrix and which is of the form
where ep+r is the last standard basis column vector in ℝp+r. The next lemma is formulated.
Lemma 3.8
The matrix 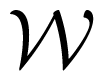
Proof
The unique solution of (69) is assured since the product of all the eigenvalues of

or
taking the property of the companion matrix



Consequently, the matrix
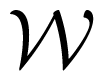
The matrices, ℘(ϑ) and
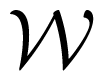
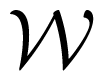
The (p + r) × (p + r) diagonal matrix (ϑ) is of the form
where φ(z) = a(z)b(z)h(z) and i = 1, . . . , p, j = 1, . . . , q and k = 1, . . . , ℓ. Whereas the (p + r) × (p + r) matrices Vαβξ and V̂αβξ are of the form
The (p + r) × (p + r) Vandermonde matrices Vαβξ and V̂αβξ are nonsingular when αi ≠ αj , βk ≠ βh, ξm ≠ ξn, αi ≠ βk, αi ≠ ξm, βk ≠ ξm for all i, j = 1, . . . , p, k, h = 1, . . . , q and m,n = 1, . . . , ℓ. The Vandermonde determinants DetVαβξ and Det V̂αβξ, are
where
Like for the Vandermonde matrices Vαβ and ,
Equation (70) is the ARMAX equivalent to (47). A combination of both equations generates a new representation of the FIM
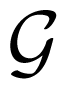
Lemma 3.9
Assume the conditions (67) to hold and consider the representations of ℘(ϑ) and 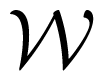
In Lemma 3.9, the FIM
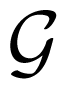
3.8. The Fisher Information Matrix of a Vector ARMA(p, q) Process
The process (6) is summarized as,
and we assume that {y(t), t ∈ ℕ}, is a zero mean Gaussian time series and {ɛ(t), t ∈ ℕ} is a n-dimensional vector random variable, such that
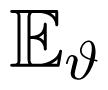
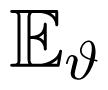
where ∂ɛ/∂ϑT is of size n×n2(p+q) and for convenience t is omitted from ɛ(t). Using the differential rules outlined in [6], yields
The substitution of representation (72) of ∂ɛ/∂ϑ T in (71) yields the FIM of a VARMA process. The purpose is to construct a factorization of the FIM F(ϑ) that should be a multiple variant of the factorization (27), so that a multiple resultant matrix property can be proved for F(ϑ). As illustrated in [6], the multiple version of the Sylvester resultant matrix (22) does not fulfill the multiple resultant matrix property. In that case even when the matrix polynomials A(z) and B(z) have a common zero or a common eigenvalue, the multiple Sylvester matrix is not neccessarily singular. This has also been illustrated in [3]. In order to consider a multiple equivalent to the resultant matrix
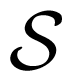
In [3], the authors prove that the tensor Sylvester matrix
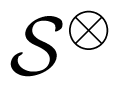
where
and
In order to obtain a multiple variant of (27), the following matrix is introduced,
where
and the matrix P(ϑ) is a multiple variant of the matrix ℘(ϑ) in (28), it is of the form
In Lemma 2.3 in [6], it is proved that the matrix M(ϑ) in (76) becomes singular if and only if the matrix polynomials A(z) and B(z) have at least one common eigenvalue-zero. The proof is a multiple equivalent of the proof of Corollary 2.2 in [5], since the equality (76) is a multiple version of (27). Consequently, the matrix M(ϑ) like the tensor Sylvester matrix
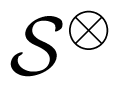
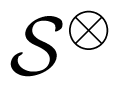
A brief summary of the contribution of [6] follows, in order to show that the FIM of a VARMA process F(ϑ) is a multiple resultant matrix two new representations of the FIM are derived. To construct such representations appropriate matrix differential rules are applied. The newly obtained representations are expressed in terms of the multiple Sylvester matrix and the tensor Sylvester matrix. The representation of the FIM expressed by the tensor Sylvester matrix is used to prove that the FIM becomes singular if and only if the autoregressive and moving average matrix polynomials have at least one common eigenvalue. It then follows that the FIM and the tensor Sylvester matrix have equivalent singularity conditions. In a numerical example it is shown, however, that the FIM fails to detect common eigenvalues due to some kind of numerical instability. The tensor Sylvester matrix reveals it clearly, proving the usefulness of the results derived in this paper.
3.9. The Fisher Information Matrix of a Vector ARMAX(p, r, q) Process
The n2(p + q + r) × n2(p + q + r) asymptotic FIM of the VARMAX(p, r, q) process (2)
is displayed according to [23] and is an extension of the FIM of the VARMA(p, q) process (6). Representation (16) of the FIM of the VARMAX(p, r, q) process is then
where
To obtain the term ∂ɛ/∂ϑ T, of size n × n2(p + q + r), the same differential rules are applied as for the VARMA(p, q) process. In Proposition 2.3 in [23], the representation of the FIM of a VARMAX process is expressed in terms of tensor Sylvester matrices, this obtained when ∂ɛ/∂ϑ T in (78) is substituted in (16), to obtain
The matrices in (79) are of the form
additionally we have Ψ(z) = Rx(z) ⊗ σ(z) and the Hermitian spectral density matrix Rx(z) is defined in (10), whereas the matrix polynomials Θ(z) and σ(z) are presented in (75). In (80), we have the pn2 × (p + q)n2 and qn2 × (p + q)n2 submatrices and of the tensor Sylvester resultant matrix . Whereas the matrices and are the upper and lower blocks of the (p+r)n2×(p+r)n2 tensor Sylvester resultant matrix . As for the FIM of the VARMA(p, q) process, the objective is to construct a multiple version of (65), this done in [23], to obtain
The matrices involved are of the form
and P(ϑ) is given in (77). Note, the matrices Φx(z), Λx(z), (z) and
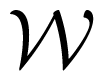
A parallel between the scalar and multiple structures is straightforward. This is best illustrated by comparing the representations (27) and (28) with (76) and (77) respectively, confronting the FIM for scalar and vector ARMA(p, q) processes. The FIM of the scalar ARMAX(p, r, q) process contains an ARMA(p, q) part, this is confirmed by (65), through the presence of the matrix ℘(ϑ) which is originally displayed in (28). The multiple resultant matrices M(ϑ) and Mx(ϑ) derived from the FIM of the VARMA(p, q) and VARMAX(p, r, q) processes respectively both contain P(ϑ), whereas the first matrix term of the matrices Φ(z) and Φx(z), which are of different size, consist of the same nonzero submatrices. To summarize, in [23] compact forms of the FIM of a VARMAX process expressed in terms of multiple and tensor Sylvester matrices are developed. The tensor Sylvester matrices allow us to investigate the multiple resultant matrix property of the FIM of VARMAX(p, r, q) processes. However, since no proof of the multiple resultant matrix property of the FIM G(ϑ) has been done yet, justifies the consideration of a conjecture. A conjecture that states, the FIMG(ϑ) of a VARMAX(p, r, q) process becomes singular if and only if the matrix polynomials A(z), B(z) and C(z) have at least one common eigenvalue. A multiple equivalent to Theorem 3.1 in [4] and combined with Proposition 2.4 in [6], but based on the representations (79) and (81), can be envisaged to formulate a proof which will be a subject for future study.
4. Conclusions
In this survey paper, matrix algebraic properties of the FIM of stationary processes are discussed. The presented material is a summary of papers where several matrix structural aspects of the FIM are investigated. The FIM of scalar and multiple processes like the (V)ARMA(X) are set forth with appropriate factorized forms involving (tensor) Sylvester matrices. These representations enable us to prove the resultant matrix property of the corresponding FIM. This has been done for (V)ARMA(p, q) and ARMAX(p, r, q) processes in the papers [4–6]. The development of the stages that lead to the appropriate factorized form of the FIM G(ϑ) (79) is set forth in [23]. However, there is no proof done yet that confirms the multiple resultant matrix property of the FIM G(ϑ) of a VARMAX(p, r, q) process. This justifies the consideration of a conjecture which is formulated in the former section, this can be a subject for future study.
The statistical distance measure derived in [7], involves entries of the FIM. This distance measure can be a challenge to its quantum information counterpart (41). Because (36) involves information about m parameters estimated from n measurements. Whereas in quantum information, like in e.g., [8–10], the information about one parameter in a particular measurement procedure is considered for establishing an interconnection with the appropriate statistical distance measure. A possible approach, by combining matrix algebra and quantum information, for developing a statistical distance measure in quantum information or quantum statistics but at the matrix level, can be a subject of future research. Some results concerning interconnections between the FIM of ARMA(X) models and appropriate solutions to Stein matrix equations are discussed, the material is extracted from the papers, [12] and [13]. However, in this paper, some alternative and new proofs that emphasize the conditions under which the FIM fulfills appropriate Stein equations, are set forth. The presence of various types of Vandermonde matrices is also emphasized when an explicit expansion of the FIM is computed. These Vandermonde matrices are inserted in interconnections with appropriate solutions to Stein equations. This explains, when the matrix algebraic structures of the FIM of stationary processes are investigated, the involvement of structured matrices like the (tensor) Sylvester, Bezoutian and Vandermonde matrices is essential.
Acknowledgements
The author thanks a perceptive reviewer for his comments which significantly improved the quality and presentation of the paper.
Conflicts of Interest
The authors have declared no conflict of interest.
References
- Dym, H. Linear Algebra in Action; American Mathematical Society: Providence, RI, USA, 2006; Volume 78. [Google Scholar]
- Lancaster, P.; Tismenetsky, M. The Theory of Matrices with Applications, 2nd ed; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]
- Gohberg, I.; Lerer, L. Resultants of matrix polynomials. Bull. Am. Math. Soc 1976, 82, 565–567. [Google Scholar]
- Klein, A.; Spreij, P. On Fisher’s information matrix of an ARMAX process and Sylvester’s resultant matrices. Linear Algebra Appl 1996, 237/238, 579–590. [Google Scholar]
- Klein, A.; Spreij, P. On Fisher’s information matrix of an ARMA process. In Stochastic Differential and Difference Equations; Csiszar, I., Michaletzky, Gy., Eds.; Birkhäuser: Boston: Boston, USA, 1997; Progress in Systems and Control Theory; Volume 23, pp. 273–284. [Google Scholar]
- Klein, A.; Mélard, G.; Spreij, P. On the Resultant Property of the Fisher Information Matrix of a Vector ARMA process. Linear Algebra Appl 2005, 403, 291–313. [Google Scholar]
- Klein, A.; Spreij, P. Transformed Statistical Distance Measures and the Fisher Information Matrix. Linear Algebra Appl 2012, 437, 692–712. [Google Scholar]
- Braunstein, S.L.; Caves, C.M. Statistical Distance and the Geometry of Quantum States. Phys. Rev. Lett 1994, 72, 3439–3443. [Google Scholar]
- Jones, P.J.; Kok, P. Geometric derivation of the quantum speed limit. Phys. Rev. A 2010, 82, 022107. [Google Scholar]
- Kok, P. Tutorial: Statistical distance and Fisher information; Oxford: UK, 2006. [Google Scholar]
- Lancaster, P.; Rodman, L. Algebraic Riccati Equations; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Klein, A.; Spreij, P. On Stein’s equation, Vandermonde matrices and Fisher’s information matrix of time series processes. Part I: The autoregressive moving average process. Linear Algebra Appl 2001, 329, 9–47. [Google Scholar]
- Klein, A.; Spreij, P. On the solution of Stein’s equation and Fisher’s information matrix of an ARMAX process. Linear Algebra Appl 2005, 396, 1–34. [Google Scholar]
- Grenander, U.; Szegő, G.P. Toeplitz Forms and Their Applications; University of California Press: New York, NY, USA, 1958. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods, 2nd ed; Springer Verlag: Berlin, Germany; New York, NY, USA, 1991. [Google Scholar]
- Caines, P. Linear Stochastic Systems; John Wiley and Sons: New York, NY, USA, 1988. [Google Scholar]
- Ljung, L.; Söderström, T. Theory and Practice of Recursive Identification; M.I.T. Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Hannan, E.J.; Deistler, M. The Statistical Theory of Linear Systems; John Wiley and Sons: New York, NY, USA, 1988. [Google Scholar]
- Hannan, E.J.; Dunsmuir, W.T.M.; Deistler, M. Estimation of vector Armax models. J. Multivar. Anal 1980, 10, 275–295. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Topics in Matrix Analysis; Cambridge University Press: New York, NY, USA, 1995. [Google Scholar]
- Klein, A.; Spreij, P. Matrix differential calculus applied to multiple stationary time series and an extended Whittle formula for information matrices. Linear Algebra Appl 2009, 430, 674–691. [Google Scholar]
- Klein, A.; Mélard, G. An algorithm for the exact Fisher information matrix of vector ARMAX time series. Linear Algebra Its Appl 2014, 446, 1–24. [Google Scholar]
- Klein, A.; Spreij, P. Tensor Sylvester matrices and the Fisher information matrix of VARMAX processes. Linear Algebra Appl 2010, 432, 1975–1989. [Google Scholar]
- Rao, C.R. Information and the accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc 1945, 37, 81–91. [Google Scholar]
- Ibragimov, I.A.; Has’minskiĭ, R.Z. Statistical Estimation. In Asymptotic Theory; Springer-Verlag: New York, NY, USA, 1981. [Google Scholar]
- Lehmann, E.L. Theory of Point Estimation; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Friedlander, B. On the computation of the Cramér-Rao bound for ARMA parameter estimation. IEEE Trans. Acoust. Speech Signal Process 1984, 32, 721–727. [Google Scholar]
- Holevo, A.S. Probabilistic and Statistical Aspects of Quantum Theory, 2nd ed; Edizioni Della Normale, SNS Pisa: Pisa, Italy, 2011. [Google Scholar]
- Petz, T. Quantum Information Theory and Quantum Statistics; Springer-Verlag: Berlin Heidelberg, Germany, 2008. [Google Scholar]
- Barndorff-Nielsen, O.E.; Gill, R.D. Fisher Information in quantum statistics. J. Phys. A 2000, 30, 4481–4490. [Google Scholar]
- Luo, S. Wigner-Yanase skew information vs. quantum Fisher information. Proc. Amer. Math. Soc 2004, 132, 885–890. [Google Scholar]
- Klein, A.; Mélard, G. On algorithms for computing the covariance matrix of estimates in autoregressive moving average processes. Comput. Stat. Q 1989, 5, 1–9. [Google Scholar]
- Klein, A.; Mélard, G. An algorithm for computing the asymptotic Fisher information matrix for seasonal SISO models. J. Time Ser. Anal 2004, 25, 627–648. [Google Scholar]
- Bistritz, Y.; Lifshitz, A. Bounds for resultants of univariate and bivariate polynomials. Linear Algebra Appl 2010, 432, 1995–2005. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: New York, NY, USA, 1996. [Google Scholar]
- Golub, G.H.; van Loan, C.F. Matrix Computations, 3rd ed; John Hopkins University Press: Baltimore, USA, 1996. [Google Scholar]
- Kullback, S. Information Theory and Statistics; John Wiley and Sons: New York, NY, USA, 1959. [Google Scholar]
- Klein, A.; Spreij, P. The Bezoutian, state space realizations and Fisher’s information matrix of an ARMA process. Linear Algebra Appl 2006, 416, 160–174. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Klein, A. Matrix Algebraic Properties of the Fisher Information Matrix of Stationary Processes. Entropy 2014, 16, 2023-2055. https://doi.org/10.3390/e16042023
Klein A. Matrix Algebraic Properties of the Fisher Information Matrix of Stationary Processes. Entropy. 2014; 16(4):2023-2055. https://doi.org/10.3390/e16042023
Chicago/Turabian StyleKlein, André. 2014. "Matrix Algebraic Properties of the Fisher Information Matrix of Stationary Processes" Entropy 16, no. 4: 2023-2055. https://doi.org/10.3390/e16042023



