Entropy Principle and Recent Results in Non-Equilibrium Theories
Abstract
: We present the state of the art on the modern mathematical methods of exploiting the entropy principle in thermomechanics of continuous media. A survey of recent results and conceptual discussions of this topic in some well-known non-equilibrium theories (Classical irreversible thermodynamics CIT, Rational thermodynamics RT, Thermodynamics of irreversible processes TIP, Extended irreversible thermodynamics EIT, Rational Extended thermodynamics RET) is also summarized.PACS Classification: 03.50.-z, 05.70.Ln, 05.70.Ce1. Introduction
In continuum physics the entropy principle constitutes a valuable tool in modeling material properties. In rational thermodynamics (RT) [1] Coleman and Noll were the first to formulate it as follows [2]:
The constitutive equations, which characterize the material properties of continuous media, must be assigned in such a way that second law of thermodynamics is satisfied along arbitrary thermodynamic processes.
These authors also proposed a rigorous mathematical procedure to exploit the requirement above, currently referred to as Coleman-Noll procedure [2,3]. Afterwards, Liu [4] developed an alternative and elegant method of exploitation, based on the Lagrange multipliers and known as Liu procedure. Hauser and Kirchner [5] recognized that the Liu procedure constitutes a special case of a more general result on linear programming [6].
On the other hand, the Coleman-Noll approach requires an appropriate formulation of second law. In continuum physics [2,7] it is assumed that:
The rate of entropy production per unit volume σ(s), defined as
where ρ is the mass density, s is the specific entropy, J is the entropy-flux density (hereafter referred to as entropy flux), r the rate of heat supply per unit of mass and T the absolute temperature, is nonnegative along any thermodynamic process.
For the entropy flux Coleman and Noll postulated the constitutive equation where q is the heat-flux density (hereafter referred to as heat flux), and T the temperature.
When dealing with the formulation above, one should look for an appropriate constitutive equation not only for the entropy flux but also for the entropy density, and for an appropriate definition of temperature in situations far from equilibrium. In extended irreversible thermodynamics (EIT), taking the fluxes as independent variables, the three questions mentioned above give the following answers [8–13]:
in processes which are not too far from equilibrium, the extended entropy is the local equilibrium entropy plus a negative contribution proportional to the square of the fluxes; the corresponding coefficient is proportional to the relaxation time of the corresponding flux and inversely proportional to the respective transport coefficient; thus, the non-equilibrium contributions to the entropy are related to relaxational contributions to generalized transport equations;
the entropy flux is the Coleman-Noll entropy flux plus a non-equilibrium contribution due to higher-order fluxes;
the absolute temperature, given by the reciprocal of the derivative of the extended entropy with respect to the internal energy, differs from the local-equilibrium temperature and depends on the fluxes; it is related to the average kinetic energy of the particles in the plane perpendicular to the fluxes, and it is in general different from the temperatures of the other degrees of freedom, which may have different values.
Some conceptual problems arise by analyzing the different mathematical methods for the exploitation of the entropy principle. First of all, the entropy principle itself, such as formulated by Coleman and Noll, could appear as an arbitrary assumption, since nothing prevents second law of thermodynamics to restrict the processes instead of the constitutive equations. Thus, Muschik and Ehrentraut [14] proposed the following amendment to the second law:
In the state space, any curve which represents a reversible process, belongs to the equilibrium subspace.
As a consequence of this statement, they proved that for regular processes, i.e., for classical solutions of the system of governing equations, the second law of thermodynamics necessarily restricts the constitutive equations and not the thermodynamic processes. In this way, the classical Coleman–Noll approach follows by a rigorous proof (see Section 5, Theorem 2).
It is worth noting that if one applies the classical Coleman–Noll or Liu procedures, weakly nonlocal continuum theories [15,16], taking the gradients of the unknown variables as independent state variables, result to be not compatible with second law. Such a severe consequence seems to be related to the insufficiency of the standard analysis of the entropy inequality in case of weakly nonlocal continua. For example, according to the usual approaches, thermodynamic principles deny the existence of both higher grade elasticity [17] and Korteweg fluids [18]. These obstacles can be circumvented by several means (generalized entropy flux, interstitial working, microforce balance, phase fields, etc. . . .). All these theories modify in different ways either first or second law of thermodynamics, so that we have a non uniform approach with respect to the classical structure of continuum theories. For example, as a possible remedy to the incompatibility with second law of Korteweg fluids, Dunn and Serrin introduce an additional rate of supply of mechanical energy, the interstitial working, engendered by long–range interactions among the molecules [18], which results in an energy extra–flux u into the local balance of energy (first law of thermodynamics). Alternative approaches suppose that the entropy flux J is affected by additional mechanical terms, due to long–range forces. Among them, the most celebrated one is the Müller approach, who, by kinetic considerations, proposed a more general entropy flux J, that is a constitutive quantity, together with an entropy density that needs to be determined by the compatibility with the second law [7]. This is tantamount to introduce in the local form of second law an entropy extra–flux , [7].
An alternative method for circumventing that problem is to generalize the classical exploitation procedures, by regarding the governing equations for the gradients entering the state space as additional constraints for the entropy inequality, [19–21].
Recently Fabrizio, Lazzari and Nibbi [22], and Amendola, Fabrizio and Golden [23], proposed a new procedure to achieve generalizations of the laws of thermodynamics, which consists in expressing them in terms of internal powers. According to their suggestion, for some classes of nonlocal materials, an extension of first law of thermodynamics, and not only of second law, is necessary. They propose the following balance power laws for first and second laws of thermodynamics, respectively,
where is the internal mechanical power density, is the internal heat power density and is the internal entropy power density.
In [22], the authors analyze several different materials, which arise in electromagnetism, in the study of phase transitions and also in other physical processes, as those describing phase separation by means of Cahn-Hilliard’s equation. For all these materials they derive the form of the RHS either of Equation (2) or of Equation (3), getting so explicit constitutive equations for the energy or the entropy extra-flux. It is shown that this formulation highlights, without ambiguity, the contribution of the internal powers in the variation of the thermodynamic potentials.
In classical irreversible thermodynamics (CIT) [24], the entropy principle is exploited by a phenomenological procedure, which regards the entropy production as a bilinear function of thermodynamical forces and fluxes [15,25]. Nowadays, this approach has ramifications into the general equation for non-equilibrium reversible-irreversible coupling (GENERIC) [26,27]. Mainly two major directions have been followed in the literature for the specification of force-flux relations. On the one hand, the so-called transport coefficients may depend on the forces themselves, in which case we call the relation quasi-linear. On the other hand, force-flux relations are also often represented in potential form, with the flux given by the derivative with respect to the force of a so-called dissipation potential. The second law of thermodynamics is respected by requiring certain properties of the potential, primarily its convexity. It can be proved that every potential-based force-flux relation can be cast into quasi-linear form, while the reverse statement does not hold true [27]. It is worth noting that GENERIC can be formulated either in a quasi-linear form [26] or in a dissipation-potential based form [28].
A different perspective has been open in rational extended thermodynamics (RET) [11,29], in which the principle is exploited to determine the appropriate constitutive equations (of local type) assuming a priori that the system is formed by balance laws equations. Concavity arguments postulated a priori for the entropy density permit to determine the main field which renders the system of field equations symmetric hyperbolic. That way, the properties of causality and predictability for the physical model are ensured [30].
The formulation (1) of the second law is not always appropriate when dealing with micro/nano-systems, in which quantum and confinement effects may become important. In such a case, a suitable form of second law is represented by the maximum entropy principle (MEP), proposed by Jaynes in connection with information theory [31,32], which asserts that:
The thermodynamic systems evolve naturally toward states corresponding to a distribution function f (x, ξ, t) which maximizes the entropy
where kB is the Boltzmann constant and f dx dξ is the number of particles in the volume dx dξ of the phase space centered at (x, ξ) and included in R3 × R3.
Thus, it seems to be quite natural to investigate what is the relation between the two statements above. Recent results have shown that the procedure of MEP for the closure of the moments equations for rarefied gases, complies with the recent macroscopic approach of extended thermodynamics to real and perfect gases [33–35].
Although entropy maximization in isolated systems is a well-known procedure, it becomes problematic in non equilibrium situations. For instance, entropy maximization around an equilibrium steady state, submitted to further additional constraints on fluxes, or higher-order moments (which are null at equilibrium) is not so evident nor well-known, but it is not in contradiction with maximization in equilibrium. Nonetheless, several quantum systems, such as interacting fermionic and bosonic gases, semiconductor heterostructures with confined carrier transport, require a quantum formulation of MEP in situations out of equilibrium. In achieving that task, the main difficulty is to define, in non equilibrium situations, an appropriate quantum entropy that explicitly incorporates quantum statistics [36,37]. For instance, in the formulation of hydrodynamic subband models for charge carriers in semiconductors in presence of confinement effects in one or two directions, a crucial problem, in order to apply the maximum entropy principle, is an appropriate formulation of entropy for a 2D or 1D electron gas which combines a semiclassical description in the transport direction and quantum effects in the transversal direction [38,39].
As far as the relation between macroscopic and microscopic approaches is concerned, one should observe that in kinetic theory higher order weakly nonlocal continuum extensions can be obtained by Chapmann-Enskog expansion. However, the expansion beyond first order results in unstable equations. Thus, the family of Burnett equations cannot be much improved, contrary to serious efforts [40,41]. The Grad approach [42], which replaced the Chapmann-Enskog method in some modern thermodynamic theories, has been used to create agreement between the kinetic and the local continuum theories up to the limits of continuum mechanics. Although this method gives more satisfactory results with respect to stability, it does not comply with weakly nonlocal continuum theories [43]. In Section 4, the Grad method and its application in RET are illustrated in detail.
The examples above show that the proper formulation of the entropy principle in continuum physics is still an open problem. The aim of this paper is to provide an overview on the state of the art and on recent researches on this topic, which represents a milestone in thermodynamics of continuous media.
To achieve that task, different approaches, corresponding to the different point of view of the authors on non-equilibrium continuum theories, are presented and illustrated by some recent applications. In this way, different thermodynamic theories are analyzed.
The foundation of different theories in the last decades has stimulated several discussions into the thermodynamic community and produced many progresses, which regard both the mathematical tools of investigation and the understanding of new physical phenomena. Moreover, if we look at the different schools of thermodynamics with more attention, we discover that these are not so far as it could appear at the first sight, since several connections emerge. A further aim of this presentation is just to point out the similarities between the various approaches.
Then, in Section 2, Péter Ván illustrates the role of the entropy principle in classical irreversible thermodynamics. In Section 3, David Jou analyzes the application of the entropy principle in extended irreversible thermodynamics. In Section 4, Tommaso Ruggeri shows the consequences of the entropy principle in rational extended thermodynamics. In Section 5, Vito Antonio Cimmelli presents some classical results of rational thermodynamics and recent results regarding the mathematical analysis of the entropy inequality.
Throughout the paper, summation with respect to repeated indices will be assumed. Moreover we adopt the following notations:
t f —partial time derivative of f
k f, k = 1, 2, . . . n—partial derivative of f with respect to the coordinate xk
ḟ = ∂t f + vi∂i f—material time derivative of f
x · y = xi yi—scalar product between vectors x and y
X : Y = Xij Yij—scalar product between tensors X and Y
∇ ≡ (∂i), i = 1, 2, . . . n—Nabla operator
Δ ≡ (∂ii)—Laplace operator
∇(∇ · x) ≡ ∂i(∂jxj), i, j = 1, 2, . . . n—Gradient of Divergence of x
A(ij)—symmetric part of tensor Aij
A〈ij〉 —symmetric and traceless part of tensor Aij
AT —transpose of tensor A
Rn—the vector space of the n-tuples of real numbers x1 . . . xn
the word “density” means the amount of a given quantity per unitary volume
the word “specific” means the amount of a given quantity per unitary mass
The problems illustrated in the present paper have been discussed during the “12th Joint European Thermodynamics Conference” (JETC 2013), held in Brescia, Italy, from July 1 to July 5, 2013.
It is worth observing that, although in our analysis second law of thermodynamics plays a fundamental role, the present review is not devoted to the wide topic of the different formulations of second law, but to the more restricted one of the entropy principle, i.e., the constitutive principle which requires that the constitutive equations which in continuum physics characterize the material properties, must be assigned in such a way that second law of thermodynamics is satisfied along arbitrary thermodynamic processes.
The authors gratefully acknowledge the chairman of the conference, Prof. Gian Paolo Beretta, and the staff of JETC 2013, for the perfect organization, the friendly ambient and the opportunity of several interesting discussions on new trends in non-equilibrium thermodynamics.
2. The Entropy Principle in Classical Irreversible Thermodynamics
In his pioneering works about reciprocal relations Lars Onsager established a uniform approach of different interactions in discrete (homogeneous) thermodynamic bodies, where the basic variables are the classical extensive thermodynamic variables [44,45]. His main concern was the relation of phenomenological and statistical treatments with the help of fluctuation theory and also a phenomenological explanation in the form of variational principles, based on dissipation functions (see also [46,47]). Classical irreversible thermodynamics as a field theory has been started by Eckart [48–51] and was developed and applied in different cases by Prigogine, de Groot, Mazur and many others [24,52].
CIT constructs evolution equations for dissipative phenomena. Instead of variational principles the thermodynamic compatibility of continuum material properties plays a key role in the methodology. Eckart established the connection between homogeneous thermodynamic bodies and classical continua with the help of the hypothesis of local equilibrium. According to this hypothesis one assumes the validity of the Gibbs relation and the corresponding equations of state for densities or specific quantities of the extensive thermodynamic variables—that is local equilibrium—and introduces the entropy inequality as a balance. There are two crucial points of this procedure:
- (1)
What is internal energy? How could one separate mechanics and thermodynamics, distinguish between motion and equilibrium?
- (2)
What is the form of the entropy current density?
The answers of these questions are technically simple. The internal energy is the difference between the conserved total energy and the kinetic energy. One component simple fluids are characterized by the internal energy and the mass. Their Gibbs relation, expressed with specific quantities is
Here the extensive quantities are the specific internal energy ɛ, the specific entropy s and the specific volume V = 1/ρ, while p denotes the scalar static pressure and T the temperature. Therefore the partial derivatives of the specific entropy are:
In this simple case the entropy inequality (1) can be constructed by calculating the material time derivative of the specific entropy through the Gibbs relation:
In the expression above we denoted by vi the components of the velocity field and eliminated the time derivatives with the help of balances of mass and energy
where Tij denote the components of the Cauchy stress and the specific heat supply has been neglected. We can identify the entropy current density in the last divergence term as the product of the reciprocal temperature and the conductive current density of the internal energy, the heat flux:
Then the entropy balance
follows, where δij are the components of the identity tensor. We may recognize that the inequality (10) can be solved assuming a linear relationship between the thermodynamic fluxes—the heat flux qi and the stress Tij + pδij, and the thermodynamic forces—the gradient of the reciprocal temperature ∂i(1/T) and the gradient of the velocity ∂jvi. The linear coefficient matrix must be positive definite. For isotropic materials, represented by isotropic functions, one obtains the Fourier law of heat conduction and the Newtonian viscous stress, with three positive scalar parameters:
Here λF = λ/T2 is the Fourier heat conduction coefficient, ηv and η are the bulk and the shear viscosities.
In case of several components and more complex materials one generalizes the previous procedure and try to obtain this quadratic form of the entropy production as a sum of product of thermodynamic fluxes and forces. The linear relationship with symmetric and positive definite coefficient matrix is assumed for less symmetric materials, too. In this respect the concepts of crystal physics proved to be instructive [53,54]. The extension of these ideas for more complex thermodynamic systems is a powerful and useful theory of classical continuum physics [55].
In the previous heuristic treatment one can identify several problematic points, where a deeper analysis is necessary for further developments:
- (1)
Material frame indifference or objectivity. The best parameters from an experimental point of view are those that characterize the material and do not depend on experimental conditions. Therefore the theoretical separation of motion related and material properties is crucial. In CIT material time derivatives are used instead of frame dependent partial ones, and conductive current densities instead of frame dependent local ones. This seems to work in case of fluids, but for solids one cannot avoid a more detailed analysis of the basic kinematic fields, the balance structure and the constitutive relations. In spite of various mathematical formulations of the principle of material frame indifference [56–59], its proper meaning is still a controversial topic in continuum physics. For example, there are cases in which the frame indifference is violated by the effect of Coriolis forces [60–62], although that effect is small under most circumstances, because it depends on the degree that mean free paths of atoms are bent by the Coriolis force. Two final remarks are worth of mention.
The weakly nonlocal extension of the constitutive state space is a safe procedure, because the gradient is a covector, that does not depend on the motion, e.g., does not transform by a Galilean transformation [63,64].
In RET, weakly nonlocal constitutive equations are derived by truncated balance laws (see Section 4 for more details), so that they do not need to satisfy any constitutive principle.
- (2)
Solution of the inequality. The mentioned Onsagerian linear relationship is a robust choice for solving the quadratic inequality, but only one possibility. One can find infinitely many more functions that could result in nonnegative entropy production. Are there different, or even better solutions than the linear one? The example of plasticity demonstrates the physical relevance of this question. The thermodynamic theory is based on a first order homogeneous form of the entropy production instead of the mentioned quadratic, second order homogeneous one [65,66].
- (3)
Constitutive character. In the previous treatment the constitutive functions are fixed at the end of the procedure, with the help of the quadratic flux-force structure. For example, the heat flux turned out to be proportional to the temperature gradient. However, can be the heat flux a function of other variables, like the second derivative of the internal energy? How can we go beyond these experimentally safe classical examples in case of more general state spaces? What are the conditions that lead to a soluble, possibly quadratic form of the entropy production?
In the following, we focus on these last questions. Exploring the conditions behind of classical theory, we show some possible generalizations and the way toward extensions.
2.1. The Role of State Spaces
The limitations of classical irreversible thermodynamics in its original form became more and more evident soon after the appearance of the monograph of de Groot and Mazur [24]. The criticism of Truesdell clarified the imprecise and heuristic mathematics of the theory [1]. He initiated a more exact, rational approach, that rejected the thermostatic foundations together with the Onsagerian reciprocal relations. However, in several cases Truesdell has not solved but only made understandable the problems.
Other challenges came from the experimental observations and from the part of statistical theories. Thermodynamic compatibility of rheology and plasticity are old challenges, relativistic fluids and power law tail statistics provide new ones. Any new approaches of thermodynamics of irreversible processes (TIP) that generalize CIT should answer these challenges, when keeping the universal applicability and uniting character of the theory as a framework of dissipative gases, fluids and solids.
From this point of view the Truesdellian program of rationalization encountered various difficulties. For instance, the extension of the state space of elastic solids with gradients of the basic state variables (e.g., strain) was forbidden by mathematically rigorous analysis of the second law [17]. Moreover, these kind of attempted gradient extensions were proved to be untenable because of stability reasons [67]. Therefore the research in these directions either based on local constitutive state spaces without gradients or the theories have chosen different foundations. The first approach is compatible with the moment series expansion of the kinetic theory and therefore local state spaces are among the basic postulates in rational extended thermodynamics (RET). Gradient dependence can be introduced by eliminating higher order moments in the hierarchy [68]. Examples of different frameworks for weakly nonlocal theories are the statistically motivated phase field theory [69,70], and GENERIC with the separation of the ideal and dissipative parts of the evolution equations from the start of the construction [26].
However, the mathematical methods, the Coleman-Noll and Liu procedures, are neutral, and one should scrutinize the applied conditions and background concepts also from a physical point of view. In the following we compare the heuristic methods to the more precise ones. In order to focus on the second law and simplify the treatment, we choose an abstract notation, that hides the details of the particular continua together with the aspects of material frame indifference.
The formal vector of the densities of extensive quantities zα spans the basic state space zα ∈

if the material is considered at rest. The entropy inequality (1) is written as
where ρs is the entropy density and Jk is the entropy current density. Then the hypothesis of local equilibrium requires an entropy density depending only on the basic state ρs = ρs(zα). The classical form of the entropy current Equation (9) is generalized as
Here denotes the entropic intensive quantity conjugated to zα and double indices denote summation both for the vector components (i, j, k) and for the state variables (α, β). The entropy production can be calculated by substituting Equations (12) and (14) into Equation (13):
We may recognize the quadratic flux-force structure and identify the current densities of the extensives, , as thermodynamic fluxes and the gradients of the intensives, ∂kΓα as thermodynamic forces. Finally, the linear solution of the inequality is
if the symmetric part of the conductivity matrix is positive definite.
In this procedure the constitutive quantities are the extensive fluxes , the entropy density ρs, and also the entropy current density Jk. Moreover, the fluxes, as constitutive functions, are not local, they are not only functions of the basic state variables but depend on the gradients of the extensives, too. An other observation is that the entropy inequality is constrained by the balances. Then we may ask, whether the entropy inequality selects among the solutions of the balances—then it is a restriction of the processes −, or, alternatively, it can be considered as a selection of materials, as it is implicitly assumed. The second possibility is definitely more convenient for any experimental validation and also expresses our physical (or philosophical) expectation. On the other hand, the question arises, whether our method of substitution is too naive and the dependence of the constitutive functions on the gradients may lead to a different form the entropy production. Moreover, one may ask whether constitutive functions that depend on higher order gradients are compatible with the second law without further conditions, or not. These kind of observations lead to an amendment of the classical formulation of the second law [14], and also to more involved mathematical methods (see Section 5). In order to separate the conditions from the consequences we repeat the previous derivation with the help of Liu procedure.
Let us assume that the constitutive functions , Jk and ρs depend on the unknown fields and also on their gradients, so that our constitutive state space is first order weakly nonlocal:
The balances Equation (12) are considered as constraints, with the help of Λα Lagrange-Farkas multipliers. Therefore the entropy inequality can be written as:
In this case the vector of highest derivatives is (∂tzα, ∂t∂kzα), and therefore the corresponding coefficients are zero, leading to the following Liu equations (see Section 5):
According to the second Liu equation there is local equilibrium, the entropy does not depend on the gradient of the state space. The first Liu Equation (18) identifies the Lagrange-Farkas multipliers with the entropic intensives. We may also recognize that the form Equation (14) of the entropy flux is a solution of the third Liu Equation (20). Substituting back these solutions of the Liu equations into Equation (17) one obtains the dissipation inequality in the following form:
This is identical to Equation (15). Therefore, the choice of the first order weakly nonlocal constitutive state space and the balance structure of the evolution equations enforced a local entropy density function and the classical form of the entropy current density turned out to be compatible.
Moreover,
is a solution of Equation (20), too, with the additive local vector Kk [7]. Let us remark, that there is no restriction regarding the antisymmetric part, therefore (22) is only one possible solution of Equation (20). The assumption of zero antisymmetric part in Equation (20) ensures the existence of a scalar potential whose derivative by ∂kzα is the vector field (see e.g., [71]).
Let us observe, that the final result of this simple derivation, the entropy production in the form of Equation (21), corresponds only to the structure of the second, thermal term in Equation (10). The first, mechanical term is different. Classical heat conduction and diffusion is without memory and inertia, mechanics is not. The realization of this difference leads to theories of extended thermodynamics [46,47,72] as we will see in the next sections.
Remarks
- (1)
The extension of the basic state space by additional variables or/and higher order gradients has two conceptually important consequences.
In case of higher order weak nonlocality it is necessary to introduce the gradients of the constraints (e.g., the balances) as independent new restrictions, too [19,20,25].
In case of internal variables (without balances as constraints) one can derive the complete evolution equations with thermodynamic methods and a weakly nonlocal extension provides also natural boundary conditions. The thermodynamic approach can substitute variational considerations. For example evolution equations of generalized continua can be obtained with the help of the entropy principle also in the ideal, nondissipative limit [73,74].
- (2)
Writing about entropy principle in continuum physics we should mention the method of GENERIC (General Equation of Reversible and Irreversible Coupling) [26]. GENERIC separates the dissipative and nondissipative parts of the evolution equations by construction. The structure of GENERIC evolution equation is the following
The evolution of the nondissipative part is generated by the functional derivative of the energy E and the related antisymmetric operator-matrix L. The evolution of the dissipative part is governed by the functional derivative of the entropy S and the corresponding symmetric operator-matrix M. The second law is introduced by the symmetric positive semidefinite property of M for the dissipative part. M and L have other properties (in a bracket formulation) to ensure the expected properties and the compatibility of the two parts. Therefore the constitutive state space of GENERIC is inherently weakly nonlocal (functional derivatives), and enforces the linear constitutive structure (matrix formalism) in an operator sense. The comparison of the entropy principle with the other theories is not straightforward because of the different basic structures.
3. The Entropy Principle in Extended Irreversible Thermodynamics
The entropy principle in extended irreversible thermodynamics (EIT) is analogous to that in CIT, but with some formal and conceptual differences which we examine here. One starts with an entropy and an entropy flux which depend on the fluxes, besides on the classical variables. As said in the introduction, not too far from equilibrium the entropy is the local equilibrium entropy minus some expressions quadratic in the fluxes, and the entropy flux is the classical entropy flux plus a correction proportional to the product of the flux of the flux times the flux itself. In principle, these non-equilibrium contributions are not identified a priori, but depend on coefficients whose physical meaning will be interpreted later. From here, using the definition (1) for the entropy production, one is led for the entropy production to a quadratic form which is a sum of products of fluxes times generalized thermodynamic forces, and it is required that the constitutive equations are submitted to the restriction that the entropy production is positive definite. The main differences with the entropy principle in CIT are [8–10]:
The thermodynamic forces are more general than their local equilibrium counterparts, and in them appear the time derivatives and the gradients of the fluxes, as a consequence of using an entropy and entropy flux which depend on the fluxes.
Since the fluxes are considered as independent variables, the constitutive equations do not aim to express the fluxes in terms of thermodynamic forces, but to express the evolution equations for the fluxes., i.e., to give the time derivative of the fluxes in terms of classical thermodynamic forces, the fluxes, and the gradients of the fluxes.
As a consequence of (1), it is more natural in EIT to express the thermodynamic forces (containing the time derivatives of the fluxes) in terms of the fluxes and of the gradients of the fluxes. The presence of these gradients allows to couple fluxes of different tensorial orders (as for instance, a vector with the divergence of a tensor or a gradient of a scalar, a tensor with the gradient of a vector, and so on). Thus, the so-called Curie principle of CIT, stating that fluxes and forces of different tensorial orders are not coupled to each other, [24,26,53,54] is fulfilled.
Since the corresponding evolution equations are not exact equations but approximate equations, requiring that the entropy production is positive may be interpreted as giving a limit of validity to these equations; thus, whereas the restrictions of the entropy principle on exact evolution equations could establish that such equations must be valid for any process, the entropy principle as applied to approximate evolution equations may indicate that these equations are only valid for a range of processes, but not for every process. This is not in contradiction with the amendment to the second law proposed by Muschik and Ehrentraut [14], specified in the the introduction, because that amendment implicitly refers to exact constitutive equations [14,75].
The temperature appearing in the Gibbs equations, i.e., the reciprocal of the partial derivative of the entropy with respect to the internal energy, is not the local-equilibrium temperature but depends also on the fluxes. In fact, the several definitions of temperature (caloric, kinetic), when applied to the non-equilibrium system under a heat flux, lead to different values, which reduce to the same value when the non-equilibrium contributions quadratic in the flux are negligible [13].
Two other points worth of comment are the following ones:
The non-classical contributions to the entropy and entropy flux may be given a microscopic physical meaning by fluctuation theory, namely, by combining the generalized entropy with the Einstein’s equation for the probability of fluctuations to obtain the second moments of the fluctuations of the fluxes, which coincide with the usual forms of the fluctuation-dissipation theorems [76,77].
The non-classical contributions to the entropy and entropy flux may also be compared with the corresponding second-order expressions obtained from kinetic theory [76,77], or from information theory. Up to the second order in the fluxes, these microscopic expressions coincide with the macroscopic expressions phenomenologically derived from extended irreversible thermodynamics.
After the evolution equations for the fluxes have been formulated, one is able to give a physical interpretation to the several coefficients appearing in such equations (which are related to the coefficients of the non-equilibrium contributions to the entropy and the entropy flux) in terms of the classical transport coefficients, the relaxation times of the fluxes, the correlation lengths of the fluxes, and so on [78,79]. As a simple illustration we mention the situation related to the so-called Guyer-Krumhansl equation for heat transfer in rigid conductors, which takes into account relaxation effects and non-local effects, in the form [80–82]
where λ is the thermal conductivity, τ the relaxation time of the heat flux and ℓ the mean free path of the heat carriers. The corresponding entropy and entropy flux are
with seq the local-equilibrium entropy.
The second term in Equation (25), i.e., the non-classical contribution to the entropy, has been given in [8] a phenomenological intuitive interpretation. Namely, assume a small volume element of a system with energy ɛ in the presence of a heat flux q, and suddenly isolate it. The heat flux will decay from the initial value q to 0. This relaxation process will produce some amount of entropy. The entropy of the final equilibrium state reached after the relaxation has occurred will be the local equilibrium entropy corresponding to the value of ɛ, namely seq(ɛ). This entropy will be equal to the initial entropy s(ɛ, q) plus the entropy produced during the heat flux relaxation. Thus, s(ɛ, q) may be written as s(ɛ, q) = seq(ɛ)−srel, where srel is the entropy produced during relaxation. This is precisely the form (25). In local-equilibrium theory, the latter term is neglected. This interpretation is complementary to the kinetic-theory interpretation and the fluctuation theory interpretation mentioned two paragraphs above, but more direct and intuitive.
When the mean free path is negligible, Equation (24) reduces to Cattaneo’s equation [80,83]
Equation (26) yields the classical entropy flux, while Equation (25) remains unaltered. Finally, when the relaxation time and the mean free path are both negligible, Equation (24) reduces to Fourier’s law
while Equations (25) and (26) yield the classical entropy and the classical entropy flux. Thus, we infer that the presence of non nonlocal terms in the entropy flux is related to the presence of higher-order gradients in the evolution equation for the heat flux [12].
Absolute temperature is given by the reciprocal of the derivative of the entropy with respect to the internal energy (at constant values of the other extensive variables). When the extended entropy (25) is used instead of the local-equilibrium entropy, the resulting absolute temperature is [13]
with the (temperature dependent) specific heat at constant volume . Note that T differs from the local-equilibrium temperature Teq and depends on the fluxes [13].
Relation (29) is purely formal unless a process of measuring it is specified. In equilibrium, all the many possible operational definitions of temperature lead to the same value, and all the thermometers will indicate it. However, this is not so out of equilibrium, where different kinds of thermometers yield different values for the temperature. In particular, the temperature defined in (29) may be related to the average kinetic energy of the particles in the plane perpendicular to the fluxes, and it is in general different from the ‘temperatures’ of the other degrees of freedom, which may have different values.
In order to show the important role played by the nonlocal constitutive Equation (26), let us consider a cylindrical nanodevice of radius r0, and thickness h0, acting as a steady heat source at constant temperature T0, connected to a graphene circular layer, of outer radius rg, and the thickness hg), which removes the heat from that source. We analyze the steady-state situation in an isotropic layer, in which the heat removed is equal to the heat dissipated, thus allowing the temperature to remain constant.
This situation can be studied starting from the hydrodynamic-like equation
which, in steady states and when the heat flux may be neglected with respect to its spatial derivative, as it often happens in nanosystems, is a direct consequence of the Guyer-Krumhansl heat-transport Equation (24), [84]. Let us observe that in 2D steady-state situations wherein the heat diffuses radially away from a point source, the heat has only one component q given by
with r as the radial distance from the center of the hot spot, and Γ = Q0/ (2πhg), Q0 being the constant amount of heat per unit time irradiated by the point source. Equation (31) is derived under the hypothesis that the lateral heat transferred from the heated graphene layer to the neighboring environment is negligible. The coupling of Equations (30) and (31) leads to
Equation (32) points out that for r < ℓ the temperature gradient dT/dr is positive, whereas for r > ℓ the temperature gradient dT/dr becomes negative, i.e., the temperature profile shows the surprising presence of a hump, which seems to contradict second law of thermodynamics, since for r < ℓ the temperature increases if the distance from the heat source decreases. The reality of such a contradiction may be checked by focusing the attention on the entropy flux (26), which in the case of radial heat propagation becomes
Thus, in a generic annular region between two radial distances r1 and r2, such that r1 < r2, the inequality (1) implies
wherein J (r1) is the incoming entropy flux, and J (r2) is the outgoing one. Owing to Equation (33), the inequality (34) yields
Moreover, since the conservation of the total heat flux across each circular zone implies 2πr1q (r1) = 2πr2q (r2), we have
From this relation it follows that when λT > ℓ2Γ/r2 (or in the limit case of Γ ℓ2/ (λTr2) → 0), then inequality (36) is not violated if T1 > T2. On the other hand, when ℓ < r1, r2 the condition λT > ℓ2Γ/r2 holds. Then we conclude that for radial distances from the center of the hot point larger than the mean free path, as expected, the larger the radial distance, the smaller the temperature.
When r1, r2 < ℓ, instead, then λT < ℓ2Γ/r2, and the inequality (34) changes in
which is not violated for T1 < T2. Then, for radial distances from the center of the hot point smaller than the mean free path, the larger the radial distance, the bigger the temperature, so that the temperature hump arises.
Thus, the nonlocal form (26) of the entropy flux, indicates that in some situations it is possible to have a heat transfer from lower to higher temperature, at the condition that the inhomogeneity in the heat flux is high enough and the dimension of the system is of the same order of magnitude, (or smaller) of the mean free path of the heat carriers.
Another field in which nonlocal interactions are important is the analysis of thermoelectric effects, i.e., the direct conversion of temperature differences to electric voltage and vice-versa. Frequently used conversion devices are represented by nanostructured crystals, in which the heat is carried by phonons and electrons. Their thermodynamical efficiency may be evaluated through the parameter ZT, being Z the so called figure-of-merit, defined as
∈ being the Seebeck coefficient, σe the electrical conductivity, and λe and λp the thermal conductivities due to electrons and phonons, respectively.
Let us focus our attention on a cylindrical nanowire with transversal radius R, such that ℓe < R < ℓp, where ℓe is the mean free path of the electrons and ℓp is the mean free path of the phonons. If the nanowire is assumed to be isotropic, then the heat flux on each cross section propagates radially. In such a case it is realistic to suppose that, due to the reduced dimension of the radius with respect to the phonon mean free path, the effects of the interaction between the phonons and the wall of the nanowire are not limited to a thin layer close to the wall but pervade the whole system. According with this point of view, we suppose that the phonon heat flux is [85,86]
where
represents the heat flux in the bulk, calculated by solving the stationary Guyer-Krumhansl Equation (24) for the phonon heat flux, and is the wall contribution to the heat flux, for which we postulate the constitutive equation [86]
Cp being a non-negative temperature-dependent numerical coefficient characterizing the walls, the value of which is smaller than unit. The influence of is important especially in a thin layer near the walls, the thickness of which is the order of ℓp (i.e., the so-called Knudsen layer). Far from the boundary, the wall contribution in Equation (41) would decrease, in such a way that when the phonon mean free path is negligible with respect to the radial distance (or to the characteristic size of the system), then would become negligible. However, in the present case that layer pervades the whole transversal section, so that the wall contribution arising from Equation (41) is constant. Thus, the radial profile of the total heat flux is [85,86]
while, the figure-of-merit may be calculated to be [85]
As it is possible to observe, the figure-of-merit depends on R (size dependency), and this fact allows to control its value by modulating the physical dimensions of the system. For increasing values of the ratio Knp = ℓp/R, Z decreases and tends linearly to the limit value Zlim = ∈2σe/λe. Moreover, it emerges that a further control of Z may be obtained by controlling the material coefficient Cp.
4. The Entropy Principle in Rational Extended Thermodynamics
Modelling non-equilibrium phenomena in which steep gradients and rapid changes occur represents a challenging task which has been tackled in the case of gas by means of two complementary approaches: the continuum approach and the kinetic approach.
The continuum model consists in describing the system by means of macroscopic equations (e.g., fluid-dynamic equations) obtained on the basis of conservation laws and appropriate constitutive equations. As an example, classical irreversible thermodynamics (CIT), which relies on the assumption of local thermodynamic equilibrium (LTE), has proven to be a useful and sound theory characterized by a systematic and comprehensive theoretical structure [24]. In this framework, the Navier-Stokes-Fourier (NSF) theory [24,87] has gained much popularity mainly due to its practical usefulness in many applications (see Section 2). Nonetheless, CIT and NSF suffer of some limits: since the mathematical structure of these theories is characterized by a system of differential equations of parabolic type, an infinite speed is predicted for the propagation of signals—an issue which has been addressed as the “paradox of heat conduction” [83]. Moreover, the applicability of the classical macroscopic theory is inherently restricted to processes characterized by small Knudsen numbers (dense gas), and the transport coefficients associated to the dissipation processes are not provided by the theory except for the sign.
On the other hand, the approach based on the kinetic theory, which postulates that the state of the gas can be described by a velocity distribution function whose evolution is governed by the Boltzmann equation, is applicable to processes characterized by a large Knudsen number, and transport coefficients naturally emerge from the theory itself. Nevertheless the range of applicability Boltzmann equation is limited to rarefied and monatomic gas.
Rational extended thermodynamics is a phenomenological theory aiming at filling the gap between this two limit cases.
After the well known observation of Cattaneo in the case of a rigid heat conductor [83] and the kinetic 13 moment model due to Grad [42], the first approach of a phenomenological extended thermodynamics (ET) was proposed by Müller, based on the modification of the Gibbs relation [88].
It was observed by Ruggeri in [89] that, in this approach, the entropy production depends strongly of the choice of the entropy flux and for different entropy flux there are different field equations. The differential system is not a priori in the form of balance laws and this implies from mathematical point of view that there is not ever the possibility to define weak solutions and to study shock waves.
Taking into account that the most clear situation in which the NSF theory is not valid is when the gas is very rarefied, Liu and Müller [90] in a classic context and Liu, Müller and Ruggeri in a relativistic framework [91] developed a new restyling of modern ET that was called rational extended thermodynamics [11]. The main difference was that a priori the mathematical structure of RET is based on a hierarchy of balance laws that have the same structure of the moments of the distribution function in Boltzmann equation truncated at some arbitrary order N; the theory, under this respect, resembles the kinetic approach, but the closure is achieved by means of the universal principles of continuum theory: the entropy principle, the objectivity principle and the principles of causality and stability.
More precisely, the kinetic theory of monatomic gases is based on the assumption that the state of the gas can be described by the distribution function f (x, ξ, t). The rate of change of the velocity distribution function in the absence of external forces is determined by the Boltzmann equation
where the collision integral Q( f ) represents the rate of change of the distribution function f due to collisions.
Finding solution of (44) is, in general, an extremely complicated task; however, one is usually interested in the evolution of macroscopic observable quantities. One way to circumvent direct solution of the Boltzmann equation is to define macroscopic quantities by averaging f over the velocity space (moments of the distribution function)
where m represents the mass of the particles, and to determine appropriate governing equations for these new quantities. It is easily seen that the moments of the distribution function satisfy an infinite hierarchy of balance laws in which the flux in one equation becomes the density in the next one
where
with Pll = 0.
The balance laws obtained for the collision invariants m, mξi and mξ2/2 (ξ2 = ξjξj) turn out to be the conservation laws of mass, momentum and energy, since the corresponding production terms are null, and therefore the first 13 moments are identified as the macroscopic variables commonly used
where ρ is the mass density, ρvi is the momentum (being vi the macroscopic gas velocity), ρɛ is the internal energy density, qi is the heat flux,
is the stress tensor, p, Π and Sij denote, respectively, the pressure, the dynamical pressure and the deviatoric part of viscous stress tensor (traceless). Taking into account (46) and (47) we have the relation 3p = 2ρɛ and Π = 0, typical conditions for rarefied monatomic gas.
When we cut the infinite hierarchy (45) at the density with tensor of rank N and we choose as field the densities u ≡ (F, Fk1, Fk1k2, . . . Fk1k2...kN), we have the problem of closure because the last flux and the production terms are not in the list of the densities. The basic idea of RET [11] is to consider the truncated system as a phenomenological system of continuum mechanics, and to consider the above-mentioned quantities as local constitutive functions to be assigned
According to the continuum theory, restrictions on the constitutive equations come only from universal principles, i.e., the entropy principle, the objectivity principle and the principle of causality and stability (convexity of the entropy).
4.1. The 13 Field Theory
An important example of the procedure outlined above is given by the “13-moment theory”, in which the truncated system includes only the quantities F (interpreted as the mass density), Fi (momentum density), Fll (energy density), Fi1i2 (momentum flux), and Flli (energy flux) which are expressed in Equation (46). This is a particular case of system (45) with N = 3
The closure procedure is very complex. To achieve that task, first we need to require the Galilean invariance of the system. Hence, as a consequence of a general theorem for generic balance laws proved in [92], we infer an explicit polynomial dependence of the densities, fluxes and production on the velocity. Then exploiting the entropy principle by using Theorem 6 of Section 5, it is possible (for processes not far from equilibrium state) to obtain a complete closure in which all coefficients are prescribed only by the knowledge of the thermal and caloric equations of state. The closure is proved to be coincident to the system of equations obtained in the framework of the kinetic theory by means of the closure procedure proposed by Grad [42]. The closed system rewritten using the material derivative reads
where τS and τq are the relaxation times which relate to the viscosity and heat conductivity. It is possible to prove that the differential system is symmetric hyperbolic in the main field components (Lagrange multipliers associated to the system (48)).
Remark. We need to observe a misunderstanding point about the Lagrange multipliers. In fact the Lagrange multipliers introduced by Liu [4] are relative to the non-balance form of a differential system like Equation (49). These quantities are not in general a field. The main field, which is instead a vector of independent variables is the particular set of Lagrange multipliers of the system in balance form (48). Therefore the technique described in Theorem 6 is similar to the one proposed by Liu for very special choice of Lagrange multipliers (for more detail the reader can see [92]).
The obtained closed system may be considered as the extension of the Navier-Stokes-Fourier theory for rarefied monatomic gases. In fact, by performing the Maxwellian iteration [93], the Navier-Stokes-Fourier theory is derived from the 13-moment theory.
4.2. Molecular Extended Thermodynamics of Moments and Maximum Entropy Principle
In the case of a large number of moments it is too difficult to proceed with a pure macroscopic theory (as the 13-moments theory) and it is necessary to recall that the Fs are moments of a distribution function f. An alternative method for achieving the closure of the system of equations is provided by MEP, which has its roots in statistical mechanics and information theory [31,32,94]. Originally motivated by the similarity of RET and moment equations derived from the Boltzmann equation on one hand, and by the observation made by Kogan [95] according to which the Grad’s distribution function maximizes the entropy on the other hand, MEP was first proposed by Dreyer [35], then generalized by Müller and Ruggeri to the case of any number of moments [11], and later proposed again and popularized by Levermore [96]. More precisely, suppose to close the system (45) retaining the densities until the tensorial index N. We have the system of balance law
where, the densities F, the fluxes Fj and the productions P are:
with
The MEP procedure states that actual distribution function f is the one which maximizes the physical entropy (4) under the constraints that its moments (51)1 are prescribed. Thus, the approximate distribution function comes out as solution of a variational problem, with constraints and yields the following solution [34]
where λ ≡ (λ, λi1, λi1i1, . . . , λi1i2...iN) is the Lagrange multipliers vector. In equilibrium it is possible to prove that the approximated distribution function reduces to the usual Maxwellian fE. For both mathematical (convergence) and physical (not so large Knudsen number) reasons, the maximizer (52) is expanded in the neighborhood of local equilibrium where all the moments except hydrodynamic ones can be regarded as small. Therefore, the distribution function can be approximated as
where fE denotes Maxwellian distribution in local equilibrium (the local Maxwellian) and λE are Lagrange multipliers evaluated at local equilibrium state.
Plugging (53) into (51)1, we obtain a linear algebraic system that permits to evaluate the Lagrange multipliers λ̃ in terms of the densities F
(FE denotes the equilibrium values). Inserting the Lagrange multipliers as function of the densities solution of (54) into the truncated fluxes (51)2 and source terms (51)3, the truncated system of moment Equation (50) becomes closed. The complete equivalence between entropy principle and MEP was proved by Boillat and Ruggeri [34]. It is also proved that the closed balance laws system can be put into symmetric hyperbolic form using the main field u′ which coincides with Lagrange multipliers λ. Moreover, the same authors put in evidence that the moments closure gives a nesting theories of principal subsystems. In fact, it was proved that if the closure is obtained with two different truncation orders M < N, then the system of order M is a principal subsystem of the system of order N [97]. The main consequence is that the maximum characteristic velocity increases with the index N. Boillat and Ruggeri were able to deduce a lower bound estimate for the maximum characteristic velocity in terms of the truncated index N [34]
where cS is the sound velocity. Therefore, λmax becomes unbounded when N → ∞. Moreover the same authors proved an equivalent inequality in the case of relativistic theory both for non-degenerate [98] and degenerate [99] gas. In this case, as we aspect, the limit of λmax for N → ∞ is the light velocity.
4.3. Rational Extended Thermodynamics of Polyatomic and Dense Gases
For the case of rarefied monatomic gases, the well-established RET theory, endowed with MEP to achieve the closure, has proven to be very successful. Even in those cases in which the 13-moment theory is not so satisfactory (problems involving high-frequency sound waves, light scattering, or shock waves structure [11]), RET provides the right theoretical framework for building theories with higher number of moments which have given results in excellent agreement with the experience.
Unfortunately the RET theory, being strictly connected with the kinetic theory, suffers from the same limit as the Boltzmann equation, which is notoriously valid only for rarefied monatomic gases since the internal energy ɛ and the pressure p are assumed to be connected by the relation 2ρɛ = 3p. In the case of rarefied polyatomic gases, the rotational and vibrational degrees of freedom—which are not present in the simple rarefied monatomic gases model—come into play [? ], and in the case of dense gases, as the average distance between the constituent molecules is finite, the interaction between the molecules cannot be neglected. From a mathematical standpoint, these effects are responsible for intrinsic changes in the structure of the emerging equations of moments that prevent from building a simple hierarchy of equations as in the case of monatomic gases (in particular, the internal energy density is no longer simply related to the pressure).
A RET theory of dense gases and of rarefied polyatomic ones has recently been developed by Arima, Taniguchi, Ruggeri and Sugiyama which adopts the 14-moment: the mass density, velocity, shear stress, dynamic pressure, energy and heat flux as independent fields [100]. This theory provides two parallel hierarchies. One of two hierarchies consists of the balance equations for the mass density, momentum density and momentum flux (momentum-like hierarchy), and the other one consists of the balance equations for the energy density and energy flux (energy-like hierarchy). These hierarchies cannot be merged with each other since the internal energy density (the intrinsic part of the energy density) is no longer related to the pressure (one of the intrinsic part of the momentum flux)—as it is in the monatomic gas case. By adopting the closure by the RET theory to this 14-moment theory, the constitutive equations are determined explicitly with the thermal and caloric equations of state. The theory includes as a singular limit the 13-moment theory for rarefied monatomic gases [101] and this new approach has also been applied to the derivation of a 6-moment theory [102] which extends the Meixner’s model [103,104]. The validity of the theory has been confirmed by comparing its predictions to experimental evidence, for rarefied polyatomic gases, in the case of ultrasonic waves [105] and shock waves [106,107].
As far as the kinetic counterpart is concerned, a crucial step towards the development of a theory of rarefied polyatomic gases is the work by Borgnakke and Larsen [108] in which the distribution function is assumed to depend on an additional continuous variable representing the internal energy of a molecule, thus allowing to take into account the exchange of energy (other than translational) in binary collisions. This model was initially used for Monte Carlo simulations of polyatomic gases, and later it has been applied to the derivation of appropriate Boltzmann equation by Bourgat, Desvillettes, Le Tallec and Perthame [109].
Recently Pavić, Ruggeri and Simić have proven [33], using the MEP that the kinetic model for rarefied polyatomic gases presented in [108,109] yields appropriate macroscopic balance laws in agreement with the 14-moment theory, and presents a natural generalization to polyatomic gases of the classical procedure of MEP valid for monatomic ones. In fact, the two hierarchies of moment equations obtained with the distribution function presented in [33] are consistent with the hierarchies presented in [100]. In particular, it has been shown that the momentum-like hierarchy is related to the classical moments of the distribution function, and the energy-like hierarchy is related to the moments with an additional continuous variable representing the internal energy of a molecule. The result obtained by MEP is in agreement with the macroscopic approach given in [100].
More precisely, the 14 field RET theory of dense gases adopts the following 14 independent fields
whose evolution is governed by the balance equations
where Fijk and Gppik are the fluxes of Fij and Gppi, respectively, and Pij and Qppi are the productions with respect to Fij and Gppi, respectively. The balance equations of F, Fi and Gii are, respectively, the conservation laws of mass, momentum and energy, therefore their productions vanish. There are two parallel series in the balance equations; the one starts from the balance equation with the mass density (F-hierarchy) and the other from the balance equation with the energy density (G-hierarchy). In each series, the flux in one equation becomes the density in the next equation.
In the case of 14 moments it is possible to deduce using the previous hierarchy (56) the closure of the system also for dense gas [100].
In the case of rarefied polyatomic gases, with the thermal and caloric equations of state
where D is related to the degrees of freedom of a molecule given by the sum of the space dimension 3 for the translational motion and the contribution from the internal degrees of freedom (φ ≥ 0) (for monatomic gases, D = 3), the structure of the balance Equation (56) emerges naturally for the moments defined in the kinetic theory [33]. In the present case the idea is to consider an additional parameter in the distribution function f (t, x, ξ, I) defined on extended domain [0, ∞)×R3 × R3 ×[0, ∞). Its rate of change is determined by the Boltzmann equation which has the same form as for monatomic gas but collision integral Q( f ) takes into account the influence of internal degrees of freedom through collisional cross section (Bourgat, Desvillettes, Le Tallec and Perthame [109], see also Borgnakke and Larsen [108]). Pavić, Ruggeri and Simić [33] proved the agreement with the binary hierarchy (56) and the KT, provided we choose the moments
where
The closure with both the method of Entropy Principle and MEP, leads to the following differential system for polyatomic rarefied gas
The entropy density and the entropy flux are expressed as
and concavity of the entropy density is ensured in equilibrium provided D > 3. The modified Gibbs equation arises a posteriori by differentiating (60).
Remarks
- (1)
The previous results are very similar to the ones of the EIT but now all the coefficients in the system (59) and in the entropy density (60) and entropy flux (61) are explicitly determined.
- (2)
The limit D → 3 of monatomic gas is a singular limit but it is possible to prove that the 14 equations and the solutions of the system (59) converge to the 13 equations and solutions of monatomic gas (49) with Π = 0, provided the initial data are chosen compatible with the monatomic gas, i.e., Π(x, 0) = 0, [101].
- (3)
Using the procedure of Maxwellian iteration the Navier Stokes equations emerge as limit case of (59)4,5, while Equation (59)6 reduces to the Fourier law. These results together with similar ones obtained for Fick’s and Darcy’s law convinced one of us (T. R.) that equations that are non local in space are not real constitutive equations but approximations of balance laws equations (as the present case) and the real constitutive equations are local and, as consequence, the differential systems of mathematical physics are hyperbolic rather than parabolic [29]. A further consequence of this conjecture is that these non local equations do not need to satisfy the so called objectivity principle because are approximation of balance laws and the objectivity principle still continues to be valid only for the “authentic” local constitutive equations. However these limit non-local equations are useful not only because they are used in normal physical situations but also because they permit to obtain the evaluation of non-observable quantities such as the velocity or the temperature of each constituent of a mixture.
- (4)
Although the differential system of RET is very complex, it is possible to give some qualitative analysis. In fact, not only every nesting theories of RET are governed by symmetric hyperbolic systems with the property of well posedness of local (in time) Cauchy problem (see Section 5) but there can exists also global smooth solutions due to the overlap between the first 5 conservation laws and the remaining dissipative ones. In fact, for generic hyperbolic systems of balance laws (121), endowed with a convex entropy law, and dissipative, the so called Kawashima-Shizuta K-condition [110] becomes a sufficient condition for the existence of global smooth solutions, provided the initial data are sufficiently smooth (Hanouzet and Natalini [111], Wen-An Yong [112], Bianchini, Hanouzet and Natalini [113], see also the Dafermos book [114]).
Theorem [Global Existence]
Assume that the system of balance laws is strictly dissipative and the K-condition is satisfied. Then there exists δ > 0, such that, if ||u(x, 0)||2 ≤ δ, there is a unique global smooth solution, which verifies
Moreover Ruggeri and Serre have proved, in the one-dimensional case, that the constant states are stable [115].
Theorem [Stability of Constant State]
Under natural hypotheses of strongly convex entropy, strict dissipativeness, genuine coupling and “zero mass” initial for the perturbation of the equilibrium variables, the constant solution stabilizes
Recently Lou and Ruggeri [116] have observed that there exists a weaker K-condition that is a necessary (but unfortunately not sufficient) condition for the global existence of smooth solutions. It was proved that the assumptions of the previous theorems are fulfilled in both classical [117] and relativistic [118], [119] RET and also in the case of mixture of gas with multi-temperatures [120].
5. Exploitation of the Entropy Principle
5.1. The Entropy Principle in RT: Coleman-Noll and Liu Procedures
Let us consider a local state space

We suppose that the evolution of the basic fields zα is ruled by the set of balance equations [8,14]
with as the components of the flux of zα, and rα as either the productions of zα or the source terms.
The dissipation inequality reads [8,14]
with s the entropy density, Jk the components of the entropy flux and σ the entropy production density, which has to be nonnegative.
Thus, the set of governing equations, evaluated on the state space, reads
In Equation (64), the entropy density s and the entropy flux density J are constitutive quantities so that, by taking into account the state space (62) we obtain the dissipation inequality
The inequality above is linear in the ω time derivatives ∂tzα and on the 6ω space derivatives . We call these 7ω quantities higher derivatives. In an arbitrarily fixed point (x0, t0), let us introduce the vector y ∈ Rn, n = 7ω, given by
We call y process-direction vector. That way, in (x0, t0) we can write the balance equations and the entropy inequality as follows
where A is a matrix, B and C are vectors and D is a scalar. All these quantities depend on the elements of the state space evaluated in (x0, t0), so that
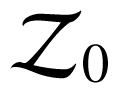
Theorem 1
[14]. In any point (x0, t0) of the space-time, the process-direction vectors can take arbitrary values.
Proof
Since Equation (65) is a system of differential equations of first order in time, suitable (global) initial conditions
must be assigned. By successive differentiations with respect to space, from Equation (70) the relations
ensue.
From Equation (71), we argue that 6ω of the 7ω higher derivatives (67) follow by the initial conditions z(x, t0). The remaining ω higher derivatives ∂tzα(x, t0) are determined by the balance Equation (65). Now, let us evaluate Equations (70) and (71) in an arbitrary but fixed point (x0, t0). We get so
The 7ω real numbers in Equations (72) and (73) can be arbitrarily chosen, changing the global initial conditions (70), and the 6ω of them in (73), (the higher derivatives), can be changed without influencing the coefficients of the higher derivatives in the system (65), since these quantities depend on the elements of the state space only. This is enough to prove your assertion
The problem now is to exploit the new dissipation inequality obtained by the inequality (66) after having taken the balances (65) into account.
In the light of the previous result, it is worth investigating if, for arbitrary initial conditions, A, B, C and D allow only solutions y of Equation (68) leading to a nonnegative entropy production density or whether there are solutions giving rise to a negative entropy production.
We have two possibilities, each of them excluding the other one:
- (1)
in (x0, t0) all (local) solutions of the balance equations have to satisfy the second law, i.e.,
- (2)
in (x0, t0) there are (local) solutions of the balance equations which satisfy the second law and others which do not, i.e.,
In (x0, t0) a process-direction vector y is said
reversible if
admitted if
forbidden if
Axiom 1
[14]. Except in equilibria, reversible process-direction vectors do not exist.
Theorem 2
[14]. If Axiom 1 is true, then the entropy inequality
is necessarily a restriction on the constitutive equations and not on the processes.
Proof
Let us suppose that in nonequilibrium second law represents a restriction on the processes, i.e., that there exist nonequilibrium solutions of the balance equations which satisfy the second law and others which do not. Let us denote by y1 and y2 an admitted process-direction vector and a forbidden one, and let us prove that, in such a case, there exists a process-direction vector
with
which is reversible.
In fact, let us evaluate Equation (68) first in y1 and multiply them by a scalar α, and then in y2 and multiply them by the scalar β = 1 – α. Thus,
Moreover, since y1 is an admitted process-direction vector while y2 is a forbidden one, the entropy production densities σ1 and σ2 in correspondence of them will be
It is worth observing that y3 satisfies the system of balance laws (68). In fact, by addition of (83) to (84), we obtain
On the other hand, the entropy production density corresponding to y3, namely
has not definite sign, and therefore nothing prevents that y1 and y2 are such that
However, since σ3 < 0 characterizes processes which do not exist in nature, for real ones we have σ3 = 0, so that y3 is a reversible process-direction, contradicting so Axiom 1.
Moreover, the following relation, corresponding to reversible processes, holds
Equation (90) yields the following value of α
As a direct consequence of the admissibility of y1 we infer α ≤ 1. Moreover, by inequalities (85) and (86), it follows that D – B · y2 > 0 and B · (y1 – y2) > 0, from which we conclude that α is positive.
Due to the result above, presupposing the validity of Axiom 1, we are forced to conclude that in correspondence of nonequilibrium states, the process-direction vectors are either all admissible or all forbidden. On the other hand, since the real processes are necessarily admissible, the second hypothesis is false. As a consequence, in nonequilibrium second law cannot exclude forbidden process-direction vectors (since they do not exist) but it may only restrict the constitutive equations. This completes the proof.
In rational thermodynamics (RT) the sole balance equations are the balances of mass, linear momentum, angular momentum and energy [1–3], which locally read
where bi are the components of the specific external force and r is the specific heat supply. The system above is closed by assigning suitable constitutive equations for Ti j and qi. The state space can be either local or weakly nonlocal. The local unbalance of entropy is postulated in the form (1), and the entropy flux is assumed either in the Coleman-Noll form [2] , or in the Müller’s one [7] (see Section 1). In this more general case, in virtue of the balance of energy, the local entropy inequality reads
with the Helmholtz free energy ψ given by the Legendre transformation ψ = ɛ – T s [3]. The relation above is referred to as Clausius-Duhem inequality [1].
Alternative approaches introduce an additional rate of supply of mechanical energy, the interstitial working, engendered by long–range interactions among the molecules [18], or by diffusion of matter through the system [121], which results in an energy extra–flux u into the local balance of energy. In this case, the Clausius-Duhem inequality becomes
Without loss of generality we can pursue our analysis under the hypothesis that the relation (95) holds. For a system at rest with the state space (62), it reads
Thus, it is easy to verify that in an arbitrary but fixed point (x0, t0) the inequality above may be rewritten as
where B̃ and à are vectors and D̃ is a scalar, all depending on
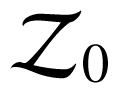
Theorem 3
[3]. Let B̃ ∈ Rn, Ã ∈ Rn and D̃ ∈ ℝ two given vectors (independent of y), and a given scalar, respectively. Then, the inequality
is satisfied for arbitrary y ∈ Rn if, and only if,
Proof
The proof is straightforward. It is clear that the conditions (100) are sufficient to satisfy (99). On the other hand, should B̃ – Ã be different from 0, being y arbitrary, it could be chosen in such a way that the inequality (99) could be easily violated. Thus, it is necessary that B̃ – Ã = 0, and, as a consequence, D̃ ≤ 0
Equations (100) constitute a set of a priori constraints, to be satisfied by the constitutive equations in (x0, t0), to ensure that the entropy inequality is fulfilled for arbitrary process-direction vectors. On the other hand, since (x0, t0) is arbitrary, we can write the relations (100) in any point (x, t), getting so a set of global conditions ensuring that the entropy inequality is fulfilled along arbitrary thermodynamic processes.
The technique illustrated so far is known in literature as Coleman-Noll procedure. Since the form of B̃, Ã and D̃ depends on the way in which Equations (68) are substituted into the inequality (69), the restrictions (100) can take different form, depending on the type of substitution. This problem motivated Liu [4] to develop an alternative method, which is known as Liu procedure, based on earlier results of linear programming [6]. The Liu procedure is based on the following algebraic lemma.
Theorem 4
[4]. Let
Then the following statements are equivalent:
- (1)
- (2)
there exists Λ ∈ Rn, with Λ ≠ 0, such that
- (3)
there exists Λ ∈ Rn, with Λ ≠ 0, such that
Proof
It is trivial that 2 implies 1. To see that 2 and 3 are equivalent, let us observe that the inequality (102) can be rearranged as follows
Being y arbitrary, Equation (105) is true if, and only if, Equation (103) and Equation (104) hold. Thus, to complete the proof, it is sufficient to show that 1 implies 3. Then, let
Similarly, let
Observe that H0, , S 0 and are all linear subspaces of Rn. Then, if x ∈ S 0, for any y ∈ S we have x+y ∈ S . By definition, 1 implies S ⊂ H, and we claim that this implies S 0 ⊂ H0. In fact, if we suppose that S 0 ⊄ H0, then there exists x ∈ S 0 such that x ∉ H0, i.e., Ax = 0 and B · x ≠ 0. Since S 0 is a linear subspace of Rn, for any a ∈ ℝ it follows that ax ∈ S 0, which implies, for any y ∈ S , that y + ax ∈ S . But
Since x ∉ H0, i.e., B · x ≠ 0, there exists a ∈ ℝ such that B · (y + ax) – D < 0, which allows to conclude that y + ax ∉ H.. Hence, S ⊄ H, which contradicts our initial assumption. Therefore, we must have S 0 ⊂ H0. That implies , because if z ∈ then z · x = 0∀z ∈ S 0 ⊂ H0. Observe that, by definition, and also the n vectors of Rn formed by the elements of the columns of A, let us call them u1, . . . un, belong to . On the other hand, since we know from linear algebra that is spanned by u1, . . . un. Thus, there exists Λ ∈ Rn, with Λ ≠ 0, such that B = ΛA, which is Equation (103). Finally, for any y ∈ S , i.e., such that Ay = C we get B · y – D = ΛA · y – D = Λ · Ay – D = Λ · C – D ≥ 0 by definition. This completes the proof
A simple but meaningful application of this procedure can be seen in Section 2, and the results are shown in Equations (18)–(21). More refined applications are illustrated in Section 4.
For the sake of simplicity all the results above have been proved for a system at rest, in the case that only the first-order gradients of the unknown quantities enter the state space. It is worth noting that the proofs may be given in more general situations, i.e., for moving systems, with the higher-order gradients of the zα to enter the state space. The readers interested to this problem are referred to the original papers by Muschik and Ehrentraut [14] for Theorem 2, by Coleman and Gurtin [3] for Theorem 3, and by Liu [4] for Theorem 4.
Although Coleman-Noll and Liu procedures are quite different, it can be proven that for some class of materials they lead to the same results [122].
5.2. Thermodynamics with Internal Variables: The Onsager Procedure
An interesting situation arises when the state pace is spanned by ω internal variables aα, i.e.,
The internal variables of state constitute an important tool in dealing with nonequilibrium processes involving complex thermodynamical systems. This is the case in the inelastic behavior of solids or in the relaxation effects in thermo-viscous fluids [123,124]. These non-equilibrium parameters, whose nature depends on the phenomenon at hand, are introduced through ordinary differential equations, called kinetic equations, on the basis of physical experiments. The entropy principle can help to determine the form of the kinetic equations, which can be written as
where the fα are supposed to be regular functions of their arguments. In this case, the entropy inequality on the state space reads
Both the ω quantities and the 3ω quantities ∂kaα are referred to as generalized thermodynamic forces while the ω time derivatives ∂taα are called thermodynamic rates and the 3ω elements generalized thermodynamic fluxes, [24,72]. Thus, the inequality above can be put in the form
where x and y are vectors of Rω whose components are the ω thermodynamic forces and the ω thermodynamic rates ∂taα, respectively, while X and Y are ω × 3 matrices, whose components are the 3ω thermodynamic fluxes , and the 3ω thermodynamic forces ∂kaα, respectively.
In the inequality above, the time and space derivatives of aα can be regarded as unknown functions of the elements of the state space. Thus, in a linear approximation, we are allowed to express these quantities as linear functions of the thermodynamic forces , and of the thermodynamic fluxes [24], namely,
with L, M, N, and P as suitable tensors defined on the state space.
Theorem 5
For isotropic systems, if L and P are positive semidefinite, the linear relations (111) and (112) are sufficient to ensure that the local entropy production is nonnegative along arbitrary thermodynamic processes.
Proof
As first observed by Truesdell [1], the theory of representation of isotropic tensor functions [125] implies that for isotropic systems the linear relationships (111) and (112) hold if, and only if, M = N = 0. Thus, the inequality (110) becomes
which is always satisfied if L and P are positive semidefinite
Remarks
- (1)
It is worth noting that the vanishing of M and N for isotropic materials was known for a long time in classical irreversible thermodynamics, and referred to as Curie Principle, [24,53,54]. It asserts that for isotropic systems the thermodynamic forces and fluxes of different tensorial character do not couple. Truesdell, [1], was the first to observe that this statement does not correspond to any physical principle but is a straightforward consequence of the theory of representation of isotropic tensor functions [125]. Due to the result above, the linear relationship (111) reduces to
which represents the set of ordinary differential equations we are looking for. That way, the form of the kinetic equations is determined by the constitutive equation of the specific entropy [126]. Such a method is often referred to as the Onsager procedure.
- (2)
Since x and X are not independent, as both are functions of the elements of the state space, the positive semi-definiteness of L and P is not necessary to ensure that the entropy production is always nonnegative. More precise information can be obtained by the Coleman-Noll analysis of the Clausius-Duhem inequality, which reads now
The necessary and sufficient conditions to satisfy (115) along arbitrary thermodynamic precesses are [3]
Thus, we conclude that the Onsager procedure is capable to provide less information with respect to Coleman-Noll and Liu ones. However, it is the sole method which can lead to a set of differential equations as thermodynamic restrictions, since the Coleman-Noll procedure restricts the functions fα only by the unilateral differential constraint (116)2.
5.3. Quasi-Linear First Order Hyperbolic Systems and Discontinuity Waves
In continuum physics the systems of governing equations often my be also put in the first-order quasi-linear form
with the unknown N-column vector u(x, t) = (u1, u2, . . . uN)T, where A0 and Ai are real N × N matrices and f is a N-column vector too. The most important consequence of nonlinearity is that non regular solutions may occur and propagate through the medium as waves.
A wave is a moving surface ∑ represented mathematically by the equation
which defines the wave front. The unit normal n on ∑ and the normal speed V of ∑, are given by
Weak waves have a continuous velocity across the front but a jump of the acceleration. Meantime, the unknown fields uα, α = 1, . . . N, are continuous across the front but their gradients are discontinuous, with the jump pointing in the normal direction. The symbols F+ and F− will denote the limits of F on the side of ∑ with positive and negative normal, respectively. The quantities Πα = [∂iuα] ni, where [F] = F+ – F− is the jump of F along the normal, are called amplitudes of the acceleration wave, and their evolution is ruled by a Bernoulli equation [127–129]. The wave speeds and the amplitudes of the acceleration waves are given, respectively, by the eigenvalues λ and the eigenvectors r of the following eigenvalue problem
The system (117) is said hyperbolic in the t-direction if detA0 ≠ 0, and the problem (120) has only real eigenvalues (characteristic speeds) and N independents right eigenvectors. The system (117) is said symmetric if A0 is positive definite and Ai = Ai T. Any symmetric system is hyperbolic.
A remarkable consequence of the symmetry is the well-posedness of the Cauchy problem under very general conditions [30]. In fact, for any symmetric system, the Cauchy problem with initial data in a Sobolev space Wp,2 with p ≥ 4, has a unique solution u ∈ Wp,2 in the neighborhood of the initial manifold [130].
5.4. Balance Laws and Entropy Principle
A particular case of the quasi-linear first order system (117) is the system of balance laws
compatible with a supplementary balance law
with h0 = −ρs and hk = −Jk − ρsvk.
Theorem 6
[92,131,132]. The constitutive equations for the system of balance laws (121) compatible with the entropy inequality (122) are those and only those for which there exist four potentials, called generators, and a privileged field u′, called main field, such that
Moreover, if h0 is a convex function of u, then the field equations form a symmetric hyperbolic system and the Cauchy problem is well-posed under suitable smooth initial data.
Proof
The compatibility of (123) with (124) implies the existence of a particular set of Lagrange multiplier u′ such that [132]:
As the system (121) is quasi-linear and the entropy inequality must be valid for any solutions we have: [4,92]
The condition (127) may be written as
Supposing that the map (u ⇔ u′) is invertible, we may choose the multipliers u′ as new field variables. Therefore, from (129) we obtain
where we have put
From (130) we have
and we conclude that the entropy principle implies that the vectors Fβ are gradients of the four potentials with respect to the components of the new field u′. This was not the case for the field u and therefore u′ will henceforth be called the main field [132].
Moreover, the production term F is admissible, if and only if it satisfies the residual inequality (128). If we insert (132) into the original system (121), it becomes
or, equivalently
where the matrices Aα are the Hessian matrices of with respect to the components of u′, namely
Obviously they are all symmetric. Now we choose the components of the field u to coincide with the densities F0, which we may do without essential loss of generality, and we assume that h0 is a strictly convex function of u. In this case it is granted that it is possible to choose u′ as field. Indeed from (129), when β = 0, we obtain
and therefore the Jacobian matrix
is positive definite and the map from u to u′ is globally invertible. Moreover from (131), evaluated for β = 0, we observe that is the Legendre transformation of h0 and therefore is also a convex function of u′. Indeed we have
Thus, by (135) it follows that the matrix A0 is positive definite. We have in this case that all matrices Aβ are symmetric and A0 is also positive definite. Consequently our system (134) is a symmetric hyperbolic system in the sense of Friedrichs and Lax [133]
5.5. Generalization of the Classical Exploitation Procedures
New mathematical problems arise when dealing with higher-grade materials, namely those materials with higher-order gradients in the state space. In such a case, since the number of balance laws is smaller than that of the state variables, we have some time derivatives that appear into the entropy inequality but not in the system of balance laws. As a consequence, in the inequality (99) the dimension of B̃ and y is, in general, higher than that of Ã. Hence, it may be rearranged as follows
where yA includes the higher derivatives which appear into the entropy inequality as well as in the balance equations, while yB includes the higher derivatives which enter the entropy inequality but not the balance laws. The vectors B̃A and B̃B are formed consequently. By (139), the following thermodynamic restrictions ensue (see Theorem 3)
Since the components of the vector B̃B are the partial derivatives of the specific free energy with respect to some of its arguments, the second of the restrictions (140) results in the independence of the thermodynamic potentials with respect to some state variables, and this fact may lead to the thermodynamic incompatibility of important classes of materials. A meaningful example is constituted by Korteweg fluids. Capillarity effects in fluids can be modeled through the presence of density gradients in the elastic part of the Cauchy stress tensor. Such an idea has been introduced in 1901 by the Dutch physicist D. J. Korteweg, who proposed the following constitutive equation for the elastic part of the Cauchy stress
where p is the pressure of the fluid, while α̃, β̃, γ̃ an δ̃ are suitable material functions of ρ and the temperature T, [134]. The hypothesis above requires the second derivatives of the mass density to enter the state space. However, if we investigate the thermodynamic compatibility of Equation (141) by the Coleman-Noll procedure, from one side, by the first of the restrictions (140) we get that the stress can be calculated by partial derivation of the free energy, from the other side, by the second of the restrictions (140) it follows that the free energy cannot depend on the gradients of ρ. As a consequence, Equation (141) results to be incompatible with second law, i.e., it does not exist in nature. Since such a result does not comply with the experimental evidence, it is necessary to deal with more general situations, allowing the thermodynamic compatibility of Equation (141). We already observed that there are different approaches which allow this compatibility by modifying in different ways either first or second law of thermodynamics, so that we have a non uniform approach with respect to the classical structure of continuum theories.
However, it is possible to regard this problem from a purely mathematical point of view, by considering a wider set of governing equations, some of them not in the balance form, by taking the gradients of the basic balance laws up to the order of the gradients entering the state space. That way, the number of differential constraints to be taken into account is always equal to the number of thermodynamic variables. Moreover, since both the Coleman-Noll and Liu procedures reduce the exploitation to an algebraic problem in an arbitrary point of the space-time (see Theorems 1–4 above), and since in a fixed point a function and its derivatives are independent quantities, the additional constraints are independent of the original ones. Thus, it is worth investigating:
- (1)
what is the form of the entropy inequality once the gradients of the balance laws have been taken into account;
- (2)
what is the new set of thermodynamic restrictions implied by this new, generalized, entropy inequality.
From now on, we pursue our analysis by considering the Liu procedure only. Similar conclusions may be achieved for the Coleman-Noll one [20]. For the sake of simplicity, we will limit to analyze first-order non locality only, so that
In the classical Liu procedure, the obtained entropy inequality (Liu inequality) is linear with respect to those time derivatives which cannot be expressed through the balance laws as functions of the elements of the state space. Moreover, it is linear also with respect to the spatial gradients which are one order higher with respect to the order of the gradients entering the state space. In the extended procedure, instead, gradients which are two orders higher with respect to the order of the gradients in the state space, enter the entropy inequality [19,21]. Moreover, the obtained entropy inequality, (extended Liu inequality), is no longer linear with respect to the spatial gradients which are one order higher than that one of the gradients in the state space. Hence, in what follows, we distinguish between higher derivatives and highest derivatives [20,21]. The higher derivatives are the spatial derivatives whose order is higher than that one of the gradients entering the state space. The highest derivatives are both the time derivatives of the elements of the state space which cannot be expressed through the governing equations as functions of the basic fields, and the higher derivatives whose order is the highest one.
Let us introduce in (x0, t0) the vector of the highest derivatives
which, in the present case, is an element of Rm, with m = 14ω. We call X higher-order process-direction vector. Let us define further the new process-direction vector, which is given by
and is an element of Rn, with n = 6ω. The answer to the questions 1. and 2. above is given in the propositions below. For the proofs, let us refer to [21] the readers interested.
Theorem 7
[21]. In any point (x0, t0) of the space-time the vectors Y and Y take arbitrary values.
Theorem 8
[21]. In any point (x0, t0) of the space-time the set of governing equations i.e., the fundamental balance laws and their gradient extensions, and the extended Liu inequality take the form
where the p×m matrix E and the vector H ∈ Rm depend on the elements of the state space
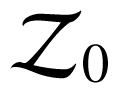
Theorem 9
[135]. If Axiom 1 is true, then second law of thermodynamics in the form (146) is necessarily a restriction on the constitutive equations and not on the processes.
Theorem 10
[21]. The inequality (146) may be rewritten as
where a is a n × n matrix, the vectors h and e belong to Rm, the vectors b and d are elements of Rn and c ∈ ℝ. Moreover, such a relation holds for arbitrary X ∈ Rm and y ∈ Rn if, and only if,
and a is positive semidefinite.
The result above does not prevent the constitutive equations to depend on the whole set of the thermodynamic variables. However, particular solutions of Equations (148) and (149) can result in the independence by some of the variables.
That way, the thermodynamic compatibility of higher-order nonlocal theories can be achieved without any change of first or second law of thermodynamics.
Let us consider now an initial value problem with non-regular data. In particular, let us focus our attention on initial conditions suffering jump discontinuities across a surface, which could lead to non-regular solutions. They can be written as [135,136]
where Ω0 is the discontinuity surface at a fixed instant t0, is the side of Ω0 with positive normal and is the side with the negative one. As a consequence, the up-scripts + and − will denote the value of the fields on and respectively.
Finally, let us consider the following projections of the state space
onto and , respectively
On the other hand, the balance equations and the entropy inequality in an arbitrary point of and , respectively, and at an arbitrary time t0, read [136]
where Z+ and Z − denote the process directions in an arbitrary point of
and
, respectively, and at an arbitrary time t0, while
and
denote the the state spaces
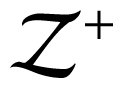
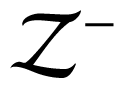
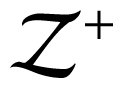
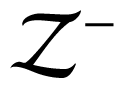
Axiom 2
[136]. Except in equilibria, reversible process directions in an arbitrary point of and, and at an arbitrary time t0, do not exist.
The meaning of Axiom 2 is straightforward. Since Axiom 1 expresses the well-known experimental evidence that reversible thermodynamic transformations in

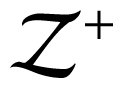
The main consequence of the axiom above, is the following.
Theorem 11
[136]. If Axiom 2 is true, then, on and, second law of thermodynamics is necessarily a restriction on the constitutive equations and not on the processes.
6. Conclusions and Perspectives
We have examined different approaches to non-equilibrium thermodynamics starting from different applications of the entropy principle in different thermodynamic theories. We have pointed out that, in spite of the apparent differences, the theories present several similarities.
We reviewed the methods of exploitation of the entropy inequality and showed that they are robust from the mathematical point of view, unless in CIT, in which some methodologies are rather heuristic and not based on rigorous mathematical proofs (see [1], Lecture 7, for an extensive discussion).
In RT (Rational Thermodynamics) the entropy principle is characterized by the following properties: The entropy inequality in postulated in the form (1). The dissipative fluxes are constitutive quantities. The entropy current density is given by the heat flux divided the local-equilibrium temperature. The entropy inequality is exploited by the Coleman-Noll or Liu procedures.
In CIT (Classical Irreversible Thermodynamics), it is characterized by the following properties: Local equilibrium, usually given in the form of a classical Gibbs relation or, equivalently, by a local entropy function. Heuristic state spaces. Entropy current density as in RT. Solution of the entropy inequality in the form of thermodynamic fluxes and forces. Balance form of evolution equations.
In TIP (Thermodynamics of Irreversible Processes):
Gibbs relation is not necessary, but possible. The state spaces are extended including weak nonlocality. Entropy current density is calculated. A solution of the entropy inequality is obtained in the form of thermodynamic fluxes and forces. Balance form of evolution equations is not required.
The entropy principle in EIT (Extended Irreversible Thermodynamics) is characterized by: Generalized Gibbs relation, with the dissipative fluxes as new variables. Generalized entropy current. Solution of the entropy inequality either in the form of thermodynamic fluxes and forces or by Coleman-Noll or Liu procedures. Balance form of evolution equations. Compatibility with the structure of kinetic theory, with transport coefficients not necessarily calculated.
The entropy principle in RET (Rational Extended Thermodynamics) has the following distinguishing properties: Rigorous compatibility with moment series expansion of kinetic theory, e.g., transport coefficients are calculated. Gibbs relation as consequence of the general mathematical structure. Balance form of evolution equations, and generalized entropy current density. Entropy inequality (beyond H-theorem) used in the closure and also in the construction of a symmetric system of governing equations.
In general, we can say that with more compatibility with kinetic theory the continuum theories loose from their universality, because they can be applied for a restricted class of materials, but gain in predictability, because the mathematical structure becomes more rigorous and material quantities can be calculated.
6.1. Comparison of the Various Approaches
All the presented theories are able to reproduce important physical phenomena. Moreover, also local and nonlocal theories seem to be not so far as it could appear at a first sight. For instance, although the Guyer-Krumhansl Equation (24) cannot be directly obtained in RET [11], since its derivation requires that the gradient of the heat flux enters the constitutive equations, one can obtain it through a suitable approximation of the system of RET. In fact, according to the point of view expressed by one of us (T. R.) in Section 4, the nonlocal constitutive equations should be considered as balance equations in truncated form. Furthermore, although the presence of the spatial gradients into the constitutive equations makes the nonlocal theories parabolic, so that finite speeds of propagation, in a classical mathematical sense, cannot be expected, all the theories are capable to satisfy the causality requirement.
As we pointed out in Section 4, in RET the requirements of causality and predictability are achieved by applying the entropy principle to find the main field which symmetrizes the system of field equations.
In weakly nonlocal theories (RT, EIT, TIP) instead, finite speeds of propagation can be obtained in generalized sense, by observing that a correct estimation of the speed of propagation of the perturbations requires to compare the order of magnitude of the solution of the system of balance equations with that of the error affecting the experimental data which the theory aims to fit [137]. Thus, if in a finite interval of time the solution of the system of balance laws is bigger than the experimental error only in a compact domain, then such a solution is experimentally zero outside this domain. As a consequence, it has propagated with finite speed, because not all the points of the space have been reached in a finite time [138]. This point of view complies with a classical result proved by Fichera in his celebrated defense of Fourier theory [139], whose meaning is that the measurements of temperature and heat flux are valid only within the limits of observation, which, in turn, depend on the sensitivities of measuring instruments.
In his article Fichera also commented an observation made by Maxwell [140], namely that the sensible propagation of heat, so far from being instantaneous, is instead a very slow process, and that the time taken for the bulk of the heat to propagate is proportional to the square of the distance.
This idea suggests a second line of defense of Fourier theory [141], which has been provided with a rigorous measure-theoretic foundation by Day [141,142] and Day and Saccomandi [143,144].
Of course, the arguments above loose their validity in a relativistic context, where the experimental evidence—always confirmed until now—imposes the speed of light as upper bound for the velocity of propagation of thermomechanical disturbances. Thus, in this case the system of balance laws must be necessarily hyperbolic. A generalized constitutive principle, which is compatible with parabolic theories in the classical case but also forces the theories to be hyperbolic in the relativistic one, has been proposed in [138].
In RT memory effects, as those arising in heat conduction with finite speed, are often modeled through integral constitutive equations [145]. In such a case the balance equations are difficult to solve, and sometime the well posedness of the relevant Cauchy problem is not guaranteed [146]. Another possibility, used both in RT [147–149] and in CIT [150] is to introduce internal state variables [123,126]. Such an approach leads to more simple systems of equations. Nonetheless, although internal variables are always measurable, in the sense that one can always manage to detect and to measure them [123], they are in general “not controllable”, i.e., their value on the boundary cannot be conditioned through the direct action of external forces [123,124]. Hence it is difficult to assign appropriate boundary conditions, [151,152]. The determination of suitable boundary conditions is a serious problem also in extended theories, since often the physical meaning of the higher order fluxes is not clear [153]. Moreover, since in these theories the number of field equations is not fixed, an important problem is the determination of the appropriate number of equations, i.e., of the step at which the system of balance laws should be truncated [154].
Some final comments are in order.
First we observe that, according to the results of kinetic theory, extended thermodynamics is not a single theory, but a family of theories, each of which is extracted by an hierarchy of infinite balance equations. Nonetheless, each theory has a finite number of equations, which is determined according to a general criterion established in [154]. Such a criterion, which requires to evaluate, by physical considerations, the steepness of the rapid thermodynamic changes in the nonequlibrium processes at hand, can be formulated as follows: If one expects that a process is “steep of

When the boundary value of higher order fluxes cannot be determined by direct measurements, one can use the so called fluctuation principle, according to which the systems on the boundary adjust naturally to the mean values of the fluctuating boundary values [153]. On the other hand, the information obtained by this principle should be merged with the consideration that the boundary conditions do not depend only on the properties of the system, and on external forces or fluxes, but also on particular features of the walls (smooth or rough, polar or non-polar, rigid or elastic, electrically charged or neutral, and so on). These characteristic should be taken into account in calculating the mean of the fluctuating boundary values.
There are subtle differences between EIT and RET, the most important one being the choice of the state space. A further difference is the starting point of the theories, since EIT assumes a modified Gibbs equation and does not require balance laws a priori, while RET starts from the balance structure dictated by kinetic theory. The first approach is more general while the second approach is well-suited for a restricted class of materials (e.g., rarefied monoatomic gases, polyatomic and dense gases). However, it provides more accurate models of these materials, determining all the material properties from the thermal and caloric equations of state. Also, it leads to a satisfactory qualitative analysis of shock wave propagation.
Some authors consider CIT with internal variables the real counterpart of EIT and RET [123,124]. In this respect the fluxes are regarded as special extensive internal variables with a kinetic equation in the balance form [123,124]. Moreover, internal variables seem to work also for solids, while for these materials is more difficult to develop extended thermodynamics models. Although internal variables are, “in general”, not controllable, often we can control them. This is the case, for instance, of the Ginzburg-Landau theory, in which the value of the phase-field on the boundary can be obtained by physical considerations on the properties of the phase transition [69,70]. In other cases the values of the internal variable on the boundary are dictated by second law of thermodynamics [152].
A comparative analysis of the main properties of the different thermodynamic theories is resumed in the tables below. In Table 1 we compare the different thermodynamic theories on the base of their properties of predictability, causality and agreement with kinetic theories. In Table 2, instead, a comparison is made by taking into account the number of equations, the type of constitutive equations and the way in which boundary conditions can be assigned.
It is worth observing that what we presented above is only a first tentative scheme of comparison. The detailed comparison and classification of the different theories with respect to the properties mentioned above could be the subject of a future separate review.
At this point, it seems natural to investigate if there exists a more general approach to non-equilibrium thermodynamics which encompasses all the previous ones. This important problem, which still remains to be solved, is left to the young generations of thermodynamicists.
Acknowledgments
Vito Antonio Cimmelli acknowledges the financial support from the University of Basilicata, research project Equazioni costitutive non locali in fisica del continuo, and from the Italian National Group of Mathematical Physics GNFM-INdAM.
David Jou acknowledges the financial support from the Dirección General de Investigación of the Spanish Ministry of Economics and Competitiveness under grant FIS No. 2012-33099, and the Direcció General de Recerca of the Generalitat of Catalonia under grant No. 2009-SGR-00164.
Tommaso Ruggeri acknowledges the financial support from the University of Bologna Farb Project 2012 Termodinamica Estesa dei Processi di Non Equilibrio dalla Macro-alla-Nano-Scala, and from the Italian National Group of Mathematical Physics GNFM-INdAM. Péter Ván acknowledges the financial support from OTKA, under grants K81161 and K104260.
Conflicts of Interest
The authors declare no conflicts of interest.
- Author ContributionsIn this article Péter Ván illustrated the role of the entropy principle in classical irreversible thermodynamics; David Jou analyzed the application of the entropy principle in extended irreversible thermodynamics; Tommaso Ruggeri showed the consequences of the entropy principle in rational extended thermodynamics; Vito Antonio Cimmelli presented some classical results of rational thermodynamics and recent results regarding the mathematical analysis of the entropy inequality. All 4 authors were fully involved in: substantial conception and design of the paper; drafting the article and revising it critically for important intellectual content; final approval of the version to be published.
- In memory of Prof. Witold KosińskiOne day before the receipt of the proofs of this article, the authors have learned of the untimely death of Prof. Witold Kosiński, from the Polish-Japanese Institute of Information Technology in Warsaw and Institute of Mechanics and Applied Computer Science at Kazimierz-Wielki University in Bydgoszcz. For all of them Witold was a dear colleague and a renowned scientist. For V. A. Cimmelli he was also a memorable teacher and a sincere friend. The authors remember him with affection and they wish to dedicate this article to his memory.
References
- Truesdell, C. Rational Thermodynamics, 2nd ed; Springer: New York, NY, USA, 1984. [Google Scholar]
- Coleman, B.D.; Noll, W. The thermodynamics of elastic materials with heat conduction and viscosity. Arch. Ration. Mech. Anal 1963, 13, 167–178. [Google Scholar]
- Coleman, B.D.; Gurtin, M.E. Thermodynamics with internal state variables. J. Chem. Phys 1967, 47, 597–613. [Google Scholar]
- Liu, I.-S. Method of Lagrange multipliers for exploitation of the entropy principle. Arch. Ration. Mech. Anal 1972, 46, 131–148. [Google Scholar]
- Hauser, R.A.; Kirchner, N.P. A historical note on the entropy principle of Müller and Liu. Continuum Mech. Thermodyn 2002, 14, 223–226. [Google Scholar]
- Farkas, G.Y. A Fourier-féle mechanikai elv alkalmazásai. Mathematikai és Természettudományi Értesít˝o 1894, 12, 457–472. (In Hungarian). [Google Scholar]
- Müller, I. On the entropy inequality. Arch. Ration. Mech. Anal 1967, 26, 118–141. [Google Scholar]
- Jou, D.; Casas-Vázquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 4th ed; Springer: Berlin, Germany, 2010. [Google Scholar]
- Lebon, G.; Jou, D.; Casas-Vázquez, J. Understanding Nonequilibrium Thermodynamics; Springer: Berlin, Germany, 2008. [Google Scholar]
- Jou, D.; Casas-Vázquez, J.; Criado-Sancho, J.M. Thermodynamics of Fluids Under Flow; Springer: Berlin, Germany, 2000. [Google Scholar]
- Müller, I.; Ruggeri, T. Rational Extended Thermodynamics, 2nd ed; Springer: New York, NY, USA, 1998. [Google Scholar]
- Lebon, G.; Jou, D.; Casas-Vázquez, J.; Muschik, W. Weakly nonlocal and nonlinear heat transport in rigid solids. J. Non-Equilib. Thermodyn 1998, 23, 176–191. [Google Scholar]
- Casas-Vázquez, J.; Jou, D. Temperature in non-equilibrium states: A review of open problems and current proposals. Rep. Prog. Phys 2003, 66, 1937–2023. [Google Scholar]
- Muschik, W.; Ehrentraut, H. An amendment to the second law. J. Non-Equilib. Thermodyn 1996, 21, 175–192. [Google Scholar]
- Ván, P. Weakly nonlocal irreversible thermodynamics. Ann. Physik 2003, 12, 142–169. [Google Scholar]
- Ván, P. Weakly Nonlocal non-equilibrium thermodynamics—variational principles and second Law. In Applied Wave Mathematics—Selected Topics in Solids, Fluids, and Mathematical Methods; Quak, E., Soomere, T., Eds.; Springer: Berlin, Germany, 2009; pp. 153–186. [Google Scholar]
- Gurtin, M.E. Thermodynamics and the possibility of spatial interaction in elastic materials. Arch. Ration. Mech. Anal 1965, 19, 339–352. [Google Scholar]
- Dunn, J.E.; Serrin, J. On the thermomechanics of the interstitial working. Arch. Ration. Mech. Anal 1985, 88, 95–133. [Google Scholar]
- Cimmelli, V.A. An extension of Liu procedure in weakly nonlocal thermodynamics. J. Math. Phys 2007, 48, 113510:1–113510:13. [Google Scholar]
- Cimmelli, V.A.; Sellitto, A.; Triani, V. A generalized Coleman-Noll procedure for the exploitation of the entropy principle. Proc. R. Soc. A 2010, 466, 911–925. [Google Scholar]
- Cimmelli, V.A.; Oliveri, F.; Triani, V. Exploitation of the entropy principle: Proof of Liu Theorem if the gradients of the governing equations are considered as constraints. J. Math. Phys 2011, 52, 023511:1–023511:15. [Google Scholar]
- Fabrizio, M.; Lazzari, B.; Nibbi, R. Thermodynamics of nonlocal materials: Extra fluxes and internal powers. Continuum Mech. Thermodyn 2011, 23, 509–525. [Google Scholar]
- Amendola, G.; Fabrizio, M.; Golden, M. Thermodynamics of a non-simple heat conductor with memory. Q. Appl. Math 2011, 69, 787–806. [Google Scholar]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; North-Holland Publishing Company: Amsterdam, The Netherland, 1962. [Google Scholar]
- Ván, P. Exploiting the second law in weakly non-local continuum physics. Period. Polytech. Ser. Mech. Eng 2005, 49, 79–94. [Google Scholar]
- Öttinger, H. C. Beyond Equilibrium Thermodynamics; Wiley Interscience Publishers: Hoboken, NJ, USA, 2005. [Google Scholar]
- Hütter, M.; Svendsen, B. Quasi-Linear versus Potential-Based Formulations of Force-Flux Relations and the GENERIC for Irreversible Processes: Comparisons and Examples. Continuum Mech. Thermodyn 2013, 25, 803–816. [Google Scholar]
- Grmela, M. Multiscale Equilibrium and Nonequilibrium Thermodynamics in Chemical Engineering. Adv. Chem. Eng 2010, 39, 75–129. [Google Scholar]
- Ruggeri, T. The Entropy Principle from Continuum Mechanics to Hyperbolic Systems of Balance Laws: The Modern Theory of Extended Thermodynamics. Entropy 2008, 10, 319–333. [Google Scholar]
- Müller, I. Extended Thermodynamics: A Theory of Symmetric Hyperbolic Field Equations. Entropy 2008, 10, 477–492. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev 1957, 106, 620–630. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics II. Phys. Rev 1957, 108, 171–190. [Google Scholar]
- Pavic, M.; Ruggeri, T.; Simic, S. Maximum entropy principle for rarefied polyatomic gases. Phys. A 2013, 392, 1302–1317. [Google Scholar]
- Boillat, G.; Ruggeri, T. Moment equations in the kinetic theory of gases and wave velocities. Continuum Mech. Thermodyn 1997, 9, 205–212. [Google Scholar]
- Dreyer, W. Maximisation of the Entropy in Non-Equilibrium. J. Phys. Math. Gen 1987, 20, 6505–6517. [Google Scholar]
- Trovato, M.; Reggiani, L. Maximum entropy principle and hydrodynamic models in statistical mechanics. Rivista del Nuovo Cimento 2012, 35, 99–266. [Google Scholar]
- Trovato, M.; Reggiani, L. Quantum Maximum Entropy Principle for Fractional Exclusion Statistics. Phys. Rev. Lett 2013, 110, 020404:1–020404:5. [Google Scholar]
- Mascali, G.; Romano, V. A non parabolic hydrodynamical subband model for semiconductors based on the maximum entropy principle. Math. Comput. Model 2012, 55, 1003–1020. [Google Scholar]
- Camiola, V.D.; Mascali, G.; Romano, V. Numerical simulation of a double-gate MOSFET with a subband model for semiconductors based on the maximum entropy principle. Continuum Mech. Thermodyn 2012, 24, 417–436. [Google Scholar]
- Struchtrup, H. Macroscopic Transport Equations for Rarefied Gas Flows; Springer: Heidelberg, Germany, 2005. [Google Scholar]
- Kremer, G.M. An Introduction to the Boltzmann Equation and Transport Processes in Gases; Springer: Berlin, Germany, 2010. [Google Scholar]
- Grad, H. On the kinetic theory of rarefied gases. Comm. Pure Appl. Math 1949, 2, 331–407. [Google Scholar]
- Gorban, A.N.; Karlin, I. Hilbert’s 6th Problem: Exact and approximate hydrodynamic manifolds for kinetic equations. Bull. Am. Math. Soc 2014, 5, 186–246. [Google Scholar]
- Onsager, L. Reciprocal relations of irreversible processes I. Phys. Rev 1931, 37, 405–426. [Google Scholar]
- Onsager, L. Reciprocal relations of irreversible processes II. Phys. Rev 1931, 38, 2265–2279. [Google Scholar]
- Onsager, L.; Machlup, S. Fluctuations and irreversible processes. Phys. Rev 1953, 91, 1505–1512. [Google Scholar]
- Machlup, S.; Onsager, L. Fluctuations and irreversible processes II: Systems with kinetic energy. Phys. Rev 1953, 91, 1512–1515. [Google Scholar]
- Eckart, C. The thermodynamics of irreversible processes, I: The simple fluid. Phys. Rev 1940, 58, 267–269. [Google Scholar]
- Eckart, C. The thermodynamics of irreversible processes, II: Fluid mixtures. Phys. Rev 1940, 58, 269–275. [Google Scholar]
- Eckart, C. The thermodynamics of irreversible processes, III: Relativistic theory of the simple fluid. Phys. Rev 1940, 58, 919–924. [Google Scholar]
- Eckart, C. The thermodynamics of irreversible processes, IV: The theory of elasticity and anelasticity. Phys. Rev 1940, 73, 373–382. [Google Scholar]
- Prigogine, I. Etude thermodinamique des phénomènes irréversibles; Desoer; Liège, Belgium, 1947. (In French) [Google Scholar]
- Billings, A.R. Tensor Properties of Materials; Wiley-Interscience: London, UK, 1969. [Google Scholar]
- Curie, M.P. Sur la symétrie dans les phènoménes physiques, symétrie d’un champ électrique et d’un champ magnetique. J. Phys. Theor. Appl 1894, 3, 393–415. (In French). [Google Scholar]
- Kjelstrup, S.; Bedeaux, D. Non-equilibrium Thermodynamics of Heterogeneous Systems; World Scientific: Singapore, 2008. [Google Scholar]
- Noll, W. Space-time Structures in Classical Mechanics. In The Foundations of Mechanics and Thermodynamics (Selected papers by Walter Noll); Springer: Berlin, Germany, 1974; pp. 204–210. [Google Scholar]
- Liu, I.-S. On Euclidean objectivity and the principle of material frame-indifference. Continuum Mech. Thermodyn 2003, 16, 177–183. [Google Scholar]
- Fülöp, T.; Ván, P. Kinematic quantities of finite elastic and plastic deformations. Math. Meth. Appl. Sci 2012, 35, 1825–1842. [Google Scholar]
- Muschik, W.; Restuccia, L. Systematic remarks on objectivity and frame-indifference, liquid crystal theory as an example. Arch. Appl. Mech 2008, 78, 837–854. [Google Scholar]
- Müller, I. On the frame dependence of stress and heat flux. Arch. Ration. Mech. Anal 1972, 45, 241–250. [Google Scholar]
- Heckl, M.; Müller, I. Frame dependence, entropy, entropy flux, and wave speed in mixtures of gases. Acta Mech 1983, 50, 71–95. [Google Scholar]
- Barbera, E.; Müller, I. Inherent Frame Dependence of Thermodynamic Fields in a Gas. Acta Mech 2006, 184, 205–216. [Google Scholar]
- Matolcsi, T.; Ván, P. Can material time derivative be objective? Phys. Lett. A 2006, 353, 109–112. [Google Scholar]
- Matolcsi, T.; Ván, P. Absolute time derivatives. J. Math. Phys 2007, 48, 053507:1–053507:19. [Google Scholar]
- Maugin, G.A. The Thermomechanics of Nonlinear Irreversible Behaviors: An Introduction; World Scientific: Singapore, 1999. [Google Scholar]
- Houlsby, G.T.; Puzrin, A.M. Principles of Hyperplasticity; Springer: London, UK, 2006. [Google Scholar]
- Müller, I.; Weiss, W. Thermodynamics of irreversible processes—Past and present. Eur. Phys. J. H 2012, 37, 139–236. [Google Scholar]
- Ruggeri, T. Can constitutive equations be represented by non-local equations? Quart. Appl. Math 2012, 70, 597–611. [Google Scholar]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Modern Phys 1977, 49, 435–479. [Google Scholar]
- Penrose, O.; Fife, P.C. Thermodynamically consistent models of phase-field type for the kinetics of phase transitions. Phys. D 1990, 43, 44–62. [Google Scholar]
- Liu, I.-S. Entropy flux relation for viscoelastic bodies. J. Elast 2007, 90, 259–270. [Google Scholar]
- Gyarmati, I. On the Wave Approach of Thermodynamics and some Problems of Non-Linear Theories. J. Non-Equilib. Thermodyn 1977, 2, 233–260. [Google Scholar]
- Berezovski, A.; Engelbrecht, J.; Maugin, G.A. Generalized thermomechanics with dual internal variables. Arch. Appl. Mech 2011, 81, 229–240. [Google Scholar]
- Ván, P.; Papenfuss, C.; Berezovski, A. Thermodynamic approach to generalized continua. Continuum Mech. Thermodyn 2013. [Google Scholar] [CrossRef]
- Muschik, W. Aspects of Non-equilibrium Thermodynamics; World Scientific: Singapore, 1990. [Google Scholar]
- Luzzi, R.; Vasconcellos, R.; Ramos, J.G. Statistical Foundations of Irreversible Thermodynamics; Teubner: Leipzig, Germany, 2001. [Google Scholar]
- Eu, B.C. Kinetic Theory and Irreversible Thermodynamics; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Lebon, G.; Jou, D.; Casas-Vázquez, J. Questions and answers about a thermodynamic theory of third type. Contemp. Phys 1992, 33, 41–51. [Google Scholar]
- Jou, D.; Restuccia, L. Mesoscopic transport equations and contemporary thermodynamics. Contemp. Phys 2011, 52, 465–474. [Google Scholar]
- Tzou, D.Y. Macro-to Microscale Heat Transfer. The Lagging Behaviour; Taylor and Francis: New York, NY, USA, 1997. [Google Scholar]
- Guyer, R.A.; Krumhansl, J.A. Solution of the linearized phonon Boltzmann equation. Phys. Rev 1966, 148, 766–778. [Google Scholar]
- Guyer, R.A.; Krumhansl, J.A. Thermal conductivity, second sound and phonon hydrodynamic phenomena in nonmetallic crystals. Phys. Rev 1966, 148, 778–788. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Sellitto, A.; Cimmelli, V.A.; Jou, D. Entropy flux and anomalous axial heat transport at the nanoscale. Phys. Rev. B 2013, 87, 054302:1–054302:7. [Google Scholar]
- Sellitto, A.; Cimmelli, V.A.; Jou, D. Thermoelectric effects and size dependency of the figure-of-merit in cylindrical nanowires. Int. J. Heat Mass Transf 2013, 57, 109–116. [Google Scholar]
- Alvarez, F.X.; Cimmelli, V.A.; Jou, D.; Sellitto, A. Mesoscopic description of boundary effects in nanoscale heat transport. Nanoscale Syst. MMTA 2012, 1, 112–142. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Pergamon Press: London, UK, 1958. [Google Scholar]
- Müller, I. Zum Paradoxon der Warmeleitungstheorie. Zeitschrift fr̈ Physik 1967, 198, 329–344. (In German). [Google Scholar]
- Ruggeri, T. Symmetric-hyperbolic system of conservative equations for a viscous heat conducting fluid. Acta Mech 1983, 47, 167–183. [Google Scholar]
- Liu, I.-S.; Müller, I. Extended thermodynamics of classical and degenerate ideal gases. Arch. Ration. Mech. Anal 1983, 83, 285–332. [Google Scholar]
- Liu, I.-S.; Müller, I.; Ruggeri, T. Relativistic thermodynamics of Gases. Ann. Phys 1986, 169, 191–219. [Google Scholar]
- Ruggeri, T. Galilean invariance and entropy principle for systems of balance laws. Continuum Mech. Thermodyn 1989, 1, 3–20. [Google Scholar]
- Ikenberry, E.; Truesdell, C. On the pressure and the flux of energy in a gas according to Maxwell’s kinetic theory. J. Ration. Mech. Anal 1956, 5, 1–54. [Google Scholar]
- Kapur, J.N. Maximum Entropy Models in Science and Engineering; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Kogan, M.N. On the Principle of Maximum Entropy. In Rarefied Gas Dynamics; Brundin, C.L., Ed.; Academic Press: New York, NY, USA, 1967; Volume I. [Google Scholar]
- Levermore, C.D. Moment Closure Hierarchies for Kinetic Theories. J. Stat. Phys 1996, 83, 1021–1065. [Google Scholar]
- Boillat, G.; Ruggeri, T. Hyperbolic Principal Subsystems: Entropy Convexity and Subcharacteristic Conditions. Arch. Ration. Mech. Anal 1997, 137, 305–320. [Google Scholar]
- Boillat, G.; Ruggeri, T. Maximum Wave Velocity in the Moments System of a Relativistic Gas. Continuum Mech. Thermodyn 1999, 11, 107–111. [Google Scholar]
- Boillat, G.; Ruggeri, T. Relativistic Gas: Moment Equations and Maximum Wave Velocity. J. Math. Phys 1999, 40, 6399–6404. [Google Scholar]
- Arima, T.; Taniguchi, S.; Ruggeri, T.; Sugiyama, M. Extended thermodynamics of dense gases. Continuum Mech. Thermodyn 2011, 24, 271–292. [Google Scholar]
- Arima, T.; Taniguchi, S.; Ruggeri, T.; Sugiyama, M. Monatomic Rarefied Gas as a Singular Limit of Polyatomic Gas in Extended Thermodynamics. Phys. Lett. A 2013, 377, 2136–2140. [Google Scholar]
- Arima, T.; Taniguchi, S.; Ruggeri, T.; Sugiyama, M. Extended thermodynamics of real gases with dynamic pressure: An extension of Meixner’s theory. Phys. Lett. A 2012, 376, 2799–2803. [Google Scholar]
- Meixner, J. Absorption und Dispersion des Schalles in Gasen mit chemisch reagierenden und anregbaren Komponenten. I. Teil. Ann. Physik 1943, 43, 470–487. (In German). [Google Scholar]
- Meixner, J. Allgemeine theorie der Schallabsorption in Gasen und Flüssigkeiten unter Berücksichtigung der Transporterscheinungen. Acoustica 1952, 2, 101–109. (In German). [Google Scholar]
- Arima, T.; Taniguchi, S.; Ruggeri, T.; Sugiyama, M. Dispersion relation for sound in rarefied polyatomic gases based on extended thermodynamics. Continuum Mech. Thermodyn 2013, 25, 727–737. [Google Scholar]
- Taniguchi, S.; Arima, T.; Ruggeri, T.; Sugiyama, T. Thermodynamic theory of the shock wave structure in a rarefied polyatomic gas: Beyond the Bethe-Teller theory. Phys. Rev. E 2014, 89, 013025:1–013025:11. [Google Scholar]
- Taniguchi, S.; Arima, T.; Ruggeri, T.; Sugiyama, M. Effect of dynamic pressure on the shock wave structure in a rarefied polyatomic gas. Phys. Fluids 2014, 26, 016103:1–016103:15. [Google Scholar]
- Borgnakke, C.; Larsen, P.S. Statistical Collision Model for Monte Carlo Simulation of Polyatomic Gas Mixture. J. Comput. Phys 1975, 18, 405–420. [Google Scholar]
- Bourgat, J.-F.; Desvillettes, L.; Le Tallec, P.; Perthame, B. Microreversible collisions for polyatomic gases. Eur. J. Mech. B Fluid 1994, 13, 237–254. [Google Scholar]
- Shizuta, Y.; Kawashima, S. Systems of equations of hyperbolic-parabolic type with applications to the discrete Boltzmann equation. Hokkaido Math. J 1985, 14, 249–275. [Google Scholar]
- Hanouzet, B.; Natalini, R. Global existence of smooth solutions for partially dissipative hyperbolic systems with a convex entropy. Arch. Rational Mech. Anal 2003, 169, 89–117. [Google Scholar]
- Yong, W.A. Entropy and global existence for hyperbolic balance laws. Arch. Ration. Mech. Anal 2004, 172, 247–266. [Google Scholar]
- Bianchini, S.; Hanouzet, B.; Natalini, R. Asymptotic Behavior of Smooth Solutions for Partially Dissipative Hyperbolic Systems with a Convex Entropy. Comm. Pure Appl. Math 2007, 60, 1559–1622. [Google Scholar]
- Dafermos, C. Hyperbolic Conservation Laws in Continuum Physics; Springer: Berlin, Germany, 2001. [Google Scholar]
- Ruggeri, T.; Serre, D. Stability of constant equilibrium state for dissipative balance laws system with a convex entropy. Quart. Appl. Math 2004, 62, 163–179. [Google Scholar]
- Lou, J.; Ruggeri, T. Acceleration Waves and Weak Shizuta-Kawashima Condition. Suppl. Rend. Circ. Mat. Palermo 2006, 78, 187–200. [Google Scholar]
- Ruggeri, T. Global existence of smooth solutions and stability of the constant state for dissipative hyperbolic systems with applications to extended thermodynamics. In Trends and Applications of Mathematics to Mechanics; Springer: Berlin, Germany, 2005. [Google Scholar]
- Ruggeri, T. Entropy principle and Relativistic Extended Thermodynamics: Global existence of smooth solutions and stability of equilibrium state. Il Nuovo Cimento B 2004, 119, 809–821. [Google Scholar]
- Ruggeri, T. Extended Relativistic Thermodynamics. In General Relativity and the Einstein Equations; Choquet, B.Y., Ed.; Oxford University Press: Oxford, UK, 2009; pp. 334–340. [Google Scholar]
- Ruggeri, T.; Simić, S. On the Hyperbolic System of a Mixture of Eulerian Fluids: A Comparison Between Single and Multi-Temperature Models. Math. Meth. Appl. Sci 2007, 30, 827–849. [Google Scholar]
- Gurtin, M.E.; Vargas, A.S. On the Classical Theory of Reacting Fluid Mixtures. Arch. Ration. Mech. Anal 1971, 43, 179–197. [Google Scholar]
- Triani, V.; Papenfuss, C.; Cimmelli, V.A.; Muschik, W. Exploitation of the Second Law: Coleman-Noll and Liu Procedure in Comparison. J. Non-Equilib. Thermodyn 2008, 33, 47–60. [Google Scholar]
- Maugin, G.A.; Muschik, W. Thermodynamics with Internal Variables. Part I. General Concepts. J. Non-Equilib. Thermodyn 1994, 19, 217–249. [Google Scholar]
- Maugin, G.A.; Muschik, W. Thermodynamics with Internal Variables. Part II. Applications. J. Non-Equilib. Thermodyn 1994, 19, 250–289. [Google Scholar]
- Smith, G.F. On isotropic functions of symmetric tensors, skew–symmetric tensors and vectors. Int. J. Eng. Sci 1971, 9, 899–916. [Google Scholar]
- Verhás, J. Thermodynamics and Rheology; Kluwer Academic Publisher: Dordrecht, The Netherland, 1997. [Google Scholar]
- Boillat, G. La propagation des Ondes; Gauthier-Villars: Paris, France, 1965. [Google Scholar]
- Boillat, G.; Ruggeri, T. On the evolution law of the weak discontinuities for hyperbolic quasi-linear systems. Wave Motion 1979, 1, 149–152. [Google Scholar]
- Ruggeri, T. Stability and Discontinuity Waves for Symmetric Hyperbolic Systems. In Non-linear Wave Motion; Jeffrey, A., Ed.; Longman: London, UK, 1989; pp. 148–161. [Google Scholar]
- Fisher, A.; Marsden, D.P. The Einstein evolution equations as a first order quasilinear symmetric hyperbolic system. Comm. Math. Phys 1972, 28, 1–38. [Google Scholar]
- Boillat, G. Sur l’existence et la recherche d’équations de conservation supplémentaires pour les systémes hyperboliques. C. R. Acad. Sci. Paris A 1974, 278, 909–912. [Google Scholar]
- Ruggeri, T.; Strumia, A. Main field and convex covariant density for quasi-linear hyperbolic systems. Relativistic fluid dynamics. Ann. Inst. H. Poincaré, Section A 1981, 34, 65–84. [Google Scholar]
- Friedrichs, K.O.; Lax, P.D. Systems of conservation equations with a convex extension. Proc. Natl. Acad. Sci. USA 1971, 68, 1686–1688. [Google Scholar]
- Korteweg, D.J. Sur la forme qui prennent les equations du mouvement des fluids si l’on tient compte des forces capillaires par des variations de densité considérables mais continues et sur la théorie de la capillarité dans l’hypothèse d’une variation continue de la densité. Arch. Néer. Sci. Exactes 1901, 6, 1–24. (In French). [Google Scholar]
- Triani, V.; Cimmelli, V.A. Entropy principle, non-regular processes, and generalized exploitation procedures. J. Math. Phys 2012, 53, 063509. [Google Scholar]
- Triani, V.; Cimmelli, V.A. Interpretation of Second Law of Thermodynamics in the presence of interfaces. Continuum Mech. Thermodyn 2012, 24, 165–174. [Google Scholar]
- Cimmelli, V.A. Different thermodynamic theories and different heat conduction laws. J. Non-Equilib. Thermodyn 2009, 34, 299–333. [Google Scholar]
- Cimmelli, V.A. On the causality requirement for diffusive-hyperbolic systems in non-equilibrium thermodynamics. J. Non-Equilib. Thermodyn 2004, 29, 125–139. [Google Scholar]
- Fichera, G. Is the Fourier theory of heat propagation paradoxical? Rendiconti del Circolo Matematico di Palermo 1992, 41, 5–28. [Google Scholar]
- Maxwell, J.C. Theory of Heat, 2nd ed.; Longman: London, UK, 1872. [Google Scholar]
- Day, W.A. Two Lines of Defense of Fourier’s Theory of Heat Propagation. In Homage to Gaetano Fichera; Cialdea, A., Ed.; Aracne Editrice: Rome, Italy, 2000; pp. 147–159. [Google Scholar]
- Day, W.A. A note on the propagation of temperature disturbances. Quart. Appl. Math 1997, 55, 565–572. [Google Scholar]
- Day, W.A.; Saccomandi, G. On the propagation of the bulk of a mass subject to periodic convection and diffusion. Quart. Appl. Math 1999, 57, 561–572. [Google Scholar]
- Day, W.A.; Saccomandi, G. On rates of propagation for Burgers’ equation. Rendiconti Lincei. Matematica e Applicazioni 1998, 9, 149–156. [Google Scholar]
- Gurtin, M.E.; Pipkin, A.C. A general theory of heat conduction with finite wave speed. Arch. Ration. Mech. Anal 1968, 31, 113–126. [Google Scholar]
- Fichera, G. Avere una memoria tenace crea gravi problemi. Arch. Ration. Mech. Anal 1979, 70, 101–112. [Google Scholar]
- Coleman, B.D.; Fabrizio, M.; Owen, D.R. The thermodynamics of second sound in crystals. Arch. Ration. Mech. Anal 1982, 80, 135–158. [Google Scholar]
- Morro, A.; Ruggeri, T. Second sound and internal energy in solids. Int. J. Non-Linear Mech 1987, 22, 27–36. [Google Scholar]
- Cimmelli, V.A.; Kosiński, W. Nonequilibrium semi-empirical temperature in materials with thermal relaxation. Arch. Mech 1991, 43, 753–767. [Google Scholar]
- Ván, P.; Fülöp, T. Universality in heat conduction theory: Weakly nonlocal thermodynamics. Ann. Physik 2012, 524, 470–478. [Google Scholar]
- Waldman, L. Non-equilibrium thermodynamics of boundary conditions. Z. Naturforschg 1967, 22, 1269–1286. [Google Scholar]
- Cimmelli, V.A. Boundary conditions in the presence of internal variables. J. Non-Equilib. Thermodyn 2002, 27, 15–33. [Google Scholar]
- Barbera, E.; Müller, I.; Reitebuch, D.; Zhao, N.R. Determination of boundary conditions in extended thermodynamics via fluctuation theory. Continuum. Mech. Thermodyn 2004, 16, 411–425. [Google Scholar]
- Müller, I.; Reitebuch, D.; Weiss, W. Extended thermodynamics consistent in order of magnitude. Continuum. Mech. Thermodyn 2003, 15, 113–146. [Google Scholar]
| Predictability | Causality | Agreement with kinetic theories | |
|---|---|---|---|
| CIT | Yes, to be proved case by case | Yes, in the generalized sense | Not considered |
| EIT | Yes, to be proved case by case | Yes, in the generalized sense | Yes |
| RET | Yes, in general | Yes, in general | Yes |
| RT | Yes, to be proved case by case | Yes, in the generalized sense | Not considered |
| Number of field equations | Constitutive equations | Boundary conditions | |
|---|---|---|---|
| CIT | Finite | Weakly nonlocal | Experiments |
| EIT | Finite, from an infinite hierarchy | Weakly nonlocal | Experiments or fluctuation theory |
| RET | Finite, from an infinite hierarchy | Local | Experiments or fluctuation theory |
| RT | Finite | Weakly nonlocal | Experiments |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cimmelli, V.A.; Jou, D.; Ruggeri, T.; Ván, P. Entropy Principle and Recent Results in Non-Equilibrium Theories. Entropy 2014, 16, 1756-1807. https://doi.org/10.3390/e16031756
Cimmelli VA, Jou D, Ruggeri T, Ván P. Entropy Principle and Recent Results in Non-Equilibrium Theories. Entropy. 2014; 16(3):1756-1807. https://doi.org/10.3390/e16031756
Chicago/Turabian StyleCimmelli, Vito Antonio, David Jou, Tommaso Ruggeri, and Péter Ván. 2014. "Entropy Principle and Recent Results in Non-Equilibrium Theories" Entropy 16, no. 3: 1756-1807. https://doi.org/10.3390/e16031756







