Ensemble Entropy for Monitoring Network Design
Abstract
: Information-theory provides, among others, conceptual methods to quantify the amount of information contained in single random variables and methods to quantify the amount of information contained and shared among two or more variables. Although these concepts have been successfully applied in hydrology and other fields, the evaluation of these quantities is sensitive to different assumptions in the estimation of probabilities. An example is the histogram bin size used to estimate probabilities to calculate Information Theory quantities via frequency methods. The present research aims at introducing a method to take into consideration the uncertainty coming from these parameters in the evaluation of the North Sea’s water level network. The main idea is that the entropy of a random variable can be represented as a probability distribution of possible values, instead of entropy being a deterministic value. The method consists of solving multiple scenarios of Multi-Objective Optimization Problem in which information content is maximized and redundancy is minimized. Results include probabilistic analysis of the chosen parameters on the resulting family of Pareto fronts, providing additional criteria on the selection of the final set of monitoring points.1. Introduction
Data collection is crucial in hydrology and water resources because it is an activity that generates information about past and current states of water systems to ultimately assist informed decisions. For this purpose, monitoring sensors are positioned in strategic places in such a way that the highest information content about the state of an area is obtained, observing the limitations in the number of available sensors to do so.
Literature on design of hydrometric monitoring network started to be popular in the 1960s after the International Hydrological Decade (1965–1974) brought global attention to the need for hydrometric data [1,2]. Some of the explored methods, which were mainly based on statistical analyses, include regression techniques [3,4], cross correlation reduction [5–8] and geostatistical analyses [9,10], among others.
Information-theory provides conceptual methods to quantify the amount of information contained in single random variables and contained and shared among two or more random variables. Information content of single variables can be estimated using the concept of Marginal Entropy (H), as described by [11]. Similarly, information content of two or more variable can be estimated using the concept of Joint Entropy (JH). To quantify the amount of information shared among two or more variables Mutual Information (I) is a popular measure [12].
Entropy-based methods for hydrology studies started to be popular after the seminal paper [13], and its application in monitoring network design and evaluation was exploited for several authors for multi-purpose networks [14], water quality [15], groundwater quality [16–19], air pollution [20] and rainfall gauging stations [21–24]. In general, these approaches are based on the fact that the information that is shared among stations should be as little as possible, thus ensuring minor redundancy. Recent publications on entropy-based criterion for hydrometric network evaluation include [25,26].
In recent years different authors have exploited the concept of Total Correlation to quantify the information content that is shared within a set of two or more stations, as a generalization of the Mutual Information concept used studies applying pair-wise station analysis [23,27,28]. This is the case of the distribution of water level monitors in polders [29,30] and in river systems [24,31].
Although Information Theory concepts have been successfully applied in hydrology and other fields [32], the evaluation of these quantities is sensitive to different assumptions in the estimation of probabilities. An example is the histogram bin size used to estimate probabilities to calculate Entropy quantities via frequency methods. Consequently, entropy-based values depend on some assumptions that may affect the final locations of monitors. Knowing the uncertainty associated to these assumed parameters makes it possible to select a solution that is less sensitive to their changes.
This paper introduces a method to take into consideration the uncertainty coming from these assumptions in the evaluation of the North Sea’s water level network. The network is evaluated in a multi-objective optimisation framework to ensure that the set of resulting sensors are simultaneously informative and non-redundant. Entropy parameters are then sampled for the optimised network in order to estimate the robustness of the solutions given the changes in the baseline assumptions.
2. Methods
2.1. Information Theory Quantities for Monitoring Design
From the Information Theory perspective, an accepted approach to set of stations that form a monitoring network is to consider that the information content of the set is maximum, whereas, at the same time, the redundancy among each station of the set is minimum [29,31]. The first objective, maximising information content of the set, can be assessed with the expression for Joint Entropy (JH). For a set of M random variables with n unique records, JH is defined as, Equation (1):
where pi1...iM is the joint probability of the M variables. The second objective, minimisation of redundancy of the set, is evaluated using the concept of Total Correlation (C), defined as Equation (2):
where H(Xi) is the marginal entropy of the variable i with x unique records, defined as:
where px is the probability that Xi equals the outcome x, P(Xi = x).
2.2. Multi-Objective Optimisation (MO)
MO consists of searching for a set of decision variables such that simultaneously optimize independent objective functions. Usually objective functions conflict with each other, so the word optimisation suggests having a compromise among the objectives. According to the discussion in previous section, the MO problem can be posed as shown in Equation (4) for two objective functions:
where Xi (i = 1,2,...,M) are the decision variables, each one representing a potential station location with available time series data. A way to solve the problem is by using evolutionary algorithms. In particular, the Non-dominated Sorting Genetic Algorithm (NSGA-II) [33], is utilised in this manuscript. The solution of the MO problem is the set Yi (i = 1,2,...,M) chosen among all sets Xi (i = 1,2,...,M) containing the most informative sensor locations that are simultaneously the least redundant that forms a Pareto front of quasi-optimal solutions.
2.3. Ensemble Entropy in Monitoring Network Design
Although the approach described so far has been applied in different studies (see e.g., [29–31,34]), the estimation of the Information Theory quantities presented in Section 2.1 is sensitive to different assumptions in the calculation of probabilities. An example is the histogram bin size used to estimate probabilities via frequency methods. In particular, we analyse the quantization method suggested in [29], which consists of filtering out noise in the data series by converting an analog signal into a discrete pulse with the application of the mathematical floor function. Therefore, the conversion of an analog value x to a quantized value xq, which is rounded to the nearest multiple of a, is performed by:
where a is given by the quotient of the difference between the maximum and the minimum of the time series and the bin-size used in frequency analysis. We introduce parameter γ as a numeric factor used to normalise data series coming from multiple sources. Equation (5) is then used to transform time series from different locations and normalise them in order to allow for fair comparisons. The transformed time series are then composed by different symbols whose probabilities of occurrence are obtained by frequency analysis. These probabilities are then used to evaluate Equations (1)–(3) and therefore the MO problem formulated in Equation (4).
This paper aims at introducing a method to take into consideration the uncertainty coming from assumptions of parameters γ and a in the monitoring network design problem, with the purpose of finding a solution as independent as possible to their assumptions. In other words, the final solution should vary only marginally if different parameter values γ and a are assumed. In addition, rather than choosing the single solution on the Pareto front that meets the optimal MO solution, the proposed methodology provides an ensemble of suitable solutions from which decision makers can make a choice incorporating other factors such as the cost of the monitoring network.
The main idea of the method is that the entropy of a random variable can be represented as a probability distribution of possible values, instead of entropy being a deterministic value. The method is called ensemble entropy, and it consists of the following steps:
- (1)
Assume a value for parameters γ and a in Equation (5)
- (2)
Obtain the transformed (i.e., normalised and quantized) time series D by applying Equation (5), for each data record of each sensor location (i.e., each Xi).
- (3)
Solve the optimisation problem formulated in Equation (4), obtaining the Pareto quasi-optimal vector Yi of sensor locations, each one having its corresponding time data series Di
- (4)
Take S different sample combinations for parameters γ and a in Equation (5)
- (5)
For each sample combination j (j = 1,2,...,S) of values γ and a:
- (a)
Obtain the transformed (i.e., normalised and quantized) time series Dij* by applying Equation (5) for each data record of quasi-optimal sensor location (i.e., each Yi).
- (b)
Evaluate JH and C with Equations (1) and (2) respectively, using the transformed time series Dij*
- (6)
Evaluate the two-dimensional distribution of JH and C in the original Pareto front of quasi-optimal sensor locations.
The method can consider any sampling strategy for parameters γ and a. As a first approach, and in order to avoid assuming any particular probability distribution, we use equal intervals for sampling.
3. Case Study: Water Levels in the North Sea
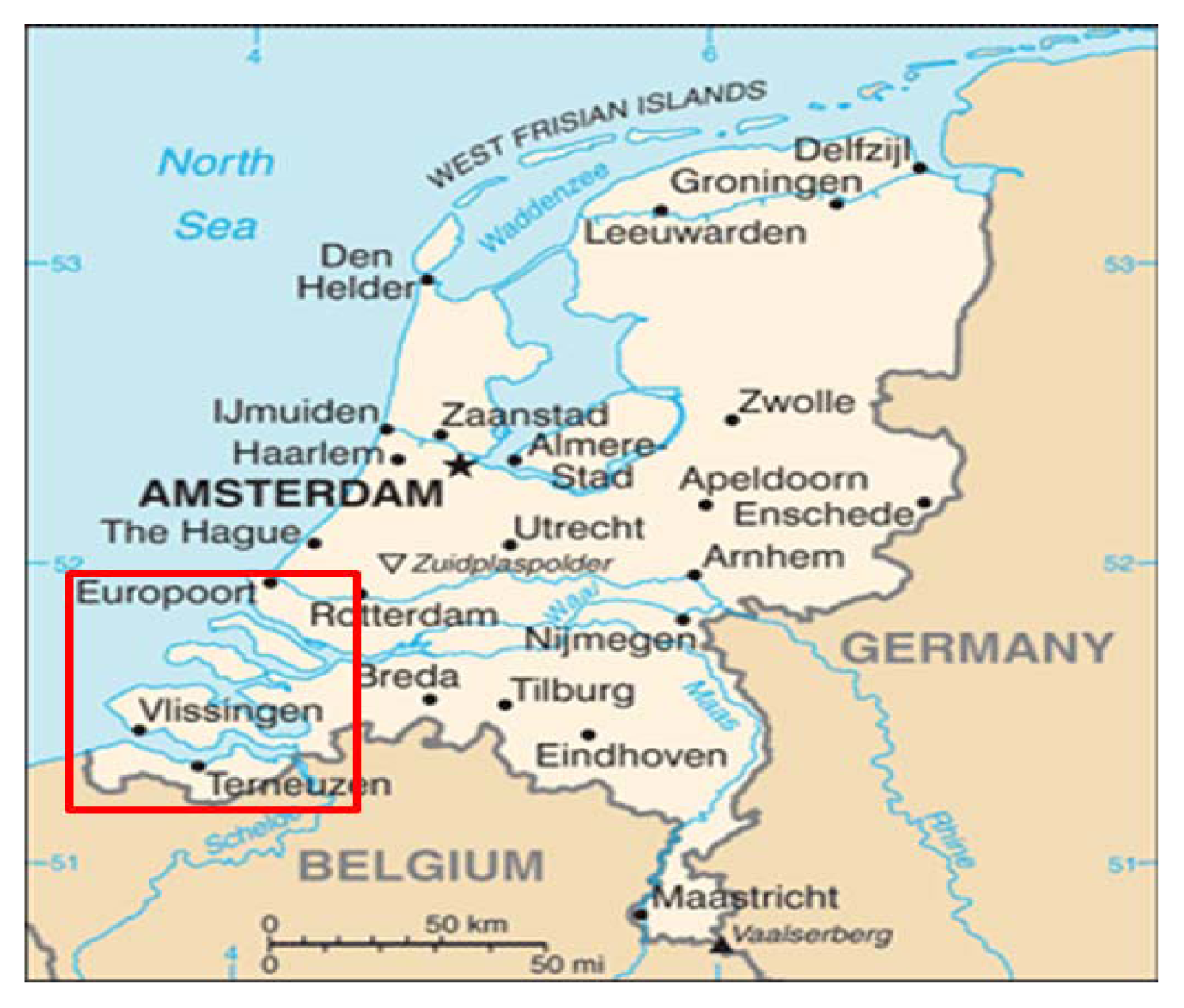
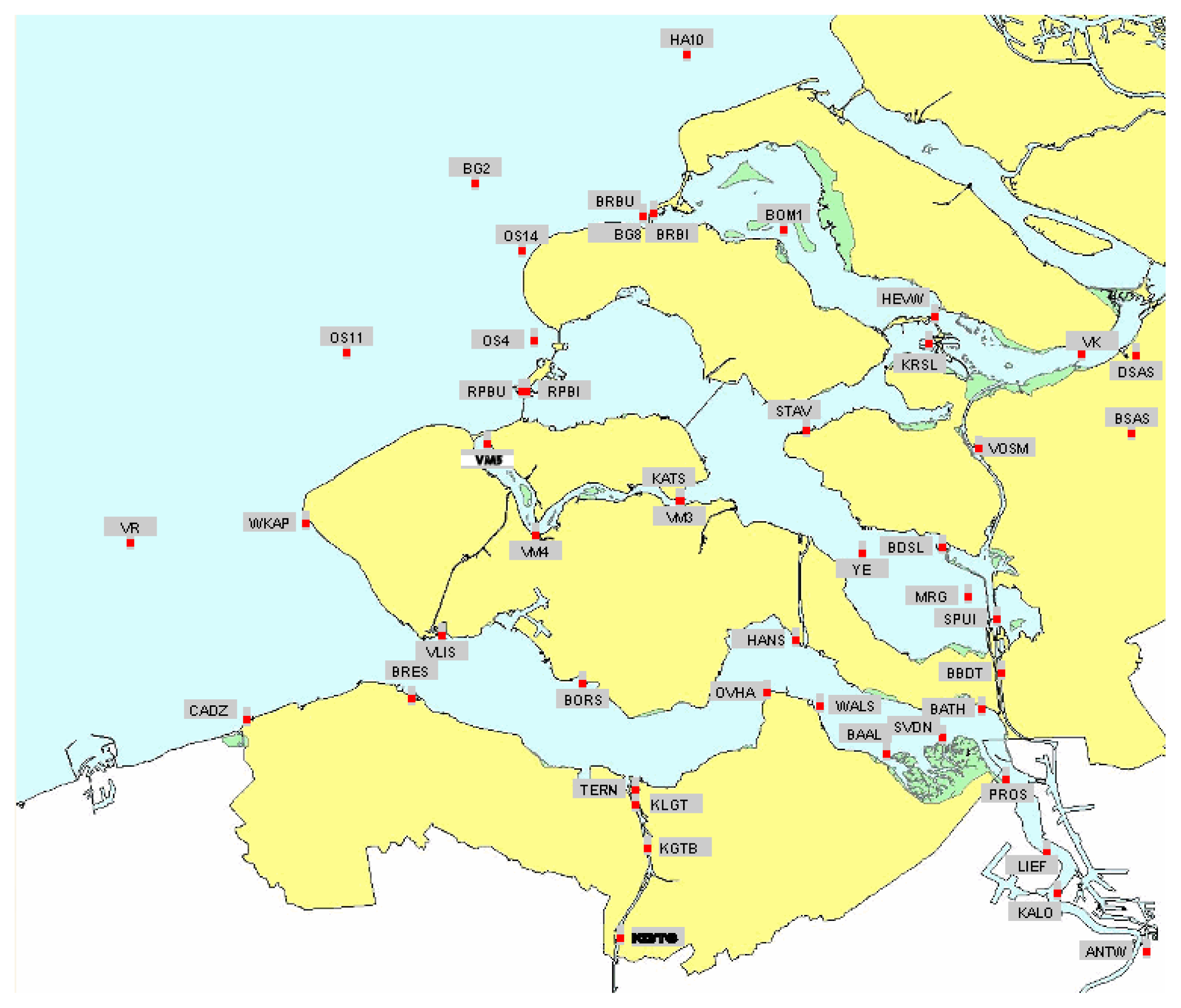
The city of Rotterdam is one of the most important ship transit cities in the world, an important port that is significant for the economy of The Netherlands, Figure 1. In addition, the country is below sea level, makes it a priority to monitor the water levels of the North Sea, which are normally affected by storms and tidal processes. For this reason, the sea is being measured by the monitoring network presented in Figure 2. However, as the operation and maintenance of this monitoring network demand a serious amount of resources, it is necessary to optimise the number of the stations installed. To this end, data series are the water stage values gauged by a network of 47 sensors deployed in the delta of the Netherlands, Figure 2. Data series used in this study are collected with 10 minutes resolution time and cover a period from 2007 to 2008.
4. Results and Discussion
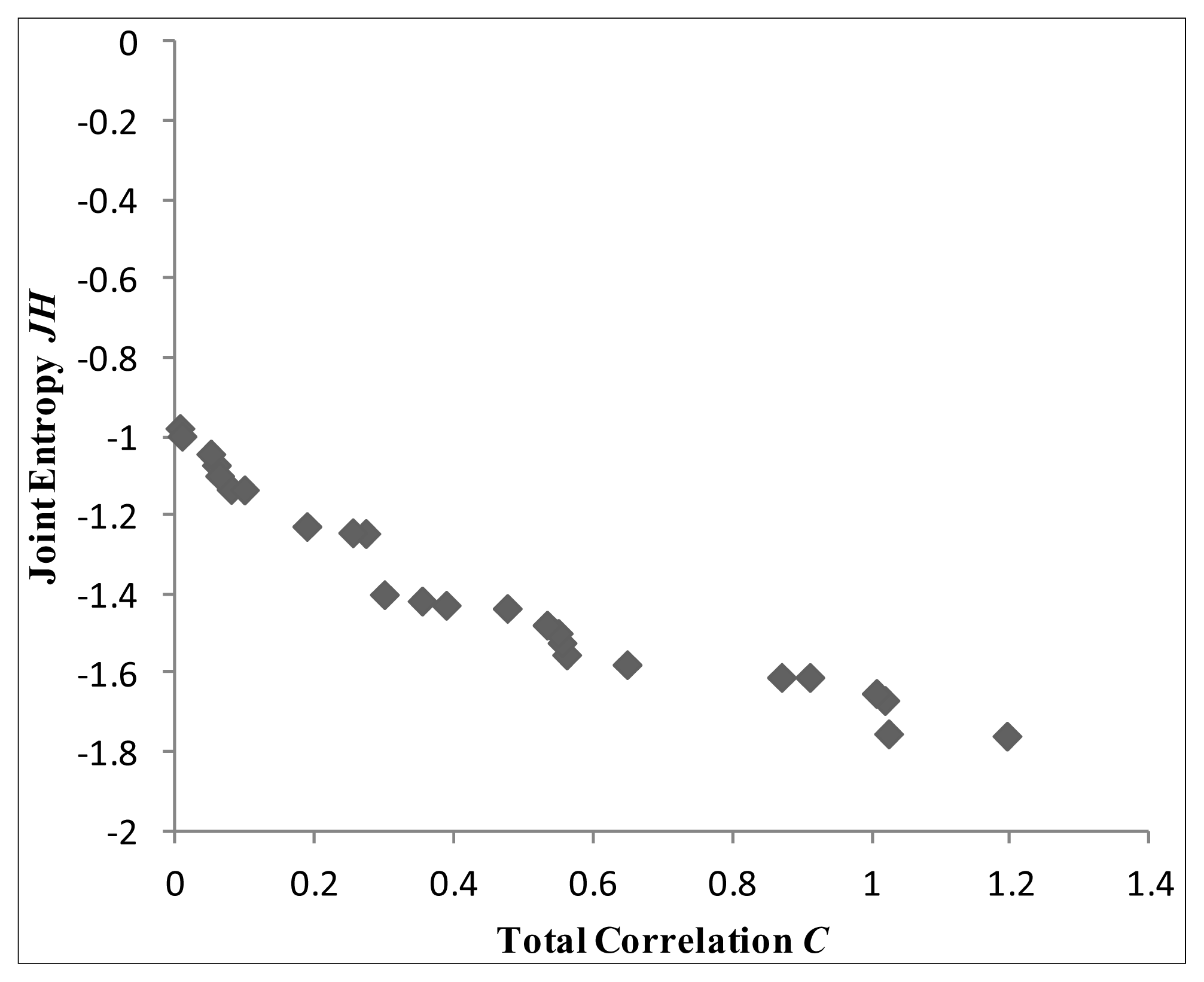
This section presents the results of the methodology presented in Section 2.3, for the optimisation of the locations of three monitoring sensors. In the first place, both parameters γ and a are assumed equal to 1 and 7 correspondingly, and all the available time series are transformed using Equation (5). The optimisation problem, formulated in Equation (4), is then solved for three variables X1, X2, X3 using the multi-objective optimisation algorithm NSGA-II, obtaining the Pareto quasi-optimal shown in Figure 3, of 100 solutions. Details on NSGA-II algorithm and parameters can be found in [33] and are not elaborated further in this paper.
The following step in the proposed methodology is to take S different sample combinations for parameters γ and a in Equation (5). In our case we sampled both parameters from 1 to 10, which means that 100 possible transformed series are generated for each sensor and therefore S = 100. Subsequently, each of the 100 combinations of parameters is used to transform via Equation (5) all the records of the set of locations depicted in Figure 3. The quantities JH and C are then evaluated for each set and each transformed time series with Equations (1) and (2) respectively. Finally, the two-dimensional distribution of JH and C in the original Pareto front of quasi-optimal sensor locations is evaluated.
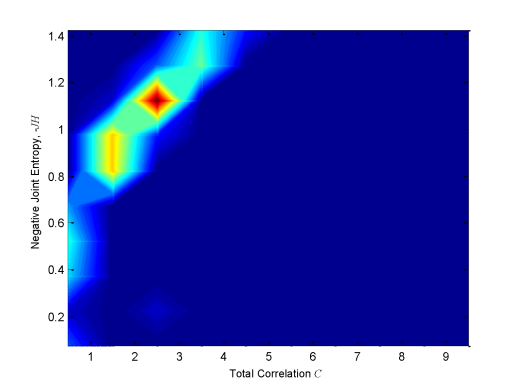
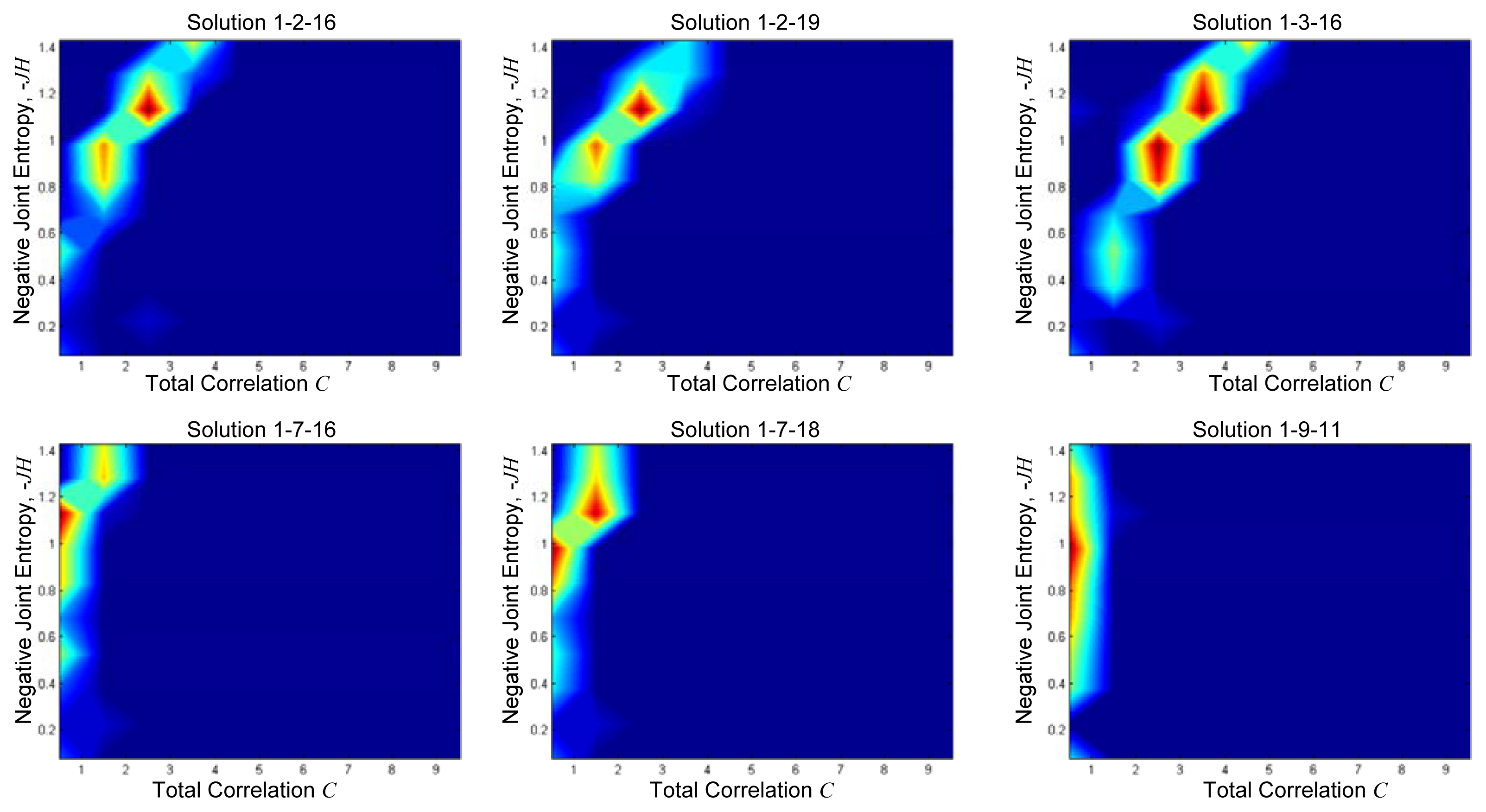
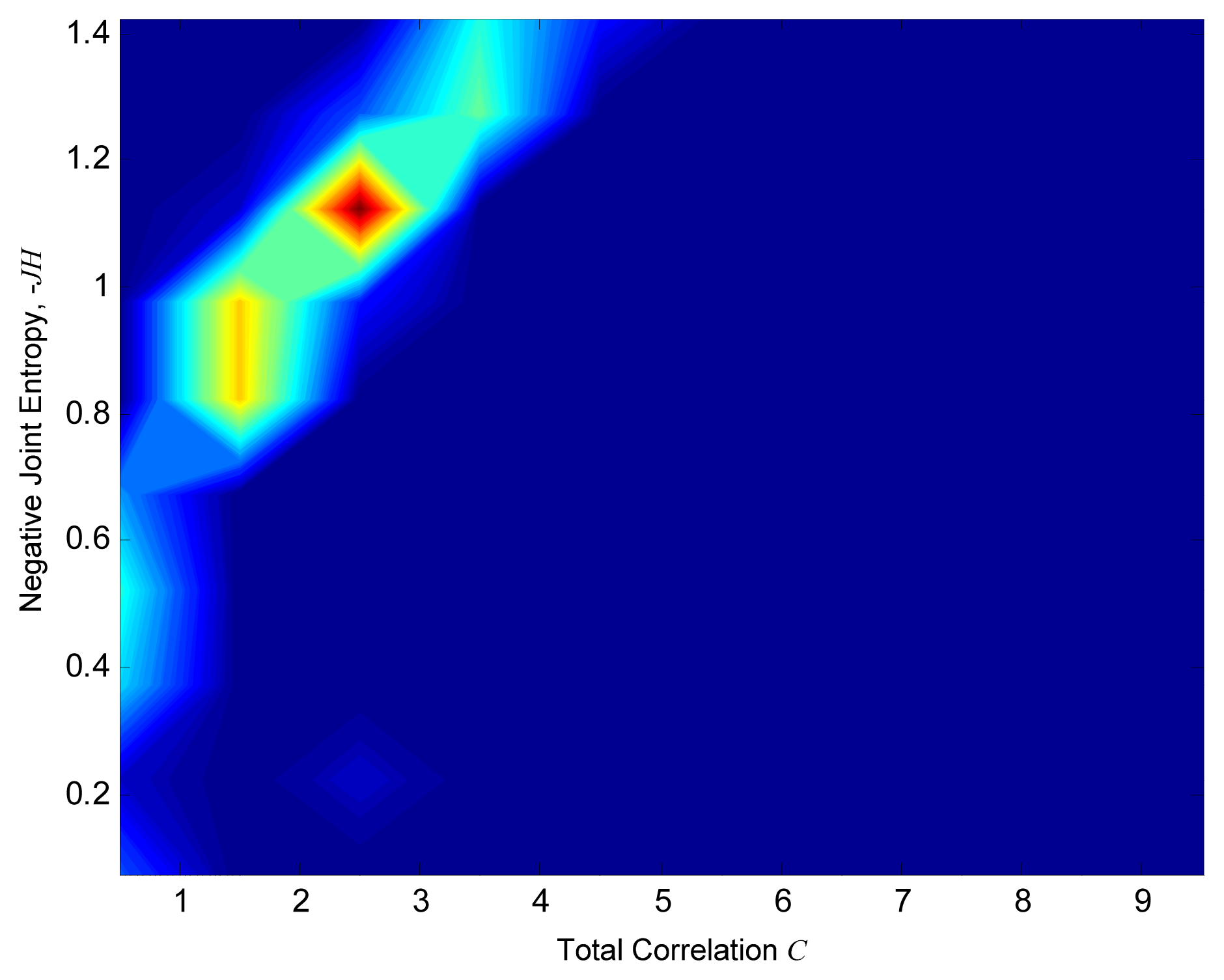
Figure 4 shows intermediate results of two-dimensional frequency distribution of JH and C for ten divisions in both axes for some of the sets of monitors represented by a point in Figure 3. In the plots, the red area corresponds to the most probable JH and C values of the considered vector. Indeed, even if the vector is normalized varying the values of γ and a, it is possible to define which JH and C values have a high frequency of occurrence. While for lower number of quasi-optimal sets, colour intensity is lighter and more disperse. In order to summarize the results, all the distributions have been summed up at each axes division. The result is shown in Figure 5. It can be seen how the Pareto front is now smooth, and shows that parameters change for the estimation of Information Theory quantities has an important effect on the results. It is interesting to note that in Figure 5 the red area is more localized than for plots in Figure 4. Therefore, it is possible to define the most probable and thus, less uncertain combination of JH and C among all. The lighter colored area corresponds to less probable and more uncertain JH and C combinations. In this way Figure 5 can be seen as the plot of the uncertainty linked to JH and C solutions: the reddish the color, the more certain the combination.
Because Figure 5 is the sum of the 2D distributions of all quasi-optimal sensors location, it can be helpful to determine the best optimal set as the one with the most probable JH and C combination. Three solutions presented in Figure 4 are represented on a map in Figure 6. Monitors of solutions 1, 2, 16 (green triangles) and 1, 3, 16 (red stars) are located in the south-east of the North Sea. Particularly, they are concentrated in the inland part of the delta close to Antwerp. Their corresponding 2D distributions (Figure 4) present a well shaped Pareto front with best solutions (red area) corresponding to the best one of Figure 5. This means that both solutions are representative of the overall best solution. On the other hand, monitors of the other solution (1, 9, 11) are more spread over the area. Indeed, one is in the upper part, one in south-east, the other in the south west. The Pareto front in Figure 4 is flat and almost parallel to the y axis.
5. Conclusions
In this work a method to take into consideration the uncertainty coming from water monitoring sensors optimization through Information Theory is presented. The main idea is that the entropy of a random variable can be represented as a probability distribution of possible values, instead of entropy being a deterministic value. Entropy determination implies the estimation of marginal and joint probability of each data series. The problem is faced transforming each data series value in a quantized one through two parameters γ and a. They are hypothesized equal to a given value and goodness of this choice is investigated as follows. Once variables are transformed, it is possible to determine the frequency of occurrence of each data series outcome and therefore, estimate its probability. The method includes solving multiple scenarios of Multi-Objective Optimization Problem in which information content (JH) is maximized and redundancy (C) is minimized. The Problem is solved through a non-sorting genetic algorithm and quasi-optimal solutions sets are plotted on a Pareto front. To determine the uncertainty linked to the γ and a values choice, the water level values corresponding to these quasi-optimal sets are then normalized varying γ and a from 1 to 10 and the corresponding JH and C values are computed. A new Pareto is then plotted, representing the 2D distribution of JH and C. In this way it is possible to determine which range of combination of JH and C is the most probable varying γ and a for each quasi-optimal set. Summing up all solutions, results are summarized. This final Pareto front has a more smoothed shape and defines more precisely the most probable combination of JH and C (i.e., the most frequent). Therefore, this Pareto front can be used to determine the uncertainty due to parameters values choice to estimate data series probability and consequently the information and redundant information contents. This work aims to define the uncertainty when dealing with entropy estimation and moreover, to make aware about the effect that this uncertainty could have on linked study. Indeed, the resulting family of Pareto fronts, as well as the summarized version of it, provides additional criteria on the selection of the final set of monitoring points. In particular, the solution at C = 2.5 and JH = 1.15 appears to be repetitive in the ensemble of solutions and that is closer to the origin (ideal point). This can be used as an additional criterion when selecting the final set of monitors, lowering the uncertainty when choosing the best sensors location among all.
Acknowledgments
Part of this research was carried out with funds from the FP7 WeSenseIt project. The data used is made freely available by the Dutch Ministry of Infrastructure and Environment (Rijkswaterstaat) at http://www.hmcz.nl/nl/water-en-weer_verwachtingen-water_kust_zeeuwse-wateren.htm.
Conflicts of Interest
The authors declare no conflict of interest.
- Author ContributionsAll the authors contributed to the manuscript. Alfonso, Ridolfi, Napolitano and Russo have contributed to the research methods and the results have been discussed among all authors. The contributions by sections are: Alfonso: Abstract, Introduction, Methods, Results, Discussion and Conclusions; Ridolfi: Methods, Results and Discussion; Gaytan-Aguilar: Case study; Napolitano: Introduction; Russo: Conclusions.
References
- Vose, R.S.; Schmoyer, R.L.; Steurer, P.M.; Peterson, T.C.; Heim, R.; Karl, T.R.; Eischeid, J.K. The global historical climatology network: Long-term monthly temperature, precipitation, sea level pressure, and station pressure data; Oak Ridge National Laboratory: Oak Ridge, TN, USA; July; 1992. [Google Scholar] [CrossRef]
- Mishra, A.K.; Coulibaly, P. Developments in hydrometric network design: A review. Rev. Geophys 2009, 47. [Google Scholar] [CrossRef]
- Moss, M.E.; Karlinger, M.R. Surface water network design by regression analysis simulation. Water Resour. Res 1974, 10, 427–433. [Google Scholar]
- Moss, M.E. Design of surface water data networks for regional information. Hydrol. Sci. Bull 1976, 21, 113–127. [Google Scholar]
- Bonaccorso, B.; Cancelliere, A.; Rossi, G. Network design for drought monitoring by geostatistical techniques. Eur. Water 2003, 3, 9–15. [Google Scholar]
- Fiering, M.B. An optimization scheme for gaging. Water Resour. Res 1965, 1, 463–470. [Google Scholar]
- Volkmann, T.H.; Lyon, S.W.; Gupta, H.V.; Troch, P.A. Multicriteria design of rain gauge networks for flash flood prediction in semiarid catchments with complex terrain. Water Resour. Res 2010, 46. [Google Scholar] [CrossRef]
- Thomas, D.M.; Benson, M.A. Generalization of Streamflow Characteristics from Drainage-Basin Characteristics; Water Supply Paper; US Government Printing Office: Washington, DC, USA, 1970. [Google Scholar]
- Kanevski, M.; Parkin, R.; Pozdnukhov, A.; Timonin, V.; Maignan, M.; Demyanov, V.; Canu, S. Environmental data mining and modeling based on machine learning algorithms and geostatistics. Environ. Model. Softw 2004, 19, 845–855. [Google Scholar]
- Krause, A.; Singh, A.; Guestrin, C. Near-optimal sensor placements in gaussian processes: Theory, efficient algorithms and empirical studies. J. Mach. Learn. Res 2008, 9, 235–284. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Techn. J 1948, 27, 379–423. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Amorocho, J.; Espildora, B. Entropy in the assessment of uncertainty in hydrologic systems and models. Water Resour. Res 1973, 9, 1511–1522. [Google Scholar]
- Caselton, W.F.; Zidek, J.V. Optimal monitoring network designs. Stat. Probabil. Lett 1984, 2, 223–227. [Google Scholar]
- Harmancioglu, N.B.; Fistikoglu, O.; Ozkul, S.D.; Singh, V.P.; Alpaslan, M.N. Water Quality Monitoring Network Design; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Caselton, W.F.; Husain, T. Hydrologic networks: Information transmission. J. Water Resour. Plan. Manag. Divis 1980, 106, 503–520. [Google Scholar]
- Mogheir, Y.; Singh, V.P. Application of information theory to groundwater quality monitoring networks. Water Resour. Manag 2002, 16, 37–49. [Google Scholar]
- Mogheir, Y.; de Lima, J.; Singh, V.P. Characterizing the spatial variability of groundwater quality using the entropy theory: I. Synthetic data. Hydrol. Process 2004, 18, 2165–2179. [Google Scholar]
- Mogheir, Y.; Singh, V.P.; de Lima, J. Spatial assessment and redesign of a groundwater quality monitoring network using entropy theory, gaza strip, palestine. Hydrogeol. J 2006, 14, 700–712. [Google Scholar]
- Zidek, J.V.; Sun, W.; Le, N.D. Designing and integrating composite networks for monitoring multivariate Gaussian pollution elds. J. R. Stat. Soc. Ser. C 2000, 49, 63–79. [Google Scholar]
- Krastanovic, P.F.; Singh, V.P. Evaluation of rainfall networks using entropy: II. Applications. Water Resour. Manag 1992, 6, 295–314. [Google Scholar]
- Krstanovic, P.F.; Singh, V.P. Evaluation of rainfall networks using entropy: I. Theoretical development. Water Resour. Manag 1992, 6, 279–293. [Google Scholar]
- Husain, T. Hydrologic uncertainty measure and network design. Water Resour. Bull 1989, 25, 527–534. [Google Scholar]
- Ridolfi, E.; Montesarchio, V.; Russo, F.; Napolitano, F. An entropy approach for evaluating the maximum information content achievable by an urban rainfall network. Nat. Hazards Earth Syst. Sci 2011, 11, 2075–2083. [Google Scholar]
- Mishra, A.K.; Coulibaly, P. Hydrometric network evaluation for canadian watersheds. J. Hydrol 2010, 380, 420–437. [Google Scholar]
- Li, C.; Singh, V.P.; Mishra, A.K. Entropy theory-based criterion for hydrometric network evaluation and design: Maximum information minimum redundancy. Water Resour. Res 2012, 48. [Google Scholar] [CrossRef]
- Yang, Y.; Burn, D.H. An entropy approach to data collection network design. J. Hydrol 1994, 157, 307–324. [Google Scholar]
- Filippini, F.; Galliani, G.; Mantovani, M.; Screpanti, F. Optimization criteria for configuring a network of monitoring stations. Environ. Softw 1994, 9, 77–88. [Google Scholar]
- Alfonso, L.; Lobbrecht, A.; Price, R. Information theory-based approach for location of monitoring water level gauges in polders. Water Resour. Res 2010, 46. [Google Scholar] [CrossRef]
- Alfonso, L.; Lobbrecht, A.; Price, R. Optimization of water level monitoring network in polder systems using information theory. Water Resour. Res 2010, 46. [Google Scholar] [CrossRef]
- Alfonso, L.; He, L.; Lobbrecht, A.; Price, R. Information theory applied to evaluate the discharge monitoring network of the magdalena river. J. Hydroinf 2013, 15, 211–228. [Google Scholar]
- Singh, V.P. The use of entropy in hydrology and water resources. Hydrol. Process 1997, 11, 587–626. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput 2002, 6, 182–197. [Google Scholar]
- Ridolfi, E.; Alfonso, L.; Di Baldassarre, G.; Dottori, F.; Russo, F.; Napolitano, F. An entropy approach for the optimization of cross-section spacing for river modelling. Hydrol. Sci. J 2013, 59, 1–12. [Google Scholar]

© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Alfonso, L.; Ridolfi, E.; Gaytan-Aguilar, S.; Napolitano, F.; Russo, F. Ensemble Entropy for Monitoring Network Design. Entropy 2014, 16, 1365-1375. https://doi.org/10.3390/e16031365
Alfonso L, Ridolfi E, Gaytan-Aguilar S, Napolitano F, Russo F. Ensemble Entropy for Monitoring Network Design. Entropy. 2014; 16(3):1365-1375. https://doi.org/10.3390/e16031365
Chicago/Turabian StyleAlfonso, Leonardo, Elena Ridolfi, Sandra Gaytan-Aguilar, Francesco Napolitano, and Fabio Russo. 2014. "Ensemble Entropy for Monitoring Network Design" Entropy 16, no. 3: 1365-1375. https://doi.org/10.3390/e16031365