Entropy: From Thermodynamics to Hydrology
Abstract
: Some known results from statistical thermophysics as well as from hydrology are revisited from a different perspective trying: (a) to unify the notion of entropy in thermodynamic and statistical/stochastic approaches of complex hydrological systems and (b) to show the power of entropy and the principle of maximum entropy in inference, both deductive and inductive. The capability for deductive reasoning is illustrated by deriving the law of phase change transition of water (Clausius-Clapeyron) from scratch by maximizing entropy in a formal probabilistic frame. However, such deductive reasoning cannot work in more complex hydrological systems with diverse elements, yet the entropy maximization framework can help in inductive inference, necessarily based on data. Several examples of this type are provided in an attempt to link statistical thermophysics with hydrology with a unifying view of entropy.PACS Codes: 89.70.Cf; 05.70.-a; 92.40.-t; 02.50.Fz1. Introduction
Uncertainty is the only certainty there is, and knowing how to live with insecurity is the only security.
(Paulos [1], quoting his father)
Entropy is etymologized from the ancient Greek ἐvτρoπία but was introduced as a scientific term by Rudolf Clausius only in 1865, although the concept appears also in his earlier works (see [2]). The rationale for introducing the term is explained in his own words [3] (p. 358, which indicates that he was not aware of the existence of the word ἐvτρoπία in ancient Greek):
We might call S the transformational content of the body […]. But as I hold it to be better to borrow terms for important magnitudes from the ancient languages, so that they may be adopted unchanged in all modern languages, I propose to call the magnitude S the entropy of the body, from the Greek word τρoπή, transformation. I have intentionally formed the word entropy so as to be as similar as possible to the word energy; for the two magnitudes to be denoted by these words are so nearly allied their physical meanings, that a certain similarity in designation appears to be desirable.
In addition to its semantic content, this quotation contains a very important insight: the recognition that entropy is related to transformation and change and the contrast between entropy and energy, where the latter is a quantity that is conserved in all changes. This meaning has been more clearly expressed in Clausius’ famous aphorism [4]:
Die Energie der Welt ist konstant [The energy of the world is constant].
Die Entropie der Welt strebt einem Maximum zu [The entropy of the world strives to a maximum].
In other words, entropy and its ability to increase (as contrasted to energy and other quantities that are conserved) is the driving force of change. This property of entropy has seldom been acknowledged; instead in common perception entropy is typically identified with disorganization and deterioration as if change can only have negative consequences.
Mathematically, the thermodynamic entropy, S, is defined in the same Clausius’ texts through the equation dS = dQ/T, where Q and T denote heat and temperature. The definition, however, applies to a reversible process only. The fact that in an irreversible process dS > dQ/T makes the definition imperfect and affected by circular reasoning, as, in turn, a reversible process is one in which the equality holds.
Two decades later, in 1877, Ludwig Boltzmann [5,6] gave entropy a statistical content as he related it to probabilities of statistical mechanical system states, thus explaining the Second Law of thermodynamics as the tendency of the system to run toward more probable states, which have higher entropy. The statistical concept of entropy was advanced later in the works of Gibbs in thermodynamics and von Neumann in quantum mechanics. In 1948 Shannon [7] used an essentially similar, albeit more general, entropy definition to describe the information content, which he also called entropy at von Neumann’s suggestion [8,9]. According to the latter definition, entropy is a probabilistic concept, a measure of information or, equivalently, uncertainty (see next section). A decade later, Jaynes [10] introduced the principle of maximum entropy thus equipping the entropy concept with a powerful tool for logical inference.
More than half a century later, the meaning of entropy is still debated and a diversity of opinion among experts is encountered [11]. In particular, despite having the same name, probabilistic (or information) entropy and thermodynamic entropy are still regarded by many as two distinct notions having in common only the name. The classical definition of thermodynamic entropy (as above) does not give any hint about similarity with the probabilistic entropy. The fact that the former is a dimensionless quantity and the latter has units (J/K) has been regarded as an argument that the two are dissimilar. Even Jaynes [12], the founder of the maximum entropy principle, states:
We must warn at the outset that the major occupational disease of this field is a persistent failure to distinguish between the information entropy, which is a property of any probability distribution, and the experimental entropy of thermodynamics, which is instead a property of a thermodynamic state as defined, for example by such observed quantities as pressure, volume, temperature, magnetization, of some physical system. They should never have been called by the same name; the experimental entropy makes no reference to any probability distribution, and the information entropy makes no reference to thermodynamics. Many textbooks and research papers are flawed fatally by the author’s failure to distinguish between these entirely different things, and in consequence proving nonsense theorems.
Nevertheless, the units of thermodynamic entropy are only an historical accident, related to the arbitrary introduction of temperature scales [13,14]. In a recent book, Ben-Naim [15] has attempted to replace altogether the concept of entropy with the concept of information. However, such a replacement is unnecessary or even meaningless if we accept that the two concepts are identical. As recently has been shown (Koutsoyiannis [16]) the formal probability theory can produce the thermodynamic entropy of gases without difficulties and without the need of strange assumptions (e.g., the indistinguishability of particles). The logical basis of the latter study includes the following points.
- (a)
The classical definition of thermodynamic entropy is not necessary; it can be abandoned and replaced by the probabilistic definition.
- (b)
The thus defined entropy is the fundamental thermodynamic quantity, which supports the definition of all other derived ones. For example, the temperature is defined as the inverse of the partial derivative of entropy with respect to the internal energy (see Equation (26)).
- (c)
The entropy retains its dimensionless character even in thermodynamics, thus rendering the unit of kelvin an energy unit, a tiny submultiple of the joule (i.e., 1 K = 0.13806505 yJ = 1.3806505 × 10−23 J).
- (d)
The entropy retains its probabilistic interpretation as a measure of uncertainty, leaving aside the traditional but obscure “disorder” interpretation.
- (e)
The tendency of entropy to reach a maximum is the driving force of natural change. This tendency is formalized as the principle of maximum entropy [10], which can be regarded both as a physical (ontological) principle obeyed by natural systems, as well as a logical (epistemological) principle applicable in making inference about natural systems.
The present study is an extension of the previous one [16] in the field of hydrology. Thermodynamics is one of the pillars of hydrology and in this respect entropy has been in use, albeit indirectly and implicitly, in most hydrological studies (as well as in all geosciences, see e.g., [17,18]). The probabilistic formalization of entropy has not been used in hydrology for long. Only in the 1960s did the pioneering study by Leopold and Langbein [19], which relies on Boltzmann’s definition of entropy (see Section 2.3), appear. In the 1970s hydrologists began to use Shannon’s definition of entropy (see Section 2.1) mainly for parameter estimation of models [20] and probability distributions [21], while in the early 1980s some doctoral theses on the use of entropy in hydrology were conducted [22,23]. Extensive reviews on the use of entropy in applications in hydrology and water resources have been provided by Singh [24,25]. Additional hydrological studies which rely on entropy will be referred to later on.
The aim of this paper is not to derive new results. In fact no new results are presented. At the same time it is not a review paper. It presents some known results from a different perspective trying (a) to unify the notion of entropy in thermodynamic and statistical/stochastic approaches and (b) to show the power of entropy and the principle of maximum entropy in inference, both deductive and inductive. The capability for deductive reasoning is illustrated by deriving the law of phase change transition of water from scratch by using probabilistic entropy (Section 3). Although the law is very old (Clausius-Clapeyron), the derivation provided is new and constitutes an ideal example of how by maximizing entropy, i.e., uncertainty, at the microscopic level we can derive a physical law which virtually expresses certainty at a macroscopic level. Such deductive reasoning cannot work in more complex hydrological systems with diverse elements, yet the entropy maximization framework can help in inductive inference, necessarily based on data. Several examples of this type are provided (Section 4). Overall, the paper is written as a self-contained study with a pedagogic style in an attempt to help students of the entropy topic to avoid some confusion which all of us may have experienced. For this reason, the paper also contains a logical and mathematical foundation of the concepts used (Section 2) as well as several side derivations necessary to make the presentation complete (Section 3 and Appendix).
2. Logical and Mathematical Foundation
2.1. Entropy = Uncertainty
The definition of entropy relies on probability theory and is very economic as it only needs the concept of a random variable and its distribution function. Before discussing this definition it is useful to make two notes about the notation used: (a) for random variables the Dutch convention [26] is followed, according to which an underlined symbol denotes a random variable, while the same symbol not underlined represents a value (or realization) of the random variable; (b) entropy is denoted by Φ to avoid confusion with the classical thermodynamic entropy S (the original symbol used by Clausius), which has some (mostly logistic) differences (e.g., it is regarded to be a dimensional quantity, while Φ is dimensionless). Some texts use the symbol H for Shannon entropy; however here the symbol Φ was preferred for several reasons including historical ones: for long time, entropy used to be denoted by φ [27–29] and this is still echoed in the term tephigram (T-Φ-gram) used in meteorology.
The entropy definition follows some postulates originally set up by Shannon [7]. Assuming a discrete random variable z taking values zj with probability mass function Pj ≡ P(zj) = P{z = zj}, j = 1,…,w, the postulates, as reformulated by Jaynes [12] (p. 347), are:
- (a)
It is possible to set up a numerical measure Φ of the amount of uncertainty which is expressed as a real number.
- (b)
Φ is a continuous function of Pj.
- (c)
If all the Pj are equal (Pj = 1/w) then Φ should be a monotonic increasing function of w.
- (d)
If there is more than one way of working out the value of Φ, then we should get the same value for every possible way.
Quantification of the latter postulate is given, among others, in [8] (p. 3) and [30] (Theorem 1) and is related to refinement of partitions to which the probabilities Pj refer. From these general postulates about uncertainty, a unique (within a multiplicative factor) function Φ is defined. For discrete variables, for which probabilities satisfy the obvious relationship:
the entropy is defined as:
where E[ ] denotes expectation. Extension of the above definition for the case of a continuous random variable z with probability density function f(z), where:
is possible, although not contained in Shannon’s [7] original work. This extension involves some additional difficulties. Specifically, if we discretize the domain of z into intervals of size δz, then (2) would give an infinite value for the entropy as δz tends to zero (the quantity −ln p = −ln (f(z) δz)) will tend to infinity). However, if we involve a (so-called) “background measure” with density h(z) and take the ratio (f(z) δz)/(h(z) δz) = f(z)/h(z), then the logarithm of this ratio will generally not diverge. This allows the definition of entropy for continuous variables as (see e.g. [12], p. 375, and [30]):
The background measure h(z) can be any probability density, proper (with integral equal to 1, as in Equation (3)) or improper (meaning that its integral does not converge); typically it is an (improper) Lebesgue density, i.e., a constant with dimensions [h(z)] = [f(z)] = [z−1], so that the argument of the logarithm function be dimensionless. It is easily seen that for both discrete and continuous variables the entropy Φ [z] is a dimensionless quantity. For discrete variables it can only take positive values, while for continuous variables it can be either positive or negative, depending on the assumed h(z).
2.2. The Principle of Maximum Entropy: Why Entropy is Important
As already mentioned, from a physical perspective, the tendency of entropy to become maximal (Second Law of thermodynamics) is the driving force of natural change. The counterpart of the physical law in logic is the principle of maximum entropy [10], which postulates that the entropy of a random variable z should be at maximum, under some conditions, formulated as constraints, which incorporate the information that is given about this variable. The rationale of the principle is very simple and almost self-evident: If uncertainty is not the maximum possible, then there must be some more information; but all information is already incorporated in the constraints. Compared to physical laws expressed in the form of equations (e.g., equality of conserved quantities), the ME principle, as a variational law, is extremely more powerful: it can determine infinitely many (or even uncountably many) unknown probabilities.
To illustrate the ME principle we start with the simple example of determining the probabilities of the outcomes of a die throw. The example may look trivial. However, as will be seen later on, with the same reasoning we can infer more interesting things, such as the saturation vapour pressure in the atmosphere. The logic in the two cases is the same: we maximize the uncertainty with respect to the state of a die or a water molecule. For the die the entropy is:
The equality constraint is:
Inequality constraints about probabilities (0 ≤ Pi ≤ 1) are not necessary to include in optimization in this case. The solution of the optimization problem (e.g. by the Lagrange method) yields a single maximum:
The entropy is Φ = −6 (1/6) ln (1/6) = ln 6. In this case, the application of the ME principle (a variational law) is equivalent to the principle of insufficient reason (Bernoulli-Laplace; an equation form). It is noted that entropy and information are complementary to each other. When we know (observe) that the outcome is i (Pi = 1, Pj = 0 for j ≠ i), the entropy is zero.
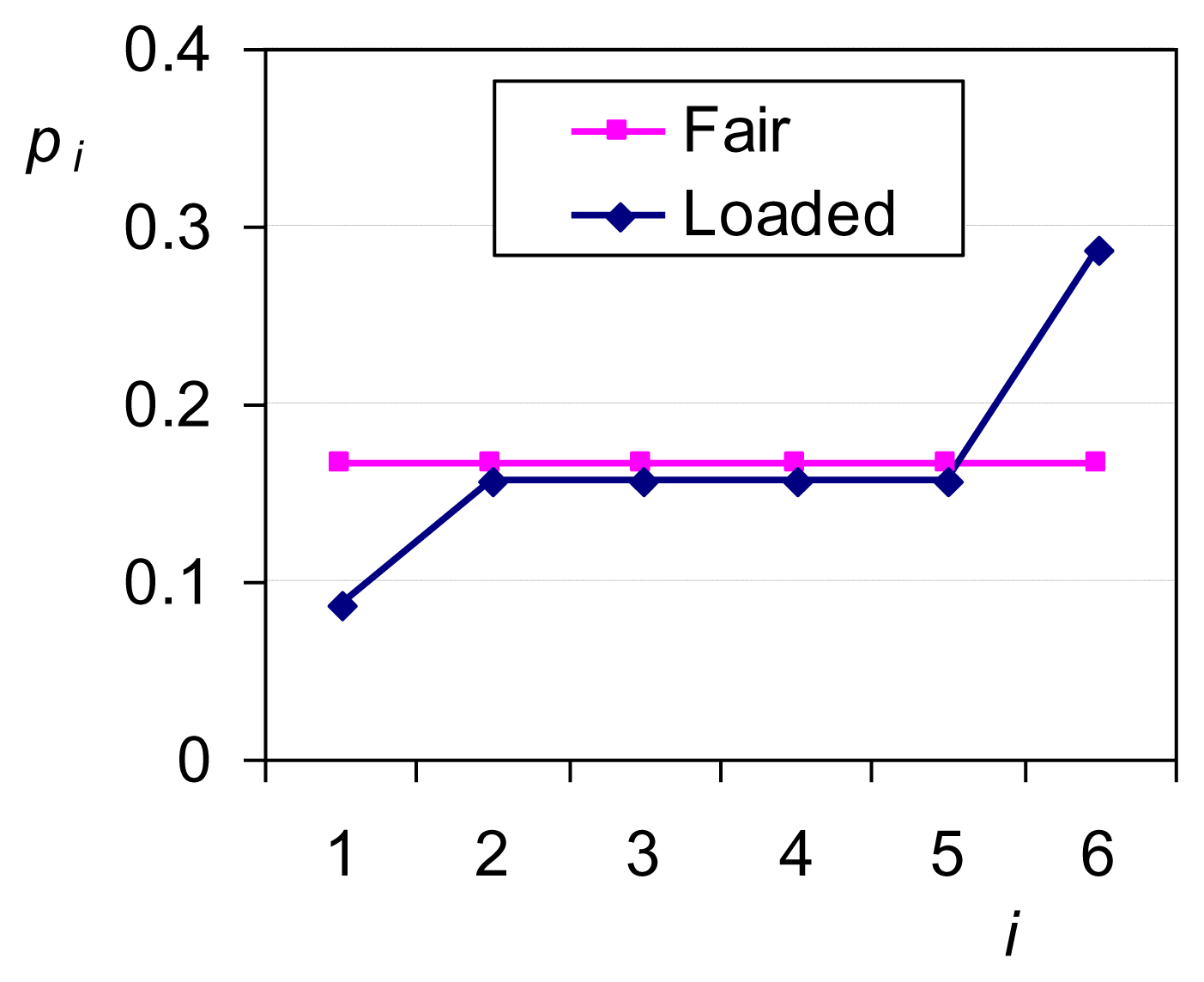
While in this simple case the principle of insufficient reason works equally well as the ME principle, in fact the latter is more powerful as it can perform in any type of problems, in which uniformity is a priori excluded. To see this let us assume that the die is loaded and that we have prior information that P6 – P1 = 0.2 ≠ 0. What is the probability that the outcome of a die throw will be i in this case? For the entropy maximization we only need to consider the additional constraint P6 – P1 – 0.2 = 0 (e.g., with an additional Lagrange multiplier). The solution of the optimization problem is a single maximum depicted in Figure 1. The entropy is Φ = 1.732, smaller than in the case of equiprobability, where Φ = ln 6 = 1.792. The decrease of entropy in the loaded die derives from the additional information incorporated in the constraints.
2.3. Maximum Entropy and Uniformity
As in the die case, entropy maximization without constraints, except the obvious Equation (1), results in equal probabilities for all outcomes. The entropy for w equiprobable outcomes is:
This corresponds to the original Boltzmann’s definition of entropy, according to which the entropy is the logarithm of the number of possible configurations of the phase space (or in probability terms the number of possible outcomes). However, when compared to Equation (8), Equation (2) provides a more general definition, applicable also to cases where, due to constraints, equiprobability is not possible, or where the number of possible outcomes or configurations is infinite. In other words, in the general case, the entropy equals the expected value of the minus logarithm of probability (rather than just the minus logarithm of probability).
A similar result is obtained for continuous variables z. Entropy maximization without constraints, except Equation (3), over a finite interval (or volume, in a vector space) Ω, will result in uniform probability density i.e. f(z) = 1/Ω, if we also assume a constant background measure density, h(z) = h. The maximized entropy then becomes:
Again this corresponds to the original Boltzmann’s definition of entropy, in this case giving the entropy in terms of the logarithm of the volume of the accessible phase space Ω. Yet Equation (4) provides a more general definition than Equation (9), applicable in every case, even if the volume of phase space is infinite.
An important characteristic of the general entropy definitions in Equations (2) and (4) is that they both are independent of the specific metric that is used to define the random variables which describe a physical phenomenon. This is obvious in Equation (2), which is an expression of probabilities and does not involve values of the random variables at all. It is less obvious in Equation (4) and in fact, if we assume h(z) ≡ 1 as most probability texts do (e.g., [31], p. 565), the entropy value is not unique but changes if a transformation z → y(z) is applied. However, this problem is resolved if entropy is defined as in Equation (4) and the transformation is applied also to h(z). Indeed it is easy to show that the entropy value is invariant under the transformation z → y(z) (i.e., Φ [y] = Φ [z]). The reason is that both f and h transform in the same way under a change of variables [12] (pp. 375–376). However, as has been already noted, in continuous variables the entropy value changes if a different background measure is chosen. Also, in both continuous and discrete random variables the entropy changes in coarse grained descriptions of the system, in which probabilities refer to elements of partitions of the basic set, rather than elementary events.
2.4. Expected Values as Constraints: General Solution
In the most typical application of the ME principle, we wish to infer the probability density function f(z) of a continuous random variable z (scalar or vector) for constant background measure (for simplicity taken h(z) = 1) with constraints formulated as expectations of functions gj(z). In other words, the given information, which is used in maximizing entropy, is expressed as a set of constraints formed as:
The resulting maximum entropy distribution (by maximizing entropy as defined in Equation (4) with constraints (10) and the obvious additional constraint (3)) is [31] (p. 571):
where λ0 and λj are constants determined such as to satisfy Equations (3) and (10), respectively. The resulting maximum entropy is:
Typical results for the most common constraints are provided in Table 1.
3. Application to Simple Physical Systems
3.1. ME Applied to the Uncertain Motion of a Particle
In this section we will derive physical laws which are extensively used in hydrology—in particular the law for the phase transition of water—applying the same method with which we derived the probabilities of a die outcome in Section 2.2 and the probability distribution functions in Table 1. We consider a motionless cube with edge a (volume V = a3) containing spherical particles of mass m0 (e.g., monoatomic molecules) in fast motion, in which we cannot observe the exact position and velocity. A particle’s state is described by six variables, three indicating its position xi and three indicating its velocity ui, with i = 1, 2, 3 (three degrees of freedom); all are represented as random variables, forming the vector z = (x1, x2, x3, u1, u2, u3).
The constraints for position are:
While these are inequality constraints, those for velocity are equality constraints given in terms of integrals over feasible space Ω, i.e., (0, a) for each xi and (−∞, ∞) for each ui. Specifically, the conservation of momentum is E[m0 ui] = m0 ∫Ω ui f(z) dz = 0 (because the cube is not in motion), so that:
Likewise, conservation of energy yields E[m0 ||u||2/2] = (m0/2) ∫Ω ||u||2 f(z) dz = ɛ, where ɛ is the kinetic energy of the particle (known as thermal energy) and ; thus, the constraint is:
In general, the expectation E[ui] represents the macroscopic velocity of the motion, while ui – E[ui] represents velocity fluctuation at a microscopic level. If E[ui] ≠ 0 (if the cube was moving), then the macroscopic and microscopic kinetic energies should be treated separately, the latter being ɛ = E[m0 (||u − E[u]||)2/2].
By dimensional considerations we define the background measure in terms of universal constants, i.e., the Planck constant h = 6.626 × 10−34 J·s and the proton mass mp. It is easily verified that h(z) = (mp/h)3 (dimensions L–6 T3), thereby giving the entropy as:
Application of the principle of maximum entropy with constraints as in Equations (3), (13), (14) and (15) gives the distribution of z (see proof in Appendix 1 and in [16]) as:
The marginal distribution of each of the location coordinates xi is uniform in [0, a], i.e.:
The marginal distribution of each of the velocity coordinates ui is derived as:
This is Gaussian with mean 0 and variance 2ɛ/3m0 (= 2 × energy per unit mass per degree of freedom). The marginal distribution of the velocity magnitude ||u|| is:
This is known as the Maxwell–Boltzmann distribution.
The entropy then results as:
where e is the base of natural logarithms.
From Equation (17) we readily observe that the joint distribution f(z) is a product of functions of z’s coordinates x1, x2, x3, u1, u2, u3. This means that all six random variables are jointly independent. The independence results from entropy maximization. From Equations (17) and (19) we also observe the symmetry with respect to the three velocity coordinates, resulting in uniform distribution of the energy ɛ into ɛ/3 for each direction or degree of freedom. This is known as the equipartition principle and is again a result of entropy maximization.
3.2. Extension for Many Particles
The coordinates of N identical monoatomic molecules which are in motion in the same cube of volume V form a vector Z = (z1,…, zN) with 3N location coordinates and 3N velocity coordinates. If E is the total kinetic energy of the N molecules and ɛ = E/N is the energy per particle, then following a similar approach we find [16] the entropy as:
The resulting Equation (22) is fully consistent with the probabilistic character of entropy and also with the thermodynamic content of entropy [16]. It is noted that the equation found in literature, known as the Sackur-Tetrode equation (after H. M. Tetrode and O. Sackur, who developed it independently at about the same time in 1912) differs from Equation (22) in the last term, which is N ln (V/N) instead of N ln V. To derive the Sackur-Tetrode expression, an assumption is made (inspired from quantum physics) that particles are indistinguishable. This assumption is problematic and here is avoided (see details in [16]).
3.3. Extension to Many Degrees of Freedom
The number of microscopic degrees of freedom β that can store energy in a particle depend on the particle architecture and interactions. Thus, in gases:
A monoatomic molecule has β = 3 translational degrees of freedom, corresponding to the three components of the velocity vector, as already described.
A diatomic molecule (e.g., of N2 or O2 which are the most typical in the atmosphere) has a linear structure; thus, in addition to the kinetic energy it has rotational energy at two axes perpendicular to the line defined by the two atoms; in total it has β = 5 degrees of freedom.
A triatomic, not linear, molecule (e.g., H2O), or a more complex one, has three rotational degrees of freedom or β = 6 degrees of freedom in total.
In solids and liquids there are degrees of freedom associated to vibrational energy. Generalizing Equations (21) and (22) for β degrees of freedom we obtain the entropy per molecule as:
where c incorporates all related physical and mathematical constants. Likewise, the total entropy of N molecules is:
3.4. Definition of Internal Energy and Temperature
In gases, the internal energy EI equals the thermal energy (ɛI = ɛ, EI = E). In liquids and solids, the bonds between molecules are associated with dynamic energy; denoting the dynamic energy per molecule as –ξ, we write:
where ξ = 0 for gases and ξ > 0 for liquids and solids.
Temperature is defined to be the inverse of the partial derivative of entropy with respect to energy, i.e.,
The definition is based on the internal energy, but assuming constant ξ, there is no difference if we take the thermal energy instead. Since entropy is dimensionless and EI is energy, temperature has also dimensions of energy (J). As already mentioned, this contradicts the common practice of using different units of temperature, such as K or °C. To distinguish from the common practice, we use the symbol θ (instead of T which is in K) and we call θ the natural temperature (instead of absolute temperature for T). From Equations (23), (24) and (26) we obtain:
or the temperature is twice the particle’s kinetic energy per degree of freedom.
3.5. The Law of Ideal Gases
We consider again the cube of edge a containing N identical molecules of a gas, each with mass m0 and β degrees of freedom. We consider a time interval dt; any particle at distance from the bottom edge dx3 ≤ −u3dt will collide with the cube edge (x3 = 0). From Equation (20), generalized for β degrees of freedom, the joint distribution function of (x3, u3) of a single particle is:
Thus, the expected value of the momentum q(dt) of molecules colliding at the cube edge (x3 = 0) within time interval dt is:
According to Newton’s second law, the force exerted on the edge is F = 2E[q(dt)]/dt and the pressure is p = F/a2 = 2 N ɛ/(β V), or finally (by using Equation (27)):
where v := V/N is the volume per particle. This is the well-known law of ideal gases written for natural temperature and derived by pure deduction based on maximization of probabilistic entropy.
3.6. Phase Change and Saturation Vapour Pressure
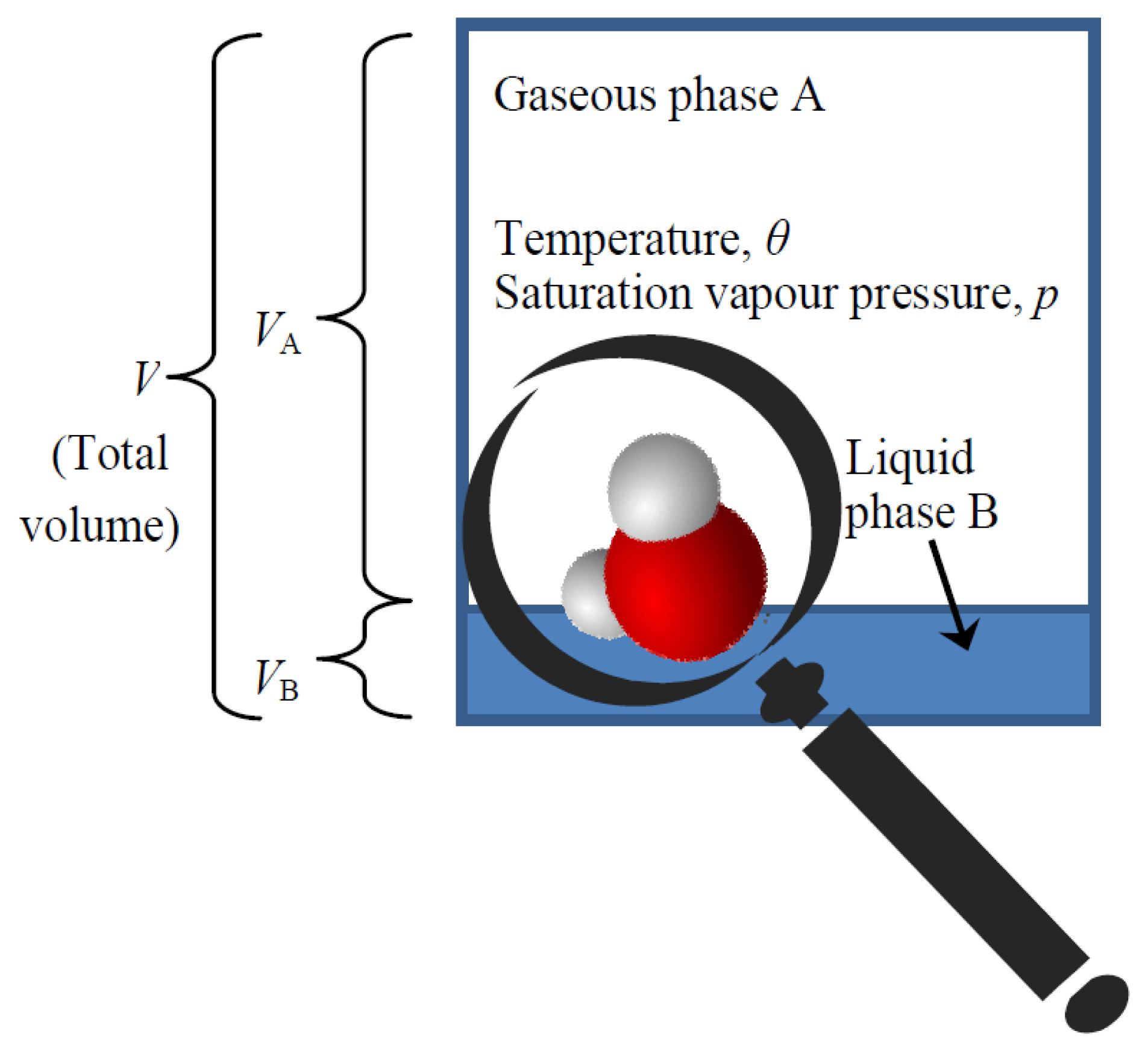
We have now almost everything to derive the law determining the equilibrium of liquid and gaseous phase of water, known as the Clausius-Clapeyron equation, which is very important in hydrology. Again this law will be derived by maximizing probabilistic entropy, i.e. uncertainty. In particular, the law is derived by studying a single molecule (see Figure 2) and maximizing the combined uncertainty of its state related to:
- (a)
its phase (whether gaseous, denoted as A, or liquid, denoted as B);
- (b)
its position in space; and
- (c)
its kinetic state, i.e., its velocity and other coordinates corresponding to its degrees of freedom and making up its thermal energy.
Furthermore, it is assumed that water vapour behaves as an ideal gas, so that Equation (30) holds. As its molecule has a 3-dimensional (not linear) structure, the rotational energy is distributed into three directions, so that the total number of degrees of freedom (translational and rotational) is:
Liquid water will be assumed incompressible, so that the volume per particle is:
where VB is the volume occupied by the liquid phase and NB is the number of particles in that phase. The number of degrees of freedom in the liquid phase is greater than βA because of the “social behaviour” of water molecules. Specifically, in addition to the translational and rotational degrees of freedom of individual molecules, there are local clusters with low energy vibrational modes that can be thermally excited. The average number of degrees of freedom per molecule (individual and collective involving more than one water molecules) is very high (e.g., [32]):
For a molecule to move from the liquid to gaseous phase, an amount of energy ξ to break its bonds with other molecules needs to be supplied (phase change energy). The partial entropies of the two phases, i.e., the entropies conditional on the particle being in the gaseous (A) or liquid (B) phase, are:
The total entropy is [16]:
or:
The two phases are in open interaction and the constraints are:
The calculations of entropy maximization are shown in Appendix 2. The resulting saturation vapour pressure is:
Assuming that at some temperature θ0, p(θ0) = p0, we write Equation (39) in a more convenient and dimensionally consistent manner as:
This is the final form of the proposed equation quantifying phase change. Equation (40) can be anchored at the triple point of water, in which θ0 = 37.714 yJ = 273.16 K, p0 = 6.11657 hPa [33], while an optimized value of the constant ξ/θ0 based on accurate measurements is ξ/θ0 = 24.861.
The Newton-Raphson method applied to Equation (40) gives the approximation:
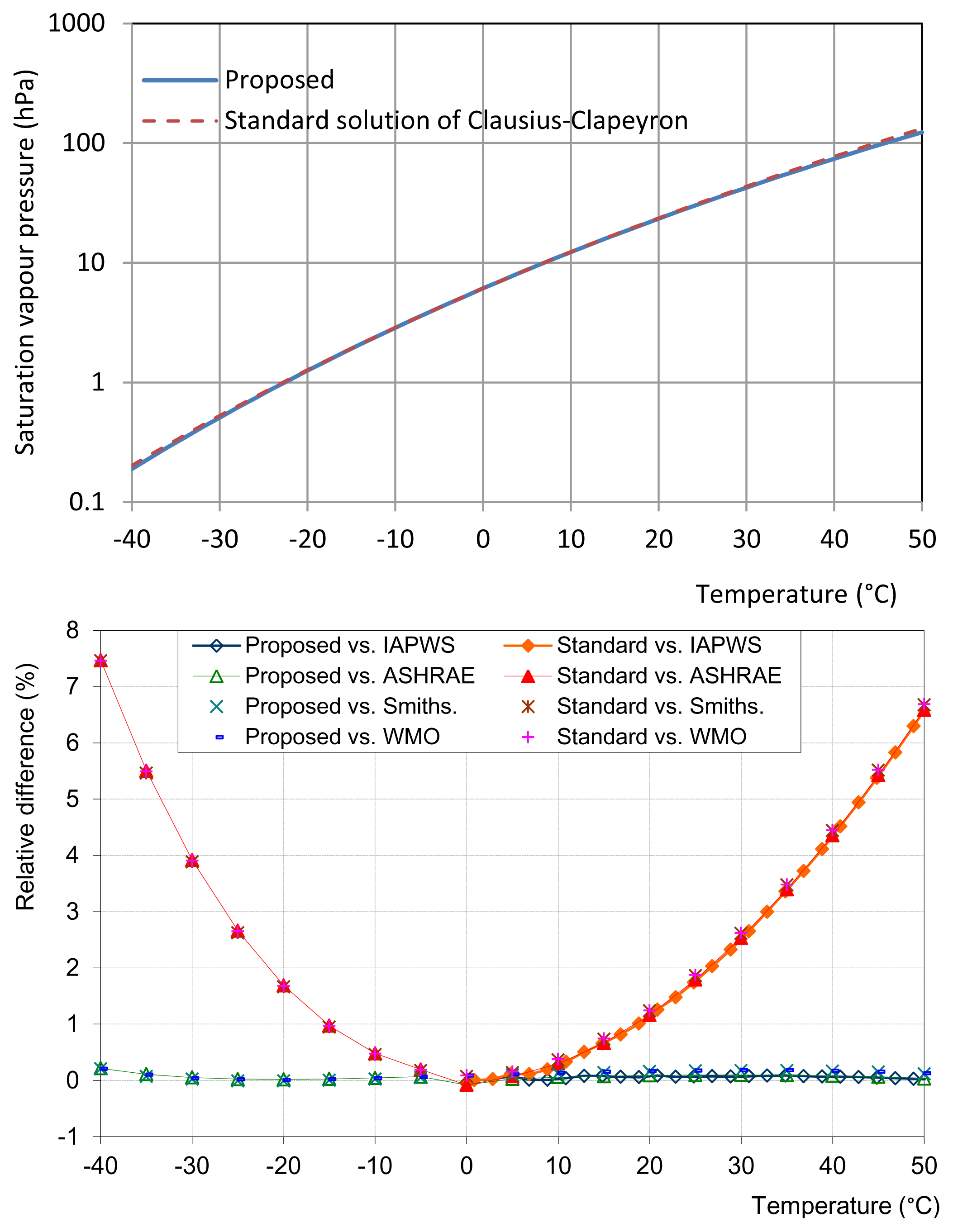
The latter is the standard solution of the Clausius-Clapeyron equation appearing in books, which however is an inconsistent approximate description of the phenomenon [34]. Figure 3 (upper) compares the proposed Equation (40) with the standard Equation (41); they seem indistinguishable. However, the lower panel of the figure, which compares relative differences from measurements, clearly indicates the superiority of Equation (40) derived here. A slightly more accurate version, based on experimental values of specific heats, instead of using integral degrees of freedom, can be found in [34] (the slight differences are in the numerical values of the constants, i.e., (βB/2 − βA/2 − 1) = 5.06 and ξ/θ0 = 24.921).
4. Application to Complex Hydrological Systems
4.1. From Statistical Thermodynamics of Systems with Identical Elements to Hydrological Systems
The law of phase change constitutes an amazing example of how we can derive, based on deductive reasoning, a virtually deterministic law by maximizing entropy (i.e., uncertainty). The key that made this possible is the huge number of identical elements involved in the phenomenon. This does not happen in higher levels of macroscopization, which are associated with higher complexity and diverse elements, each of them being a macroscopic entity per se and all of them being not so many as in typical thermodynamic systems (Figure 4).
Due to higher complexity, the probabilistic description is even more imperative in hydrological systems. Maximization of entropy (i.e., uncertainty) should provide the way to deal with the complex macroscopic hydrological systems. This contrasts the recent research trend in hydrology (and other disciplines), which invested hopes to the power of computers that would enable faithful and detailed representation of the diverse system elements. This research trend was based on the idea that the hydrological processes could be modelled using merely “first principles”, thus resulting in (deterministic) “physically-based” models which would tend to approach in complexity the real world systems. The aspiration of detailed and exact deterministic modelling traces a research direction that is wrong and opposite to the parsimonious way that Nature works.
In high-level macroscopic hydrological systems we expect to encounter more difficulties in comparison to simple thermodynamic systems. The constraints in entropy extremization do not necessarily coincide with those in classical statistical thermophysics. In particular, the mean μ and variance σ2 are important indices of the statistical behaviour (see [35]) with an intuitive conceptual meaning, but they are not constrained by physical laws as in the kinetic theory of gases—rather they are estimated from data. In addition, independence among different elements and across time (as assumed in the derivations of the previous section) is most often invalidated in high-level macroscopic systems. This, combined with the diversity of elements, entails that all laws should remain probabilistic. High-level macroscopic quantities in hydrological systems will never approach the near certainty of low-level macroscopic quantities in typical thermodynamic systems—regardless of progress in computers and algorithms. Inevitably, physically-based hydrological models are stochastic models (cf. [36]).
4.2. Towards Adaptation of the ME Framework for Nonnegative Random Variables
Typically for continuous random variables ranging in (−∞, +∞) the Lebesgue measure is used in the entropy function, so that h(z) = constant = 1/[z] where [z] denotes the physical unit in which the quantity z is expressed. The background measure h(z) determines the way of measuring distances d between values of z; the Lebesgue measure corresponds to the Euclidean distance, d(z, z′) = |z′ − z|.
However, most hydrometeorological variables are non-negative physical quantities unbounded from above (e.g., precipitation, streamflow, temperature—natural or absolute). In positive physical quantities (e.g., rainfall depth) often the Euclidean distance is not a proper metric; sometimes we use a logarithmic distance d(z, z′) = |ln(z′/z)|, as shown in the example of Table 2.
In an attempt to merge/unify the Euclidean and logarithmic distance, we heuristically introduce the generalized background measure for nonnegative variables:
where p is a characteristic scale parameter, which also serves as a physical unit for z; for p → ∞, h(x) tends to the Lebesgue measure. According to this generalized measure, the distance of any point z from 0 is:
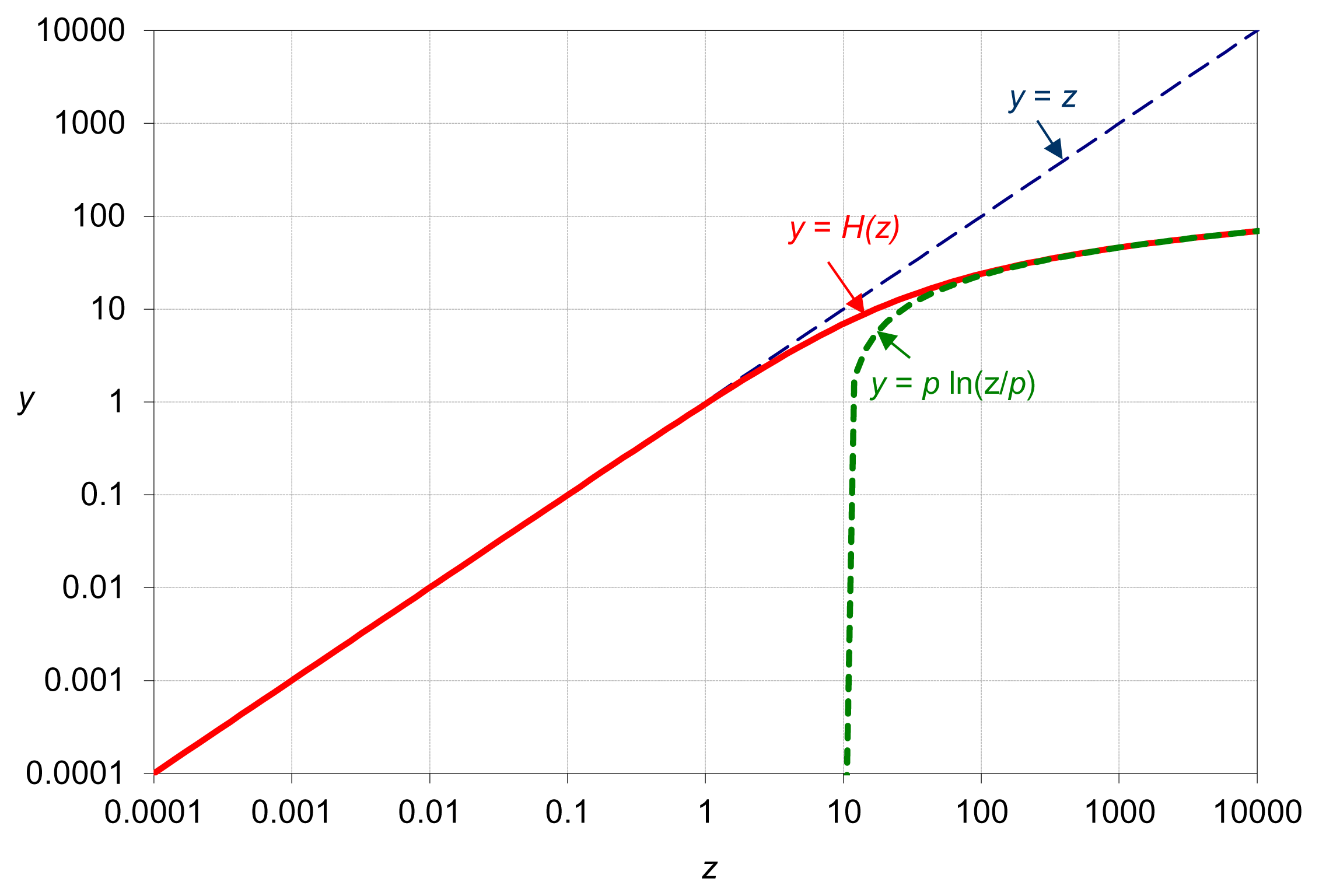
An example plot for H(z) is given in Figure 5. Hence, the distance between any two points z and z′ is:
For small z values, i.e., z < z′ << p, the distance is d(z, z′) = p ln (1 + (z′ − z)/(p + z)) ≈ z′ − z (Euclidean distance). For large values, p << z < z′, d(z, z′) ≈ p ln (z′/z) (logarithmic distance). We notice that both H(z) and d(z, z′) have the same units as z (physical consistency).
4.3. ME Distribution with a Single Constraint
For the background measure defined in (42) the entropy is:
It is reasonable to replace constraints of raw moments with those of generalized moments introduced in [37]. The simplest constraint is the preservation of a “generalized mean”, i.e.:
The entropy maximizing distribution (derived by the general methodology in [31], p. 571) is:
where λ1 is a Lagrange multiplier and A is such that (3) holds. By renaming parameters (p = λ/κ, λ1 = (1 + 2κ)/λ) we obtain the typical expression of the two-parameter Pareto distribution:
with mean μ = λ/(1 − κ), standard deviation , generalized mean mp = λ and entropy Φp [z] = E[−ln(f(z) (λ/κ + z)] = ln(eκ).
By setting κ = 0 and applying L’Hôpital’s rule we recover the exponential distribution f(z) = (1/λ) exp(−z/λ), whose basic statistics are μ = σ = λ. For a specified p the generalized mean of the exponential distribution is mp = p exp(p/λ) Γp/λ(0) and the entropy Φp [z] = ln(eλ/p) − mp/p (as can be found after algebraic manipulations in (45)); clearly Φp [z] is smaller than ln(eλ/p) which corresponds to the Pareto distribution.
Figure 6 provides a comparison of the two density functions, Pareto, fP(z), with κ = 0.15 and λP = 0.9 and exponential, fE(z), with λE = 0.953. The parameters are chosen so that both distributions have the same mp = 0.9 for p = λP/κ = 6. Their raw means are μP = 1.059 > μE = 0.953 and their entropies are ΦpP = −0.897 > ΦpE = −0.897 − 0.9/6. The enhanced uncertainty resulting from the proposed framework (Pareto distribution) in comparison to classical statistical mechanics (exponential distribution) is reflected in the distribution tail, where in the Pareto case it is a scaling law and produces much more frequent and intense extreme events.
It is recalled (Table 1) that in classical statistical mechanics a constrained mean results in exponential distribution with σ/μ = 1 while the case σ/μ > 1 is unattainable if the Lebesgue measure is used as background one. This problem is resolved with the above described framework: In the Pareto distribution . For σ/μ < 1 the above framework does not suffice as neither the exponential nor the Pareto distribution are compatible with this condition. Obviously, an additional constraint is needed for the entropy maximization. Koutsoyiannis [35] provided an exploratory framework using two constraints, mean and variance, while Papalexiou and Koutsoyiannis [37] provided a detailed modelling framework using generalized constraints.
4.4. Validation for the Marginal Distributions of Hydrometeorological Variables
The exploratory study already mentioned [35], using a somewhat different entropy maximization framework (and occasionally Tsallis entropy, which is not used here), concluded that the ratio σ/μ gives enough information to determine the general shape of the probability distribution. Large values (σ/μ > 1) entail Pareto distribution while small values (σ/μ << 1) support a normal distribution. The results were tested against several hydrometeorological time series.
Here we present results of this study which provide comparison of theoretical maximum entropy distributions with empirical distributions. Figure 7 shows the distribution of intense daily rainfall worldwide. Daily rainfall series above threshold from 168 stations worldwide each having at least 100 years of measurements were standardized by mean and merged (period covered 1822–2002; 17,922 station-years of data). For this sample, σ/μ = 1.19 > 1, which gives a Pareto ME distribution with κ = 0.15. Indeed, the Pareto distribution gives a very good fit to the empirical one while other distributions also plotted in Figure 7 depart significantly.
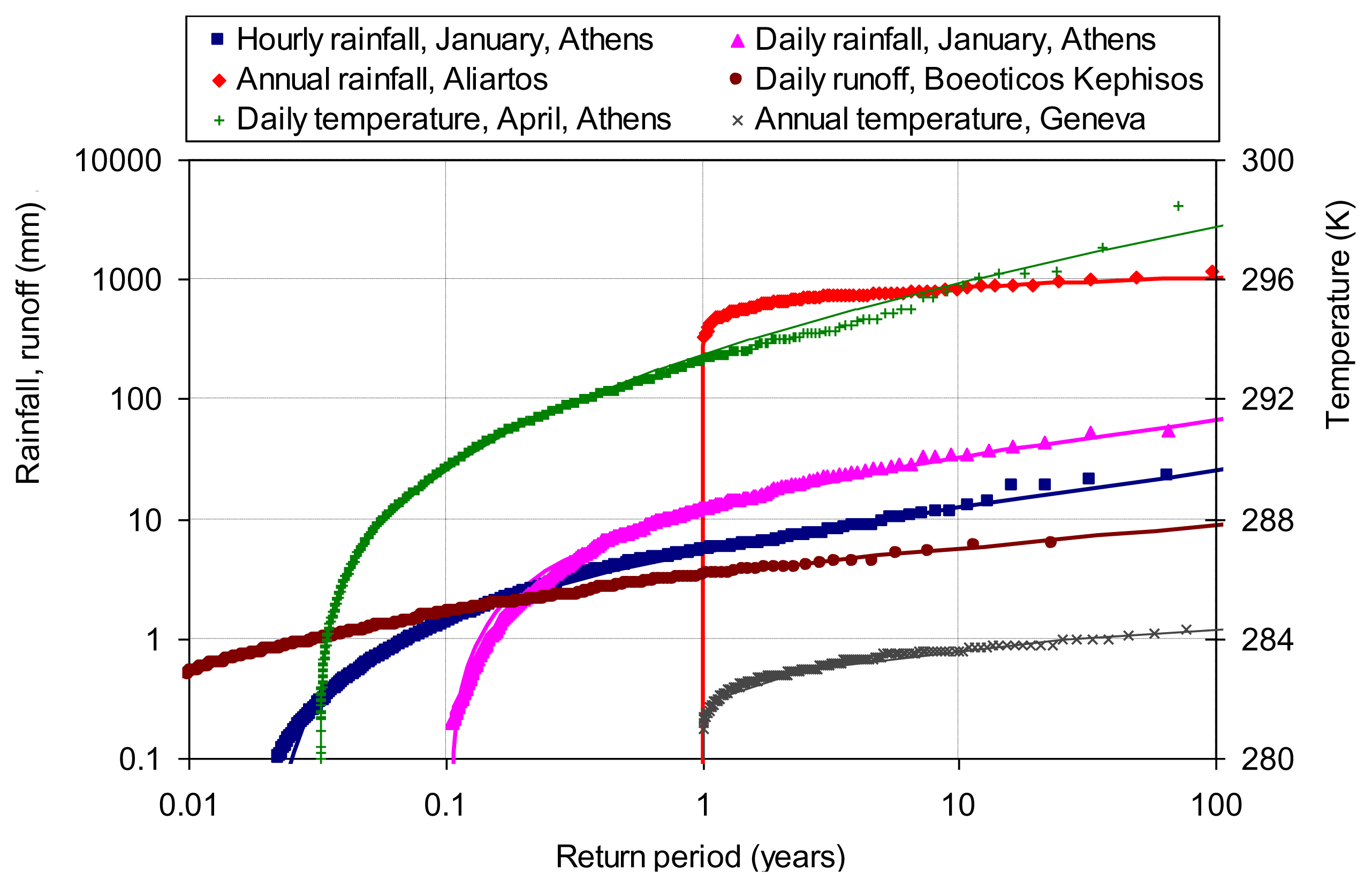
Figure 8 shows the distribution of rainfall, runoff and temperature at four sites and at scales from hourly to annual. In particular the data series and their respective coefficients of variation are (a) hourly rainfall in January at Athens, Greece, σ/μ = 1.47; (b) daily rainfall in January at Athens, σ/μ = 1.39; (c) annual rainfall at Aliartos, Greece, σ/μ = 0.24; (d) daily runoff at Boeoticos Kephisos, Greece, σ/μ = 1.19; (e) daily temperature in April at Athens, σ/μ = 0.0095; and (f) annual temperature at Geneva, σ/μ = 0.0024. These values of the coefficient of variation support the Pareto distribution for hourly and daily rainfall and runoff, the truncated normal distribution for annual rainfall and the normal distribution for temperature. These distributions give good fits to the empirical ones, as seen in Figure 8.
4.5. Systems Evolving in Time: Entropy and Clustering
Clustering (e.g., of similar events in time, of stars in space, etc.) is a universal behaviour and it can be hypothesized that it has some connection with maximum entropy, even though intuitively nonuniformity seems to contradict maximum entropy. To investigate this we can explore the entropy of two synthetic series of “extreme” events, in a period of 1,000 “years”, each having probability of occurrence in each “year” P =1/10 (Figure 9). The first series (R) is composed of random points in time, without clustering, while the second (C) was produced so as to have a clustering effect. The entropies of the two series are equal: ΦC = ΦR = (1/10) ln(10) + (9/10) ln(10/9) = 0.33. However, if we view the series at a decadal time scale, the entropy of the clustered series is higher: the entropy estimates, considering the probabilities of all possible numbers of extreme events (from 0 to 10), are ΦC = 1.29 > ΦR = 1.23. This simple example shows that clustering increases entropy (i.e., uncertainty) at aggregate time scales.
This idea was exploited in modelling rainfall occurrence, which is known to be characterized by clustering behaviour [38]. It has been shown that the observed behaviour can be explained by maximizing, for a range of scales, the entropy of the binary-state rainfall process using two constraints representing the observed occurrence probabilities at two time scales (1 and 2 hours). As shown in Figure 10, the entropy maximization with only two parameters determined from only two data points (the minimal information required to evaluate constraints) give impressively good predictions for all time scales.
4.6. Maximum Entropy Production and Scaling in Time
The dependence structure (expressed in terms of autocorrelogram, periodogram or climacogram, which are transformations of each other) of continuous-state processes evolving in continuous time can be determined by entropy extremization. Koutsoyiannis [9] suggested the use of entropy production in logarithmic time (EPLT) in a continuous time representation of the process of interest. EPLT is defined as:
with z(t) being a cumulative stochastic process (notice the different meaning of the symbol φ here and in section 3). The specific assumptions are: (a) Lebesgue background measure (assumption good for σ/μ << 1); (b) constrained mean μ and variance σ2; and (c) constrained lag-one autocorrelation ρ. Constraints (b) and (c) are formulated for a single observation time scale but the extremization of entropy production is made at asymptotic time scales, i.e., t → 0 and t → ∞. Constraint (b) results in Gaussian marginal distribution, hence (see Table 1):
where γ(t) := Var [z(t)]. Such extremization of entropy production yields two simple solutions:
A (non-scaling) Markov process (the AR(1) process in discrete time, or the Ornstein–Uhlenbeck process in continuous time).
A (scaling) Hurst-Kolmogorov (HK) process (due to Hurst [39] and Kolmogorov [40]).
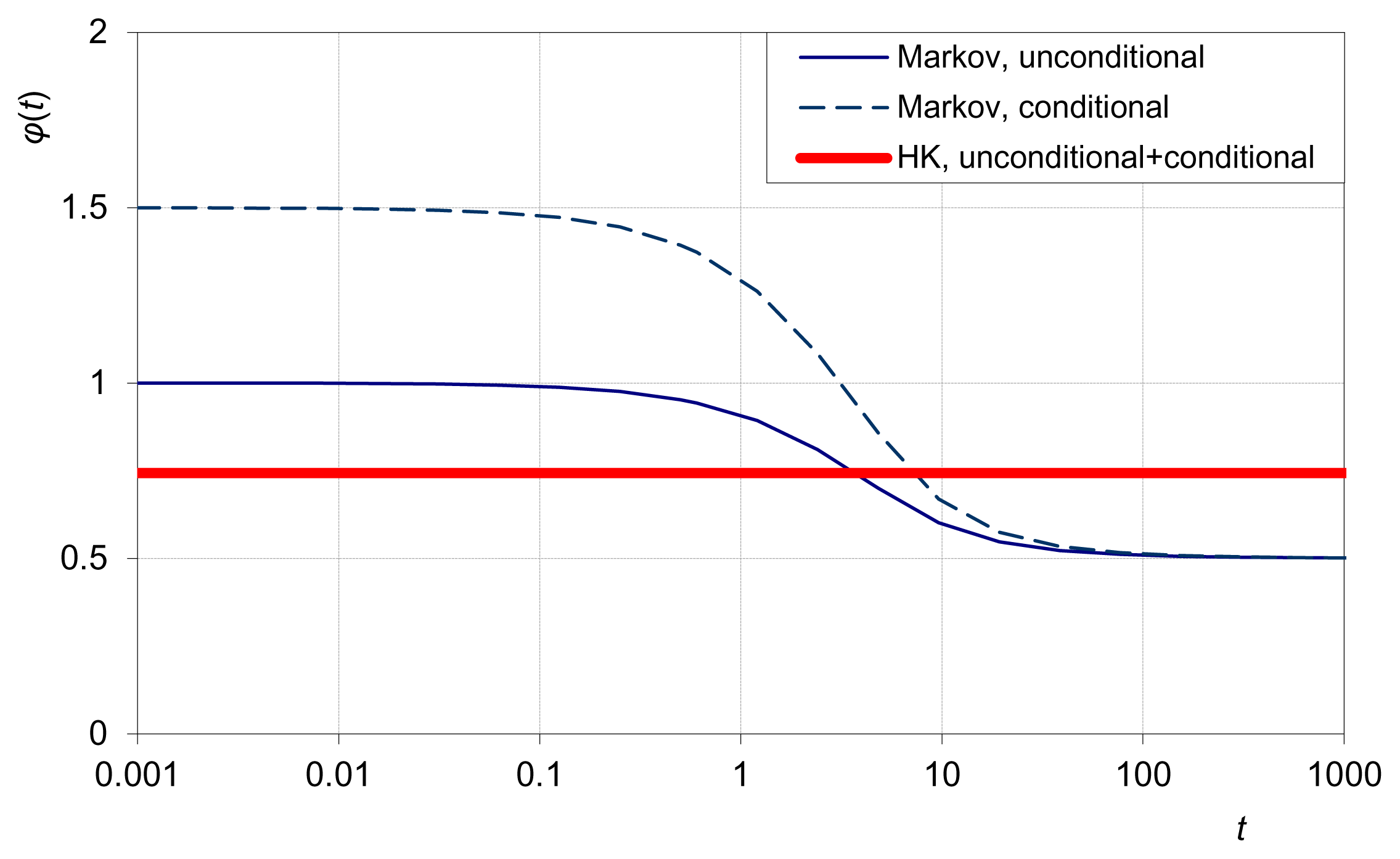
In particular, as t → 0, the EPLT is maximized by the Markov process, which however minimizes EPLT as t → ∞. In contrast, as t → ∞, the EPLT is maximized by an HK process. The HK process has constant EPLT = H, where H is the Hurst coefficient—the half of the exponent of the power law γ(t) = t2H γ(1). Actually, this power law can serve as a definition of the HK process. The two EPLT extremimizing solutions are depicted in Figure 11 in terms of the implied EPLT variation through time.
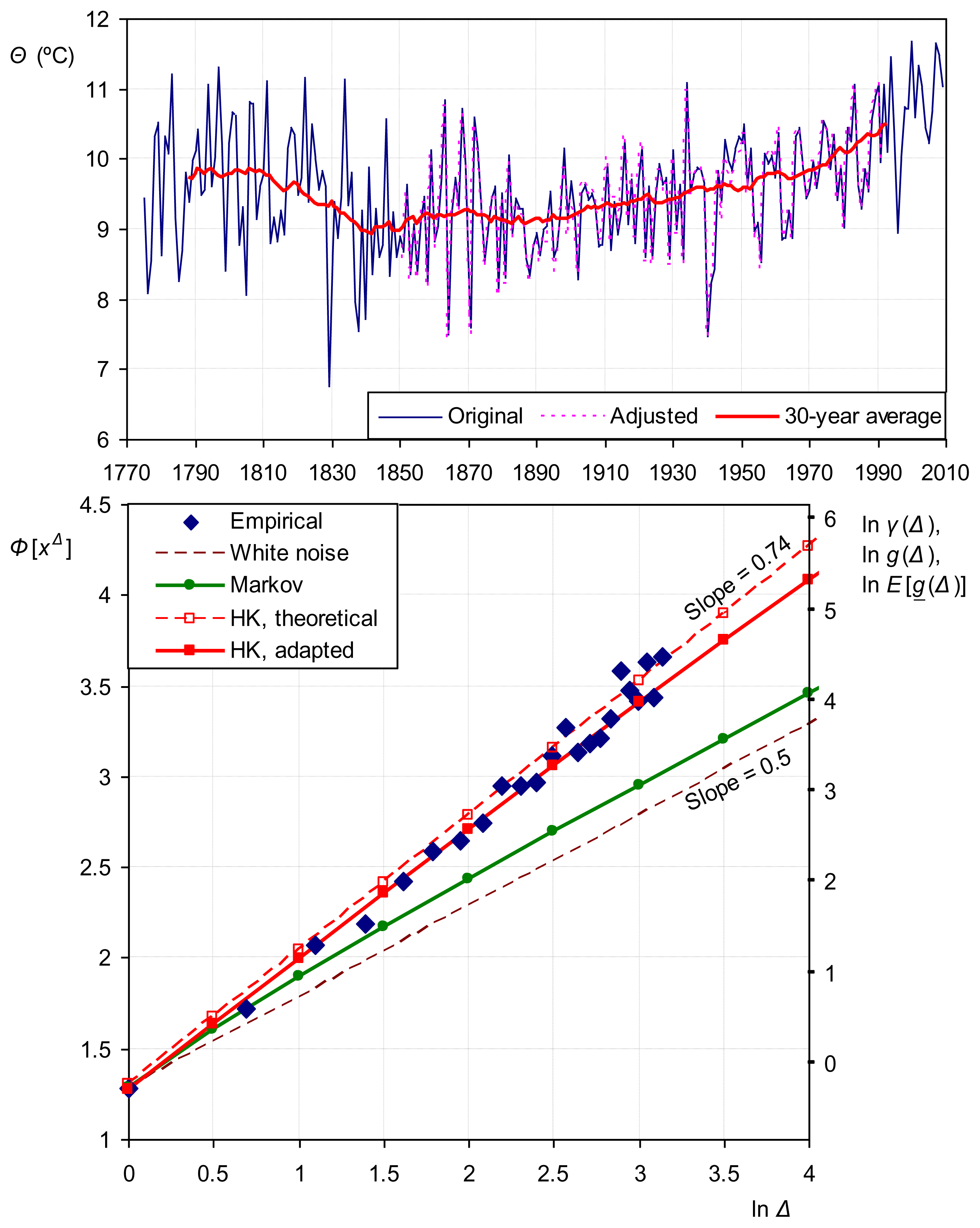
Application to the annual temperature of Vienna (one of the longest available instrumental methods) is shown in Figure 12. The low coefficient of variation (σ/μ = 0.0031 for temperature expressed in K or J), suggests Gaussian distribution and this is indeed verified by the data. As shown in the figure, the HK model (H = 0.74) is appropriate, while the Markov model (ρ = 0.3) is inappropriate. This suggests that entropy maximization at arbitrary long time (rather than that on short time) determines the long-term behaviour of the process.
4.7. Maximum Entropy and the Emergence of Linearity in Highly Nonlinear Systems
Hydrological processes (e.g., rainfall, runoff) are highly nonlinear if modelled using deterministic dynamical systems methods. The same processes, if approached macroscopically in stochastic terms, exhibit impressively linear behaviour (after the processes are transformed to Gaussian). Linearity in stochastic terms is a result of the principle of maximum entropy [31] (pp. 575–577) and makes our macroscopic descriptions as simple and parsimonious as possible. Figure 13 gives two examples of linear statistical laws using long data series.
4.8. Maximum Entropy and Parsimonious Stochastic Modelling
As already mentioned, modelling complex hydrological processes without data is impossible. It is a common problem that the data do not suffice to fit a model, particularly when the model has many parameters. Here the principle of maximum entropy can help to deduce some of the parameters, while other parameters are estimated from data.
A typical example of this type is the multivariate stochastic modelling, which involves vectors and matrices of parameters with very many elements. We consider the prediction w of the monthly flow one month ahead, conditional on a number s of other variables with known values that compose the vector z, using the linear model:
where a is a vector of parameters (T denotes transpose) and v is the prediction error, assumed to be independent of z; for simplicity, all elements of z are assumed normalized and with zero mean and unit variance.
For the model to take account of both short-range and long-range dependence (HK behaviour), a possible composition of z may include [42]: (a) the flows of a few previous months of the same year, and (b) all available flow measurements of the same month on previous years. The model parameters are estimated from:
where η := Cov[w, z] and H := Cov[z, z] (see [43]).
Altogether, the vector η and the matrix H may contain numerous items, typically of the order of 103–104 (e.g., for a dimensionality 100, if we have 100 years of observations: 100 + 100 × 100 = 10,100 items—albeit reduced due to symmetry of matrix). Traditionally, the items of such covariance matrices and vectors have been estimated directly from data; this is totally illogical (100 years of data cannot support the statistical estimation of 1,000–10,000 parameters). An alternative approach is to use data to estimate a couple of parameters per month and derive all other “unestimated” parameters by maximizing entropy. Such entropy maximization is in fact very simple; it only needs a generalized Cholesky decomposition of the matrix H (assuming that H = B BT, where B is a lower triangular matrix to be calculated by maximizing entropy). Using this approach, Koutsoyiannis et al. [42] were able to reduce a number of 1,872 model parameters to be estimated to only 26.
5. Conclusions
Entropy is none other than uncertainty quantified and its tendency to become maximal is not a curse; rather it is blessing. This tendency constitutes the driving force of change and evolution; also, it offers the basis to understand and describe Nature. By maximizing entropy, i.e., uncertainty, we can describe the behaviour of physical systems; such description is essentially probabilistic.
However, if a system is composed of numerous identical elements, the uncertainty, despite being maximal at the microscopic level, in the macroscopic description it becomes as low as to yield a physical law that is in effect deterministic. This is the case in the equilibrium of liquid water and water vapour (Clausius-Clapeyron equation).
Extremal entropy considerations provide a theoretical basis in modelling hydrological processes. However, at high macroscopization levels there is no hope to derive deterministic laws. Only stochastic modelling is feasible. Linking statistical thermophysics to hydrology with a unifying view of entropy as uncertainty is a promising scientific direction. Uncertainty and entropy are not enemies of science that should be eliminated. Rather they are important objects to be studied and understood.
Acknowledgments
I thank Pierre Hubert and Levent Kavvas for their invitations to talk about entropy in Melbourne (IUGG, 2011) and Davis (2013), respectively. Ideas from these talks were reworked to produce this paper, where reworking was partly funded by the Greek General Secretariat for Research and Technology through the research project “Combined REnewable Systems for Sustainable ENergy DevelOpment” (CRESSENDO). Finally, I am grateful to the Entropy Guest Editor Nathaniel A. Brunsell and Managing Editor Jely He for their invitation to make this paper, as well as to two reviewers for their encouraging comments.
Appendix
Appendix 1: Proof of Equations (17–21)
According to Equation (11) and taking into account the equality constraints (3), (14) and (15), the ME distribution will have density:
This proves that the density will be an exponential function of a second order polynomial of (u1, u2, u3) involving no products of different ui>. The f(z) in Equation (17) is of this type, and thus it suffices to show that it satisfies the constraints. Note that the inequality constraint (13) is not considered at this phase but only in the integration to evaluate the constraints. That is, the integration domain will be Ω: = {0 ≤ x1 ≤ a, 0 ≤ x2 ≤ a, 0 ≤ x3 ≤ a, −∞ < u1 < ∞, −∞ < u2 < ∞, −∞ < u3 < ∞}. We denote by ∫Ω dz the integral over this domain. It is easy then to show (the calculation of integrals is trivial) that:
Thus, all constraints are satisfied. To find the marginal distribution of each of the variables we integrate over the entire domain of the remaining variables; due to independence this is very easy and the results are given in Equations (18) and (19). To find the marginal distribution of ||u|| (Equation (20)), we recall that the sum of squares of n independent N(0, 1) random variables has a χ2(n) distribution [44] (pp. 219, 221); then we use known results for the density of a transformation of a random variable [44] (p. 118) to obtain the distribution of the square root, thus obtaining Equation (20).
To calculate the entropy, we observe that and ln h(z) = 3 ln (mp/h). Thus, the entropy is derived as follows:
This can be written as in Equation (21).
Appendix 2: Proof of (39)
Based on the assumption of Equation (32), if V is the total volume, then that of the gaseous phase is:
Using Equation (A4), (34) becomes:
We wish to find the conditions which maximize the entropy φ in Equation (35) under constraints (37) and (38) with unknowns ɛA, ɛB, πA, πB. We form the function ψ incorporating the total entropy φ as well as the two constraints with Langrage multipliers κ and λ:
To maximize ψ, equating to 0 the derivatives with respect to ɛA and ɛB, we obtain:
By virtue of Equation (27), this obviously results in equal temperature θ in the two phases, i.e.,
Equating to 0 the derivatives with respect to πA and πB, we obtain:
It can be seen that the first term of ∂ψ/∂πB equals −vB/vA and is negligible since vB << vA. After eliminating λ, substituting κ from Equation (A8), and making algebraic manipulations, we get:
On the other hand, from Equation (34), the entropy difference is:
Substituting θ for ɛA and ɛB from Equation (A8) and using the ideal gas to express vA in terms of θ and p we obtain:
Combining Equations (A10) and (A12), and eliminating (φA − ln πA) − (φB − ln πB), we find Equation (39).
Conflicts of Interest
The author declares no conflict of interest.
References
- Paulos, J.A. A Mathematician Plays the Stock Market; Basic Books: New York, NY, USA, 2003. [Google Scholar]
- Clausius, R. A contribution to the history of the mechanical theory of heat. Phil. Mag 1872, 43, 106–115. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat: With Its Applications to the Steam-Engine and To the Physical Properties of Bodies; J. van Voorst: London, UK, 1867. Available online: http://books.google.gr/books?id=8LIEAAAAYAAJ accessed on 10 January 2014.
- Clausius, R. Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie. Annalen der Physik und Chemie 1865, 125, 353–400. (In German). [Google Scholar]
- Boltzmann, L. Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht. Wien. Ber 1877, 76, 373–435. (In German). [Google Scholar]
- Swendsen, R.H. Statistical mechanics of colloids and Boltzmann’s definition of the entropy. Am. J. Phys 2006, 74, 187–190. [Google Scholar]
- Shannon, C.E. The mathematical theory of communication. Bell Syst. Tech. J 1948, 27, 379–423. [Google Scholar]
- Robertson, H.S. Statistical Thermophysics; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Koutsoyiannis, D. Hurst-Kolmogorov dynamics as a result of extremal entropy production. Physica A 2011, 390, 1424–1432. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev 1957, 106, 620–630. [Google Scholar]
- Swendsen, R.H. How physicists disagree on the meaning of entropy. Am. J. Phys 2011, 79, 342–348. [Google Scholar]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge Univ. Press: Cambridge, UK, 2003. [Google Scholar]
- Atkins, P. Four Laws that Drive the Universe; Oxford Univ. Press: Oxford, UK, 2007. [Google Scholar]
- Kalinin, M.; Kononogov, S. Boltzmann’s constant, the energy meaning of temperature, and thermodynamic irreversibility. Meas. Tech 2005, 48, 632–636. [Google Scholar]
- Ben-Naim, A. A Farewell to Entropy: Statistical Thermodynamics Based on Information; World Scientific Pub: Singapore, 2008. [Google Scholar]
- Koutsoyiannis, D. Physics of uncertainty, the Gibbs paradox and indistinguishable particles. Studies in History and Philosophy of Modern Physics 2013, 44, 480–489. [Google Scholar]
- Brunsell, N.A.; Schymanski, S.J.; Kleidon, A. Quantifying the thermodynamic entropy budget of the land surface: is this useful? Earth Syst. Dynam 2011, 2, 87–103. [Google Scholar]
- Ruddell, B.L.; Brunsell, N.A.; Stoy, P. Applying information theory in the geosciences to quantify process uncertainty, feedback, scale. Eos 2013, 94, 56–56. [Google Scholar]
- Leopold, L.B.; Langbein, W.B. The Concept of Entropy in Landscape Evolution; US Government Printing Office: Washington, DC, USA, 1962. [Google Scholar]
- Sonuga, J.O. Principle of maximum entropy in hydrologic frequency analysis. J. Hydrol 1972, 17, 177–191. [Google Scholar]
- Jackson, D.R.; Aron, G. Parameter estimation in hydrology: The state of the art. J. Am. Water Resour. Assoc 1971, 7, 457–472. [Google Scholar]
- Harmancioglu, N. Measuring the Information Content of Hydrological Processes by the Entropy Concept (In Turkish). Ph.D. Thesis, Ege University, İzmir, Turkey, 1980. [Google Scholar]
- Bendjoudi, H. Application du concept d’entropie dans les sciences de l’eau (In French). Ph.D. Thesis; École Nationale Supérieure des Mines de Paris: Paris, France, 1983. Available online: http://hydrologie.org/THE/BENDJOUDI.pdf accessed on 7 February 2014. [Google Scholar]
- Singh, V.P. The use of entropy in hydrology and water resources. Hydrol. Process 1997, 11, 587–626. [Google Scholar]
- Singh, V. Hydrologic synthesis using entropy theory: Review. J. Hydrol. Eng 2011, 16, 421–433. [Google Scholar]
- Hemelrijk, J. Underlining random variables. Stat. Neerl 1966, 20, 1–7. [Google Scholar]
- Perry, J. The Thermodynamics of Heat Engines. Nature 1903, 67, 602–605. [Google Scholar]
- Swinburne, J. Entropy. Nature 1904, 70, 54–55. [Google Scholar]
- Ewing, J., LXII. The specific heat of saturated vapour and the entropy-temperature diagrams of certain fluids. Lond. Edinb. Dubl. Phil. Mag. J. Sci 1920, 39, 633–646. [Google Scholar]
- Uffink, J. Can the maximum entropy principle be explained as a consistency requirement? Studies in History and Philosophy of Modern Physics 1995, 26, 223–261. [Google Scholar]
- Papoulis, A. Probability, Random Variables and Stochastic Processes, 3rd ed; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Fraundorf, P. Heat capacity in bits. Am. J. Phys 2003, 71, 1142–1151. [Google Scholar]
- Wagner, W.; Pruss, A. The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar]
- Koutsoyiannis, D. Clausius-Clapeyron equation and saturation vapour pressure: simple theory reconciled with practice. Eur. J. Phys 2012, 33, 295–305. [Google Scholar]
- Koutsoyiannis, D. Uncertainty, entropy, scaling and hydrological stochastics, 1, Marginal distributional properties of hydrological processes and state scaling. Hydrol. Sci. J 2005, 50, 381–404. [Google Scholar]
- Montanari, A.; Koutsoyiannis, D. A blueprint for process-based modeling of uncertain hydrological systems. Water Resour. Res 2012. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. Entropy based derivation of probability distributions: A case study to daily rainfall. Adv. Water Resour 2012, 45, 51–57. [Google Scholar]
- Koutsoyiannis, D. An entropic-stochastic representation of rainfall intermittency: The origin of clustering and persistence. Water Resour. Res 2006. [Google Scholar] [CrossRef]
- Hurst, H.E. Long term storage capacities of reservoirs. Trans. Am. Soc. Civil Engrs 1951, 116, 776–808. [Google Scholar]
- Kolmogorov, A.N. Wienersche Spiralen und einige andere interessante Kurven in Hilbertschen Raum. Dokl. Akad. Nauk URSS 1940, 26, 115–118. (In German). [Google Scholar]
- Papalexiou, S.M.; Koutsoyiannis, D.; Montanari, A. Can a simple stochastic model generate rich patterns of rainfall events? J. Hydrol 2011, 411, 279–289. [Google Scholar]
- Koutsoyiannis, D.; Yao, H.; Georgakakos, A. Medium-range flow prediction for the Nile: A comparison of stochastic and deterministic methods. Hydrol. Sci. J 2008, 53, 142–164. [Google Scholar]
- Koutsoyiannis, D. A generalized mathematical framework for stochastic simulation and forecast of hydrologic time series. Water Resour. Res 2000, 36, 1519–1533. [Google Scholar]
- Papoulis, A. Probability and Statistics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]






| Constraints for the continuous variable z | Resulting distribution f(z) and entropy Φ (for h(z) = 1) |
|---|---|
| z bounded in [0, w]; no equality constraint | f(z) = 1/w (uniform) Φ = ln w |
| z unbounded from both below and above | |
| No constraint or constrained mean μ | not defined |
| Constrained mean μ and variance σ2 | (Gaussian) |
| Nonnegative z unbounded from above | |
| No equality constraint | not defined |
| Constrained mean μ | f(z) = (1/μ) exp(−z/μ) (exponential) Φ = ln (eμ) |
| Constrained mean μ and variance σ2 with σ < μ | f(z) = A exp(− ((z − α)/β)2/2) (truncated Gaussian tending to exponential as σ → μ); the constants A, a and β are determined from the constraints and Φ from (12) |
| As above but with σ > μ | not defined |
| Euclidean Distance | Logarithmic Distance | |
|---|---|---|
| z = 0.1 mm, z′ = 0.2 mm | 0.1 mm | ln 2 |
| z = 100 mm, z′ = 100.1 mm | 0.1 mm | ln 1.001 |
| z = 100 mm, z′ = 200 mm | 100 mm | ln 2 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Koutsoyiannis, D. Entropy: From Thermodynamics to Hydrology. Entropy 2014, 16, 1287-1314. https://doi.org/10.3390/e16031287
Koutsoyiannis D. Entropy: From Thermodynamics to Hydrology. Entropy. 2014; 16(3):1287-1314. https://doi.org/10.3390/e16031287
Chicago/Turabian StyleKoutsoyiannis, Demetris. 2014. "Entropy: From Thermodynamics to Hydrology" Entropy 16, no. 3: 1287-1314. https://doi.org/10.3390/e16031287





