The Maximum Error Probability Criterion, Random Encoder, and Feedback, in Multiple Input Channels
Abstract
: For a multiple input channel, one may define different capacity regions, according to the criterions of error, types of codes, and presence of feedback. In this paper, we aim to draw a complete picture of relations among these different capacity regions. To this end, we first prove that the average-error-probability capacity region of a multiple input channel can be achieved by a random code under the criterion of maximum error probability. Moreover, we show that for a non-deterministic multiple input channel with feedback, the capacity regions are the same under two different error criterions. In addition, we discuss two special classes of channels to shed light on the relation of different capacity regions. In particular, to illustrate the roles of feedback, we provide a class of MAC, for which feedback may enlarge maximum-error-probability capacity regions, but not average-error-capacity regions. Besides, we present a class of MAC, as an example for which the maximum-error-probability capacity regions are strictly smaller than the average-error-probability capacity regions (first example showing this was due to G. Dueck). Differently from G. Dueck’s enlightening example in which a deterministic MAC was considered, our example includes and further generalizes G. Dueck’s example by taking both deterministic and non-deterministic MACs into account. Finally, we extend our results for a discrete memoryless two-input channel, to compound, arbitrarily varying MAC, and MAC with more than two inputs.1. Introduction
The behavior of a multiple user channel is quite different from that of a point-to-point channel. For example, it is well known that the choice of the error criterion, i.e., the average or maximum probability of error, makes no difference for the capacity of a point-to-point channel; whereas G. Dueck [1] showed that, maximum-error-probability capacity regions of multiple access channel (MAC), two way channel (TWC), and interference channel (IC) can be strictly smaller than their average-error-probability capacity regions. It is worth mentioning that this had been pointed out in an earlier work by R. Ahlswede [2]. Nevertheless, the two criterions may lead to the same capacity region for an MAC as well, as such an example was presented by P. Vanroose in [3].
The difference of the two capacity regions could be intuitively explained as follows. For a channel with two inputs, two senders may not always well cooperate (although in most cases they may cooperate well). If the criterion of maximum probability of error is used, the worst case has to be counted. As a direct consequence, the capacity region in this case may be strictly smaller than the one under the criterion of average error probaility (where only the average case is considered). This also explains why for a broadcast channel (BC), which is a channel with one single input, the maximum-error-probability capacity region is always equal to the average-error-probability capacity region [4] (p.293).
In network information theory, a lot of excellent work has been done on the criterion of average error probability (for example c.f. [5]). However, the progress of research on the criterion of maximum error probability seems to be relatively slow. As a comparison, for a discrete memoryless MAC, to determine its maximum-error-probability capacity region is still a challenging open problem even today; whilst its average-error-probability capacity region was completely determined in early of 70’s of the last century [6,7].
Another interesting issue is feedback. It is well known that feedback may not increase the capacity of a point-to-point memoryless channel [8]; whilst it may enlarge the capacity region of a multiple user channel (e.g., [9–14]). Remarkably, feedback may not increase the capacity region of a physical degraded BC [15], as to a point-to-point channel. Moreover, the capacity region of a multiple-user channel with feedback also depends on the error criterion used. As shown in Dueck’s example in [1], the maximum-error-probability capacity region of an MAC, even when feedback is present, may be strictly smaller than its average-error-probability region without feedback. Therefore, for a MAC with feedback, the capacity regions under two different error criterions may be different. To clear the clouds, an investigation on the difference made by error criterions in coding theorems for multiple user channels with feedback, is necessary.
Finally, let us take a look at the impact on the capacity regions made by different types of codes, i.e., deterministic and random codes. If the criterion of average probability of error is used, obviously the capacity regions of a channel for both deterministic codes and random codes are the same. Actually, the proofs of most direct coding theorems are based on this fact. So, when speaking of average-error-probability capacity region, (without or with feedback,) one does not have to distinguish which types of codes are employed. As a direct consequence, a point-to-point channel has only one capacity, no matter which criterion of error is considered, whether feedback is present or not, and which type of codes are employed. And, the same applies to a BC without feedback. However, this is not applicable to an MAC, IC, or TWC, since their maximum- and average-error-probability regions might be different when deterministic codes are employed. Therefore, there is no reason to believe that for them, random codes and deterministic codes have the same maximum-probability-error capacity region. In fact, we shall see in this paper, that random codes may have a larger maximum-error-probability capacity region than deterministic codes.
In general, for an MAC or IC, we can define the following 6 capacity regions:
average-error-probability capacity regions, without and with feedback;
maximum-error-probability capacity regions of random codes, without and with feedback;
maximum-error-probability capacity regions of deterministic codes, without and with feedback.
Similarly, when speaking of capacity region of a TWC, we must distinguish which type of codes and error criterion are used.
We observe that the relations of these capacity regions of MAC, IC, and TWC are similar, due to the fact that they all have multiple inputs. We refer to them as multiple input channels. The goal of the paper is to clarify the relation of the capacity regions of multiple input channels, but not to determine them. To simplify the discussion, we first assume that all channels have two inputs, and then extend them to the general case.
First, we show that the average-error-probability capacity region for a multiple input channel may be achieved by a random code under the criterion of maximum probability of error, no matter whether feedback is present or not. Thus, we reduce the above “6 capacity regions” to 4 of them. By definition, a random code for a two-input channel may have two random encoders, or one random encoder and one deterministic encoder. Notice that a deterministic encoder can be considered as a “special random encoder”. Therefore, capacity region of random codes with two random encoders may not be smaller than that of random codes with one random encoder and one deterministic encoder, no matter maximum or average error criterion to be considered. For the same reason, no matter which criterion of error to be used, the capacity region of random codes with one random encoder and one deterministic encoder may not be smaller than the capacity region of deterministic codes. On the other hand, for random codes with two random encoders, the maximum-error-probability capacity region may not be larger than its average-error-probability capacity region, which is equal to average-error-probability capacity region of deterministic codes. We propose a coding scheme, which achieves the average-error-probability capacity region by employing a random code under the criterion of maximum probability of error. In our coding scheme, randomization at one encoder is sufficient. Therefore, the maximum-error-probability capacity regions of random codes with two random encoders, and one random encoder and one deterministic encoder must be the same.
Consider the remaining 4 capacity regions. Recall that for a MAC which employs deterministic codes, feedback may enlarge the average- and maximum-error-probability capacity regions; and the maximum-error-probability capacity region may be strictly smaller than the average-error-probability capacity region. In particular, G. Dueck [1] gave an example of a deterministic channel and showed that, the maximum-error-probability capacity region of a MAC with feedback or TWC may be strictly contained by its average-error-probability capacity region, even when the feedback is absent. So, it nature for us to ask whether maximum-error-probability capacity region for a multiple input channel with feedback may be larger than the average-error-probability capacity region for the same channel when the feedback is absent. This motivate us to study maximum-error-probability capacity region with feedback. In contrast to Dueck’s example, in this paper, we demonstrate that, for a non-deterministic discrete memoryless or Gaussian MAC and IC with feedback, the average- and maximum-error-probability capacity regions are always the same, as well as for a TWC. This tells us that only the deterministic channel may possibly have the properties in [1]. By combining our result and Cover-Leung bound [10], it is not difficult to find a MAC such that its maximum-error-probability capacity region with feedback is strictly larger than its average-error-probability capacity region without feedback. As a conclusion, we obtain a complete picture about the relation of the capacity regions of a multiple input channel.
The choice of criterion of error makes no difference for random codes.
The maximum-error-probability capacity region for deterministic codes without feedback is contained by all the other capacity regions; and, the contained relation can be strict.
The average-error-probability capacity region with feedback contains all the other capacity regions; and, the containing relation can be strict.
The maximum-error-probability capacity region for deterministic codes with feedback may be strictly larger than, or strictly smaller than the average-error-probability capacity region without feedback.
For deterministic codes with feedback, if the channel is deterministic, the choice of criterion of error makes a difference; whereas if the channel is non-deterministic, it makes no difference.
When deterministic codes are employed, feedback may enlarge both the average- and maximum-error-probability capacity regions. However, the reasons may be different. To illustrate it, we provide a class of MAC, for which feedback may enlarge the maximum-error-probability capacity regions, but not the average-error-probability capacity regions. As the contraction channel (the channel used by G. Dueck in [1] to show that the maximum-error-probability capacity region of a multiple input channel may be strictly smaller than its average-error-probability capacity region), is deterministic, we are especially interested in having a non-deterministic example. For this purpose, we generalize the contraction channel to a class of MAC, which contains both deterministic and non-deterministic MACs, and show that, for all channels in the class, maximum-error-probability capacity regions are strictly smaller than average-error-probability capacity regions.
Moreover, we extend above results to compound channels, arbitrarily varying channels, and channels with more than two inputs. It turns out that for a random code under the criterion of maximum probability of error, to achieve the average-error-probability capacity region of an arbitrarily varying MAC, a randomization at one encoder is not sufficient any longer; and it is necessary to have randomization at both encoders. This leads us to the 3rd capacity region of an arbitrarily varying MAC, which we shall call semi-average-error-probability capacity region.
The rest of the paper is organized as follows. In the next section, we briefly describe our problems and review the contraction channel which was introduced in [1]. In Section 3, we prove that the average-error-probability capacity region of a multiple input channel can be achieved by a random code under the criterion of maximum probability of error. In Section 4, we show that for a non-deterministic discrete memoryless channel with feedback, and a Gaussian channel with feedback, the maximum-error-probability capacity region is always equal to the average-error-probability capacity region. To better illustrate the results of random coding and coding with feedback, we provide two examples in Section 5. In Section 6, the results are extended to compound channels, arbitrarily varying channels, and channels with more than two inputs. Finally we conclude the paper by a brief discussion in Section 7.
2. Problem Description and Previous Work
2.1. Channel Codes and their Error Criterion
Consider a MAC, which has two inputs and one output. Two senders aim to send messages from their own message sets i, i = 1, 2 to a receiver, who accesses the output of the channel. A code C for the MAC is specified by its encoding functions φi, i = 1, 2 and decoding function ψ. Note that the encoding functions φi, i = 1, 2 are two mappings from the message sets i, i = 1, 2 to the two input alphabets of the channel, respectively; whilst the decoding function ψ is a mapping from the output space of the channel to the message set1×2.
Consider an IC, which has two inputs and two outputs. Two senders aim to send their own messages from sets1 and2 to two receivers, respectively. Similarly, a code C for the IC is specified by its the encoding functions φi, i = 1, 2 and the decoding functions ψj, j = 1, 2. In general case, the capacity region of an IC remains unknown; and, the best inner bound is due to T. S Han and K. Kobayashi [16].
For a MAC/IC, we say that feedback from the output y(j) (for a MAC, the output index j = 1; whilst for an IC, j ∈ {1, 2}) is available at the encoder i for i ∈ {1, 2}, if the codeword sent by the i-th sender, not only depends on the message mi, but also the output y(j) causally. I. e., the codeword can be written as
where ; and is the symbol sent by the sender i at the time t.
A TWC has two inputs and two outputs, and is used by two users for exchanging messages. The first user sends messages to the first input of the channel, and receives messages from the second output of the channel; and the second user sends messages to the second input, and receives messages from the first output. The symbol sent by a user at the time t depends on not only the message that he/she wants to send, but also the output that he/she has received before the time t. A user decodes the messages according to not only the output that he/she received, but also the message sent by him/her. TWC was introduced by C. E. Shannon in his milestone paper [17]. It was actually the first model in network information theory. In the case that the users encode only according to their own messages, respectively, but not the outputs received by them, we refer the channel as a TWC without feedback. In other words, a TWC without feedback is an “IC”, for which his/her own message of a user can be used in decoding.
To distinguish MAC, IC, and TWC from point-to-point channels and BC, we refer them as multiple input channels. Note that in general a MAC may have more than two inputs. In the following, we first consider a MAC with only two inputs; and results obtained will be extended to the general case later.
It is well known that, a discrete channel
for a MAC (or
for an IC/TWC), is memoryless if for all
, and all y = (y1, y2, . . . , yn) ∈

where

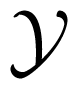
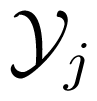
For a multiple input channel, let pe (C, (m1, m2)) be the error probability of a given code C for the message pair (m1, m2) ∈ 1 ×2 (i.e., the probability, that the decoder of the MAC, or at least one decoder of the IC or TWC, does not correctly decode, when the messages m1 and m2 are sent simultaneously through the channel). Then the average probability of error and maximum probability of error of the code are defined as
respectively, where Mi = |i|, i = 1, 2.
We say that an encoder i is random, if it can choose the codewords randomly, where i ∈ {1, 2}. That is, in the case that feedback is absent, the encoder i first generates a random key Ki, and then chooses a codeword according to the message to be sent, and the outcome of the random key; whilst in the case that feedback is present, the choice of codeword is additionally according to the received output of channel via the feedback causally. If the i-th encoder is random, accordingly we denote its encoding function by capital Greek Φi.
In this paper, we assume that the random key is uniformly distributed. A random code may have two random encoders, or one random encoder and one deterministic encoder. If a random code has two random encoders, we assume that the two random keys K1 and K2 are independent. We shall see in the next section that the number of random encoders makes no difference in the capacity regions of an (ordinary) multiple input channel. However, we shall see in Subsection 6.2, that random codes with two random encoders, and random codes with one random encoder and one deterministic encoder may have different capacity regions for an arbitrarily varying MAC. Thus, we do not need to distinguish the number of random encoders, when speaking of the capacity region, until Subsection 6.2.
For a random code Cr, the error probability pe(Cr, (m1, m2)) for a fixed message pair (m1, m2) is a function of the random keys, and thus is a random variable. Therefore, it must be replaced by its expectation in the definitions of error probabilities. That is, the average probability of error and maximum probability of error of the random code Cr are defined as
respectively, where E is operator of expectation. Obviously randomcodesmay not have a capacity region smaller than deterministic codes, because by definition, a deterministic code is a “special random code”.
The capacity regions of a multiple input channel are defined in a standard way. According to the presence of feedback, criterions of probabilities of error, and types of codes (random or deterministic), formally one might have 8 capacity regions.
As a matter of fact, every random code such that its average probability of error defined by (3) is smaller than a given number, has a realization with an average probability of error (defined in Equation (1) smaller than the same number. So, the type of codes makes no difference, if the criterion of the average error probability is employed. Therefore, we may simply speak of average-error-probability capacity region, and do not need to distinguish the type of codes.
For the criterion of the average probability of error, we have two capacity regions for a given channel W. We denote them by ̄(W) and ̄f (W), respectively, according to whether feedback is absent or present.
For the criterion of maximum probability of error, one may define capacity regions of random codes without and with feedback, denoted by r(W) and r,f (W), respectively; and, capacity regions of deterministic codes without and with feedback, denoted by d(W) and d,f (W), respectively.
As a special kind of random codes, deterministic codes may not have larger capacity regions than random codes; and, feedback may not reduce capacity regions. Therefore, relationship of the six capacity regions are presented as follows.
Remarks 2.1
We have the following observations:
- (1)
By definition, a multiple input channel may have different kinds of feedback; and, its capacity regions may depend on the kinds of feedback. Nevertheless, we denote the capacity regions with different kinds of feedback by the same notation. It makes no problem in this paper, since we are interested in the relation between the capacity regions, but not the capacity regions themselves. And, the kinds of feedback are also clear by the context.
- (2)
Let Cr be a random code with a random encoder Φ1 and a deterministic encoder φ2 for a multiple input channel. Then {Φ1(m1) : m1 ∈ 1} is not necessary to be a set of independent random variables. However, one can obtain a random code with the same rate, the same average and maximum probabilities of error for the same channel, from Cr, such that, m1 ∈ 1 are independent. The reasons are the followings:
- (1)
For, one can simply choose values of for all m1 ∈ 1, randomly and independently according to marginal distribution of Φ1(m1), and keep the deterministic encoder and the decoder(s) unchanged.
- (2)
Then { , mi ∈ i} is a set of independent random variables with the same marginal distribution as pe(Cr, (m1, m2)), for all (m1, m2) ∈ 1 × 2. That is, we have that
- (3)
Thus, without loss of generality, one may assume that {Φ1(m1), m1 ∈ 1} and {pe(Cr, (m1, m2)), m1 ∈ 1} for m2 ∈ 2, are sets of independent random variables.
By the same reason, for a random code with two random encoders Φi, i = 1, 2, we may also assume Φi(mi), mi ∈ i, i = 1, 2 are independent and pe(Cr, (m1, m2)), m1 ∈ 1 are conditionally independent, given Φ2(m2) = x(2).
- (3)
We may also assume that the decoder (decoders) of a random code accesses (access) the random key(s) generated by encoder(s), and decodes (decode) according to the outcome(s) of the key(s). In this case, the decoder(s) is (are) random. The code is often referred as a correlated random code in coding theorems of arbitrarily varying channels. One may have a random code with deterministic decoder(s), from a correlated random code with vanishing key rate(s), by sending the outcome(s) of random key(s) to decoder(s), if the capacity region of deterministic codes has non-empty topological interior.
2.2. Dueck’s Contraction Channel
In [1] G. Dueck showed by an example that, for MAC and TWC, maximum-error-probability capacity regions can be strictly smaller than their average-error-probability capacity regions. Without being pointed out explicitly in [1], the same example also implies that the maximum-error-probability capacity region of an IC may be strictly contained in its average-error-probability capacity region.
Dueck’s contraction channel is a discrete memoryless channel with a generic W :



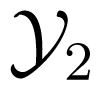
Let g be a function from



Let W1 be a channel W1 :






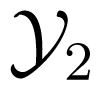



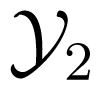

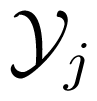
Dueck [1] considered the following scenarios:
(1) TWC
- (1.w)
TWC without feedback, or IC: There are two users in the communication system, say user 1 and user 2. The user 1 (user 2) accesses the first (second) message set 1 (2) and the second (first) output of the channel with the alphabet , and sends messages to the first (second) input of the channel with alphabet . No feedback is available. It is easy to see that, for this channel, their own messages may not help them to decode. So TWC and IC have the same capacity region.
- (1.f)
TWC with feedback: In addition to (1.w), the feedbacks from the second output to the first encoder and from the first output to the second encoder are available. That is, the channel is used as the standard TWC in Shannon’s sense [17].
(2) MAC
- (2.w)
MAC without feedback: Two senders send their messages to two inputs of the channel independently; and a single receiver, who wants to decode both messages, accesses both outputs. That is, by combining two outputs as one single output, we use the channel as an MAC. No feedback is available.
- (2.f)
MAC with feedback: In addition to (1.w), the feedbacks from the output to both encoders are available.
Notice that a codeword x(2), which is sent to the second input of the contraction channel, always can be recovered from both outputs correctly with probability 1; and, the second output is a function of the first output of the channel. Therefore, one may assume that the receiver only accesses the first output of channel in scenario (2). Moreover, a code is decodable in scenario (1) if and only if it is decodable in scenario (2). Thus, its capacity regions in scenarios (1.w) and (2.w) are the same; and, its capacity regions in scenarios (1.f) and (2.f) are the same.
Let ̄ be the average-error-probability capacity region of channels in scenarios (1) and (2). Define
where h(·) is the binary entropy function. Dueck [1] proved that the maximum-error-probability capacity regions in all the above four scenarios are contained by out, which is strictly smaller than ̄.
3. Randomization at One Encoder Enhances Codes with Maximum Error Probability
In this section, we show that randomization at one encoder may enhance a code under the criterion of maximum error probability for a multiple input channel, without or with feedback, to achieve the average-error-probability capacity region. That is, for a multiple input channel W, r(W) = ̄(W) and r,f (W) = ̄f (W).
First, let us recall Chernoff bound which will be applied in this paper repeatedly.
Lemma 3.1
Let V1, V2, . . . VL be L independent random variables such that EVl ≤ α < β/3 and 0 ≤ Vl ≤ 1 with probability 1, for l = 1, 2, . . . , L, and positive real numbers α and β. Then
Proof
where the equality in (a) holds because V1, V2, . . . VL are independent; (b) follows from the inequality for x ∈ [0, 1]; (c) holds because Vl ≤ 1 with probability 1; (d) follows from the assumption that EVl ≤ α; and (e) follows from the inequality 1 + x ≤ ex. That is (7).
Theorem 3.2
Let W be a multiple input channel. Then
provided that ̄(W) has a non-empty topological interior; and
provided that ̄f (W) has a non-empty topological interior.
Moreover, ̄(W) has a non-empty topological interior if and only if r(W) has a non-empty topological interior; and, ̄f (W) has a non-empty topological interior if and only if r,f (W) has a non-empty topological interior.
Proof
Since r(W) ⊂ ̄(W) and r,f (W) ⊂ ̄f (W), it is sufficient to show that, (1) ̄(W) is achievable by a randomcode with maximum error probability and without feedback, if it has a non-empty topological interior; and, (2) ̄ f (W) is achievable by a random code with maximum error probability and with feedback, if it has a non-empty topological interior. Both are proven in the same way.
Let ̄(W) or ̄f (W) have a non-empty topological interior; (R1, R2) be a rate pair in ̄(W) or ̄f (W), and λ, ε > 0. Then, for a sufficiently large n, there exists a deterministic code C of length n, with the encoding function φi, i = 1, 2, suitable decoder(s), and rate pair (at least) ( ), such that the average probability of error
where i, i = 1, 2, are the two message sets. Let
for m2 ∈ 2; and,
and 2,1 = 2\2,0. Then it follows from (10) and Markov inequality that
This gives us or . By using the same encoding functions and decoding function(s), while deleting messages in2,1, we have a subcode C0 of C, such that for all (m1, m2) ∈ 1×2,0, pe(C0, (m1, m2)) = pe(C, (m1, m2)).
Next we construct a code with a random encoder and a deterministic encoder under the criterion of maximum error probability. To this end, we let ∑ be the permutation group on 1; and, σ̃k, k = 1, 2, . . . n2, be i.i.d. random permutations uniformly distributed on ∑, where n is the length of code C. Then for all m1,, and all k,
For a σ ∈ ∑, we define σ(C0) as a code with the same message sets as C0, encoding functions φ1,σ(·) = φ1(σ(·)) and φ2,σ(·) = φ2(·), and a suitable modification in decoder(s) (i.e., by decoding the first message to be if the decoding result in C0 is ). Then, we have that pe(σ(C0), (m1, m2)) = pe(C0, (σ(m1), m2)), for all (m1, m2) ∈ 1 ×2,0. Thus by Equation (13), we have that for all k ∈ {1, 2, . . . , n2}, (m1, m2) ∈ 1×2,0,
where (a) and (b) hold by Equations (13) and (11), respectively; and (c) follows from (12) and the fact m2 ∈ 2,0. Consequently, by Chernoff bound, i.e., Lemma 3.1 (taking L = n2,), and (14), we obtain that for all fixed (m1, m2) ∈ 1×2,0,
Thus, by union bound, we have that with a probability at least (as n → ∞), (σ̃1, σ̃2, . . . σ̃n2) has a realization (σ1, σ2, . . . , σn2), such that for all (m1, m2) ∈ 1×2,0,
Now we are ready to construct a random code C̃r with a random encoder and a deterministic encoder. Our code consists of two blocks.
We first prepare a code C fulfilling the criterion of average probability error, choose its subcode C0, and then find permutation groups (σ1, σ2, . . . , σn2), satisfying (16).
Encoders
The first sender uniformly at random generates a “key” K1 from {1, 2, . . . , n2}, and then sends the outcome k1 of K1 in the first block, by using a code with average probability of error . At the same time, the second sender sends a suitably chosen dummy codeword to help the transmission. Then, the first sender sends the codeword φ1,σk1 (m1) through the channel in the second block, if he/she wants to send the message m1 and the outcome of the key is k1. At the same time, to send the message m2, the second sender sends φ2,σk1 (m2)(= φ2(m2)) through the channel. That is, the two senders send their messages by using the code σk1 (C0) in the second block. Notice that the second sender does not need to know the outcome of the key, because his/her encoding function does not depend on the permutation σk1 . The ratio of the length of the first block in the whole length of the code can be arbitrarily small, when n is sufficiently large, because the key rate vanishes, as n increases. Thus, the rates of code are larger than Ri − ε, i = 1, 2, respectively, if n is sufficiently large.
Decoder(s)
At the receiver(s), first the key is decoded as k̂; then the second block is decoded by using the decoding function of the code σk̂(C0).
Error Analysis
Let 0 be the event, of that an error occurs in the first block; and be its complement. Then, for all (m1, m2) ∈ 1×2,0,
where (a) holds since pe(C̃r(m1, m2)) ≤ 1 with probability 1; (b) holds since the average probability of error in the first block is no larger than ; (c) follows from the code construction; (d) follows from (16). Thus we complete the proof of Theorem 3.2.
The part of the proof will be used in the next section and Section 6, for readers’ convenience, we summary them as the following lemma:
Lemma 3.3
Let C be a deterministic code of length n for a multiple input channel, without or with feedback, with average probability of error, and a message set1×2.
- (1)
Then, there is a subcode C0 of C, with a message set 1 × 2,0, such that 2,0 ⊂ 2,, and Qe(m2) < 2λ1, for Qe(m2) as defined in Equation (11), and m2 ∈ 2,0.
- (2)
Let σ̃k, k = 1, 2, . . . , n2, be i.i.d. random permutations uniformly distributed on ∑, then Equation (15) holds for C0 as described in 1).
- (3)
Therefore, there are n2 permutations σk, k = 1, 2, . . . , n2 on 1 such that (16) holds.
Next, let us look into the reason why the average- and maximum-error-probability capacity regions of deterministic codes for a multiple input channel may be different. The two senders of a multiple input channel may cooperate only in the choice of codebook, since they must choose codewords independently due to the independence of messages. The combinations of the codeword pairs sent by them may be “good” or “bad”. Intuitively, comparing to the whole codebooks, the bad combinations are very few. Thus their contributions to the average probability of error can be ignored, when the codebooks are sufficiently large. On the other hand, if the criterion of maximum probability of error is used, one must consider the probability of error for “worst combination of codeword pairs”. To guarantee the worst combinations of codeword pairs to be correctly decoded with a high probability, the capacity region for codes satisfying the criterion of maximum probability of error often must be reduced. The randomization at an encoder plays a similar role to probability algorithms in theory of computation, or mixed strategies in game theory, mixing the good and bad combinations. As a consequence, the average-error-probability capacity regions are achievable.
The proof of the theorem tells us that adding randomness with a vanishing rate at one single encoder is sufficient for a code fulfilling the criterion of maximum error probability to achieve the average-error-probability capacity region. That is, the cost for the randomization is very low. This suggests us to use random coding in the network communication, because in any sense a small maximum probability of error is better than a small average probability of error, although in most cases the latter is acceptable.
By Theorem 3.2, the 6 capacity regions in (5) can be actually reduced to 4 capacity regions. Namely, (5) can be represented by
So far we have known that there is a MAC W, such that ̄(W) ⊊ ̄f (W); and, there are MAC, IC, and TWC W, such that d(W) ⊂ d,f (W) ⊊ ̄(W). In the next section, we shall apply Lemma 3.3 to non-deterministic and Gaussian multiple input channels with feedback, and show that for all non-deterministic discrete memoryless and Gaussian multiple input channels W,
By applying Cover-Leung inner bound [10], it is not hard to find a non-deterministic discrete memoryless MAC W, such that ̄(W) ⊊ ̄f (W), which with (19) yields that ̄(W) ⊊ d,f (W). Thus, we have a complete picture of the relation of the capacity regions of multiple input channels. That is, all contained relations in (18) may possibly be strict; and, d,f (W) may be strictly contained by, and strictly contain ̄ (W). Therefore, the relations in (18) may not be simplified further.
4. An Application to Feedback
In this section, we apply Lemma 3.3 to non-deterministic discrete memoryless and Gaussian multiple input channels with feedback.
An output of a multiple input channel is deterministic, if the output is a function of inputs. That is, for a deterministic output, no matter what input letters are input to the channel, at the output the channel always outputs a letter with probability 1. We say that the output is non-deterministic, if it is not deterministic. A multiple input channel is non-deterministic, if it has at least one non-deterministic output. Throughout this section, we assume that feedback from a non-deterministic output is available at least at one encoder, say the first encoder, if a multiple input channel is non-deterministic. Obviously, the contraction channel is deterministic. Here, by Gaussian channels we mean discrete-time additive Gaussian noise channels in the sense of [5] (93,137–138,438) or [18] ([Chapter 15]). It is easy to see from the following that, the result in Corollary 4.1 is true for all multiple input channels with the property (*) below, although for simplicity, we assume that the channel is non-deterministic discrete memoryless channels or Gaussian.
(*) There is a positive α such that for all β > 0, γ > 0 and a sufficiently large integer n0, there exist two codewords x(i), i = 1, 2 of length n0, and a subset A in an output space, whose output is sent to the first encoder as a feedback, such that
with probability at least 1 − β, the output sequence falls in A;
A can be partitioned into a = 2n0(α+o(1)) parts with nearly equal probability, i.e., the probability of each part is in ( ) when (x(1), x(2)) are the input to the channel.
Typically, we require that β → 0 and γ → 0 as n0 → ∞.
Obviously, for a non-deterministic discrete memoryless or a Gaussian multiple input channel, one may always choose a pair of codewords (x(1), x(2)) of length n0, such that the random output of the channel has positive entropy n0α, when x(1) and x(2) are sent to the channel. It is easy to see that, by taking the set of typical sequences as A, by AEP, one can partition A into (nearly) 2n0α parts with nearly equal probabilities. For instance, for a non-deterministic discrete memoryless channel, there are about 2n0(α+o(1)) output typical sequences with nearly equal probabilities, if the output entropy is n0α. Thus, one may partition the typical sequences into a = 2n0(α+o(1)) parts, such that each part contains nearly equal number of typical sequences, and therefore has nearly equal probability, similarly for a Gaussian channel. That is, (*) follows.
Feedback in memoryless channel usually may play the following 3 roles:
- (1)
Reducing Size of the Decoding List: The idea was introduced by C. E. Shannon in his pioneering work [8]. In short, the receiver lists all messages, which are possibly to be sent to him/her. Initially, the list contains all messages in the message sets. At each time t, the receiver reduces the list according to the output symbols, that he/she has received so far. Finally, the receiver decodes the message, when only one single message remains in the list. The senders learn the list via feedback, and thus can effectually cooperate with the receiver(s) to work on the list (instead of the whole sets of the messages).
- (1)
(2) Shifting the Private Messages to the Common Messages: Perhaps, it is the most common way to use feedback to enlarge capacity regions (e.g., [9,10,19] and etc). One difficulty for the senders of an multiple input channel (without feedback) to cooperate is that, their (private) messages are independent. When feedback is present, a sender can obtain certain information about the message sent by the other sender(s), via his own inputs and previous outputs, which he has received via feedback. Thus, he/she can shift the information from the private messages (of the other encoder) to the common messages, and cooperate with the other encoder(s) to resend them.
- (1)
(3) Extracting Common Randomness: Finally, receiver(s ) may extract a common randomness, or “a random key” from the output(s) and sends (send) it to the sender(s) via feedback. Thus, they may use the common randomness to help transmission (e.g., [20,21]).
The feedback will play the 3rd role in the following corollary. That is, by the property (*), we shall use a block of length n0 to generate a random key of size a. Then by using the random key, we shall “mix the good and bad combinations” of input codeword pairs.
Note that
Therefore, if the topological interior of ̄f (W) is empty, then the topological interior of d,f (W) is empty too. For simplicity of the discussion and ignoring this trivial case, we assume that the topological interior of ̄f (W) is not empty.
Corollary 4.1
For a non-deterministic discrete memoryless or Gaussian multiple input channel W, such that the topological interior of ̄f (W) is not empty, we have that
Proof
By (20), it is sufficient for us to show that, all (R1,R2) ∈ ̄f (W) is achievable by (deterministic) codes under the criterion of maximum probability of error and with feedback. For any given λ, ε > 0 and a sufficiently large n, we first find a code C of length n with feedback, such that its average probability of error is at most , and , i = 1, 2, where 1×2 is the message set of C. Then we find a subcode C0 of C and permutation groups (σ1, σ2, . . . , σn2) as described in Lemma 3.3. Next, we choose (x(1), x(2)) with the smallest possible n0 in the property (*) such that
Obviously, can be arbitrarily small, by choosing a sufficiently large n, since an integer n0 no less than is sufficient, and , as n → ∞.
We assume that the channel is a MAC. Our code consists of two blocks. In the first block, two senders send x(1) and x(2) (in the property (*)) respectively, no matter what messages they want to send. After the first block, both the first sender and the receiver learn the output y of the first block. In the case that y does not fall into A, the receiver declares an error, and we denote this error event by 0. By assumption, we have that
In the case that 0 does not occur, we assume that y falls into the k-th subset in the partition of A. Then in the second block, two senders send message m1 and m2, respectively, by using the code σk(C0) as described in Lemma 3.3. Recall (16). We have that for any fixed (m1, m2), the probability of error in the second block is upper bounded by
which with (22) together implies that, the total probability of error of the code for the MAC is upper bounded by . Moreover, by choosing sufficiently small , the rates of code may be larger than Ri − ε, i = 1, 2.
Notice that the second sender does not need to know k although he/she may know it. That is, the statement of the corollary still holds in the case that the feedback is available at one encoder only.
Differently from an MAC, a TWC or IC has two outputs. Let A be in any of outputs. Then a receiver accessing the other output, may not know the outcome of the random key. Thus, we need an additional block, for the first encoder to inform him/her the outcome of the key. This can be done by using a code with feedback and with average error probability at most . Thus as in the proof of Theorem 3.2, the total maximum probability of error may not exceed λ. Again, because the rate of random key as n → ∞, a vanishing rate is sufficient for the block. Thus, the total rates of code are not smaller than Ri − ε, i = 1, 2. This completes our proof.
Remark 4.2
Now, among the capacity regions of Gaussian MAC, only the maximum-error-probability capacity region without feedback is unknown, because the average-error-probability capacity region of a Gaussian MAC with feedback was determined by H. Ozarow [11]; and, by Corollary 4.1, it is equal to the maximum-error-probability capacity region of the same channel. We conjecture that the maximum-error-probability capacity region of a Gaussian MAC would be strictly smaller than the average-error-probability capacity region, when the feedback is absent. However, a proof or disproof has not been discovered so far. It would be very appreciated, if one might point out its existence. Otherwise, it would be a good problem for future research.
Corollary 4.1 tells us that, for a non-deterministic channel with feedback, the error criterion makes no difference on its capacity region. But, it is not always true in the general case, because we have learnt from the contraction channel [1], which is a deterministic channel, that its maximum-error-probability capacity region of deterministic codes with feedback is strictly smaller than its average-error-probability capacity region without feedback. Now we know from Corollary 4.1, that one can find neither example of non-deterministic channel nor example of Gaussian channel, which leads us to a similar result as in [1]. So, Corollary 4.1 actually provides a counterpart of Dueck’s case [1]. By comparing these two cases, we see an essential difference between deterministic and non-deterministic multiple user channels. The reason behind the difference is that: for a non-deterministic channel, one can build a common randomness through the feedback and use it to mix the “good cases” and “bad cases”; but for a deterministic channel, it is impossible. In this sense, noise may help transmission when feedback is present. We have seen this phenomenon from arbitrarily varying channel [20]. We will illustrate it in more details by examples in the next section.
5. Examples
Motivated by the following, we present two subclasses of MAC, as examples, in this section.
We have seen that one can apply feedback, not only for shifting the private messages to the common messages, but also for extracting common randomness, to help the transmission under the criterion of the maximum probability of error. On the other hand, the common randomness may not help the transmission under the criterion of the average probability of error, as random codes and deterministic codes have the same average-error-probability capacity region. So, it is expected that there exists a multiple input channel, for which feedback may enlarge the maximum-error-probability capacity region, but not the average-error-probability capacity region.
We wonder if there is a non-deterministic MAC, whose average- and maximum-error-probability capacity regions are different, since Dueck’s contraction channel is special for being deterministic.
First let us recall an inner bound on the average-error-probability capacity regions of discrete memoryless MAC W with feedback, due to T. M. Cover and C. S. K. Leung [10], which will be used in this section:
where

for all (u, x1, x2, y) ∈
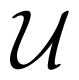


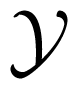

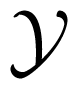
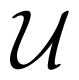
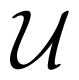


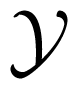
It was shown by F. M. J. Willems [22] that, the inner bound is tight, when the second input of the MAC is uniquely determined by the first input and the output of the MAC. We denote by
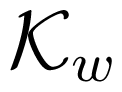
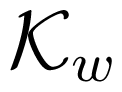
5.1. A Class of MAC, for which Feedback Does not Enlarge Average-Error-Probability Capacity Region
We say that a MAC W is in the class
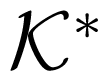
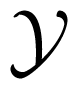


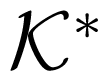
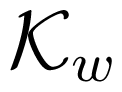
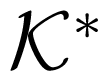
The maximum-error-probability capacity region of channels in with feedback was obtained by R. Ahlswede and N. Cai [23], where the channels in were referred as semi-noisy deterministic MAC, based on the 1st role of feedback: reducing size of the decoding list. It is easy to see that both the contraction channel in [1] and noiseless binary switching MAC in [3] belong to this subclass .
As
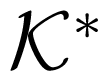
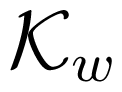
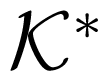
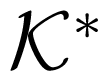
In fact, for all channels in
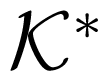
Proposition 5.1
(i) For all W ∈
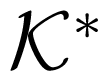
(ii) For all,
Proof
Since (ii) immediately follows from (i) and Corollary 4.1, it is sufficient for us to show (i).
To show (i), we only need to verify that, the average-error-probability capacity region of any channel in
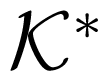
where (X1, X2, Y ) are a triple of random variables with a joint distribution PX1X2Y (x1, x2, y) = PX1(x1)PX2(x2)W(y|x1, x2), for all (x1, x2, y) ∈


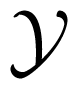

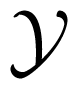
To this end, we fix a W ∈
due to the fact that by definition of
as X1 and X2 are independent. Then the bounds on R2 and R1 + R2 in (27) can be rewritten as
respectively. In addition, we notice that R1 ≤ I(X1; Y|X2) and R2 ≤ H(X2) imply that R1 + R2 ≤ I(X1; Y|X2) + H(X2). Thus for a W ∈
On the other hand, since for (U, X1, X2, Y ) ∈

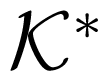
That is, cl(W) is contained in the convex hull of ′(W; X1, X2). This completes our proof.
By Proposition 5.1, feedback may not enlarge the average-error-probability capacity region of a MAC in
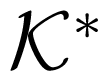
Feedback may not enlarge the average-error-probability capacity region of a MAC in
![Entropy 16 01211f20]()
Cover-Leung bound was obtained by the technique of shifting the private messages to the common messages. That is, a sender may obtain some information about the message sent by the other sender, via his/her own inputs and previous outputs of the channel, which he/she learnt from the feedback. Then he/she may shift the information from the private messages of the other sender to common messages, and cooperate with the other sender to resend it. The key idea is that the “common message” is more easily to be sent, under the cooperation of two senders. A premise is that the common message should be unknown by the receiver, because otherwise it is not necessary to be resent. For a MAC in
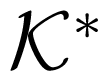
Feedback can enlarge the maximum-error-probability capacity region of a MAC in
However, one can apply the 3rd role of feedback i.e., extracting common randomness from feedback for mixing the “good cases” and the “bad case”. This may enlarge the maximum-error-probability capacity region, when the worst case is considered.
5.2. Generalized Contraction MAC
In the previous subsection, we have that for a channel W in , d,f (W) = R̄(W) = R̄f (W). To have an example in , for which feedback enlarges the maximum-error-probability capacity region, but does not enlarge the average-error-probability capacity region, we need an example in , for which d(W) ⊊ R̄ (W). To this end, we extend the contraction channel to generalized contraction MACs as follows.
Let W̃ be a (point-to-point) channel with input alphabet
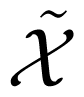

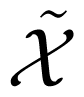
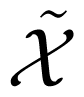


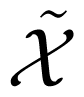
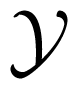
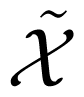

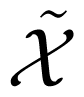

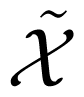


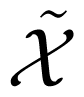
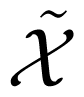

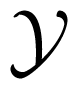


for all x1 ∈


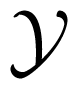
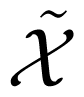
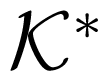
Since the generalized contraction channels are in
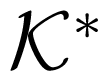
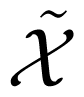
where (a) holds since J is a function of X1; (b) holds since J is a function of Y ; (c) holds since J and X2 are independent. Next we let PX2(1) = p and Pr(J = 1) = q. Continue with the above inequality,
where h(q) is the binary entropy of q. Note that in (d) the equality holds if and only if I(X1; Y |J = 0, X2 = 1) = I(X1; Y |J = 1, X2 = 0) = γ*; or, equivalently both PX1|J (·|0) and PX1|J (·|1) are optimal input of W̃. By the symmetry, we assume that . Consequently, the average-error-probability capacity region of a generalized contraction MAC W is the convex hull of rectangles
To show that the maximum-error-probability capacity region of a generalized contraction MAC is strictly smaller than its average-error-probability capacity region, we need an outer bound on the maximum-error-probability capacity region. G. Dueck [1] elegantly applied vertex isoperimetric theorem in the binary Hamming space, to derive an outer bound of the maximum-error-probability capacity region of the contraction channel. Along his way, we will derive our outer bound.
The isoperimetric problem is a basic problem in combinatorics, which asks how large at least, the boundary of a subset with a given cardinality in a discrete metric space has to be. Its asymptotic version is known as “Blowing Up Lemma”, by people in Information Theory (e.g., c.f. [4,24]). The vertex isoperimetric theorem in the binary Hamming space first was discovered by K. H. Harper [25]. Its different proofs were then given by G.O.H. Katona [26], P. Frankl and Z. Füredi [27]. The theorem says that, the optimal configurations have a nested structure. In this paper, we only need its simplified version as given below. More about the isoperimetric theorem can be found in [26] or [27].
For a subset


where dH is the Hamming distance. The following lemma is a simplified version of isoperimetric theorem in the binary Hamming space.
Lemma 5.2
[25] Let

Let C be a code with maximum probability of error λ and block length n, with codebooks
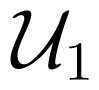
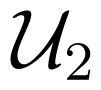
without loss of generality, we may assume
, since we are interested in the asymptotic rates of the codes. For j = (j1, j2, . . . jn) ∈ {0, 1}n, we denote
and partition
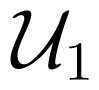
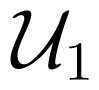
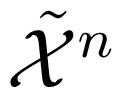
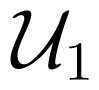
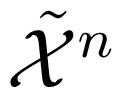
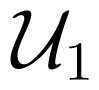
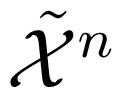
where dH(j,
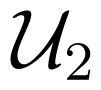
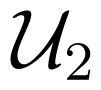
Now we have to maximize the right hand side of (35). By Lemma 5.2 and (33), we have that Γl(
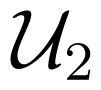
which is maximized by by Lemma 5.2. That is,
where |z|+ = max{0, z}. Thus by s (33) and (36) for , we have an outer bound of the maximum-error-probability capacity region of W :
Because for a fixed p, the function h(q′) + (q′ − p)γ* achieves the maximum value at
and for γ* ≥ 0, and if and only if γ* = 0, the outer bound can be rewritten as
In particular, when W̃ is the identity channel on {a, b}, γ* = 1 and , W becomes the contraction channel, and the outer bound (38) becomes Dueck’s outer bound (6). It is easy to verify that, if γ* > 0, the outer bound in (38) is always strictly smaller than the average-error-probability capacity region, the convex hull of ″(p), in (31), since for any fixed ,
if γ* > 0. That is, for any (nontrivial) generalized contraction MAC, the maximum-probability-error capacity region is always strictly smaller than the average-error-probability capacity region. In particular, by Corollary 4.1 and Proposition 5.1, we have that for all non-deterministic generalized contraction MAC W,
6. Extensions
In this section, we extend our results to compound channels, arbitrarily varying channels, and channels with more than two inputs. For the sake of simplicity, we will focus on the discrete memoryless MAC. As one can see, it is not that difficult to extend the results in Subsections 6.1 and 6.3 to Gaussian MAC and other multiple input channels. However, it is not very easy to extend Theorem 3.2 to arbitrarily varying Gaussian channel defined in the sense of [28], due to the following reason. By its definition, a Gaussian arbitrarily varying MAC with average power constraint Λ to the state sequences, is possibly governed by any state sequence with average power not exceeding Λ. In our coding scheme, we need to send the outcome of random key by a block with a vanishing rate. This would not work, when a state sequence, such that powers of its components in the “small block” are much larger than Λ, and powers in the rest part are slightly smaller than Λ, governs the channel.
6.1. Extension to Compound MAC
A compound MAC



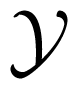
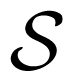
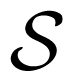
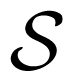
if the sequences
, j = 1, 2 are sent to the channel, and the channel is governed by the state s. Similarly, for deterministic a code C (random code Cr) with message set 1 × 2, we denote by pe(C; (m1, m2); s) (pe(Cr; (m1, m2); s)) for mj ∈ j, j = 1, 2 and s ∈
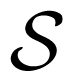
respectively; and, for a random code Cr,
respectively. In the following, we extend the results in Sections 3, 4 to compound channels.
First we extend Theorem 3.2 by showing that
for all compound channels

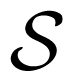
if and only if m2 ∈ 2,1(s). Then, by Markov inequality, we have that
, for all s ∈
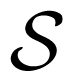
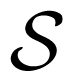
By applying Lemma 3.3-(2) to each channel in the set of

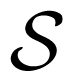
Then by the union bound, with probability at least
, there is a realization of (σ̃1, σ̃2, . . . , σ̃n2), (σ1, σ2, . . . , σn2), such that for all (m1, m2)∈ 1 × 2,0 and all s ∈
We omit the rest parts of the proof of of (44), since they follow exactly the proof of Theorem 3.2.
The extension of Corollary 4.1 to a compound MAC is straightforward. The proof follows from the argument in Section 4. Note that the definition of the non-deterministic compound channel slightly makes a difference here. If we define a non-deterministic compound MAC as a compound MAC, such that there is a pair of input letter (x1, x2), for which no y and s are with W(y|x1, x2, s) = 1, then the same as in Section 4, we can spend a block to build the common randomness. However, it seems more natural to define a non-deterministic compound MAC as an compound MAC, such that for all s ∈
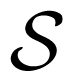


6.2. Extension to Arbitrarily Varying MAC
Similar to a compound MAC, an arbitrarily varying MAC (AVMAC)
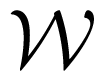


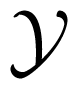
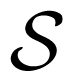
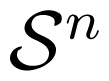
if the sequences
, j = 1, 2, are sent to the channel, and the channel is governed by the state sequence s = (s1, s2, . . . , sn). For a given deterministic code C (random code Cr) with message set 1× 2, we denote by pe(C; (m1, m2); s) (pe(Cr; (m1, m2); s)) for mj ∈ j, j = 1, 2, and s ∈
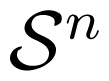
respectively; and, for a random code Cr,
respectively.
According to our knowledge, most known works on AVMAC focused on the average-error-probability capacity regions. By elimination technique, J. H. Jahn [29] proved that, the average-error-probability capacity regions of random correlated codes and deterministic codes are the same, provided that the average-error-probability capacity region has a non-empty topological interior. Thereafter, it became a key problem to find conditions for which the average-error-probability capacity region of an AVMAC has a non-empty the topological interior. In [30], J. A. Gubner found a necessary condition and conjectured that it is also sufficient. Eventually, R. Ahlswede and N. Cai [31] proved that his conjecture is true. Since random codes and deterministic codes for an AVMAC in general may have different average-error-probability capacity regions, we add the subscript “d” to the capacity region of deterministic codes. However, we assume in the following that the average-error-probability capacity region has a non-empty topological interior, in which case the average-error-probability capacity regions of random and deterministic codes are the same [29].
Actually, one can define the 3rd kind of probabilities of error, which we call semi-average probability of error:
Accordingly, we denote the semi-average error probability capacity regions of deterministic codes, without and with feedback by ̃d (
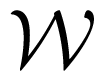
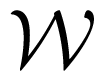
The difference among the criterions of the average, semi-average, and maximum error probability regions is obvious. At first, we have that
Secondly, we observe that ̃d(
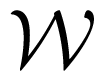
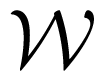
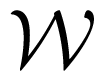
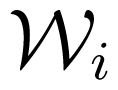
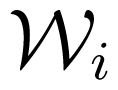
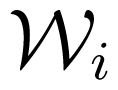

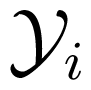
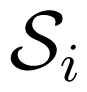
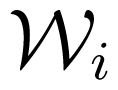
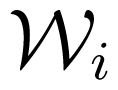
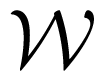

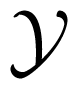

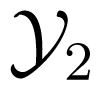
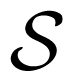
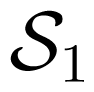
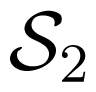


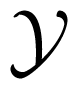
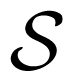
for all x1 ∈


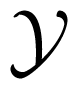
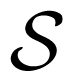
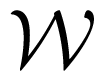
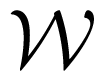
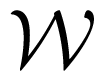
respectively. Obviously we have that
i.e., indeed, the three capacity regions are different. Similarly we can see the difference, when feedback is present.
We have discussed in Section 3 that, randomization at one single encoder is sufficient for a random code under the criterion of maximum probability of error to achieve the average-error-probability capacity region, and therefore the number of random encoders makes no difference for an (ordinary) MAC. Now, we shall see that it does make a difference for an AVMAC. Let r,d (
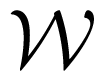
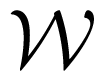
Theorem 6.1
For an AVMAC
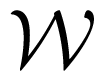
Proof
To show (53), we first show that
This can be done by simply modifying the proof of Theorem 3.2, similar to the extension to compound channels in last subsection. For a λ > 0 and any pair of rates (R1, R2) ∈ ̃d(
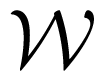
for all m2 ∈ 2 and s ∈
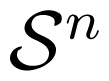
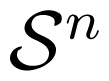
By (56), the code C already has the property of C0 in Lemma 3.3, which is needed by us. Thus, it is sufficient to show that, (by replacing C0 in Lemma 3.3-(2) with C,) the set of random permutations in Lemma 3.3 has a realization (σ1, σ2, . . . , σn2), such that for all (m1, m2) ∈ 1× 2, s ∈
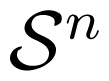
since the rest part of the proof will directly follow from the proof of Theorem 3.2, similar to proof of extension to compound channel in the last subsection. Applying Lemma 3.3 to all s ∈
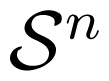
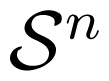
That is, with a probability no less than , a realization satisfying (57) exists.
Next, we show the opposite relation
To do that, we have to prove that, given Cr,d having a random encoder Φ1 and a deterministic encoder φ2, with the maximum probability of error
, one can always construct a deterministic code C′ with the same rate and semi-average probability of error λ. It is done by choosing a realization of Cr,d. Note that by Remark 2.1-(2), we may for a fixed m2 ∈ 2 and s ∈
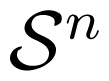
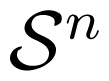
Consequently, applying the union bound, we have
which can be arbitrarily close to 0, for a sufficiently large n, since M1 exponentially increases as n increases. This implies that Cr,d has a realization with semi-average probability of error at most λ, i.e., (59).
Now we proceed to the proof of (54). Notice that under our assumption, ̄d(
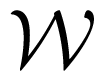
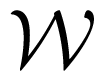
Similarly to the proof of Theorem 3.2, for a deterministic code C for
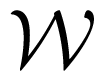

Next we randomly, independently and uniformly generate n2 random permutations , k = 1, 2, . . . , n2 on i for i = 1, 2, respectively. Then, similarly to the proof of Theorem 3.2, we have that , k1 = 1, 2, . . . , n2, k2 = 1, 2, . . . , n2, are n4 independent random variables with expectations
for all fixed (m1, m2) ∈ 1 × 2 and s ∈
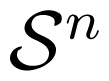
As a direct consequence, by the union bound, with a probability at least has a realization { , ki = 1, 2, . . . , n2, i = 1, 2}, such that for all (m1, m2), s, we have
Now we construct a two-block random code by using the code C and the realization. That is, the two encoders randomly generate two keys Ki, i = 1, 2 from {1, 2, . . . , n2}, and send them in the first block independently, by using a code with average error probability at most . In the second block, they use the code to sent their messages, if the outcomes of Ki are ki, i = 1, 2. Then the total maximum probability of error may not be larger than λ, if the average probability of error in the first block is no larger than . That is, (60) holds, which completes the proof of the theorem.
Similarly to in Section 3, here we have the following corollary.
Corollary 6.2
For an AVMAC
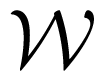

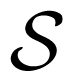
Remarks 6.3
- (1)
The random codes in Theorem 6.1 seems to be slightly different from the random codes in [29]. In Theorem 6.1, we assume that the two encoders choose codewords according to the outcomes of two random keys, respectively; and, the decoder does not know the outcomes of the keys (initially). In [29] J. H. Jahn assumed that the decoder knows the keys. But in the case that the capacity region has a non-empty topological interior, they are equivalent. This is because (as we did,) in this case the encoders may send the outcomes of keys to the decoder and by elimination technique, a block with a vanishing rate is sufficient for the purpose.
- (2)
The assumption in Corollary 6.2 greatly simplified the problem. The problem would become very complicated when the assumption is violated (i.e., in the case that for all xi ∈
, i = 1, 2, there exist an s ∈
and a y ∈
with W(y|x1, x2, s) = 1). In this case, the conclusion in the corollary likely does not hold any more. For a (point-to-point) AVC, the maximum-error-probability capacity with feedback may be positive, but strictly smaller than its average-error-probability capacity, if for all input letter x, there are a state s and an output letter y such that W(y|x, s) = 1 [20].
6.3. Extension to Multiple Input MAC
The results in Sections 3 and 4 can be easily extended to an MAC with I inputs for I > 2. As the proof of the extension is very similar to the proof in Sections 3 and 4, we just give a brief outline as follows. Suppose that we are given a deterministic code C with average probability of error . Let φi, i = 1, 2, . . . , I, be its encoding functions.
To find a “good” subcode: It follows from Markov inequality that, C contains a subcode C0 with message sets i, i = 1, 2, . . . , I − 1, I,0 ⊂ I, , and
for all mI ∈ I,0, where i, i = 1, 2, . . . , I, are message sets of C.
Existence of permutations for construction of a random code: Similarly to the proofs in Section 3 and Subsection 6.2, define a code (σ(1), σ(2), . . . , σ(I−1))(C0), for a set of permutations σ(i) on i, i = 1, 2, . . . , I − 1 i.e., by taking φi(σ(i)(·)) for i = 1, 2, . . . , I − 1, φI (·), as encoding function, and properly choosing a decoding function. Randomly and independently generate n2 permutations , ki = 1, 2, . . . , n2 on i, for i = 1, 2, . . . , I −1. Apply Chernoff bound to show that there exists a realization of the random permutations, { , ki = 1, 2, . . . , n2, i = 1, 2, . . . I − 1} such that
for all (m1, m2, . . . , mI−1, mI)∈ 1× 2 × . . .× I−1× I,0.
Constructing a random code with maximum probability of error: Construct a random code under the criterion of maximum probability of error, with I − 1 random encoders and a deterministic encoder, in two blocks such that the outcomes of random keys are sent in the first block, and messages are sent in the second block.
Constructing a deterministic code with feedback for non-deterministic MAC: Construct deterministic code with feedback under the criterion of maximum probability of error in two blocks, such that common randomness between the i-th encoders and the decoder, for i = 1, 2, . . . I − 1, are generated in the first block; and, messages are sent in the second block. Here C is understood as a code with feedback.
7. Discussions
In [32], R. Ahlswede defined 6 capacities for AVC and discussed their relation. Readers who are familiar with AVC, may recognize that a multiple input channel has properties similar to AVC, especially when the criterion of maximum probability of error is considered; and, our results are similar to those in [32]. A (point-to-point) AVC can be regarded as an MAC or IC, where an input is controlled by a malicious user. The similarity is caused by the fact that for both AVC and multiple input channels under the criterion of maximum error probability, one must consider the “bad combination” of input codewords. For multiple input channels, this is due to the fact that the senders may not always cooperate properly. A user might be considered to be “malicious” by other users, if they do not cooperate well. This can be reflected by the following fact. For a random code under the criterion of maximum error probability, to achieve the average-error-probability capacity region of an I input channel, one needs I − 1 random encoders; and, for arbitrarily varying I input channel, one needs one more random encoder. A difference is that, for an MAC the receiver has to decode the messages from both input; and, for an IC, a receiver may decode the message not to be sent to him/her, as a side information; whereas it is impossible for a receiver of an AVC to decode the state sequence.
We have seen that randomization at encoders serves as an efficient way to solve the problem caused by the bad combination of input codewords. As in many cases, a perfect cooperation in network communication is impossible, this suggests us to employ random codes.
So far we have known very little about the maximum-error-probability capacity regions. One reason is that in most cases a small average probability of error is acceptable. Perhaps, another reason is that, to determine the maximum-error-probability capacity regions is much harder than to determine the average-error-probability capacity regions. Nevertheless, from a theoretical point of view, to well understand the multiple user channels, exploring their maximum-error-probability capacity regions is necessary. Likely, the study on the maximum-error-probability capacity regions is closely related to the study on AVCs.
Acknowledgements
The author would like to thank Yanling Chen for many discussions and helpful suggestions in details for revising the paper. This work was partially supported by grant from the National Natural Science Foundation of China (Ref. No. 61271174).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dueck, G. Maximal error capacity regions are smaller than average error capacity regions for multi-user channels. Probl. Contr. Inform. Theor 1978, 7, 11–19. [Google Scholar]
- Ahlswede, R. On two-way communication channels and a problem. Proceedings of the Zarankiewiez, Sixth Prague Conference on Information Thery, Statistical Decision Functions and Random Processes, Prague, Czech, 19–25 September 1971.
- Vanroose, P. Code construction for the noiseless binary switching multiple-access channel. IEEE Trans. Inform. Theor 1988, 34, 1100–1106. [Google Scholar]
- Csiszár, I.; Körner, J. Information Theory: Coding Theorem for Discrete Memoryless Sytems, 2nd ed; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Gamal, A.E.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Ahlswede, R. Multi-way communication channels. Proceedings of the 2nd International Symposium on Information Theory, Tsahkadsor, Armenian USSR, 2–8 September 1971; Publishing House of the Hungarian Academy of Sciences: Budapest, Hungary, 1973; pp. 23–52. [Google Scholar]
- Liao, H. A coding theorem for multiple access communications. Proceedings of the International Symposium on Information Theory, Asilomar, USA, 1972.
- Shannon, C.E. The zero-error capacity of a noisy channel. IRE Trans. Inform. Theor 1956, 2, 8–19. [Google Scholar]
- Gaarder, N.T.; Wolf, J.K. The capacity region of a multiple-access discrete memoryless channel can increase with feedback. IEEE Trans. Inform. Theor 1975, 21, 100–102. [Google Scholar]
- Cover, T.M.; Leung, C.S.K. An achievable rate region for the multiple-access channel with feedback. IEEE Trans. Inform. Theor 1981, 27, 292–298. [Google Scholar]
- Ozarow, L.H. The capacity of the white gaussian multiple access channel with feedback. IEEE Trans. Inform. Theor 1984, 30, 623–629. [Google Scholar]
- Ozarow, L.H.; Leung, C.S.K. An achievable region and outer bound for the Gaussian broadcast channel with feedback. IEEE Trans. Inform. Theor 1984, 30, 667–671. [Google Scholar]
- Kramer, G. Capacity results for the discrete memoryless network. IEEE Trans. Inform. Theor 2003, 49, 4–21. [Google Scholar]
- Bross, S,I.; Lapidoth, A. An improved achievable region for the discrete memoryless two-user multiple-access channel with noiseless feedback. IEEE Trans. Inform. Theor 2005, 51, 811–833. [Google Scholar]
- El Gamal, A. The feedback capacity of degraded broadcast channels. IEEE Trans. Inform. Theor 1978, 24, 379–381. [Google Scholar]
- Han, T.S.; Kobayashi, K. A new achievable rate region for the interference channel. IEEE Trans. Inform. Theor 1981, 27, 49–60. [Google Scholar]
- Shannon, C.E. Two-way communication channels, Berkeley, CA, USA, 20 June – 30 July 1960; University of California Press: Berkeley, CA, USA, 1961; I, pp. 611–644.
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed; Wiley: Weinheim, Germany, 2006. [Google Scholar]
- Dueck, G. The zero error feedback capacity region of a certain class of multiple-access channels. Probl. Control Inform. Theory 1985, 14, 89–103. [Google Scholar]
- Ahlswede, R.; Cai, N. The AVC with noiseless feedback and maximal error probability: A capacity formula with a trichotomy. In Numbers, Information, and Complexity (Festschrift for Rudolf Ahlswede); Althöfer, I., Cai, N., Dueck, G., Khachatian, G., Pinsker, MS., Sarkozy, A., Wegener, I., Zhang, Z., Eds.; Kluwer: Dordrecht, The Netherlands, 2000; pp. 151–176. [Google Scholar]
- Ahlswede, R.; Cai, N. Transmission, Identification and Common Randomness Capacities for Wire-tape Channels with Secure Feedback from the Decoder. In General Theory of Information Transfer and Combinatorics; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2006; Volume 4123, pp. 257–274. [Google Scholar]
- Willems, F.M.J. The feedback capacity region of a class of discrete memoryless multiple access channels. IEEE Trans. Inform. Theor 1982, 28, 93–95. [Google Scholar]
- Ahlswede, R.; Cai, N. Seminoisy deterministic multiple-access channels: Coding theorems for list codes and codes with feedback. IEEE Trans. Inform. Theor 2002, 48, 2153–2162. [Google Scholar]
- Alhswede, R.; Gács, P.; Körner, J. Bounds on Conditional Probabilities with Application in Muli-User Communication. Probab. Theor. Relat. Field 1976, 34, 157–177. [Google Scholar]
- Harper, K.H. Optimal numberings and insperimetric problems on graphs. J. Comb. Theory 1966, 1, 385–393. [Google Scholar]
- Katona, G.O.H. The Hamming-sphere Has Minimum Boundary. Studia Sci. Math. Hugar 1975, 10, 131–140. [Google Scholar]
- Frankl, P.; Füredi, Z. A short proof for a theorem of harper about hamming-spheres. Discrete Math 1981, 34, 311–313. [Google Scholar]
- Csiszár, I.; Narayan, P. Capacity of the gaussian arbitrarily varying channel. IEEE Trans. Inform. Theor 1991, 31, 18–26. [Google Scholar]
- Jahn, J.H. Coding of arbitrarily varying multiuser channels. IEEE Trans. Inform. Theor 1981, 27, 212–226. [Google Scholar]
- Gubner, J.A. On the deterministic-code capacity of the multiple-access arbitrarily varying channel. IEEE Trans. Inform. Theor 1990, 36, 262–275. [Google Scholar]
- Ahlswede, R.; Cai, N. Arbitrarily varying multiple-access channels part I, Ericson’s symmetrizability is adequate, Gubner’s conjecture is true. IEEE Trans. Inform. Theor 1999, 45, 742–749. [Google Scholar]
- Ahlswede, R. Elimination of correlation in random codes for arbitrarily varying channels. Probab. Theor. Relat. Field 1978, 44, 159–175. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cai, N. The Maximum Error Probability Criterion, Random Encoder, and Feedback, in Multiple Input Channels. Entropy 2014, 16, 1211-1242. https://doi.org/10.3390/e16031211
Cai N. The Maximum Error Probability Criterion, Random Encoder, and Feedback, in Multiple Input Channels. Entropy. 2014; 16(3):1211-1242. https://doi.org/10.3390/e16031211
Chicago/Turabian StyleCai, Ning. 2014. "The Maximum Error Probability Criterion, Random Encoder, and Feedback, in Multiple Input Channels" Entropy 16, no. 3: 1211-1242. https://doi.org/10.3390/e16031211



