The Elusive Nature of Entropy and Its Physical Meaning
Abstract
: Entropy is the most used and often abused concept in science, but also in philosophy and society. Further confusions are produced by some attempts to generalize entropy with similar but not the same concepts in other disciplines. The physical meaning of phenomenological, thermodynamic entropy is reasoned and elaborated by generalizing Clausius definition with inclusion of generated heat, since it is irrelevant if entropy is changed due to reversible heat transfer or irreversible heat generation. Irreversible, caloric heat transfer is introduced as complementing reversible heat transfer. It is also reasoned and thus proven why entropy cannot be destroyed but is always generated (and thus overall increased) locally and globally, at every space and time scales, without any exception. It is concluded that entropy is a thermal displacement (dynamic thermal-volume) of thermal energy due to absolute temperature as a thermal potential (dQ = TdS), and thus associated with thermal heat and absolute temperature, i.e., distribution of thermal energy within thermal micro-particles in space. Entropy is an integral measure of (random) thermal energy redistribution (due to heat transfer and/or irreversible heat generation) within a material system structure in space, per absolute temperature level: dS = dQSys/T = mCSysdT/T, thus logarithmic integral function, with J/K unit. It may be also expressed as a measure of “thermal disorder”, being related to logarithm of number of all thermal, dynamic microstates W (their position and momenta), S = kBlnW, or to the sum of their logarithmic probabilities S = −kB∑pilnpi, that correspond to, or are consistent with the given thermodynamic macro-state. The number of thermal microstates W, is correlated with macro-properties temperature T and volume V for ideal gases. A system form and/or functional order or disorder are not (thermal) energy order/disorder and the former is not related to Thermodynamic entropy. Expanding entropy to any type of disorder or information is a source of many misconceptions. Granted, there are certain benefits of simplified statistical descriptions to better comprehend the randomness of thermal motion and related physical quantities, but the limitations should be stated so the generalizations are not overstretched and the real physics overlooked, or worse discredited.1. Introduction
What is the underlying nature of “entropy” and why does it always increase? Why is entropy so intriguing and mysterious, unique and universal, as if it is a miraculous property of natural, material systems? How does it encompass and quantify all processes at all natural space and time scales, governed by the Second Law of Thermodynamics? And many other elusive and debatable issues, as if entropy is among the deepest unresolved mysteries in nature, defying our common sense. Entropy is the most used and often abused concept in science, but also in philosophy and society. Further confusions are produced by some attempts to generalize entropy with similar, but not the same concepts in other disciplines. Von Neumann once remarked that “whoever uses the term ‘entropy’ in a discussion always wins since no one knows what entropy really is, so in a debate one always has the advantage.”
The historian of science and mathematician, Truesdell, explains in his essay of Method and Taste in Natural Philosophy: “Heads have split for a century trying to define entropy in terms of other things. Entropy, like force, is an undefined object, and if you try to define it, you will suffer the same fate as the force-definers of the seventeenth and eighteenth centuries: Either you will get something too special or you will run around in a circle.” Trying to reason, understand, and explain fundamental concepts are daunting endeavors, and different from understanding other concepts derived from the fundamental ones. However, there is factual reality that we should be always aware of and guided by. The fundamental interactions and their inter-relations, along with subtle reasoning, may help to resolve ambiguities and close the needed loops. “Going in a circle” does not mean we are not going anywhere, as long as we succeed in comprehension of subtle “circular” interactions, including interrelated (“chicken-and-egg”) causes-and-effects.
The intention of this treatise is not a review of vast entropy literature, but presentation of this author’s long-contemplated reflections on physical meaning of entropy, and to put certain physical and philosophical concepts in perspective. Only two seminal references and two related publications by the author, in addition to three popular references to illustrate certain misconceptions, are cited. The classical, phenomenological thermodynamics today has unjustifiably a dubious status. Some modern physicists regard classical thermodynamics as an obsolete relic. Often, mostly due to lack of dubious comprehension, thermodynamics is considered as an engineering subject, and thus not as the most fundamental science of energy and nature. The phenomenological thermodynamics has the supremacy over other disciplines, due to its logical reasoning based on the fundamental laws and without the regard to the system complex dynamic structure, and even more complex related interactions.
There are many puzzling issues surrounding thermodynamics and the nature of heat, including subtle definitions and ambiguous meaning of very fundamental concepts. In modern times, there is a tendency by some scientists to unduly discredit thermal energy as being indistinguishable from other internal energy types. Romer [1] argues that “Heat is not a noun,” and proposes to remove it from the dictionary. Ben-Naim [2] titles his book “A Farewell To Entropy,” while Leff [3] in a series of articles entitled “Removing the Mystery of Entropy and Thermodynamics,” argues surprisingly, that “Entropy can be introduced and understood without ever mentioning heat engines,” and against the “thermal energy” concept in favor of more modern and well-defined “internal energy.” Some consider the tabulated Thermodynamic Internal Energy (u = U/m, per unit mass) to be thermal energy, although it represents all energy types stored as kinetic and potential energy of constituent microstructure, thus thermal and mechanical elastic energy in simple compressive substances, in addition to chemical and nuclear internal energies. In more complex system structure there may be more energy types.
Entropy is related to thermal motion of a system microstructure, the latter gives rise to all thermal phenomena and related properties, namely, temperature, thermal or heat capacity, thermal energy and entropy, among others. Due to conversion of thermal energy to other energy forms, like mechanical work in heat engine, and also spontaneous and unavoidable dissipation of all other energy forms to thermal energy via so called heat generation, additional issues and often confusions arise. However, entropy is well-defined material system macro-property, precisely measured, and tabulated and/or correlated, for practical use in engineering and science. Entropy should be further reasoned, refined and explained for what it is, and not be misrepresented as something it might be or is not.
2. From Carnot’s Ingenious Reasoning of Reversible Cycles to Clausius’ Definition of Entropy
Sadi Carnot (1824) laid ingenious foundations for the Second Law of Thermodynamics and discovery of Entropy before the Frist Law of energy conservation was even known (Joule, 1843), and long before thermodynamic concepts were established in the second half of the nineteenth century. In historical context, it is hard to comprehend now, how Carnot then, at age 28, ingeniously and fully explained the critical concepts of reversible thermo-mechanical processes and the limits of converting heat to work at inception of the heat engines’ era, when nature of heat was not fully understood. No wonder that Sadi Carnot’s “Réflexions sur la puissance motrice du feu (Reflections on the Motive Power of Fire [4]),” original treatise published in 1824, was not noticed at his time, when his ingenious reasoning of ideal heat engine reversible cycles, is not fully recognized, and may be truly comprehended by a few, even nowadays.
Carnot paved the way for his followers to define and prove that entropy is a state function, a material property conserved in ideal, reversible cycles (Clausius Equality—definition of entropy property), that entropy could not be destroyed since it will imply more efficient than ideal cycles, but is always generated (locally and globally, thus overall increased) due to dissipation of any and all work potentials to heat, causing generation of entropy in irreversible cycles (Clausius Inequality—definition of entropy generation); thereby, quantifying all reversible and irreversible processes and providing generalization of the Second Law of Thermodynamics. Note that Carnot erroneously assumed that the same caloric (heat) passes through the engine and extracts (produces) work by lowering its temperature, similar to how the same water flow passes through the water-wheel and produces work by lowering its elevation potential. This error, considering the knowledge at the time, in no way diminishes Carnot’s ingenious reasoning and conclusions about limiting, reversible processes and its accurate limitations of heat to work conversion [5].
The consequence of a process and cycle reversibility is most ingenious and far-reaching, see elsewhere [5]. Carnot’s simple and logical reasoning that mechanical work is extracted in heat engine due to the caloric (heat) passing from high to low temperature, led him to a very logical conclusion that any heat transfer from higher to lower temperature (like in a heat exchanger), without extracting possible work (like in a reversible heat engine), will be an irreversible loss of work potential [4,5]. Then he expended his logical reasoning to conclude that all reversible (ideal) heat engines, working between the same heat reservoirs, must have equal and maximum possible efficiency. Otherwise, if one with smaller efficiency is reversed and coupled with another, the impossible “perpetual motion” will be achieved. The maximum engine efficiency dependence on the reservoirs’ temperatures only, is functionally expressed by Equation (1):
What a simple and logical, ingenious reasoning! The maximum, limiting efficiency of heat engine does not depend on the medium used in the engine or its design, but only depends on (and increases with) the temperature difference between the heat source and heat sink, similar to the water wheel output dependence on the waterfall height difference.
After the First Law of energy conservation was later established (after Sadi Carnot’s death), it was simple to derive the Carnot cycle efficiency, η = (QH–QL)/QH = [f(TH)–f(TL)]/f(TH), that led to a very important correlation deduced for a reversible Carnot cycle between any two temperature levels, say T1 and T2, i.e.,
The above function f(T) could be arbitrary, but non-negative and increasing function of temperature, thus defining an absolute, thermodynamic temperature scale, say f(T) = θ = T ≥ 0 (for simplicity, but could be another non-negative and increasing function), independent of the system used for measurement (i.e., thermometer). This simple, thermodynamic temperature scale happened to be the same as the absolute temperature scale obtained using an ideal gas thermometer with constant specific heat [5].
The Carnot ratio equality, Q/T = constant (named in Carnot’s honor, Equation (2)), is much more important than what it appears at first. Actually, the “Carnot Ratio Equality” is probably the most important equation in Thermodynamics and among the most important equations in natural sciences. Carnot’s ingenious reasoning opened the way to the generalization of Thermodynamic reversibility and energy process-equivalency, definition of absolute thermodynamic temperature, and a new thermodynamic material property “Entropy”, as well as the Gibbs Free Energy, one of the most important Thermodynamic functions for the characterization of electro-chemical systems and their equilibriums, thus resulting in the formulation of the universal and far-reaching Second Law of thermodynamics [5,6].
3. Clausius Equality (Entropy) and Inequality (Entropy Generation)
Another important consequence of the Carnot ratio equality, Equation (2), for a Carnot cycle working between the two different, but constant temperature thermal-reservoirs, TH and TL < TH, is:
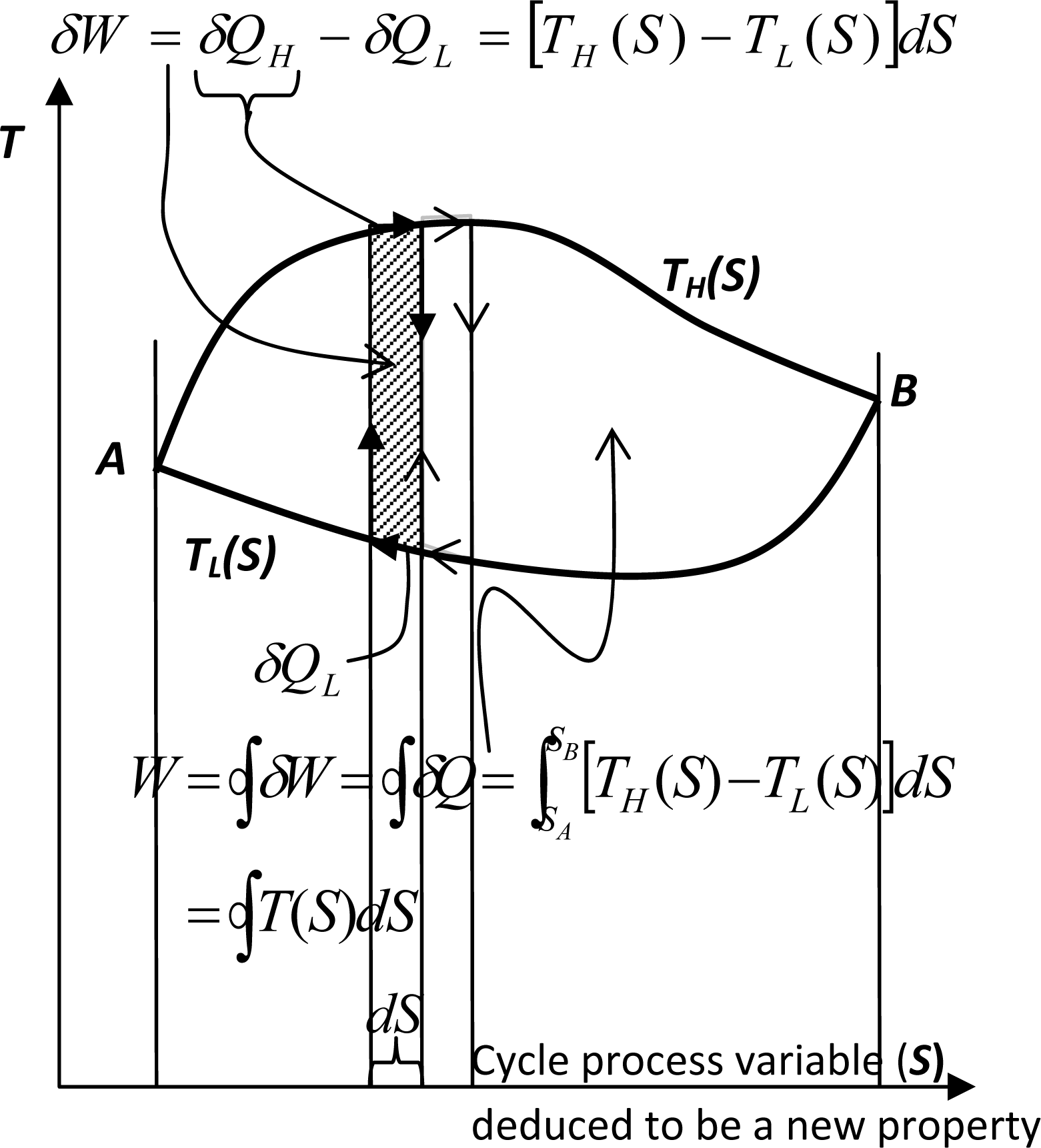
Or in general, a reversible cycle, working between the variable temperature thermal-reservoirs, see Figure 1, could be accomplished with an infinite number of coupled, infinitesimally small Carnot cycles, each working between two temperature reservoirs at specified temperatures and finite temperature difference. After the cycle-integration of Equation (3), for infinitely many Carnot cycles of infinitesimally small heat transfer δQ, we obtained the following equation:
Equation (4) is well-known Clausius equality (more about Clausius inequality later), which defines new fundamental property entropy, since its integral is independent on process path between any two given points A and B, namely (compare with Equation (4)):
Let us reiterate: The reversible process/cycle equivalency, deduced by Sadi Carnot, has resulted in the Clausius equality (Equation (4)). Efficiency of any reversible cycle between any two given reservoirs’ temperatures cannot be smaller than any other cycle efficiency. Thus, all reversible cycle efficiencies, between the two thermal reservoirs, must be the same and maximum possible. This subtle reasoning allowed for definition of the absolute Thermodynamic temperature, and deduction, and thus proof based on Carnot’s reasoning, of the Clausius equality, Equation (4), and the definition of the new property, entropy, up to an arbitrary reference value, Equation (5).
An additional consequence of Carnot’s reasoning is that non-reversible (irreversible) cycles must have smaller efficiency than maximum possible reversible efficiency. Otherwise, if equal they would be reversible, and if bigger would be impossible, hence, allowing deduction (and thus proof) of the Clausius inequality based on the same Carnot’s subtle reasoning. We have to keep in mind that Carnot’s reasoning is based on the impossibility of making an autonomous machine (to spontaneously produce work on its own), which would be equivalent of having higher efficiency of such a cycle than a related reversible cycle, thus destroying entropy. I in turn, it is equivalent to the deduced Clausius inequality (see next), the latter in limit being an equality for reversible cycles.
Namely, as reasoned by Carnot and reemphasized above and elsewhere [5], for real irreversible (Irr) cycles, the heat engine efficiency is smaller than for reversible cycles (Rev, otherwise the Irr cycle will be reversible or impossible), i.e., for everything else being the same, then WIrr < WRev. Therefore, we can reason the proof of the well-known Clausius inequality as follows:
Considering the inequality, Equation (6), and expending on derivation of Clausius equality, Equation (4) (recall that T is non-negative absolute temperature), we have the following: , or for both, reversible and irreversible cycles:
Everything reasoned above is deduced from the impossibility to have a cycle with higher efficiency than a reversible cycle, and thus equivalent to “impossibility of heat to be transferred spontaneously (without any external influence) from colder to warmer body/reservoir, nor it is possible to construct any device to achieve it in an autonomous process (a process without any external influences).” A new material property, entropy, was defined using the cyclic Clausius equality, Equations (4) and (5) [6].
The cyclic Clausius inequality, Equation (7), affirms that cycle net-influx of the new quantity, entropy, within a cyclic process must be negative (i.e., must be net-outflux), since the working medium comes back to the same state (and thus the same all properties) after completing the cycle. This implies that all real, irreversible cyclic processes must generate (produce) the new property entropy, equal to the generated heat from lost cycle work potential per relevant absolute temperature, which in limit is zero, thus entropy being conserved in reversible processes. Therefore, it would be impossible to have a cyclic process that destroy entropy, since it would be equivalent to the spontaneous heat transfer from a colder to a hotter body against a thermal forcing, or to produce work from heat within a single reservoir, from within an equilibrium without a due forcing. The ‘process forcing’ has to be ‘uniquely directional,’ and so is the process energy transfer. It cannot be one way or the opposite way at will, thus defying directionality of forcing and existence of stable equilibrium. Similar reasoning has been further extended to all types of energy processes and thus establishing universality of the Second Law of entropy generation and energy degradation.
4. Physical Meaning of Entropy: Thermal Displacement of Thermal Energy (Dynamic Thermal-Volume)
During reversible, boundary heat transfer δQBry without work interactions, thus no volume (V) change for simple compressible substance system (Sys), the system temperature within a volume will be uniform and equal to its boundary (Bry) temperature at any instant (TBry = TSys = T), i.e.,:
There is a tacit distinction between entropy transfer across the boundary surface δSBry (flux quantity δSBry = ṠBrydt) and change (e.g., storage) of entropy property within the material system dSSys (in time dt) that occupies space volume V, and the two are the same only for reversible processes, Equation (8). We also note that process irreversibility is associated with a material system occupying a volume (it is a volumetric phenomenon) and could not be defined for an energy flux crossing a system boundary having no thickness, thus the distinction between differentials ‘δ’ for flux and ‘d’ for system.
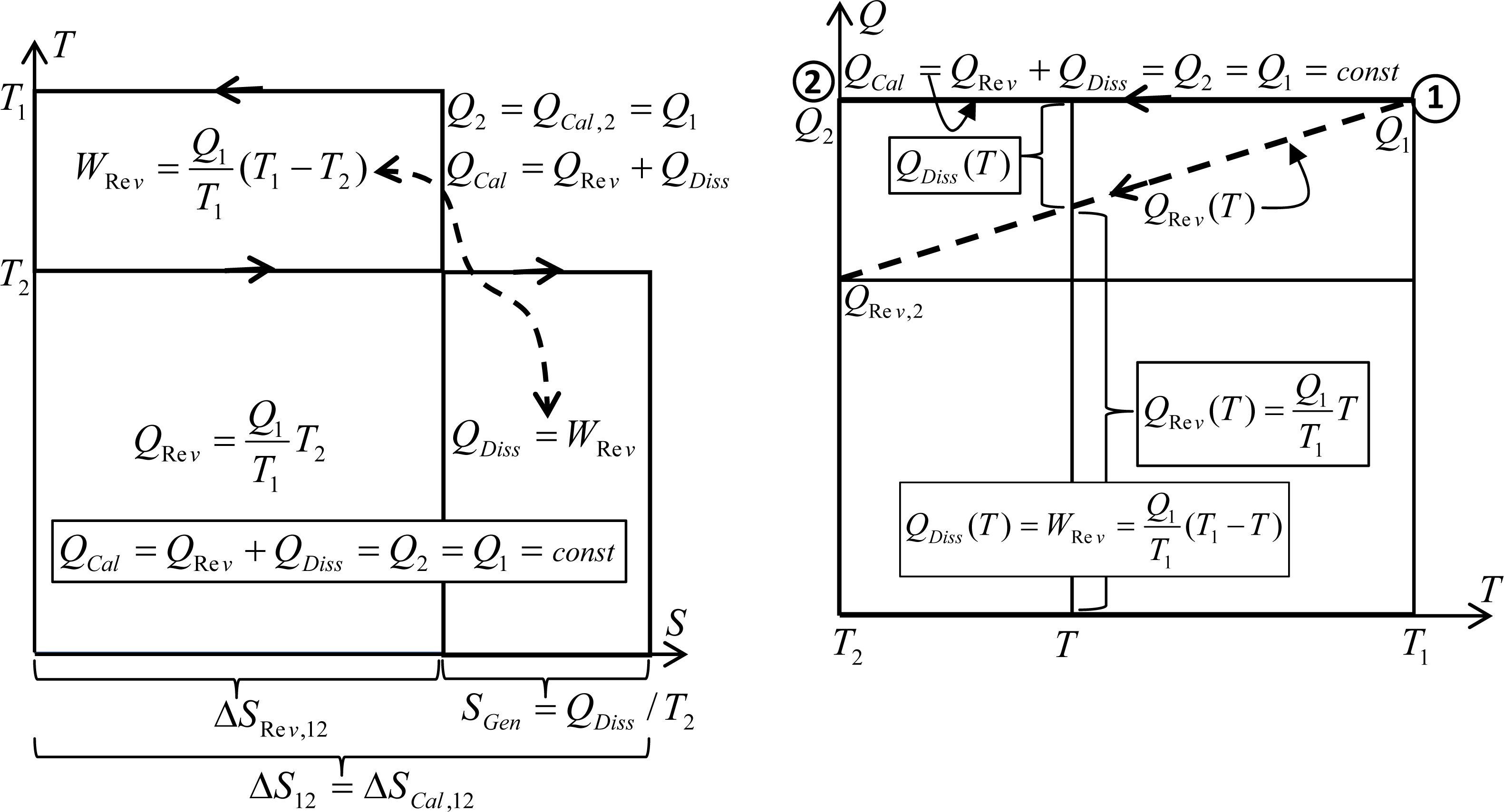
There is an important peculiarity about heat transfer processes without any work interactions (like within heat exchangers): no heat conversion to work like in heat engine, and no other than ‘thermal work potential’ dissipation and heat generation, therefore the thermal energy (like original caloric) is conserved on its own. We like to name such processes, without work interactions, as “caloric processes” or caloric heat transfer. We also could define “reversible heat transfer” at infinitesimally small temperature difference, as an ideal limiting case, achieved by an ideal Carnot cycle, when the heat source and sink are at a finite temperature difference, so that work potential is extracted, instead of being dissipated as heat, like in the above caloric processes, while heat transfer takes place at infinitesimally small temperature difference at each temperature level (dT→0) [7]. Therefore, during the reversible heat transfer from higher to lower temperature reservoirs, see Figure 2 (left), the work potential is extracted and less heat is reversibly transferred (QRe v,2 = Q1T2/T1) to the reservoir at lower temperature (consider it to be a system, T = TSys = T2), for the amount of the extracted work (as per the Carnot ratio or Carnot efficiency, and energy conservation), so the entropy is conserved since no entropy was generated in the reversible cycle (note QRe v/T = constant).
However, during a caloric process the work potential is completely dissipated into self-generated heat at lower temperature (QDiss = WRev), which after being added to the equally reduced reversible heat at lower temperature (QRe v), will result in conserved heat or thermal energy (QCal = QRe v + QDiss = const; i.e., caloric process) with increased, generated entropy in the amount of dissipated work potential per relevant absolute temperature, see Figure 2 (left).
Considering the fact that entropy is defined for reversible processes, as per the Clausius equality, it may be deduced that system entropy increase due to irreversible heat generation, is the same as if it is transferred from an internal (within) boundary, the same as entropy increase during corresponding, reversible heat transfer. Therefore, for irreversible caloric processes (without external work interactions as defined above), the entropy may be conveniently measured and calculated in the same manner as for reversible heat transfer, i.e.,
During caloric heating (i.e., a system isochoric process without work interactions), the system thermal or heat capacity, CV,Sys, will govern its temperature and entropy increase, regardless of the heat source temperature, the latter if higher, will cause the lesser source entropy change, resulting in source-system process irreversibility with entropy generation.
Furthermore, based on the above reasoning, since any dissipated work type may be considered as a (generated) heat source for the system, the Clausius entropy definition could be extended and generalized for any process, including work interactions, as follows:
Note that QGen = QDiss = WLoss also includes the Carnot work-potential loss during ‘caloric’ heat transfer at finite temperature difference, so the boundary entropy transfer could be ‘considered to be reversible’ as in reversible processes (no ‘volumetric-process’ entropy generation through a boundary surface).
We could further generalize the Clausius entropy definition so that entropy change is equal to all thermal heat stored within the system, dQSys = δQBry(Re v) + δQGen per relevant, absolute system temperature TSys (at location where the heat is stored within a system), since it is irrelevant if entropy is changed due to reversible heat transfer or irreversible heat generation, i.e.,
Note that for reversible processes, WLoss = QGen = 0, then QSys = QBry = QRev, and for caloric processes QSys = QCal. Furthermore, for reversible adiabatic process, QSys = QRev + QGen = 0, thus isentropic process. However, for irreversible adiabatic process, there will be irreversible loss of work potential within (instead of being extracted or stored) which will dissipate and convert to heat, i.e., generate heat (and thus entropy) within, and be stored within the system, QSys = WLoss = QGen > 0, thus resulting in irreversible entropy increase (Equation (11)). Accounting for all irreversibly-generated heat may be elaborate, except for reversible processes (being zero) and caloric processes (caloric heat conserved), Equation (9).
Entropy is associated with the system heat stored and not with the work transferred, only with the work lost within the system, and thus generated heat, as if it is transferred from some internal, thermal boundary within. As already stated, it is irrelevant if the heat is stored (as thermal energy) within the system by (reversible) boundary heat transfer or generated within.
For compressible ideal gas (PV = mRT) with constant specific heats CV and CP = kCV, and the gas constant R = CP−CV, the entropy change, and thus entropy, could be determined from the Clausius definition and the First Law of energy conservation within a reference (Ref) constant, i.e.,
As seen from Equation (12), entropy increases with an increase of temperature and volume, thus it could be considered as “thermal dynamic-volume” or general “thermal displacement.” However, during the reversible change of volume due to work transfer, temperature will change accordingly, and there will be no change of entropy, since the latter is not associated with work, but only due to heat transfer, if any. In Statistical Thermodynamics it is shown that entropy could be derived (for simple systems like mono-atomic ideal gas) as a function of thermal-motion momentum (thus function of temperature) and space position (thus function of volume) of microscopic particles of the material system.
Therefore, dQSys = TSysdSSys = dUThermal, is valid in general, and it demonstrates that entropy is a thermal displacement (dynamic thermal-volume) of thermal energy, i.e., “system heat,” due to temperature as a thermal potential. It is similar to physical (mechanical) volume being the displacement for mechanical energy, dWSys(IN) = PSys (−dVSys) = −dWSys(OUT) = −PSysdVSys = dUMechanical, due to pressure as a mechanical (elastic) potential. Thus, the differential change of internal energy, dU = [(TdS) + (−PdV)]Sys = dUThermal + dUMechanical, to be elaborated in another manuscript, may be resolved into thermal and mechanical components. Note that change of temperature alone (without entropy change) will not cause the heat transfer (as during isentropic expansion when mechanical energy is extracted, the latter not related to entropy); the same way, the change of force (pressure) without displacement (volume change), will not cause the work transfer. The stored system heat increases the system thermal energy that is distinguished from the system internal, mechanical (elastic) energy, which will be a subject of another manuscript. For example, the heating or compressing an ideal gas with the same amount of energy will result in the same temperature and internal energies, but different states, with different volumes and entropies, and similar for other material substances.
In conclusion, entropy is a thermal displacement, an integral measure of (random) thermal energy redistribution (due to heat transfer and/or irreversible heat generation due to energy degradation) within a system mass and space, per absolute temperature level: dS = dSSys = dQSys/TSys with J/K unit. Note that adjective ‘thermal’ is critically important, since similar but non-thermal phenomena are not related to thermodynamic entropy.
5. Physical Meaning of Entropy: A Measure of Thermal Disorder
Statistical Thermodynamics deals with microscopic structures and dynamic interactions of microparticles with an objective to describe thermo-physical properties of a classical system as a statistical average of all possible and relevant microstates, described by positions and momenta of microparticles. In principle, we can reason and derive Classical Thermodynamics from relevant statistics of microstates’ dynamics, down to quantum behavior of molecules and atoms. However, in reality, there are many obstacles, ambiguities and limitations due to complex microstructure and interactions at many different micro-, nano-, subatomic- and quantum- levels. Note that the statistical results are feasible for very few simple and idealized systems.
As already stated, the thermal random, fluctuation-motion of microparticles gives rise to thermal macro-properties, like temperature, thermal energy, heat capacity, and entropy, among others. Temperature is a measure of average kinetic energy of relevant microparticles, or the kinetic energy of thermal motion of a representative microparticle, while the thermal energy is the sum of all kinetic and potential energies related to the thermal motion of all microparticles, which also give rise to thermal heat capacity. When thermal motion ceases, virtually all thermal properties vanish at absolute zero temperature.
The entropy may also be expressed as a logarithmic measure of all possible thermal-microstates, W, that “correspond to or are consistent with” a given system macro-state. Thus, all real complexity is transferred to properly “counting” microstates W, to match the bulk entropy macro-state, the thermal displacement property, dS = dQSys/T = mCSysdT/T, thus logarithmic integral function, with J/K unit, as accurately deduced by Clausius and precisely measured in laboratories for any system of interest. Since, for the classical systems (as continuum media), the number of microstates is actually infinite, thus uncountable, there is a need for proper discretization (discrete ranging/grouping) of the microstates to obtain a proper, countable set, e.g., if the positions (x) and momenta (p) of ideal gas molecules are within certain, relevant δx and δp ranges of each others, respectively.
Boltzmann first hypothesized that entropy is related to the probability of microstates corresponding to related macro-state. Regardless of what Boltzmann thought at the time, the well-known correlation:
In Statistical Thermodynamics, “entropy” is also expressed as uncertainty of all molecular positions due to their thermal random motion (thermal randomness, thermal fluctuations, or thermal disorder). The adjective ‘thermal’ is critically important, but often overlooked in the literature. At absolute zero temperature the thermal motion ceases and the position of the molecules are fixed/certain in pure crystalline substance, defining the absolute zero entropy (the Third Law of Thermodynamics). For not purely crystalline substance (as ‘randomly frozen’ solid solution structures), the positions of the molecules are not uniquely determined and entropy is not exactly zero at absolute temperature (but some residual value); however, no uncertainty due to thermal motion.
The thermal-motion randomness or thermal disorder, as related to the entropy, was generalized by Gibbs as “a (logarithmic) measure” of sum of all microstates’ uncertainties, i.e., probabilities pi, i.e.,
With an increase of thermal disorder, i.e., an increase of microparticle momenta (temperature) and space they occupy (volume), more information is required for its characterization than in more ordered systems, which could be described via related probabilities of microstates, thus generalizing disorder as Shanon’s information entropy. However, the Gibbs or von Neumann quantum (based on the number of possible quantum microstates), or Shanon or other probabilistic entropy descriptions, are also statistical as Boltzmann's. Actually they all reduce to the Boltzmann expression for fully-randomized, with uniform probability of all W microstates, where pi = 1/W = constant << 1, thus simply reducing Equation (14) to Equation (13).
Again, a statistical interpretation is important as a metaphor only: The sum of the logarithmic function of probabilities of all possible discrete microstates, pi’s, that could occur during the “random thermal fluctuations” of a given macrostate. The adjectives: possible, could occur, consistent random fluctuations (thus thermal), and the holistic meaning of the statement, have deep meanings, and could not be evaluated for any real system, but only scaled for the trivial ones.
Entropy is generated when work potential is lost, i.e., dissipated (randomly equi-partitioned) via heat generation into the thermal energy at a given absolute temperature within the space occupied by the system, including caloric processes, and when expansion (elastic) work potential is lost, i.e., energy randomly redistributed within enlarged volume instead of being extracted as work (volume displacement against the surrounding equilibrium pressure), as demonstrated by the entropy dependence on temperature and volume for an ideal gas of N microparticles [R = CP−CV = CV(k−1) = kBN/m]:
The above (Equations (16) and (17)) correlate the statistical number of microstates W with temperature T and volume V, macro-properties for ideal gas. Granted, there are certain benefits of simplified statistical descriptions to better comprehend the randomness of thermal motion and related physical quantities, but the limitations should be stated so the generalizations are not overstretched and the real physics overlooked, or worse discredited.
6. Conclusions: Physical Meaning of Entropy
As already stated, the elusive nature of entropy is due to the elusive nature of heat and related thermal motion of the material structure, the latter also coupled with other than thermal phenomena, and the conversion of other energy types to thermal heat. The uniqueness and universality of entropy come from the fact that all processes in the universe, at all time and space scales are due to forced displacement of mass-energy, as the “cause-and-effect” of directional forcing of energy transfer (as driving force for all processes) from higher to lower energy density/potential. Therefore, the spontaneous processes are due to work-potential forcing, accompanied with its dissipation to heat and entropy generation, and thus the work potential reduction, in limit to zero when equilibrium is reached.
In general, for all processes, with different functional, natural or man-made material structures, including functional devices, the work potential (a measure of non-equilibrium) could be transferred in different ways, as forced energy displacement, to accomplish different functions and objectives, including life processes and evolution. The forced energy displacement is always accompanied with dissipation of any and all energy types to heat or thermal energy (including thermal energy to itself as transferred from higher to lower temperature) and thus contributes to the irreversible entropy generation at all space and time scales. The thermal macro-phenomena and related properties, including entropy, could be defined as statistical averages (of enough-large number) of micro-particles. Note that on an individual microscale the “Thermodynamics becomes Dynamics.” In ideal, reversible processes the entropy is conserved, but there is no way to destroy entropy, even when heat is converted to work since entropy is not associated with work. Destruction of entropy would be equivalent to spontaneous heat transfer from lower to higher temperature, or to have heat engine with higher efficiency than ideal, reversible Carnot cycle, against the directional, thermal forcing and against the equilibrium existence in nature [5].
An individual microparticle alone (an atom or a molecule, etc.) does not have a certain temperature or possesses a defined amount of heat or thermal energy, nor a specified amount of entropy (all being thermal macro-properties of larger assembly of micro-particles), unless a microparticle is part of thermal, random chaotic interactions of large number of microparticles. On a small individual scale (without interactions with other particles), a microparticle entropy is non-existent, thus zero. However, within a collective larger structure with thermal random interactions/collisions, its entropy increases with spatial and other types of displacements, in limit to infinity (thus relativity of zero and infinity). These, thermal parameters characterize the collective physical state of atoms and molecules, be they solids, liquids or gases. The temperature, heat stored or thermal energy, and entropy are macroscopic properties reflecting the random (thermal) collective behavior of the constituents within a system. While temperature represents the average kinetic energy of all the system’s particles (i.e., the kinetic energy of a representative particle), the stored heat, or thermal energy represents the total amount of kinetic- and potential thermal-energy possessed by all the particles in the system. Similarly, entropy quantifies chaotic displacements of thermal disorder within a system - the displacement of randomly disordered energy, i.e., thermal energy without a defined, but chaotic structure. Note again that adjective ‘thermal’ is critically important, but often overlooked! Moreover, the intermolecular phenomena are coupled and thus elusive. In addition to thermal interactions, giving rise to temperature, heat and entropy, the nature and strength of mutual attractions between atoms and molecules in solids and liquids give rise to other macroscopic properties such as hardness, elasticity and tensile strength in solids, viscosity in liquids, and similar.
Entropy is a thermal displacement (dynamic thermal-volume) of thermal energy due to temperature as a thermal potential (dQ = TdS), and thus associated with thermal heat and absolute temperature, i.e., distribution of thermal energy within thermal (randomly moving) micro-particles in space. It is an integral measure of (random) thermal energy redistribution (due to heat transfer and/or irreversible heat generation due to energy degradation, the latter being multifaceted and somewhat elusive) within a material system structure in space, per absolute temperature level: dS = dQSys/T = mCSysdT/T with J/K unit. Entropy may be also expressed as a measure of thermal disorder, being related to logarithm of number of all thermal, dynamic microstates W (based on microparticles’ position and momenta), S = kBlnW, or to the weighted sum of their logarithmic probabilities S = −kB∑pilnpi, that correspond to, or are consistent with the given thermodynamic macro-state. Note that the meanings of “all relevant adjectives” are deeply important to reflect reality, and as such, “disorder” has metaphoric description for real systems.
Some like to generalize the entropy concept as being a “measure of any disorder,” and imply its destruction when order is created, as in evolution of life. However, during any process, natural or man-made, of creating or destroying any order or disorder, i.e., transforming any material structure, work potential will be always dissipated into heat, and entropy will always be produced, i.e., generated.
Expanding classical entropy concept to other types of disorder or information is ‘overreaching’ and could be a source of many misconceptions. A system form and/or functional order or disorder is not (thermal) energy order/disorder, and the former is not related to Thermodynamic entropy, see Figure 3.
Entropy is increasing from perfectly-ordered (uniquely defined) crystalline structure at zero absolute temperature (absolute zero reference) during the reversible heating (entropy transfer) and/or entropy generation during irreversible energy conversion (loss of work-potential to generated thermal energy), i.e., energy degradation or random equi-partition within a system material structure and space, per absolute temperature level. Furthermore, entropy of a system for a given state is the same, regardless whether it is reached by reversible heat transfer or irreversible heat or irreversible work dissipation.
The fundamental laws and physical phenomena could not be ‘governed’ by mathematical modeling and calculation outcomes as suggested by some [2,3], but the other way around. The energy, temperature, and especially entropy are subtle and elusive, but well-defined and precisely measured as physical quantities, and used as such. Any new approach should be correlated with existing knowledge, with the limitations clearly and objectively presented.
The phenomenological thermodynamics has the supremacy due to logical and holistic reasoning based on the fundamental laws and without regard to the systems’ complex dynamic structures and even more complex interactions; thus its importance and supremacy should not be marginalized.
Nothing occurs locally, nor globally in the universe, without mass-energy exchange and entropy production/generation. The miracles are until we comprehend and explain them!
Conflicts of Interest
The author declares no conflict of interest.
References
- Romer, R.H. Heat is not a noun. Am. J. Phys 2001, 69, 107. [Google Scholar] [CrossRef]
- Ben-Naim, A. Farewell to Entropy: Statistical Thermodynamics Based on Information; World Scientific: Singapore, Singapore, 2008. [Google Scholar]
- Leff, H.S. Removing the mystery of entropy and thermodynamics—Part II. Phys. Teach 2012, 50, 87–90. With comments by Kostic, M., available online: http://goo.gl/mXYGv (accessed on 14 February 2014). [Google Scholar]
- Carnot, S. Reflections on the Motive Power of Heat (English translation by R.H. Thurston); Chapman & Hall Ltd.: London, UK, 1897. Available online: http://www.kostic.niu.edu/Sadi-Carnot-Reflections.html (accessed on 14 February 2014).
- Kostic, M. Revisiting the second law of energy degradation and entropy generation: From Sadi Carnot’s ingenious reasoning to holistic generalization. AIP Conf. Proc 2011, 1411, 327. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat (English translation by Browne, W.R.); McMillan and Co.: London, UK, 1879. Available online: http://www.kostic.niu.edu/Clausius-Mechanical-Theory-of-Heat.html (accessed on 14 February 2014).
- Kostic, M. Irreversibility and reversible heat transfer: The quest and nature of energy and entropy. Proceedings of the IMECE2004, Anaheim, California, USA, November 13–19, 2004; ASME Proceedings, ASME: New York, NY, USA, 2004. [Google Scholar]

© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kostic, M.M. The Elusive Nature of Entropy and Its Physical Meaning. Entropy 2014, 16, 953-967. https://doi.org/10.3390/e16020953
Kostic MM. The Elusive Nature of Entropy and Its Physical Meaning. Entropy. 2014; 16(2):953-967. https://doi.org/10.3390/e16020953
Chicago/Turabian StyleKostic, Milivoje M. 2014. "The Elusive Nature of Entropy and Its Physical Meaning" Entropy 16, no. 2: 953-967. https://doi.org/10.3390/e16020953
APA StyleKostic, M. M. (2014). The Elusive Nature of Entropy and Its Physical Meaning. Entropy, 16(2), 953-967. https://doi.org/10.3390/e16020953




