A Simplified Algorithm for the Topological Entropy of Multimodal Maps
Abstract
: A numerical algorithm to compute the topological entropy of multimodal maps is proposed. This algorithm results from a closed formula containing the so-called min-max symbols, which are closely related to the kneading symbols. Furthermore, it simplifies a previous algorithm, also based on min-max symbols, which was originally proposed for twice differentiable multimodal maps. The new algorithm has been benchmarked against the old one with a number of multimodal maps, the results being reported in the paper. The comparison is favorable to the new algorithm, except in the unimodal case.1. Introduction
Let f be a continuous self-map of a compact interval, [a, b] ⊂ ℝ, with a finite number of turning (or critical) points. Such maps are generically called multimodal. Then, the topological entropy of f [1,2], h(f), can be calculated (along with other possibilities) with the formula:
In [5] (Section 7), a numerical algorithm to compute the topological entropy of multimodal maps was proposed. Let us point out that this algorithm generalizes and hence includes a previous one for unimodal maps published in [6]. The algorithm builds on Equation (1) by calculating ℓn with the help of the min-max symbols of f [5–8], a generalization of the kneading symbols [9,10]. The min-max symbols of a multimodal map not only locate the iterates of its critical values up to the precision set by the partition defined by its critical points, as the kneading symbols do, but they also display their minimum/maximum (or “critical”) character. The interesting point is that such an additional information supposes virtually no extra computational cost. Indeed, it can be read recursively from a look-up table once the min-max symbols of the critical values are known.
In this paper, we propose a related algorithm, which actually approximates the value of h(f) given by a closed formula involving also the min-max symbols of f. The new algorithm eliminates a formal restriction that, as it turns out, unnecessarily marred the applicability of the algorithm of [5]. At the same time, it simplifies the computation scheme of the latter. We elaborate upon these two points briefly.
With regard to the formal restriction, the theoretical results of [5] refer to twice differentiable multimodal maps only. However, numerical simulations with piecewise linear maps of constant slope (and alternating sign) suggested that the algorithm of [5] could be applied as well to just continuous maps. In this paper, we justify the extension of the results from smooth to just continuous maps. Although the proof turns out to be straightforward, this generalization was not explored in the previous papers [5,6], just because these followed the original approach in [7,8], which only considered twice differentiable maps for simplicity.
As for the simplification of the computation scheme, this has to do with the boundary conditions (or the lack of them). Indeed, the algorithm of [5] keeps track of the orbits of the boundary points, thus calculating the exact value of the lap number, ℓn, in each computation loop. On the contrary, the new algorithm dispenses with those orbits, because they do not affect the limit in Equation (1). In fact, Theorem 3 below shows that, as far as the computation of h(f) is concerned, one may assume that f is boundary-anchored, i.e., f ({a, b}) ⊂ {a, b}. The result is a compact expression for the lap number, ℓn, that makes possible a closed formula for h(f).
In sum, we fill a theoretical gap in the application of the algorithm in [5] by showing that the continuity of the maps suffices. Moreover, we abridge the numerical scheme by approximating ℓn in Equation (1) with a formula, which is exact only for boundary-anchored maps, but which provides the correct limit in Equation (1) for h(f).
This paper is organized as follows. To make the paper self-contained, we review in Section 2 all the basic concepts, especially the concept of min-max sequences, needed in the following sections. Most importantly, we extend in Theorem 1 the transition rules for min-max symbols from twice differentiable multimodal maps [5] to just continuous ones. In Section 3, we introduce some instrumental results, which lead, in Section 4, together with Theorem 3, to a closed formula for h(f) containing the min-max symbols of f (Theorem 4). A formal proof of Theorem 3 has been shifted to the Appendix in order not to interrupt the flow of ideas. Section 5 contains the main result of the paper, namely, an algorithm for the topological entropy of (not necessarily smooth) multimodal maps, which approximates the value of h(f) given in Theorem 4. As a way of illustration, this algorithm is put to the test in Section 6. First, the new, abridged algorithm is benchmarked in Sections 6.1 to 6.3 against the full-pledged one [5] using smooth uni-, bi- and tri-modal maps, respectively, borrowed from [5,6]. Finally, in Section 6.4, we also compare both algorithms via piecewise linear, four- and five-modal maps of known topological entropy. It turns out that, except in the unimodal case, the new algorithm outperforms the old one.
2. Min-Max Sequences
For the reader’s convenience, we use the same notation as in [5] throughout. Let I be a compact interval, [a, b] ⊂ ℝ, and f : I → I a piecewise monotone continuous map. Such a map is called l-modal if f has precisely l turning points (i.e., points in (a, b), where f has a local extremum). Sometimes, we speak also of multimodal maps, in general, or of unimodal maps in the particular case l = 1. Furthermore, assume henceforth that f has local extrema at c1 < … < cl and is strictly monotone in each of the l + 1 intervals:
In this case, we write f ∈ l(I). When the interval, I, is clear from the context or unimportant for the argument, we write just l.
Since the results we obtain below for the calculation of the topological entropy do not depend on the shape of f, i.e., on whether f(c1) is a maximum (positive shape) or a minimum (negative shape), we assume, unless otherwise stated, that f has a positive shape. This implies that f(codd) are maxima, whereas f(ceven) are minima, where here and hereafter “even” and “odd” stand for even and odd subindices, respectively. Hence, f is strictly increasing on the intervals Iodd and strictly decreasing on the intervals Ieven. The points, f(ci), 1 ≤ i ≤ l, are called the critical values of f, although no differentiability of f at ci is assumed when so doing.
Theorem 1. Let f ∈ l have a positive shape, and n ≥ 1. Then:
- (a)
If fn(x) = codd, then fn+1(x) is a maximum. If fn(x) = ceven, then fn+1(x) is a minimum.
- (b)
If fn(x) is a minimum, then:
- (c)
If fn(x) is a maximum, then:
Proof. (a) This is a trivial consequence of f having a positive shape.
(b) Suppose that fn(x0) is a minimum with fn(x0) ∈ Iodd. Therefore, there exists a neighborhood of x0, U(x0), such that fn(x0) ≤ fn(x) for all x ∈ U(x0). Without restriction, we may assume that U(x0) ⊂ f−n(Iodd). It follows that:
If fn(x0) ∈ Ieven, then we derive from fn(x0) ≤ fn(x) that fn+1(x0) ≥ fn+1(x) for all x ∈ U(x0), because this time, fn(U(x0)) ⊂ Ieven, an interval where f is decreasing.
(c) This case follows similarly to (b).□
The itinerary of x ∈ I under f is a symbolic sequence:
The itineraries of the critical values,
Definition 1 [5–8]. The min-max sequences of an l-modal map f,
Thus, the min-max symbols have an exponential-like notation, where the “base” belongs to the alphabet, {m, M}, and the “exponent” is a kneading symbol. The extra information of a min-max symbol, , as compared to a kneading symbol, , is contained, therefore, in the base, which tells us whether fn(ci) is a minimum (m) or a maximum (M). Theorem 1 shows that once the symbol, , of a map with a positive shape is known, the symbol, , can be read from the table:
Let us mention for completeness that if f ∈ l has a negative shape, then the transition rules from to read:
The transition rules in Equations (2) and (3) substantiate our claim in the Introduction that, from the point of view of the computational cost, min-max sequences and kneading sequences are virtually equivalent.
Therefore, the kneading symbols of f ∈ l, along with its initial min-max symbols, i.e.,
A final ingredient (proper of min-max sequences) is the following. Let the i-th critical line, 1 ≤ i ≤ l, be the line y = ci in the Cartesian product I × I. Min-max symbols split into bad and good symbols with respect to the i-th critical line. Geometrically, good symbols correspond to local maxima strictly above the line y = ci or to local minima strictly below the line y = ci. All other min-max symbols are:
Bad symbols appear in all results of [5,6] concerning the computation of the topological entropy of f ∈ l via min-max symbols. In this sense, we may say that bad symbols are the hallmark of this approach.
3. Auxiliary Results
Let , 1 ≤ i ≤ l, stand for the number of interior simple zeros of f ν(x) − ci, ν ≥ 0, i.e., solutions of x − ci = 0 (ν = 0) or solutions of f ν(x) = ci, x ∈ (a, b), with fμ(x) ≠ ci for 0 ≤ μ ≤ ν −1 and f ν′ (x) ≠ 0 (ν ≥ 1). Geometrically, is the number of transversal intersections on the Cartesian plane (x, y) of the curve y = fν (x) and the straight line y = ci, over the interval (a, b). Note that for all i.
To streamline the notation, set:
Furthermore, define:
(ν≥ 1, 1 ≤ i≤ l), that is, collects the upper and lower indices (k,κ) of the bad symbols with respect to the i-th critical line in all the initial blocks:
Finally, set:
We say that f ∈ l is boundary-anchored if f{a, b} ⊂ {a, b}. This boundary condition boils down to:
Theorem 2.Let f ∈ l be boundary-anchored. Then:
Proof. Suppose for the time being that f is twice differentiable on [a, b] without any restriction at the boundaries. In this case, it was proved in ([5], Theorem 5.3) that:
Therefore, the boundary conditions (12) or (13) allow us to express with the help of some , ,..., , 1 ≤ k ≤ l, via Equations (14) and (10). Sum the Equation (14) over i from one to l to obtain the compact relation:
4. A Closed Formula for the Topological Entropy of Multimodal Maps
According to [11] (Lemma 4.4), the topological entropy of a multimodal map depends only on the kneading sequences, i.e., on the itineraries of the critical values, but not on the itineraries of the boundary points. This entails that one may assume without restriction boundary conditions (12) or (13) when calculating the topological entropy of l-modal maps with a positive or negative shape, respectively. A formal justification is given by the following theorem.
Theorem 3. Let f ∈l(I). Then, there exists F ∈ l(J), where J⊃I, such that h(F) = h(f) and F is boundary-anchored.
See [9] (Lemma 7.7) and [11] (proof of Lemma 4.4). For the reader’s convenience, a proof of Theorem 3 is given in the Appendix.
This being the case, Equations (1) and (17) yield the following result.
Theorem 4. Let f ∈ l. Then,
Equation (18) provides a closed expression for h(f), which includes the min-max symbols of f.
5. A Simplified Algorithm for the Topological Entropy
An offshoot of the preceding section is that, when it comes to calculating the topological entropy of a multimodal map, one can resort to Equation (18), whether the map is boundary-anchored or not. Loosely speaking,
As a matter of fact, the numerical algorithm below estimates h(f) by to the desired precision. The core of the algorithm consists of a loop over ν. Each time the algorithm enters the loop, the values of sν−1 and Sν−1 are updated to sv and Sv, and the current estimation of h(f) is compared to the previous one. Note that the computation of , 1 ≤ i ≤ l, requires ,, see Equation (10), while the computation of , 1 ≤ i ≤ l, requires , and , see Equation (14).
We summarize next the algorithm resulting from Equation (18) in the following scheme (“A → B” stands for “B is computed by means of A”).
- (A1)
Parameters: l ≥ 1 (number of critical points), ɛ > 0 (dynamic halt criterion) and nmax ≥ 2 (maximum number of loops).
- (A2)
Initialization:, and (1 ≤ i ≤ l).
- (A3)
First iteration: For 1≤ i ≤ l,
- (A4)
Computation loop. For 1 ≤ i ≤ l and ν ≥ 2, keep calculating , and according to the recursions:
until (i)or else, (ii) ν = nmax + 1.- (A5)
Output. In case (i), output:
In case (ii), output “Algorithm failed”.
As said above, Algorithms (A1)–(A5) simplify the original algorithm [5], which formally consists of the same five steps above, but is based on the exact value of the lap number, ℓν. This entails that the new algorithm needs more loops to output h(f) with the same parameter ɛ in the halt criterion shown in Equation (21), although this does not necessarily mean that the overall execution time will be longer, since now, less computations are required. In fact, we will find both situations in the numerical simulations of Section 6.
Furthermore, given a halt criterion, ɛ, the execution time depends, as well, on the units (i.e., on the base of the logarithm), whichever algorithm is used. For instance, if logarithms to base e are used (i.e., h(f) in nats) and ν = nnat is the first time that the halt criterion,
Therefore, if the the halt criterion:
Two final remarks:
R1. The parameter ɛ does not bound the error , but the difference between two consecutive estimations; see Equation (21). The number of exact decimal positions of h(f) can be found out by taking different ɛ’s, as we will see in the next section. Equivalently, one can control how successive decimal positions of stabilize with growing ν. Moreover, the smaller h(f), the smaller ɛ has to be chosen to achieve a given approximation precision.
R2. According to [4] (Theorem 4.2.4), for any ν. We may expect, therefore, that the numerical approximations (22) converge from above to the true value of the topological entropy with ever more iterations, in spite of the relation holding in general for boundary-anchored maps only.
6. Numerical Simulations
In this section, we compute the topological entropy of a variety of multimodal maps. To this end, a code for arbitrary l was written with PYTHON and run on an Intel(R) Core(TM)2 Duo CPU. All the numerical results will be given with six decimal positions for brevity.
Thus, in Section 6.1 to 6.3, we calculate the entropy of families of uni-, bi- and tri-modal maps, respectively, taken from [6] (unimodal case) and [5] (general case). Except for particular values of the parameters, these maps are not boundary-anchored. The purpose of our choice is to compare our entropy plots with the plots published in those references. To complete the picture, we will consider non-smooth maps in Section 6.4. The natural choices are piecewise linear maps of a constant slope, because, in this case, the exact value of the topological entropy is known. In all sections, we are going to compare numerically the performance of the algorithm presented in Section 5 with the general algorithm presented in [5] (Section 7) by means of single maps. For brevity, we shall refer to them as the new algorithm and the old one, respectively.
As for the units, the nat is the usual choice in applied mathematics and physics, while the bit is the standard unit in information theory and communication technologies. In the following subsections, we are actually going to use both of them despite the fact that, as shown in Section 5, computations with Napierian logarithms are faster, to a given precision. To be specific, we use bits in Sections 6.2 and 6.3 for the sake of comparison with the results published in [5], which are given in that unit.
6.1. Simulation with One-Modal Maps
Let α> 0, −1 < β ≤ 0 and fα,β : [−(1 +β), (1 +β)] → [−(1 +β), (1 +β)] be defined as ([6], Equation (29)):
These maps have the peculiarity of showing direct and reverse period-doubling bifurcations when the parameters are monotonically changed (see Figure 3a in [6]).
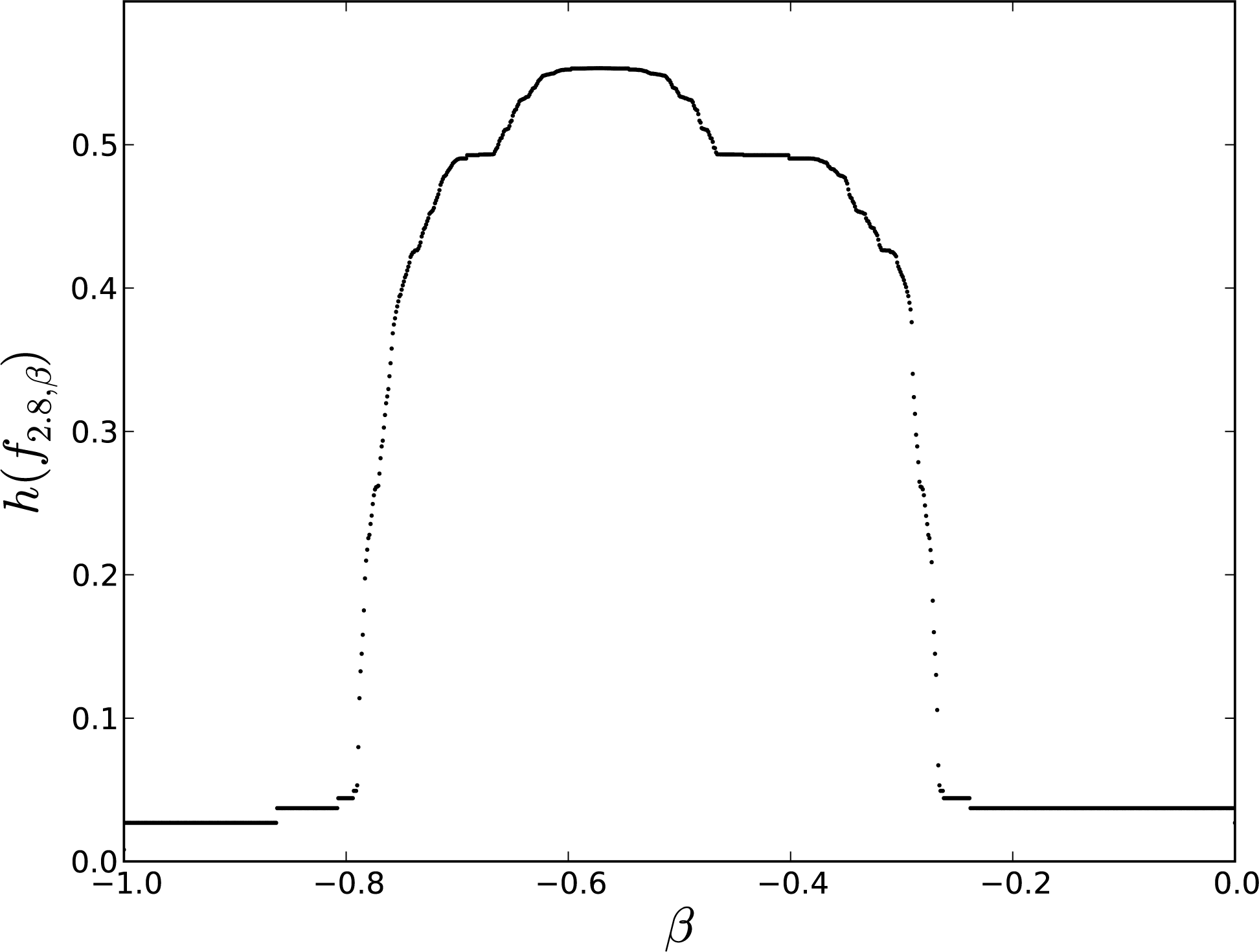
Figure 1 shows the plot of h(f2.8,β) vs.β calculated with the algorithm of Section 7. Here, ɛ = 10−4, and the parameter, β, was increased in steps of Δβ = 0.001 from β= −0.999 to β= 0. Upon comparing Figure 1 with Figure 3b of [6], we see that both plots coincide visually, except for the two vanishing entropy tails. We conclude that ɛ = 10−4 is not small enough to obtain reliable estimations of the topological entropy for vanishing values of h(f2.8,β). This fact can also be ascertained numerically by taking different values of ɛ, as we do in the table below.
To compare the convergence speed and execution time of the old and the new algorithm, we have computed h(f2.8,−0.5) with both algorithms for different ɛ’s. The number of loops, n, needed to achieve the halt condition ɛ = 10−d, 4 ≤ d ≤ 7, and the execution time, t (in seconds), are listed in Table 1. The columns, hold, nold and told, were obtained with the old algorithm, while the columns, hnew, nnew and tnew, were obtained with the new one. For ɛ = 10−4, it exceptionally holds told > tnew; otherwise told < tnew. Furthermore, we conclude from Table 1 that h(f) = 0.52... nats with either algorithm and ɛ = 10−6, both decimal digits being exact. If ɛ = 10−7, the old algorithm fixes the third decimal digit, h(f) = 0.524... nats, whereas the new algorithm does not.
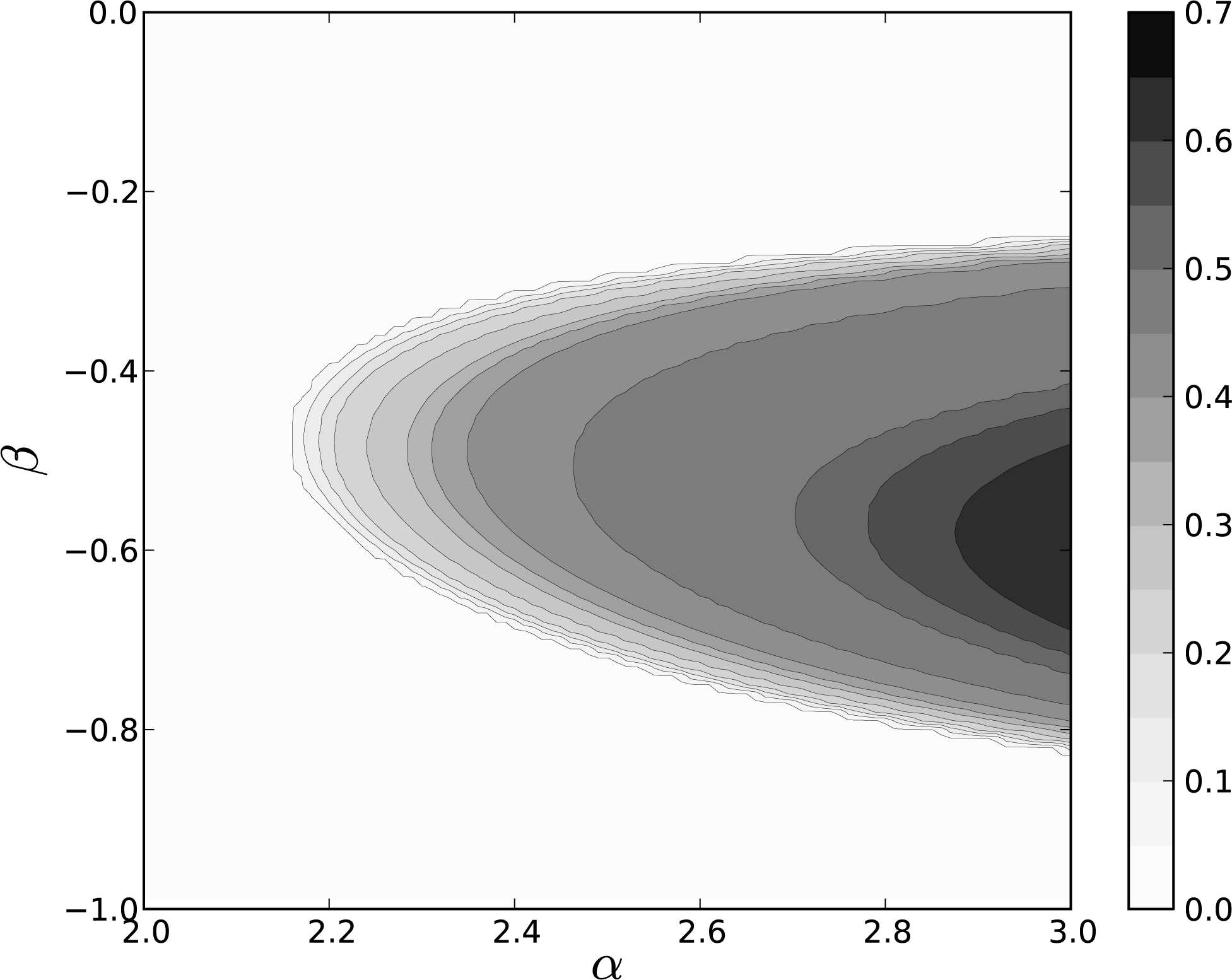
Figure 2 depicts the values of h(fα,β) for 2 ≤ α ≤ 3, −1 < β ≤ 0, ɛ = 10−4 and Δα Δβ = 0.01.
6.2. Simulation with Two-Modal Maps
Let 0 ≤ υ2 < υ1 ≤ 1 and fυ1,υ2 : [0, 1] → [0, 1] be defined as ([5], Section 8.1):
These maps have convenient properties for numerical simulations, as they share the same fixed critical points,
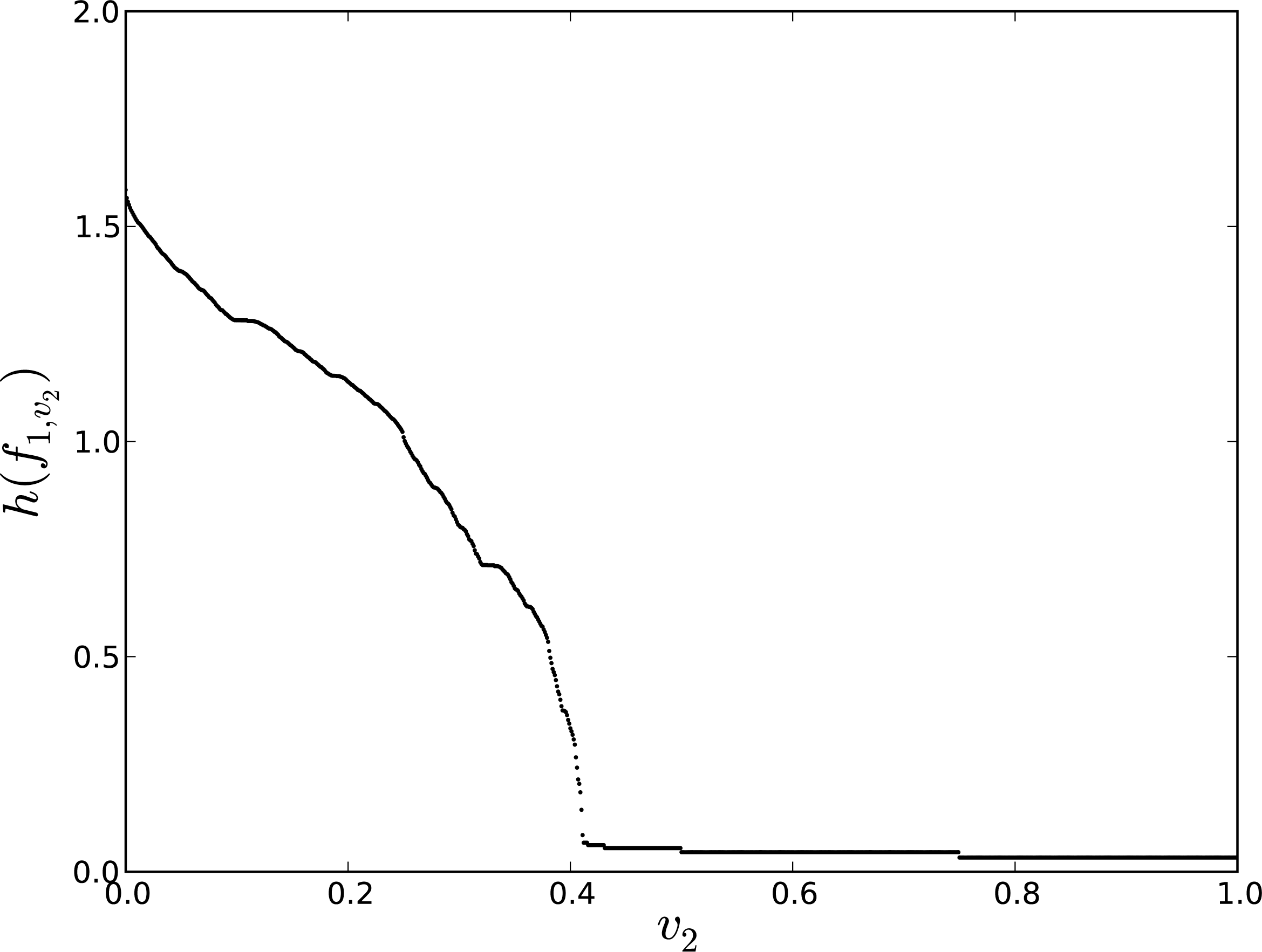
Figure 3 shows the plot of h(f1,υ2) vs. υ2, 0 ≤ υ2 < 1, computed with the new algorithm, ɛ = 10−4, and Δυ2 = 0.001. Again, this plot coincides visually with the same plot computed with the old algorithm [5] (Figure 4), except for the vanishing entropy tail, which indicates that ɛ = 10−4 is too large a value for obtaining accurate estimates in that parametric region.
Table 2 displays the performance of the new algorithm as compared to the old one when computing h(f0.9,0.1). This time, told > tnew for ɛ = 10−d, 4 ≤ d ≤ 7 (as in Table 1). Furthermore, we obtain two correct decimal digits of the topological entropy, h(f0.9,0.1) = 0.60... bits, with both algorithms and ɛ = 10−6.
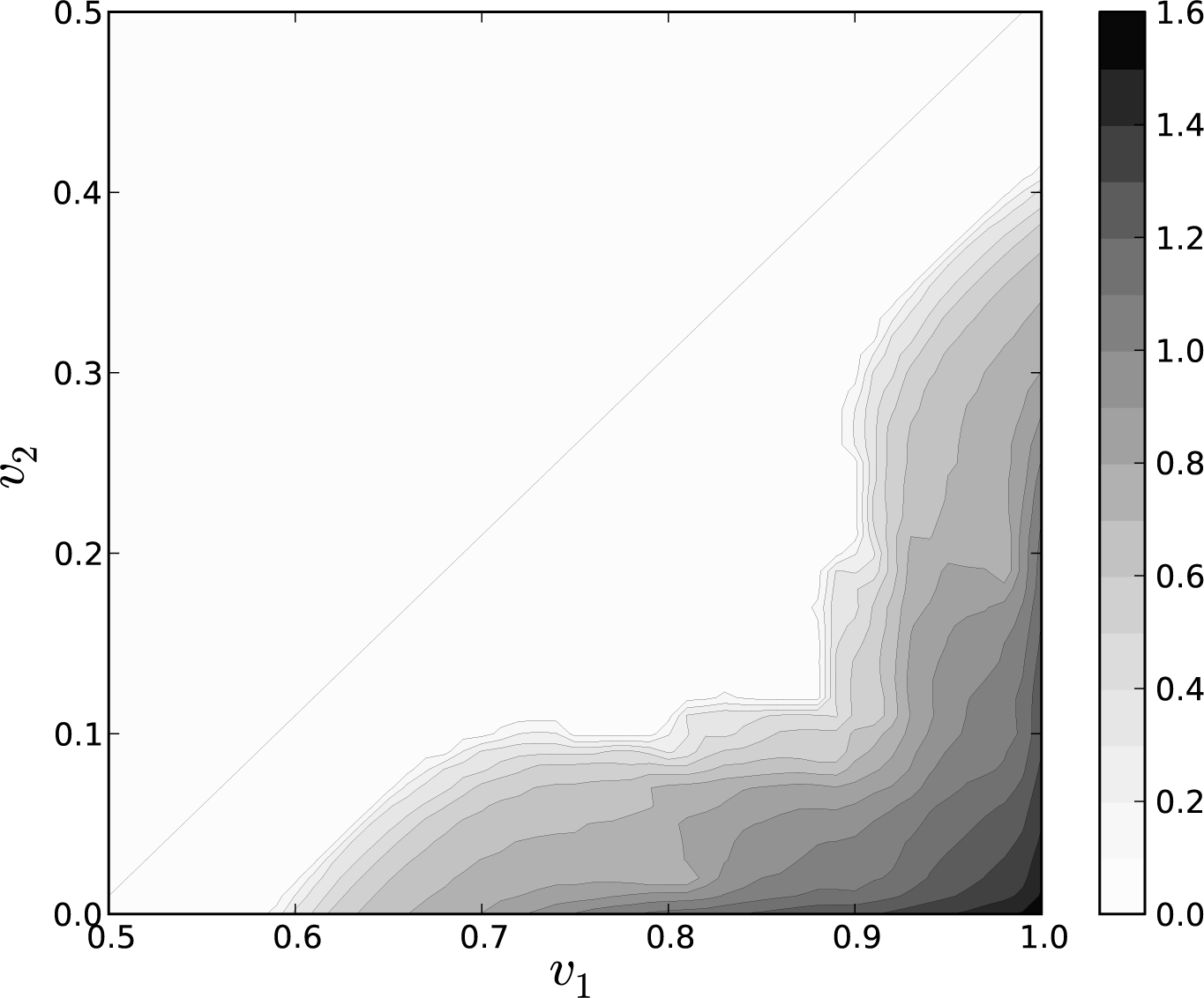
Figure 4 depicts the values of h(fυ1,υ2) for 0 ≤ υ2 ≤ υ1 − 0.5, ɛ = 10−4, and Δυ1, Δυ2 = 0.01.
6.3. Simulation with Three-Modal Maps
Consider next the three-modal maps, fυ2,υ3 : [0, 1] → [0, 1], defined by the quartic polynomials [5] (Section 8.2):
Moreover, this family verifies fυ2,υ3(0) = 0, fυ2,υ3(c2) = υ2, f(c3) = υ3 and:
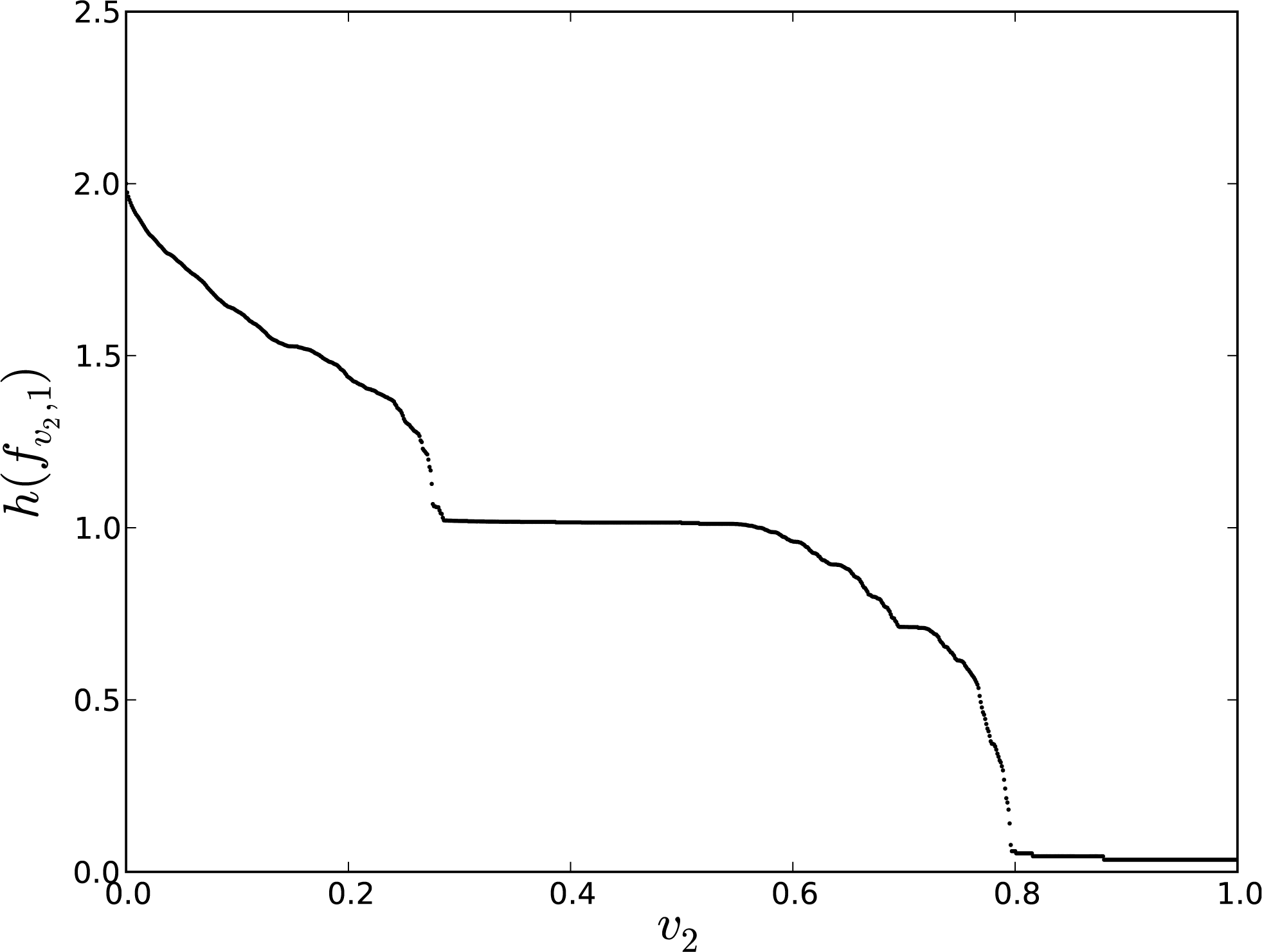
Figure 5 shows the plot of h(fυ2,1) vs. υ2, 0 ≤ υ2 < 1, computed with the new algorithm, ɛ = 10−4, and Δυ2 = 0.001. Once more, this plot coincides visually with the same plot computed with the old algorithm (see Figure 7 (left) in [5]), except for the vanishing entropy tail, which again indicates that ɛ = 10−4 is too large a value for obtaining accurate estimates in that parametric region.
Table 3 displays the performance of the new algorithm as compared to the old one when computing h(f0.7,1). Furthermore, this time, told > tnew for ɛ = 10−d, 4 ≤ d ≤ 7 (as in Tables 1 and 2). Furthermore, we obtain two correct decimal digits of the topological entropy, h(f0.7,1) = 0.69... bits, with both algorithms and ɛ = 10−6.
Figure 6 depicts the values of h(fυ2,υ3) for υ2 + 0.3 ≤ υ3 ≤1, ɛ = 10−4 and Δυ2, Δυ3 = 0.01.
6.4. Simulation with Higher Multimodal Maps
Last, but not least, we are going to compare the performances of the old and new algorithms with the four- and five-modal maps of Figure 7. These are piecewise linear maps on [0, 1], with constant slope s = ±1.5, critical points:
Table 4 summarizes the computational performance of both algorithms with the four-modal map. As happened with the two- and three-modal maps (Tables 2 and 3), the new algorithm needs more computation loops, but less execution time than the old one for all ɛ = 10−d, 4 ≤ d ≤ 7.
Likewise, Table 5 summarizes the computational performance of both algorithms with the five-modal map. It is worth noting that now, both algorithms need the same number of loops for all halt criteria ɛ, and yet, the new algorithm is faster.
As in the preceding simulations, we conclude from Tables 4 and 5 that both algorithms determine two correct decimal positions of the topological entropy of the corresponding map, h(f) = 0.40... nats. However, this time, the halt criterion ɛ = 10−6 does not suffice; here, one has to set ɛ = 10−7 to achieve the same precision.
A concluding observation. As anticipated in remark R2 of Section 5 and illustrated in Tables 1 and 5, the values of hnew converge from above with ever more computation loops (or smaller values of the parameter, ɛ). This property follows for hold from ([4] (Theorem 4.2.4).
7. Conclusions
The main contributions of this paper are the following.
- (i)
In Theorem 1, we proved that the transition rules for min-max symbols in Equations (2) and (3), which were derived in [5] for twice differentiable multimodal maps, actually hold true for just continuous ones.
- (ii)
As a result of Theorem 1, we conclude that the validity of formula (15), which was proved in ([5], Theorem 5.3) for twice differentiable multimodal maps, can be extended to continuous maps. For subsequent applications, only the particularization of Equation (15) to boundary-anchored maps (Theorem 2) is needed.
- (iii)
The results reviewed and proved in Sections 2 and 3 lead to closed formula (18) for the topological entropy of multimodal maps. Previously, we proved in Theorem 3 that, although ℓn clearly depends on the boundary conditions, the limit does not.
- (iv)
The numerical algorithm proposed in Section 5 for the computation of h(f) amounts to a recursive scheme to approximate the limit in closed formula (18).
This algorithm is a simplification and, at the same time, a generalization of the recursion scheme proposed in [5] for h(f). Indeed, it is a simplification, because Equation (15) was used in [5] to compute the lap number, ℓv, while the abridged expression in Equation (14) is used here. In other words, the new algorithm does not track the orbits of the endpoints. Additionally, it is also a generalization, because we proved in Theorem 2 that Equation (14) (and Equation (15) for that matter) holds not only for twice differentiable maps (as assumed in [5], (Theorem 5.3)) but also for just continuous ones. By the way, this point was numerically checked in Section 6.4.
The performances of both algorithms, old and new, were compared in Section 6.1 to 6.4 using smooth and non-smooth l-modal maps with 1 ≤ l ≤ 5. In view of the results summarized in Tables 1 and 5, the old algorithm performs better in the unimodal case, while the opposite occurs in the other multimodal cases.
Acknowledgments
We thank our referees for their constructive criticism. We are also grateful to José S. Cánovas and María Muñoz Guillermo (Universidad Politécnica de Cartagena, Spain) for clarifying discussions and to Víctor Jiménez (Universidad de Murcia, Spain) for the elegant proof in the Appendix. This work was financially supported by the Spanish Ministerio de Economía y Competitividad, grant MTM2012-31698.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
Let g : X → X be a continuous map of a compact Hausdorff space, X, into itself. A point, x ∈ X, is non-wandering with respect to the map, g, if for any neighborhood, U, of x, there is an n ≤ 1 (possibly depending on x), such that fn(U) ∩ U ≠ ∅. Fixed and periodic points are examples of non-wandering points. The closed set of all non-wandering points of g is called its non-wandering set and denoted by Ω(g). According to ([4], Lemma 4.1.5),
Furthermore, if:
To prove Theorem 3, suppose that f is an l-modal self-map of the compact interval, I, with a positive shape (the proof for maps with a negative shape is analogous).
Set I = [a, b], and J = [a′, b′] with a′ ≤ a < b ≤ b′. If f(a) = a, choose a′ = a; if f(b) = a (l odd) or f(b) = b (l even), choose b′ = b. For definiteness, we suppose the most general situation, namely, a′ < a and b < b′. Let F : J → J be such that: (i) F is strictly increasing on [a′, a]; (ii) F |[a,b] = f; and (iii) F is strictly decreasing (l odd) or strictly increasing (l even) on [b, b′]. In particular, F may be taken as piecewise linear on [a′, a] ∪ [ b, b′]. Thus, F ∈ l(J) has the same critical points and values as f, the same shape and is boundary-anchored. Note that the shape enters in how f is extended to F .
Moreover, it is easy to check that Ω(F) = Ω (f) ∪ C, where C is a closed and F -invariant set that only contains fixed points. Thus, h(F |C) = 0 and, according to Equations (A1) and (A2),
References
- Adler, R.; Konheim, A.; McAndrew, M. Topological entropy. Trans. Am. Math. Soc 1965, 114, 309–319. [Google Scholar]
- Walters, P. An Introduction to Ergodic Theory; Springer Verlag: New York, NY, USA, 2000. [Google Scholar]
- Misiurewicz, M.; Szlenk, W. Entropy of piecewise monotone mappings. Stud. Math 1980, 67, 45–63. [Google Scholar]
- Alsedà, L.; Llibre, J.; Misiurewicz, M. Combinatorial Dynamics and Entropy in Dimension One; World Scientific: Singapore, Singapore, 2000. [Google Scholar]
- Amigó, J.M.; Dilão, R.; Giménez, A. Computing the topological entropy of multimodal maps via min-max sequences. Entropy 2012, 14, 742–768. [Google Scholar]
- Dilão, R.; Amigó, J.M. Computing the topological entropy of unimodal maps. Int. J. Bifurc. Chaos 2012, 22, 1250152. [Google Scholar]
- Dias de Deus, J.; Dilão, R.; Taborda Duarte, J. Topological entropy and approaches to chaos in dynamics of the interval. Phys. Lett. A 1982, 90, 1–4. [Google Scholar]
- Dilão, R. Maps of the Interval Symbolic Dynamics, Topological Entropy and Periodic Behavior (in Portuguese), Ph.D. Thesis, Instituto Superior Técnico, Lisbon, Portugal. 1985.
- Milnor, J.; Thurston, W. On Iterated Maps of the Interval. In Dynamical Systems, Lectures Notes in Mathematics 1342; Alexander, J.C., Ed.; Springer: Berlin, Germany, 1988; pp. 465–563. [Google Scholar]
- De Melo, W.; van Strien, S. One-Dimensional Dynamics; Springer: New York, NY, USA, 1993. [Google Scholar]
- Milnor, J.; Tresser, C. On entropy and monotonicity of real cubic maps. Commun. Math. Phys 2000, 209, 123–178. [Google Scholar]


| hold | nold | told | hnew | nnew | tnew | |
|---|---|---|---|---|---|---|
| ɛ = 10−4 | 0.531968 | 81 | 0.031076 | 0.534106 | 101 | 0.021248 |
| ɛ = 10−5 | 0.526645 | 253 | 0.179558 | 0.527305 | 318 | 0.193149 |
| ɛ = 10−6 | 0.524935 | 797 | 1.684213 | 0.525142 | 1,004 | 1.912784 |
| ɛ = 10−7 | 0.524391 | 2,519 | 16.369158 | 0.524456 | 3,174 | 18.900032 |
| hold | nold | told | hnew | nnew | tnew | |
|---|---|---|---|---|---|---|
| ɛ = 10−4 | 0.619682 | 195 | 0.286922 | 0.622100 | 218 | 0.253133 |
| ɛ = 10−5 | 0.606568 | 613 | 2.665108 | 0.607310 | 688 | 2.485049 |
| ɛ = 10−6 | 0.602385 | 1938 | 26.238006 | 0.602622 | 2173 | 24.890648 |
| ɛ = 10−7 | 0.601062 | 6125 | 271.074381 | 0.601137 | 6871 | 265.198039 |
| hold | nold | told | hnew | nnew | tnew | |
|---|---|---|---|---|---|---|
| ɛ = 10−4 | 0.710321 | 162 | 0.422875 | 0.711709 | 177 | 0.351586 |
| ɛ = 10−5 | 0.699339 | 511 | 4.028703 | 0.699793 | 557 | 3.448455 |
| ɛ = 10−6 | 0.695855 | 1,615 | 39.882275 | 0.696000 | 1,759 | 34.853025 |
| ɛ = 10−7 | 0.694752 | 5,105 | 417.489291 | 0.694798 | 5,561 | 368.900286 |
| hold | nold | told | hnew | nnew | tnew | |
|---|---|---|---|---|---|---|
| ɛ = 10−4 | 0.421218 | 160 | 0.697776 | 0.422215 | 169 | 0.576800 |
| ɛ = 10−5 | 0.410476 | 503 | 6.583444 | 0.410776 | 533 | 5.747668 |
| ɛ = 10−6 | 0.407051 | 1,589 | 65.236068 | 0.407147 | 1,683 | 57.951979 |
| ɛ = 10−7 | 0.405967 | 5,021 | 678.706894 | 0.405997 | 5,321 | 616.59469 |
| hold | nold | told | hnew | nnew | tnew | |
|---|---|---|---|---|---|---|
| ɛ = 10−4 | 0.420542 | 152 | 0.848166 | 0.420542 | 152 | 0.644305 |
| ɛ = 10−5 | 0.410239 | 480 | 8.231152 | 0.410239 | 480 | 6.501711 |
| ɛ = 10−6 | 0.406978 | 1,515 | 81.429872 | 0.406978 | 1,515 | 65.307619 |
| ɛ = 10−7 | 0.405944 | 4,788 | 864.376277 | 0.405944 | 4,788 | 695.24749 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Amigó, J.M.; Giménez, Á. A Simplified Algorithm for the Topological Entropy of Multimodal Maps. Entropy 2014, 16, 627-644. https://doi.org/10.3390/e16020627
Amigó JM, Giménez Á. A Simplified Algorithm for the Topological Entropy of Multimodal Maps. Entropy. 2014; 16(2):627-644. https://doi.org/10.3390/e16020627
Chicago/Turabian StyleAmigó, José M., and Ángel Giménez. 2014. "A Simplified Algorithm for the Topological Entropy of Multimodal Maps" Entropy 16, no. 2: 627-644. https://doi.org/10.3390/e16020627





