A Relationship between the Ordinary Maximum Entropy Method and the Method of Maximum Entropy in the Mean

Abstract

There are two entropy-based methods to deal with linear inverse problems, which we shall call the ordinary method of maximum entropy (OME) and the method of maximum entropy in the mean (MEM). Not only does MEM use OME as a stepping stone, it also allows for greater generality. First, because it allows to include convex constraints in a natural way, and second, because it allows to incorporate and to estimate (additive) measurement errors from the data. Here we shall see both methods in action in a specific example. We shall solve the discretized version of the problem by two variants of MEM and directly with OME. We shall see that OME is actually a particular instance of MEM, when the reference measure is a Poisson Measure.

1. Introduction

During the last quarter of the XIX-th century Boltzmann proposed a way to study convergence to equilibrium in a system of interacting particles through a quantity that was that was a Lyapunov functional for the dynamics of the system, and increased as the system tended to equilibrium. A related idea was used at the beginning of the XX-th century by Gibbs to propose a theory of equilibrium statistical mechanics. The difference between the approaches was in the nature of the microscopic description. In the late 1950s, Jaynes in [1] turned the idea into a variational method to determine a probability distribution given the expected value of a few random variables (observables to use the physical terminology). This procedure is called the method of maximum entropy. This methodology has proven useful in a variety of problems well removed from the standard statistical physics setup. See Kapur (1989) [2] for example, or the Kluwer Academic Press collection of Maximum Entropy and Bayesian Methods or the volume by Jaynes (2003) [3].

As it turns out, similar procedures had come up in the actuarial and statistical literature, see for example the works by Esscher (1932) [4] and by Kullback (1957) [5]. Jaynes’s procedure was further extended in Decarreau et al. (1992) [6], and Dacunha-Castelle and Gamboa (1990) [7]. Such extension has proven a powerful tool to deal with linear inverse problems with convex constraints. See Gzyl and Velásquez (2011) [8] for example. This method uses the standard variational technique as a stepping stone in a peculiar way.

Besides providing a more general type of solutions to the OME problem, we shall verify in two different ways that the standard solution of the OME is actually a particular case of the more general MEM approach to solve linear inverse problems with convex constraints.

The paper is organized as follows. In the remainder of this section we shall state the two problems whose solutions we want to relate. These consists in obtaining a positive, continuous function satisfying some integral constraints. In the next section we shall recall the basics of MEM. In section three we continue with the same theme and examine specific choices of set up to implement the method. Section 4 is devoted to the issue of obtaining the problem by the OME from the solution by the MEM.

In section five we implement both approaches numerically to compare their performance in one simple example. The idea of using two different choices of prior is to emphasize the flexibility of the MEM.

1.1. Statement of the First Problem

Even though the problem considered is not in its most general form, it is enough for our purposes and can be readily extended. We want to find a continuous positive function x(t) : [0, 1] → [0, ∞) such that

$${\int }_0^1{k}_i(t)x(t)dt=\mathit{m};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,M$$

(1)

Typically {k_i(t) : i = 1, ..., M} a collection of measurable functions defined on [0, 1] describing some sort of observations made on a random variable whose density we want to estimate. These could be ordinary moments t^n_i for some collection {n₁, ..., n_M} of integers. Or they could be fractional powers t^a_i for some collection {a₁, ..., a_M} of reals. This problem appears when our information consists of the values of a Laplace transform at points {a₁, ..., a_M} and we map our problem onto [0, 1] by means of the change of variables s → t = e^−s. Or the k_i(t) could be trigonometric polynomials. In such case we refer to Equation (1) as a generalized moment problem. When x(t) is required to be a probability density, we shall consider k₁(t) ≡ 1 on [0, 1]. It is also apparent that the convex constraint is the positivity constraint on x(t).

1.2. Statement of the Second Problem

Clearly Equation (1) is a particular case of the following more general problem: Let k(s, t) : [a, b] × [0, 1] → ℝ. Let $𝒦$ ⊂ $𝒞$([0, 1]) be a cone contained in the class of continuous functions, and let m(s) : [a, b] → ℝ be some continuous function. We want to find x(t) ∈ $𝒦$ satisfying the integral constraints

$${\int }_0^{1}k(s,t)x(t)dt=m(s),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}s\in [a,b]$$

(2)

We remark that when x(t) is a density and k(s, t) ≡ 1, them m(s) ≡ 1. Clearly the integral constraints could be incorporated into $𝒦$, but it is convenient to keep both separated. For what comes below, and to relate to the first problem, we shall restrict ourselves to the convex set of continuous density functions. Such type of problems were considered for example in [9] or in much grater generality in [10] or and more recently in [11] where applications and further references to related work are collected. As mentioned above, the setup can be relaxed considerable at the expense of technicalities. For example, one can consider the kernel k to be defined on the product S₁ × S₂ of two locally compact, separable metric spaces, and dt could be replaced by some σ–finite measure ν(dt) on (S₂, $ℬ$(S₂)). But let us keep it as simple as possible.

2. The Maximum Entropy in the Mean Approach

The basic intuition behind the MEM goes as follows. We search for a stochastic process with independent increments {X(t)|t ∈ [0, 1]} defined on some auxiliary probability space (Ω, $ℱ$, Q) such that

$$dX(t)=X(t+\delta )-X(t)\in 𝒦,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\in [0,1]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\delta >0$$

(3)

$$\frac{d{E}_P[X(t)]}{dt}=x(t);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\text{some}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}P\ll Q$$

(4)

$$E_P\left[{\int }_0^{1}k(s,t)dX(t)\right]={\int }_0^{1}k(s,t)x(t)dt=m(t)$$

(5)

Here the measure P on (Ω, $ℱ$) is yet to be determined. If it exists, notice that x(t) ∈ $𝒦$ automatically. The integral with respect to dX(t) is to be understood in the Itô sense.

As we want to implement the scheme numerically, it is more convenient to discretize Equation (2) and then to bring in the MEM. It is at this point where the regularity properties of k(s, t) and x(t) come in to make life easier. Consider a partition of [a, b] into M equal adjacent intervals and a partition of [0, 1] into N adjacent intervals. Let {s_i|i = 1, ..., M} and respectively {t_j|j = 1, ..., N} be the center points of those intervals. Let us set A_ij = A(i, j) = k(s_i, t_j). Also, set x_j ≡ x(j) = x(t_j)/N and finally m_i ≡ m(i) = m(s_i).

Comment We chose x_j = x(t_j)/N because when x(t) is a density, we want its discretized version to satisfy ∑_j x_j = 1.

With these changes, the discretized version of the second problem becomes: Given M real numbers m_i : i = 1, ..., M, determine positive numbers x_j : j = 1, ..., N such that

$$\sum _{j=1}^N{A}_{ij}{x}_j=m_i,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,M$$

(6)

To assemble the model, consider Ω = [0, ∞)^N with $ℱ$ = $ℬ$(Ω) the usual Borel sets. To make things really simple, let q_j(dξ_j) be N copies of a Measure q(dξ) on ([0, ∞), $ℬ$([0, ∞))) and let

$$Q(d\xi )=\prod _{j=1}^N{q}_j(d{\xi }_j)$$

be the reference measure. Note that with respect to Q the coordinate maps X_j ≡ X(j) : Ω → [0, ∞) defined by X_j(ξ) = ξ_j satisfy the positivity constraints and are independent. With this notation, the original discretized problem (6) is transformed

$$\text{Determine}\hspace{0.17em}\text{a}\hspace{0.17em}\text{probality}\hspace{0.17em}\text{measure}\hspace{0.17em}P\ll Q\hspace{0.17em}\text{such}\hspace{0.17em}\text{that}\hspace{0.17em}{E}_P[\mathbf{AX}]=\mathbf{m}$$

(7)

Note that if such a measure P is found, then x_j = E_P [X_j] satisfies Equation (6). It is to determine P where the OME comes in as a stepping stone.

3. Solution of Equation (7) by MEM

The notation will be as at the end of the previous section. For the purpose of comparison, we shall solve Equation (7) using two different measures. First we shall consider a product of exponential distributions on Ω and then we shall consider a product of Poisson distributions. Let us first develop the generic procedure, and then particularize for each choice of reference measure.

At this point we mention that the only requirement on the reference measure $Q(d\mathit{\xi })={\Pi }_{j=1}^N{q}_j(d{\xi }_j)$ is the following:

Assumption We shall require the closure of the convex hull generated by the support of Q to be exactly Ω.

Let us consider the convex set $𝒫$(Q) = {P measure on(Ω, $ℱ$), P << Q} on which we define the following concave functional

$$S_Q(P)=-{\int }_{\Omega }\text{ln}\left(\frac{dP}{dQ}\right)\hspace{0.17em}dP$$

(8)

whenever ln(dP/dQ) is P–integrable and equal −∞ otherwise. This is the negative of the Kullback-Leibler divergence between P and Q. It is a standard result that S_Q(P) is concave in P and we have

Lemma 3.1. Suppose that P, Q and R are probability measures on (Ω, $ℱ$) such that P << Q, P << R and R << Q, then S_R(P) ≤ 0, and

$$S_Q(P)=S_R(P)-\int dP\text{ln}\left(\frac{dR}{dQ}\right)$$

(9)

Proof. The verification of the first assertion is easy invoking Jensens’ inequality. The second follows readily from the fact that $\frac{dP}{dQ}=\frac{dP}{dR}/\frac{dQ}{dR}$.

We want to consider the following consequence of this lemma. Let us define R by dR_λ(ξ) = ρ_λ(ξ)dQ(ξ) where

$${\rho }_{\mathbf{\lambda }}(\mathit{\xi })=\frac{e^{-<\mathbf{\lambda },\text{A}\mathit{\xi }>}}{Z(\mathbf{\lambda })}$$

(10)

where Z(λ) is the obvious normalization factor, which is given by

$$Z(\mathbf{\lambda })=\int e^{-<\mathbf{\lambda },\mathbf{A}\mathit{\xi }>}dQ\mathit{\xi }$$

The idea behind the maximum entropy method, comes from the realization that for such R, when P satisfies the constraints, substituting Equation (10) in the integral term in Equation (9), we obtain that

$$\Sigma (\mathbf{\lambda })\equiv \text{ln}Z(\mathbf{\lambda })+<\mathbf{\lambda },\text{m}>\ge S_Q(P)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}\text{any}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\lambda }\in {ℝ}^M$$

(11)

Thus, whenever {λ ∈ ℝ^M |Z(λ) < ∞} we expect the problem to have a solution, and whenever the class of P′s satisfying the constraints Equation (7) is non-empty, a minimizer of the convex function Σ(λ) is expected to exist. Actually, Csiszar in [12,13] proved the existence of such P′s. Actually a different (a perhaps more physicist oriented) proof was provided more recently in [14]. It is actually a simple exercise to verify the following

Proposition 3.1. Suppose that a measure P satisfying (7) exists and that the minimum of Σ(λ) is reached at λ^* in the interior of {λ ∈ ℝ^M |Z(λ) < ∞}, then the probability P^* that maximizes S_Q(P) and satisfies Equation (7) is given by

$$d{P}^{*}(\mathbf{\xi })=\frac{e^{-<{\mathit{A}}^{†}{\mathbf{\lambda }}^{*},\mathit{\xi }>}}{Z({\mathbf{\lambda }}^{*})}dQ(\mathit{\xi })$$

(12)

We are using A^† to denote the transpose of A With that result, the next step consists of computing

$$x^{*}(j)={\int }_{\Omega }{\xi }_{i}d{P}^{*}(\mathit{\xi })$$

(13)

Let us now examine two possible choices for Q.

3.1. Exponential Reference Measure

Since we want positive x_j, we shall first try all factor q(dξ) = μe^−μξdξ, which has [0, ∞) as support. A simple computation yields that

$$Z(\mathbf{\lambda })=\prod _{j=1}^N\frac{\mu }{\mu +{({\mathit{A}}^{†}\mathbf{\lambda })}_j}$$

For the purpose of modeling one has to chose μ large enough such that μ + (A^†λ)_j is positive. Another simple computation (as in the verification of the preceding proposition), yields

$$x_j^{*}=\frac{1}{\mu +{({\mathit{A}}^{†}{\mathbf{\lambda }}^{*})}_j}$$

(14)

Observe that the method has just shifted the mean of each exponential to a new value. We let the reader to write down P^* explicitly to verify this assertion.

3.2. Poisson Reference Measure

This time, instead of a product of exponentials, we shall consider a product of Poisson measures, i.e., we take

$$q(d\xi )=e^{-\mu }\sum _{k\ge 0}\frac{{\mu }^k}{k!}{∊}_{\left\{k\right\}}(d\xi )$$

Here we use ∊_{a}(dξ) to denote the unit point mass (Dirac delta) at a. Certainly the convex hull of the non-negative integers is [0, ∞). Notice that now

$$Z(\mathbf{\lambda })=\prod _{j\ge 0}^N\text{exp}\left(-\mu (1-e^{-{({\mathit{A}}^{†}\mathbf{\lambda })}_j})\right)$$

from which we obtain

$$\Sigma (\mathbf{\lambda })=-\mu \sum _{j=1}^N\left(1-e^{-{({\mathit{A}}^{†}\lambda )}_j}\right)+<\mathbf{\lambda },\mathit{m}>$$

Notice now that if λ^* minimizes that expression, then the estimated solution to Equation (7) is

$$x_j^{*}=e^{-{({\mathit{A}}^{†}{\mathbf{\lambda }}^{*})}_j}$$

(15)

3.3. The MEM Approach to the Original Problem

Consider Equation (1) again. This time we shall consider a Poisson point process on ([0, 1], $ℬ$([0, 1]) with intensity dt. By this we mean a base probability space (Ω, $ℱ$, Q) on which a collection of random measures {N(A) : A ∈ $ℬ$([0, 1])} (the point process) is given, which has the following properties:

(1)

N(A) is a Poisson random variable with intensity (mean)|A|,

(2)

Q – almost everywhere A → N(A) is an integer valued measure

(3)

For any disjoint A₁, ..., A_k the N(A₁), ..., N(A_k) are independent

From these, it is clear that for any λ ∈ ℝ^M the random variable ${\int }_0^1<\mathbf{\lambda }$, k(t) > N(dt) satisfies

$$E_Q\left[e^{-{\int }_0^1<\mathbf{\lambda },{\mathit{k}}_{(t)>N(dt)}}\right]=\text{exp}\left(-{\int }_0^{1}dt\left(\text{exp}\left(-<\mathbf{\lambda },\mathit{k}(t)>\right)-1\right)\right)$$

where k(t) is the vector of generalized moments appearing in Equation (1). Clearly, here we again denote the previous quantity by Z_Q(λ, k), and again Σ(λ) = ln (Z_Q(λ)) + <λ, m>. This function is convex on {λ ∈ ℝ^M |Z_Q(λ) < ∞}. When a minimizer λ^* exists in the interior of that domain, then P^* with density

$$\frac{d{P}^{*}}{dQ}=\frac{e^{-{\int }_0^1<{\mathbf{\lambda }}^{*},{\mathit{k}}_{(t)>N(dt)}}}{Z_Q({\mathbf{\lambda }}^{*})}$$

is such that

$$x_{\infty }^{*}(t)\equiv \frac{d{E}_{P^{*}}[N[0,t]]}{dt}=e^{-<{\mathbf{\lambda }}^{*},{\mathit{k}}_{(t)>}}$$

(16)

solves Equation (1).

4. OME from MEM

4.1. Discrete Case

We shall now relate the last result to the standard (ordinary) method of maximum entropy. Suppose that the unknown quantities x_j in Equation (3) are indeed probabilities, and that m₁ = 1 and A_1j = 1 for all j = 1, ..., N. It is easy to verify using the first equation of the set Equation (3) that $\text{exp}(-{\lambda }_1)=1/\zeta ({\mathbf{\lambda }}_r^{*})$ where λ_r = (λ₂, ..., λ_M) and

$$\zeta ({\mathbf{\lambda }}_r)=\sum _{j=1}^N{e}^{-{\sum }_{i=2}^M{\lambda }_i{A}_{i,j}}$$

From this, Equation (15) becomes

$$x_j^{*}=\frac{e^{-{\sum }_{i=2}^M{\lambda }_i^{*}{A}_{i,j}}}{\zeta ({\mathbf{\lambda }}_r^{*})}$$

which is the solution to Equation (3) by the OME method.

4.2. Continuous Case as Limit of the Discrete Case

This is the second place in which our discretization procedure enters. First rewriteEquation (15)$x_j^{*}$ as x^*(t_j)/N, from which Equation (15) becomes

$$x^{*}(t_j)=\frac{e^{-{\sum }_{i=2}^M{\lambda }_i^{*}{A}_{i,j}}}{\frac{1}{N}\zeta ({\mathbf{\lambda }}_r^{*})}$$

(17)

One may want to argue as follows: Notice as well, that given any t ∈ [0, 1] as N → ∞, there is a sequence t_j(N) converging to t. In addition, it is clear that

$$\frac{1}{N}\zeta ({\mathbf{\lambda }}_r^{*}))\to {\int }_0^1{e}^{-{\sum }_{i=2}^M{\lambda }_i{k}_i(t)dt}$$

and therefore

$$x^{*}(t)=\frac{e^{-{\sum }_{i=2}^M{\lambda }_i^{*}{k}_i(t)}}{{\int }_0^1{e}^{-{\sum }_{i=2}^M{\lambda }_i^{*}{k}_i(s)}ds}$$

which we would like to identify as the solution (1) provided by the OME method. The problem with the procedure is that the λ^* depends on N and changes along the way. Let us indicate a possible way to overcome this issue.

For each N denote by A_j(N) the blocks of the partition of [0, 1], and suppose that the partitions refine each other as N increases (consider dyadic partitions for example). For each N denote the maxentropic solution described in Equation (17) by $x_N^{*}(t_j)$ and define the piecewise constant (continuous) density

$${\tilde{x}}_N(t)=\sum _j{x}_N^{*}(t_j)I_{A_j(N)}(t)$$

Clearly, x̃_N satisfies Equation (1), but it is not the density that maximizes the entropy. Actually, one can rapidly verify that

$$S({\tilde{x}}_N)\le S({\tilde{x}}_{N+1})\le S({\tilde{x}}_{\infty })$$

We shall relate x̃_∞ to the $x_{\infty }^{*}$ displayed in Equation (16) below. The remaining part of the argument is to verify that λ_N → λ_∞ (in an obvious notation) as N → ∞. This is simple to say, but hard to prove. A way around the convergence of the λ_N issue is provided by [12].

4.3. The Full Continuous Case

Here we show how to obtain the OME solution to Equation (1) from the MEM solution Equation (16) without the labor described in the previous section. The argument is similar to the one mentioned above. As k₁(t) = 1, we can isolate ${\lambda }_1^{*}$ and rewrite $x_{\infty }^{*}(t)$ as

$$x^{*}(t)=\frac{e^{-{\sum }_{i=2}^M{\lambda }_i^{*}{k}_i(t)}}{{\int }_0^1{e}^{-{\sum }_{i=2}^M{\lambda }_i^{*}{k}_i(s)}ds}$$

(18)

That this solves Equation (1) is due to the fact that the equations that determine λ^* in the full MEM and in the OME cases coincide. This happens because of the special form of Z_Q(λ) when the underlying auxiliary process is the Poisson point process

5. Numerical Examples

To compare the output of the three methods, we consider a simple example in which the data consists in a few values of the Laplace transform of the density of a Γ(a, b) density. Observe that if S denotes the original random variable, then T = e^−S denotes the corresponding random variable with range mapped onto [0, 1]. The values of the Laplace transform of S are the fractional (non-necessarily integer) moments of T. The maxentropic methods yield the density x(t) of T, from which the density of S is to be obtained by the change of variable f_S(s) = e^−sx(e^−s).

If we let {α₁ = 0, α₂, ..., α_M} and k_i(t) = t^α_i be M given powers of T, the corresponding moments to be used in Equation (1) are m_i = (b/(α_i + b))^a, with m₁ = 1. To be specific, let us consider a = b = 1, and α₂ = 1/5, α₃ = 1/4, α₄ = 1/3, α₅ = 1/2, α₆ = 5, α₇ = 10, α₈ = 15, α₉ = 20 from which we readily obtain the values of the 9 generalized moments m_i. To finish, we take N = 100 partition points of [0, 1].

5.1. Exponential Reference Measure

We shall set μ = 10 as a number high enough so that the positivity conditions mentioned in Section (3.1) holds. The function to be minimized to determine the λs is

$$\Sigma (\mathbf{\lambda })=N\text{ln}\mu -\sum _{j=1}^N\text{ln}\left(\mu +{({\mathit{A}}^{†}\mathbf{\lambda })}_j\right)+<\mathbf{\lambda },\mathit{m}>$$

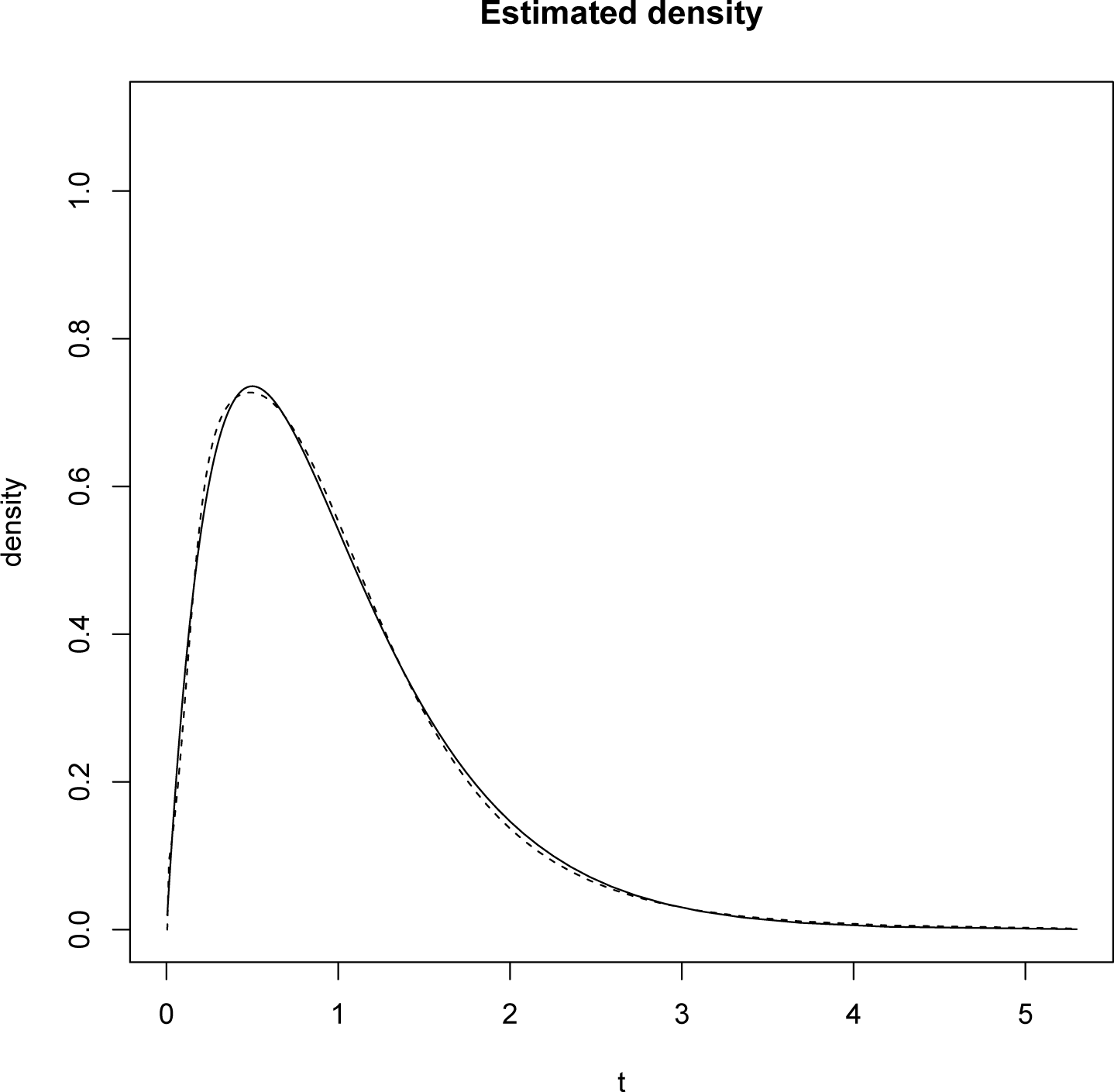
To find the minimizer, we use the Barzilai-Borwein code available for R, see [15]. Once the optimal λ is obtained it is inserted in Equation (14). That is the density of T on [0, 1]. To plot the density on [0, ∞) we perform the change of variables mentioned above and the result is plotted in the Figure 1.

We point out that the L₁ norm of the difference between the reconstructed and the original densities is 0.0283 rounding at the fourth decimal place.

5.2. The Poisson Reference Measure

In reference to the setup of Section 3.3 we set μ = 5 this time. The function to be minimized this time is

$$\Sigma (\mathbf{\lambda })=-\mu \sum _{j=1}^N\left(1-e^{-{({\mathit{A}}^{†}\mathbf{\lambda })}_j}\right)+<\mathbf{\lambda },\mathit{m}>$$

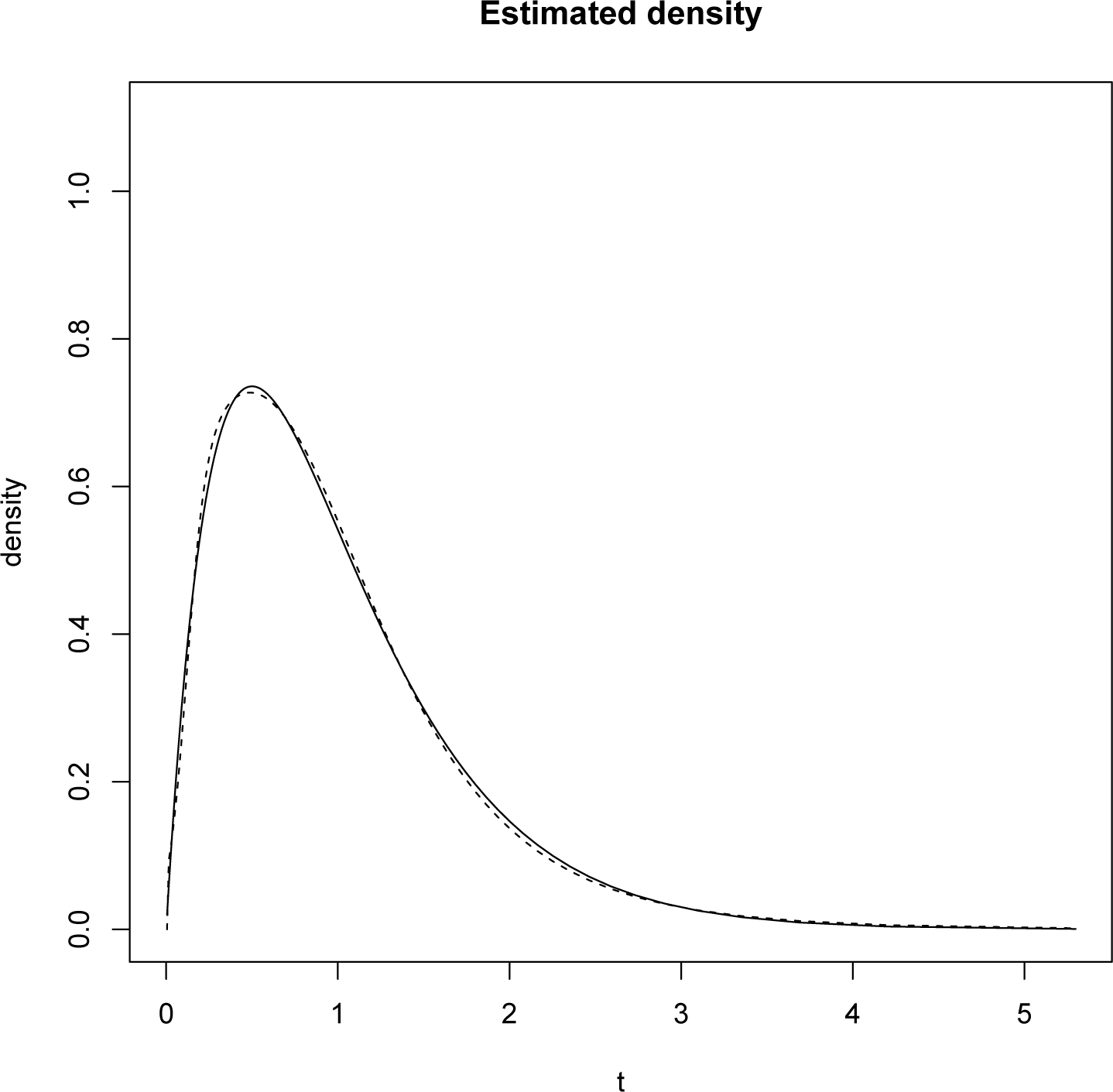
Once the minimizing λ^* has been found, the routine is as above: the density on [0, 1] is mapped onto a density on [0, ∞) by means of a change of variables. The result obtained is displayed on Figure 2.

The L₁ norm of the difference between the reconstructed and the original densities is 0.00524.

5.3. The OME Method

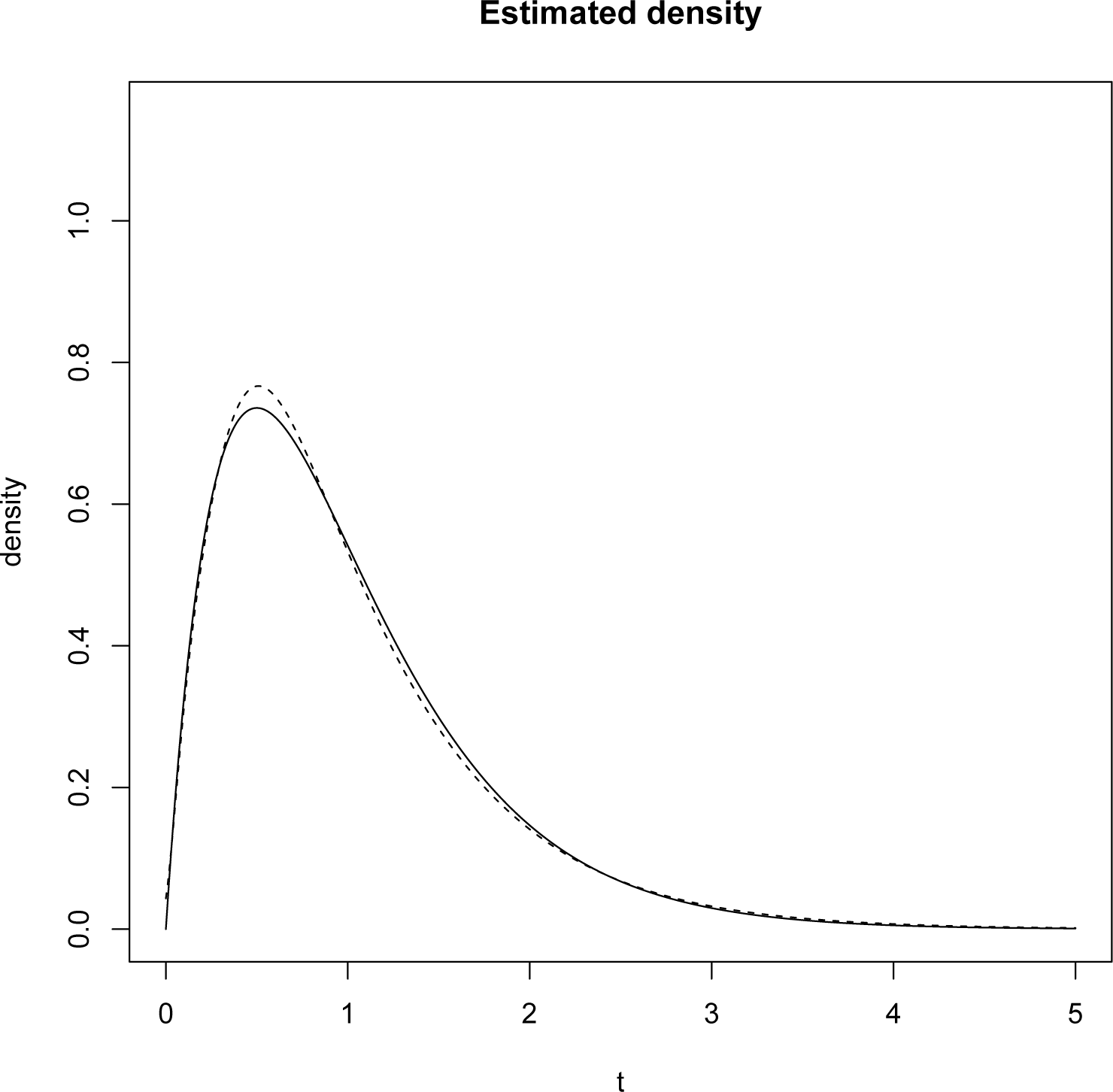
In this case, to determine λ^* we have to minimize

$$\Sigma (\mathbf{\lambda })={\int }_0^1{e}^{-<\mathbf{\lambda },{\mathit{k}}_{(t)}>}dt+<\mathbf{\lambda },\mathit{m}>$$

which clearly is the same thing as minimizing

$$\Sigma (\mathbf{\lambda })=-{\int }_0^1\left(1-e^{-<\mathbf{\lambda },{\mathit{k}}_{(t)}>}\right)dt+<\mathbf{\lambda },\mathit{m}>$$

as mentioned at the end of Section 4.3. The result, after the change of variables is displayed in Figure 3.

The L₁ norm of the difference between the reconstructed and the original densities is 0.03479.