Characterization of Rare Events in Molecular Dynamics
Abstract
: A good deal of molecular dynamics simulations aims at predicting and quantifying rare events, such as the folding of a protein or a phase transition. Simulating rare events is often prohibitive, especially if the equations of motion are high-dimensional, as is the case in molecular dynamics. Various algorithms have been proposed for efficiently computing mean first passage times, transition rates or reaction pathways. This article surveys and discusses recent developments in the field of rare event simulation and outlines a new approach that combines ideas from optimal control and statistical mechanics. The optimal control approach described in detail resembles the use of Jarzynski’s equality for free energy calculations, but with an optimized protocol that speeds up the sampling, while (theoretically) giving variance-free estimators of the rare events statistics. We illustrate the new approach with two numerical examples and discuss its relation to existing methods.1. Introduction
Rare but important transition events between long-lived states are a key feature of many systems arising in physics, chemistry, biology, etc. Molecular dynamics (MD) simulations allow for analysis and understanding of the dynamical behavior of molecular systems. However, realistic simulations for interesting (large) molecular systems in solution on timescales beyond microseconds are still infeasible even on the most powerful general purpose computers. This significantly limits the MD-based analysis of many biological equilibrium processes, because they often are associated with rare events. These rare events require prohibitively long simulations because the average waiting time between the events is orders of magnitude longer than the timescale of the transition characterizing the event itself. Therefore, the straightforward approach to such a problem via direct numerical simulation of the system until a reasonable number of events has been observed is impractically excessive for most interesting systems. As a consequence, rare event simulation and estimation are among the most challenging topics in molecular dynamics.
In this article, we consider typical rare events in molecular dynamics for which conformation changes or protein folding may serve as examples. They can be described in the following abstract way: The molecular system under consideration has the ability to go from a reactant state given by a set A in its state space (e.g., an initial conformation) to a product state described by another set B (e.g., the target conformation). Dynamical transitions from A to B are rare. The general situation we will address is as follows:
The system is (meta)stable, with the sets A and B being two of its metastable sets in the sense that if the system is put there, it will remain there for a long time; transitions between A and B are rare events.
The sets A and B are separated by an unknown and, in general, rough or diffusive energy landscape (that will be denoted by V).
know which parts of state space such reactive trajectories visit most likely, i.e., where in state space do we find transition pathways or transition channels through which most of the probability current generated by reactive trajectories flows and
characterize the rare event statistically, i.e., compute the transition rate, the free energy barrier, the mean first passage time or even more elaborated statistical quantities.
The molecular dynamics literature on rare event simulations is rich. Since the 1930s, transition state theory (TST) [1,2] and extensions thereof based on the reactive flux formalism have provided the main theoretical framework for the description of transition events. TST can, however, at best deliver rates and does not allow one to characterize transition channels. It is based on partitioning the state space into two sets with a dividing surface in between, leaving set A on one side and the target set B on the other, and the theory only tells how this surface is crossed during the reaction. Often, it is difficult to choose a suitable dividing surface, and a bad choice will lead to a very poor estimate of the rate. The TST estimate is then extremely difficult to correct, especially if the rare event is of the diffusive type, where many different reaction channels co-exist. Therefore, many techniques have been proposed that try to go beyond TST.
These different strategies approach the problem by sampling the ensemble of reactive trajectories or by directly searching for the transition channels of the system. Most notable among these techniques are (1) Transition Path Sampling (TPS) [3]; (2) the so-called String Methods [4], or optimal path approaches [5–7] and variants thereof; (3) techniques that follow the progress of the transition through interfaces, like Forward-Flux Simulation (FFS) [8], Transition Interface Sampling (TIS) [9] or the Milestoning techniques [10,11]; and (4) methods that drive the molecular system by external forces with the aim of making the required transition more frequent while still allowing one to compute the exact rare event statistics for the unforced system, e.g., based on Jarzynski’s and Crook’s identity [12,13]. All of these methods consider the problem in continuous state space, i.e., through reactive trajectories or transition channels in the original state space of the molecular system. They all face substantial problems, e.g., if the ensemble of reactive trajectories and/or transition channels of the system under consideration are too complicated (multi-modal, irregular, essentially high dimensional) or they suffer from too large variance of the underlying statistical estimators. We should moreover stress that each of these methods has its specific scope of application; some methods are mainly useful for computing transition rates, whereas others can be used to compute transition pathways or free energy differences.
Our aim is (A) to review some of these methods based on a joint theoretical basis and (B) to outline a new approach to the estimation of rare event statistics based on a combination of ideas from optimal control and statistical mechanics. In principle, this approach allows for a variance-free estimation of rare event statistics in combination with much reduced simulation time. The rest of the article is organized as follows: We start with a precise characterization of reactive trajectories, transition channels and related quantities in the framework of Transition Path Theory (TPT) in Section 2. Then, in Sections 3 and 4, we discuss the methods from classes (1)–(3) and characterize their potential problems in more detail. In Section 5, we consider methods of type (4) as an introduction to the presentation of the new optimal control approach that is outlined in detail in Sections 6 and 7, including some numerical experiments.
Alternative, inherently discrete methods, like Markov State Modeling, that discretize the state space appropriately and try to compute transition channels and rates a posteriori based on the resulting discrete model of the dynamics will not be discussed herein and are considered in the article [14] in a way related to the presentation at hand. We should further mention that not all rare event problems in molecular dynamics are related to sampling the underlying Gibbs–Boltzmann statistics, e.g., nucleation events under shear [15] or genuine nonequilibrium systems without a stationary probability distribution [16].
2. Reactive Trajectories, Transition Rates and Transition Channels
Since our results are rather general, it is useful to set the stage somewhat abstractly. To this end, we borrow some notation from [17] and consider a system whose state space is ℝn and denote by Xt the current state of the system at time t. For example, Xt may be the set of instantaneous positions and momenta of the atoms of a molecular system. We assume that the system is ergodic with respect to a probability (equilibrium) distribution μ and that we can generate an infinitely long equilibrium trajectory {Xt}t∈ℝ where, for technical reasons, we let the trajectory start at time t = −∞. The trajectory will go infinitely many times from A to B and each time the reaction happens. This reaction involves reactive trajectories that can be defined as follows: Given the trajectory {X(t)}t∈ℝ, we say that its reactive pieces are the segments during which Xt is neither in A or B, came out of A last and will go to B next. To formalize things, let
Given the ensemble of reactive trajectories, we want to characterize it statistically by answering the following questions:
- (Q1)
What is the probability of observing a trajectory at x ∉ (A ∪ B) at time t, conditional on t ∈ R?
- (Q2)
What is the probability current of reactive trajectories? This probability current is the vector field jAB(x) with the property that given any separating surface S between A and B (i.e., the boundary of a region that contains A but not B), the surface integral of jAB over S gives the probability flux of reactive trajectories between A and B across S.
- (Q3)
What is the transition rate of the reaction, i.e., what is the mean frequency kAB of transitions from A to B?
- (Q4)
Where are the main transition channels used by most of the reactive trajectories?
Question (Q1) can be answered easily, at least theoretically: The probability density to observe any trajectory (reactive or not) at point x is μ(x). Let q(x) be the so-called committor function, that is the probability that the trajectory starting from x reaches first B rather than A. If the dynamics are reversible, then the probability that a trajectory we observe at state x is reactive is q(x)(1 − q(x)), where the first factor appears since the trajectory must go to B rather than A next, and the second factor appears since it needs to come from A rather than B last. Now, the Markov property of the dynamics implies that the probability density to observe a reactive trajectory at point x is
2.1. Transition Path Theory (TPT)
In order to give answers to the other questions, we will exploit the framework of transition path theory (TPT), which has been developed in [17–20] in the context of diffusions and has been generalized to discrete state spaces in [21,22]. In order to review the key results of TPT, let us consider diffusive molecular dynamics in an energy landscape V : ℝn → ℝ:
For these kind of dynamics, Questions (Q2) and (Q3) have surprisingly simple answers: The reactive probability current is given by
Figure 1 illustrates these quantities for the case of a 2D three well potential with two main wells (the bottoms of which we take as A and B in the following) and a less significant third well. The three main saddle points separating the wells are such that the two saddle points between the main wells and the third well are lower in energy than the saddle point between the main wells, such that in the zero temperature limit, we expect that almost all reactive trajectories take the route through the third well across the two lower saddle points. We observe that the committor functions for low and higher temperatures exhibit smooth isocommittor lines separating the sets A and B, as expected. The transition channels computed from the associated reactive current also show what one should expect: For a lower temperature, the channel through the third well and across the two lower saddle points is dominant, while for a higher temperature, the direct transition from A to B across the higher saddle point is preferred.
These considerations can be generalized to a wide range of different kinds of dynamics in continuous state spaces, including, e.g., full Langevin dynamics, see [17–20].
This example illustrates that TPT in principle allows us to quantify all aspects of the transition behavior underlying a rare event. We can compute transition rates exactly and even characterize the transition mechanisms if we can compute the committor function. Deeper insight using the Feynman–Kac formula yields that the committor function can be computed as the solution of a linear boundary value problem, which for diffusive molecular dynamics reads
2.2. Transition Path Sampling (TPS)
TPS has been developed in order to sample from the probability distribution of reactive trajectories in so-called “path space”, which means nothing else than the space of all discrete or continuous paths starting in A and ending up in B equipped with the probability distribution generated by the dynamics through the ensemble of associated reactive trajectories. Let PT denote the path measure on the space of discrete or continuous trajectories {Xt}0≤t≤T of length T. The path measure of reactive trajectories then is
TPS is a Metropolis Monte-Carlo (MC) method for sampling ({Xt}0≤t≤T)) that uses explicit information regarding the path measure PT, such as Equation (5), with MC moves that are based on a perturbation of a precomputed reactive trajectory [3,24]. It delivers an ensemble of reactive trajectories of length T that (under the assumption of convergence of the MC scheme) is representative for and thus allows one to compute respective expectation values, like the probability to observe a reactive trajectory or the reactive current. However, its potential drawbacks are obvious: (1) A typical reactive trajectory is very long and rather uninformative (cf. Figure 1), i.e., the computational effort of generating an entire ensemble of long reactive trajectories can be prohibitive; (2) convergence of the MC scheme in the infinite dimensional path space can be very poor; and (3) the limitation to a pre-defined trajectory length T can lead to biased statistics of the TPS ensemble. Advanced TPS schemes try to remedy these drawbacks by combining the original TPS idea with interface methods [9]. Even though TPS can be used no matter whether the underlying dynamics is deterministic or stochastic, the algorithm is usually used in connection with deterministic Hamiltonian dynamics [3].
3. Finding Transition Channels
Whenever a transition channel exists, one can try to approximate the center curve of the transition channel instead of sampling the ensemble of reactive trajectories. If the center curve (also: principal curve) is a rather smooth object, then such a method would not suffer from the extensive length of reactive trajectories. Several such methods have been introduced; they differ with respect to the definition of the transition channel and the corresponding center or principal curve.
3.1. Action-Based Methods
Rather than sampling the probability distribution of reactive pathways, such as Equation (4), one can try to obtain a representative or dominant pathway, e.g., by computing the pathway that has maximum probability under PT. For the case of diffusive molecular dynamics, the path measure PT has a probability density relative to a (fictitious) uniform measure on the space of all continuous paths in ℝn of length T that are generated by Brownian motion; the relative density reads
The fact that the Euler discretization of the path density ℓ, with I∊ interpreted in the sense of Itô integrals, corresponds to the probability density of the Euler-discretized reaction path with respect to Lebesgue measure has led to the idea that by minimizing the Onsager–Machlup action over all continuous paths φ:[0, T ] → ℝn going from A to B, one can find the dominant reactive path φ* = argminφ I∊ (φ) in the sense of a maximum likelihood estimator. The hope is that this path, often also called the optimal path or most probable path, on the one hand, contains information on the transition mechanism and, on the other hand, is much smoother and easier to interpret than a typical reactive trajectory. Note, however, that the actual probability that the solution of Equation (2) remains in a small neighborhood of a given path φ(·) is exponentially small in the size of the neighborhood.
In [7], a comparison between the Onsager–Machlup action and its zero temperature limit has been given using gradient descent methods, raising issues regarding the correct interpretation of the minimizers of I∊ (that need not exist) as most probable paths. In [5], the dominant reaction pathway method has been outlined, which uses a simplified version of the Onsager–Machlup functional that leads to a computationally simpler optimization problem and is applicable to large-scale problems, e.g., protein folding [6]. However, even if the globally dominant pathways can be computed, such that the optimization does not get stuck in local minima, and even if we ignore the issues regarding the correct interpretation of minimizers, the resulting pathways in general do not allow one to gain statistical information on the transition (like rates, currents, mean first passage times).
Another action-based method that has been introduced in [26] is the MaxFlux method, which seeks the path that carries the highest reactive flux among all reactive trajectories of a certain length. The idea is to compute the path of least resistance by minimizing the functional
3.2. String Method and Variants
There are several other methods that entirely avoid the computation of reactive trajectories, but try to reconstruct the less complex transition channels or pathways instead, analyzing the energy landscape of the system. One group of such techniques, like the Zero Temperature String method [4], the Geometric Minimum Action method [30] or the Nudged Elastic Band method [31], concentrate on the computation of the minimal energy path (MEP), i.e., the path of lowest potential energy between (a point in) A and (a point in) B. Under diffusive molecular dynamics and for vanishing temperature, the MEP is the path that transitions take with probability one [32]. It turns out that the MEP in this case is the minimizer of the Onsager–Machlup action (5) in the limit ∊ → 0. For non-zero temperature and a rugged energy landscape, the MEP will in general be not very informative and must be replaced by a finite-temperature transition channel. This is done by the finite-temperature string (FTS) method [33] based on the following considerations: Firstly, the isocommittor surfaces Γα, α ∈ [0, 1], of the committor q are taken as natural interfaces that separate A from B. Secondly, each Γα is weighted with the stationary distribution μ to find reactive trajectories crossing it at a certain point x ∈ Γα,
The FTS method allows one to compute single transition channels in rugged energy landscapes as long as these are not too extended and rugged. Compared to methods that sample the ensemble of reactive trajectories, it has the significant advantage that the string, that is, the principal curve inside the transition channel, is rather smooth and short, as compared to the typical reactive trajectories. The FTS further allows one to compute the free energy profile F = F (α) along the string,
4. Computing Transition Rates
The computation of transition rates can be performed without computing the dominant transition channels or similar objects. There is a list of rather general techniques, with Forward Flux Sampling (FFS) [8], Transition Interface Sampling (TIS) [9] and Milestoning [10] as examples, that approximate transition rates by exploring how the transition progresses from one to the next interface that separates A from B.
4.1. Forward Flux Sampling (FFS)
The first step of FFS is the choice of a finite sequence of interfaces Ik, k = 1, . . .,N, in state space between A and B = IN. The transition rate kAB comes as the product of two factors: (1) the probability current JA of all trajectories leaving A and hitting I1; and (2) the probability
FFS has been demonstrated to be quite general in approximating the flux of reactive trajectories through a given set of interfaces; it can be applied to equilibrium, as well as nonequilibrium systems, and its implementation is easy (see [16,38]). The interfaces used in FFS are, in principle, arbitrary. However, the efficiency of the sampling of the reactive hitting probabilities ℙ(Ik+1|Ik) crucially depends on the choice of the interfaces. In practice, the efficiency of FFS will drop dramatically if one does not use appropriate surfaces, and totally misleading rates may result from this. Ideally, one would like to choose these surfaces, so that the computational gain offered by FFS in optimized, but in practice, this is not a trivial task; see [39]. The same is true for TIS that couples TPS with progressing from interface to interface.
4.2. Milestoning
Milestoning [10] is similar to FFS in so far as it also uses a set of interfaces Ik, k = 1, . . .,N that separate A and B = IN. In contrast to FFS and TIS, the fundamental quantities in Milestoning are the hitting time distributions (τ), i = 1, . . .,N − 1, where (τ) is the probability that a trajectory starting at t = 0 at interface Ii hits Ii±1 before time τ. Trajectories that make it to milestone Ii must come from milestones Ii±1 and vice versa. In the original algorithm, these distributions are approximated as follows [10]: For each milestone Ii, one first samples the distribution μ constrained to Ii. Based on the resulting sample, we start a trajectory from each point, which is terminated when it reaches one of its two neighboring milestones Ii±1. The hitting times are recorded and collected into two distributions (τ).
These local kinetics are then compiled into the global kinetics of the process: For each i, one defines Pi(t) as the probability that the process is found between Ii−1 and Ii+1 at time t and that the last milestone hit was Ii. Milestoning is based on a (non-Markovian) construction of Pi(t) from the (τ). Its efficiency comes from two sources: (1) It does not require the computation of long reactive trajectories but only short ones between milestones (which therefore should be ‘close enough’); (2) It is easily parallelizable. Its disadvantage is the dependence on the milestones that have to be chosen in advance: It can be shown that Milestoning with perfect sampling allows one to compute exact transition rates or mean first passage times if the interfaces are given by the isocommittor surfaces (which in general are not known in advance) [40]; if the interfaces are chosen inappropriately, the results can be rather misleading.
5. Nonequilibrium Forcing and Jarzynski’s Identity
The computation of reliable rare event statistics suffers from the enormous lengths of reactive trajectories. One obvious way to overcome this obstacle is to force the system to exhibit the transition of interest on shorter timescales. Therefore, can we drive the molecular system to make the required transition more frequently but still compute the exact rare event statistics for the unforced system?
As was shown by Jarzynski and others, nonequilibrium forcing can in fact be used to obtain equilibrium rare event statistics. The advantage seems to be that the external force can speed up the sampling of the rare events by biasing the equilibrium distribution towards a distribution under which the rare event is no longer rare. We will shortly review Jarzynski’s identity before discussing the matter in more detail.
5.1. Jarzynski’s Identity
Jarzynski’s and Crook’s formulae [12,13] relate the equilibrium Helmholtz free energy to the nonequilibrium work exerted under external forcing: Given a system with energy landscape V (x), the total Helmholtz free energy can be defined as
Algorithmic application prohibitive. Despite the fact that Jarzynski’s and Crook’s formulae are used in molecular dynamics applications [43], their algorithmic usability is limited by the fact that the likelihood ratio between equilibrium and nonequilibrium trajectories is highly degenerate, and the overwhelming majority of nonequilibrium forcings generate trajectories that have almost zero weight with respect to the equilibrium distribution that is relevant for the rare event. This leads to the fact that most rare event sampling algorithms based on Jarzynski’s identity have prohibitively large variance. Recent developments have reduced this problem by sampling just the reversible work processes based on Crook’s formula, but could not fully remove the problem of large variance [44]; see also [45]. Because of this, we will approach the problem of variance reduction subsequently.
5.2. Cumulant Generating Functions
In order to demonstrate how to improve approaches based on the idea of driving molecular systems to make rare events frequent, we first have to introduce some concepts and notation from statistical mechanics: Let W be a random variable that depends on the sample paths of (Xt)t≥0, i.e., on molecular dynamics trajectories of the system under investigation. Further, let P be the underlying probability measure on the space of continuous trajectories as introduced in Section 2.2 (but without the restriction to a given length T). We define the cumulant generating function (CGF) of W by
Optimal reweighting.
The CGF admits a variational characterization in terms of relative entropies. To this end, let Q be another probability measure, so that P is absolutely continuous with respect to Q, i.e., the likelihood ratio dP/dQ exists and is Q-integrable. Then, using Jensen’s inequality again,
Let W be bounded from above, with E[exp(−σW)] < ∞. Then
6. Optimal Driving from Control Theory
When Xt denotes stochastic dynamics, such as Equation (2), the above variational formula admits a nice interpretation in terms of an optimal control problem with a quadratic cost. To reveal it, we first need some technical assumptions.
- (A1)
We define Q = [0, T) × O where T ∈ [0, ∞] and O ⊂ ℝn is a bounded open set with smooth boundary ∂O. Further, let τ < ∞ be the stopping time
i.e., τ is the stopping time that either t = T or Xt leaves the set O, whichever comes first.- (A2)
The random variable W is of the form
for some continuous and nonnegative functions f, g : ℝn → ℝ, which are bounded from above and at most polynomially growing in x (compare Jarzynski’s formula).- (A3)
The potential V : ℝn → ℝ in Equation (2) is smooth, bounded below and satisfies the usual local Lipschitz and growth conditions.
Log transformation of the cumulant generating function. In order to arrive at the optimal control version of the variational formula (9), we introduce the logarithmic transformation of ψσ as
Optimal control problem. Equation (12) is a Hamilton–Jacobi–Bellman (HJB) equation and is recognized as the dynamic programming equation of the following optimal control problem: minimize
Form of optimal control. In more detail, one can show (e.g., see ([47] (Section IV.2))) that assumptions (A1)–(A3) above imply that Equation (12) has a classical solution (i.e., twice differentiable in x, differentiable in t and continuous at the boundaries). Moreover, vσ satisfies
The function vσ is called the value function or optimal-cost-to-go for the optimal control problems (13) and (14). Specifically, vσ(x, t) measures the minimum cost needed to drive the system to the terminal state when started at x at time t. We briefly mention the two most relevant special cases of (13) and (14).
6.1. Case I: The Exit Problem
We want to consider the limit T → ∞. To this end, call τO = inf{t > 0: Xt ∉ O} the first exit time of the set O ⊂ ℝn. The stopping time τ = min{T, τO} then converges to τO, i.e.,
6.2. Case II: Finite Time Horizon Optimal Control
If we keep T < ∞ fixed while letting O grow, such that diam(O) → ∞, where diam(O) = sup{r > 0: r(x) ⊂ O, x ∈ O} is understood as the maximum radius r > 0 that an open ball r(·) contained in O can have, it follows that
6.3. Optimal Control Potential and Optimally Controlled Dynamics
The optimal control u* that minimizes the functional in Equation (13) is again of gradient form and given by
Remarks. Some remarks are in order.
- (a)
Monte-Carlo estimators of the conditional CGF
that are based on the optimally controlled dynamics have zero variance. This is so because the optimal control minimizes the variational expression in Equation (9), but at the minimum, the random variable inside the expectation must be almost surely constant (as a consequence of Jensen’s inequality and the strict convexity of the exponential function). Hence, we have a zero-variance estimator of the conditional CGF.- (b)
The reader may now wonder as to whether it is possible to extract single moments from the CGF (e.g., mean first passage times). In general, this question is not straightforward to answer. One of the difficulties is that extracting moments from the CGF requires one to take derivatives at σ = 0, but small values of σ imply strong penalization, which renders the control inactive and, thus, makes the approach inefficient. Another difficulty is that reweighting the controlled trajectories back to the original (equilibrium) path measure can increase the variance of a rare event estimator, as compared to the corresponding estimator based on the uncontrolled dynamics. As yet, the efficient calculation of moments from the CGF by either extrapolation methods or reweighing is an open question and currently a field of active research (see, e.g., [48,49]).
- (c)
Jarzynski’s identity relates equilibrium free energies to averages that are taken over an ensemble of trajectories generated by controlled dynamics, and the reader may wonder whether the above zero-variance property can be used in connection with free energy computations à la Jarzynski (cf.[45]). Indeed, we can interpret the CGF as the free energy of the nonequilibrium work
where f is the nonequilibrium force exerted on the system under driving it with some prescribed protocol ξ : [0, T ] → ℝ; in this case, the dynamics Xt depend on ξt, as well, and writing down the HJB equation according to Equation (19) is straightforward. However, even if we can solve Equation (19), we do not get zero-variance estimators for the free energyThe reason for this is simple: Jarzynski’s formula requires that the initial conditions are chosen from an equilibrium distribution, say, π0 the equilibrium distribution corresponding to the initial value ξ0 of the protocol, but optimal controls are defined point-wise for each state (t, Xt) andIn other words:- (d)
A similar argument as the one underlying the derivation of the HJB equation from the linear boundary value problem yields that Jarzynski’s formula can be interpreted as a two-player zero-sum differential game (cf.[50]).
7. Characterize Rare Events by Optimally Controlled MD
Now, we illustrate how to use the results of the last section in practice. We will mainly consider the case discussed in Section 6.1 regarding the statistical characterization of hitting a certain set.
7.1. First Passage Times
Roughly speaking, the CGF encodes information about the moments of any random variable W that is a functional of the trajectories (Xt)t≥0. For example, for f = ∊ and T → ∞, we obtain the CGF of the first exit time from O, i.e.,
7.2. Committor Probabilities Revisited
It is not only possible to use the moment generating function to collect statistics about rare events in terms of the cumulant generating function, but also to express the committor function directly in terms of an optimal control problem (see Section 2.1 for the definition of the committor qAB between to sets A and B). To this end, let σ = 1, and suppose we divide ∂O into two sets B ⊂ ∂O and A = ∂O \ B (i.e., τO is the stopping time that is defined by hitting either A or B). Setting
Setting v(x) = − ∊log qAB(x) yields the equality
Remarks. Some remarks on the committor equation follow:
- (a)
The logarithmic singularity of the value function at “reactant state” A has the effect that the control will try to avoid running back into A, for there is an infinite penalty on hitting A. In other words, by controlling the system, we condition it on hitting the “product state” B at time t = τO. Conditioning a diffusion (or general Markov) process on an exit state has a strong connection with Doob’s h-transform, which can be considered a change-of-measure transformation of the underlying path measure that forces the diffusion to hit the exit state with probability one [51].
- (b)
The optimally controlled dynamics has a stationary distribution with a density proportional to
where we used β = 1/∊.
7.3. Algorithmic Realization
For the exit problem (“Case I”, above), one can find an efficient algorithm for computing the conditional CGF γ(σ;x) or, equivalently, the value function vσ(x) in [52]. The idea of the algorithm is to exploit that, according to Equations (20) and (21), the optimal control is of gradient form. The latter implies that the value function can be represented as a minimization of the cost functional over time-homogeneous candidate functions C for the optimal bias potential, in other words,
The algorithm that finds the optimal C works by iteratively minimizing the cost functional for potentials C from a finite-dimensional ansatz space, i.e.,
Remarks. Let us briefly comment on some aspects of the gradient descent algorithm.
- (a)
The minimization algorithm for the value function belongs to the class of expectation-maximization algorithms (although, here, we carry out a minimization rather than a maximization), in that each minimization step is followed by a function evaluation that involves computing an expectation. In connection with rare events sampling and molecular dynamics problems, a close relative is the adaptive biasing force (ABF) method for computing free energy profiles, the latter being intimately linked with cumulant generating functions or value functions (cf. Section 5). In ABF methods (or its variants, such as metadynamics or Wang–Landau dynamics), the gradient of the free energy is estimated on the fly, running a molecular dynamics simulation, and then added as a biasing force to accelerate the sampling in the direction of the relevant coordinates [53,54]. The biasing force eventually converges to the derivative of the free energy, which is the optimal bias for passing over the relevant energy barriers that are responsible for the rare events [55].
- (b)
The number of basis functions needed depends mainly on the roughness of the value function, but is independent of the system dimension. For systems with clear time scale separation, it has been moreover shown [56] that the optimal control is independent of the fast variables; hence, we expect that the algorithm can be efficient, even for large-scale systems, provided that some information about the relevant collective variables and a reasonable initial guess are available. Yet, the question remains: How many basis functions are needed to approximate the optimal control up to a given accuracy? Controlling the error in the value function and the resulting optimal control is particularly important, as a wrong (e.g., suboptimal) bias potential may lead to Monte-Carlo estimators that may have a larger variance than the vanilla rare event estimator, as has been pointed out in [57,58]. The first results in this direction have been obtained in [59], in which error bounds for the CGF for suboptimal controls have been derived, and [60], which discusses the approximation error of the Galerkin approximation of the corresponding HJB equations; see also [61]for a related discussion regarding so-called log-efficient estimators for rare events.
7.4. Numerical Examples
In our first example, we consider diffusive molecular dynamics as in Equation (2) with ∊ = 0.1 and V being the five-well potential shown in Figure 2. We first compute the CGF of the first passage time as discussed in Section 7.1, using the gradient descent algorithm described in Section 7.3 with 10 Gaussian ansatz functions that are centered around the critical points of the potential energy function. The resulting optimal control potential (21) after roughly 20 iterations of the gradient descent is displayed in Figure 2 for different values of σ. As the set O, we take the whole state space, except a small neighborhood of its global minimum of V, so that its complement Oc is identical to the vicinity of the global minimum and the exit time τO is the first passage time to Oc. Figure 2 shows that the optimal control potential alters the original potential V significantly in the sense that for σ > 0, the set Oc is the bottom of the only well of the potential, so that all trajectories starting somewhere else will quickly enter Oc.
This case is instructive: For the unperturbed original dynamics, the mean first passage time Ex(τO) takes values of around 104 for x > −2. For the optimally controlled dynamics, the mean first passage times into Oc are less than five for σ = 0.1, 0.5, 1.0, so that the estimation of Ex(τO) resulting from the optimal control approach requires trajectories that are a factor of at least 103 shorter than the ones we would have to use by direct numerical simulation of the unperturbed dynamics.
Figure 3 shows the optimal control potentials for computation of the committor qAB, as described in Section 7.2. We observe that the optimal control potential exhibits a singularity at the boundary of the basin of attraction of the set A. That is, it prevents the optimally controlled dynamics from entering the basin of attraction of A and, thus, avoids the waste of computational effort by unproductive returns to A.
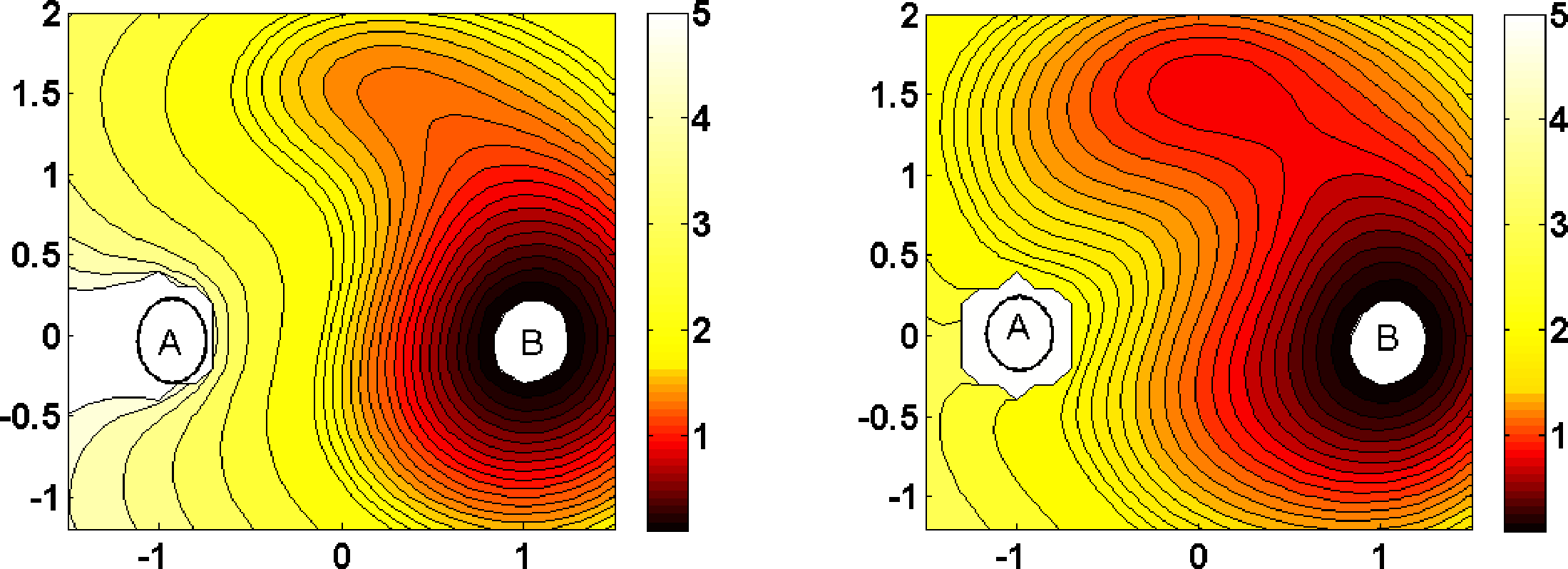
In our second example, we consider two-dimensional diffusive molecular dynamics as in Equation (2) with the energy landscape V being the three-well potential shown in Figure 1. In Figure 4, the optimal control potential for computing the committors qAB between the two main wells for two different temperatures ∊ = 0.15 and ∊ = 0.6 are displayed. The numerical solution is based on a Galerkin approximation of the log-transformed HJB equation, using precomputed committor functions as the basis set; see [60] for details.
As in our former experiment, we observe that the optimal control potential prevents the dynamics from returning to A; in addition, it flattens the third well significantly, such that the optimally controlled dynamics in any case quickly goes into B. For ∊ = 0.15, a TPS sampling of reactive trajectories between the two main wells, precisely from A to B with A and B, as indicated in Figure 4, results in an average length of 367 for reactive trajectories based on the original dynamics. For the optimally controlled dynamics, we found an average length of 1.3.
8. Conclusions
We have surveyed various techniques for the characterization and computation of rare events occurring in molecular dynamics. Roughly, the approaches fall into two categories: (a) methods that approach the problem by characterizing the ensemble of reactive trajectories between metastable states or (b) path-based methods that target dominant transition channels or pathways by minimization of suitable action functionals. Methods of the first type, e.g., Transition Path Theory, Transition Path Sampling, Milestoning or variants thereof, are predominantly Monte-Carlo-type methods for generating one very long or many short trajectories, from which the rare event statistics can then be estimated. Methods that belong to the second category, e.g., MaxFlux, Nudged-Elastic Band or the String Method, are basically optimization methods (sometimes combined with a Monte-Carlo scheme); here, the objectives are few (single or multiple) smooth pathways that describe, e.g., a transition event. It is clear that this classification is not completely unambiguous, in that action-based methods for computing most probable pathways can be also used to sample an ensemble of reactive trajectories. Another possible classification (with its own drawbacks) is along the lines of the biased-unbiased dichotomy that distinguishes between methods that characterize rare events based on the original dynamics and methods that bias the underlying equilibrium distribution towards a new probability distribution under which the rare events are no longer rare. Typical representatives of the second class range from biasing force methods, such as ABF or metadynamics, up to genuine nonequilibrium approaches based on Jarzynski’s identity for computing free energy profiles. The problem often is that rare event estimators based on an ensemble of nonequilibrium trajectories suffer from large variances, unless the bias is cleverly chosen.
We have described a strategy to find such a cleverly chosen perturbation, based on ideas from optimal control. The idea rests on the fact that the cumulant generating function of a certain observable, e.g., the first exit time from a metastable set, can be expressed as the solution to an optimal control problem, which yields a zero variance estimator for the cumulant generating function. The control acting on the system has essentially two effects: (1) Under the controlled dynamics, the rare events are no longer rare, as a consequence of which the simulations become much shorter; (2) The variance of the statistical estimators is small (or even zero if the optimal control is known exactly). We should stress that, depending on the type of observable, the approach only appears to be a nonequilibrium method, for the optimal control is an exact gradient of a biasing potential; hence, the optimally perturbed system satisfies a detailed balance, which is one criterion for thermodynamic equilibrium. Future research should address the question as to whether the approach is competitive for realistic molecular systems, how to efficiently and robustly extract information about specific moments rather than cumulant generating functions and how to extend it to the more general observables or the calculation of free energy profiles.
Acknowledgments
The authors are grateful to Eric Vanden-Eijnden, Giovanni Ciccotti, Frank Pinski and Christoph Dellago for valuable discussions and comments. Ralf Banisch and Tomasz Badowski hold scholarships from the Berlin Mathematical School (BMS). This work was supported by the DFG Research Center “Mathematics for key technologies” (MATHEON) in Berlin.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eyring, H. The activated complex in chemical reactions. J. Chem. Phys 1935, 3, 107–115. [Google Scholar]
- Wigner, E. Calculation of the rate of elementary association reactions. J. Chem. Phys 1937, 5, 720–725. [Google Scholar]
- Bolhuis, P.G.; Chandler, D.; Dellago, C.; Geissler, P. Transition path sampling: Throwing ropes over rough mountain passes, in the dark. Annu. Rev. Phys. Chem 2002, 59, 291–318. [Google Scholar]
- E, W.; Ren, W.; Vanden-Eijnden, E. String method for the study of rare events. Phys. Rev. B 2002, 66, 052301. [Google Scholar]
- Beccara, S.; Skrbic, T.; Covino, R.; Faccioli, P. Dominant folding pathways of a WW domain. Proc. Natl. Acad. Sci. USA 2012, 109, 2330–2335. [Google Scholar]
- Faccioli, P.; Lonardi, A.; Orland, H. Dominant reaction pathways in protein folding: A direct validation against molecular dynamics simulations. J. Chem. Phys 2010, 133, 045104. [Google Scholar]
- Pinski, F.; Stuart, A. Transition paths in molecules: Gradient descent in path space. J. Chem. Phys 2010, 132, 184104. [Google Scholar]
- Allen, R.; Warren, P.; ten Wolde, P.R. Sampling rare switching events in biochemical networks. Phys. Rev. Lett 2005, 94, 018104. [Google Scholar]
- Moroni, D.; van Erp, T.; Bolhuis, P. Investigating rare events by transition interface sampling. Physica A 2004, 340, 395–401. [Google Scholar]
- Faradjian, A.K.; Elber, R. Computing time scales from reaction coordinates by milestoning. J. Chem. Phys 2004, 120, 10880–10889. [Google Scholar]
- Olender, R.; Elber, R. Calculation of classical trajectories with a very large time step: Formalism and numerical examples. J. Chem. Phys 1996, 105, 9299–9315. [Google Scholar]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett 1997, 78, 2690–2693. [Google Scholar]
- Crooks, G. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721–2726. [Google Scholar]
- Sarich, M.; Bansich, R.; Hartmann, C.; Schütte, C. Markov state models for rare events in molecular dynamics. Entropy 2014, 16, 258–286. [Google Scholar]
- Allen, R.J.; Valeriani, C.; Tanase-Nicola, S.; ten Wolde, P.R.; Frenkel, D. Homogeneous nucleation under shear in a two-dimensional Ising model: Cluster growth, coalescence, and breakup. J. Chem. Phys 2008, 129, 134704. [Google Scholar]
- Berryman, J.T.; Schilling, T. Sampling rare events in nonequilibrium and nonstationary systems. J. Chem. Phys 2010, 133, 244101. [Google Scholar]
- E, W.; Vanden-Eijnden, E. Towards a theory of transition paths. J. Stat. Phys 2006, 123, 503–523. [Google Scholar]
- E, W.; Vanden-Eijnden, E. Metastability, Conformation Dynamics, and Transition Pathways in Complex Systems. In Multiscale Modeling and Simulation; Springer: Berlin, Germany, 2004; pp. 35–68. [Google Scholar]
- Metzner, P.; Schütte, C.; Vanden-Eijnden, E. Illustration of transition path theory on a collection of simple examples. J. Chem. Phys 2006, 125, 084110. [Google Scholar]
- E, W.; Vanden-Eijnden, E. Transition-path theory and path-finding algorithms for the study of rare events. Annu. Rev. Phys. Chem 2010, 61, 391–420. [Google Scholar]
- Metzner, P.; Schütte, C.; Vanden-Eijnden, E. Transition path theory for Markov jump processes. Multiscale Model. Sim 2009, 7, 1192–1219. [Google Scholar]
- Metzner, P. Transition Path Theory for Markov Processes: Application to Molecular Dynamics. Ph.D. Thesis, Freie Universit¨at Berlin, Berlin, Germany. 2007. [Google Scholar]
- Noé, F.; Schütte, C.; Vanden-Eijnden, E.; Reich, L.; Weikl, T. Constructing the full ensemble of folding pathways from short off-equilibrium trajectories. Proc. Natl. Acad. Sci. USA 2009, 106, 19011–19016. [Google Scholar]
- Chandler, D. Finding Transition Pathways: Throwing Ropes over Rough Montain Passes, in the Dark; World Scientific: Singapore, Singapore, 1998. [Google Scholar]
- Dürr, D.; Bach, A. The Onsager-Machlup function as Lagrangian for the most probable path of a diffusion process. Commun. Math. Phys 1978, 60, 153–170. [Google Scholar]
- Berkowitz, M.; Morgan, J.D.; McCammon, J.A.; Northrup, S.H. Diffusion-controlled reactions: A variational formula for the optimum reaction coordinate. J. Chem. Phys 1983, 79, 5563–5565. [Google Scholar]
- Huo, S.; Straub, J.E. The MaxFlux algorithm for calculating variationally optimized reaction paths for conformational transitions in many body systems at finite temperature. J. Chem. Phys 1997, 107, 5000–5006. [Google Scholar]
- Zhao, R.; Shen, J.; Skeel, R.D. Maximum flux transition paths of conformational change. J. Chem. Theory Comput 2010, 6, 2411–2423. [Google Scholar]
- Cameron, M. Estimation of reactive fluxes in gradient stochastic systems using an analogy with electric circuits. J. Comput. Phys 2013, 247, 137–152. [Google Scholar]
- Vanden-Eijnden, E.; Heymann, M. The geometric minimum action method for computing minimum energy paths. J. Chem. Phys 2008, 128, 061103. [Google Scholar]
- Jonsson, H.; Mills, G.; Jacobsen, K. Nudged Elastic Band Method for Finding Minimum Energy Paths of Transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne, B.J., Ciccotti, G., Coker, D.F., Eds.; World Scientific: Singapore, Singapore, 1998. [Google Scholar]
- Freidlin, M.; Wentzell, A.D. Random Perturbations of Dynamical Systems; Springer: New York, NY, USA, 1998. [Google Scholar]
- E, W.; Ren, W.; Vanden-Eijnden, E. Finite temperature string method for the study of rare events. J. Phys. Chem. B 2005, 109, 6688–6693. [Google Scholar]
- Ren, W.; Vanden-Eijnden, E.; Maragakis, P; E, W. Transition pathways in complex systems: Application of the finite-temperature string method to the alanine dipeptide. J. Phys. Chem 2005, 123, 134109. [Google Scholar]
- Vanden-Eijnden, E.; Venturoli, M. Revisiting the finite temperature string method for the calculation of reaction tubes and free energies. J. Phys. Chem 2009, 130, 194103. [Google Scholar]
- Allen, R.; Frenkel, D.; ten Wolde, P.R. Simulating rare events in equilibrium or nonequilibrium stochastic systems. J. Chem. Phys 2006, 124, 024102. [Google Scholar]
- Allen, R.; Frenkel, D.; ten Wolde, P.R. Forward flux sampling-type schemes for simulating rare events: Efficiency analysis. J. Chem. Phys 2006, 124, 194111. [Google Scholar]
- Becker, N.B.; Allen, R.J.; ten Wolde, P.R. Non-stationary forward flux sampling. J. Chem. Phys 2012, 136, 174118. [Google Scholar]
- Kratzer, K.; Arnold, A.; Allen, R.J. Automatic, optimized interface placement in forward flux sampling simulations. J. Chem. Phys 2013, 138, 164112. [Google Scholar]
- Vanden-Eijnden, E.; Venturoli, M.; Ciccotti, G.; Elber, R. On the assumptions underlying milestoning. J. Chem. Phys 2008, 129, 174102. [Google Scholar]
- Latorre, J.; Hartmann, C.; Schütte, C. Free energy computation by controlled Langevin processes. Procedia Comput. Sci 2010, 1, 1591–1600. [Google Scholar]
- Lelièvre, T.; Stoltz, G.; Rousset, M. Free Energy Computations: A Mathematical Perspective; Imperial College Press: London, UK, 2010. [Google Scholar]
- Isralewitz, B.; Gao, M.; Schulten, K. Steered molecular dynamics and mechanical functions of proteins. Curr. Opin. Struct. Biol 2001, 11, 224–230. [Google Scholar]
- Vaikuntanathan, S.; Jarzynski, C. Escorted free energy simulations: Improving convergence by reducing dissipation. Phys. Rev. Lett 2008, 100, 190601. [Google Scholar]
- Oberhofer, H.; Dellago, C. Optimum bias for fast-switching free energy calculations. Comput. Phys. Commun 2008, 179, 41–45. [Google Scholar]
- Dai Pra, P.; Meneghini, L.; Runggaldier, W. Connections between stochastic control and dynamic games. Math. Control Signals Syst 1996, 9, 303–326. [Google Scholar]
- Fleming, W.; Soner, H. Controlled Markov Processes and Viscosity Solutions; Springer: New York, NY, USA, 2006. [Google Scholar]
- Awad, H.; Glynn, P.; Rubinstein, R. Zero-variance importance sampling estimators for markov process expectations. Math. Oper. Res 2013, 38, 358–388. [Google Scholar]
- Badowski, T. Importance Sampling Using Discrete Girsanov Estimators. Ph.D. Thesis, Freie Universit¨at Berlin, Berlin, Germany. 2013. in preparation. [Google Scholar]
- Fleming, W. Risk sensitive stochastic control and differential games. Commun. Inf. Syst 2006, 6, 161–178. [Google Scholar]
- Day, M. Conditional exits for small noise diffusions with characteristic boundary. Ann. Probab 1992, 20, 1385–1419. [Google Scholar]
- Hartmann, C.; Schütte, C. Efficient rare event simulation by optimal nonequilibrium forcing. J. Stat. Mech. Theor. Exp 2012, 2012, P11004. [Google Scholar]
- Darve, E.; Rodriguez-Gomez, D.; Pohorille, A. Adaptive biasing force method for scalar and vector free energy calculations. J. Chem. Phys 2008, 128, 144120. [Google Scholar]
- Lelièvre, T.; Rousset, M.; Stoltz, G. Computation of free energy profiles with parallel adaptive dynamicss. J. Chem. Phys 2007, 126, 134111. [Google Scholar]
- Lelièvre, T.; Rousset, M.; Stoltz, G. Long-time convergence of an adaptive biasing force methods. Nonlinearity 2008, 21, 1155–1181. [Google Scholar]
- Zhang, W.; Latorre, J.; Pavliotis, G.; Hartmann, C. Optimal control of multiscale diffusions using reduced-order models. J. Comput. Dynam 2013. submitted. [Google Scholar]
- Dupuis, P.; Wang, H. Importance sampling, large deviations, and differential games. Stochast. Stochast. Rep 2004, 76, 481–508. [Google Scholar]
- Dupuis, P.; Wang, H. Subsolutions of an isaacs equation and efficient schemes for importance sampling. Math. Oper. Res 2007, 32, 723–757. [Google Scholar]
- Zhang, W.; Hartmann, C.; Weber, M.; Schütte, C. Importance sampling in path space for diffusion processes. Multiscale Model. Sim 2013. submitted. [Google Scholar]
- Banisch, R.; Hartmann, C. Meshless Discretizations of LQ-type stochastic control problems. SIAM J. Control Optim 2013. submitted. [Google Scholar]
- Vanden-Eijnden, E.; Weare, J. Rare event simulation of small noise diffusions. Commun. Pure Appl. Math 2012, 65, 1770–1803. [Google Scholar]



© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hartmann, C.; Banisch, R.; Sarich, M.; Badowski, T.; Schütte, C. Characterization of Rare Events in Molecular Dynamics. Entropy 2014, 16, 350-376. https://doi.org/10.3390/e16010350
Hartmann C, Banisch R, Sarich M, Badowski T, Schütte C. Characterization of Rare Events in Molecular Dynamics. Entropy. 2014; 16(1):350-376. https://doi.org/10.3390/e16010350
Chicago/Turabian StyleHartmann, Carsten, Ralf Banisch, Marco Sarich, Tomasz Badowski, and Christof Schütte. 2014. "Characterization of Rare Events in Molecular Dynamics" Entropy 16, no. 1: 350-376. https://doi.org/10.3390/e16010350



