Modeling Potential Energy Surfaces: From First-Principle Approaches to Empirical Force Fields
Abstract
: Explicit or implicit expressions of potential energy surfaces (PES) represent the basis of our ability to simulate condensed matter systems, possibly understanding and sometimes predicting their properties by purely computational methods. The paper provides an outline of the major approaches currently used to approximate and represent PESs and contains a brief discussion of what still needs to be achieved. The paper also analyses the relative role of empirical and ab initio methods, which represents a crucial issue affecting the future of modeling in chemical physics and materials science.1. Introduction
Most, if not all, of computer simulations using particles require the specification of the system potential energy as a function of particles’ coordinates [1]. The most ab initio methods, such as those discussed in [2], represent systems as made of electrons and atomic nuclei, and Coulomb’s law is sufficient to account for every interaction. In all other cases, particles represent composite objects, such as atoms or atomic nuclei, dressed by core electrons, possibly embedded into a sea of valence electrons described at some approximate level of a many-body theory. Then, all the relevant interactions need to be worked out on a case by case basis, and the effort required to determine inter-particle forces may represent a sizeable fraction of the work to be done to investigate condensed matter systems [3].
The sections that follow contain an overview of modeling approaches and a discussion of their relative merits and limitations. Needless to say, the variety of systems and methods, together with the shear size of the knowledge accumulated over decades, impose strict limits to the scope of this presentation. First of all, the focus is on atomistic models, i.e., models in which the number and geometry of interaction centers follows the distribution of atoms closely. A second major branch of modeling, concerning coarse graining approaches, is the subject of a separate contribution (see [4]).
Moreover, again, for limitations of space, the discussion that follows mainly concerns the most restrictive picture of interatomic interactions, based on the assumption that the potential energy of a system of N atoms can be expressed as a single-valued function of their 3N coordinates {Ri,i = 1, ..., N}, which represents the so-called potential energy surface (PES) of the system. This assumption relies, first of all, on the so-called Born-Oppenheimer approximation [5], whose validity is loosely attributed to the ∼3–4 orders of magnitude difference in the mass of electrons and atomic nuclei, giving rise to a clear separation of the characteristic energy and time scales for the motion of electrons and atomic nuclei. Then, for any given instantaneous configuration of the atomic cores, electrons will be able to reach their electronic ground state, justifying the single-value assumption for the system potential energy. Experience shows that this “adiabatic assumption” is fairly well justified for a wide variety of systems and thermodynamic conditions. To be precise, it turns out that some cases are left out of this picture and often represent systems and phenomena of great interest. Methods suitable to deal with these cases are discussed in [6].
Computational science and simulation, in particular, always have a practical and an algorithmic aspect to them, and a central theme of research is the development of efficient ways to approximate and represent PESs. The availability of simple and computationally-convenient models of inter-particle interactions, for instance, has been instrumental in the dawning of computer simulation. Since then, the two complementary stages of determining the relevant interactions and of working out their structural, thermodynamic and dynamical consequences have cross fertilized each other, so much that the terms, modeling and simulation, often appear together in the title of books, papers, conferences, workshops and funding proposals.
Nowadays, the general perception of atomistic modeling is that of an overwhelmingly important and successful field, steadily expanding its reach towards more complex systems, which in this context means systems combining a wider variety of chemical bonds. In this respect, it is clear that much remains to be done, for instance, to bring under the cover of simulation heterogeneous systems and interfaces at which organic, semiconducting and metal phases meet each other or to model systems in which chemical transformations take place.
During the last few decades, ab initio simulation methods have progressively come to play the role of the elephant in the (modeling) room. Methods, such as density functional theory [7,8] and ab initio molecular dynamics [9], could, in principle, replace all other approaches, reducing the variety of modeling problems to just one, concerning the effective and accurate representation of the energy of valence electrons in the field of atomic nuclei or ionic cores.
Up to now, this replacement has not been pervasive, mainly because of the size and time limitations of ab initio methods running on present day computers and partly because the approximations that make ab initio computations feasible still somewhat limit their accuracy on the energy scale of thermal motion, especially for molecular systems whose properties are determined by weak interactions among closed shell molecules. Ab initio modeling, however, is progressing and extending its reach. For what concerns atomistic simulation, therefore, empirical and semi-empirical models might eventually be squeezed out by the combination of ab initio methods and coarse-grained approaches. Simple models of atom-atom interactions, however, are likely to retain their appeal, because of their unique ability to represent and rationalize the microscopic forces underlying the properties and behaviors of condensed matter systems.
2. The Potential Energy Surface (PES) of a Many-Atom System
From a physicist point of view, ordinary matter consists of an assembly of electrons and atomic nuclei, evolving according to the laws of quantum mechanics. The non-relativistic limit is adequate for many of the systems and properties of interest for the present discussion, and unless differently specified, we shall restrict ourselves to this case.
Let us therefore consider a system made of N electrons and K nuclei, and let {ri, i = 1, ..., N} and {Rα, α = 1, ..., K} be the coordinates of electrons and nuclei, respectively. The corresponding linear momenta are denoted by {pi} and {Pα}. In the absence of external fields, the system Hamiltonian is:
Let us assume that the system is described by a many-body wave function, Ψ(r1, ..., rN; R1, ..., Rk; t), whose time evolution is determined by the time-dependent Schrodinger equation:
The first important step towards the definition of a potential energy surface for the atomic nuclei is provided by the Born-Oppenheimer approximation (BO), which, under suitable and often verified conditions, opens the way to a separate description of the time evolution of electrons and nuclei [5]. The intuitive justification of BO is the observation that the motion of electrons and nuclei takes place over different time scales, since Mα/m is at least Mn/m ∼1, 800, and usually approaches 2ZαMn/m, where Mn is the mass of a nucleon (proton or neutron). Moreover, the ratio of vibrational and rotational excitations is again ∼ . Experimental data confirm that, indeed, typical electronic excitations are of the order of a few eV; vibrational energies reach up to a few hundred meV, and even for small molecules, the separation of rotational levels is of the order of 1 meV. The conclusion is that the excitation of electrons, because of vibrational or rotational motion, is very unlikely. We can therefore represent the motion of electrons as taking place in the slowly varying field of the nuclei. Consistently with these qualitative arguments, the BO approximation breaks down whenever the energy of relevant electronic excitations becomes comparable to typical vibrational energies (or, much less likely, comparable to rotational energies). In those cases, vibrational and electronic excitations need to be considered on the same footing.
The core of the so-called adiabatic approximation can be given a semi-rigorous mathematical formulation in the following way [5]. Let us re-write Ĥ0 as:
For every choice of the nuclear coordinates, {Rα, α = 1, ..., K}, the eigenvalue problem:
The functions, ψj, are a basis for the Hilbert space spanned by the electron coordinates, and we can represent Ψk as follows:
The equation for Ψk becomes:
Neglecting these non-diagonal terms, the equations for the electronic and ionic coordinates are decoupled, and the picture emerging from this manipulation of Equation (6) is that of nuclei evolving on the potential energy surfaces Uj[{Rα}] = Ej({Rα}) + 〈ψj | T̂ion | ψj〉. This last expression, corresponding to the so-called Born-Huang approximation [10], represents, in fact, an upper bound for the system’s potential energy. A lower bound, instead, is given by the original BO approximation, i.e., Uj[{Rα}] = Ej({Rα}).
The nuclear motion in general is quantum mechanical, and, depending on initial conditions, it might occur on any of the Uj potential energy surfaces (PESs). More precisely, since the equations for different j’s are separated, it will take place on a single surface of index j, provided the starting point is consistent with this choice. This condition, that we identify with adiabatic motion, underlies most of the simulations that are routinely carried out in computational-condensed matter physics. Moreover, again, in most cases, but with noticeable exceptions, the relevant PES corresponds to the electronic ground state, and the scale of times and energies of interest allows the usage of classical dynamics instead of quantum mechanics [6].
The following sections are devoted to the discussion of the general properties of PESs, and of computationally tractable approaches to approximate them. Before doing that, it might be interesting to consider briefly when the BO approximation and the conditions for adiabatic motion are no longer valid.
An estimate of the 〈ψm | T̂ion | ψj〉 terms can be obtained by perturbation theory, showing that the strength of the non-diagonal coupling is proportional to:
Far from being the exception, violations of the BO approximation are pervasive. They occur often, but not exclusively, at the so-called conical intersections [11], playing a major role in chemical reactions and, for instance, challenging our ability to model catalysis [12]. Apparent non-BO effects are routinely highlighted by clever experiments [13,14].
Metals, whose occupied states are immediately contiguous in energy to the empty states, may appear as the most obvious candidates for large deviations from the BO picture. In the vicinity of the Fermi surface, however, single particle excitations are the only relevant excitations, but the coupling of each of these excitations to the nuclear motion (through Equation (11)) is vanishingly small. Collective electron excitations, such as plasmons, couple to the atomic motion, but their energies are of the order of several eV and, thus, are comparable to, if not higher than, those of closed shell atoms and molecules. As a result, vibrational properties of metals are generally well described by adiabatic dynamics. Exceptions are represented by Kohn anomalies, resulting from the nesting of reciprocal lattice vectors with the Fermi surface. Metals also provide the setting for a type of BO violation qualitatively different from those considered until now, represented by superconductors, in which the coupling of the electron and nuclear motion changes the symmetry of the ground state.
The isolated system picture underlying the BO decoupling has been generalized in [15–17] to the case of electrons and nuclei evolving in an external time-dependent potential. It was shown, in particular, that the full wave function can be factorized exactly into an electronic and a nuclear wave function, again opening the way to the definition of a time-dependent PES. The picture is less simple than in the static case, since it involves the introduction of a Berry vector potential and of Berry-Pancharatnam geometric phases [18,19] into the problem. This approach has already provided the basis for the real-time simulation of molecular systems in strong (laser) external fields. For completeness, I mention that some details of the formal framework might still need to be worked out for a fully rigorous treatment [20].
3. Properties of Potential Energy Surfaces
Basic features of the PES can be anticipated even without an explicit solution of the standard electronic problem in Equation (5). A surprisingly realistic intuition of what a PES looks like was outlined in elegant Latin prose long before quantum mechanics [21], based on an atomistic hypothesis and on the assumption that the still undiscovered atoms felt each other mainly at short distances.
The modern interpretation confirms this picture and adds a wealth of microscopic detail. The direct Coulomb repulsion among nuclei, unscreened by electrons at short distances, prevents the close contact of atoms and their eventual collapse. The kinetic energy of the electrons tightly bound to the nuclei will provide an additional repulsive contribution, resulting from the need to preserve the Pauli principle. On the other hand, the formation of chemical bonds gives rise to attractive potentials, binding atoms together. Even in the case of inert species, subtle quantum mechanical effects give rise to dispersion forces, which provide a weak, but pervasive, attraction.
Arguably, the simplest and most intuitive picture of atomic interactions is provided by pair potential models, in which the system energy is written as:
Computations and comparison with experiments have shown that an expression of this kind is suitable for rare gases [22] and for simple ionic compounds [23]. Systems and models of this kind have been instrumental in establishing computer simulation as a quantitative research tool in condensed matter and in chemical physics.
Needless to say, the scope of pair potentials is very narrow, and limitations of this model were already apparent well before the dawn of computer simulation, based on the results of lattice dynamics models in metals and semiconductors.
One could think of the pair potential expression as being only the lowest order approximation of the PES into an n-body expansion of the form:
More fruitful than the systematic expansion of Equation (13) has been the introduction of the cluster potential idea [25,26], loosely and sometimes more closely based on the bond-order concept introduced by Pauling [27]. In this approach, a fixed and low number of terms is retained; the expression looses its character of a systematic series to become an asymptotic expansion. Each of the few terms that are retained describe low-order potentials whose strength depends on the local environment. Approaches of this kind have given origin to the most popular family of potentials used to simulate metals and metallic alloys and also to some important approaches to approximate the PES of semi-conductors, which are discussed in the following sections.
4. Many-Body Interactions: Metals and Metal Alloys
Metals and their alloys posed an early challenge to the pair or few-body potential picture, since their basic properties manifest essential many-body interactions [28].
The successful and physically-motivated incorporation of these effects into tractable models in the early eighties of the last century has spawned a vast simulation activity, aiming, at first, at reproducing phase diagrams, then at analyzing in detail surfaces and interfaces and further progressing towards the prediction of mechanical properties through multi-scale approaches. Physical metallurgy is currently one of the most active and productive subfields of atomistic simulation [29,30].
Many-body interactions in metals were first identified by the analysis of their elastic properties. For instance, the elastic constants of cubic materials consisting of atoms interacting via spherically symmetric pair potentials have to satisfy the so-called Cauchy relations, stating, for instance, that C12 = C44. The violation of this relation, known in the solid state literature as a Cauchy anomaly, is the rule more than the exception in metals, unambiguously pointing to a deviation from the pair potential picture.
These features were first rationalized by considering the basic representation of a metal, as made of ions embedded into a sea of valence electrons. Since the major ingredient, i.e., the homogeneous electron gas could be solved analytically, and, at least for sp metals, the electron-ion interaction is weak, the full problem could be attacked by perturbation theory [28,31]. Carried up to the second order, this approach provides an expression for the system total energy that consists of a large volume (or, equivalently, density) term and a pair potential contribution. The volume term is able to account for the Cauchy anomaly. In simple metals, such as the alkalis, the pair potential is relatively soft at short distances and oscillates at large distances, reflecting Friedel oscillations. These features explain the bccstructure of these systems at normal conditions and provide a clue to understand more complex structures adopted by the lighter alkali metals at very low temperature or found in slightly more complex systems, such as alloys, or heavier sp metals, such as gallium, indium or tin.
Approaches of this kind are now mainly of historical interest, since most of the cases relevant for applications involve transition metals, and in those systems, the valence electron-ion interaction is by no means weak; the perturbation expansion cannot be limited to the second order and becomes rapidly untreatable beyond that point [32]. Besides these fundamental problems, other practical difficulties concern the definition and the zero-order solution of an electron gas problem suitable for inhomogeneous systems and for alloys. Electron gas perturbative approaches, therefore, could not solve problems, such as the inward relaxation of crystal surfaces, the quantitative description of stacking faults or the overestimation by pair potentials of the vacancy formation energy in metals.
To overcome these problems, new models have been proposed in [33–35], conforming to the cluster-potential idea [26], and representing low-order approximations to a bond-order potential. The embedded atom model (EAM) of [33,34], loosely based on density functional theory, has the broadest appeal, and for this reason, it is used here as a representative of a wider class of models.
According to EAM, each metal ion, i, at position Ri gains an energy, E[ρe(Ri)], upon being immersed into the valence electron distribution at density ρe(Ri) and interacts with neighboring ions by a short range repulsive pair potential, V2(R). The energy of N metal atoms, therefore, is:
The picture is completed by a prescription to compute the electron density, ρe, at the position, Ri, of each atomic core. EAM represents such a density as the sum of contributions from every other atom:
Parameters and auxiliary functions, such as t(R), E[ρe] and V2(R), could be computed from first principles [36], but this approach has been only moderately successful. Far more effective has been the strategy of adopting the EAM potential energy expression as a general framework, relying on fitting experimental quantities to tune a few parameters distributed into the functional form.
The success of EAM has been due to its ability to overcome the limitations of simpler models, easily accounting for the Cauchy anomaly, the reduced value of the vacancy formation energy, the inward relaxation of compact metal surfaces and the reconstruction of more open ones. Its broad acceptance relies also on the many and physically appealing properties of the model, discussed in a number of publications, such as the ease of extending EAM to alloys or the close relation with pair potentials in the case of homogeneous systems at constant volume.
From the computational point of view, the efficiency of EAM is due to the pair potential form of both the repulsive contribution, V2, and the embedding density expression in Equation (15). The time required to carry out a simulation based on EAM is expected to be twice that of a pair potential model, since a pass on all atom pairs is required to compute the repulsive potentials and the embedding density, while a second pass is needed to compute forces on atoms arising from the embedding energy. With suitable lists of neighbors, and depending on the range of V2(R) and of t(R), EAM can be used to carry out MDsimulations for systems of 104 atoms over several nanoseconds using laptops or inexpensive PCs. Supercomputers extend these ranges to several million atoms, and μs time scales.
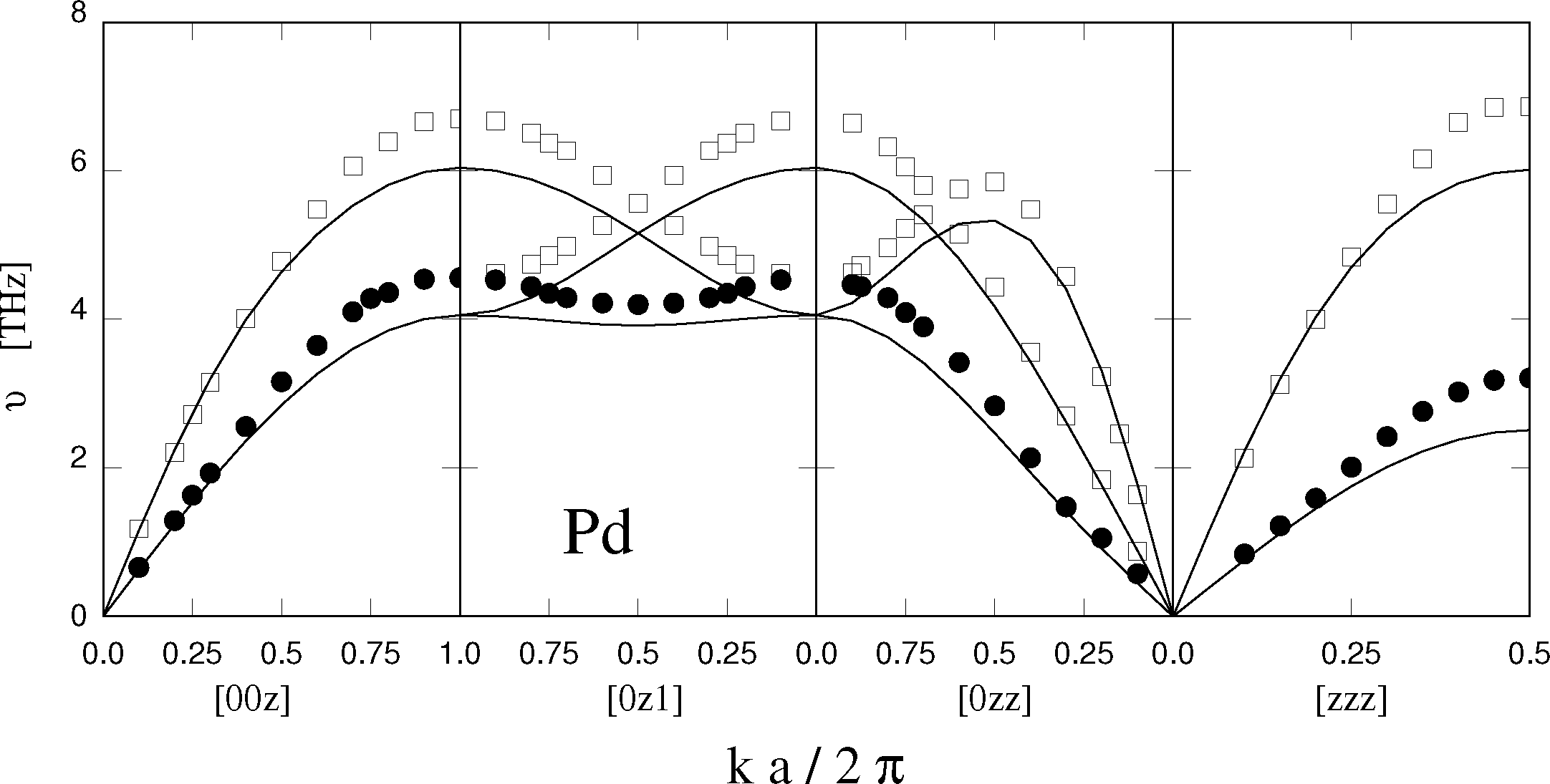
Needless to say, an empirical and approximate approach, such as EAM, cannot provide the final answer to the problem of modeling metals, and transition metals, in particular. A comprehensive discussion of inaccuracies and limitations identified during thirty years of applications is beyond the scope of this short review, and only two examples are briefly mentioned here. Phonons in transition metal crystals, a property routinely measured by inelastic neutron scattering, are not well reproduced by EAM. The elastic constants usually enter the fitting of the potential, and thus, the low-frequency acoustic phonons close to the Γ-point of the first Brillouin zone are usually well reproduced. Higher frequency modes at the zone boundary, however, turn out to be too soft with respect to the experimental data (see Figure 1). Transition metal clusters from a few to several thousand atoms are important for catalysis and represent a basic ingredient of nanotechnology. EAM neglects the details of the electronic structure of the atoms, leaving out quantum mechanical effects, such as Jahn-Teller. Thus, EAM is unable to quantitatively reproduce the structure and cohesive properties of the very small aggregates as provided by density functional computations. Beyond ∼100 atoms, cluster properties are expected to evolve more continuously with size, approaching those of bulk phases beyond 104 atoms. EAM has been used extensively to investigate clusters across this range, but a quantitative validation of the model is still lacking and difficult to achieve, since more ab initio computations become too expensive to carry out, and experiments find it difficult to probe this range of cluster sizes.
A step beyond EAM, needed to quantitatively model the fine details of the structure, thermodynamics and dynamics of transition metal systems, requires the introduction of explicit angular terms into the potential energy expression. This can be achieved through a conceptually simple extension of EAM, known as modified EAM (MEAM) [34], or resorting to a chemically accurate bond-order potential model, including the directionality of d and f electron orbitals, as well as the distinction of σ, π, δ, ..., bonding, anti-bonding and non-bonding orbitals [37].
The MEAM is somewhat more complex to use than EAM, and probably for this reason, it has been less extensively applied. Moreover, its ability to quantitatively overcome the limitations of the simpler model is not always so apparent. The other approaches, more closely based on the bond order approach, appear to be cumbersome to use in simulations, and the number of applications based on these models has been limited.
Because of the inclusion of angularly dependent forces, the scope of MEAM could, in principle, cover semiconductors. Successful applications have been published [34], but more specific models, described in the following section, have received broader attention in this subfield.
5. Semiconductors and Insulators
Semiconductor materials, exemplified by silicon, germanium, gallium arsenite, etc., are characterized by fairly open and complex structures of relatively low coordination, stabilized by sizeable angular forces, arising from the directionality of covalent bonds. Apart from elemental systems, most inorganic semiconductors are characterized, in fact, by a combination of covalent and ionic bonding. Several of these systems, most notably silicon and germanium, turn into metals upon melting.
Despite the difficulty of reproducing these properties by few-body potentials, the urgency of investigating the elements and compounds that fueled the electronic revolution stimulated the first bold attempts. The two- and three-body potential for silicon proposed by Stillinger and Weber [39] arguably has been the most representative example of this first generation of models.
Despite their interest, approaches of this kind have been only moderately successful, and once again, the bond-order concept [27] proved more fruitful. Its application to semiconductors was first discussed by Abell [25] before being used in a more empirical setting by Tersoff [40,41] and extended by Brenner [42] to a wider class of systems and problems.
According to these models, the potential energy of an assembly of N atoms of coordinates {Ri} is written as:
This form has obvious analogies with the EAM case. The difference is that Bij not only counts neighbors, as the embedding density does, but takes into account also the angular correlation among their mutual positions. This addition is required to enforce the dominance of tetrahedral sp3 coordination, but also to carve a secondary role for other structures, from the sp2 bonding of graphite, to the octahedral coordination of liquid silicon and germanium [40,41].
Parallel to the EAM case for metals, potentials of this type replaced previous models and established a new standard in modeling semiconducting systems. Success, however, has been somewhat less pervasive than in the case of EAM, for reasons that are relatively easy to identify. First of all, interactions in semiconductors are more complex and propagate at a longer range, since screening is not as effective as in metals. Moreover, semiconducting alloys and compounds give rise to partially Coulombic interactions, whose combination with covalent bonding has seldom been modeled, even by bond-order potentials.
Furthermore, in this case, the systematic improvement beyond the semi-empirical Tersoff and Brenner potentials has to rely on the analytical development of chemically accurate bond-order models [43]. Work along these lines is underway and has shown promising developments, but current models still appear fairly difficult to implement in molecular dynamics or Monte Carlo packages.
An important development of Brenner’s scheme has been the introduction of reactive force fields, able to describe chemical transformations in the system under consideration. The majority of the parameterizations and applications published until now concern organic systems, but potentials of this kind are mentioned here for their similarity with models first introduced for semiconductor systems. Prototypical examples of a reactive force field are the so-called ReaxFF [44] and the REBOpotential [45]. Both models require a massive parametrization effort, and for this reason, they appear to be fairly ad hoc and system specific.
A different line of attack to modeling semiconducting systems is suggested by the observation that in many cases, force fields of the form currently used to model organic systems and consisting on stretching, bending and torsion might indeed provide a good representation of structural and dynamical properties of semiconductors and of network insulators, such as silica. Models of this kind, in fact, were developed well before the age of computer simulation, and extensively used in lattice dynamics studies of semiconductors and insulators [46]. The problem of these models is that, mainly because of the established tradition, the topology of bonds is kept fixed, bonds are harmonic and can neither form nor break. These models, therefore, describe only low amplitude oscillations around a pre-assigned minimum of the potential energy surface. Removing these inessential constraints by introducing rules to break, form and interchange bonds results in a far more realistic picture. It was shown, for instance, that such a reactive force field model of silica undergoes melting at approximately the right conditions [47] (see Figure 2), and the same model has been used to provide an intriguing view of the amorphous silica surface at length and time scales unachievable by other methods [48].
Progressively increasing the electronegativity difference in compound semiconductors enhances the charge transfer among atoms, widening the band gap and turning the system into an ionic insulator. In the limit of strongly ionic materials, of course, pair potentials are adequate, but only a few compounds belong to this class, such as, for instance, alkali-halides or the oxides and chlorides of Group IIA and Group IIB metals. In between ionic insulators and polar semiconductors, there is a vast number of systems, including technologically relevant compounds, such as ceramics, transition metal oxides, ferroelectric and ferroid materials, minerals and bio-minerals, in particular, for which no current model is fully satisfactory. One of the major issues for these systems is the inclusion of polarizability into ionic and polar models [49]. Unfortunately, simulation approaches using polarizable models require either the minimization at every step of a polarization energy functional or the inclusion into the model of charged shells [50]. These last represent electronic degrees of freedom and react to electric fields on a time scale much faster than that of ionic vibrations [51]. Both methods are significantly at a disadvantage with respect to cases in which the potential energy is an explicit function of the atomic coordinates, and the simulation of systems bound by a combination of covalent and ionic forces appears to be split between oversimplified pair potential models and ab initio approaches.
6. Force Fields for Molecular Systems
Although every material ultimately consists of atoms, many systems are more easily understood as being made of molecules.
Modeling the PES of small and relatively unreactive species, such as N2,O2, CO, CO2, but, also, PF6, BF4, BH4, etc., requires only a slight extension of the pair-potential picture. Each molecule is represented by a small number of interaction centers, which may or may not coincide with atoms in number and position. The intra-molecular configuration is enforced by constraints representing rigid bonds or, less often, by harmonic springs, while centers on different molecules interact pair-wise. Because of their simplicity, models for small inorganic molecules have been used since the early days of computer simulation. Perhaps the most remarkable observation concerning these systems is that the quantitative details of their PES are still under investigations and require surprisingly sophisticated models to be reproduced [52,53].
Conspicuously absent in the list of small unreactive and supposedly simple molecules is water, whose peculiar properties and special role have motivated an extraordinary modeling effort, which is discussed separately in Section 7.
A specialized subfield of modeling simple species concerns systems in which a weakly bound molecular fluid is physisorbed on an inert solid surface, such as MgO, mica, graphite and flat or stepped transition metal surfaces. In this case, the effect of the solid substrate on the molecular fluid often is represented as an external field. In the case of crystal surfaces, the in-plane dependence of the field strength can be expanded in plane waves, whose wave vectors reflect the periodicity and symmetry of the surface lattice [54].
6.1. Organic Molecular Systems
In many respects, organic molecular systems are not so different from any other molecular systems, but the range and impact of their applications together with the explosive expansion of simulation in bio-physics and bio-chemistry amply justify a separate discussion. Systems of interest in this context include polymers, hydrocarbons, sugars, cellulose, etc., but also the endless variety of biological molecules, from phospholipids to proteins and nucleic acids. Other molecular organic systems of biological interest include drugs, simple nutrients, signal molecules, such as hormones, metabolic species, such as ATP, GTP, NADP, coenzymes, including vitamins, and prosthetic groups.
The modeling and simulation of systems of this kind arguably is the computational condensed matter activity with the largest economic relevance, both directly via the commercialization of packages and force fields and indirectly through the impact it has on applied research.
Despite the complexity of the structures they form, the PESs of organic systems turns out to be approximated fairly well by simple analytic expressions. First of all, the organic and biological species of interest are made primarily of light elements, forming strong covalent bonds through their s and p orbitals, giving origin to closed shell molecules. Systems of this kind, therefore, can be thought of as consisting of atoms connected by a fixed topology of bonds, with inter-molecular, i.e., non-bonded, interactions consisting of pair-wise Coulomb and dispersion forces. Because of their sp character, intra-molecular angular forces are relatively simple. Whenever d electron metals are involved, as in metal centers and in prosthetic groups, modeling becomes far more challenging.
In the standard cases, the PES of organic and biological systems is written as the sum of contributions from bonded (Ub) and non-bonded (Unb) interactions:
The bonded energy, in turn, is given by the sum of two-, three- and four-body terms from atoms joined by one ({ij}), two ({ijk}) and three ({ijkl}) consecutive covalent bonds:
Non-bonded interactions are written as.
The remarkable and, to same extent, unique property of the PES of organic and biological systems is that the bonds, whose properties are described in Equation (18), are fairly transferable, meaning that the equilibrium length, stiffness, etc., of a given organic bond is nearly the same in a large number of homologous compounds. Highlighting these similarities and exploiting them to endow the model with broad transferability is the most challenging and most rewarding part of modeling organic molecular systems.
The parametrization and, especially, validation of these potentials may require sizeable computations and are the playground of large collaborations, since it requires the convergence of several types of complementary expertise. Any single system might be analyzed by ab initio computations to derive intra-molecular force constants and atomic charges. These need to be complemented by suitable coefficients for the dispersion part, which are usually obtained by fitting measured properties, such as the equilibrium density and enthalpy per molecule or the molecular diffusion constant.
Generic potentials covering large classes of compounds and widely used by the community include Amber [55], CHARMM [56], OPLS [57] and Gromos [58]. More specialized parameterizations, tuned on the properties of specific families of compounds, are too many to be listed.
In many respects, the most uncertain part of the parametrization is the choice of coefficients for the non-bonded interactions. The definition of atomic charges is not unique, and different methods provide fairly different results. The most popular approach [59] attributes charges by fitting the electrostatic potential outside gas-phase molecules, as provided by ab initio computations. The method is physically sound, but the fit becomes ill conditioned whenever the molecular size exceeds ∼ 15–20 atoms or when the geometry is compact, thus reducing the number of multipolar momenta whose modulus is significantly different from zero. Constraints and minimum conditions on the size of individual charges do improve the fit [60], but the choice of these parameters remains fairly uncertain. For each individual system, the error introduced by the choice of the charge may be compensated for by the selection of the dispersion coefficients. In fact, it has been observed many times that it was possible to accurately reproduce the target properties of condensed phases such as the density or the molecular diffusion even starting from the fairly different charges provided by different methods. Unfortunately, this cancellation of errors limits the transferability of the potential, since an equivalent compensation might not occur when a given organic molecule is transferred into a different environment.
Especially for large biological systems, computational cost considerations have motivated approximations and shortcuts that might reduce the size of the simulated system. One obvious saving is obtained by representing CH2 and CH3 groups in aliphatic chains by a single particle. This united-atoms approximation is fairly well justified, since these groups are small and and the non-bonded potential arising from them is fairly spherical. Moreover, the motion of hydrogen in each of these groups is frozen by quantum effects up to fairly high temperature.
A second more drastic approximation concerns systems in solution. Since, especially in biochemistry, one is interested in the properties of the solute, implicit solvent models [61] have been developed to replace the effect of the solvent by suitable modifications of the solute force field. In many respects, implicit solvent models are a special case of coarse graining and, as such, are left out of our discussion.
In summary, the force field modeling of organic and biological systems is a largely successful enterprise, validated by a vast number of applications and supporting the research of a large portion of the simulation community. Furthermore, in this case, and almost needless to say, the vast simulation activity has highlighted many cases of inaccuracies or outright failures. The general feeling, however, is that the scale of most of these simulations is too large to allow, at present, the usage of significantly more sophisticated and more expensive approaches. Polarizability is likely to be the single most relevant missing ingredient, but the available methods to include it into simulations are still fairly expensive, and for this reason, explicitly polarizable models have been used only for a limited number of large-scale studies.
At present, a very active research field is the development of force fields for organo-metallic complexes, which represent prosthetic groups in proteins or active groups in a variety of organic opto-electronic devices and are important also for homogeneous catalysis. Peculiar difficulties are represented by the variety of coordination numbers, sometimes corresponding to different spin states, thus pointing to multiple PESs fairly close in energy. Moreover, the structure of organo-metallic complexes is characterized by the importance of quantum mechanical effects, such as Jahn-Teller, or by the so-called trans influence, defined as the “tendency of a ligand to selectively weaken the bond trans to itself” [62]. Models to include these effects in empirical PES models might turn out to be too complex to be used in practice. A more promising alternative is provided by QM/MMapproaches, using classical force fields for most of the system and resorting to ab initio methods for the challenging portion around the metal center.
An intriguing subset of mainly, but not exclusively, organic compounds is represented by the so-called room temperature ionic liquids [63], defined as molecular ionic systems whose melting temperature is below 100°. Prototypical systems are made by an alkane substituted imidazolium cation, joined to an organic or inorganic anion. Systems of this kind are relevant here, not only because of the intense simulation activity that concerns them, but mainly because they provide a bridge between different classes of bonding and, thus, pose special modeling problems.
The bulk of the extensive simulation work carried out at present relies on Amber-like force fields, with specialized parameterizations (see, for instance, [64,65]). Models of this kind are fairly successful, but issues concerning polarizability and the attribution of partial charges to atoms become particularly important for these systems. Despite these difficulties, a number of simulations have successfully addressed the properties of very complex systems, consisting of room temperature ionic liquids in combination with a variety of solvents and neutral organic compounds, including bio-molecular species (see Figure 3).
A few carbon systems, such as fullerenes, carbon nanotubes and graphene, lie at the boundary between inorganic and organic species and even blur the distinction between covalent and metal character. Not surprisingly, systems of this kind have been represented by a variety of models, from Tersoff-Brenner to a molecular force field, such as those described in this section.
7. Water
Because of its fundamental role in life and of its widespread and generally benign presence in nature, water has always been the object of interest and fascination. In this respect, computational physicists and chemists are no exception, although the reasons for their interest are somewhat different from those of the rest of humankind. A number of measurements have highlighted a wide variety of peculiarities, if not anomalies, in the properties of water [67]. These include the surprising expansion of water upon freezing, the density anomaly observed at 4 °C at ambient pressure, and, more in general, the non-monotonic variation of several physics-chemical properties in the vicinity of this remarkable density maximum. Other peculiar features consist in the wide temperature range of super-cooling, the high liquid-vapor critical temperature and the large value of the latent heat of the liquid water-ice transition.
To a large extent, these anomalous behaviors are embodied into the PES of water systems and arise from the strength and directionality of the hydrogen bond network that provides the bulk of water cohesion. In part, however, they are due to the light mass of the water molecule, causing non-negligible quantum effects that influence the properties of hydrogen bonds. Heavy water, for instance, is already somewhat different from ordinary water, so much that D2O is known to have peculiar and generally adverse biological effects. This duality of potential energy versus quantum mechanical effects poses apparent and significant problems to modeling [68]. Potentials tuned on the exact PES of water do not reproduce its properties when used in a classical simulation. On the other hand, potentials tuned on experimental properties of water do not necessarily reflect the details of the exact PES.
Work to provide a quantitative and comprehensive description of water properties is still in progress [69,70]. In the meantime, a vast number of simulations in which water is the unique or an essential component are being carried out with a variety of simple potentials, reflecting the basic atomistic and electronic structure of the water molecule. Two major families are in use: TIPnP[71–73], with n = 3, 4 and 5, and SPC [74–77], both based on fixed charges (rigid ions) and centers of short range interactions, joined by rigid or harmonic bonds.
Models of this kind allow the routine simulation by MD of systems of 50 × 103 water molecules solvating whole proteins, covering times well in excess of 100 ns. Results are generally good, and a large number of successful applications clearly validate these models, at least up to the accuracy needed for these large-scale applications. However, it is fair to say that no single model of the rigid ion type is able to provide a uniformly satisfactory account of water properties over a wide range of regimes and thermodynamic conditions. Several of these models, in particular, do not display the experimental density maximum of water or place it at (P, T)conditions far from the experimental ones [69,70]. The liquid-vapor coexistence curve is also poorly predicted by rigid ion models, unless the potential parameters are explicitly adjusted for this purpose. In such a case, however, the accurate description of some other quantity might need to be sacrificed. The description of critical properties, that are accurately known from measurements, are only moderately well reproduced [78].
Water clusters and droplets are another, distinct subfield of water research. Thermodynamic and spectroscopic data are available from experiments, but are not sufficiently detailed to provide a full description of structural and dynamical properties. In this case, state-of-the-art quantum chemistry computations supplement the experimental information [79]. Once again, it turns out that rigid ion models are only moderately successful in predicting their properties and usually fail to reproduce the reduced binding of very small clusters. The oxygen-oxygen equilibrium distance in the water dimer, for instance, is greatly underestimated by popular models, and its cohesive energy is correspondingly overestimated. These discrepancies decrease in importance with increasing cluster size, but the convergence to the bulk cohesive properties, reliably described by current DFTmodels of water, is fairly slow (See Table 1). In these small systems, the rigid-ion assumption, or, in other terms, the lack of polarizability, again seems to be the major problem. The molecular dipole moment of water, for instance, changes from μ = 1.855 D in the gas phase molecule, to nearly μ = 3 D in ice and in liquid water, but rigid ion models cannot reproduce this change. Moreover, within rigid-ion models, hydrogen bonds have only a Coulombic origin, contradicting the results of experiments and quantum chemistry computations showing that both Coulomb and covalent contributions are important [80] and change in slightly different ways upon changing the aggregation state of water.
Somewhat surprisingly, the inclusion of polarizability into simple models has not resulted yet into the systematic improvement of the description of the properties for extended water systems [84], while it has been more successful for clusters.
All these difficulties have stimulated a large number of new attempts. It might be worth mentioning the representation of electron polarizability via classical [85] and quantum [86] Drude oscillators, the application to water [87] of the empirical valence band (EVB) theory [88] and the usage of polarizable Thole models [89].
Ab initio modeling, discussed in more detailed below, will eventually provide the method of choice to study water [90]. Until now, however, approaches of this kind using standard approximations for the exchange-correlation energy (see next section) have given rather mixed results [91].
8. The Ab initio Route
Over the last twenty years, the art of representing PES as a function of atomic coordinates has seen its role increasingly challenged by the explosive growth of ab initio simulation methods.
As discussed in Section 2, the exact PES of a system made by N electrons evolving in the field of K nuclei can be determined point by point by computing the energy eigenvalues of the Ĥele Hamiltonian:
For what concerns the direct application of ab initio methods to simulation, however, progress came primarily through the advent of density functional theory, whose recognized theoretical and practical foundation is provided by the Hohenberg-Kohn (HK) theorem [92] and by the seminal paper by Kohn and Sham (KS) [93]. In a very schematic way, density functional theory in the popular Kohn-Sham formulation represents the ground state electron density, ρ(r), in terms of an auxiliary set of non-interacting electron orbitals {ϕi(r), i = 1, ..., K}, generally known as the Kohn-Sham orbitals:
Then, according to KS, the system ground state energy is the minimum of the unique and universal functional:
Methods to solve this problem have been developed and discussed in a vast numbers of papers and textbooks [7,8]. The accuracy of the solution depends on the functional used to approximate UXC[ρ], and on the choice of the basis used to represent the orbitals. Popular choices for the exchange-correlation energy are generalized gradient corrections, such as PBE [82], or hybrid functionals, such as B3LYP [94]. Basis sets range from atomic orbitals to wavelets, but plane waves [95,96] and Gaussian functions [97] are probably the most widely used choice for implementations tuned on molecular dynamics applications.
The solution of the standard problem in Equation (5) obtained through Equation (22) is restricted to the ground state PES. Even within this limited scope, the PES itself can only be determined point by point. Nevertheless, the KS energy expression can be used to evolve the atomic positions in time, thus opening the way to MD, provided one can: (i) minimize Equation (22) fast enough; and (ii) evaluate forces on the atoms through:
Atoms evolve on the adiabatic PES implicitly defined by Equation (22) classically or quantum mechanically. The validity of a classical time evolution for the atoms according to Newton’s equations relies on conditions discussed in detail in Chapter [6]. Outside these conditions, one could resort to a path integral approach, as done, for instance, in [99].
The method can be extended to simulate the atomic dynamics on the single PES of an electronically excited state [100], provided the different symmetry of the ground and excited state allows a meaningful definition of both PESs by density functional methods. As apparent from the discussion of the Born-Oppenheimer approximation, multiple PESs close in energy make it impossible to disentangle the ionic and electron dynamics, and in these cases, resorting to semiclassical or to more accurate quantum mechanical approaches [6] is mandatory.
Somewhat simplified versions of the density-functional-based MD, resorting to localized bases and relying on a self-consistent tight-binding approach have been developed [101,102] and provide a cheaper and popular alternative to unrestricted DFT methods. The price to be paid is a slight limitation in the quality of the solution, as well as occasional failures of the method.
The amazing success of density-functional-based simulation methods is due to the fact that they represent the only method endowed with truly predictive power, which can be used for systems of several hundred atoms, with up to a few thousand valence electrons. ab initio simulation, therefore, is the method of choice whenever we cannot guess a suitable representation of the PES or when we need an accuracy that cannot be provided by the empirical models that are available. Ab initio simulation is also strictly required for systems whose structure is affected by electronic effects, such as Jahn-Teller, and also enjoys a clear advantage in describing spin-polarization effects or systems undergoing chemical transformations and non-stoichiometric compounds exhibiting different valence states.
Well known drawbacks are represented by the computational cost that limits the size and especially the time scale of ab initio simulations, even though the reach of the method is constantly expanding. At present, large computations running on state-of-the-art facilities may involve ∼ 1, 000 atoms and ∼4, 000–5, 000 valence electrons. Early problems with metals have been progressively eased by approaches relying on the accurate step-by-step minimization of the KS energy functional. Problems, however, remain with transition and, especially, rare-earth metals, for which standard exchange-correlation approximations give unsatisfactory results, and quantum chemistry hybrid methods fail fairly spectacularly [103]. Progress is being achieved with methods incorporating strong correlation at some approximate level, such as LSD+U [104].
Difficulties remain also in the limit of weakly interacting molecular systems. Furthermore, in this case, early methods lacked essential components, such as the dispersion interaction, which in molecular systems provide a good portion of cohesion. Dispersion interactions are now increasingly included in ab initio simulations [81], especially for molecular systems and for water, in particular. Results are encouraging, although not yet in full quantitative agreement with experiments. However, the accuracy, reliability and computational efficiency of these methods are improving rapidly.
The major problem in current MD applications of ab initio methods arguably is that achieving accurate results for difficult systems, such as transition metals and oxides or molecular systems, still require an extensive preliminary calibration stage and system-specific exchange correlation approximations [105], effectively spoiling the ab initio character of these methods. Perhaps more importantly, these adjustments of the model decrease their reliability for systems exhibiting different bonding types, since the improvement on one type might worsen the description of the other type.
Most of the cost of KS-DFT computations is due to the representation of the density in terms of KS orbitals. Approaches relying on genuine density functional formalism, such as a refined Thomas-Fermi method, could enjoy a huge computational advantage, but no successful scheme has emerged during the years, and only very idealized Gordon-Kim approaches [106] have been used with some success.
9. Conclusions
Explicit or implicit expressions of the PES of condensed matter systems represent the basis of our ability to simulate them, possibly understanding and sometimes predicting their properties by purely computational methods. For this reason, the development of approximations and efficient representations of PES is the focus of an intense research effort, involving a sizable portion of the computational community.
Such a modeling activity is an art as much as a science. It is a science in the systematic derivation of interatomic forces from more fundamental interactions. It is an art in the invention of effective ways to incorporate new ideas in physically transparent and computationally efficient mathematical expressions. Like many other forms of art, it relies on a big deal of craftsmanship, required in the stage of parameterizing force fields, validating them and incorporating them into widely used computer packages, using sophisticated programming techniques, tuned on state-of-the-art computational hardware.
It should be apparent from the discussion of the previous sections that the last thirty years have seen an amazing enhancement of our ability to model a wide variety of systems at the atomistic level, fueling the explosive growth of simulation studies, while, at the same time, being driven by it. Equally amazing, however, is the extent of what we are still unable to model satisfactorily. Interfaces between different materials, for instance, are intrinsically difficult to describe by simple approaches. Excluding ab initio, no reliable, general and widely accepted model is available to simulate water and electrolyte solutions in contact with neutral or charged electrodes, organic and biological molecules on solid surfaces or the junction of metal and semiconducting phases. Even homogeneous phases, such as non-stoichiometric oxides, still represent a formidable challenge for models suitable for simulating 104 atoms over 100 ns or more. Systems undergoing chemical transformations are another sore point, even though methods, such as ReaxFF and REBO, are achieving progress in this direction.
At this stage, strategic decisions on the directions and aims of the modeling effort have to take into account the rapid growth of ab initio methods, which easily account for the intermixing of different bonding categories, cover electrostatic polarizability, provide information on excited state PES and may include magnetic interactions and spin effects through their approximate description of exchange.
The rapid progress of methods and computational equipment implies that the foreseeable future spans at most ten to fifteen years from now. Over this time, empirical models of PES will continue to play an important and useful role in the atomistic simulation of large systems (N ≃ 104 atoms) over times in excess of 100 ns. Most biochemistry and biophysics simulations fall into this class.
On the longer run, however, the general picture of modeling might indeed change. First of all, the domain proper to atomistic modeling concerns the investigation of the microscopic details underlying larger-scale phenomena. In this context, the scales of interest rarely exceed ∼ 104 atoms and correspondingly short times of less than ∼ 10 ns. Beyond this range, simulation may become the exclusive domain of coarse graining and multi-scale approaches, provided refined versions of these methods are developed over the next few years.
Ab initio methods already represent the method of choice for systems for which we do not have reliable approximations of their PES, for phenomena that can be represented by 100 to 1, 000 atoms and that take place within a 50–100 ps time span. Mixed QM/MM approaches extend this reach and represent the most appealing method to treat systems, such as protein reaction centers, organometallic catalysts, etc., in which a small portion of a large system needs to be represented in full chemical detail.
The parallel development of ab initio and of refined coarse graining and multi-scale methods, therefore, could greatly shrink the role of empirical PES approximations in atomistic simulation. Even these likely developments, however, might not mark the end of atomistic potential models, since simple and transparent representations of PES will continue to provide the conceptual basis to rationalize the properties of condensed matter systems in terms of atoms, of molecules and of their microscopic interactions.
Acknowledgments
I thank Carlo Pierleoni for useful discussions and for a careful reading of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Frenkel, D.; Smit, B. Understanding Molecular Simulation, 2nd ed; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Morales, M.A.; Clay, R.; Pierleoni, C.; Ceperley, D.M. First-principle methods: A perspective from quantum Monte Carlo. Entropy 2014, 16, 287–321. [Google Scholar]
- Finnis, M. Interatomic Forces in Condensed Matter; Oxford Series on Materials Modeling: Oxford, UK, 2010. [Google Scholar]
- Delle Site, L. What is a multiscale problem in molecular dynamics? Entropy 2014, 16, 23–40. [Google Scholar]
- Ziman, J.M. Electrons and Phonons; Oxford University Press: Oxford, UK, 1960; Chapter 5. [Google Scholar]
- De Carvalho, F.F.; Bouduban, M.E.F.; Curchod, B.F.E.; Tavernelli, I. Nonadiabatic molecular dynamics based on trajectories. Entropy 2014, 16, 62–85. [Google Scholar]
- Martin, R.M. Electronic Structure, Basic Theory and Practical Methods; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Kaxiras, E. Atomic and Electronic Structure of Solids; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett 1985, 55, 2471–2474. [Google Scholar]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Oxford University Press: Oxford, UK, 1954. [Google Scholar]
- Yarkony, D.R. Diabolical conical intersections. Rev. Mod. Phys 1996, 68, 985–1013. [Google Scholar]
- Kroes, G.J.; Gross, A.; Baerends, E.J.; Scheffler, M.; McCormack, D.A. Quantum theory of dissociative chemisorption on metal surfaces. Acc. Chem. Res 2002, 35, 193–200. [Google Scholar]
- Bowman, J.M. Beyond born-oppenheimer. Science 2008, 319, 40. [Google Scholar]
- White, J.D.; Chen, J.; Matsiev, D.; Auerbach, D.J.; Wodtke, A.M. Conversion of large-amplitude vibration to electron excitation at a metal surface. Nature 2005, 433, 503–505. [Google Scholar]
- Abedi, A.; Maitra, N.T.; Gross, E.K.U. Exact factorization of the time-dependent electron-nuclear wave function. Phys. Rev. Lett 2010, 105, 123002. [Google Scholar]
- Abedi, A.; Maitra, N.T.; Gross, E.K.U. Correlated electron-nuclear dynamics: Exact factorization of the molecular wavefunction. J. Chem. Phys 2012, 137, 22A530. [Google Scholar]
- Hunter, G. Conditional probability amplitudes in wave mechanics. Int. J. Quantum Chem 1975, 9, 237–242. [Google Scholar]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. Ser. A 1984, 392, 45–57. [Google Scholar]
- Pancharatnam, S. Generalized theory of interference, and its applications. Proc. Indian Acad. Sci. A 1956, 44, 247–262. [Google Scholar]
- Sutcliffe, B. Is there an exact potential energy surface? Theor. Chem. Acc 2012, 131. [Google Scholar] [CrossRef]
- Boscovich, R.J. Theoria Philosophiae Naturalis; Venice, Italy, 1758.
- Lennard-Jones, J.E. On the determination of molecular fields. Proc. R. Soc. Lond. A 1924, 106, 463–477. [Google Scholar]
- Fumi, F.G.; Tosi, M.P. Ionic sizes and Born repulsive parameters in the NaCl-type alkali halides. J. Phys. Chem. Solids 1964, 25, 31–43. [Google Scholar]
- Carlsson, A.E.; Ashcroft, N.W. Pair potentials from band theory: Application to vacancy-formation energies. Phys. Rev. B 1983, 27, 2101–2110. [Google Scholar]
- Abell, G.C. Empirical chemical pseudopotential theory of molecular and metallic bonding. Phys. Rev. B 1985, 31, 6184–6196. [Google Scholar]
- Carlsson, A.E. Beyond Pair Potentials in Elemental Transition Metals and Semiconductors. In Solid State Physics: Advances in Research and Applications; Ehrenreich, H., Turnbull, D., Eds.; Academic Press: Boston, MA, USA, 1990; Volume 43, pp. 1–91. [Google Scholar]
- Pauling, L. The Nature of the Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960. [Google Scholar]
- Hafner, J. From Hamiltonians to Phase Diagrams; Springer: Berlin, Germany, 1987. [Google Scholar]
- Handbook of Materials Modeling; Yip, S., Ed.; Springer: Berlin, Germany, 2005.
- In Comprehensive Nuclear Materials; Basic Aspects of Radiation Effects in Solids/Basic Aspects of Multi-Scale Modeling. Konings, R.J.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2012; Volume 1.
- Dagens, L.; Rasolt, M.; Taylor, R. Charge densities and interionic potentials in simple metals. Phys. Rev. B 1975, 11, 2726–2734. [Google Scholar]
- Moriarty, J.A. First-principles interatomic potentials in transition metals. Phys. Rev. Lett 1985, 55, 1502–1505. [Google Scholar]
- Daw, M.S.; Baskes, M.I. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals. Phys. Rev. Lett 1983, 50, 1285–1288. [Google Scholar]
- Baskes, M.I. Application of the embedded-atom method to covalent materials: A semiempirical potential for silicon. Phys. Rev. Lett 1987, 59, 2666–2669. [Google Scholar]
- Rosato, V.; Guillope, M.; Legrand, B. Thermodynamical and structural properties of f.c.c. transition metals using a simple tight-binding model. Philos. Mag. A 1989, 59, 321–336. [Google Scholar]
- Jacobsen, K.W.; Nørskov, J.K.; Puska, M.J. Interatomic interactions in the effective-medium theory. Phys. Rev. B 1987, 35, 7423–7442. [Google Scholar]
- Drautz, R.; Pettifor, D.G. Valence-dependent analytic bond-order potential for transition metals. Phys. Rev. B 2006, 74, 174117. [Google Scholar]
- Miiller, A.P.; Brockhouse, B.N. Crystal dynamics and electronic specific heats of palladium and copper. Can. J. Phys 1971, 49, 704–723. [Google Scholar]
- Stillinger, F.; Weber, T. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B 1985, 31, 5262–5271. [Google Scholar]
- Tersoff, J. New empirical model for the structural properties of silicon. Phys. Rev. Lett 1986, 56, 632–635. [Google Scholar]
- Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 1988, 37, 6991–7000. [Google Scholar]
- Brenner, D.W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 1990, 42, 9458–9471. [Google Scholar]
- Pettifor, D.G.; Oleinik, I.I. Analytic bond-order potentials beyond Tersof-Brenner. I. Theory. Phys. Rev. B 1999, 59, 8487–8499. [Google Scholar]
- Van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A., III. ReaxFF: A reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar]
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys.: Condens. Matter 2002, 14, 783–802. [Google Scholar]
- Keating, P.N. Effect of invariance requirements on the elastic strain energy of crystals with application to the diamond structure. Phys. Rev 1966, 145, 637–645. [Google Scholar]
- Cabriolu, R.; Del Popolo, M.G.; Ballone, P. Melting of a tetrahedral network model of silica. Chem. Phys. Phys. Chem 2009, 11, 10820–10823. [Google Scholar]
- Cabriolu, R.; Ballone, P. Thermodynamic properties and atomistic structure of the dry amorphous silica surface from a reactive force field model. Phys. Rev. B 2010, 81, 155432. [Google Scholar]
- Ponder, J.W.; Wu, C.; Ren, P.; Pande, V.S.; Chodera, J.D.; Schnieders, M.J.; Haque, I.; Mobley, D.L.; Lambrecht, D.S.; DiStasio, R.A.; et al. Current status of the AMOEBA polarizable force field. J. Phys. Chem. B 2010, 114, 2549–2564. [Google Scholar]
- Dick, B.G.; Overhauser, A.W. Theory of the dielectric constants of alkali halide crystals. Phys. Rev 1958, 112, 90–103. [Google Scholar]
- Mitchell, P.J.; Fincham, D. Shell model simulations by adiabatic dynamics. J. Phys.: Condens. Matter 1993, 5, 1031–1038. [Google Scholar]
- Rezaei, M.; Sheybani-Deloui, S.; Moazzen-Ahmadi, N.; Michaelian, K.H.; McKellar, A.R.W. Spectroscopic evidence for a planar cyclic CO trimer. J. Chem. Phys 2013, 138, 071102. [Google Scholar]
- Visser, G.W.M.; Hesselmann, A.; Jansen, G.; Wormer, P.E.S.; van der Avoird, A. New CO-CO interaction potential tested by rovibrational calculations. J. Chem. Phys 2005, 122, 054306. [Google Scholar]
- Righi, M.C.; Ferrario, M. Potential energy surface for rare gases adsorbed on Cu(111): Parameterization of the gas/metal interaction potential. J. Phys.: Condens. Matter 2007, 19, 305008. [Google Scholar]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M., Jr; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc 1995, 117, 5179–5197. [Google Scholar]
- Patel, S.; Brooks, C.L., III. CHARMM fluctuating charge force field for proteins: I parameterization and application to bulk organic liquid simulations. J. Comput. Chem 2004, 25, 1–16. [Google Scholar]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc 1996, 118, 11225–11236. [Google Scholar]
- Schuler, L.D.; Daura, X.; van Gunsteren, W.F. An improved GROMOS96 force field for aliphatic hydrocarbons in the condensed phase. J. Comp. Chem 2001, 22, 1205–1218. [Google Scholar]
- Chandra Singh, U.; Kollman, P.A. An approach to computing electrostatic charges for molecules. J. Comput. Chem 1984, 5, 129–145. [Google Scholar]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charge. J. Phys. Chem 1993, 97, 9620–9631. [Google Scholar]
- Roux, B.; Simonson, T. Implicit solvent models. Biophys Chem 1999, 78, 1–20. [Google Scholar]
- Pidcock, A.; Richards, R.E.; Venanzi, L.M. 195Pt31P nuclear spin coupling constants and the nature of the trans-effect in platinum complexes. J. Chem. Soc. A 1966, 1707–1710. [Google Scholar]
- Welton, T. Room-temperature ionic liquids. Solvents for synthesis and catalysis. Chem. Rev 1999, 99, 2071–2084. [Google Scholar]
- Canongia Lopes, J.N.; Deschamps, J.; Padua, A.A.H. Modeling ionic liquids using a systematic all-atom force field. J. Phys. Chem. B 2004, 108, 2038–2047. [Google Scholar]
- Canongia Lopes, J.N.; Deschamps, J.; Padua, A.A.H. Modeling ionic liquids using a systematic all-atom force field. J. Phys. Chem. B 2004, 108, 11250. [Google Scholar]
- Bingham, R.; Ballone, P. Computational study of room-temperature ionic liquids interacting with a POPC phospholipid bilayer. J. Phys. Chem. B 2012, 116, 11205–11216. [Google Scholar]
- Brovchenko, I.; Oleinikova, A. Multiple phases of liquid water. Chem Phys Chem 2008, 9, 2660–2675. [Google Scholar]
- Billeter, S.R.; King, P.M.; van Gunsteren, W.F. Can the density maximum of water be found by computer-simulation. J. Chem. Phys 1994, 100, 6692–6699. [Google Scholar]
- Guillot, B.; Guissani, Y. How to build a better pair potential for water. J. Chem. Phys 2001, 114, 6720–6733. [Google Scholar]
- Guillot, B. A reappraisal of what we have learnt during three decades of computer simulations on water. J. Mol. Liquids 2002, 101, 219–260. [Google Scholar]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- Mahoney, M.W.; Jorgensen, W.L. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys 2000, 112, 8910–8922. [Google Scholar]
- Abascal, J.L.F.; Sanz, E.; Garcia Fernandez, R.; Vega, C. A potential model for the study of ices and amorphous water: TIP4P/Ice. J. Chem. Phys 2005, 122, 234511. [Google Scholar]
- Berendsen, H.J.C.; Postma, J.P.M.; von Gunsteren, W.F.; Hermans, J. Intermolecular Forces; Pullman, P., Ed.; Reidel: Dordrecht, Holland, 1981. [Google Scholar]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem 1987, 91, 6269–6271. [Google Scholar]
- Dang, L.X.; Pettitt, B.M. Simple intermolecular model potentials for water. J. Phys. Chem 1987, 91, 3349–3354. [Google Scholar]
- Wu, Y.; Tepper, H.L.; Voth, G.A. Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys 2006, 124, 024503. [Google Scholar]
- Chialvo, A.A.; Cummings, P.T. Molecular-based modeling of water and aqueous solutions at supercritical conditions. Adv. Chem. Phys 1999, 109, 115–205. [Google Scholar]
- Temelso, B.; Archer, K.A.; Shields, G.C. Benchmark structures and binding energies of small water clusters with anharmonicity corrections. J. Phys. Chem. A 2011, 115, 12034–12046. [Google Scholar]
- Khaliullin, R.Z.; Bell, A.T.; Head-Gordon, M. Electron donation in the water-water hydrogen bond. Chem.-Eur. J 2009, 15, 851–855. [Google Scholar]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem 2006, 27, 1787–1799. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett 1996, 77, 3865–3868. [Google Scholar]
- Bingham, R.J.; Ballone, P. Energy, structure and vibrational modes of small water clusters by a simple many-body potential mimicking polarization effects. Mol. Phys 2013. [Google Scholar] [CrossRef]
- Chen, B.; Potoff, J.J.; Siepmann, I.J.I. Adiabatic nuclear and electronic sampling Monte Carlo simulations in the Gibbs ensemble: Application to polarizable force fields for water. J. Phys. Chem. B 2000, 104, 2391–2401. [Google Scholar]
- Lamoureux, G.; Harder, E.; Vorobyov, I.V.; Roux, B.; MacKerell, A.D., Jr. A polarizable model of water for molecular dynamics simulations of biomolecules. Chem. Phys. Lett 2006, 418, 245–249. [Google Scholar]
- Jones, A.; Cipcigan, F.; Sokhan, V.P.; Crain, J.; Martyna, G.J. Electronically coarse-grained model for water. Phys. Rev. Lett 2013, 110, 227801. [Google Scholar]
- Day, T.J.F.; Soudackov, A.V.; Cuma, M.; Schmitt, U.W.; Voth, G.A. A second generation multistate empirical valence bond model for proton transport in aqueous systems. J. Chem. Phys 2002, 117, 5839–5849. [Google Scholar]
- Aqvist, J.; Warshel, A. Simulation of enzyme-reactions using valence-bond force-fields and other hybrid quantum-classical approaches. Chem. Rev 1993, 93, 2523–2544. [Google Scholar]
- Thole, B.T. Molecular polarizabilities calculated with a modified dipole interaction. Chem. Phys 1981, 59, 341–350. [Google Scholar]
- Zhang, C.; Wu, J.; Galli, G.; Gygi, F. Structural and vibrational properties of liquid water from van der Waals density functionals. J. Chem. Theory Comput 2011, 7, 3054–3061. [Google Scholar]
- Yoo, S.; Zeng, X.C.; Xantheas, S.S. On the phase diagram of water with density functional theory potentials: The melting temperature of ice Ih with the PBE and BLYP functionals. J. Chem. Phys 2009, 130, 221102. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev 1964, 136, B864–B871. [Google Scholar]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev 1965, 140, A1133–A1138. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys 1993, 98, 5648–5652. [Google Scholar]
- Marx, D.; Hutter, J. Modern Methods and Algorithms of Quantum Chemistry; Grotendorst, J., Ed.; John von Neumann Institute for Computing: Jülich, Germany, 2000; NIC Series; Volume 1, pp. 301–449. [Google Scholar]
- Quantum Espresso is an Open Source Distribution. Available online: http://www.quantum-espresso.org (accessed on 15 October 2013).
- Cp2k is an Open Source Distribution. Available online: http://www.cp2k.org (accessed on 15 October 2013).
- Srivastava, G.P.; Weaire, D. The theory of the cohesive energies of solids. Adv. Phys 1997, 36, 463–517. [Google Scholar]
- Morrone, J.A.; Car, R. Nuclear quantum effects in water. Phys. Rev. Lett 2008, 101, 017801. [Google Scholar]
- Frank, I.; Hutter, J.; Marx, D.; Parrinello, M. Molecular dynamics in low-spin excited states. J. Chem. Phys 1998, 108, 4060–4069. [Google Scholar]
- Soler, J.M.; Artacho, E.; Gale, J. D; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys.: Condens. Matter 2002, 14, 2745–2779. [Google Scholar]
- Porezag, D.; Frauenheim, Th.; Köhler, Th.; Seifert, G.; Kaschner, R. Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon. Phys. Rev. B 1995, 51, 12947–12957. [Google Scholar]
- Paier, J.; Marsman, M.; Kresse, G. Why does the B3LYP hybrid functional fail for metals? J. Chem. Phys 2007, 127, 024103. [Google Scholar]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar]
- Tonigold, K.; Gross, A. Dispersive interactions in water bilayers at metallic surfaces: A comparison of the PBE and RPBE functional including semiempirical dispersion corrections. J. Comp. Chem 2012, 33, 695–701. [Google Scholar]
- Tabacchi, G.; Hutter, J.; Mundy, C.J. A density-functional approach to polarizable models: A Kim-Gordon response density interaction potential for molecular simulations. J. Chem. Phys 2005, 123, 074108. [Google Scholar]


| n | 2 | 3 | 4 | 5 | 6 | 8 |
|---|---|---|---|---|---|---|
| PBE+vdW | 12.06 | 25.95 | 34.48 | 36.09 | 36.82 | 45.28 |
| SPC/Fw | 14.35 [18.99%] | 26.66 [2.7%] | 33.44 [−3.0%] | 35.10 [−2.7%] | 35.67 [−3.1%] | 40.69 [−10.1%] |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ballone, P. Modeling Potential Energy Surfaces: From First-Principle Approaches to Empirical Force Fields. Entropy 2014, 16, 322-349. https://doi.org/10.3390/e16010322
Ballone P. Modeling Potential Energy Surfaces: From First-Principle Approaches to Empirical Force Fields. Entropy. 2014; 16(1):322-349. https://doi.org/10.3390/e16010322
Chicago/Turabian StyleBallone, Pietro. 2014. "Modeling Potential Energy Surfaces: From First-Principle Approaches to Empirical Force Fields" Entropy 16, no. 1: 322-349. https://doi.org/10.3390/e16010322




