First Principles Methods: A Perspective from Quantum Monte Carlo
Abstract
: Quantum Monte Carlo methods are among the most accurate algorithms for predicting properties of general quantum systems. We briefly introduce ground state, path integral at finite temperature and coupled electron-ion Monte Carlo methods, their merits and limitations. We then discuss recent calculations using these methods for dense liquid hydrogen as it undergoes a molecular/atomic (metal/insulator) transition. We then discuss a procedure that can be used to assess electronic density functionals, which in turn can be used on a larger scale for first principles calculations and apply this technique to dense hydrogen and liquid water.1. Introduction
With the increasing computational power and the greater access to large clusters seen during the last decade, simulation methods have become an increasingly useful tool for many fields of science, including chemistry, materials science, condensed matter physics, and biophysics. In this article we explore some of the future impact of Quantum Monte Carlo in the field of first principles simulation (FPS). By this we mean reliable simulation methods that can be performed on condensed matter systems in the absence of detailed experimental information on those systems. Starting with the general Hamiltonian in Equation (1), and taking as input only the chemical compositions, masses, density, temperature etc, currently there is a hierarchy of methods that are used to perform such a simulation. In this introduction we focus on three classes of methods: the use of semi-empirical interatomic potentials together with Monte Carlo (MC) or molecular dynamics (MD) simulations, Density Functional Theory-based simulation methods, and Quantum Monte Carlo simulations.
The first member of the hierarchy uses semi-empirical interatomic potentials among effective atoms considered as point particles, the best known of which is the Lennard-Jones potential. Such potentials are routinely used in the vast majority of simulations (soft condensed matter, biophysics, materials science) and are reviewed in a different contribution to this issue [1]. The first question is how do we construct such a potential? The typical approach is to use available experimental data. However, it is well known that those potentials are not very accurate in the vast majority of systems, even if they match experimental data. Hence, though they can be used to say something about generic properties of systems, quantitative predictions for defect energies, energy barriers, melting temperatures, cannot be trusted. (If the potential has been adjusted to reproduce experimental measurements, then the method is no longer first principles, and the question becomes whether the potential is transferrable, i.e., reliable for properties that are not fitted for.) Another fundamental limitation of this approach is that it becomes difficult to construct reliable interatomic potentials for complex systems containing several types of atoms, for example a solvent with various solutes, or systems under extreme conditions, since it becomes difficult to get enough reliable experimental data to constrain all of the parameters. For these reasons, it is highly desirable to have methods that can provide reliable predictions without input from experimental measurements.
Density Functional Theory (DFT) in the Kohn-Sham formulation maps the problem of many interacting electrons in the external field of the nuclei onto a system of non-interacting electrons in external field, a one body problem, and adds electronic correlation through an exchange-correlation functional. A breakthrough in the usefulness and popularity of simulations occurred with the development of the first-principle molecular dynamics (FPMD) approach by Car and Parrinello [2], where they combined molecular dynamics and DFT to perform simulations of complex chemical systems. Due to its favorable ratio between accuracy and computational cost, DFT has become the workhorse as electronic solver in the field of first-principles simulations. In fact, the recent explosion in the popularity of first-principles methods is, to a large part, due to the success of DFT in providing a fairly accurate description of the electronic structure of materials at a reasonable computational cost. DFT also gives access to a large range of observables. While DFT has been very successful in the description of many types of materials, e.g. metals and weakly correlated systems, many of the currently available exchange-correlation functionals in DFT possess well-known limitations [3], including the failure to properly describe strongly correlated materials, self-interaction errors, etc. It is recognized that even for such a fundamental system as water, the FPMD procedure is not accurate enough, giving large errors in many basic properties including the melting temperature, the diffusion constant, the compressibility, among others [4].
In the past decade there has been an explosion of new DFT exchange-correlation functionals with various characteristics. The reason is the difficulty of making systematic improvements to the functional or judging the accuracy of a functional. If the DFT functional is considered as “variable” then how does the user, in the absence of experimental data, decide on the functional? In the case of finite molecular systems, the availability of high-level quantum chemistry methods, like Coupled-Cluster theory offers a possible path towards the improvement of approximated functionals in DFT, for example by minimizing errors in a training set between DFT and Coupled Cluster theory results at various level of accuracy (with Single, Double or Triple excitations). In fact, many exchange-correlation functionals contain optimizable parameters that are obtained from calculations on finite molecular systems (exceptions to this include LDA, PBE, among others), where results of quantum chemistry methods are routinely used as a references. In solids, accurate calculations using many-body methods are computationally expensive, which has limited their use in the development of density functionals. While there has also been considerable developments in other correlated approaches for bulk systems, such as the many-body Green’s function methods (GW approximation and Bethe-Salpeter equation), and Dynamical Mean Field Theory (DMFT), they are more expensive and still leave questions of accuracy. For reasons of space, we do not discuss these approaches further.
The third approach in our hierarchy is the use of Quantum Monte Carlo (QMC) methods, which are generalizations of the classical Monte Carlo techniques to quantum statistical physics and fundamentally based on imaginary-time path integrals. For a class of systems (bosons and systems in one dimension) such techniques provide an exact computational method. For general problems, though not exact, they are highly accurate and systematically improvable. Although there are a variety of QMC methods (ground state, variational, path integral, auxiliary field...) fundamentally they are closely related. QMC are the most accurate general methods but are less developed and require much more computational facilities than DFT methods (although the scaling of computer time versus system size is similar) limiting the systems on which such simulations can and have been performed. The largest impact to date of QMC has been in the development and improvement of DFT methods; specifically we mention the correlation energy of the electron gas [5], a fundamental component in almost all exchange-correlation functionals used in DFT. Recent calculations [6] give the corresponding correlation energies at finite electronic temperature.
Later in this paper we give an example of work in progress in this direction where QMC is used to directly rank various DFT functionals. We suggest that this benchmark quality data could be used to improve directly the best functionals. One can then envision using the highest ranked functional to develop intermolecular potentials that would then be of higher quality. Ercolessi et al. [7] have developed the force-matching procedure to find the optimal effective potential reproducing the forces appearing in an FPMD simulation. Such an approach is now feasible using QMC calculated forces and energies.
First principles simulation methods entirely based on QMC have also been developed in the last decade. These are the Coupled Electron-Ion Monte Carlo method [8] and the QMC-Molecular Dynamics [9], and have been recently reviewed in [10]. However their application to condensed phases has been limited so far to high pressure hydrogen, and hydrogen-helium mixtures because of their considerable computation cost. In this paper we will illustrate their use to investigate the dissociation of liquid molecular hydrogen under pressure, a problem which is still unsolved by DFT methods.
The article is organized as follows. We first describe in Section 2 the various QMC methods. Section 3 is devoted to few applications of QMC. In Section 3.1 we present a QMC study of high pressure phases of hydrogen. This is followed in Section 3.2 by a description of the use of these methods to provide quantitative information on the accuracy of various DFT functionals. Finally we close with a discussion in Section 4.
2. Computational Methods
In this section, we review some of the Quantum Monte Carlo methods used in the first principles modeling of condensed matter systems. Under normal conditions of temperature and pressure, such systems are described to a high degree of accuracy by the non-relativistic Hamiltonian for a collection of electrons and ions. We will use atomic units throughout the paper, where Planck’s constant ħ = me = kB = e = 4π∊0 = 1 with kB being Boltzmann’s constant, and the energy is measured in Hartrees Eh = 315, 775 K = 27.2114 eV. Note that, in these units, the energy of a hydrogen atom is 0.5Eh, the binding energy of a hydrogen molecule is 0.17Eh, the unit of length is the Bohr Radius a0 = 0.0529 nm, and the molecular equilibrium bond length is 1.4a0. The Hamiltonian of the systems reads
Finding the eigenvalues and eigenfunctions of the Hamiltonian in Equation (1) is a formidable task, impossible to do analytically except for a few simple systems such as the single hydrogen atom. In practice, numerical or approximate theoretical methods must be used. Two of the most widely applicable methods are based either on imaginary-time path integrals or density functional theory (DFT), as discussed in the following subsections.
2.1. Ground State Methods
The following ground state methods seek to evaluate expectation values of physical observables taken over the ground state wavefunction ϕ0(R):
2.1.1. Variational Monte Carlo
Variational Monte Carlo (VMC) is conceptually the simplest of the ground-state QMC methods. It works by approximating the true ground-state wavefunction ϕ0(R) with some trial wavefunction ΨT (R). Integrals like Equation (4) are then performed using Metropolis Monte Carlo sampling, with ΨT (R) in place of ϕ0(R) [11]. The accuracy of this method depends strongly on how closely ΨT (R) approximates ϕ0(R). Fortunately, the variational principle of quantum mechanics gives us a metric by which to improve the quality of trial wavefunctions. Consider the expectation value of the Hamiltonian and its variance:
A popular approach for fermionic problems is to assume a Slater-Jastrow wavefunction. This type of wavefunction possesses the correct fermionic antisymmetry, and symbolically is given by ΨT (R) = det(M(R))eJ(R). Here, M(R)ij = ϕj(ri) is a Slater determinant of single-particle orbitals. The single-particle orbitals ϕj(r) are typically taken from other quantum-chemistry methods (Hartree-Fock, DFT, etc.). J(R) is called a “Jastrow” factor, and is constructed to be symmetric under particle exchange [12,13]. The Jastrow factor is typically chosen to be a sum of species dependent one-body, two-body, and sometimes three-body functions, which are designed to capture bosonic correlations. The form of these functions can vary from analytically derived forms with few to no free parameters, like the RPA jastrow [14,15], to functions with a large number of variational parameters, like b-splines. The interested reader is encouraged to look at the references for more information on Slater-Jastrow wavefunctions [12,16]. One can also go beyond the Slater-Jastrow form; other possible choices include multi-Slater determinant expansions [17], geminals [18], etc.
VMC can be improved if we consider classes of trial wavefunctions ΨT (R, α) parameterized by α = (α1, . . ., αm) free parameters. We then minimize the energy and/or variance with respect to these parameters. Recent improvements to optimization algorithms allow the optimization of thousands of variational parameters [19,20]. Traditionally, only the Jastrow functions have been parameterized, although work has been done using parameterized single particle orbitals and multi-Slater determinantal expansions.
VMC has some advantages that keep it in use. First, it is usually computationally cheaper than more accurate QMC methods (to be discussed later). VMC can also include several different types of electron correlations (various forms of electronic wave functions). Lastly, it doesn’t suffer from a sign problem. However, it is at heart an approximate method, and does depend on the choice of trial wavefunction.
2.1.2. Projector Methods
2.1.2.1. Formalism
Projector methods attempt to stochastically project out the exact many-body ground state, allowing us to sample this distribution for Monte Carlo integration. The “projector”, or imaginary-time Green’s function G(R′, R′, β′ − β), is the operator solution to the imaginary-time Schrödinger equation:
For efficiency reasons, it is better to use the “importance-sampled” Schrödinger’s equation [12,21,22]. We obtain this by writing the original equation in terms of f(R, β) = ΨT (R)Ψ(R, β). After some algebra [12], we find that
The solution of Equation (12) satisfy the following integral equation
2.1.2.2. Diffusion Monte Carlo
In diffusion Monte Carlo (DMC) [22–24], we represent the distribution function f(R, β) as an ensemble of 3N-dimensional samples {R1, . . ., RM}, which are known as “walkers”. The average density of walkers at position R in configurational space is proportional to the distribution function f(R).
As in classical diffusion, we would then simulate Equations (13) and (14) by a Langevin-like process acting on the walkers. Assuming that the time step τ = β/M is sufficiently small, we advance from f(R, β) → f(R, β + τ) by first proposing to move each walker Ri to R′i by a drift-diffusion step, prescribed by Equation (15). Then we accumulate a weight associated with walker i, given by wi(β + τ) = wi(β)GB(R′i,Ri, τ). To calculate the expectation value of an operator ̂ over f(R, β) = ΨT (R)Ψ(R, β), we average over the ensemble of walkers, including the appropriate weights:
Branching diffusion Monte Carlo [23], by far the most used form of DMC, fixes this problem by using the weights to either replicate or kill off walkers. After each drift-diffusion step, the number of walkers associated with the single walker Ri to advance to the next time-step, is chosen to be = INT(wi(β + τ) + ξ), where ξ is a random number between [0, 1]. The weights of the replicated walkers are all adjusted to conserve the total weight of walker i as much as possible. Modern methods are typically hybrids, where the weights of walkers are carried until they exceed certain established bounds, at which point they are branched [26].
The simulation is run by initializing the starting ensemble according to f(R, 0) = |ΨT (R)|2. Assuming β is the projection time required to reach the ground-state, the simulation is incremented M = β/τ steps, at which point our ensemble is distributed according to f0(R) = ΨT (R)ϕ0(R). Samples can then be accumulated, and the simulation is run for a long enough time to achieve the desired statistical error bars.
It is important to note that since we are sampling f0(R), this corresponds to the following type of expectation value, known as a “mixed-estimate”:
2.1.2.3. Reptation Monte Carlo
Reptation Monte Carlo (RMC) is based on the path-integral representation of the projector. Assuming that β is large enough to guarantee sufficient convergence to the ground state, we begin by partitioning the full projector into M segments of time-interval τ = β/M, called “time slices”. Inserting a resolution of the identity between each short-time projector, we find the following path-integral expression for the mixed distribution 〈ΨT|ϕ0〉:
Using the short-time approximate Green’s function at the beginning of this section, we can recast this expectation value in a more traditional path-integral form:
Here, X is shorthand for the directed path X = R0, . . . ,RM. Equation (20) plays the role of a partition function in statistical mechanics, where the Π[X] = eS[X]/𝒵 is the probability of a given path X, −S[X] is the path action, which includes the trial wavefunctions at the ends of the path, as well as a sum over “link-actions” Ls(R′, R), (see Equations (22) and (23)). The form we used for the link-action comes from imposing symmetry of the normal Green’s function under the exchange of two end-points, and writing it in terms of the importance-sampled Green’s functions [28].
The versatility of reptation Monte Carlo comes from how Π[X] is sampled. In the original method [29], one takes a given path X and chooses a growth direction at random. One then proposes a new path X* by adding δ time slices to the “head” and removing δ slices from the “tail”. Acceptance or rejection of this move is based on the usual Metropolis acceptance step. This type of move is called “reptation”, reminiscent of a “reptile”, from which the method derives its name. The proposed head move is done by a sequence of drift-diffusion moves, as in DMC, and rigorously preserves detailed balance.
Most practical implementations use what’s known as the “bounce algorithm” [28]. Rather than choosing the growth direction randomly, it is set at the beginning of the simulation and is changed only after a rejection step, hence the name “bounce”. This method does not satisfy detailed balance, but does satisfy the more general stationarity condition required for Markov chain Monte Carlo. This dramatically decreases the autocorrelation time of the method, and also tames ergodicity problems that have been observed to crop up in the method.
RMC is appealing for two reasons. It gives us the same level of accuracy for the energy as DMC but correlated sampling between different configurations can be done without approximation. This is particularly useful in methods like the Coupled Electron-Ion Monte Carlo. RMC also gives us the ability to sample expectation values over the pure distribution, as seen below:
2.1.2.4. The Fixed-Node Approximation
The previous projector methods we mentioned are in principle exact for bosonic systems, since the mapping to a diffusion process is valid when ϕ0(R) ≥ 0 everywhere. However, since the wavefunction for a fermion systems must be antisymmetric under exchange, the ground state wavefunction will have as many negative configurations as positive ones (in many cases the wavefunction can be made real). We can restore the probabilistic interpretation of the wavefunction Ψ(R, β) if we factor its sign into the weight of the walker, or into the observable itself. It turns out that in doing so, we will have large and almost equal contributions to the expectation value of opposite signs. This leads to an exponentially decaying signal to noise ratio, implying that the computational effort required to treat the fermion problem directly scales exponentially. This is the well known “fermion sign problem”.
By far, the most common means of alleviating the sign-problem in both DMC and RMC is applying the “fixed-node” approximation [23,24]. We assume that the nodes of ϕ0(R) are the same as the nodes for ΨT (R). We then propagate our ensemble of walkers or our reptile strictly within restricted space where ΨT (R) doesn’t change sign. This can be implemented by rejecting moves that carry walkers across a node, or bouncing a reptile whenever a head move is proposed across a nodal surface. Though this is an uncontrolled approximation, it turns out to be an extremely good one in most cases. Fixed-node energies are proved to be upper bounds of the exact energy [16], which allows us to optimize the nodal surfaces and to compare fixed-node DMC and fixed-node RMC energies with other methods. It turns out that both of these methods are among the most accurate computational methods known for electronic systems.
2.2. Scaling of QMC Methods
Like DFT, fermionic QMC typically has scaling between (N3) and (N4) depending on the property computed and the trial function. Here N is the number of particles. In contrast, popular quantum chemistry methods like Moller-Plesset Perturbation Theory, coupled-cluster, or configuration interaction, scale at least like O(N7). This makes QMC one of the few accurate many-body theories that is able to treat bulk systems.
Unlike DFT, whose scaling prefactor is governed by the solution of a generalized eigenvalue problem, Monte Carlo methods, in general, have statistical error bars which reduce as the inverse of the square root of the sampled configurations as a consequence of the central limit theorem. This makes quantum Monte Carlo significantly more expensive than DFT to reach chemical accuracy, though it has a smaller uncontrolled bias. The necessity for a much smaller time step in projector monte carlo than in VMC can make projector monte carlo about an order of magnitude more expensive for the same statistical uncertainty.
The cost of a single N-particle monte carlo step in VMC and projector monte carlo methods are determined by the evaluation of the trial wavefunction. For bosonic trial wavefunctions with pair-wise correlations, these calculations scale like (N2) per N-particle step. If these correlations are short-ranged, linear scaling can be achieved.
For fermionic trial wavefunctions, the computational cost is determined by the evaluation of single-particle orbitals and by the evaluation of a Slater determinant. The scaling of orbital evaluations depends on whether the electrons are localized since evaluating localized orbitals can be done in constant time. For plane waves basis sets, the cost scales like (N). If we seek to include the effects of backflow, this can increase the computational cost by an additional factor of N. The remaining bottleneck is then the evaluation of the Slater determinant, which scales like (N3) per N-particle step. In theory, the cost of the determinant evaluation could be brought down by almost a factor of N if the Slater determinant is sparse, however, the crossover point is prohibitive (greater than 3000 particles for a model system) [30]. This causes VMC and projector monte carlo to realistically scale like (N3–4) depending on whether one uses backflow or not.
2.3. Finite-Temperature Methods
Next, we summarize path integral methods. These methods are similar to DMC but can treat systems at non-zero temperature: a many-body density matrix replaces the trial wave function. Concerning first principles simulations the path integral method can be used either to simulate the properties of thermal electrons or to simulate the zero point effects of light nuclei or both. For electronic simulations there are two major problems. First, the energy scale of electrons is 1 Hartree or above, thus to reach ambient temperature requires very long paths. Second, since electrons are fermions, antisymmetrization and hence the sign problem is inevitable. For a more complete overview of the method and its application to fermion systems, see [31,32] respectively.
2.3.1. Path Integrals
To begin, we define the many particle density matrix for a system in equilibrium with an external reservoir at inverse temperature β = 1/kBT (canonical ensemble)
Finally, in order to account for the particle statistics of the simulated system, we must sum over permutations , giving
2.3.2. Restricted Paths
For fermions, negative terms enter in this sum, leading to a sign problem. As was done in the previous discussion of DMC, one way to circumvent this issue is to impose a nodal constraint [33]. We define the nodal surface ϒR★β for a given point R★ and inverse temperature β to be
We have thus turned the sign-full expression for the density matrix into one which includes only terms of a single sign, allowing efficient computation. However, because ρ appears on both sides of Equation (34) (in the r.h.s. it appears into the definition of the reach), this requires a priori knowledge of the density matrix nodal structure, which is generally unknown. To escape this self-consistency issue, an ansatz density matrix that approximates the actual nodal structure, is introduced. This will give an exact sampling of the Fermi density matrix if its nodes are correct. This method is called restricted PIMC (RPIMC). The density matrix for non-interacting fermions is a Slater determinant of single-particle distinguishable density matrices, where
The nodal error, arising from using an approximate restriction is problematic since it is uncontrollable. The finite temperature variational principle is through the free energy, as opposed to the internal energy in the ground state. Thus one possible solution is to parameterize the nodal ansatz, and then minimize the free energy by varying the parameters. This will require a thermodynamic integration, in general. Systems analyzed to date suggest that the nodal error arising from the free-particle ansatz is small since the correlation from the interacting potential is fully taken into account.
2.3.3. Path Integrals for Nuclei
Even when quantum particles can be considered distinguishable, as for instance light nuclei in condensed phases, there could be substantial physical effects arising from their quantum behavior, i.e., resulting from the T̂n in Equation (1). For example in bulk hydrogen and in water, the zero point motion of the protons must be taken into account for an accurate description. Furthermore, in the crystalline phase the frequently used harmonic approximation is often inadequate since non-harmonic effects can be as significant as harmonic effects. In contrast to the situation with electrons, our ability to simulate the nuclei with current algorithms and hardware is well controlled; because the nuclei are thousands of time heavier, they are much closer to the classical limit, so that fewer path steps are needed. For hydrogen-containing compounds at room temperature, one can often get away with about few tens of imaginary time slices. A second consequence is that particle statistics (either Fermi or Bose) can typically be ignored; a notable exception is the difference between para- and ortho-hydrogen, important for modeling the low-temperature low-pressure crystals of molecular hydrogen and deuterium.
A frequent use of path integrals for nuclei occurs when DFT is used to integrate out the electronic degrees of freedom. However, one wants to use the DFT energy surface for the properties of the quantum nuclei in equilibrium, using the path integral method. To perform the path integration, it is advantageous to use molecular dynamics instead of Monte Carlo since that will allow the electronic wave functions to evolve smoothly in time, and thus reduce the time to convergence in solving the DFT self-consistency conditions. M. Ceriotti, et al. [34] have devised an ingenious noise filtering scheme to reduce the number of needed path integral steps. Assuming the density functional description of the electrons is accurate, thermodynamic (static) properties of the simulated system will be accurate. Conversely the dynamical properties are not to be trusted. In general a reliable method for quantum time correlation functions or, even worse, quantum dynamics is still missing.
2.4. Coupled Electron-Ion Monte Carlo
The QMC methods described so far, when applied to an ion-electron system, treat all particles on the same footing, either both in the ground state [35–37] or both at the same finite temperature [38–40]. However the large nucleon-electron mass ratio implies a wide separation of time and energy scales and it is a common practice to adopt the adiabatic, or Born-Oppenheimer (BO), approximation. Ignoring such an approximation in QMC causes difficulties. The imaginary time step of the path integral representation (both in DMC/RMC and PIMC) is imposed by the light electron mass. In DMC this means that nuclear “dynamics” (the speed of sampling configuration space) is much slower than electron “dynamics” requiring very long (and time consuming) trajectories. In PIMC the separation of time scales presents itself as a separation in the regions where thermal effects are relevant: in high pressure hydrogen for instance nuclear quantum effects becomes relevant below ∼2000 K where electrons are, to a very good approximation, in their ground state. Performing PIMC in this region of temperatures requires very long electronic paths causing a slowing down of the exploration of configuration space and effectively limiting the ability of PIMC to perform accurate calculations at low temperatures.
The Coupled Electron-Ion Monte Carlo method (CEIMC) is a QMC method based on the BO approximation [8]. In CEIMC a Monte Carlo calculation for finite temperature nuclei (either classical or quantum represented by path integrals) is performed using the Metropolis method with the BO energy obtained by a separate QMC calculation for ground state electrons. CEIMC has been extensively reviewed in [8,10]. Here, we only briefly report the main features of the method.
2.4.1. Penalty Method
In CEIMC the difference of BO energies of two nearby nuclear configurations in a MC attempted step, as obtained by an electronic QMC run, is affected by statistical noise which, if ignored, results in a biased nuclear sampling. To cope with this situation either the statistical noise needs to be reduced to a negligible value by long electronic calculations (very inefficient), or the Metropolis acceptance/rejection scheme needs modifications to cope with noisy energy differences. The latter strategy is implemented in the Penalty Method [41] which enforces detailed balance to hold on average over the noise distribution. The presence of statistical noise causes an extra rejection for a single nuclear move with respect to the noiseless situation. An extra “penalty” defined as the variance of the energy difference over the square of the physical temperature is added to the energy differences. Therefore running at lower temperatures requires a reduced variance to keep an acceptable efficiency of the nuclear sampling. Small variances can be obtained if correlated sampling is used to compute the energy of the two competing nuclear configurations. In an attempted nuclear MC step, a single ground state electronic run is performed with a trial wave function which is a linear combination of the wave functions of the two nuclear configurations considered. The BO energy of the two nuclear configurations is obtained by a reweighting procedure which provides energy differences with a much reduced variance with respect to performing two independent electronic runs if the “distance” between the two nuclear configurations is limited (i.e., the overlap between the trial wave functions of the two configurations is large) [42]. This strategy allows an efficient sampling of nuclear configuration space for high pressure hydrogen and helium down to temperature as low as ∼200 K.
2.4.2. Nuclear PIMC
When nuclear quantum effects are included using a path integral representation (see §2.3), the relevant inverse temperature in the penalty method is the imaginary time discretization step τ, so that no loss of efficiency is experienced when lowering the temperature (i.e., taking longer paths). For quantum protons in high pressure hydrogen, CEIMC can be used to efficiently study systems at temperatures as low as ∼200 K. In the present implementation of nuclear quantum effects in CEIMC, we introduce an effective pair potential between nuclei and use the pair density matrix corresponding to the effective potential to factorize the imaginary time propagator. The residual difference between the energy of the effective system and the BO energy of the original system is considered at the primitive approximation level of the Trotter break-up of the proton propagator [8]. In high pressure hydrogen (rs = 1.40) it is found that with this strategy, an inverse time step of τ−1 ≃ 4800 K is enough to reach convergence of the thermodynamics properties, which allows to study systems at low temperature with a limited number of time slices (≤50).
In CEIMC many-body nuclear moves are preferred to single-body moves. The reason is that even if only few nuclei are moved the entire electronic calculation must be repeated, by far the most expensive part of the method. For this reason we sample nuclear configuration by a smart Monte Carlo method [43] in the normal mode space of the path [44] with forces from the effective two body potential. This strategy allows us to simulate systems of ∼100 protons (for hydrogen) at temperature as low as 200 K with an acceptable efficiency.
2.4.3. VMC vs. RMC
The main ingredient of CEIMC is the electronic QMC engine used to compute the BO energy. As mentioned a very important aspect for the efficiency of CEIMC is the noise level which is related to the variance of the local energy. In ground state QMC (see §2.1) the “zero variance principle” applies: if the trial wave function is an eigenfunction of the Hamiltonian, the local energy is no longer a function of the electronic coordinates and a single calculation provides the exact corresponding eigenvalues. Therefore by improving the trial wave function and approaching the exact ground state, the variance of the local energy decreases to zero. In connection with CEIMC, this is important not only for the accuracy of the BO energy but also for the efficiency of the nuclear sampling since the extra rejection due to the noise is reduced for a more accurate trial wave function.
To go beyond VMC accuracy in CEIMC we have implemented Reptation QMC method (RMC) [8,29]. RMC is superior to DMC in the CEIMC context since it uses an explicit representation of the statistical weight of each path and therefore the reweighting procedure needed for estimating energy differences is easily applied. Going from VMC to RMC accuracy in CEIMC requires at least one order of magnitude more computer time. This is because it is in general more difficult to properly sample the configuration space of a 3N-dimensional path than of a 3N-dimensional point. It is analogous to the difficulty of sampling the configuration space of a long polymers with respect to point particles. For any proposed nuclear move one has to relax the electronic path to the new equilibrium state and perform long enough sampling of the electronic configuration space to compute the energy difference with the required noise level.
In order to improve the efficiency of CEIMC while keeping the RMC accuracy, we have recently developed a method, based on a peculiar thermodynamic integration, to estimate the free energy of the system with RMC based BO energy from the knowledge of the free energy of the system with VMC based BO energy [45]. This allows to extensively use VMC rather than RMC, performing RMC on selected thermodynamic states only.
2.4.4. Hydrogen Trial Wave Function
For high pressure hydrogen we have developed a quite accurate trial function of the Slater-Jastrow, single determinant, form. The Jastrow part has an electron-proton and electron-electron Random Phase Approximation (RPA) term plus two-body and three-body empirical terms depending on few variational parameters. The Slater determinants (one for each spin state) are built with single electron orbitals obtained by a self-consistent DFT solution. We have recently integrated the PWSCF-DFT solver [46] into our CEIMC code to ensure a faster and uniform convergence of the single electron orbitals in different physical conditions. Further, the argument of the orbitals are not the bare electron positions but rather the quasiparticle positions defined by the backflow transformation [47,48]. We combined both the RPA analytical form and the Gaussian-like empirical terms depending on variational parameters. Our trial wave function has a total of 13 variational parameters to be optimized [42,48].
In view of the large variability of DFT results from different exchange-correlation approximations in the dissociation region of high pressure hydrogen (see next section), one interesting question is about the sensitivity of the trial wave function to the particular form of the adopted Kohn-Sham orbitals in the Slater determinant. This is particularly relevant since the form of the orbitals determine the nodal surface of the trial wave function, the ultimate limit in the accuracy of fermionic QMC. On the one hand one could hope to further improve the quality of the trial wave function by varying the type of orbitals, on the other hand a large sensitivity to the form of the Kohn-Sham orbitals will signal a too constrained form of the wave function, probably with a large room for improvements. The recent technical advance of the CEIMC code, namely the integration of PWSCF, allowed us to test several different types of orbitals: standard local (LDA) and semilocal (GGA-PBE) approximation, a non-local functional devised to reduce the self-interaction error and improve the description of the electronic correlation in DFT (HSE [49]) and a functional devised to improve the description of the dispersion interactions which are absent in a self-consistent mean-field theory (vdW-DF2 [50–52]). In the range of coupling parameter 1.22 ≤ rs ≤ 1.44 which corresponds approximatively to the range of pressure between 200 GPa and 550 GPa according to DFT, we have considered four recently proposed candidate structures for the molecular crystal [53], namely C2/c, Cmca-12, Pbcn and P63m. For each structure we have performed parameter optimizations for the four mentioned forms of the orbitals and at eight different densities. Supercells of 96 atoms were considered for C2/c, Cmca-12 and Pbcn structures, while a supercell of 128 atoms was studied for the P63m structure. Moreover for a single structure, Pbcn, at a single value of rs = 1.35 we have performed a complete RMC study. In Figure 1 we report for all densities investigated the variational energies from the different orbitals relative to the energy of the trial function with LDA orbitals.
We note that for all structures and at all densities LDA, PBE and HSE orbitals provides trial functions of the same quality (differences are of the order of 0.2 mH/atoms = 90K). Instead the trial function with orbitals from vdW-DF2 functional provides higher energies, by roughly 0.4 mH/at with values up to 1.4 mH/atom (≃630 K). This first result is quite indicative that our trial function is flexible and general enough to be very little sensitive to the form of the orbitals. In order to check whether the observed differences from vdW-DF2 orbitals could be due to optimization problems only, we performed a complete RMC study for a single case, namely the Pbcn structure at rs = 1.35. A time step of τ = 0.005 h−1 was used, which is fairly typical in this sort of calculation. No further time step error extrapolation study has been performed. In Figure 2 the energy versus projection time is reported for all kind of orbitals. We also added results from our old DFT solver with LDA orbitals plagued by the truncation error. For all kinds of trial function we observe a very similar relaxation with projection time meaning that the quality of the trial function is similar in all cases. The differences observed at the variational level among different trial functions essentially remain along the projection and therefore in the extrapolated value for the total energy. A quantitative way to estimate the extrapolated (β → ∞) value of the total energy is to plot energy versus its variance (pure estimate) and use a linear extrapolation at small values of σ2. This plot for all studied cases is shown in the right panel of Figure 2. We see that the three kinds of orbitals, LDA, PBE and HSE all provides extrapolated energies within error bars (E0 = −0.5350(2)), while the vdW-DF2 orbitals provides a higher value (E0 = −0.5342(2)). The fact that the RMC projection is not able to remove the difference observed at the VMC level means that the nodes from the vdW-DF2 are less accurate than for the other kind of orbitals, which instead, despite their differences, provide essentially the same nodal structure. Finally we note that our old implementation of LDA orbitals provides a less accurate determination of the energy with correspondingly larger variance.
3. Applications
3.1. High-Pressure Hydrogen
Hydrogen is the simplest element of the periodic table and also the most abundant element in the Universe. Because of its simple electronic structure, it has been instrumental in the development of quantum mechanics and remains important for developing ideas and theoretical methods. In the next section we explore its use in developing DFT functionals. Its phase diagram at high pressure has received considerable attention from the first-principles simulation community due to its critical importance in many fields like planetary science, high pressure physics, astrophysics, inertial confinement fusion, among many others [10,54,55]. The phase diagram of hydrogen at high pressure contains many interesting features including: a maximum in the melting line with a subsequent negative slope [56,57], a predicted liquid-liquid transition between an insulating molecular and a conducting atomic phase [58,59], exotic molecular phases at low temperature, and a predicted metal-insulator transition in the solid phase [10,55].
The ground state structure of crystalline hydrogen across the pressure-induced molecular dissociation has been studied by DMC [35–37] which predicted molecular dissociation at density corresponding to rs ≃ 1.3. RPIMC has been applied to investigate the Warm Dense Matter regime, namely the regime of high pressure and density where thermal and pressure molecular dissociation and ionization occur simultaneously [38,39,60]. Particularly relevant for our current understanding of the phase diagram and the Equation of State (EOS) of compressed hydrogen has been the determination of the primary and secondary Hugoniots lines of deuterium which could be directly compared with experimental data [40,61]. RPIMC predictions for the principal Hugoniot of deuterium were first in disagreement with pulsed laser-produced shock compression experiments [62–64], but were later confirmed by magnetically generated shock compression experiments at the Z-pinch machine [65–70] and by converging explosive-driven shock waves techniques [71,72]. Also relevant for the development and fine tuning of simulation methods for Warm Dense Matter has been the comparison with the less demanding, but also less fundamental methods based on Density Functional Theory (either Kohn-Sham or Orbital-Free flavours). A general agreement between RPIMC and FPMD predictions for the Hugoniot lines was observed [10] except at the lowest temperatures that could be reached by RPIMC (∼10,000 K). More recently the synergetic use of Born-Oppenheimer molecular dynamics (BOMD) and RPIMC has allowed to produce first-principle based EOS’s in a wide range of physical conditions for hydrogen, helium and hydrogen-helium mixtures [73,74] instrumental in planetary modeling and crucial ingredients for the hydrodynamic codes used in the large facilities for extreme conditions experiments.
Temperatures lower than ∼10,000 K cannot be easily reached by RPIMC without reducing the level of accuracy. However, most of the interesting phenomena in high pressure hydrogen, like molecular dissociation under pressure, metallization, solid-fluid transition, a possible liquid-liquid phase transition and its interplay with melting, the various crystalline phases and the transition to the atomic phases [10], occur at lower temperature out of the reach of RPIMC. Investigating this regime by QMC methods has been the main motivation in developing CEIMC. The other motivation, as mentioned above, is the benchmark of the much more developed (and less demanding) alternative theoretical method, namely FPMD based on DFT. Indeed the numerical implementation of DFT is based on approximations (the exchange-correlation functional) the accuracy of which can only be established against experiments or, better, against more accurate theories. As mentioned earlier, QMC energy is an upper bound and therefore has an internal measure of accuracy.
CEIMC has been applied to investigate the WDM regime of hydrogen and helium and benchmark FPMD [48,75,76]. In [76] an investigation of the fully ionized state of hydrogen in a region of pressure and temperature relevant for Jovian planets found that FPMD based on the GGA-PBE exchange-correlation functional and CEIMC are in very good agreement but both deviates from a widely accepted phenomenological EOS. The agreement between the simulation methods becomes less good when approaching the molecular dissociation regime at slightly lower temperature and pressure. Both CEIMC and FPMD with different approximated functionals has been applied to investigate the Liquid-Liquid phase transition (LLPT) region in hydrogen [45,59,77]. The emerging picture is that a weak first-order phase transition occurs in hydrogen between a molecular-insulating fluid and a metallic-mostly monoatomic fluid. At higher temperature, molecular dissociation and metallization occur continuously. However the precise location of the transition line and the critical point are still matter of debate since several levels of the theory provide different locations. Within FPMD-DFT the location of the transition line depends strongly on the exchange-correlation functional employed and on whether classical or quantum protons are considered [77]. Transition lines from the PBE and vdW-DF2 approximations differ by roughly 200–250 GPa, the PBE one being located at lower pressure. The PBE melting line with quantum protons is not in agreement with experiments, which highlights the failure of the PBE approximation when employed together with the quantum description of the nuclei. On the other hand, optical properties for the vdW-DF2 approximation are in agreement with experiments supporting the use of this functional for hydrogen in the WDM regime. The LLPT line from CEIMC lies in between the lines from PBE and vdW-DF2 functionals [45,59]. However, those results were plagued by a truncation error in the calculations of the single electron orbitals which showed up only around the metallization and which resulted in biased estimates. We have now changed the DFT solver in our CEIMC code and checked the convergence. We find a roughly uniform shift of the transition line of ∼50 GPa to higher pressure and we are performing new calculations with quantum nuclei. Preliminary results, based on VMC electronic energies, suggests that, similarly to the DFT scenario, nuclear quantum effects favor molecular dissociation and become increasingly important at lower temperatures. We estimate that the transition pressure is decreased, because of nuclear quantum effects, by ∼60 GPa at 600 K and by ∼150 GPa at 300 K (from ∼430 GPa for classical nuclei to ∼290 GPa for quantum nuclei). RQMC corrections to the transition lines was previously found to be small and we expect an even smaller effect with the new CEIMC implementation since the VMC variance is roughly half of what it was in the previous code [45].
The last estimate however is for a metastable liquid state obtained by an instantaneous quenching of the fluid at higher temperature, while it is expected that the equilibrium state at 300 K and ∼290 GPa be crystalline (of unknown structure) [10]. Those results are preliminary since the calculation is performed for a small system of 54 protons (we employ Twist Averaged boundary conditions to reduce size effects on the single-electron properties with a 4 × 4 × 4 twist angle grid) and we are presently estimating size effects, both by direct size extrapolation and by the analytic treatment of size effects [78,79]. In Figure 3 we report CEIMC proton-proton g(r) at various densities along the T = 600 K isotherm to illustrate the relevance of nuclear quantum effects on the pressure dissociation. The preliminary CEIMC results suggest that, despite the good performance observed on band gap calculations in the crystalline phases [80], the vdW-DF2 exchange-correlation functional has a tendency to over-stabilize molecules.
Although our results demonstrate the power of CEIMC in predicting the physical properties of hydrogen, its use is still quite demanding in terms of computer time, a fact that limits its applicability. This is particularly true when a much larger exploration of external conditions is needed to clarify the physics. For example, to study the crystalline state of the molecular system and clarify the molecular-atomic transition mechanism in the solid state, it is necessary to consider a large number of candidate structures, some of which have very large unit cells (the recently proposed Pc structure for phase IV of molecular hydrogen [81] contains 192 proton, more than three times larger than the system considered in the LLPT). Moreover, in studying those structure at finite temperature it is important to apply a constant stress algorithm allowing the simulation box to deform and release the excess internal stress that otherwise would produce metastable states. While larger systems (>250 particles) and constant pressure algorithms are routinely applied in FP methods based on DFT, their use in conjunction with CEIMC is still problematic. Therefore, it is important to apply CEIMC and other QMC methods to validate DFT predictions and determine the most accurate functional for a given system. The same considerations apply to systems more complex than hydrogen. In the next section we will describe our effort to benchmark functionals for high pressure hydrogen and for water in condensed phase.
3.2. QMC Benchmarks of DFT
Within the Born-Oppenheimer approximation at low temperatures, the only interaction between ions and electrons comes through the potential energy surface E0(R), defined as the solution of the electronic Hamiltonian for a fixed set of ionic coordinates. E0(R) is typically approximated by EDFT (R) in first-principles calculations, and obtained from a density functional theory (DFT) calculation. Over the last several years, many-body methods for solids have been developed to the point that the prospect of developing density functionals from accurate reference calculations is now a possibility. In this section, we show how quantum Monte Carlo calculations can be used to benchmark the accuracy of DFT in the description of the potential energy surface. The quality of EDFT (R) defines the predictive capabilities of the resulting first-principles simulation. We use large sets of representative configuration from PIMD simulations, and compare the mean absolute error between accurate QMC calculations and various DFT functionals. We present preliminary calculations on high pressure hydrogen and liquid water at ambient conditions, two materials that are particularly challenging to DFT due to the subtle competition between dispersion interactions, nuclear quantum effects, hydrogen bonding, and anisotropic interactions.
3.2.1. Hydrogen
The phase diagram of hydrogen at high pressure has been extensively explored using first-principles simulations with DFT [58,59,82–85]. In spite of the large number of studies, most of the work so far has employed either the local density (LDA) [86] approximation to the exchange-correlation potential or the Perdew-Burke-Ehrzenhof (PBE) [87] generalized gradient approximation. These are two of the simplest functionals currently available in DFT. In fact, both of them suffer from self-interaction errors and lack a proper treatment of dispersion interactions, making their application in the regime of molecular dissociation questionable. Recently, the use of DFT functionals with an improved description of dispersion interactions has been employed in the study of the liquid and solid molecular phases in the neighborhood of molecular dissociation. It was found that the dissociation density changed when compared to calculations using PBE [77,80]. Since these functionals were not designed for materials at high density, and because dispersion interactions are clearly important in dense molecular hydrogen, there is a crucial need for accurate calculations that can be used to benchmark the different exchange-correlation functionals employed in first-principles simulations.
Since sufficient experimental data is not available to validate the quality of functionals in the high-pressure high-temperature regime of the phase diagram, we used fixed-node diffusion Monte Carlo (DMC) to benchmark the accuracy of several DFT functionals over a range of densities near the liquid-liquid phase transition at a temperature of T = 1000 K. Henceforth, we will refer to densities using the parameter rs. First, we ran PIMD simulations with the PBE functional for N = 54 hydrogen atoms at three densities: rs = 1.30, 1.45, 1.60. In this range of densities, the liquid goes from an insulating molecular state at rs = 1.60 to a conducting atomic liquid at rs = 1.30. The density rs = 1.45 is intermediate and close to the LLPT for this functional. After equilibration, we sampled 100 ionic configurations from uncorrelated PIMD time slices for each density. For each configuration at each density, we calculated the DMC energy, and then computed EDFT (R) for the following functionals: LDA, PBE, vdW-DF [50], vdW-DF2 [51,52,88], and HSE [49].
All QMC calculations were performed with the QMCPACK [89–91] software package. We used a Slater-Jastrow trial wavefunction with twist-averaged boundary conditions [92], employing a 3 × 3 × 3 grid of boundary conditions. For the Jastrow functions, we used real space b-splines with optimizable knots. We included spin-independent one-body proton-electron terms; a short-ranged term with the appropriate cusp condition, and a long-ranged term. We also included two long-ranged spin-dependent electron-electron functions with appropriate cusp conditions. For each configuration, linear optimization with VMC was performed for all Jastrow parameters at a single twist-angle, these parameters were subsequently used for all twists in the DMC calculations. For the DMC run, a timestep of τ = 0.05 Ha−1 and 6000 walkers were used. The orbitals were obtained from DFT using the Quantum Espresso software package [46], using the PBE functional. We used a plane wave cutoff of 210 Ry. DFT calculations were performed with a Troullier-Martins norm conserving pseudo-potential [93] with a cutoff radius of rc = 0.5a0, DMC calculations were performed with the Coulomb potential. Based on the scale of the energy differences, we found a statistical error of 0.02 mHa/particle to be sufficient for present purposes. Since we were interested in measuring the spread of energy errors in this presentation, constant energy offsets were removed from our error assessments. This means that we did not have to include energetic finite size effects, although more detailed assessments will certainly call for this.
An example of the comparison between QMC and DFT is given in Figure 4. Shown is a histogram of the energy difference between the results of DMC and the PBE functional at the three densities: ΔEDFT = EDFT − EDMC. Given that rs = 1.30 corresponds to the atomic liquid, and rs = 1.60 to the molecular liquid, we immediately see that the errors incurred by using the PBE functional are not consistent across the LLPT. As expected, PBE offers a much better description of the atomic liquid compared to the molecular phase, where self-interaction errors are larger and dispersion interactions are important. This is a well-known failure of most semi-local density functionals, which tend to favor delocalized states.
To better quantify and compare the quality of functionals, we have computed the mean absolute error (MAE) from data similar to that shown in Figure 4. This quantity is defined as MAEfunc = 〈|ΔEDFT − 〈ΔEDFT〉|〉, where the average is taken over all configurations at a particular density. Notice that we subtract the average energy difference in the definition of the MAE, since the zero of energy of each functional is modified by the use of pseudopotentials. Fluctuations of the energy differences are more significant since the structure of the liquid is only sensitive to differences. The MAE gives us one measure of the quality, or predictive capability, of a given functional as defined by the reference method, in this case DMC. We have tabulated our results in Figure 5.
There are several interesting features in Figure 5 directly related to the expected performance of these functionals in the description of hydrogen near molecular dissociation in the liquid. First, the two semi-local functionals in the comparison, LDA and PBE, have considerably different errors in the molecular and atomic regimes. As described above, the atomic regime is more accurately described in comparison to the molecular phase, leading to a potentially strong underestimation of dissociation transition pressures in both solid and liquid phases. This is consistent with recently reported simulations [77]. On the other hand, both the hybrid HSE and the functionals with improved dispersion vdW-DF and vdW-DF2 offer a more consistent level of description between the two regimes. The mean absolute errors of the HSE and vdW-DF functionals are approximately half that of the PBE functional for all densities, which indicates that these functionals more accurately capture energy differences between various liquid configurations.
3.2.2. Liquid Water
Water plays a central role in many scientific fields [94]. It is a critical component to almost all chemical, biological, and geophysical processes. As a result, it is one of the most studied substances in science, both from an experimental and a theoretical point of view. Despite such broad importance, water’s most basic property, its local structure at ambient conditions, characterized by the geometry of its underlying hydrogen-bond (H-bond) network, has remained a matter of debate for over a century [95–97]. Challenges arise because water is only ≈25 K (at room temperature) from the melting temperature of ice, where a variety of subtle and complex effects become important. While the structure is dominated by H bond between neighboring molecules, both van der Waals (vdW) interactions (which, in this context, refers to dispersion forces resulting from dynamical nonlocal electron correlations) and nuclear quantum effects (NQEs) influence the topology of the H-bond network. In fact, it is precisely these seemingly subtle effects (compared to H bonding) that are key to accurately describing ambient water, but have been (until recently) difficult or impossible to model.
Atomistic simulations have the potential to resolve these issues, particularly using first-principles methods. Providing an accurate theoretical description has been a central topic and open challenge in physical chemistry for many decades. Despite considerable focus over the last decade, to date DFT has proven insufficient for the accurate description of liquid water [4,98]. Nonetheless, much progress has occurred during the last several years. The main advances include the use of functionals that properly describe dispersion interactions in the liquid [50,52,99,100], the use of hybrid functionals [101], and the direct treatment of nuclear quantum effects [102]. The combination of all of these advances in first-principles simulations of liquid water could lead to an accurate description of its interesting properties, including its local structure. At the same time, the choice of exchange-correlation functional in DFT is still a source of complication, mainly due to the large number of possibilities and the inability to test their predictive capabilities without resorting to full first-principles calculations of a large set of observables. As in the case of hydrogen, an accurate first-principles description almost certainly requires the use of path integral methods in order to directly treat nuclear quantum effects, which makes the calculations quite computationally intensive. What is needed is a way to assess the quality of a given functional without having to resort to first-principles calculations of the liquid at the PIMD level, and if possible, a way to systematically improve them using high quality reference calculations from accurate many-body methods.
In this section, we present QMC calculations of configurations of molecules extracted from PIMD simulations of liquid water. QMC has been shown to be a reliable benchmark in the study of small water clusters [103–105], and should provide an accurate reference method to measure the quality of typical density functionals used in simulations of water. All DMC calculations were performed with the QMCPack software package [89–91]. A Troullier-Martins norm-conserving pseudo-potential [93] was used to represent both hydrogen and oxygen. In particular, we used the pseudo-potentials from the CASINO database [106,107], which were recently shown to produce accurate results in the study of small water clusters. A Slater-Jastrow trial wave-function was used. The orbitals in the Slater determinant were obtained from DFT calculations employing the PBE exchange-correlation functional. We do not expect a strong dependence of the resulting comparison on the functional used to generate the orbitals. The Jastrow term contains electron-ion, electron-electron and electron-electron-ion terms, the variational parameters were optimized at the VMC level using a variant of the linear method of Umrigar, et al. [108]. A time-step of 0.01 Ha−1 was found to be sufficiently small to produce accurate total energies and approximately 4800 walkers were used in the DMC calculations. Casula’s T-moves [109] were used to reduce locality errors, while the Model Coulomb Potential [110] and Chiesa’s [78] correction scheme were used to estimate finite-size corrections to the potential and kinetic energies respectively.
DFT calculations were performed with both Quantum Espresso (QE) [46] and VASP [111–113] simulation packages. In the case of QE calculations we employed norm-conserving Troullier-Martins pseudo-potentials, while in the case of VASP calculations we employed the Projector Augmented Wave method (PAW) [114,115]. A single pseudo-potential (constructed with PBE) was chosen in order to make a homogeneous comparison of all DFT functionals, since some of the functionals employed in this work do not yet allow for the production of pseudo-potentials. All simulations were performed at the Γ point of the supercell in order to be consistent with the corresponding DMC calculations; errors due to the lack of k-point integration were small enough to be safely discarded. We carefully tested the convergence with the plane-wave cutoff in all DFT calculations.
We present calculations for 3 different configuration sets. The first two sets, which we called TIP5P-PI-0C-ICE and TIP5P-PI-0C-LIQ, were generated with PIMD calculations on simulation cells using the semi-empirical TIP5P water model and 32 molecules [116]. As the name suggests, the PIMD calculations used to generate the configuration set were performed at T = 0 C, from stable solid and liquid phases. The third configuration set was obtained from PIMD calculations of 64 water molecules, at room temperature and density of 1 g/cm3, with the vdW-DF2 functional, which has been recently shown to provide an accurate description of the structure of water when combined with a path integral representation [117]. The number of configurations in each set is 20, 47, 50, respectively. The three configuration sets sample different aspects of the potential energy surface of liquid water. While TIP5P is a rigid molecule model, the first-principles simulations with vdW-DF2 are fully flexible, which allows us to emphasize different ranges of the molecular interactions in the liquid. On the other hand, the simulations with TIP5P in both liquid and solid phases at T = 0 C sample the configurations that either strongly favor hydrogen bonding in the solid, with those where the hydrogen-bond network has been destabilized in the liquid.
Figure 6 shows the mean absolute difference in the total energy between DMC and DFT calculations, results are separated by configuration sets in order to allow for a more clear comparison between them. Several functionals are considered including the semi-local functionals: PBE [87]; the hybrid functionals: PBE0 [49], B3LYP [119,120]; the non-local van der Waals functionals: optB88 [121], optPBE [121], optB86b [122], vdW-DF [50] and vdW-DF2 [52]; and finally functionals with the empirical van der Waals correction of Grimme, et al., (DFT-D2) [118]. While there are many interesting results in this comparison, the most noticeable feature is the large difference in the scale of the MAE between rigid and flexible molecule configurations. This is not unexpected since the larger energy fluctuations in the system are found coupled to the intramolecular degrees of freedom of the molecule. In the case of flexible molecule configurations, hybrid functionals offer a much better agreement with DMC results, producing errors typically a factor of 2 smaller than non-hybrid functionals. This result shows the fact that hybrid functionals do a much better job at describing the intramolecular potential energy surface. This is consistent with the recent calculations of Alfe, et al. [104] and with the recent calculations of the absorption spectra of bulk water at ambient conditions of Zhang, et al. [101]. On the other hand, the functionals that include an appropriate description of dispersion interactions offer a clearly better comparison with QMC in the rigid-molecule configuration sets. In this case, the intermolecular interactions are the dominant energy contribution and the lack of appropriate dispersion leads to a larger error. In this case, we can also see a small but finite improvement with the inclusion of empirically corrected vdW functionals (PBE-D, B3LYP-D), but the gain is small and can not compete with non-local vdW functionals. Notice also that the performance of hybrids in the rigid-molecule sets is comparable to the performance of semi-local functionals, due to the fact that neither of these type of functionals can properly describe dispersion interactions. Finally, the configuration set with the smallest overall MAE is the one obtained from the calculations in the solid phase close to melting, showing the fact that most of these functionals can describe hydrogen bonded configurations fairly well.
4. Discussion
Direct first-principles simulations with QMC accuracy of condensed phases systems are nowadays possible but restricted so far to the simplest first few elements of the periodic table, namely hydrogen, helium and their mixtures. Even for those simple systems, challenges are present and the computational demand is large. Nonetheless, CEIMC predictions for the liquid-liquid phase transition in hydrogen remains today the target for less accurate but faster DFT-based FP methods. While much work remains to be done in developing QMC-based FP methods, the calculations presented here show one possible use of accurate many-body calculations: using QMC to benchmark the accuracy of DFT functionals. Not only does this allow us to make a judgment of the quality of a functional before its use in first-principles simulations, but it also shows us a path for the systematic improvement of the functionals by adjusting free parameters to minimize the errors. DFT users will often point to experimental data to validate the quality of a chosen functional. What we have shown is that we can use highly-accurate QMC methods to benchmark functionals around the liquid-liquid transition of hydrogen from first-principles. In addition, this set of reference energies for the bulk system can be used to optimize the free parameters in the DFT functional to minimize the errors, and in the limit of a large data set, reproduce the quality of the more accurate many-body method in first-principles calculations using DFT. This approach will be increasingly necessary as we continue to explore matter under extreme pressures, since experimental data is often insufficient or nonexistent at geophysical/planetary scales. It will also be necessary for other situations where DFT functionals have difficulties, such as near metal-insulator transitions.
Let us consider a more general point. We suggest that, in general, it is superior to use total energies to find an interatomic potential (force field). The traditional approach is to fit experimental data, for example, the melting temperature of ice, the density of water versus temperature, etc. Clearly this procedure was necessary in the past since experimental data was all that was available. However, using this approach requires very extensive calculations including free energy or equivalent computations and ultimately only gives a few constraints. We can invoke “The Allegory of the Cave” from Plato’s The Republic. We should not look to fit the atomic potentials using the projections of the energy surface onto thermodynamic properties, but, instead to fit directly the energy surface. Thus we will obtain an interatomic potential suitable for all properties. The situation has changed since QMC methods have matured and much more computational power is available. We note that scanning potential energy surface is a task very well suited to massively parallel computers. Including total energy QMC benchmarks into the fitting procedure in addition to experimental data, can allow for much more systematic improvements. QMC thus can provide a unique role in giving total energies and is applicable to large enough systems to approximate condensed matter.
Water and hydrogen show an additional complication of using experimental data: namely because of the importance of quantum zero-point effects of the protons, fitting of the experimental data becomes particularly problematic. A common approach is to do a simulation of the classical system and assume that the effective classical system includes the effects of zero-point energy; clearly this then becomes quite approximate since the zero-point effects are not small. A complication is that the interatomic potential that results can become temperature and density dependent with all known pathologies related to the use of state dependent potentials [123]. One may need to do full PIMD simulations of the system in order to determine the best empirical potential, thus increasing the, already large, computational requirements considerably.
One aspect in determining good force fields is to find an appropriate basis set to parameterize the force field. Traditionally, these have contained few functions with very few parameters, e.g., the Lennard Jones potential with only two parameters: and σ. It is feasible today to calculate the energy and forces for millions of independent arrangements of ions. Using QMC techniques, each would come with an error estimate. Hence, we can envision fitting this data set to a force field with potentially tens of thousands of independent parameters. This will allow us to determine a completely general pair potential (say with a spline basis), a three-body potential, four-body potential, etc. However, the investigation into effective basis sets to describe these potentials becomes very important. We can imagine an integrated set of tools: QMC simulations of systems with thousands of electrons to produce data sets of energies and forces. These can be used either to tailor a DFT to a particular system, or to determine a force field. The DFT simulations and the effective force field simulations can then be used to model much larger systems. Thus simulations can thereby become much more predictive, and produce not just universal properties, but details important to applications and experiment.
Acknowledgments
Miguel Angel Morales was supported by the U.S. Department of Energy at the Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344, by LDRD Grant No. 13-LW-004 and by the Basic Energy Science (BES), DOE through the Predictive Theory and Modeling for Materials and Chemical Science program, D. M. C. and R. C. were supported by the DOE grant DE-NA0001789 and C. P. by the Italian Institute of Technology (IIT) under the SEED project grant number 259 SIMBEDD Advanced Computational Methods for Biophysics, Drug Design and Energy Research. Computer resources have been provided by the US DOE INCITE program, Lawrence Livermore National Laboratory through the 7th Institutional Unclassified Computing Grand Challenge program and PRACE Project No. 2011050781.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ballone, P. Modelling potential energy surfaces: From first-principle approaches to empirical force fields. Entropy 2014, 16, 322–349. [Google Scholar]
- Car, R.; Parinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett 1985, 55, 2471–2474. [Google Scholar]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Challenges for density functional theory. Chem. Rev 2012, 112, 289–320. [Google Scholar]
- Schwegler, E.; Grossman, J.C.; Gygi, F.; Galli, G. Towards an assessment of the accuracy of density functional theory for first principles simulations of water. II. J. Chem. Phys 2004, 121, 5400–5409. [Google Scholar]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett 1980, 45, 566–569. [Google Scholar]
- Brown, E.W.; Clark, B.K.; DuBois, J.L.; Ceperley, D.M. Path-integral monte carlo simulation of the warm dense homogeneous electron gas. Phys. Rev. Lett 2013, 110, 146405. [Google Scholar]
- Ercolessi, F.; Adams, J.B. Interatomic potentials from first-principles calculations: The force-matching method. Europhys. Lett 1994, 26, 583–588. [Google Scholar]
- Pierleoni, C.; Ceperley, D.M. The Coupled Electron-Ion Monte Carlo Method. In Computer Simulations in Condensed Matter Systems: From Materials to Chemical Biology; Ferrario, M., Ciccotti, G., Binder, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 703, pp. 641–683. [Google Scholar]
- Attaccalite, C.; Sorella, S. Stable liquid hydrogen at high pressure by a novel abinitio molecular-dynamics calculation. Phys. Rev. Lett 2008, 100, 114501. [Google Scholar]
- McMahon, J.; Morales, M.A.; Pierleoni, C.; Ceperley, D.M. The properties of hydrogen and helium under extreme conditions. Rev. Mod. Phys 2012, 84, 1607–1653. [Google Scholar]
- McMillan, W.L. Ground state of liquid He4. Phys. Rev 1965, 138, A442–A451. [Google Scholar]
- Hammond, B.L.; Lester, W.A.; Reynolds, P.J. Monte Carlo Methods in Ab Initio Quantum Chemistry; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1994; p. 304. [Google Scholar]
- Ceperley, D.; Chester, G.V.; Kalos, M. Monte Carlo simulation of a many-fermion system. Phys. Rev. B 1977, 16, 3081–3099. [Google Scholar]
- Ceperley, D. Ground state of the fermion one-component plasma: A Monte Carlo study in two and three dimensions. Phys. Rev. B 1978, 18, 3126–3138. [Google Scholar]
- Ceperley, D.; Alder, B. The calculation of the properties of metallic hydrogen using Monte Carlo. Physica B+C 1981, 108, 875–876. [Google Scholar]
- Foulkes, W.M.C.; Mitas, L.; Needs, R.J.; Rajagopal, G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys 2001, 73, 33–83. [Google Scholar]
- Morales, M.A.; McMinis, J.; Clark, B.K.; Kim, J.; Scuseria, G.E. Multideterminant wave functions in quantum Monte Carlo. J. Chem. Theory Comput 2012, 8, 2181–2188. [Google Scholar]
- Casula, M.; Attaccalite, C.; Sorella, S. Correlated geminal wave function for molecules: An efficient resonating valence bond approach. J. Chem. Phys 2004, 121, 7110–7126. [Google Scholar]
- Neuscamman, E.; Umrigar, C.; Chan, G. Optimizing large parameter sets in variational quantum Monte Carlo. Phys. Rev. B 2012, 85, 1–6. [Google Scholar]
- Clark, B.K.; Morales, M.A.; McMinis, J.B.; Kim, J.; Scuseria, G.E. Computing the energy of a water molecule using multideterminants: A simple, efficient algorithm. J. Chem. Phys 2011, 135, 244105. [Google Scholar]
- Grimm, R.; Storer, R. Monte-Carlo solution of Schrödinger’s equation. J. Comput. Phys 1971, 7, 134–156. [Google Scholar]
- Ceperley, D.; Kalos, M. Quantum Many-Body Problems. In Monte Carlo Methods in Statistical Physics; Binder, K., Ed.; Springer: Berlin/Heidelberg, Germany, 1979; Volume 7, p. 145. [Google Scholar]
- Reynolds, P.; Ceperley, D.; Alder, B.J.; Lester, W., Jr. Fixed-node quantum Monte Carlo for molecules. J. Chem. Phys 1982, 77, 5593–5603. [Google Scholar]
- Anderson, J.B. A random-walk simulation of the Schrodinger equation: H + 3. J. Chem. Phys 1975, 63, 1499. [Google Scholar]
- Caffarel, M.; Claverie, P. Development of a pure diffusion quantum Monte Carlo method using a full generalized FeynmanKac formula. I. Formalism. J. Chem. Phys 1988, 88, 1088. [Google Scholar]
- Assaraf, R.; Caffarel, M.; Khelif, A. Diffusion Monte Carlo methods with a fixed number of walkers. Phys. Rev. E 2000, 61, 4566–4575. [Google Scholar]
- Reynolds, P.J.; Barnett, R.N.; Hammond, B.L.; Lester, W.A. Molecular physics and chemistry applications of quantum Monte Carlo. J. Stat. Phys 1986, 43, 1017–1026. [Google Scholar]
- Pierleoni, C.; Ceperley, D.M. Computational methods in coupled electron-ion Monte Carlo simulations. Chem. Phys. Chem 2005, 6, 1872–1878. [Google Scholar]
- Baroni, S.; Moroni, S. Reptation quantum Monte Carlo: A method for unbiased ground-state averages and imaginary-time correlations. Phys. Rev. Lett 1999, 82, 4745–4748. [Google Scholar]
- Ahuja, K.; Clark, B.K.; de Sturler, E.; Ceperley, D.M.; Kim, J. Improved scaling for quantum Monte Carlo on insulators. SIAM J. Sci. Comput 2011, 33, 1837–1859. [Google Scholar]
- Ceperley, D.M. Path integrals in the theory of condensed helium. Rev. Mod. Phys 1995, 67, 279–355. [Google Scholar]
- Ceperley, D.M. Path Integral Monte Carlo Methods for Fermions. In Monte Carlo and Molecular Dynamics of Condensed Matter Systems; Binder, K., Ciccotti, G., Eds.; Editrice Compositori: Bologna, Italy, 1996. [Google Scholar]
- Ceperley, D.M. Fermion nodes. J. Stat. Phys 1991, 63, 1237–1267. [Google Scholar]
- Ceriotti, M.; Manolopoulos, D.E.; Parrinello, M. Accelerating the convergence of path integral dynamics with a generalized Langevin equation. J. Chem. Phys 2011, 134, 084104. [Google Scholar]
- Ceperley, D.M.; Alder, B.J. Ground state of solid hydrogen at high pressures. Phys. Rev. B 1987, 36, 2092–2106. [Google Scholar]
- Natoli, V.; Martin, R.M.; Ceperley, D.M. Crystal structure of atomic hydrogen. Phys. Rev. Lett 1993, 70, 1952–1955. [Google Scholar]
- Natoli, V.; Martin, R.M.; Ceperley, D.M. Crystal structure of molecular hydrogen at high pressure. Phys. Rev. Lett 1995, 74, 1601–1604. [Google Scholar]
- Pierleoni, C.; Ceperley, D.M.; Bernu, B.; Magro, W.R. Equation of state of the hydrogen plasma by path integral Monte Carlo simulation. Phys. Rev. Lett 1994, 73, 2145–2149. [Google Scholar]
- Magro, W.R.; Ceperley, D.M.; Pierleoni, C.; Bernu, B. Molecular dissociation in hot, dense hydrogen. Phys. Rev. Lett 1996, 76, 1240–1243. [Google Scholar]
- Militzer, B.; Ceperley, D.M.; Kress, J.D.; Johnson, J.D.; Collins, L.A.; Mazevet, S. Calculation of a deuterium double shock hugoniot from Ab Initio simulations. Phys. Rev. Lett 2001, 87, 275502. [Google Scholar]
- Ceperley, D.M.; Dewing, M. The penalty method for random walks with uncertain energies. J. Chem. Phys 1999, 110, 9812. [Google Scholar]
- Ceperley, D.M.; Dewing, M.; Pierleoni, C. The Coupled Electronic-Ionic Monte Carlo Simulation Method. In Bridging Time Scales: Molecular Simulations for the Next Decade SE-17; Nielaba, P, Mareschal, M, Ciccotti, G, Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 605, pp. 473–500. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford Science Publication, Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Tuckerman, M. Statistical Mechanics and Molecular Simulations; Oxford Graduate Texts, Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Liberatore, E.; Morales, M.A.; Ceperley, D.M. Free energy methods in coupled electron ion Monte Carlo. Mol. Phys 2011, 109, 3029–3036. [Google Scholar]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar]
- Holzmann, M.; Ceperley, D.M.; Pierleoni, C.; Esler, K. Backflow correlations for the electron gas and metallic hydrogen. Phys. Rev. E 2003, 68, 046707. [Google Scholar]
- Pierleoni, C.; Delaney, K.T.; Morales, M.A.; Ceperley, D.M.; Holzmann, M. Trial wave functions for high-pressure metallic hydrogen. Comput. Phys. Commun 2008, 179, 89–97. [Google Scholar]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys 2003, 118, 8207. [Google Scholar]
- Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D.C.; Lundqvist, B.I. Van der Waals density functional for general geometries. Phys. Rev. Lett 2004, 92, 246401. [Google Scholar]
- Román-Pérez, G.; Soler, J. Efficient implementation of a van der Waals density functional: Application to double-wall carbon nanotubes. Phys. Rev. Lett 2009, 103, 096102. [Google Scholar]
- Lee, K.; Murray, E.D.; Kong, L.; Lundqvist, B.I.; Langreth, D.C. Higher-accuracy van der Waals density functional. Phys. Rev. B 2010, 82, 081101. [Google Scholar]
- Pickard, C.J.; Needs, R.J. Structure of phase III of solid hydrogen. Nat. Phys 2007, 3, 473–476. [Google Scholar]
- Silvera, I. The solid molecular hydrogens in the condensed phase: Fundamentals and static properties. Rev. Mod. Phys 1980, 52, 393–452. [Google Scholar]
- Mao, H.K.; Hemley, R. Ultrahigh-pressure transitions in solid hydrogen. Rev. Mod. Phys 1994, 66, 671–692. [Google Scholar]
- Deemyad, S.; Silvera, I. Melting line of hydrogen at high pressures. Phys. Rev. Lett 2008, 100, 155701. [Google Scholar]
- Bonev, S.A.; Schwegler, E.; Ogitsu, T.; Galli, G. A quantum fluid of metallic hydrogen suggested by first-principles calculations. Nature 2004, 431, 669–672. [Google Scholar]
- Scandolo, S. Liquid-liquid phase transition in compressed hydrogen from first-principles simulations. Proc. Natl. Acad. Sci. USA 2003, 100, 3051–3053. [Google Scholar]
- Morales, M.A.; Pierleoni, C.; Schwegler, E.; Ceperley, D.M. Evidence for a first-order liquid-liquid transition in high-pressure hydrogen from ab initio simulations. Proc. Natl. Acad. Sci. USA 2010, 107, 12799–12803. [Google Scholar]
- Pierleoni, C.; Magro, W.R.; Ceperley, D.M.; Berne, B.J. Path Integral Monte Carlo Simulation of Hydrogen Plasma.pdf. Proceedings of the International Conference on the Physics of Strongly Coupled Plasmas, Binz, Germany, 11–15 September 1995; Kraeft, W.D., Schlanges, M., Eds.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1996. [Google Scholar]
- Militzer, B.; Ceperley, D.M. Path integral Monte Carlo calculation of the deuterium hugoniot. Phys. Rev. Lett 2000, 85, 1890–1893. [Google Scholar]
- Da Silva, L.B.; Celliers, P.; Collins, G.W.; Budil, K.S.; Holmes, N.C.; Barbee, T.W., Jr.; Hammel, B.A.; Kilkenny, J.D.; Wallace, R.J.; Ross, M.; et al. Absolute equation of state measurements on shocked liquid deuterium up to 200 GPa (2 Mbar). Phys. Rev. Lett 1997, 78, 483–486. [Google Scholar]
- Collins, G.W. Measurements of the equation of state of deuterium at the fluid insulator-metal transition. Science 1998, 281, 1178–1181. [Google Scholar]
- Celliers, P.M.; Collins, G.W.; da Silva, L.; Gold, D.M.; Cauble, R.; Wallace, R.J.; Foord, M.E.; Hammel, B.A. Shock-induced transformation of liquid deuterium into a metallic fluid. Phys. Rev. Lett 2000, 84, 5564–5567. [Google Scholar]
- Knudson, M.D.; Hanson, D.L.; Bailey, J.E.; Hall, C.A.; Asay, J.R. Equation of state measurements in liquid deuterium to 70 GPa. Phys. Rev. Lett 2001, 87, 225501. [Google Scholar]
- Knudson, M.; Hanson, D.; Bailey, J.; Hall, C.; Asay, J. Use of a Wave Reverberation Technique to Infer the Density Compression of Shocked Liquid Deuterium to 75 GPa. Phys. Rev. Lett 2003, 90, 035505. [Google Scholar]
- Knudson, M.D.; Hanson, D.L.; Bailey, J.E.; Hall, C.A.; Asay, J.R.; Deeney, C. Principal Hugoniot, reverberating wave, and mechanical reshock measurements of liquid deuterium to 400 GPa using plate impact techniques. Phys. Rev. B 2004, 69, 144209. [Google Scholar]
- Bailey, J.E.; Knudson, M.D.; Carlson, A.L.; Dunham, G.S.; Desjarlais, M.P.; Hanson, D.L.; Asay, J.R. Time-resolved optical spectroscopy measurements of shocked liquid deuterium. Phys. Rev. B 2008, 78, 144107. [Google Scholar]
- Hicks, D.G.; Boehly, T.R.; Celliers, P.M.; Eggert, J.H.; Moon, S.J.; Meyerhofer, D.D.; Collins, G.W. Laser-driven single shock compression of fluid deuterium from 45 to 220 GPa. Phys. Rev. B 2009, 79, 014112. [Google Scholar]
- Knudson, M.D.; Desjarlais, M.P. Shock compression of quartz to 1.6 TPa: Redefining a pressure standard. Phys. Rev. Lett 2009, 103, 225501. [Google Scholar]
- Boriskov, G.; Bykov, A.; Ilkaev, R.; Selemir, V.; Simakov, G.; Trunin, R.; Urlin, V.; Shuikin, A.; Nellis, W. Shock compression of liquid deuterium up to 109 GPa. Phys. Rev. B 2005, 71, 092104. [Google Scholar]
- Grishechkin, S.K.; Gruzdev, S.K.; Gryaznov, V.K.; Zhernokletov, M.V.; Ilkaev, R.I.; Iosilevskii, I.L.; Kashintseva, G.N.; Kirshanov, S.I.; Manachkin, S.F.; Mintsev, V.B.; et al. Experimental measurements of the compressibility, temperature, and light absorption in dense shock-compressed gaseous deuterium. J. Exp. Theor. Phys. Lett 2004, 80, 398–404. [Google Scholar]
- Hu, S.X.; Militzer, B.; Goncharov, V.N.; Skupsky, S. FPEOS: A first-principles equation of state table of deuterium for inertial confinement fusion applications. Phys. Rev. B 2011, 84, 224109. [Google Scholar]
- Militzer, B. Equation of state calculations of hydrogen-helium mixtures in solar and extrasolar giant planets. Phys. Rev. B 2013, 87, 014202. [Google Scholar]
- Pierleoni, C.; Ceperley, D.M.; Holzmann, M. Coupled electron-ion monte carlo calculations of dense metallic hydrogen. Phys. Rev. Lett 2004, 93, 146402. [Google Scholar]
- Morales, M.A.; Pierleoni, C.; Ceperley, D.M. Equation of state of metallic hydrogen from coupled electron-ion Monte Carlo simulations. Phys. Rev. E 2010, 81, 1–9. [Google Scholar]
- Morales, M.A.; McMahon, J.M.; Pierleoni, C.; Ceperley, D.M. Nuclear quantum effects and nonlocal exchange-correlation functionals applied to liquid hydrogen at high pressure. Phys. Rev. Lett 2013, 110, 065702. [Google Scholar]
- Chiesa, S.; Ceperley, D.; Martin, R.; Holzmann, M. Finite-size error in many-body simulations with long-range interactions. Phys. Rev. Lett 2006, 97, 6–9. [Google Scholar]
- Drummond, N.; Needs, R.J.; Sorouri, A.; Foulkes, W.M.C. Finite-size errors in continuum quantum Monte Carlo calculations. Phys. Rev. B 2008, 78, 125106. [Google Scholar]
- Morales, M.A.; McMahon, J.M.; Pierleoni, C.; Ceperley, D.M. Towards a predictive first-principles description of solid molecular hydrogen with density functional theory. Phys. Rev. B 2013, 87, 184107. [Google Scholar]
- Pickard, C.J.; Martinez-Canales, M.; Needs, R.J. Density functional theory study of phase IV of solid hydrogen. Phys. Rev. B 2012, 85, 214114. [Google Scholar]
- Desjarlais, M.P. Density-functional calculations of the liquid deuterium Hugoniot, reshock, and reverberation timing. Phys. Rev. B 2003, 68, 064204. [Google Scholar]
- Vorberger, J.; Tamblyn, I.; Militzer, B.; Bonev, S. Hydrogen-helium mixtures in the interiors of giant planets. Phys. Rev. B 2007, 75, 024206. [Google Scholar]
- Morales, M.A.; Schwegler, E.; Ceperley, D.; Pierleoni, C.; Hamel, S.; Caspersen, K. Phase separation in hydrogen-helium mixtures at Mbar pressures. Proc. Natl. Acad. Sci. USA 2009, 106, 1324–1329. [Google Scholar]
- McMahon, J.M.; Ceperley, D.M. Ground-state structures of atomic metallic hydrogen. Phys. Rev. Lett 2011, 106, 165302. [Google Scholar]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett 1996, 77, 3865–3868. [Google Scholar]
- Thonhauser, T.; Cooper, V.R.; Li, S.; Puzder, A.; Hyldgaard, P.; Langreth, D.C. Van der Waals density functional: Self-consistent potential and the nature of the van der Waals bond. Phys. Rev. B 2007, 76, 125112. [Google Scholar]
- Kim, J.; Esler, K.P.; McMinis, J.; Morales, M.A.; Clark, B.K.; Shulenburger, L.; Ceperley, D.M. Hybrid algorithms in quantum Monte Carlo. J. Phys 2012, 402, 012008. [Google Scholar]
- Esler, K.; Kim, J.; Ceperley, D.; Shulenburger, L. Accelerating quantum monte carlo simulations of real materials on GPU clusters. Comput. Sci. Eng 2012, 14, 40–51. [Google Scholar]
- Esler, K.; Kim, J.; McMinis, J. QMCPACK at http://qmcpack.cmscc.org/.
- Lin, C.; Zong, F.; Ceperley, D. Twist-averaged boundary conditions in continuum quantum Monte Carlo algorithms. Phys. Rev. E 2001, 64, 016702. [Google Scholar]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar]
- Franks, F. Water: A Matrix of Life, 2nd ed; Royal Society of Chemistry Paperbacks, Royal Society of Chemistry: Cambridge, UK, 2000. [Google Scholar]
- Ball, P. Water: Water—an enduring mystery. Nature 2008, 452, 291–292. [Google Scholar]
- Clark, G.N.; Cappa, C.D.; Smith, J.D.; Saykally, R.J.; Head-Gordon, T. The structure of ambient water. Mol. Phys 2010, 108, 1415–1433. [Google Scholar]
- Nilsson, A.; Pettersson, L. Perspective on the structure of liquid water. Chem. Phys 2011, 389, 1–34. [Google Scholar]
- Grossman, J.C.; Schwegler, E.; Draeger, E.W.; Gygi, F.; Galli, G. Towards an assessment of the accuracy of density functional theory for first principles simulations of water. J. Chem. Phys 2004, 120, 300–311. [Google Scholar]
- Zhang, C.; Wu, J.; Galli, G.; Gygi, F. Structural and vibrational properties of liquid water from van der Waals density functionals. J. Chem. Theory Comput 2011, 7, 3054–3061. [Google Scholar]
- Møgelhøj, A.; Kelkkanen, A.K.; Wikfeldt, K.T.; Schiøtz, J.; Mortensen, J.J.R.; Pettersson, L.G.M.; Lundqvist, B.I.; Jacobsen, K.W.; Nilsson, A.; Nørskov, J.K. Ab initio van der Waals interactions in simulations of water alter structure from mainly tetrahedral to high-density-like. J. Phys. Chem. B 2011, 115, 14149–14160. [Google Scholar]
- Zhang, C.; Donadio, D.; Gygi, F.; Galli, G. First principles simulations of the infrared spectrum of liquid water using hybrid density functionals. J. Chem. Theory Comput 2011, 7, 1443–1449. [Google Scholar]
- Morrone, J.; Car, R. Nuclear quantum effects in water. Phys. Rev. Lett 2008, 101, 017801. [Google Scholar]
- Santra, B.; Michaelides, A.; Fuchs, M.; Tkatchenko, A.; Filippi, C.; Scheffler, M. On the accuracy of density-functional theory exchange-correlation functionals for H bonds in small water clusters. II. The water hexamer and van der Waals interactions. J. Chem. Phys 2008, 129, 194111. [Google Scholar]
- Gillan, M.J.; Manby, F.R.; Towler, M.D.; Alfè, D. Assessing the accuracy of quantum Monte Carlo and density functional theory for energetics of small water clusters. J. Chem. Phys 2012, 136, 244105. [Google Scholar]
- Alfè, D.; Bartok, A.P.; Csanyi, G.; Gillan, M.J. Communication: Energy benchmarking with quantum Monte Carlo for water nano-droplets and bulk liquid water. J. Chem. Phys 2013, 138, 221102. [Google Scholar]
- Trail, J.R.; Needs, R.J. Smooth relativistic Hartree-Fock pseudopotentials for H to Ba and Lu to Hg. J. Chem. Phys 2005, 122, 174109. [Google Scholar]
- Trail, J.R.; Needs, R.J. Norm-conserving Hartree-Fock pseudopotentials and their asymptotic behavior. J. Chem. Phys 2005, 122, 14112. [Google Scholar]
- Umrigar, C.J.; Toulouse, J.; Filippi, C.; Sorella, S.; Hennig, R.G. Alleviation of the fermion-sign problem by optimization of many-body wave functions. Phys. Rev. Lett 2007, 98, 110201. [Google Scholar]
- Casula, M. Beyond the locality approximation in the standard diffusion Monte Carlo method. Phys. Rev. B 2006, 74, 161102. [Google Scholar]
- Fraser, L.; Foulkes, W.; Rajagopal, G.; Needs, R.; Kenny, S.; Williamson, A. Finite-size effects and Coulomb interactions in quantum Monte Carlo calculations for homogeneous systems with periodic boundary conditions. Phys. Rev. B 1996, 53, 1814–1832. [Google Scholar]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metalamorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci 1996, 6, 15–50. [Google Scholar]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar]
- Mahoney, M.W.; Jorgensen, W.L. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys 2000, 112, 8910. [Google Scholar]
- McMahon, J.M.; Morales, M.A.; Kolb, B.; Thonhauser, T. Competing nuclear quantum effects and van der Waals interactions in water. J. Phys. Chem. Letters 2013. submitted.. [Google Scholar]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem 2006, 27, 1787–1799. [Google Scholar]
- Kim, K.; Jordan, K.D. Comparison of density functional and MP2 calculations on the water monomer and dimer. J. Phys. Chem 1994, 98, 10089–10094. [Google Scholar]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem 1994, 98, 11623–11627. [Google Scholar]
- Klimeš, J.; Bowler, D.R.; Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 2010, 22, 022201. [Google Scholar]
- Klimeš, J.; Bowler, D.R.; Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 2011, 83, 195131. [Google Scholar]
- D’Adamo, G.; Pelissetto, A.; Pierleoni, C. Predicting the thermodynamics by using state-dependent interactions. J. Chem. Phys 2013, 138, 234107. [Google Scholar]
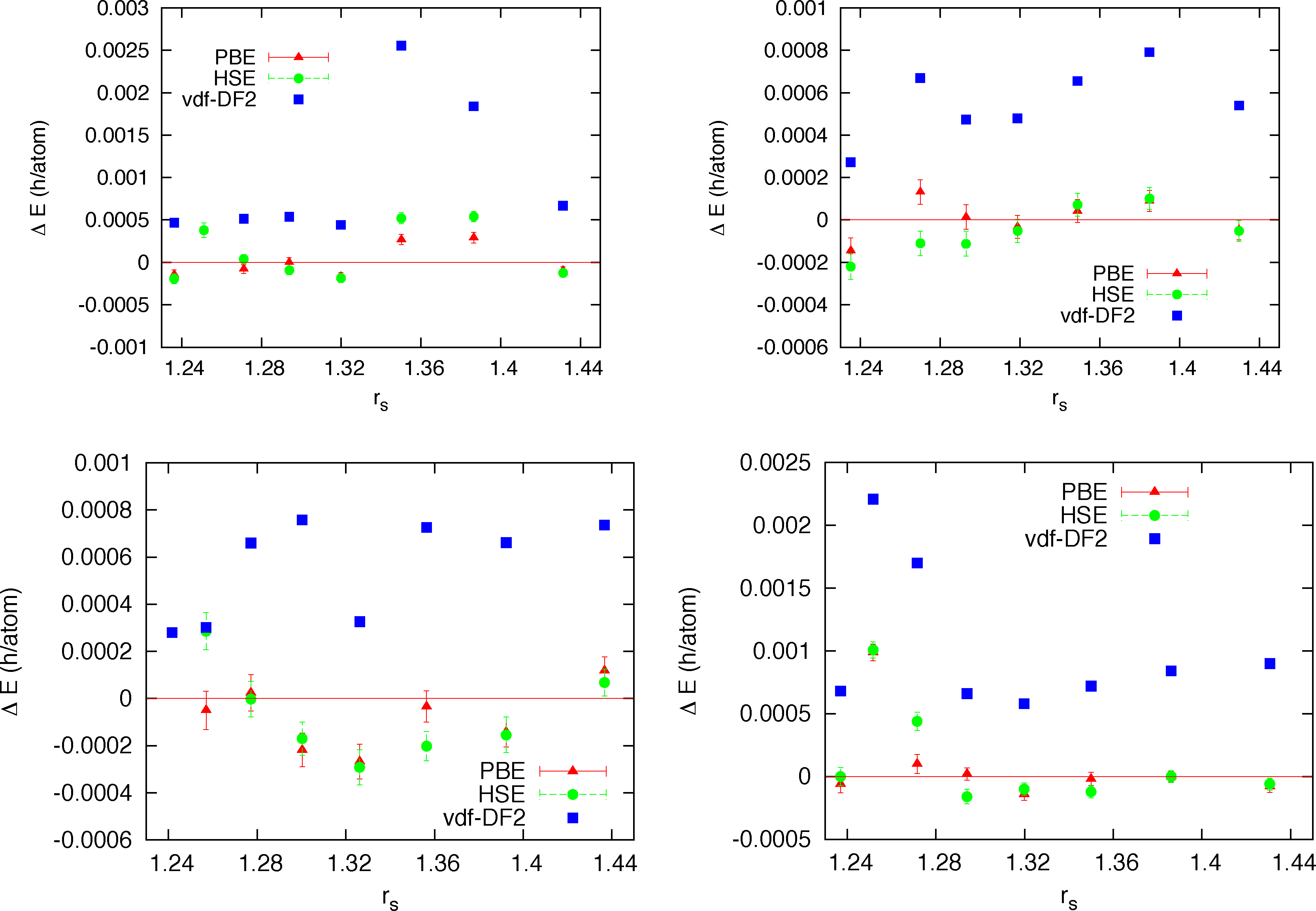
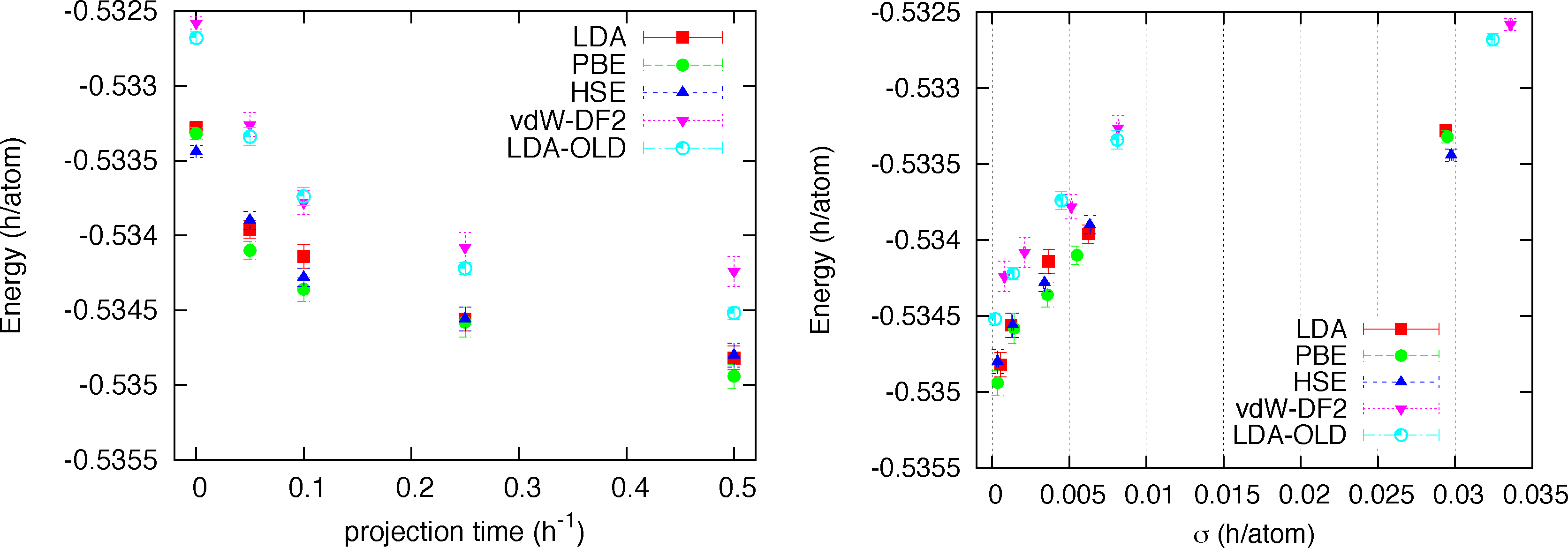
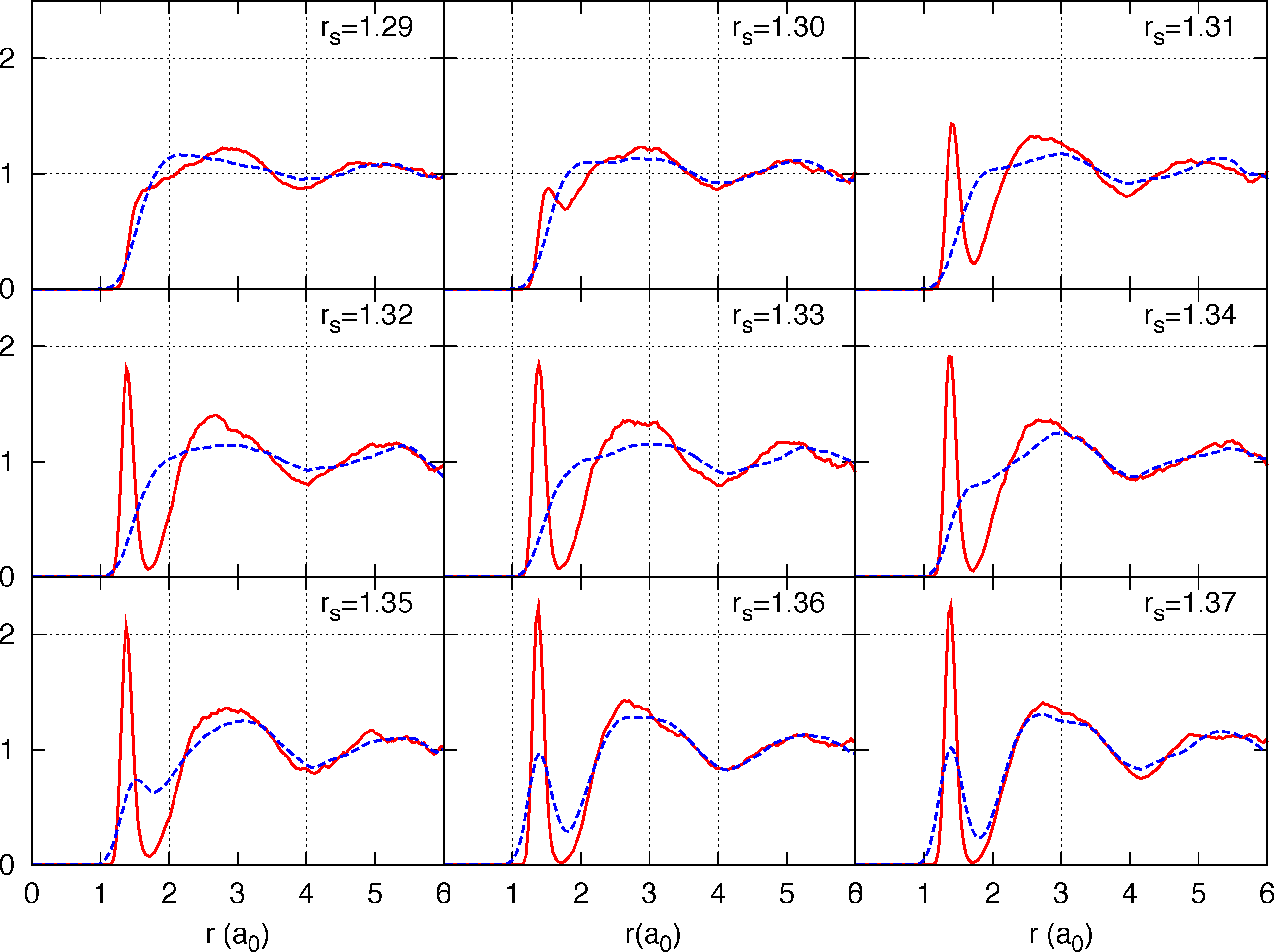
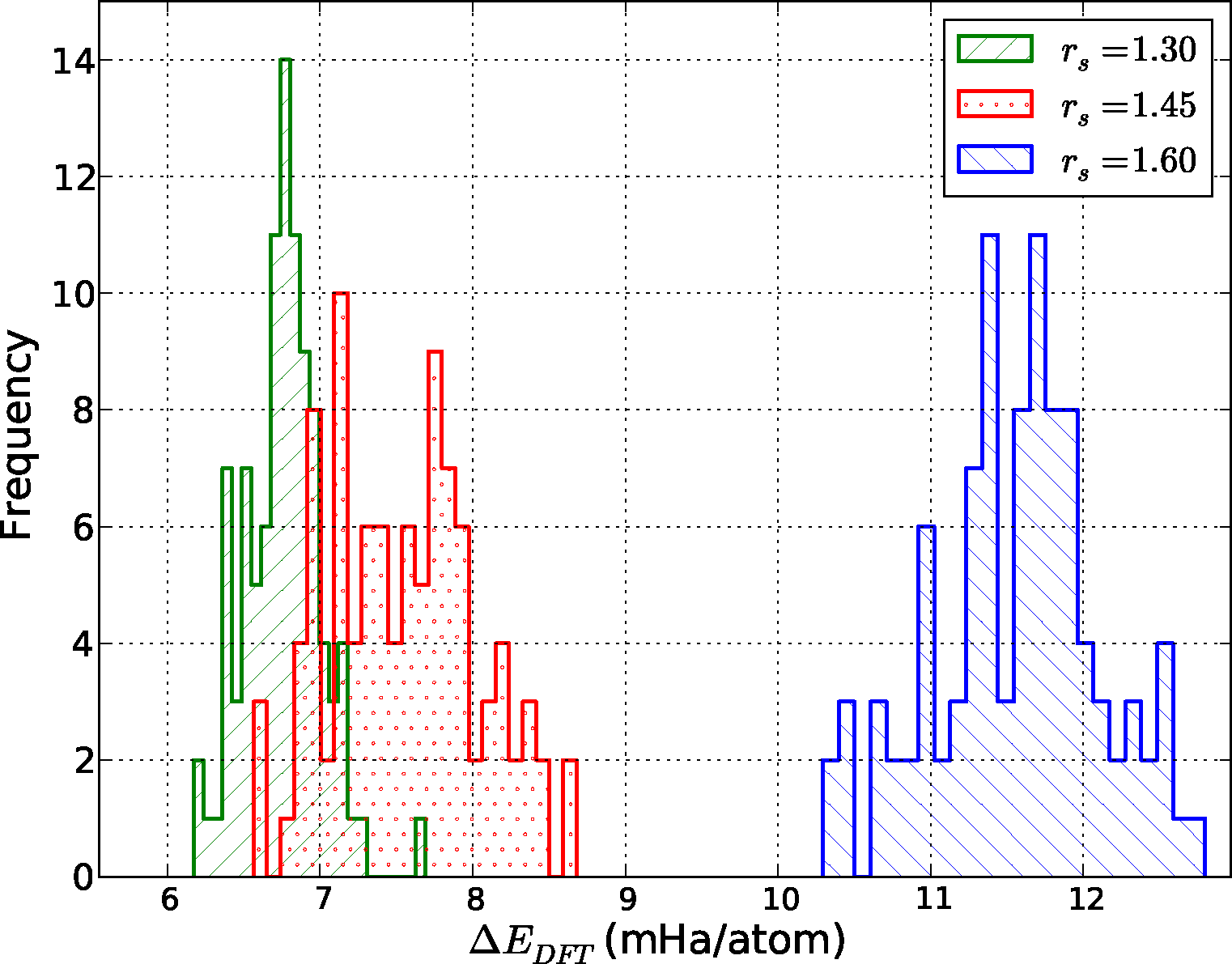
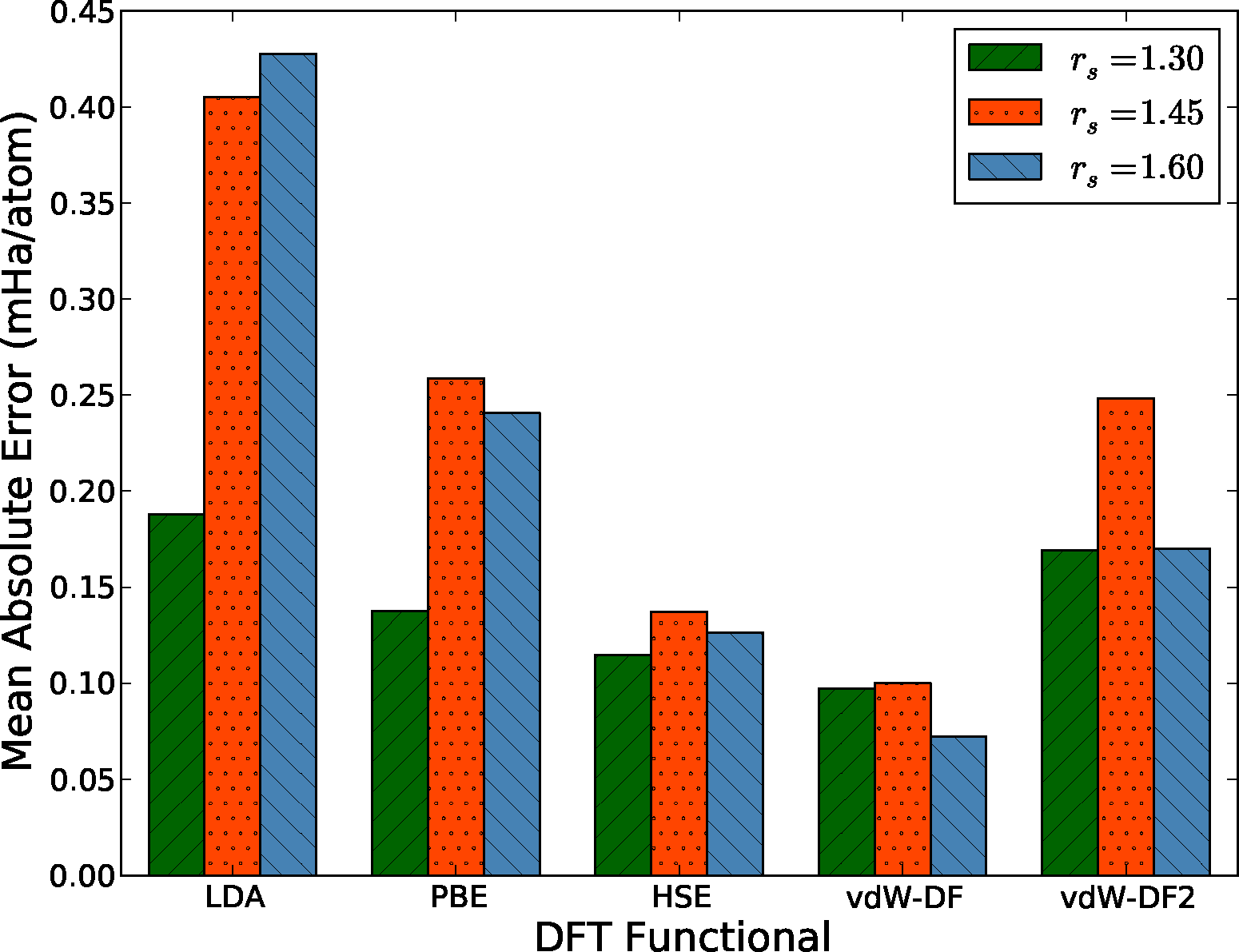
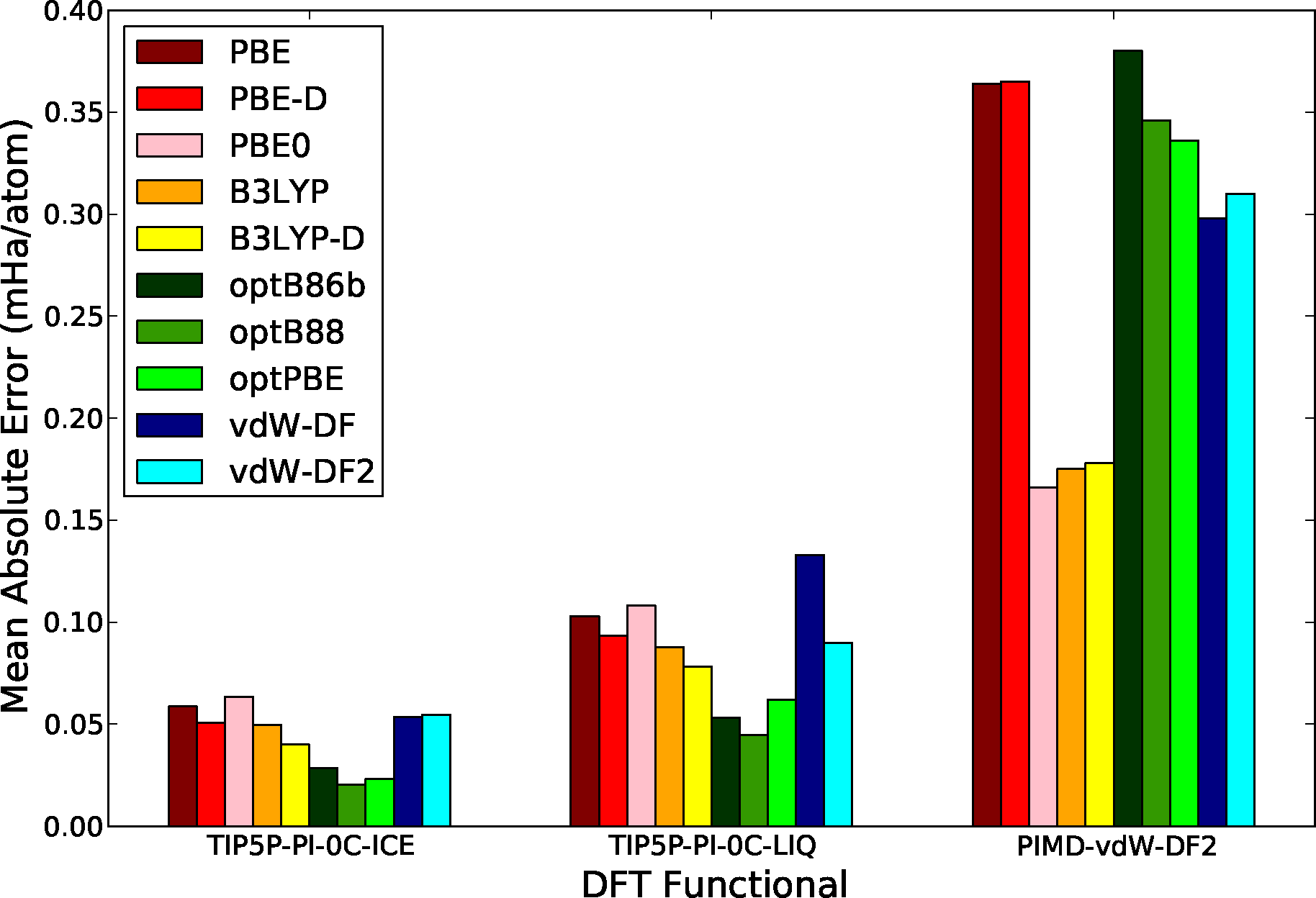
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Morales, M.A.; Clay, R.; Pierleoni, C.; Ceperley, D.M. First Principles Methods: A Perspective from Quantum Monte Carlo. Entropy 2014, 16, 287-321. https://doi.org/10.3390/e16010287
Morales MA, Clay R, Pierleoni C, Ceperley DM. First Principles Methods: A Perspective from Quantum Monte Carlo. Entropy. 2014; 16(1):287-321. https://doi.org/10.3390/e16010287
Chicago/Turabian StyleMorales, Miguel A., Raymond Clay, Carlo Pierleoni, and David M. Ceperley. 2014. "First Principles Methods: A Perspective from Quantum Monte Carlo" Entropy 16, no. 1: 287-321. https://doi.org/10.3390/e16010287




