What is a Multiscale Problem in Molecular Dynamics?
Abstract
: In this work, we make an attempt to answer the question of what a multiscale problem is in Molecular Dynamics (MD), or, more in general, in Molecular Simulation (MS). By introducing the criterion of separability of scales, we identify three major (reference) categories of multiscale problems and discuss their corresponding computational strategies by making explicit examples of applications.1. Introduction
One of the major challenges of Molecular Dynamics (MD) over the last decade has been the development and application of techniques that allow the bridging of length and time scales in a physically consistent way. The relevance of such an effort is obvious: the understanding of the microscopic origin of large-scale properties leads to a deeper knowledge of physical phenomena and, when required, to the design of physical systems with specific properties on demand. The computational and conceptual progress in bridging scales, in condensed matter, material science, chemical physics and related fields, has been rather massive, and nowadays, the expression “multiscale modeling” has become almost routine. However, what is exactly meant by multiscale modeling is not clear yet. Obviously, one must go beyond the approach of combining, in a brute force fashion, different simulation techniques designed for different scales; computers will always give an answer; however, physical consistency must not be violated beyond the level of a controlled error/approximation. In this work, we discuss a possible classification of multiscale problems and relate them to the corresponding computational techniques and to the idea of physical consistency. The paper is organized as follows. Based on the concept of scale separability, that is, how much scales can be separated in a system, we will identify three major categories: problems with “separated scales”, those with “separable scales” and those with “highly-interconnected scales”. Next, we will treat for each case some specific examples taken from applications and discuss the corresponding computational strategy. The final part will be dedicated to one (specific) emerging scale-coupling technique, that is, the adaptive resolution MD approach. This latter allows, in principle, one to describe in a unified simulation framework, the molecular (chemical) origin of large-scale properties and, thus, to interpret the multiscale idea in its full meaning.
2. Separability of Scales
Rather than providing a universal definition of multiscale, we instead introduce an objective criterion and define the idea of multiscale accordingly. The criterion in question is the “separability of scales”, that is, how much in space and time, given some properties or phenomena of interest, scales can be separated in a system. Obviously, this separation is never sharp, and scales are never exactly disjoint; for this reason, this classification must be intended only as a general reference scheme. According to the concept above, we have identified three major categories: “separated scales”, “separable scales” and “highly-interconnected scales”; below, we comment on each specific category.
Separated Scales: This corresponds to the typical situation where simulation data from a scale (let us say), A, are used as input for modeling a molecular system at scale B. Next, simulations at scale B can proceed, and the connection to scale A is no longer required. The corresponding computational strategy goes under the name of “sequential strategy”. Just to give an immediate idea, this is the typical case of molecular-based coarse graining: one needs an atomistic simulation to derive an effective coarse-grained model. Next, the coarse-grained simulation can run without any reference to atomistic details, provided that the properties of interest can be described by the coarse-grained model only.
Separable scales: As for the situation above, scale A is used to model scale B. Next, scale B evolves, but differently from the case above, in this case one needs to go back from B to A, refine the model and start again. A loop-like strategy involves the two scales, i.e., A → B → A → B........ The corresponding computational strategy is usually called a “backmapping scheme”.
Highly-interconnected scales: Scales cannot be separated at all, and actually, it is exactly the interplay between different scales that characterizes the essential physics and chemistry of the system. The corresponding computational strategy requires that the different scales are treated on the same footing in a simultaneous coupling; for this reason, the technique is named “concurrent coupling”.
Above, we have reported, for simplicity, only the case of a two scales problem; however, the extension to multiple scales is obvious. Moreover, in real applications, multiscale problems occupy the spectrum of categories given above in a sort of continuous way and, thus, require various combinations of the computational strategies reported above. It must be clarified that the separability of scales is not the only criterion possible for such a classification. An example of a complementary criterion is the one used by Berendsen: scales’ hierarchy. This stems from deciding a priori which scale is more relevant in a problem rather than looking primarily at how scales are connected [1,2]. An overview of how the idea of multiscale is interpreted in the field of condensed matter, material science, chemical physics and related disciplines, together with recent method developments and applications, can be found in [3,4]. The fact that two relevant journals in the field dedicate an entire issue to the subject is an implicit confirmation of the relevance of the idea within the community of chemists and physicists (and even beyond, e.g., to mathematicians, engineers, biologists). In the next section, we will provide few examples of problems where the abstract classification defined above finds practical application in the field of MD.
3. Separated Scales and Sequential Strategy
Let us start by discussing an example where scales can be separated in a quite good approximation, and thus, the sequential coupling strategy is appropriate. The system we will discuss is that of macromolecular samples on solid inorganic surfaces. There are two main aspects in this problem:
adhesion of the macromolecule at the surface, dominated by the specific local chemistry of the polymer moieties and by the specific reactivity of the surface;
bulk properties of the macromolecular liquid, dominated by molecular packing and by slow equilibration processes.
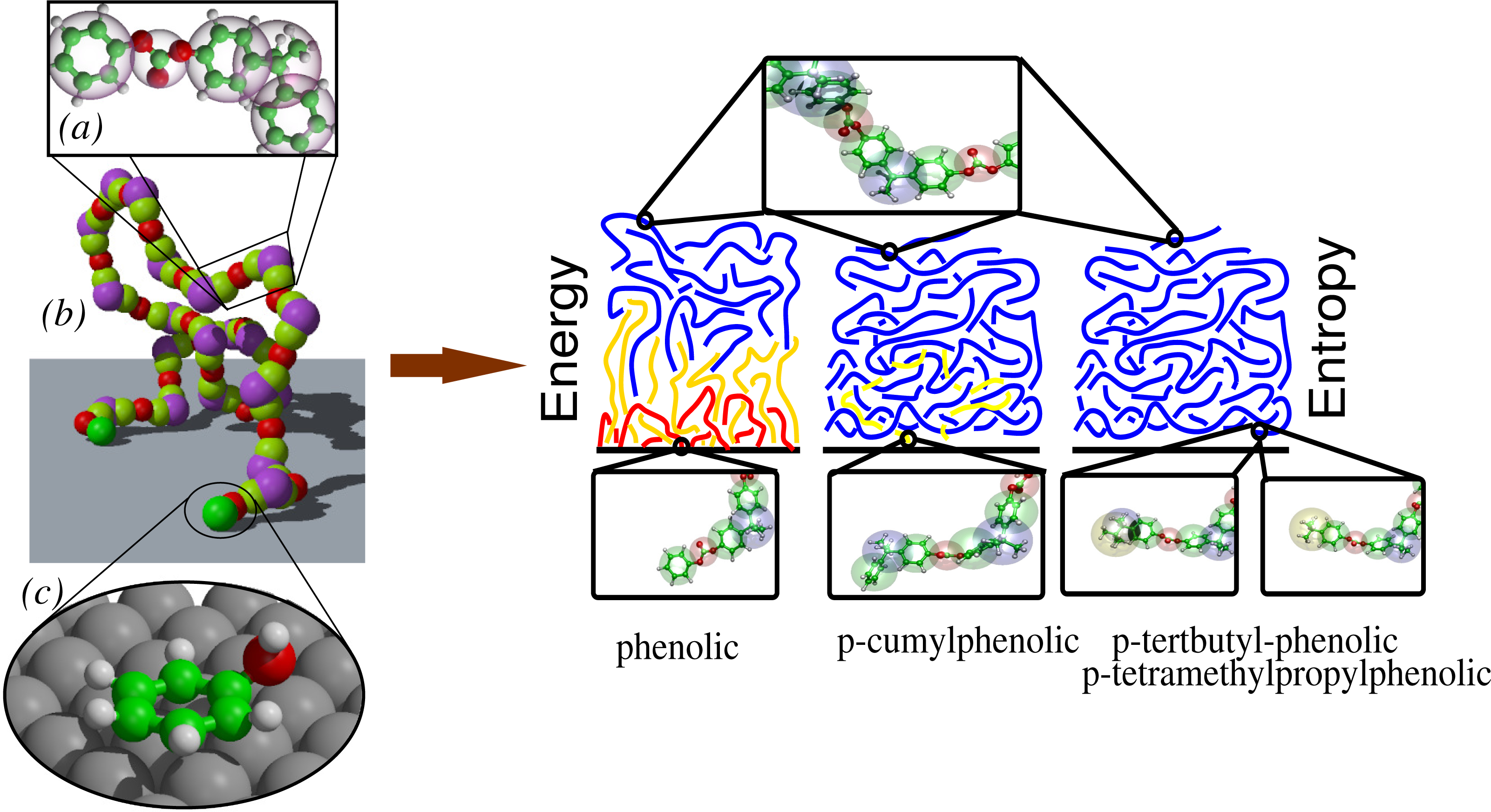
The first aspect requires the detailed description of specific chemistry and its corresponding electronic properties; thus, a quantum mechanical description is mandatory. The second aspect is dominated by the entropic character of the chain entanglements in bulk and, thus, requires classical statistical methods, which properly sample the vast configurational space of a liquid. When we put the solid surface in contact with the macromolecular liquid, the properties of interest are those at the interface. These would emerge as a result of a non-trivial combination of adhesion and molecular packing. From a methodological point of view, this implies that one must combine, in a proper consistent way, quantum mechanics and classical statistical mechanics. As an example, this idea has been put in practice for a polycarbonate melt on a surface of nickel (111) [5,6]. Figure 1 gives a pictorial explanation of the idea. First, quantum mechanical calculations are performed for each isolated polymer subgroup. However, calculations are done by taking into account all possible allowed geometries at the surface consistent with the topological constraints of the large polymer; then, an effective moiety-surface potential is derived. In parallel, a coarse-grained (bead and spring) model for the polymer, which reproduces the bulk properties of the liquid, is derived from short full atomistic simulations. Finally, a coarse-grained simulation of a large system with the quantum-based surface-polymer interaction is performed [7]. In this specific case, we found that only phenolic chain ends experience a strong attraction; internal beads or other suitable chemical modifications of the chain ends, experience the surface as a hard wall. The results of this study allow one, then, to establish whether the interface properties are energy dominated (polymers are grafted onto the surface, and this leads to a sort of brush-like interface structure) or entropy dominated (polymers are topologically confined by a purely repulsive surface, and this leads to a parallel layering of the liquid) [8–10]. The same general idea has been later on extended to the case of the adsorption of large biomolecules out of solution on metal surfaces [11–15].
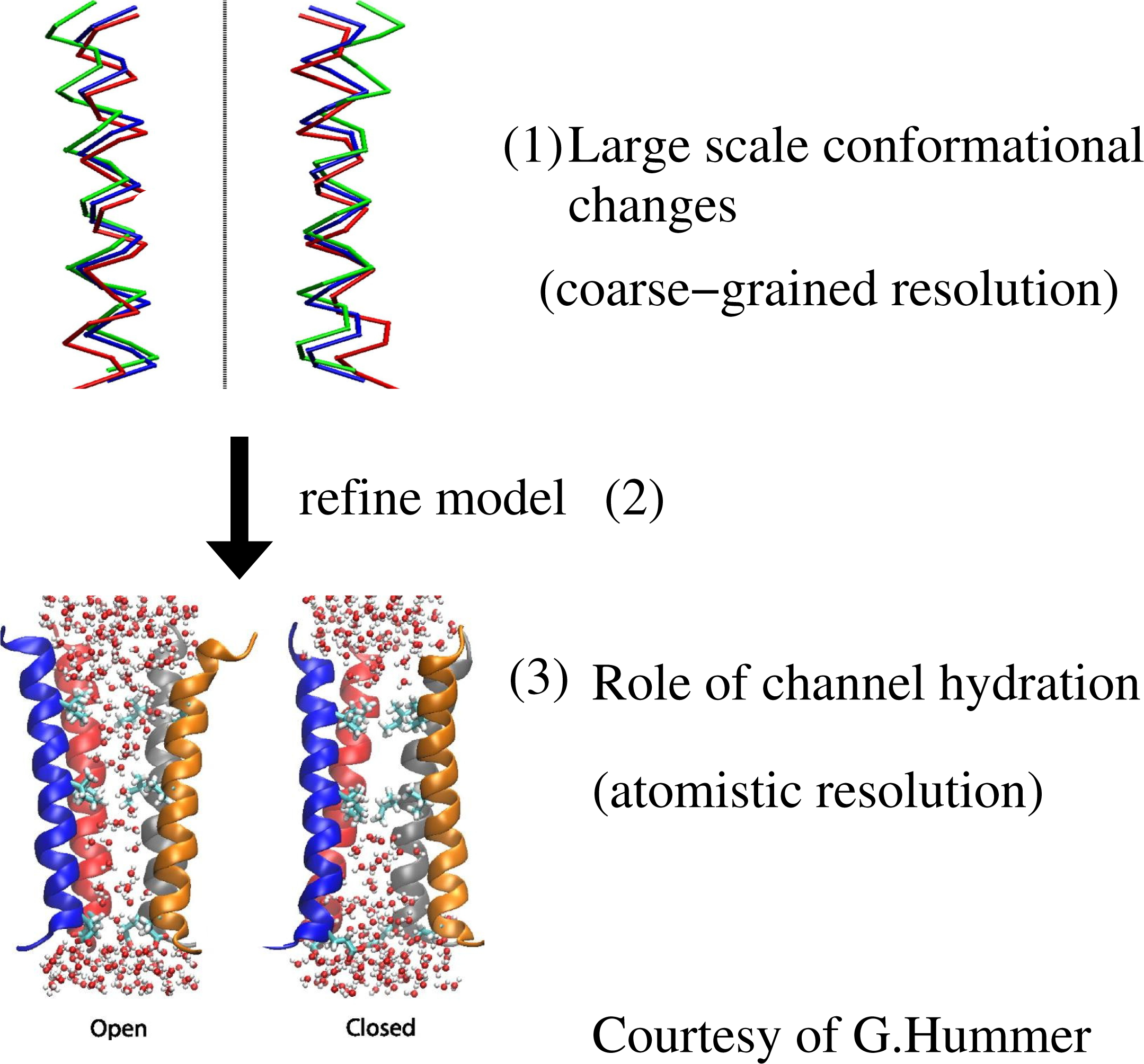
The case illustrated above is a sequential strategy in the “bottom-up” fashion, that is, from a finer to a coarser scale; however, the sequential strategy can be applied in the other direction, in a “top-down” fashion, that is, from a coarse scale down to a refined finer scale. For example, this was done by Zhu and Hummer (see, also, Figure 2 for a pictorial representation) when studying the gating transition in biological ion channels: the transition from opened to closed configuration (and vice versa) is done at a coarse-grained level and later refined at the atomistic level to study the specific role of hydration, which requires the atomistic resolution of water molecules [16,17].
In the next section, we will make a step forward and consider those cases where hopping between scales is required.
4. Separable Scales and Backmapping Strategy
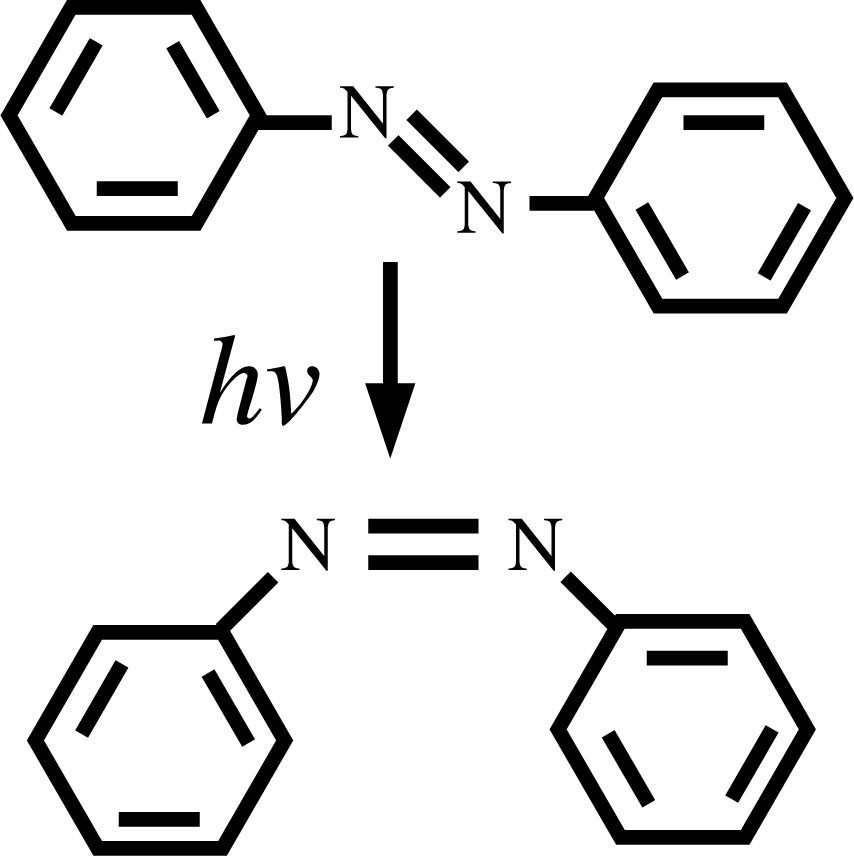
The sequential strategy of the chapter above cannot be applied when, despite a clear separation of scales in space and time, the evolution of the system requires a refinement of the coarser model as the simulation proceeds. This case of “separable”, but not fully separated, scales is illustrated in this section via the example of photoswitchable liquid crystals. The physical ingredients of the problem are the following: liquid crystals containing azobenzene groups (see Figure 3) upon illumination can isomerize by changing conformation from the trans to the cis state.
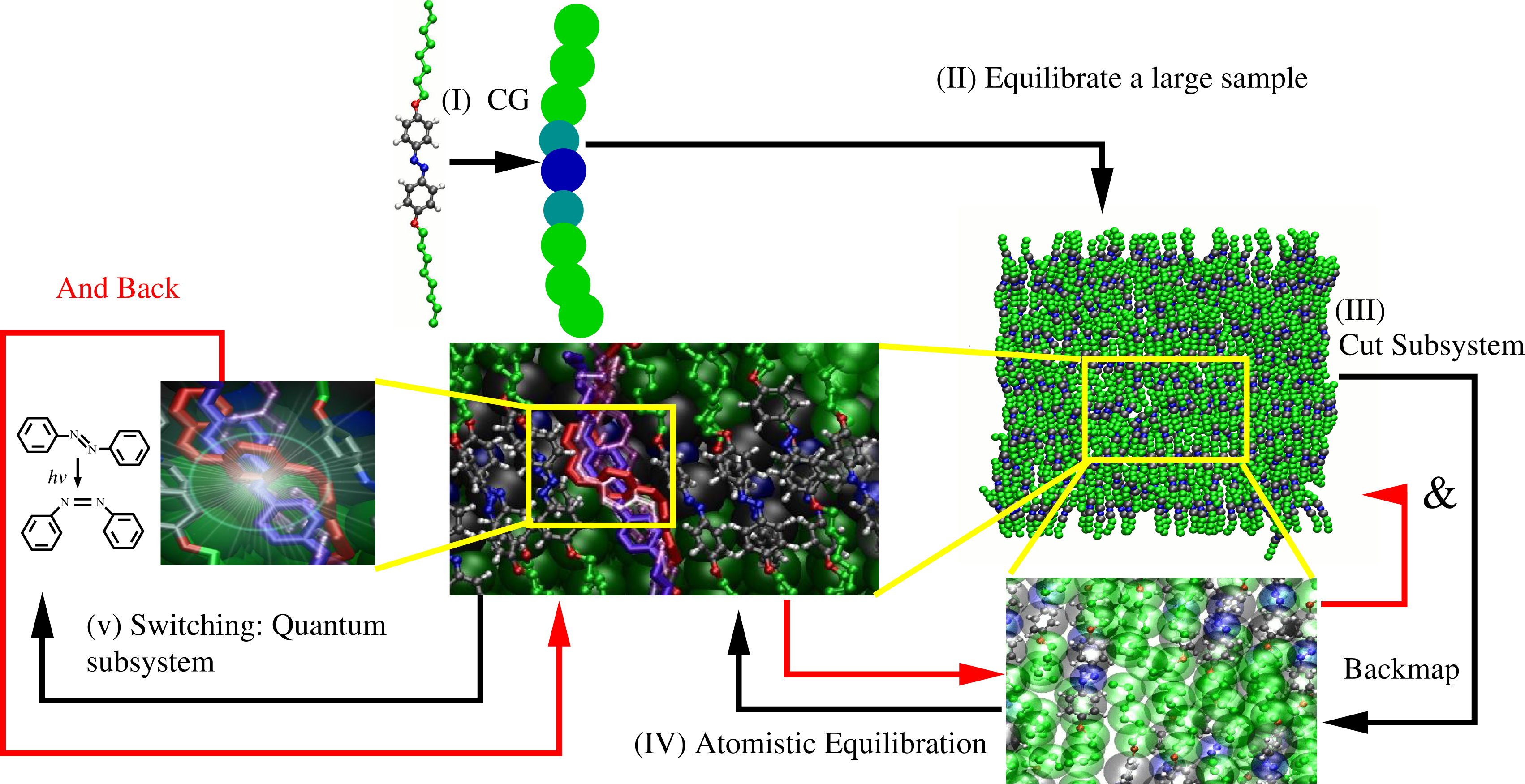
This is the basic mechanism for light-induced mesoscopic transition: upon illumination, one can have a transition from the nematic to the isotropic phase, as shown by Ikeda and Tsutsumi [18]. From the computational point of view, the scales involved are the electronic/quantum, the classical atomistic and the coarse-grained. From the quantum mechanical point of view, one must describe the photoinduced electronic excitation and the possible consequent isomerization. The classical atomistic level is then required, because as the molecule is excited, a certain intermediate conformation is taken; however, the conformation resulting from the de-excitation (i.e., staying in the trans or isomerizing in the cis state) strongly depends on the immediate atomistic environment; this, in turn, leads to a local rearrangement of the surrounding molecules. Finally, the coarse-grained scale is required to describe the large conformational response in the bulk involving the slow relaxation process of the photo-mechanical response. From the point of view of the computational strategy, one needs to link quantum, classical atomistic and coarse-grained in a consistent way [19–22]. Figure 4 illustrates the strategy. First, a coarse-grained model is derived from an all atom simulation of a relatively small system. Next, a large coarse-grained sample is simulated for long enough to have bulk equilibration. From the equilibrated system, a subsystem is cut out, and the atomistic degrees of freedom are mapped back. Next, one runs a simulation that ensures atomistic equilibration, and then, from the atomistic sample, a subsystem is cut out. Next, in this subsystem, the excitation of one molecule is allowed by treating the problem at quantum mechanical level. After the system decays from the excited state and the electronic degrees of freedom are equilibrated, the resulting configuration of the subsystem is reinserted into the the classical atomistic sample, equilibrated at the atomistic level, then, reinserted into the coarse-grained sample and equilibrated at the coarse-grained level; at this point, the loop is repeated. The meaning of separable becomes clear: time scales are separated at least by one order of magnitude (order of femtoseconds for the quantum, at least picoseconds, for the atomistic, and at least nanoseconds, for the coarse grained). Length scales are obviously separated as well, thus space and time scales are separable. However, the process at each scale is intimately linked to the response at the other scale.
At this point, it must be clarified that the idea of the example discussed above can capture, at this stage, only the response of the system to the excitation/de-excitation of one single molecule per time and cannot directly address the question of how many molecules can concurrently undergo the cis-trans transition. In order to model this more realistic scenario, one would require treating larger quantum systems in order to understand how excited molecules influence each other. At the current state-of-the-art, this would imply a prohibitive computational effort, even for the simple case of three molecules treated at the quantum level. Tests (quantum calculations) are being performed for the case of two molecules in order to understand, at a basic level, the mutual influence of excited molecules. The idea, in perspective, is that of including the information obtained by the quantum studies of one molecule and two molecules into a classical model of an azobenzene molecule that can switch mechanically from trans to cis [23], under the hypothesis that, further, many-molecule effects, at the quantum level, may be negligible. Next, one would use the multiscale simulation, including the quantum subsystem, as a reference for a test of basic consistency of the classical model. If the test is satisfactory, then the question of how many molecules can concurrently undergo the cis-trans transition could be treated at the (classical) atomistic-coarse-grained level, keeping in mind that beyond two-molecule correlations, the quantum effects in the switching process are neglected. Obviously, when larger computational resources become available, one could systematically improve the classical model, adding information from larger quantum calculations. Anyway, in the current paper, the specific strategy reported above has to be intended as a typical example of a problem where going back and forward from one scale to another is the main characteristic of the modeling idea; however, from the practical point of view, it shows also that, because of the current computational limitations, the whole complexity of the problem can only be addressed in an approximate way. Nevertheless the relevant message here is that, because of the clear separation of time and length scales, the basic strategy of going back and forward is still the optimal one, even in the case that computational resources were available for studying macroscopic systems. Finally, in the next section, we will describe the case where scales cannot be separated and, thus, a simultaneous coupling of the corresponding computational techniques and models is required.
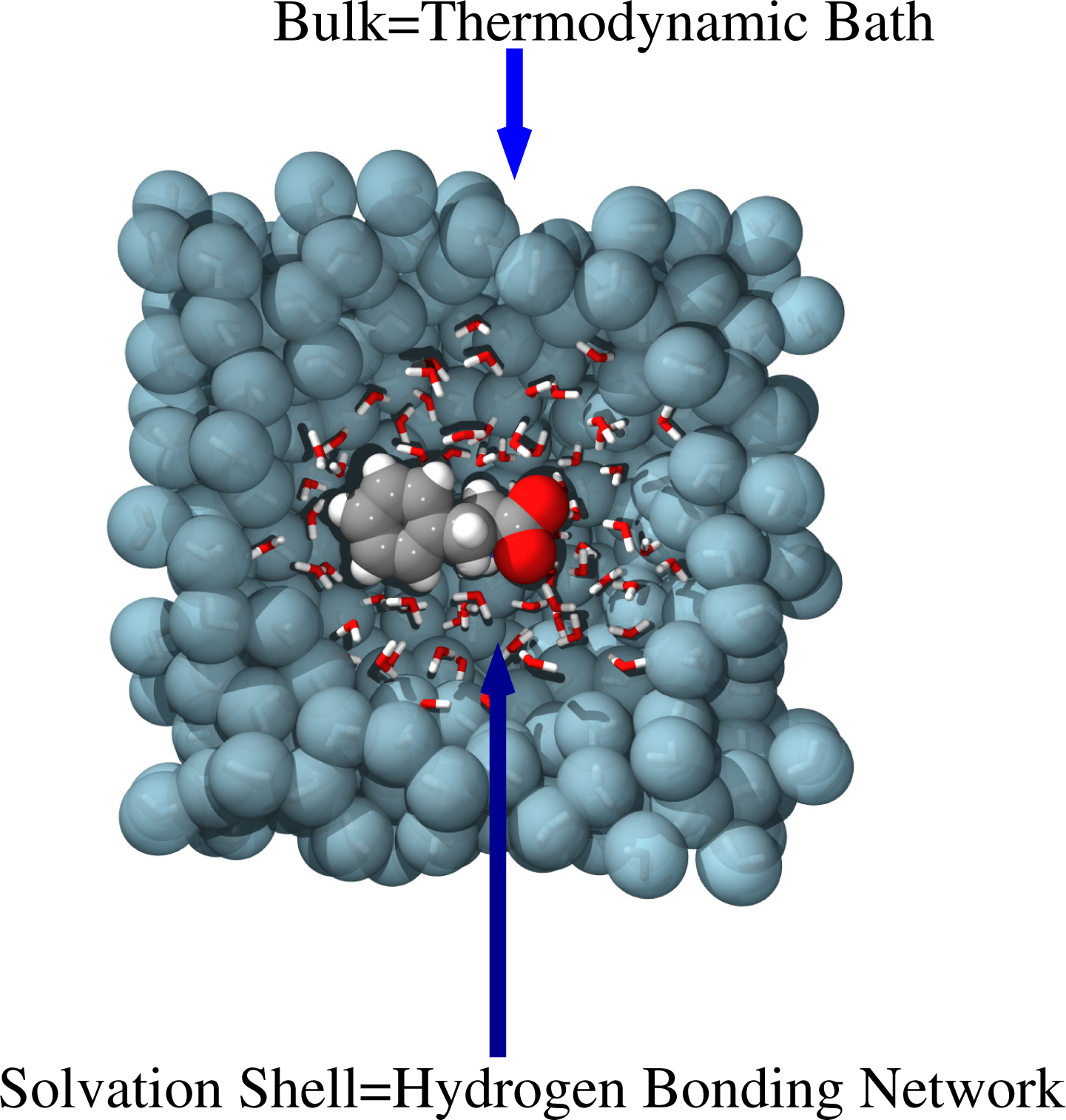
5. Highly-Interconnected Scales and Concurrent Coupling
As reported above, the backmapping strategy is rather efficient if there is a clear separation in length and time scales; however, when scales are intimately interconnected, in most of the cases, the relevant properties of the system are the expression of this interconnection. From the computational point of view, it is then mandatory to adopt strategies where, within a unified approach, all the scales are treated at the same time, i.e., a simultaneous or concurrent coupling of scales. A typical example is that reported in Figure 5 of solvation of molecules in water. High resolution—at least classical atomistic—is needed in the first hydration shells of the molecule, where the explicit formation of the hydrogen bonding network is required, as this uniquely characterizes the solvation of the specific molecule. Far away in the bulk, water plays the role of a thermodynamic bath, and thus, it may be described by coarser models, which reproduce the essential thermodynamic features (e.g., temperature and particle density fluctuations). However, the scale at which the first hydration shells evolve cannot be separated by the thermodynamic scale of the bulk, since between the two regions, there is a simultaneous exchange of information in terms of energy and (eventually) particles.
For this reason, both scales must be treated in a simultaneous fashion, taking care that the overall thermodynamics is well preserved. Popular computational approaches of this kind are, for example, the Quantum Mechanical/Molecular Mechanical (QM/MM) set-ups, where a small quantum region is coupled to a large atomistic or coarse-grained classical region, allowing free exchange of energy (though not particles, see the discussion later on) (see, e.g., [24]). The set-up mentioned above allows then for studying systems where the local process can be linked to the global behavior; for example, in situ simulation of chemical reactions and molecular excitations in solution, where the chemical reaction or the molecular excitation occurs at the quantum level in a small region of the simulation space, while the bulk solvent can be treated at the classical atomistic level [25]. Another example, relevant for mechanical engineering, is that of the crack propagation in solids. The breaking of atomic bonds in the region of the crack must be treated at the quantum level, because this is an electronic property; then, the surrounding region can be described at the classical atomistic level, so that one can see the induced crystal distortion. Finally, the bulk material is described at the continuum (finite elements) level in order to detect its macroscopic mechanical changes. However, all the scales exchange information simultaneously as the crack propagates, and thus, they are coupled in a simultaneous fashion [26]. Although the dividing line between separable scales and interconnected scales is not sharp, one can see a clear difference between the examples reported in this section and that of the azobenzene systems of the previous section. In fact, let us suppose, for example, that we were interested only in the influence of the immediate molecular neighborhood onto the excitation and de-excitation of an azobenzene molecule. In this case, a QM/MM approach would be highly appropriate, because the local liquid structure and its local fluctuations would slowly follow (and at the same time, influence) the evolution of the electronic and conformational properties of the excited molecule. In fact, in the multiscale study of the azobenzene system, the QM/MM approach was used for quantum calculations; however, the macroscopic response of the bulk cannot be predicted only by QM/MM calculations, because it would require a size for the MM system and a time scale that are, at this stage, computationally prohibitive. For this reason, the coarse-grained approach for obtaining relaxed macroscopic configurations is in this case mandatory. The three categories of problems so far discussed provide an overview of what in the literature can be classified as multiscale. However, there is an underlying general message in all the examples made: multiscale essentially means the interplay between local and global aspects (in space and time). Thus, the detailed understanding of the molecular origin of macroscopic properties requires a step forward, beyond the strategies shown so far (or their possible combinations). This will be discussed in the next chapter, where we introduce the idea of adaptive resolution simulation.
6. Molecular Origin of Macroscopic Properties: Zooming in at the Molecular Scale
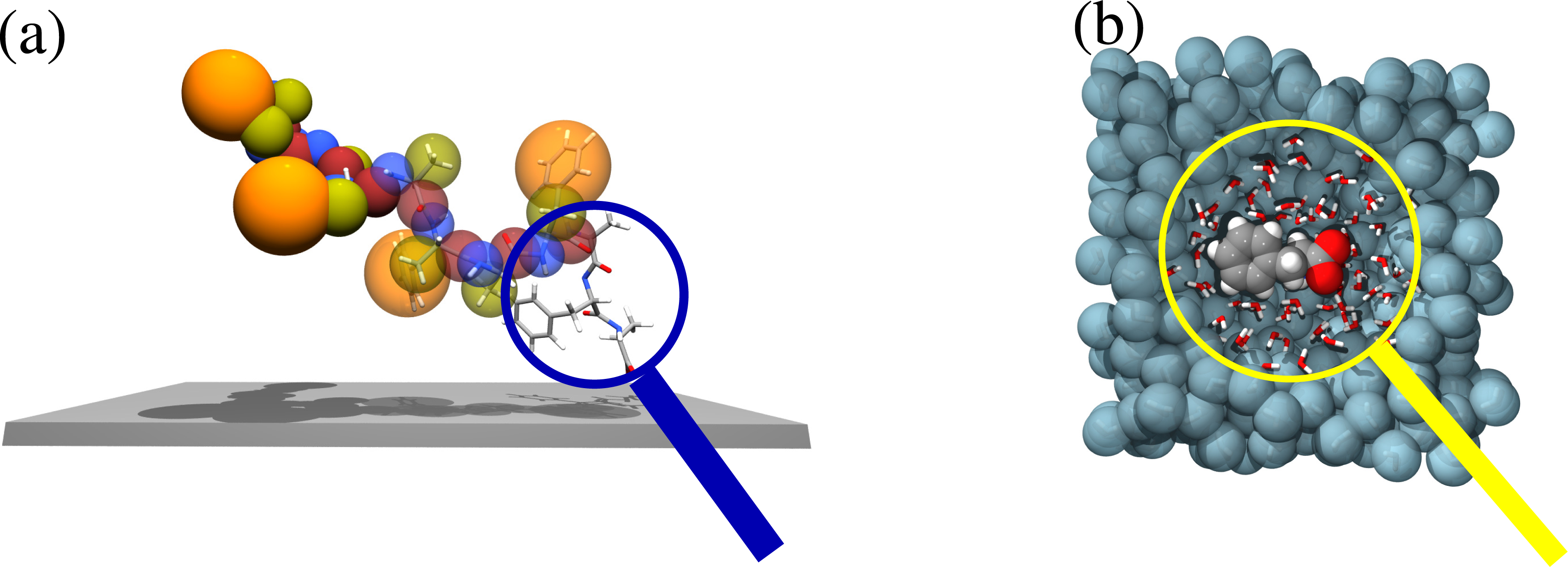
The molecular origin of macroscopic properties can be understood by zooming in (and out) in the region where the relevant microscopic physics and chemistry is taking place.
Figure 6 explains this idea for two examples previously discussed, namely, the adsorption of a large molecule on a solid surface and the solvation of a molecule in water. In the first case, while the molecule is far away from the surface, the only relevant physics is related to the proper sampling of the conformational space of the backbone; thus, a simplified bead and spring model would be sufficient for this purpose. Instead, as the molecule approaches the surface, one needs to zoom in (put the system under a magnifying glass) at the contact region and have an explicit atomistic description, so that the chemical recognition between the molecule and the surface can be properly described and be understood together with the consequent conformational rearrangement of the rest of the molecule (at a coarser scale). The same kind of idea applies to the solvation of molecules in water; the specific solvation structures of the liquid can be understood by zooming in at the hydration region around the solute: when a water molecule enters under the viewing region of the magnification glass, it must be described at the atomistic level; when it leaves, it then takes a coarse-grained description. This process requires that the high resolution region be open and allow for a free exchange of molecules. This, from the methodological point of view, implies that one must go beyond the idea of concurrent coupling to that of “adaptive resolution simulation”.
6.1. Beyond Concurrent Coupling: Adaptive Resolution Molecular Dynamics
From the methodological point of view, the essential requirements of an adaptive resolution molecular dynamics scheme are the following:
- (i)
The algorithm should change molecular resolution in a subregion of the space, leaving the rest of the system at lower resolution.
- (ii)
It should allow for free exchange of molecules from the high resolution to the low resolution region and vice versa.
- (iii)
Finally, the process of (i) and (ii) should occur under conditions of thermodynamic equilibrium: i.e., the same particle density, same temperature and same pressure all over the simulation box (ρatom = ρcg, ρatom = ρcg, Tatom = Tcg).
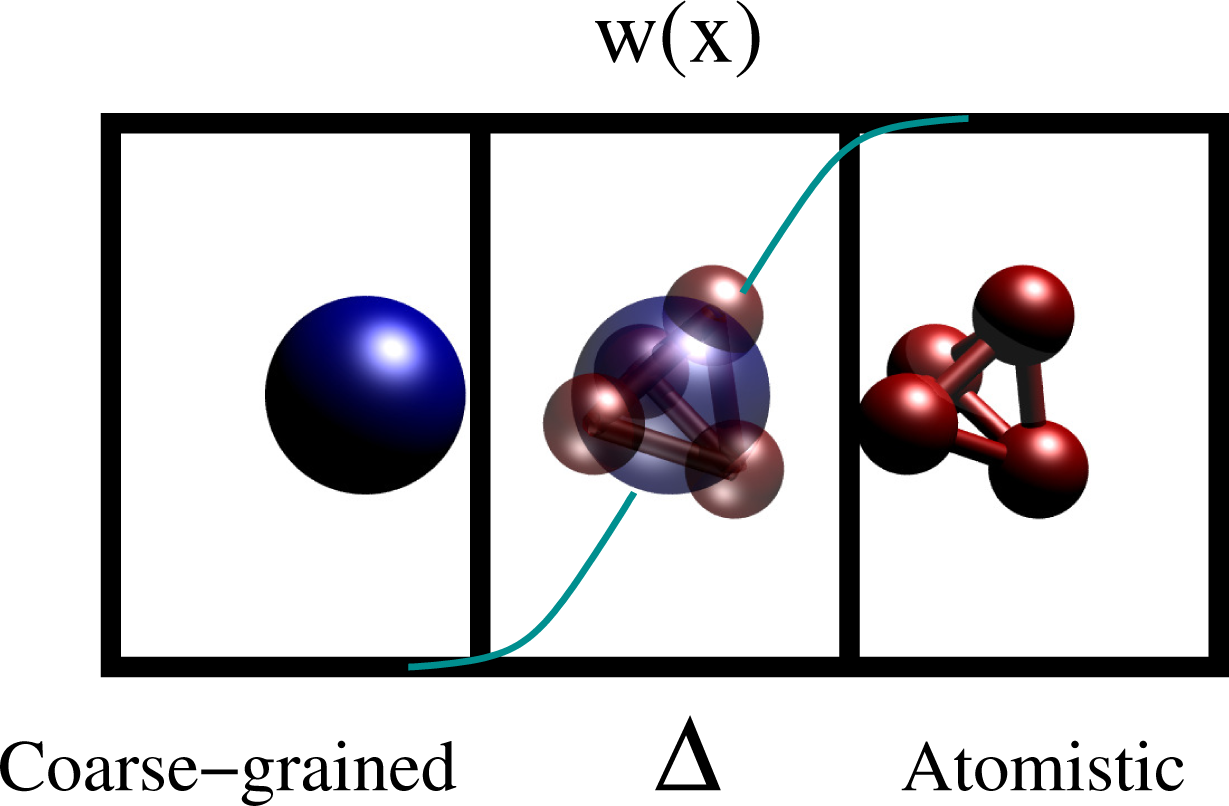
Of course, the thermodynamic state point must be the same as if the whole system was described at high resolution. Several adaptive resolution methods, which sometimes satisfy and sometime do not satisfy the requirements above, have been proposed in the last few years [27–31]. While most of the methods can switch only between two resolutions, the AdResS method has extended the idea of adaptivity from the quantum description of atoms [32–34] to the continuum description of a liquid [35,36]. The original idea was to have an on-the-fly interchange between atomistic and coarse-grained description of a liquid through a two-stage procedure. First, develop an effective, coarse-grained pair potential, Ucm, from the reference all atom simulation. Next, the atomistic and coarse-grained resolutions are coupled through an interpolation formula on the forces:
Here, α and β are the labels of two molecules, is the force derived from the atomistic potential and is the force derived from the coarse-grained potential. Xα and Xβ are the coordinates of the center of mass of, respectively, the molecule α and the molecule β. The multiplicative function, w(x), is zero in the coarse-grained region, one in the atomistic region and smooth and monotonic in an intermediate region, Δ. Figure 7 shows the idea for a test molecule (tetrahedral molecule), left, coarse grained, in Δ, a hybrid resolution according to w(x) and, on the right, atomistic.
With this set-up, two atomistic molecules interact as atomistic, coarse-grained molecules interacts with all the others as coarse-grained pairs (coarse-grained molecules do not posses any atomistic degrees of freedom), while for the other cases, molecules interact according to their coupled value of w(Xα)w(Xβ) with hybrid resolutions. This means that a molecule that goes from the atomistic to the coarse-grained region slowly looses its atomistic degrees of freedom (rotations and vibrations) and becomes an effective sphere, going through a continuous stage of hybrid resolutions in Δ. The same process, but in the opposite direction (acquiring degrees of freedom) occurs to a coarse-grained molecule moving towards the atomistic region. At this point, the “technical” meaning of “loosing” or “acquiring” degrees of freedom in the boundary (hybrid) region that divides the atomistic and the coarse-grained region must be clarified. All molecules of the system, independently of their position in space, retain the full atomistic structure. For a molecule, α, in the hybrid region, the force acting on each single atom (derived from the atomistic potential) is weighted by an amount, w(Xα), multiplied by the weight, w(Xβ), of the paired molecule, β, and, by construction, the remaining total force acting on the molecule (derived from the coarse-grained potential) is assigned to the center of mass by the weighting term, [1–w(Xα)w(Xβ)]. Since w(x) goes to zero in the coarse-grained region, the closer the molecule is to the coarse-grained region, the weaker is the force (derived from the atomistic potential) acting on each atom (and the larger the force on the center of mass). When the molecule enters into the coarse-grained region, the only force acting on the molecule is that on the center of mass, independently of the resolution of the paired molecule. The forces acting on each atomistic degrees of freedom coming from the atomistic potential are no more considered, although the underlying atomistic structure is artificially kept for technical reasons. In practice, the interactions of the atomistic degrees of freedom for this molecule are no more explicitly considered. This implies that their contributions to the dynamic evolution and to the energy of the system disappear. Moreover, the internal kinetic energy of the molecule (i.e., kinetic energy associated with rotations and internal vibrations) is also not considered in the calculation of the properties of the system (thus, effectively, the molecule behaves as a sphere). The computational gain consists of a drastically reduced number of interactions that needs to be calculated. Vice versa, when a molecule enters into the transition region, the force acting on each single atom is slowly reactivated according to the weight, w(Xβ) (and to the weight of the paired molecule, w(Xβ)). When the molecule reaches the atomistic region, we have w(Xα) = 1, and thus, it interacts in the standard full atomistic manner with molecules of the atomistic region, while for the interaction with molecules in other regions, the weight on the atomistic force depends only on the position of the paired molecule (above is commented the extreme case of the paired molecule being in the coarse-grained region). A detailed explanation of all the technical details of the implementation of this idea can be found in [37]. Obviously, in the diving boundary region between the atomistic and coarse-grained region, one must properly deactivate/reactivate the atomistic degrees of freedom. This is done by introducing an external source of heat (thermostat), which acts locally on each degree of freedom in order to assure that despite the deactivated/reactivated degrees of freedom, the temperature in this region is the same as the target one (that is, the temperature of the atomistic and of the coarse-grained systems) [38–40]. Additionally an external force derived on the basis of the first principles of thermodynamics (i.e., a force that balances the difference of the chemical potential between the atomistic region and the rest of the system) [41] is added to assure thermodynamic equilibrium. The natural question for a such molecular dynamics scheme is whether the force of Equation (1) is conservative, and the answer is negative. In fact, despite a different claim [29,42,43], it has been shown both analytically [44] and numerically [45] that within this scheme, there is no possibility of deriving Equation (1) from a potential. According to the statement above, a natural conclusion is that without a conservative force one cannot be in the microcanonical (or canonical) ensemble, and thus, even time-independent properties cannot be accurately calculated. However, it has been shown that the atomistic region (the most delicate case) is characterized by a Grand Canonical distribution [46], and thus, the method reproduces the same statistics of the equivalent region in a full atomistic system (the key property of any valid adaptive resolution method!). Moreover, an exact Hamiltonian can be written for the atomistic (and coarse-grained) region, where exact means that each term of the Hamiltonian is physically well defined without introducing any artificial (unphysical) quantity; this, then, allows for a full Grand Canonical-like formalization of the adaptive set-up [47,48]. In general, all the relevant properties (radial distribution functions, density distribution across the simulation box, molecular diffusion, particle density fluctuations and solvation structures) determined via full atomistic simulation for several liquids and solvated systems were properly reproduced (see, e.g., [27,38,41,49–53]). However, a key issue remains unresolved, that is, whether or not there exists a well-founded Hamiltonian route to adaptive resolution simulation. If a Hamiltonian approach exists, it must fulfill the following necessary requirements:
It should lead to the correct limits. That is, it should be an atomistic Hamiltonian in the atomistic region and a coarse-grained Hamiltonian in the coarse grained region
It should automatically lead, in the atomistic region, to a spatial probability distribution, which is the same as that in the corresponding subregion in a full atomistic simulation.
Recently, Potestio et al. proposed a global Hamiltonian approach of AdResS [54]. This is based on the interpolation in space of the atomistic and coarse-grained potential, that is, in this case, the potential is interpolated instead of the forces, as in the standard AdResS. The idea provides an elegant thermodynamic procedure of how to equilibrate the system, but, by construction, cannot satisfy the requirement of correct limit according to [44]. In fact, an additional force is generated by the gradient of the weighting function, w(x). This force induces an unphysical flux of particles from one region to another. In order to balance this flux, an additional field must be added to the original Hamiltonian. In [54], an elegant thermodynamic procedure is used to determine this field. However, in [44], it has been shown that such a field is a solution of a first order partial differential equation, and in order to describe a proper adaptive system, it requires that the field satisfies two boundary conditions; that is, it must be zero in the atomistic and in the coarse-grained region. Since the equation is of the first order, only one boundary condition can be used to fix the solution. Let us suppose we fix the boundary condition in the atomistic region; then, inevitably, in the coarse-grained region, the original potential is changed by an artificial, unphysical additional term. This implies that if we, ideally, shrink the atomistic region to zero, we do not recover the original coarse-grained potential. The additional term is constant in space, but strongly depends on the size of the system; although this may turn out to be a non-relevant aspect from the technical point of view, however, from the conceptual point of view, this makes the Hamiltonian, and, thus, the corresponding adaptive process, artificial. Moreover, at a more practical level, according to [48], as it stands now, the method can assure that in the atomistic region (when compared to a reference full atomistic simulation), only the first order of the probability distribution of the system, that is, the molecular number density, can be obtained with high accuracy. Higher orders, as atom-atom (or even molecule-molecule) radial distribution functions or three-body correlations, do not come automatically. Nevertheless, the approach of [54] may represent the closest (somehow “first order”) procedure for a truly adaptive Hamiltonian procedure with the further, major, advantage of the possibility of performing adaptive Monte Carlo simulations [55]. In conclusion, a truly, satisfactory, adaptive Hamiltonian has not been found yet, and my personal opinion is that this is not really needed; however, the cultural barrier in the MD community is such that, unfortunately, a method without a Hamiltonian is seen as a problem, rather than an alternative to the standard routes. The consequence is that often, the various additions to the original idea of AdResS, despite being based on clear thermodynamic arguments, are considered more at the level of practical patches, to cover, at the best, unavoidable conceptual holes, due to the lack of a Hamiltonian, rather than a natural methodological evolution per se.
On the other hand, one should keep in mind the following: the constraint that the atomistic region of the adaptive simulation should reproduce the probability distribution of the full atomistic system (that is, the key criterion to evaluate the quality of any adaptive method) can be easily implemented within the standard force-based AdResS, but (so far) not in a Hamiltonian one [48]. In [47,48], first principles, analytic/numerical conditions on the probability distribution of the system have been defined in such a way that the accuracy in the high resolution region can be controlled and systematically improved. Moreover, in [48], it has been also shown that the method is also a very powerful tool for the calculation of the chemical potential of complex liquids, at a computational cost that is orders of magnitude below that of the Insertion Particle Method, routinely used for calculating such a quantity.
7. Conclusions
We have addressed the question of how to provide a concrete meaning to the expression multiscale modeling in Molecular Dynamics (simulation). The use of the criterion of separability of scale allows for classifying multiscale problems in three main categories. Next, the most popular computational strategies adopted for each category have been discussed. In this perspective, we have underlined the role of the concurrent coupling of scales via the idea of adaptive molecular resolution. In principle, this approach can be considered a truly multiscale technique, which acts as a sort of computational microscope to determine the molecular origin of the large-scale behavior of matter. In fact, it can zoom in to the very microscopic detail and zoom out to the large-scale behavior while the simulation is running. Future developments should be focused on including electronic resolution and, thus, address the question of interfacing a quantum and a classical system in a physically-consistent way.
Acknowledgments
This work was supported by the Deutsche Forschungsgemeinschaft (DFG) within the Heisenberg program (grant code DE 1140/5-1).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berendsen, H.J.C. Simulating the Physical World, Hierarchical Modeling from Quantum Mechanics to Fluids; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Berendsen, H.J.C. Concluding remarks. Faraday Discuss 144, 467–481.
- Themed issue: Multiscale modeling of soft matter. Faraday Discuss 2010, 144, 1–494.
- Themed issue: Multiscale modeling. Phys. Chem. Chem. Phys. 2010, 13, 10381–10583.
- Delle Site, L.; Abrams, C.F.; Alavi, A.; Kremer, K. Polymers near metal surfaces: Selective adsorption and global conformations. Phys. Rev. Lett 2002, 89, 156103. [Google Scholar]
- Delle Site, L.; Kremer, K. Multiscale modeling of polymers on a surface: From ab initio Density Functional calculations of molecular adsorption to large scale properties. Int. J. Quant. Chem 2005, 101, 733–739. [Google Scholar]
- Abrams, C.F.; Delle Site, L.; Kremer, K. Dual-resolution coarse-grained/atomistic simulation of the bisphenol-a-polycarbonate/nickel interface. Phys. Rev. E 2003, 67, 021807. [Google Scholar]
- Delle Site, L.; Leon, S.; Kremer, K. BPA-PC on a Ni(111) surface: The interplay between adsorption energy and conformational entropy for different chain-end modifications. J. Am. Chem. Soc 2004, 126, 2944–2955. [Google Scholar]
- Delle Site, L.; Leon, S.; Kremer, K. Specific interaction of polymers with surface defects: Structure formation of polycarbonate on nickel. J. Phys. Condens. Matter 2005, 17, L53–L60. [Google Scholar]
- Andrienko, D.; Leon, S.; Delle Site, L.; Kremer, K. Adhesion of polycarbonate blends on a nickel surface. Macromolecules 2005, 38, 5810–5816. [Google Scholar]
- Schravendijk, P.; van der Vegt, N.F.A.; Delle Site, L.; Kremer, K. Dual scale modeling of benzene adsorption onto Ni(111) and Au(111) surfaces in explicit water. Chem. Phys. Chem 2005, 6, 1866–1871. [Google Scholar]
- Ghiringhelli, L.M.; Schravendijk, P.; Delle Site, L. Adsorption of alanine on a Ni(111) surface: A multiscale modeling oriented density functional study. Phys. Rev. B 2006, 74, 035437. [Google Scholar]
- Schravendijk, P.; Ghiringhelli, L.M.; Delle Site, L.; van der Vegt, N.F.A. Interaction of hydrated amino acids with metal surfaces: A multiscale modeling description. J. Phys. Chem. C 2007, 111, 2631–2642. [Google Scholar]
- Ghiringhelli, L.M.; Delle Site, L. Phenylalanine near inorganic surfaces: Conformational statistics vs. specific chemistry. J. Am. Chem. Soc 2008, 130, 2634–2638. [Google Scholar]
- Ghiringhelli, L.M.; Hess, B.; van der Vegt, N.F.A; Delle Site, L. Competing adsorption between hydrated peptides and water onto metal surfaces: From electronic to conformational properties. J. Am. Chem. Soc 2008, 130, 13460–13464. [Google Scholar]
- Zhu, F.; Hummer, G. Gating transitions of pentameric ligand-gated ion channels. Biophys. J 2009, 97, 2456–2463. [Google Scholar]
- Zhu, F.; Hummer, G. Pore opening and closing of a pentameric ligand-gated ion channel. Proc. Natl. Acad. Sci. USA 2010, 107, 19814–19819. [Google Scholar]
- Ikeda, T.; Tsutsumi, O. Optical switching and image storage by means of azobenzene liquid-crystal films. Science 1995, 268, 1873–1875. [Google Scholar]
- Böckmann, M.; Peter, C.; Delle Site, L.; Doltsinis, N.; Kremer, K.; Marx, D. Atomistic force field for azobenzene compounds adapted for QM/MM Simulations with applications to liquids and liquid crystals. J. Chem. Theory Comput 2007, 3, 1789–1802. [Google Scholar]
- Peter, C.; Delle Site, L.; Kremer, K. Classical simulations from the atomistic to the mesoscale and back: Coarse graining an azobenzene liquid crystal. Soft Matter 2008, 4, 859–869. [Google Scholar]
- Böckmann, M.; Marx, D.; Peter, C.; Delle Site, L.; Kremer, K.; Doltsinis, N. Multiscale modelling of mesoscopic phenomena triggered by quantum events: Light-driven azo-materials and beyond. Phys. Chem. Chem. Phys 2011, 13, 7604–7621. [Google Scholar]
- Mukherjee, B.; Delle Site, L.; Kremer, K.; Peter, C. Derivation of coarse grained models for multiscale simulation of liquid crystalline phase transitions. J. Phys. Chem. B 2012, 116, 8474–8484. [Google Scholar]
- Böckmann, M.; Doltsinis, N.; Marx, D. Azobenzene photoswitches in bulk materials. Phys. Rev. E 2008, 78, 036101. [Google Scholar]
- Warshel, A.; Lewitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol 1976, 103, 227–249. [Google Scholar]
- Röhrig, U.F.; Frank, I.; Hutter, J.; Laio, A.; VandeVondele, J.; Rothlisberger, U. QM/MM Car-Parrinello molecular dynamics study of the solvent effects on the ground state and on the first excited singlet state of acetone in water. Chem. Phys. Chem 2003, 4, 1177–1182. [Google Scholar]
- Lu, G.; Tadmor, E.B.; Kaxiras, E. From electrons to finite elements: A concurrent multiscale approach for metals. Phys. Rev. B 2006, 73, 024108. [Google Scholar]
- Praprotnik, M.; Delle Site, L.; Kremer, K. Adaptive resolution molecular dynamics simulation: Changing the degrees of freedom on the fly. J. Chem. Phys 2005, 123, 224106. [Google Scholar]
- Praprotnik, M.; Delle Site, L.; Kremer, K. Multiscale simulation of soft matter: From scale bridging to adaptive resolution. Annu. Rev. Phys. Chem 2008, 59, 545–571. [Google Scholar]
- Ensing, B.; Nielsen, S.O.; Moore, P.B.; Klein, M.L.; Parrinello, M. Energy conservation in adaptive hybrid atomistic/coarse-grain molecular dynamics. J. Chem. Theory Comput 2007, 3, 1100–1105. [Google Scholar]
- Heyden, A.; Truhlar, D.G. Conservative algorithm for an adaptive change of resolution in mixed atomistic/coarse-grained multiscale simulations. J. Chem. Theory Comput 2009, 4, 217–221. [Google Scholar]
- S.Izvekov, I.; Voth, G.A. Mixed resolution modeling of interactions in condensed-phase systems. J. Chem. Theory Comput 2009, 5, 3232–3244. [Google Scholar]
- Poma, A.B.; Delle Site, L. Classical to path-integral adaptive resolution in molecular simulation: Towards a smooth quantum-classical coupling. Phys. Rev. Lett 2010, 104, 250201. [Google Scholar]
- Poma, A.B.; Delle Site, L. Adaptive resolution simulation of liquid para-hydrogen: Testing the robustness of the quantum-classical adaptive coupling. Phys. Chem. Chem. Phys 2011, 13, 10510–10519. [Google Scholar]
- Potestio, R.; Delle Site, L. Quantum locality and equilibrium properties in low-temperature parahydrogen: A multiscale simulation study. J. Chem. Phys 2012, 136, 054101. [Google Scholar]
- Delgado-Buscalioni, R.; Kremer, K.; Praprotnik, M. Concurrent triple-scale simulation of molecular liquids. J. Chem. Phys 2008, 128, 114110. [Google Scholar]
- Delgado-Buscalioni, R.; Kremer, K.; Praprotnik, M. Coupling atomistic and continuum hydrodynamics through a mesoscopic model: Application to liquid water. J. Chem. Phys 2009, 131, 244107. [Google Scholar]
- Junghans, C; Poblete, S. A reference implementation of the adaptive resolution scheme in ESPResSo. Comput. Phys. Commun 2010, 181, 1449–1454. [Google Scholar]
- Praprotnik, M.; Delle Site, L.; Kremer, K. Adaptive resolution scheme (AdResS) for efficient hybrid atomistic/mesoscale molecular dynamics simulations of dense liquids. Phys. Rev. E 2006, 73, 066701. [Google Scholar]
- Praprotnik, M.; Kremer, K.; Delle Site, L. Adaptive molecular resolution via a continuous change of the phase space dimensionality. Phys. Rev. E 2007, 75, 017701. [Google Scholar]
- Praprotnik, M.; Kremer, K.; Delle Site, L. Fractional dimensions of phase space variables: A tool for varying the degrees of freedom of a system in a multiscale treatment. J. Phys. A 2007, 40, F281–F288. [Google Scholar]
- Poblete, S.; Praprotnik, M.; Kremer, K.; Delle Site, L. Coupling different levels of resolution in molecular simulations. J. Chem. Phys 2010, 132, 114101. [Google Scholar]
- Nielsen, S.O.; Bulo, R.E.; Moore, P.B.; Ensing, B. Recent progress in adaptive multiscale molecular dynamics simulations of soft matter. Phys. Chem. Chem. Phys 2010, 12, 12401–12414. [Google Scholar]
- Nielsen, S.O.; Moore, P.B.; Ensing, B. Adaptive multiscale molecular dynamics of macromolecular fluids. Phys. Rev. Lett 2010, 105, 237802. [Google Scholar]
- Delle Site, L. Some fundamental problems for an energy-conserving adaptive-resolution molecular dynamics scheme. Phys. Rev. E 2007, 76, 047701. [Google Scholar]
- Praprotnik, M.; Poblete, S.; Delle Site, L.; Kremer, K. Comment on: Adaptive multiscale molecular dynamics of macromolecular fluids. Phys. Rev. Lett 2011, 107, 099801. [Google Scholar]
- Fritsch, S.; Poblete, S.; Junghans, C.; Ciccotti, G.; Delle Site, L.; Kremer, K. Adaptive resolution molecular dynamics simulation through coupling to an internal particle reservoir. Phys. Rev. Lett 2012, 108, 170602. [Google Scholar]
- Wang, H.; Schütte, C.; Delle Site, L. Adaptive resolution simulation (AdResS): A smooth thermodynamic and structural transition from atomistic to coarse grained resolution and vice versa in a grand canonical fashion. J. Chem. Theory Comput 2012, 8, 2878–2887. [Google Scholar]
- Wang, H.; Hartmann, C.; Schütte, C.; Delle Site, L. Grand-canonical-like molecular-dynamics simulations by using an adaptive-resolution technique. Phys. Rev. X 2013, 3, 011018. [Google Scholar]
- Praprotnik, M.; Delle Site, L.; Kremer, K. A macromolecule in a solvent: Adaptive resolution molecular dynamics simulation. J. Chem. Phys 2007, 126, 134902. [Google Scholar]
- Praprotnik, M.; Matysiak, S.; Delle Site, L.; Kremer, K.; Clementi, C. Adaptive resolution simulation of liquid water. J. Phys. Condens. Matter 2007, 19, 292201. [Google Scholar]
- Matysiak, S.; Clementi, C.; Praprotnik, M.; Kremer, K.; Delle Site, L. Modeling diffusive dynamics in adaptive resolution simulation of liquid water. J. Chem. Phys 2008, 128, 024503. [Google Scholar]
- Lambeth, B.P.; Junghans, C.; Kremer, K.; Clementi, C.; Delle Site, L. On the locality of hydrogen bond networks at hydrophobic interfaces. J. Chem. Phys 2010, 133, 221101. [Google Scholar]
- Mukherij, D.; van der Vegt, N.F.A.; Kremer, K.; Delle Site, L. Kirkwood-Buff analysis of liquid mixtures in an open boundary simulation. J. Chem. Theory Comput 2012, 8, 375–379. [Google Scholar]
- Potestio, R.; Fritsch, S.; Espanol, P.; Delgado-Buscalioni, R.; Kremer, K.; Everaers, R.; Donadio, D. Hamiltonian adaptive resolution simulation for molecular liquids. Phys. Rev. Lett 2013, 110, 108301. [Google Scholar]
- Potestio, R.; Espanol, P.; Delgado-Buscalioni, R.; Everaers, R.; Kremer, K.; Donadio, D. Monte Carlo adaptive resolution simulation of multicomponent molecular liquids. Phys. Rev. Lett 2013, 111, 060601. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Site, L.D. What is a Multiscale Problem in Molecular Dynamics? Entropy 2014, 16, 23-40. https://doi.org/10.3390/e16010023
Site LD. What is a Multiscale Problem in Molecular Dynamics? Entropy. 2014; 16(1):23-40. https://doi.org/10.3390/e16010023
Chicago/Turabian StyleSite, Luigi Delle. 2014. "What is a Multiscale Problem in Molecular Dynamics?" Entropy 16, no. 1: 23-40. https://doi.org/10.3390/e16010023



