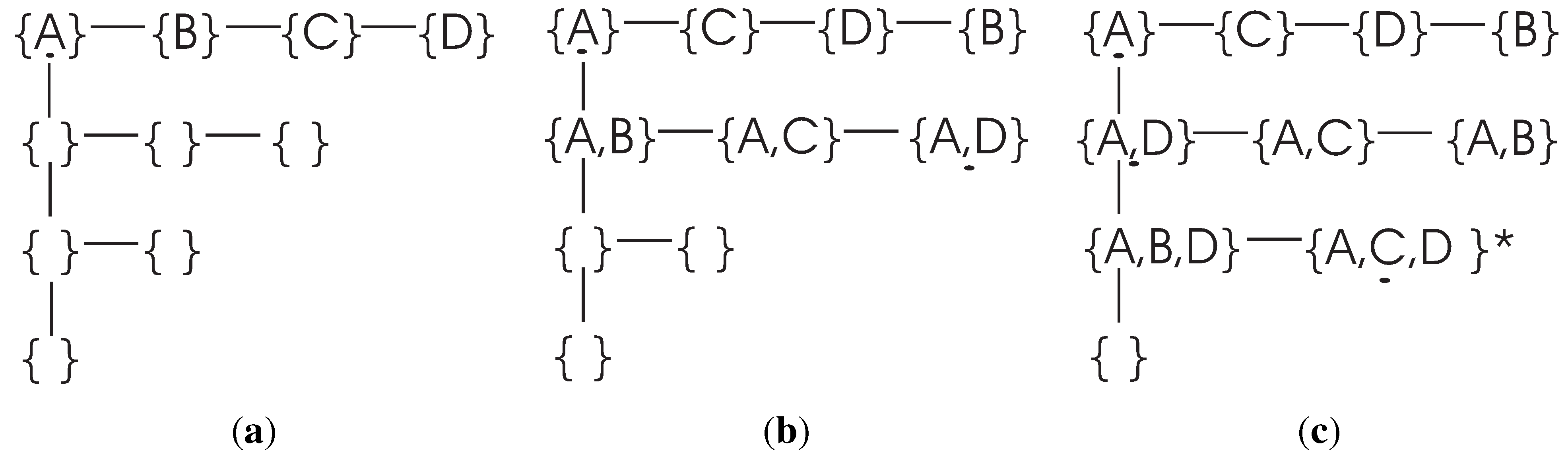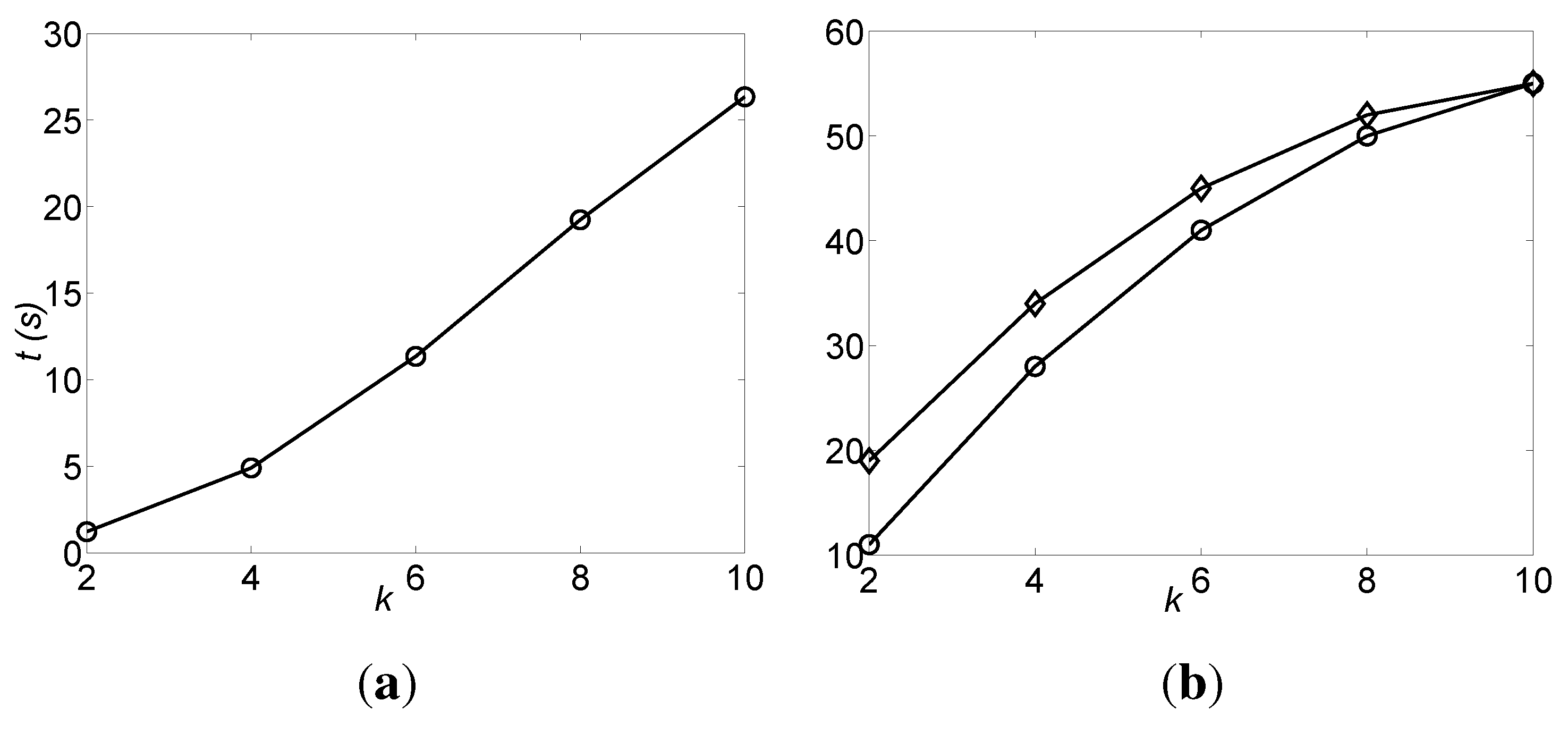Proofs of the Theorems
Theorem 15 ([34](p. 33)) If ,
.
Theorem 8 If , and X and Z are independent, then: .
Proof 1 Since X and Z are independent, based on Theorem 1, we have:Since ,
based on Theorem 5, we have .
Then, based on Theorem 15, we haveFrom Equations (11) and (12), we have .
Based on Theorem 1, we have .□
Theorem 11 In an OR BN with an indegree of k over V,
the mutual information between and
is:
Proof. Without loss of generality, we consider . In the truth table of , there are equal numbers of “0” and “1” for . Thus, .
In the truth table of
, there are
lines totally. Additionally, in the column of
, there is only one “0”, and
“1”. Thus,
There are only three possible instances for the tuple,
,
i.e., (0, 0), (0, 1) and (1, 1). By counting the numbers of these instances, and divided by the total number of lines, we have
Therefore, we obtain
□
Theorem 12 In an OR BN with an indegree of k over V,
,
,
the mutual information between and is Proof. Similar to the proof of Theorem 11, we have
Consider
and
p = 2 first. Without loss of generality, we derive
. For
, as shown in
Table A1, there are
possible instances for
,
i.e., (0,0), (0,1), (1,0) and (1,1). By counting the number of these instances and dividing by the total number of lines, we get
(bits).
Table A1.
The truth table of .
Table A1.
The truth table of .
| X1 | X2 | X3 | |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Next, we derive
. There are
possible instances for
,
i.e., (0,0,0), (0,0,1), (0,1,1), (1,0,1) and (1,1,1). Their probabilities are
Hence, we get
By generalizing three to
p, we have
From Equation (19), there is one instance of
for
. There are
instances of
for
. There are
possible instances of
with the same probabilities of
. Hence,
Finally, by combing Equations (18), (22) and (23), we have the result,
,
□
When
, from Theorem 12, we have
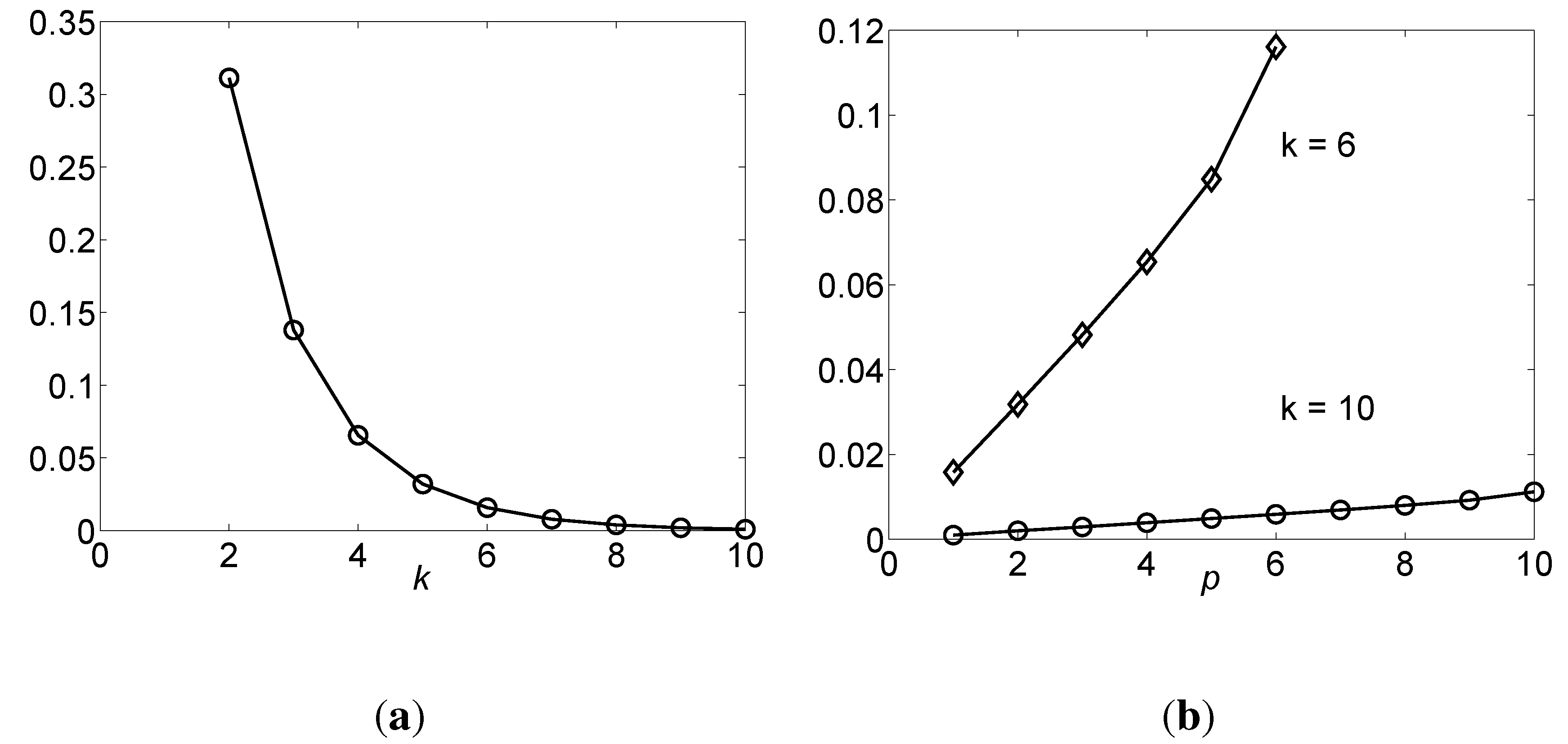
, as shown in Equation (18). This result is exactly consistent with Theorem 4, which validates Theorem 12 from another aspect. For instance, as shown in
Figure 3b, when
p = 6, the
in the curve for
k = 6 is 0.116 bits, which should be equal to
from Theorem 4. Then, from Equation (18), when
k = 6,
bits, too.
Theorem 13 In an OR BN with an indegree of k over V, , .
Proof. From Theorem 12, we have
Thus:
Since
monotonically increases
, so
; thus,
,
. Therefore,
monotonically increases with
p,
. So, we have the result.□
The correctness of Theorem 13 is also demonstrated in
Figure 3b.
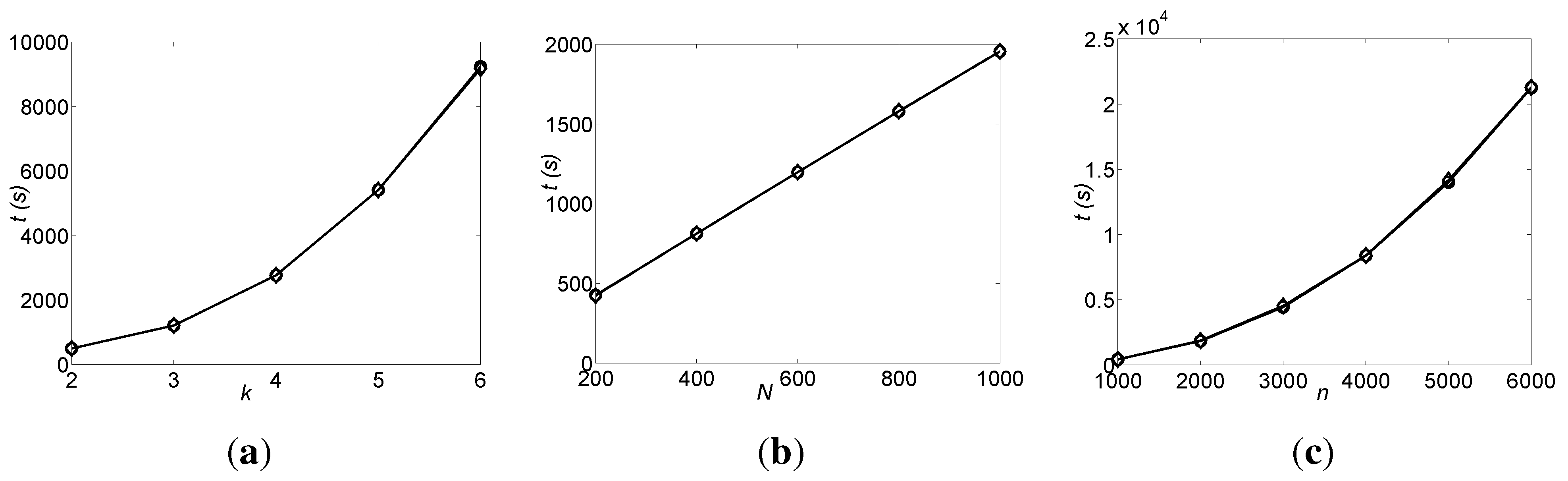
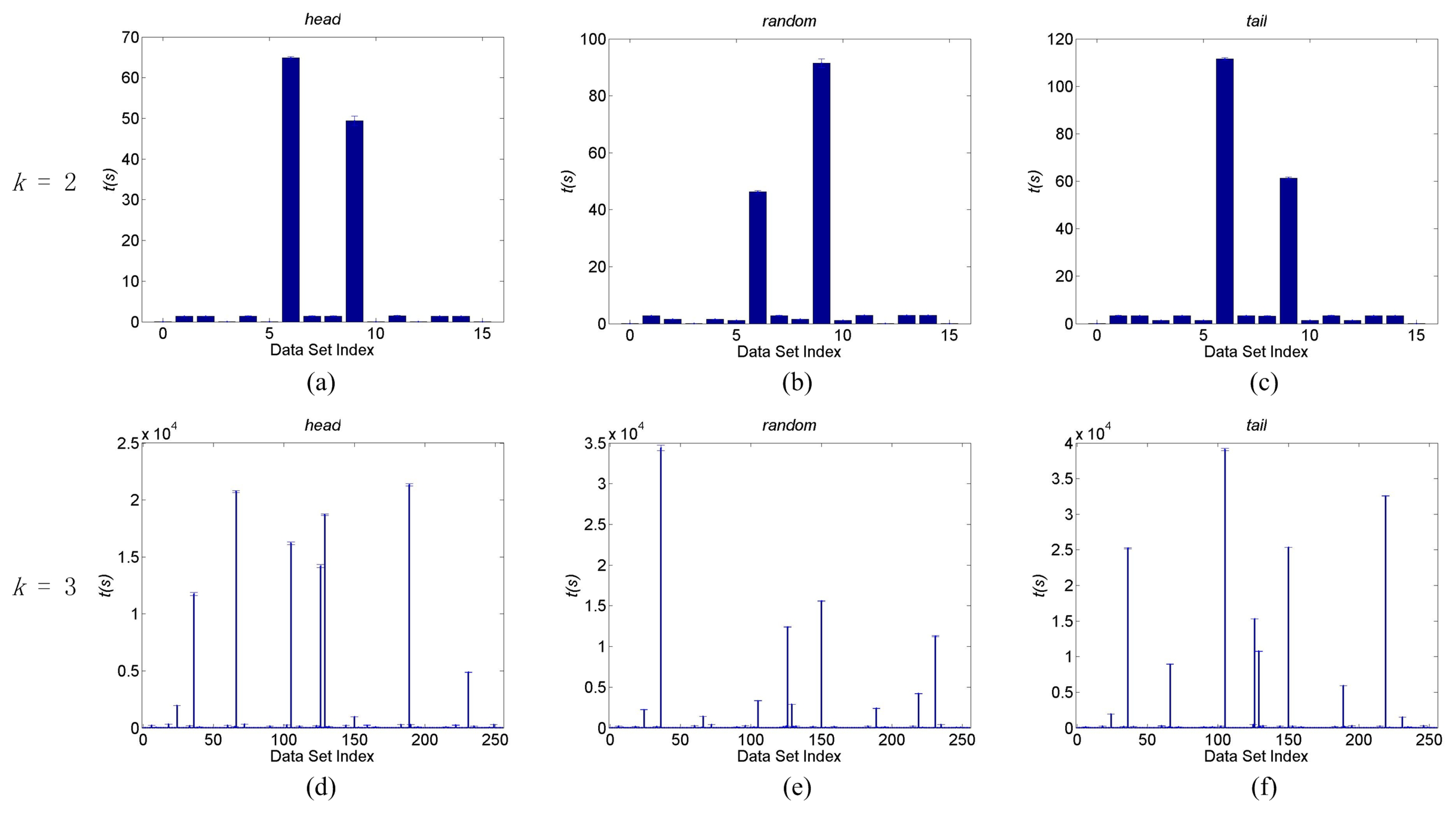
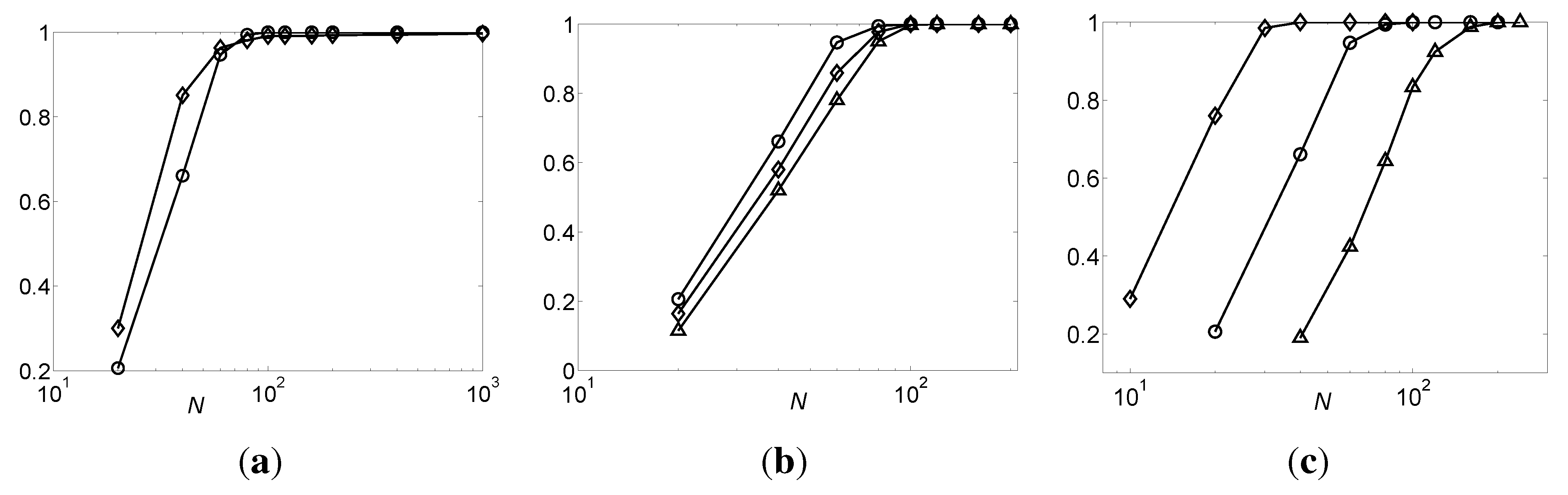
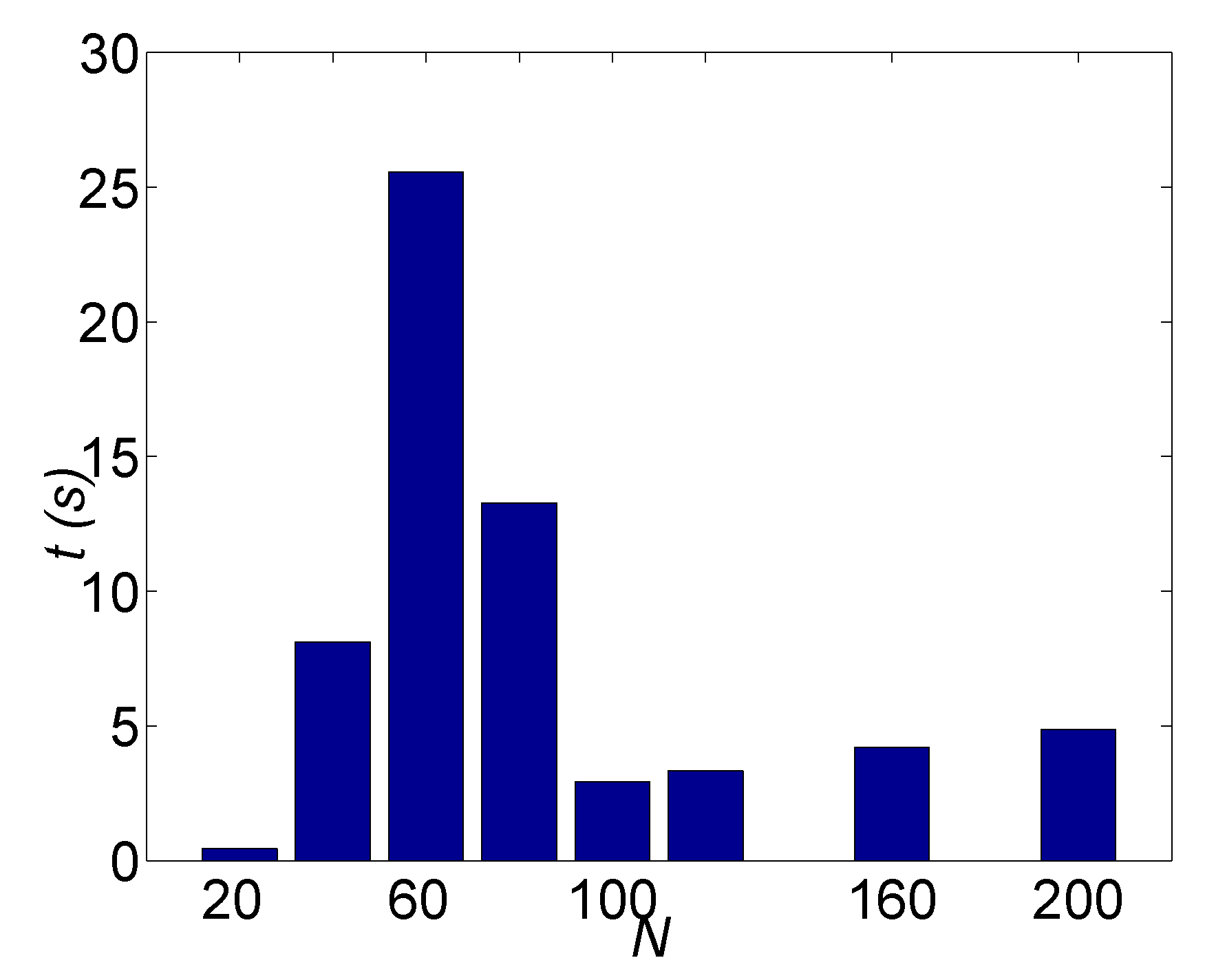
Theorem 14 For sufficiently large , if the samples are noiseless and randomly generated from a uniform distribution, then the DFL algorithm can identify an OR BN with an indegree of k in time, strictly.
Proof. The datasets are generated with the original Boolean functions of the BNs. From Theorem 6, the empirical probabilities of and in the Boolean functions, , tend to be the probabilities in the truth table of when the sample size is large enough.
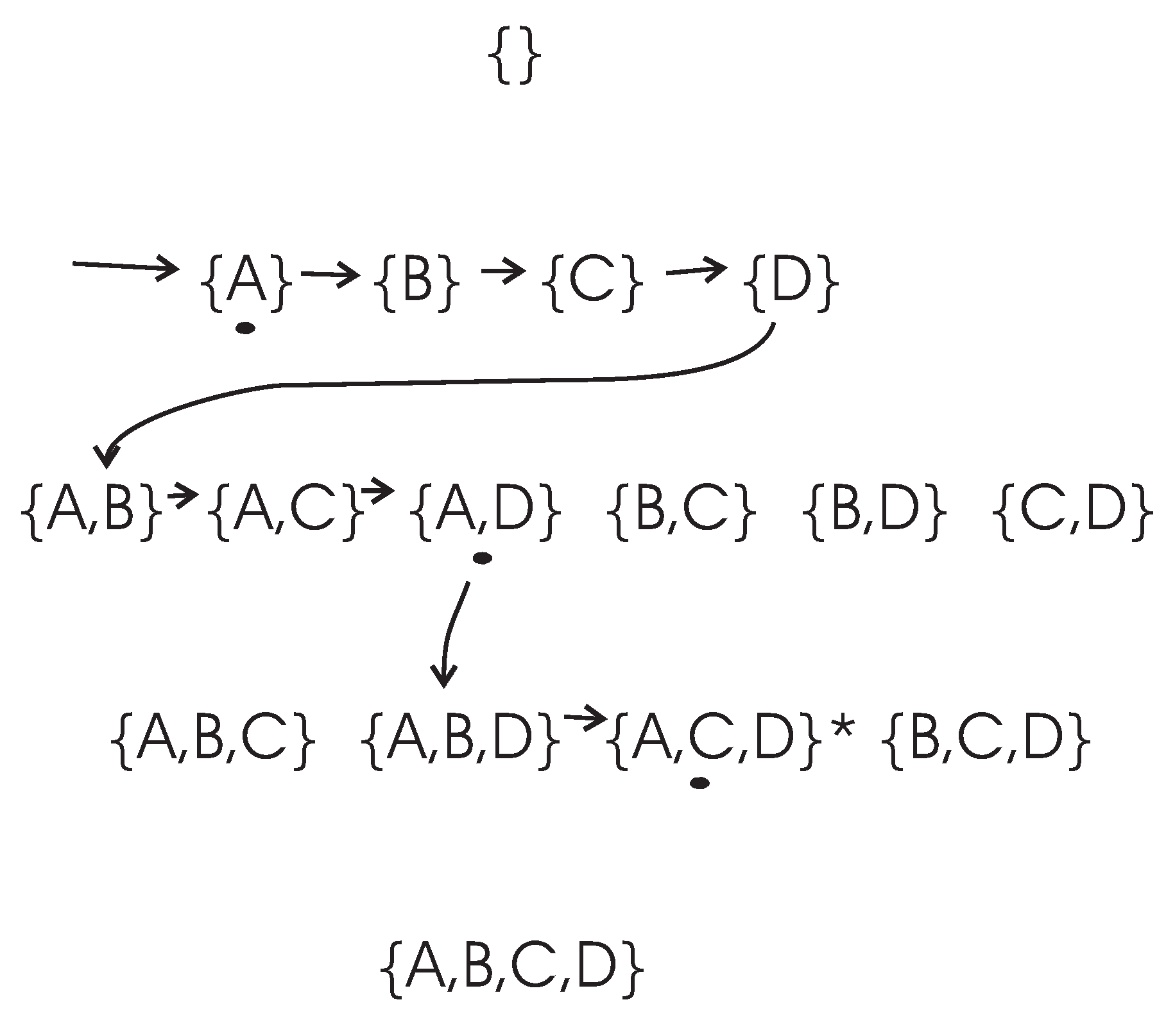
First, consider the searching process in the first layer of the search graph, like
Figure 1. From Theorem 8, we obtain
if
. Meanwhile, from Theorem 11,
. Thus,
s are listed in front of the other variables,
Zs, after the sort step in line 7 of
Table 3.
In the following, the
(subsets with
and another variable) are dynamically added to the second layer of the Δ
Tree. Now, consider the MI,
, where
Z is one of the variables in
. First, if
, from Theorem 8,
. Since
,
and
are independent variables, from Theorem 2, we get
. From Theorem 3, we have:
Second, if
, from Theorem 13, we have
After combining the results in Equations (28) and (29), we have that , is larger than the same measure when .
Therefore, in the second layer of the ΔTree, the combinations with two elements from are listed in front of other combinations, and so on so forth, until the DFL algorithm finds in the kth layer of the ΔTree, finally.
In the searching process, only
subsets are visited by the DFL algorithm. Therefore, the complexity of the DFL algorithm becomes
, where log
n is for sort step in line 7 of
Table 3 and
N is for the length of input table
T.□
Corollary 3 For sufficiently large , if the samples are noiseless and randomly generated from a uniform distribution, then the DFL algorithm can identify a generalized OR BN with an indegree of k in time, strictly.
Proof. We replace those s that are taking their inverted values with another variable, , i.e., let ; then, the resulting BN is an OR BN. does not change in the new OR BN.
To satisfy the criterion of Theorem 5, compare the MI,
, with
. We have
remains the same value as the corresponding item in . In binary systems, there are only two states, i.e., “0” and “1”. It is straightforward to obtain . Therefore, the only item changed in the is the joint entropy, . Next, we prove that .
Consider the tuple,
. If we replace “0’ of
with “1” and
vice versa, it becomes
, as shown in
Table A2. The three instances, (0, 0), (0, 1) and (1, 1), of
change to (1, 0), (1, 1) and (0, 1) of
, respectively. However, the probabilities (frequencies) of them are coincidentally equal, respectively. Thus,
.
Table A2.
The tuple and , where k is two.
Table A2.
The tuple and , where k is two.
| | | |
|---|
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 |
From Theorem 14, the results are obtained.□
Corollary 4 For sufficiently large , if the samples are noiseless and randomly generated from a uniform distribution, then the DFL algorithm can identify an AND BN with an indegree of k in time, strictly.
Proof. In an AND BN, and are equal to and in a corresponding OR BN with the same for all , respectively. Therefore, is the same as that of the corresponding OR BN. From Theorem 14, the result can be directly obtained.□
Corollary 5 For sufficiently large , if the samples are noiseless and randomly generated from a uniform distribution, then the DFL algorithm can identify a generalized AND BN with an indegree of k in time, strictly.
Proof. Similar to that of Corollary 3.□