1. Introduction
The paper gives an alternative derivation of the classical barometric and ideal gas laws. Our results coincide with those obtained from the Bohr-Sommerfeld (BS) quasi-classical approximation of Quantum Mechanics and the Boltzmann factor, but our method is more straightforward. Initially, we obtained the average force, , exerted by a corpuscle on a piston from the BS theory. The corpuscle action (area in the position-momentum, z-p, phase-space, where z denotes the corpuscle altitude and the momentum, , where is the force applied to the corpuscle, e.g., its weight, and t is time) is discrete and evenly spaced in units of the Planck constant, . Because our model is not a harmonic oscillator, the discrete corpuscle energies are unevenly spaced. Thus, going to the continuous limit converting sums into integrals, we must introduce an energy distribution, , where E denotes the energy, in the form given later. After going through these semi-classical considerations, we discovered that it was sufficient to postulate the simplicity principle, according to which the barometric law must not depend on the equations of motion. This concept, unlike quantum theory, could have been understood at the time of ancient Greece. Furthermore, we show that if the entropy is taken as the negative average value of the logarithms of the microstate probabilities, accounting for a possible uncertainty concerning the presence or not of a corpuscle, introduction and removal of separations in the cylinder containing the corpuscle does not affect the entropy.
By ideal gas, we mean a collection of non-interacting corpuscles. We may, therefore, restrict ourselves to a single corpuscle. If there is more than one corpuscle, the corpuscles are classical and, thus, distinguishable. We first suppose that we know with certainty whether a corpuscle is present or not in the cylinder, then relax this assumption. Only motion along the vertical z-axis is considered, but generalization of the barometric and ideal-gas law to three dimensions is straightforward. As said above, the corpuscle considered is submitted to an external force, , perhaps of electrical origin, w being called the corpuscle “weight”, or equivalently to a potential, . Because the presence of a corpuscle affects the potential negligibly, the latter is viewed as an external potential. We call a perfect gas an ideal gas with no external force acting on the corpuscle, except at the boundaries and with the non-relativistic approximation being made.
According to our definition, ideal gas constant-volume heat capacities depend on temperature,
θ, and volume,
h. The free expansion of an ideal gas may, therefore, entail temperature changes, while this is not the case for a perfect gas. There is full agreement between our general results and the first and second laws of thermodynamics as they are spelled out in textbooks and the usual perfect-gas laws derived by Bernoulli in the limit considered. The role of a constant force acting on the corpuscle and special-relativity have been discussed, for example, by Landsberg [
1] and Louis-Martinez [
2].
The present paper is a generalization of our previous papers [
3,
4], where our motivation is explained in more detail than here. Presently, we calculate the average forces exerted on both ends of a vertical cylinder; they are different when the corpuscle has weight. We prove the gas stability from the fact that the corpuscle round-trip time is a non-decreasing function of the energy. We show that the entropy does not vary when separating walls are introduced and removed. The entropy is not postulated to be additive or extensive: it is defined as the negative average value of the logarithms of the microstate probabilities, thereby accounting for a possible uncertainty concerning the presence or not of a corpuscle, through the concept of conditional probabilities. Our conclusion agrees with an expression for the entropy given by Landsberg and others [
1], involving an integration over the cylinder height of
, where
is the probability density that the corpuscle be at
z (or the corpuscle density for a large number of corpuscles). The difference between Landsberg’s approach and our approach is that we conceptually divide the total system into subsystems and Landsberg does not. Both approaches yield the same result. Related concepts were introduced by Peters [
5,
6].
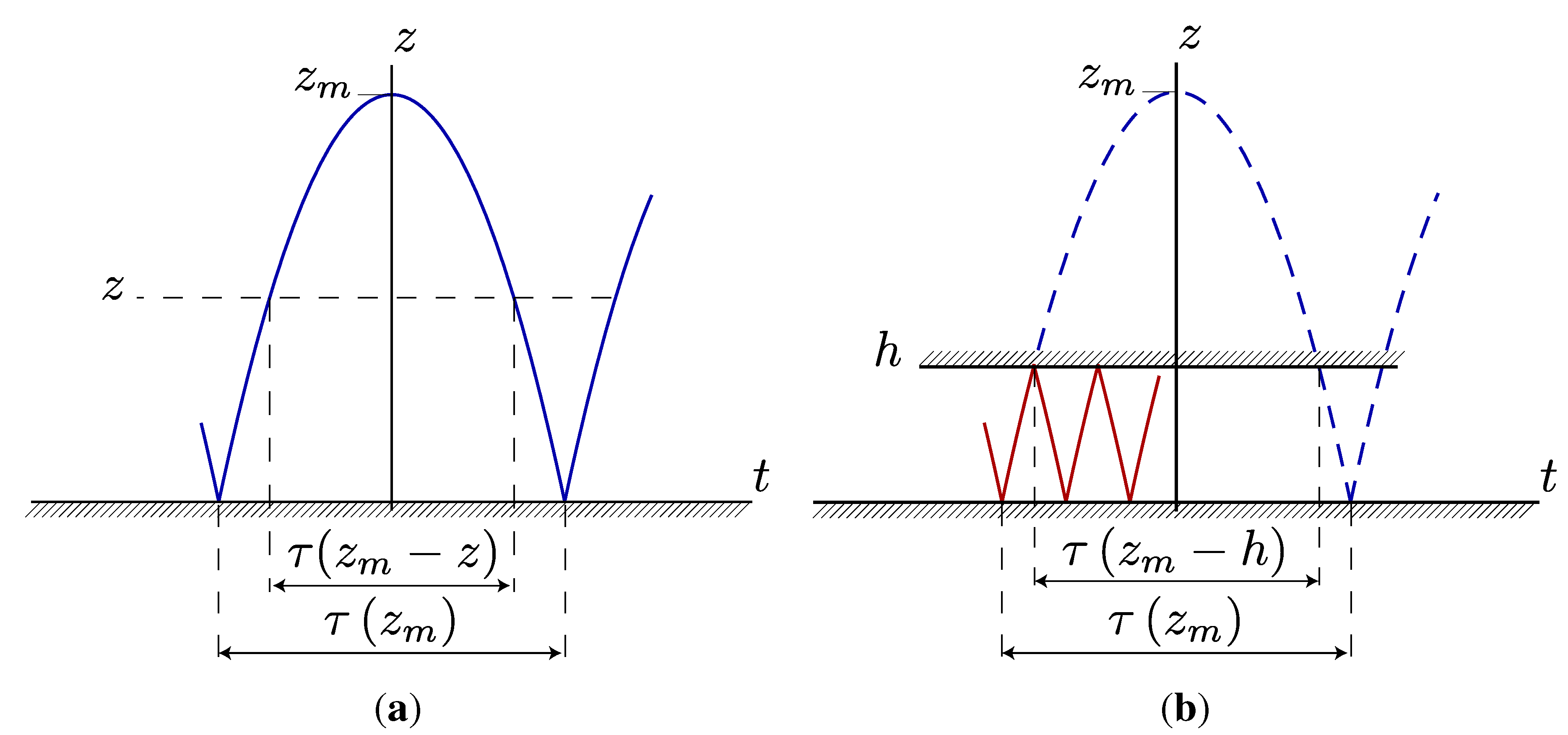
We first consider the round-trip time, , needed for a corpuscle thrown upward from the ground level, , with energy, , to reach a maximum altitude, , and come back to the ground level. If the corpuscle bounces elastically on the ground, represents the oscillation period. Since we consider only round-trip times, that is, time delays measured at some altitude, no problem of clock synchronization arises. The time during which the corpuscle is located above some altitude, , during a period is , since, under our assumption of a constant weight, the τ-function does not depend on the initial altitude or initial time. For brevity, we set in most of the present paper. The weight is easily restored from dimensional considerations. For example, the result, , should read, , in view of the fact that β has the dimension of an energy reciprocal.
We consider only thermal-equilibrium situations: If we wait a sufficiently long period of time, an isolated system ceases to evolve. We take it as an empirical result that, leaving aside general-relativity effects (According to
general relativity, thermal energy has weight, but this (so-called Tolman) effect that entails a temperature variation at equilibrium,
, where
g denotes the gravity acceleration and
c, the speed of light, is entirely negligible; see, for example, Equation (1) of [
7]. This paper gives the following interpretation of equilibrium: an (adapted) quote is: “The temperature
θ is essentially equal to
ℏ divided by the time required by the system to move from one state to the next”. This interpretation leads to the condition of temperature uniformity for weak gravity, since, in that case, time intervals do not depend significantly on altitude.), two bodies left in contact for a sufficient period of time with energy being allowed to flow from one to the other reach an equilibrium state corresponding to equal temperatures, as one can judge by our senses. Energy may flow spontaneously (
i.e., without work expenditure) from a hot body to a colder one, but the converse never occurs: the process is non-reversible (zeroth law of thermodynamics). Our
θ notation for the temperature is the one employed by Gibbs. We quote [
8]:“Gibbs, writing before the introduction of Boltzmann’s constant,
, uses
θ with the dimensions of energy for what we should today call
; consequently, his thermodynamic analog of entropy is what we should today call
and is dimensionless. In this respect Gibbs’ notation is really neater formally and more cogent physically than ours”. In our discussion, the temperature,
θ, enters solely on the basis of dimensional considerations. However, we later show that our expressions for the gas internal energy and force (or pressure) derive from the partial derivatives of the Helmholtz potential (or free energy),
. The heat delivered by the gas in reversible processes is
, an expression for the entropy,
, being given. This result enables us to prove that the formally-introduced temperature,
θ,
is a thermodynamic temperature.
To conclude, the purpose of the present paper is to show that the thermodynamics of ideal gases and, particularly, the barometric and ideal-gas laws, may be obtained solely on the basis of the Democritus model, according to which nature consists of corpuscles moving in a vacuum, plus a principle of simplicity: namely that these fundamental laws are
independent of the law of corpuscle motion. To wit, writing the corpuscle Hamiltonian (see
Appendix A) as
, the barometric and ideal-gas laws
do not depend on the
function, but the internal kinetic energy,
K, does. Thus, the Hamiltonian equations recalled in the
Appendix are unnecessary, as far as the barometric and ideal-gas laws are concerned, but they are needed (in the form of a round-trip function) for the internal energy and other quantities relevant to classical thermodynamics.
As said earlier, we consider a single corpuscle. Because of the slight thermal motion of the container wall, there is an exchange of energy between the corpuscle and the heat bath, so that the corpuscle energy slowly varies in the course of time. We are looking for averages over arbitrary, long time intervals.
2. The Barometric Law
We consider a single corpuscle moving only along the vertical
z coordinate and submitted to a constant force,
. If the corpuscle energy is
E, the maximum altitude reached is
. The round-trip time,
, is the motion period, and the time per period during which the corpuscle is above
z is (see
Figure 1a)
. It follows that the fraction of time during which the corpuscle is above
z is
. Because of thermal fluctuations, the corpuscle energy is not fixed, but must be described by a probability distribution. By invoking the simplicity principle,
i.e., by demanding independency of the
τ-function, one obtains an energy distribution proportional to
, yielding the average fraction of time during which the corpuscle is above
z as:
The result obtained for the distribution,
, is indeed:
Figure 1.
Space-time () trajectory of a unit-weight corpuscle bouncing off the ground at z=0. In (a), the maximum altitude reached by the corpuscle is , where E denotes the energy. The motion is periodic, with period , where denotes the corpuscle round-trip time at a distance, ζ, from the top of the trajectory. The time during which the corpuscle is located above z, divided by the period, is evidently . This expression holds, even if the motion is not symmetric in time. In (b), the maximum altitude is restricted to h by a piston. The motion period becomes .
Figure 1.
Space-time () trajectory of a unit-weight corpuscle bouncing off the ground at z=0. In (a), the maximum altitude reached by the corpuscle is , where E denotes the energy. The motion is periodic, with period , where denotes the corpuscle round-trip time at a distance, ζ, from the top of the trajectory. The time during which the corpuscle is located above z, divided by the period, is evidently . This expression holds, even if the motion is not symmetric in time. In (b), the maximum altitude is restricted to h by a piston. The motion period becomes .
In the integrals going from
z to
∞, we have replaced
by
. Here,
; the energy,
θ, will later on prove to be a thermodynamic temperature. In terms of the variable,
, all the integrals go from zero to infinity and cancel out. Even though there are integral signs, no integration has been performed. We simply consider an integral as a sum of terms and employ the rule of addition associativity. We have also employed the fact that
is the only function, such that
. Note that our “desired result” does not refer to a specific barometric law that would be known before hand, but to the fact (simplicity principle) that this law, whatever it is, does not depend on the equations of motion. It is postulated on the basis of common experiences that in a state of equilibrium, there exists a unique temperature. Thus, a general form of the barometric law has been obtained without invoking the Boltzmann distribution, which is presently viewed as a
consequence of the simplicity principle. For a three-dimensional configuration corresponding to real atmospheres, the same result holds: the
-function is modified; however, the barometric law does not depend on that function, and therefore, the result in Equation (
2) is unaffected. The more complicated case, where the weight,
w, depends on
z, is treated in [
4]. The result amounts to replacing
z in the above expression by a potential,
. This known result is obtained here most simply.
2.1. Reflecting Plane at
We now suppose that there is a reflecting plane located at
h, and the corpuscle is located between zero and
h. When
, the plane at
is immaterial, and the fraction of time spent by the corpuscle above
z is as before:
. When
, the fraction of time spent by the corpuscle above
z is
; see
Figure 1b. It follows that if
denotes the energy distribution, the average fraction of time spent by the corpuscle above
z (
is:
This expression is independent of the
function, according to our simplicity principle, if and only if
is selected as follows:
Using the elementary transformations given in [
4], we obtain, employing only the associativity of addition and the fact that
is the only function, such that
:
The same result is obtained if we suppose that the barometric law applies also in the presence of a reflecting plate at
h and evaluate the ratio of the integral of
from
z to
h and the integral of
from zero to
h.
Similarly, supposing that the corpuscle is located between zero and
, we obtain the probability,
, that the corpuscle be in the lower half and the probability,
, that the corpuscle be in the upper half in the form:
These expressions will be needed later on.
When the corpuscle is submitted to an arbitrary potential,
, the barometric law reads:
where
denotes the corpuscle density at
z. The details can be found in [
4]. The result is the well-known generalized Boltzmann factor that reduces to the previous one when
. However, it is obtained here from the simplicity principle alone.
4. Internal Energy
The gas internal energy,
U, is the average value of
, the gravitational energy being accounted for. First, assume that the cylinder rests on the ground level:
. The expression for
U is, using the energy distribution given in Equation (
4):
where the method employed before has been used. The mathematical details can be found in [
3]. The first term minus
θ corresponds to the kinetic energy,
K, while the second term plus
θ corresponds to the potential energy,
P. In the non-relativistic limit, the first term, minus
θ, gives the well-known expression,
. Without any force acting on the corpuscle, we have, of course,
. The internal energy,
, thus is the sum of a term,
K, the function of
θ, but not of
h, and a term,
P, obtained in analytical form, that tends to zero when
. To evaluate the first term, we need to know the round-trip time,
, to within an arbitrary proportionality factor, and an integration must be performed in that case.
The expressions given earlier for the average force,
, in Equation (
12) and the internal energy,
U, in Equation (
14) may be written, with
:
Z is a form of the (Gibbs) phase integral of
, where
is the Hamiltonian given in the
Appendix [
9]. The Planck constant,
, introduced to make
Z dimensionless plays no physical role in this paper (remember that
z should read
). All the physical results may be derived from the above expression of
.
As said above, the internal energy, U, may be written as the sum of a potential energy, P, and a kinetic energy, K. The potential energy with may be written as the ratio of the integral of from zero to h and the integral of from zero to h. In general, P must be incremented by .
The temperature, θ, introduced above only on dimensional grounds is defined to within an arbitrary constant. We may convene that , exactly as the hydrogen triple-point temperature (HTP). The value of θ at the water triple-point (WTP), for example, would then be obtained experimentally by measuring the efficiency of reversible heat engines operating with WTP as a hot bath and HTP as a cold bath. The known value is .
5. Stability
Solutions obtained for the force,
, and the energy,
U, imply stable equilibria, provided that two conditions be satisfied. Firstly, the isothermal compressibility,
, must be positive. This is readily verified, since the derivative of the force,
, given in Equation (
12), with respect to
h is negative. Secondly, one must verify that the isochoric heat capacity,
, is positive. This problem is solved below. Given that
and
are positive, it follows that the isobaric heat capacity,
, is positive, and the isentropic compressibility,
, is positive, also. Thus, let us show that
is positive. The internal energy is the sum of the potential energy,
P, which is easily seen to be an increasing function of
θ and the kinetic energy,
K.
The former may be written, according to Equation (
14):
The latter may be written as:
integrating by parts, where primes indicate derivatives with respect to the argument. In order to get
, it thus suffices to show that
, that is, letting
, for short:
Since
τ is a non-decreasing function of
E,
f is non-negative and Equation (
18) is the classical inequality regarding the moments on order of zero, one and two of the measure
μ defined by:
. Thus,
, and the expressions obtained from our simplicity principle imply the stability of the equilibria.
6. The Helmholtz Fundamental Relation
It is convenient to introduce the Helmholtz fundamental relation: . The letter A originates from the German “Arbeit”, or work, but this letter may also stand for (constant temperature) “Available work”. Indeed, the work performed at a constant temperature is the difference between the final and initial A values.
The force,
, that the corpuscle exerts on the lower piston, the force,
, that the corpuscle exerts on the upper piston and the internal energy result from the Helmholtz fundamental relation depending separately on
and
. We thus consider a cylinder whose base has been raised from
to
. The previous relations for
in Equation (
12) and for
U in Equation (
14) may be written as:
with
. Thus, if the cylinder bottom is raised to an altitude,
,
A and
U are both incremented by
. From now on, we set
for simplicity, unless specified otherwise.
We have obtained an expression for the Helmholtz fundamental relation,
, for the special case of a single corpuscle submitted to a constant force in the canonical ensemble. This fundamental relation has the same mathematical and physical content as the often-used energy fundamental relation,
, and the entropy fundamental relation,
; see [
10]. The following expressions therefore coincide with the conventional ones applicable to any working substance. Indeed, the fundamental entropy relation is obtained in parametric form from the expressions for
and
, with
θ as a parameter. Even though we cannot explicitly obtain
, it is easy to verify that
.
We have indeed:
Likewise, we obtain the well-known relation,
, if we enforce the condition,
. The Helmholtz fundamental relation will suffice for our purposes.
At a given temperature, the corpuscles are independent. Accordingly, for
N corpuscles,
and
U are simply multiplied by
N.
A is multiplied by
N, plus a function of
N that we do not specify further. It follows that if
denotes the fundamental entropy relation for a single corpuscle, the fundamental entropy relation for
N corpuscles reads
, to within an additional arbitrary function of
N. For a perfect gas, this function may be selected, such that the entropy is extensive in
h. The entropy is, in general, not extensive, but there is no reason why it should be. Let us quote Jaynes [
8]: “The question of extensivity cannot have any universally valid answer; for there are systems, for example systems with electric charge or gravitational forces, for which the scaling law does not hold because of long range interactions”.
6.1. The Energy, θ, is a Thermodynamic Temperature
We prove in this section that θ, introduced in previous sections on dimensional grounds only, is a thermodynamic temperature. We do this by showing that the efficiency of a reversible thermal cycle employing ideal gases is, , where is the cold-bath temperature and , the hot bath temperature: this is the accepted Kelvin definition of absolute temperatures.
From the law of conservation of energy, the heat released by the gas is from Equation (
19):
For any function,
, such as
,
. We employ only two independent variables, namely,
θ and
h, so-that partial derivatives are unambiguous. If the gas is in contact with a thermal bath (
θ=constant),
is the heat gained by the bath. The quantity,
S, defined above, is called “entropy”. In particular, if heat cannot go through the gas container wall (adiabatic transformation), we have
, that is, according to the above result,
. Thus, reversible adiabatic transformations are isentropic. Note that
S, here defined as the ratio of two energies, is dimensionless. It may therefore be written as the logarithm of a dimensionless quantity. The fact that
S, defined above, is a state function suffices to prove that
θ is a thermodynamic temperature.
9. Conclusions
Let us recall the concepts introduced in the present paper. One can imagine that after having introduced the notion of corpuscles moving in vacuum, Democritus observed the elastic bounces of a unit weight on a balance and defined the weight “impulse” from the motion period. Not knowing the nature of the motion, he may have thought of introducing an energy distribution, such that the average force, , does not depend on the law of motion. This, as we have seen, may be done. This distribution involves, for dimensional reasons, a quantity, θ, having the dimension of energy. Considering a thermal engine operating between two baths at temperatures , one finds, on the basis of the principles just stated, without any further assumptions, that the maximum efficiency is . This allows us to call θ the thermodynamic temperature, defined only up to a constant factor. The latter may be fixed by conceding, for example, that at the hydrogen triple point.
The present paper provides a first-principle proof of the barometric and ideal-gas laws, including a possible effect of a corpuscle weight,
w, with no knowledge of the round-trip time function,
, being required. Explicit expressions of the kinetic part of the internal energy may be obtained, however, only when the round-trip time function is known to within an arbitrary constant factor or, equivalently, when the kinetic part of the corpuscle Hamiltonian is known. The ideal-gas internal kinetic energy depends only on temperature, while the ideal-gas internal potential energy, divided by
θ, is a simple analytic function of
. Since the theory presented is strictly classical, the universal constant,
ℏ, is needed only to make the results dimensionless. We have proven the stability of the gas from the equations obtained for the force,
, and the internal energy,
U. We have also shown that, at least for ideal gases, the energy and the entropy are unchanged when a separation is introduced and considered the case of free expansion. The case of non-constant weights has been treated, based on the same concepts, in [
4], with results that agree with the Gibbs phase integral.