1. Introduction
The so-called
Landauer-Bennett (LB) thesis says that the physical implementations of logically irreversible operations
necessarily and
universally involve dissipation by at least
kln2 per bit of lost information (see Landauer [
1,
2], Bennett [
3,
4]) (The LB thesis is ascribed by Leff and Rex [
5] also to Oliver Penrose (LBP thesis), see Penrose [
6]). In this paper we argue that while dissipation may hold in interesting and even familiar situations, the thesis itself as a universal claim does not logically follow from the principles of classical mechanics. This means that the thermodynamic properties of physical processes implementing computations depend on their physical details. In this sense the LB thesis is not universal. Although there are cases in which the entropy of the universe increases during erasure (e.g.,
Figure 4,
Figure 5 and
Figure 6 below), there are also cases compatible with classical mechanics in which the entropy does not increase during erasure (see
Figure 7,
Figure 8 and
Figure 9). As far as we know there is no general characterization of the conditions in which erasure is dissipative, so that as of now it seems that there is not even a
partial proof of the conditions under which a limited thesis is true. (The LB thesis may have motivated the search for embedding logically irreversible operations within logically reversible algorithms, such as Fredkin’s gate; see Fredkin and Toffoli [
7]. However, since the LB thesis is not universal, these results, although interesting as theorems in logic, do not bear on the thermodynamics of computation.)
Rolf Landauer writes:
“Consider a typical logical process, which discards information, e.g., a logical variable that is reset to 0, regardless of its initial state. ... The erasure process we are considering must map the 1 space down into the 0 space. Now, in a closed conservative system phase space cannot be compressed, hence the reduction in the spread [in the degrees of freedom representing 1 and 0] must be compensated by a phase space expansion [in other degrees of freedom],
i.e., a heating of the irrelevant degrees of freedom, typically thermal lattice vibrations. Indeed, we are involved here in a process which is similar to adiabatic magnetization (i.e., the inverse of adiabatic demagnetization), and we can expect the same entropy increase to be passed to the thermal background as in adiabatic magnetization,
i.e.,
kln2 per erasure process. At this point, it becomes worthwhile to be a little more detailed. ... This is, however, rather like the isothermal compression of a gas in a cylinder into half its original volume. The entropy of the gas has been reduced and the surroundings have been heated, but the process is not irreversible: the gas can subsequently be expanded again. Similarly, as long as 1 and 0 occupy distinct phase space regions, the mapping is reversible. The real irreversibility comes from the fact that the 1 and 0 spaces will subsequently be treated alike and will eventually
diffuse into each other.”(Landauer [
2] p. 2, our emphasis).
In what follows we shall analyze Landauer’s idea of diffusion and put forward a condition we call blending which clarifies Landauer’s idea of diffusion. Blending in the way we define it is a necessary and sufficient condition for erasure to hold.
2. Macrostates
We start with a strictly classical mechanical underpinning of the notions that figure in the LB thesis, in particular macrostates and entropy. (By entropy we mean the Boltzmann notion of the Lebesgue measure of the macrostate of the system. For a Gibbsian version of the LB thesis, and criticism, see Maroney [
8].)
According to all the major theories of physics the universe is at each moment in some well-defined state, called a microstate (under the restrictions of relativity and a certain understanding of what is instantaneous velocity). The nature of the microstate is described by the physical theory; for example, in classical mechanics a microstate of the universe is the positions and velocities of its particles. The time evolution of the microstate is given by equations of motion that completely describe all the changes the system undergoes over time. This is all there is in mechanics. And so the reduction of thermodynamics to mechanics means that everything that we say about subsystems of the universe should be phrased in terms of statements about microstates and their time evolution. It is customary to represent the microstates of the universe as points in an abstract state space. (The theory that describes the nature of the microstates also determines the properties and dimensionality of the state space; most of these details do not matter for us here. Here we restrict attention to classical mechanics.)
It is possible (and usually non controversial) that the universe can be described as consisting of two sets of degrees of freedom which we shall call O and G, such that it is meaningful to talk about the microstate of each set separately. (Separability need not always be the case, but we assume it for convenience. Relaxing it requires certain changes in the way some of the ideas here are expressed, but the main ideas still hold.) Not every microstate is possible for every system at every time: in general, there are constraints on the universe, which determine that it can only be in certain microstates and not others; for example, its energy may be limited. Given the constraints, the set of all the microstates in which the universe may be is represented by a region in the state space called the accessible region (the energy hypersurface is an important example in the reduction of thermodynamics to mechanics). Let us consider two schemes of the structure of accessible regions.
In the first (extremely simple) example (illustrated in
Figure 1) the accessible region consists of a segment of a straight oblique line in the
OG plane. In this structure of the accessible region there is a
one-to-one correlation between the microstates of
O and the microstates of
G, and so if one knows the microstate of
O one can deduce from it the microstate of
G.
Figure 1.
Accessible region with one-to-one correlation.
Figure 1.
Accessible region with one-to-one correlation.
In the second example (see
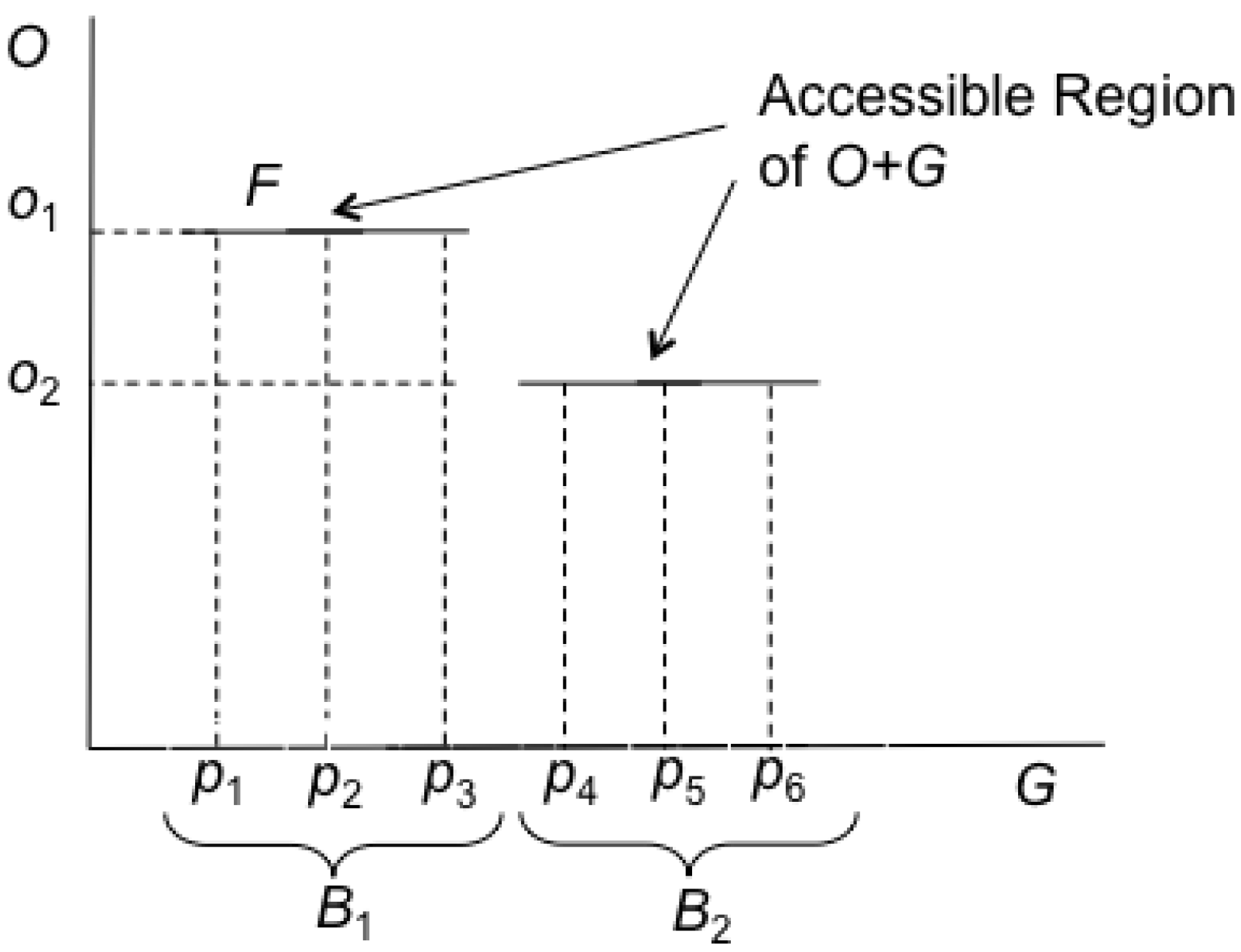
Figure 2) the accessible region of the universe consists of two horizontal line segments in the
OG plane. The correlation between
O and
G here is
one-to-many: each microstate of O is correlated with several microstates of
G. For example, the microstate
o1 of
O is correlated with the three microstates
p1,
p2 and
p3 of
G. Due to this structure of the accessible region one cannot infer the microstate of
G from the microstate of
O, even if one knows the structure of the accessible region.
The microstates
p1,
p2 and
p3 share the
physical property of being correlated with
o1; this is a physical property since it is determined by the structure of the accessible region of the
O +
G universe, and this structure, in turn, is determined by the general constraints and limitations on the possible microstates of the universe. In some very important (and possibly rare) cases, such sets of microstates of
G that are formed in virtue of one-to-many correlations with
O gain significance. And these cases are those in which the physical system
O has a special physical structure that justifies calling it
an observer which observes its environment
G. Our working hypothesis here is that the relevant notion of an observer involved here is a physical notion, and in particular that our experience of thermodynamic systems, that is, our micro correlations with our environment, can be accounted for in purely physical terms (we argue for this partially in [
9]). We will now give an account of the notion of a macrostate in these physical terms. The account of
O intended here is purely physical.
O is nothing but a physical system, a subsystem of the
O +
G universe, and whatever we say about
O, we say about
O as a purely physical system.
Figure 2.
Accessible region with one-to-many correlation.
Figure 2.
Accessible region with one-to-many correlation.
In the case of
Figure 2, we may say that when
O is in the microstate
o1,
O cannot tell whether G is in the microstates
p1,
p2 and
p3 of
G, even if
O knows the structure of the accessible region. These microstates are
indistinguishable for
O. In this case we shall say that the microstates
p1,
p2 and
p3 of
G belong to one
macrostate of
G, which we denote by
B1, and (for a similar reason) the microstates
p4,
p5 and
p6 belong to a different macrostate of
G, which we denote by
B2. It is of utmost importance to bear in mind that macrostates in statistical mechanics are sets of microstates that are grouped together because an observer does not distinguish between them. In this sense macrostates are relative to the observer’s resolution power. But this relativity is of course physical and objective. For further details about this point see our [
10] Chapter 5 and [
11].
To sum up: What is a macrostate? It is a set of microstates of G that is correlated with a microstate of O. Macrostates in this sense are objective since given classical mechanics there is, at each moment of time, a physical fact concerning the question of which set of microstates of G is correlated with each microstate of O. In this way we achieved both desiderata: we wanted macrostates to be grounded by objective facts, and we wanted these facts to be physical facts.
Macrostates, construed in this way, are objective physical facts: they are determined by the structure of the accessible region of the O + G universe; and this structure, in turn, is determined by the constraints and limitations on the possible microstates of the universe. And so we have here an account of how sets can gain ontological significance. However, it turns out that in order to endow sets of microstates with objective physical status, we must realize that an observer is part of the theory: a physical observer, but an observer nonetheless. And so it turns out that statistical mechanics cannot be made observerless.
Given this notion of a macrostate of G as a set of microstates of G that stand in correlation with a microstate of O, two more facts about the thermodynamic partition to macrostates become interesting: one concerns the special nature of the thermodynamic macrostates, and the other concerns the regularity they exhibit.
Each thermodynamic macrostate of
G consists of microstates that share two kinds of physical properties. First, they share a correlation with a microstate of
O, and this fact makes them a macrostate. Second, all the microstates in a given macrostate of
G share some property pertaining to
G alone. For example, they may share the average kinetic energy of particles, or average position in space. The difference here is crucial: we see the world in terms of macrostates because of the correlations between
O and
G; but we characterize the thermodynamic macrostates in terms that pertain to
G only, and these properties have been discovered as part of the creation of statistical mechanics. It is precisely because thermodynamic macrostates can be expressed by properties of
G alone that the correlation with the observer
O is overlooked. But this correlation is of utmost importance since without it, we would not have looked for the
G only properties, and we would not have taken them to be
physically significant. (For more on this see our [
10], Chapter 5 and [
11].
In the discussion so far we described a case where the observer
O observes the system
G directly. But observers often measure the state of the observed system indirectly, by using measuring devices. Let us describe a situation in which
O measures some quantity of
G by a measuring device
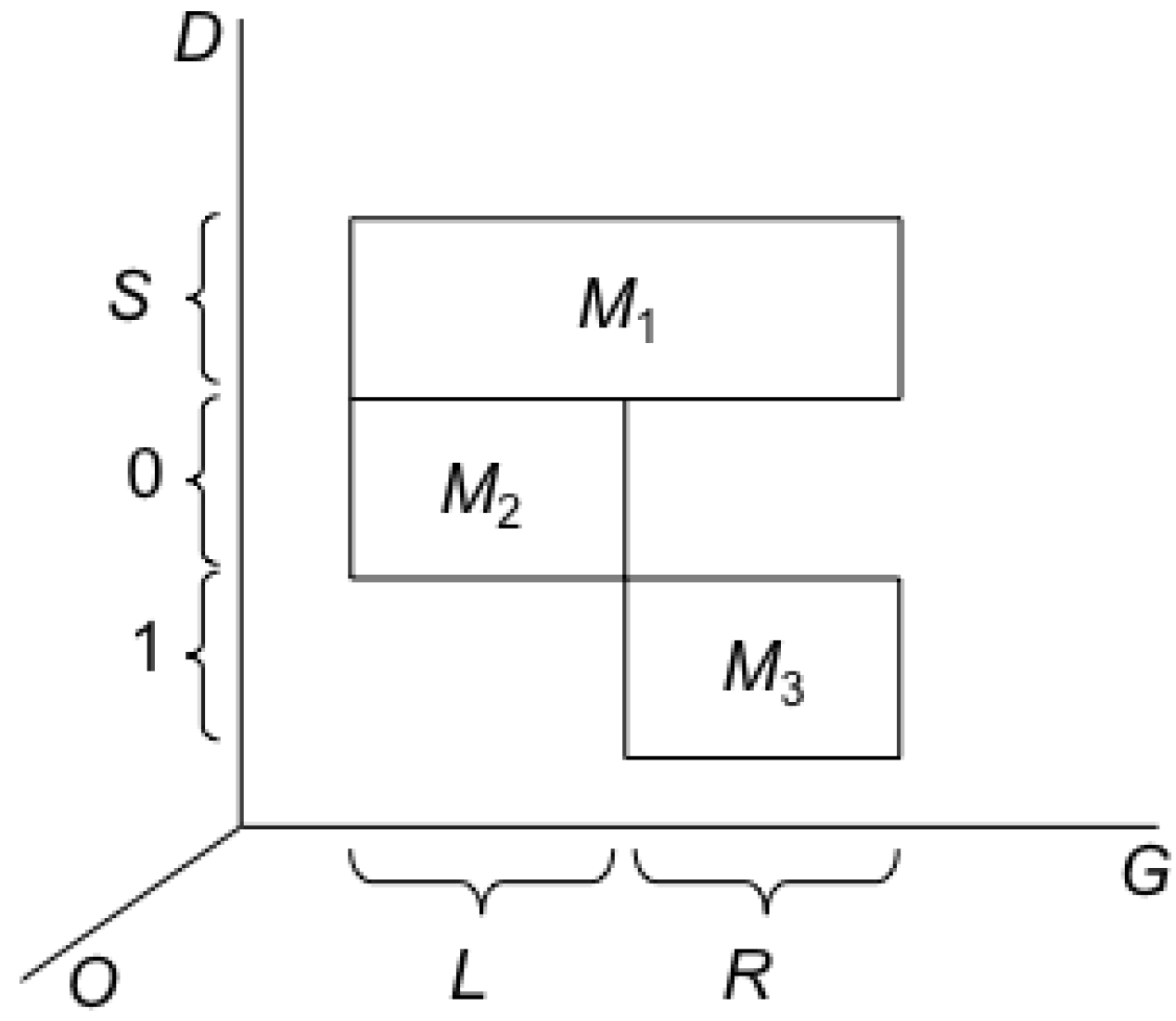
D. The state space of this case is illustrated in
Figure 3, where the vertical axis
D stands for the measuring device. The external constraints upon
O,
G and
D and the internal interactions between them determine their common accessible region.
S is the macrostate of
D representing its Ready state, and 0 and 1 are the macrostates of
D representing the measurement outcomes. Taking the macrostates of
G and the macrostates of
D together, one may talk about the macrostates of
D + G relative to
O. We reiterate that macrostates in our approach are relative to observers, and for this reason we keep the
O axis visible in our figures although for simplicity we do not depict its details. This fact is highly significant for understanding the notion of erasure (which is macroscopic). In
Figure 3 these macrostates are denoted by the two-dimensional rectangles
M1,
M2, and
M3. On the basis of this account we can understand the LB thesis to which we now turn.
Figure 3.
Macrostates of D + G.
Figure 3.
Macrostates of D + G.
3. Erasure
As already noted by Landauer [
1] (p. 149 in Leff and Rex [
5]), in classical mechanics there is no microscopic erasure because of the determinism of the dynamics. To see why note that in a trivial sense the microstate of the universe at any moment is a memory of all the microstates of the universe to the past of this moment, since given the equations of motion one can derive any microstate to the past (as well as future) from the present microstate. Therefore in classical mechanics microscopic memory can never be erased.
Another way of looking at this matter is this. In the context of the physical implementation of computation (namely, in computers), Landauer took an erasure to be a physical implementation of the function restore-to-one:
f(0) =
f(1) = 1. This is a special case of the function:
f(0) =
f(1) =
X (where
X is some standard state) in the sense that one cannot infer the initial state from the final state. However, since the classical dynamics is both deterministic and time reversal invariant it follows that two different microstates, such as those implementing the data 0 and 1, cannot both evolve to the same microstate, such as 0 or 1. And so it turns out that erasure (as well as other logically irreversible operations) can be carried out only on macrostates. (A measurement is a sort of a reversal of erasure and likewise is essentially macroscopic (see our [
10], Chapter 9.)
A necessary and sufficient condition for an erasure is what we call
blending, which has some similarity with Landauer’s notion of
diffusion. Landauer [
2], in the quotation cited in Section 1, says that the completion of an erasure requires what he calls
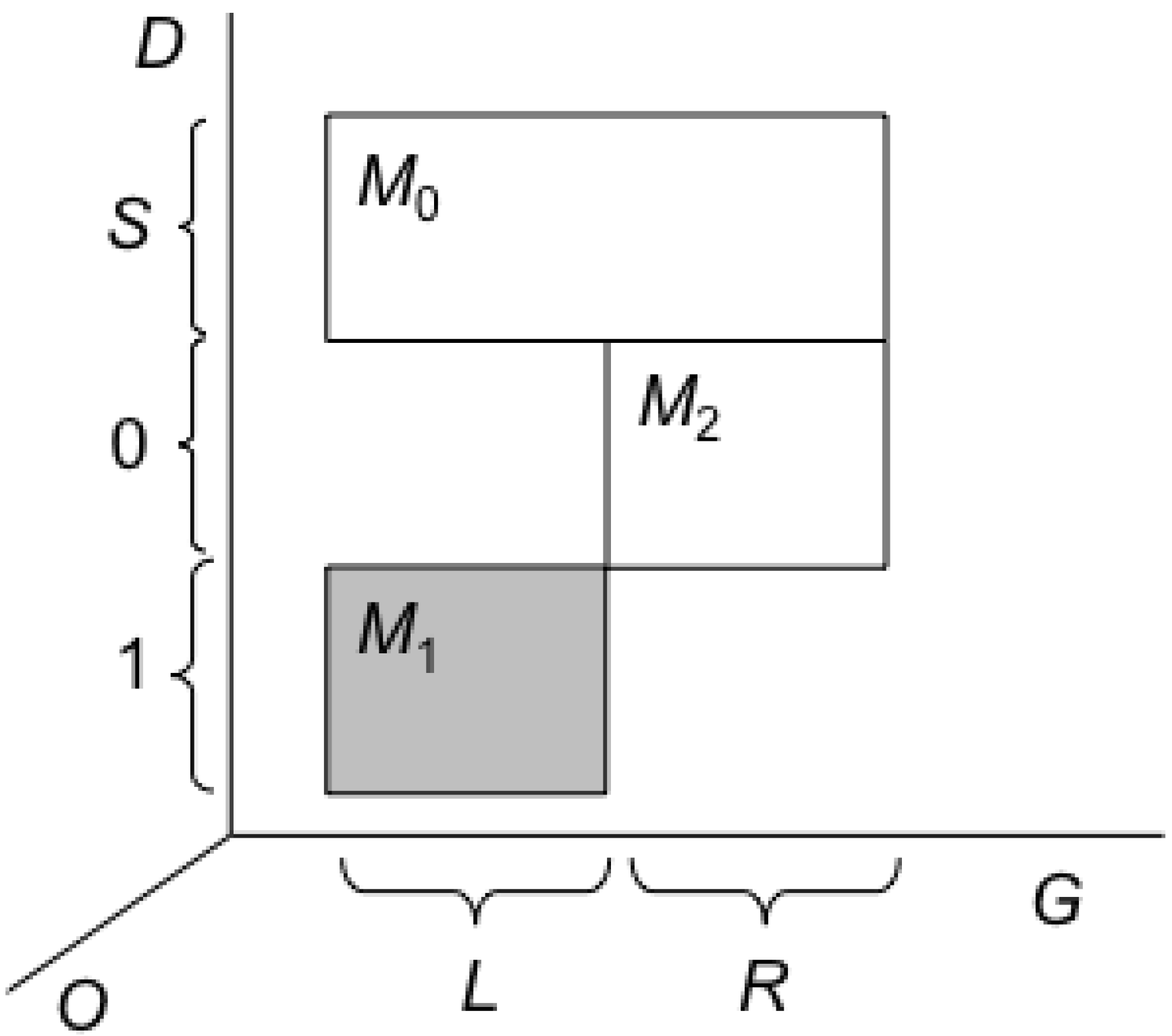
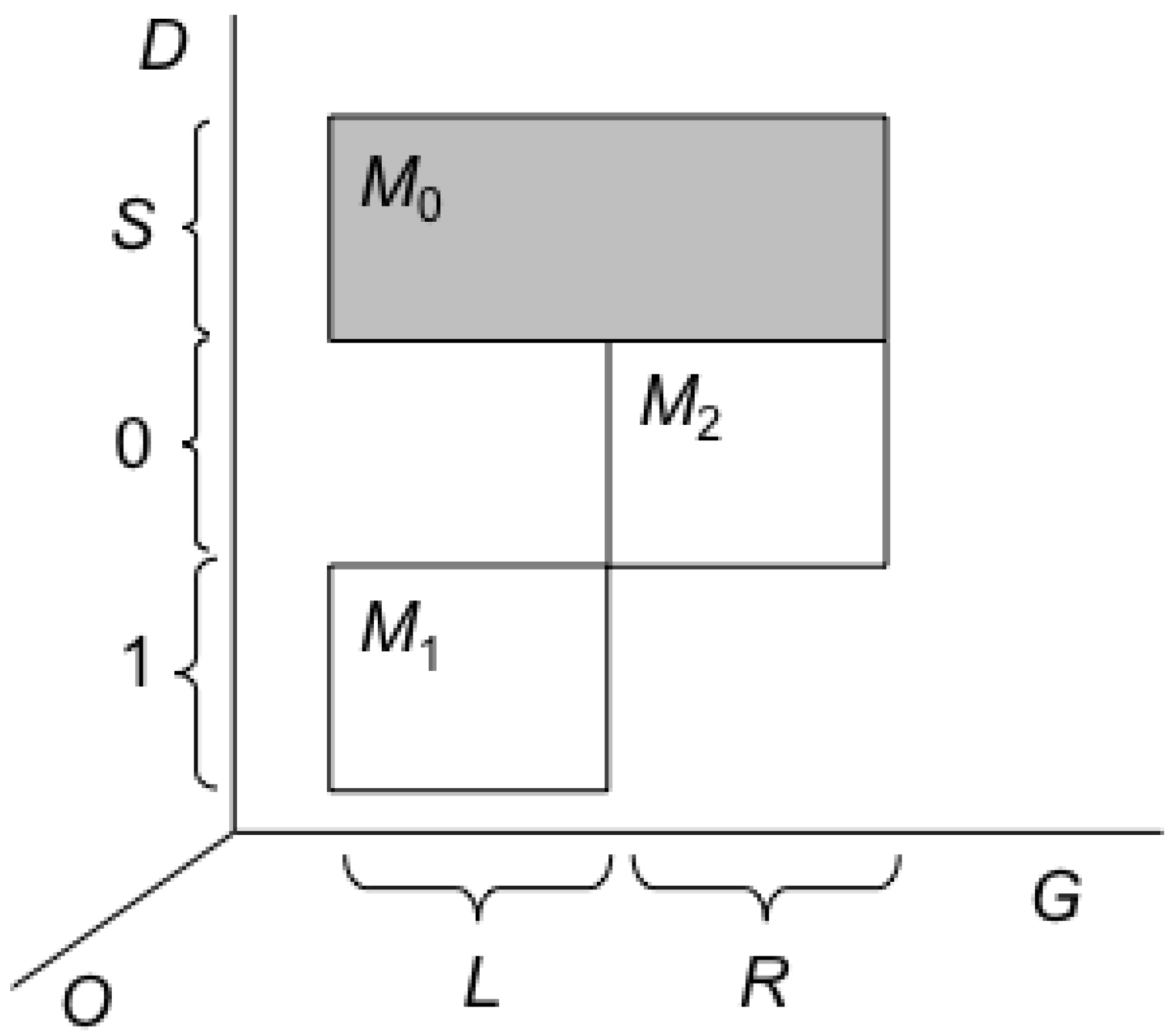
diffusion. The set up that Landauer seems to have had in mind is the following, as sketched in
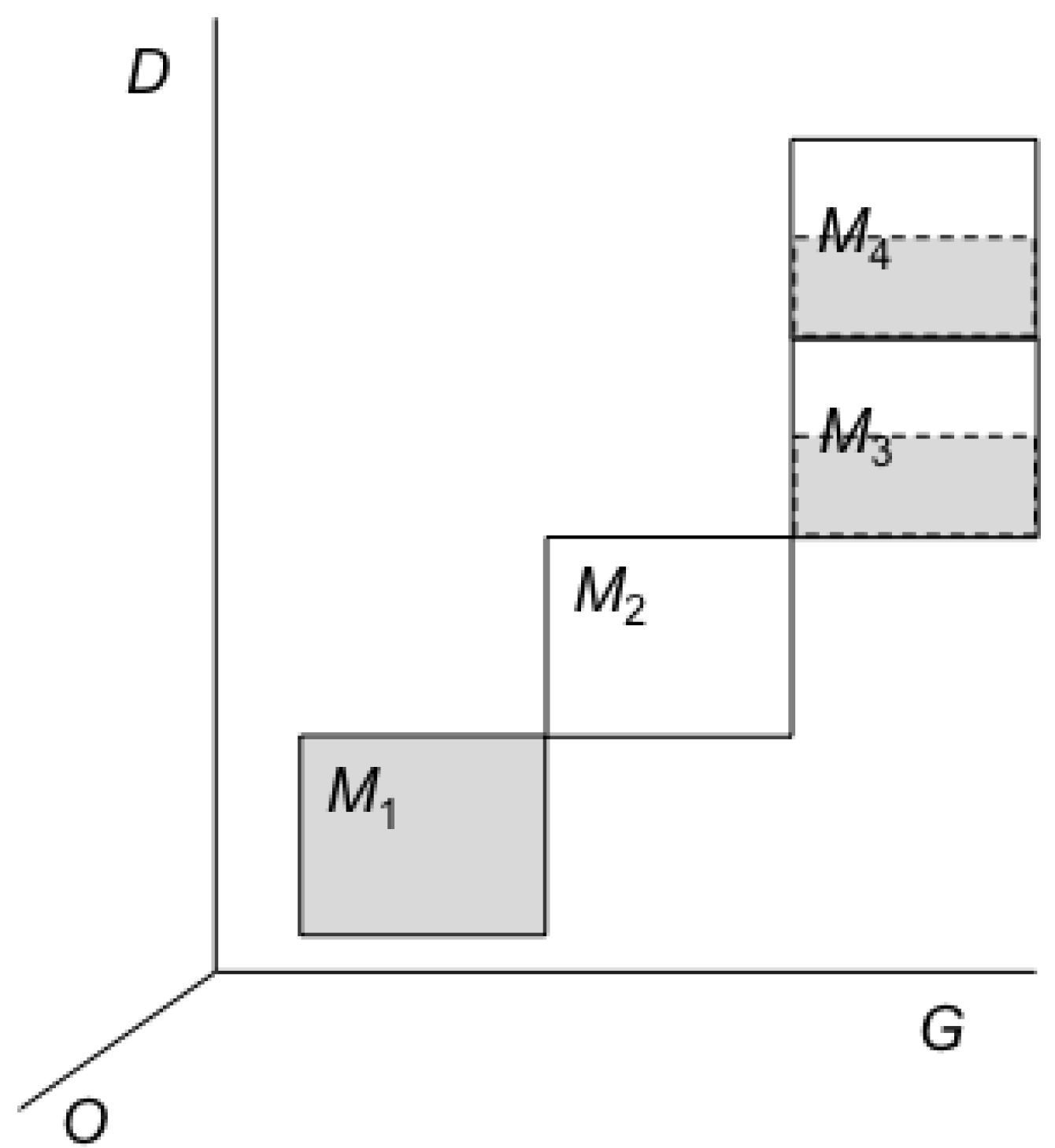
Figure 4,
Figure 5 and
Figure 6 below (the shaded areas contain the actual microstate at each case).
Figure 4.
Pre-erasure macrostate: Part a.
Figure 4.
Pre-erasure macrostate: Part a.
Figure 5.
Pre-erasure macrostate: Part b.
Figure 5.
Pre-erasure macrostate: Part b.
Figure 6.
Post-erasure macrostate.
Figure 6.
Post-erasure macrostate.
The structure of the trajectories of the universe in this case is such that trajectories that start in the region
M1 end up after some time in the region
M0, and likewise trajectories that start in the region
M2 also end up after the same time in
M0. In the figure we do not depict the regions within
M0 occupied by the end points of these two trajectories bundles (since as far as erasure is concerned these details are not relevant). This structure of trajectories implies that whether the actual pre-erasure macrostate is
M1 (which is the case in
Figure 4) or
M2 (which is the case in
Figure 5), after the erasure the macrostate will be
M0, as in
Figure 6. Since both bundles of trajectories that start in
M1 and in
M2 evolve to
M0, Liouville’s theorem requires that the Lebesgue measure of
M0 be equal to at least the sum of
M1 and
M2, and is satisfied in this case. Likewise, Liouville’s theorem is satisfied in all the cases we analyze below. Here after the two bundles of trajectories arrive at
M0 from
M1 and
M2, they diffuse or blend in
M0, in the sense that they are no longer distinguishable since the observer
O using the measuring device
D cannot infer from the final macrostate
M0 the macroscopic history of
D +
G. That is,
O cannot say, given
M0 whether the macrostate of
D +
G was
M1 or
M2. (Here we did not distinguish between the erasure of known and unknown data; see below.) Since the Lebesgue measure of
M0 (which is entropy in the Boltzmannian approach) is equal in this case to sum of the Lebesgue measures of
M1 and
M2, the entropy of
D+G increases. This case, which satisfies the
LB thesis, is often discussed in the literature (in various versions) but it is not the general case, as we shall see. (For the choice of the measure of entropy in statistical mechanics, see our [
10].)
Landauer may have thought that after some time any region of positive Lebesgue measure within
M0 contains both end points that came from
M1 and end points that came from
M2, and so it is impossible to identify sub-regions in
M0 that contain end points that belong to only one of these bundles. The idea of diffusion is indeed very important, but it can and should be generalized; and the generalization entails—as we will now see—that Landauer’s thesis concerning the entropy of erasure is not a universal theorem of mechanics. (A different argument criticizing the LB thesis is by Norton [
12]. A defense of Landauer’s thesis is in e.g. Bub [
13] and Ladyman and Robertson [
14].)
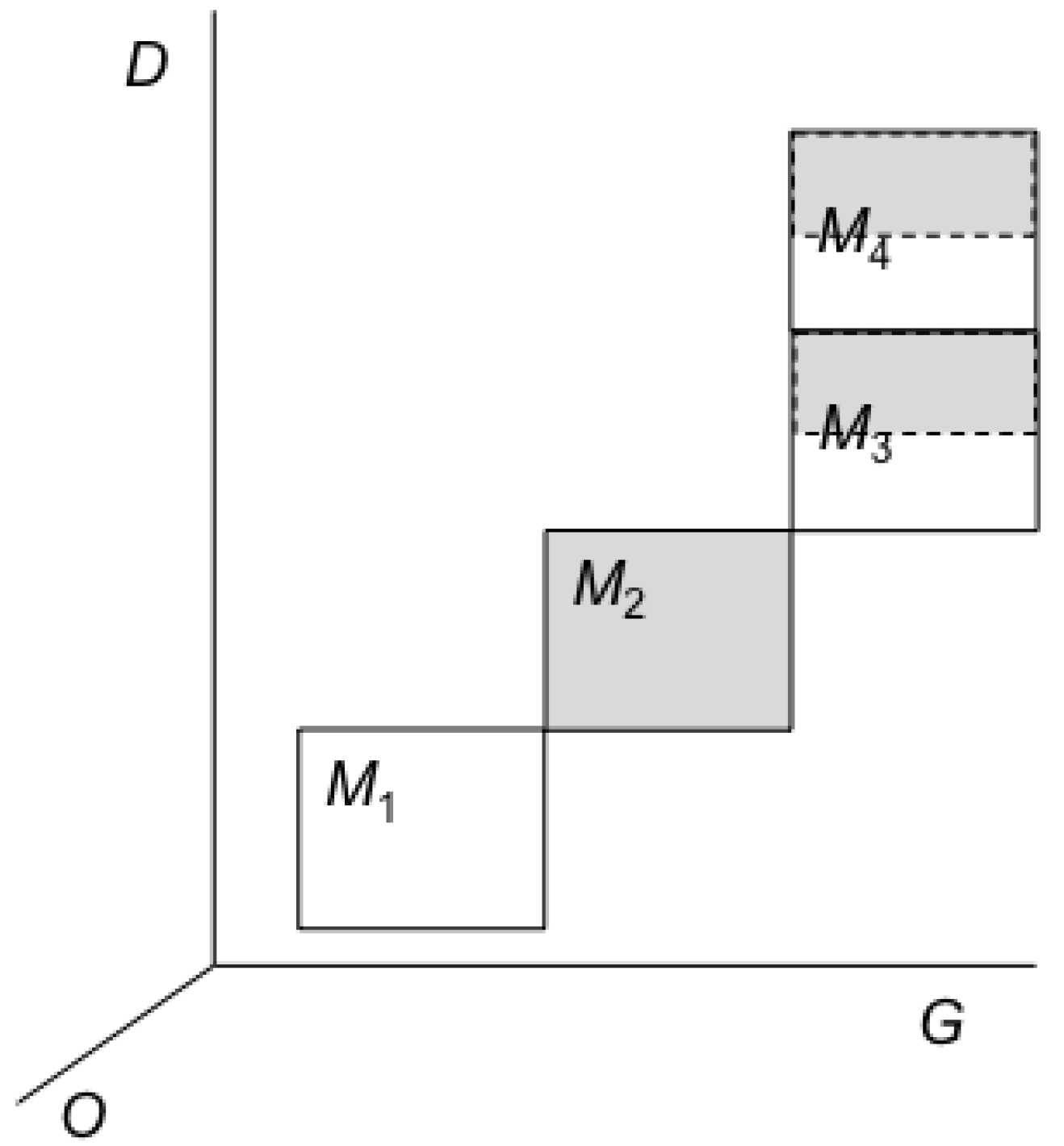
To see this, consider first
Figure 7 and
Figure 8, which illustrate the necessary and sufficient condition for erasure that we call
blending. In
Figure 7 all four macrostates have the same Lebesgue measure; and the trajectories that start in the macrostate
M1 evolve in such a way that the bundle of trajectories partly overlaps with macrostates
M3 and
M4. (In our [
10] we call this bundle of trajectories, or to be more precise, the end points at a given time of this bundle, the
dynamical blob.) The shaded areas are the initial macrostate and its evolution. In this special case, designed for simplicity, the bundle overlaps with exactly ½ of
M3 and ½ of
M4. Similarly, in
Figure 8 we see the evolution of the trajectories that start in
M2: they also evolve so that the bundle of trajectories overlaps with exactly the remaining ½ of
M3 and the remaining ½ of
M4.
Figure 7.
Blending: Part a.
Figure 7.
Blending: Part a.
Figure 8.
Blending: Part b.
Figure 8.
Blending: Part b.
By the end of this evolution,
O measures the state of
D in order to learn from it the state of
G. Here, the usual measurement process takes place (see [
10], Chapter 9). Assuming that
O is correlated with
D and
G in such a way that
O can distinguish between
M3 and
M4, a detection takes place and then the dynamical blob collapses on either
M3 or
M4, depending on which of them contains the actual microstate of
D +
G. We reiterate that in statistical mechanics macrostates are equivalence classes defined relative to an observer’s resolution power. For this reason we believe that the observer in statistical mechanics is essential (see our [
11]). Since the account of both processes of erasure and measurement in mechanics necessarily involve macrostates, we keep the reference to an observer O in our discussion although we do not go into its details. For further reading about the role of the observer in statistical mechanics see our [
10] and [
11].
By the end of this measurement, O can say only that the macrostate of D + G is the outcome of the measurement, but cannot tell which sub-region of the actual macrostate contains the actual microstate, for this is the very idea of the notion of a macrostate. Since M4 (and similarly M3) contain end points that started out in both M1 and M2, that is, if the blobs that started in M1 and M2 blend within M3 and M4, O cannot infer from M4 (or M3, depending on the actual outcome of the erasure) which macrostate M1 or M2 was the case before the erasure. In this special case the final macrostate detected by O is either M3 or M4, and since the Lebesgue measure of M3 and M4 is equal to the Lebesgue measure of the initial macrostate (M1 or M2), the entropy of D + G did not change during the erasure.
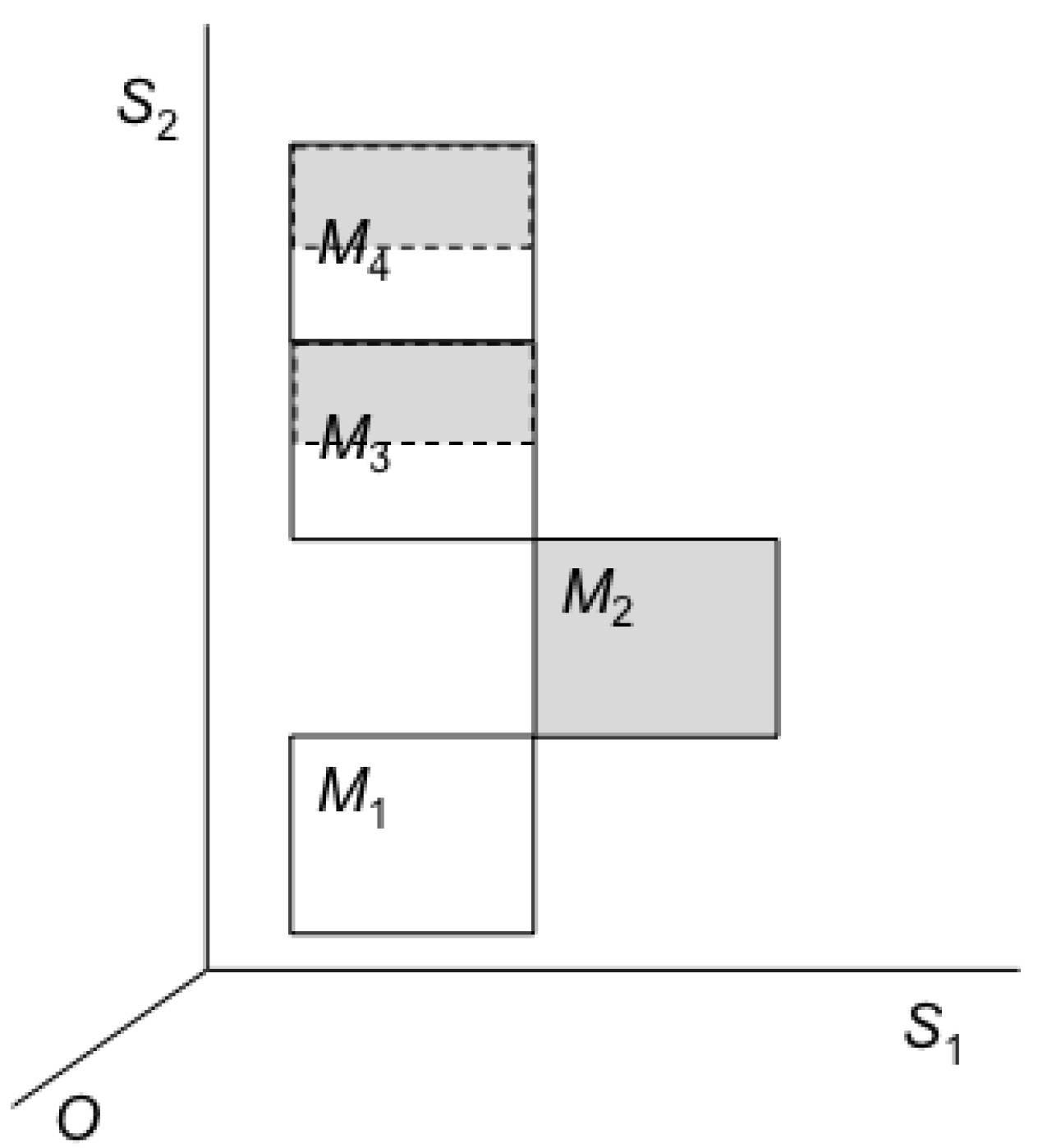
The case in which the correlations between
O and
D +
G are such that
O can distinguish between the macrostates
M3 and
M4 is special: in general this correlation can be either finer or coarser. An example of an erasure with a
coarser correlation is illustrated above in
Figure 6. An example of an erasure with a
finer correlation is given in
Figure 9, in which the regions
M3,
M4,
M5 and
M6 are macrostates. It is very important to realize that there is
no intrinsic connection between blending (or diffusing), which depends on the structure of trajectories in the blobs, and the entropy, which is fixed by the measure of the macrostates. It seems to us that Landauer [
1,
2] had in mind a
blending dynamics that takes place within a given macrostate. But what we have just seen is that blending may equally take place
across different macrostates (each of which may be of a smaller Lebesgue measure than the initial macrostate).
Figure 9.
Blending across macrostates and entropy decrease.
Figure 9.
Blending across macrostates and entropy decrease.
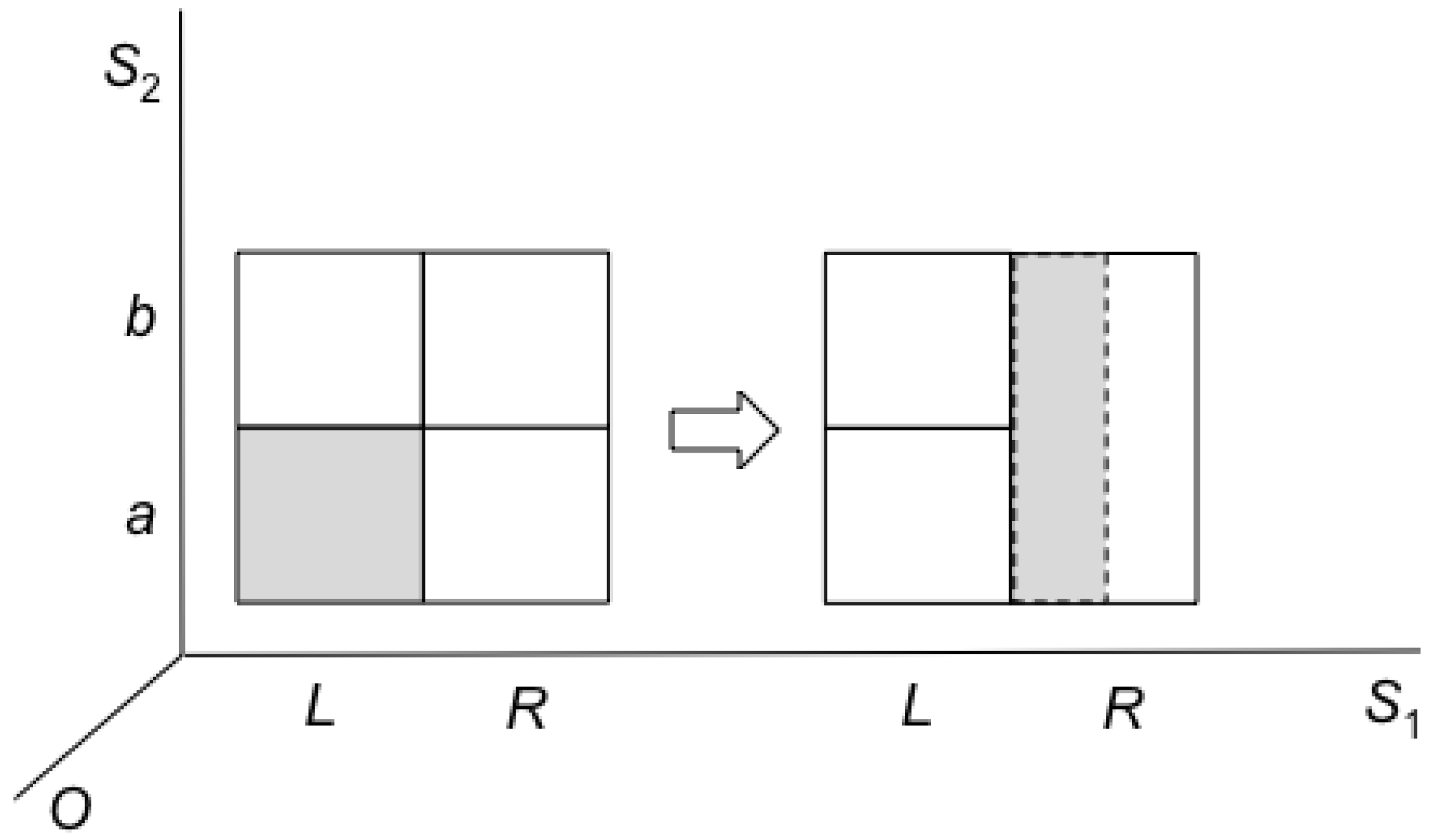
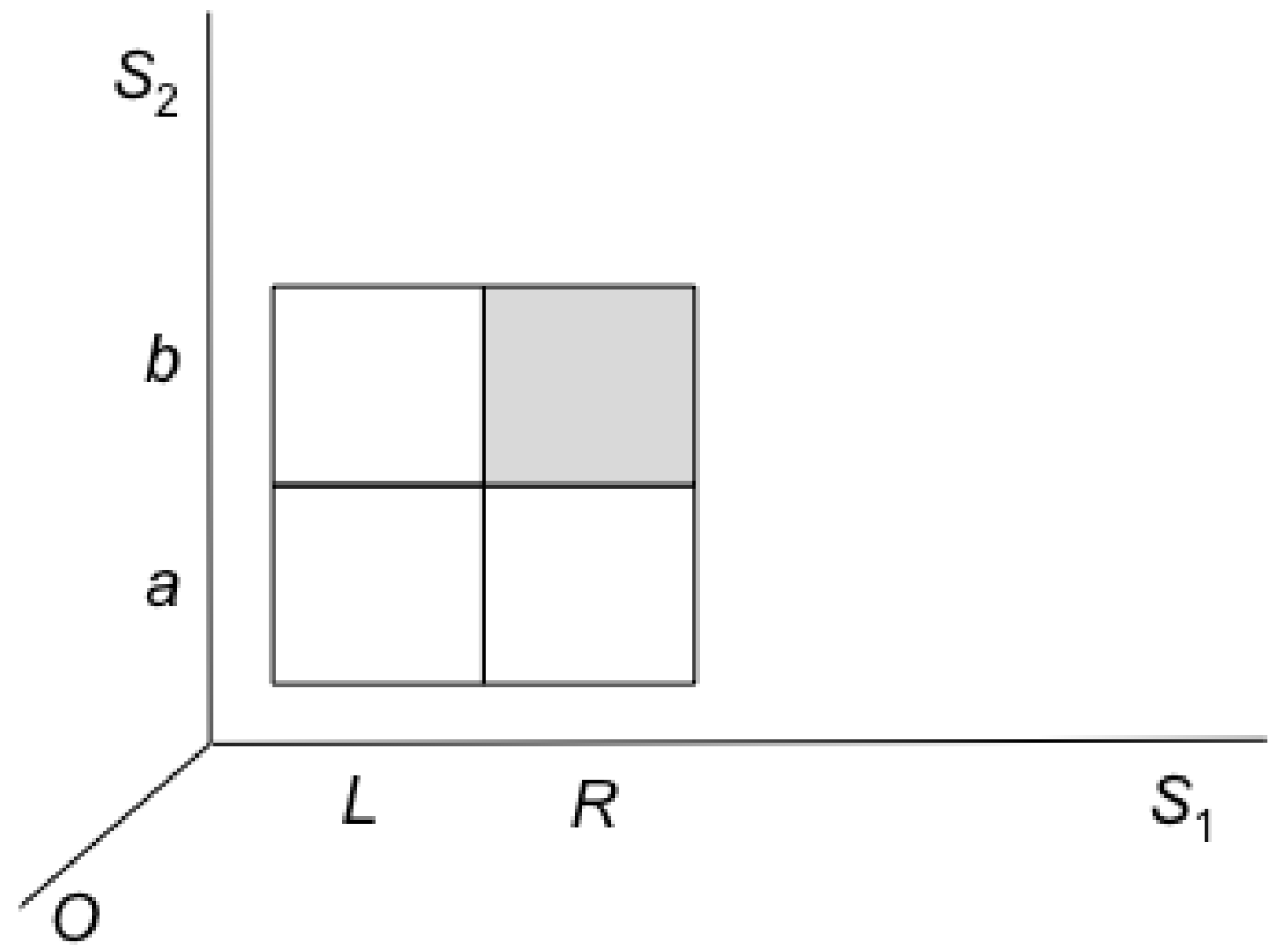
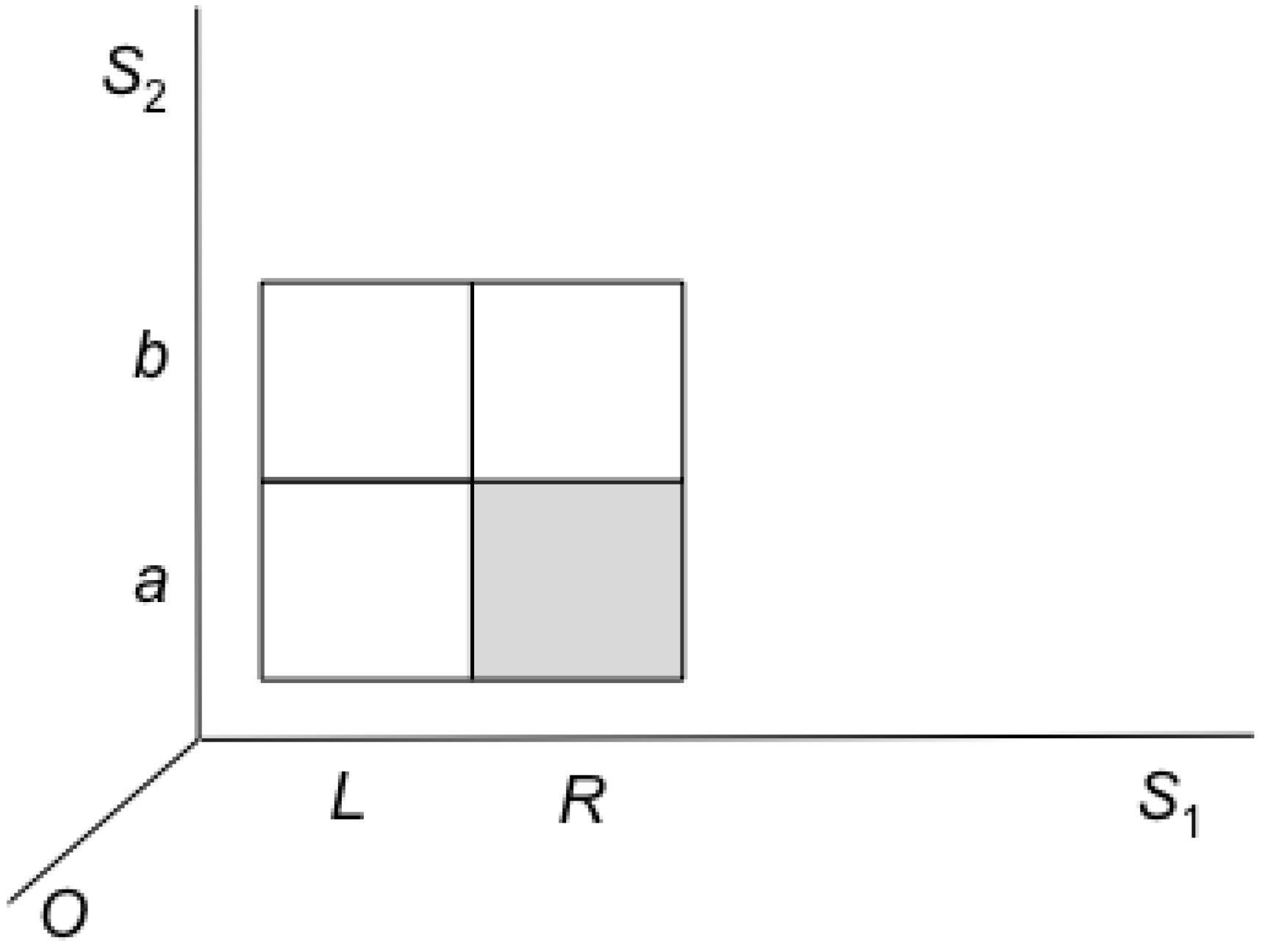
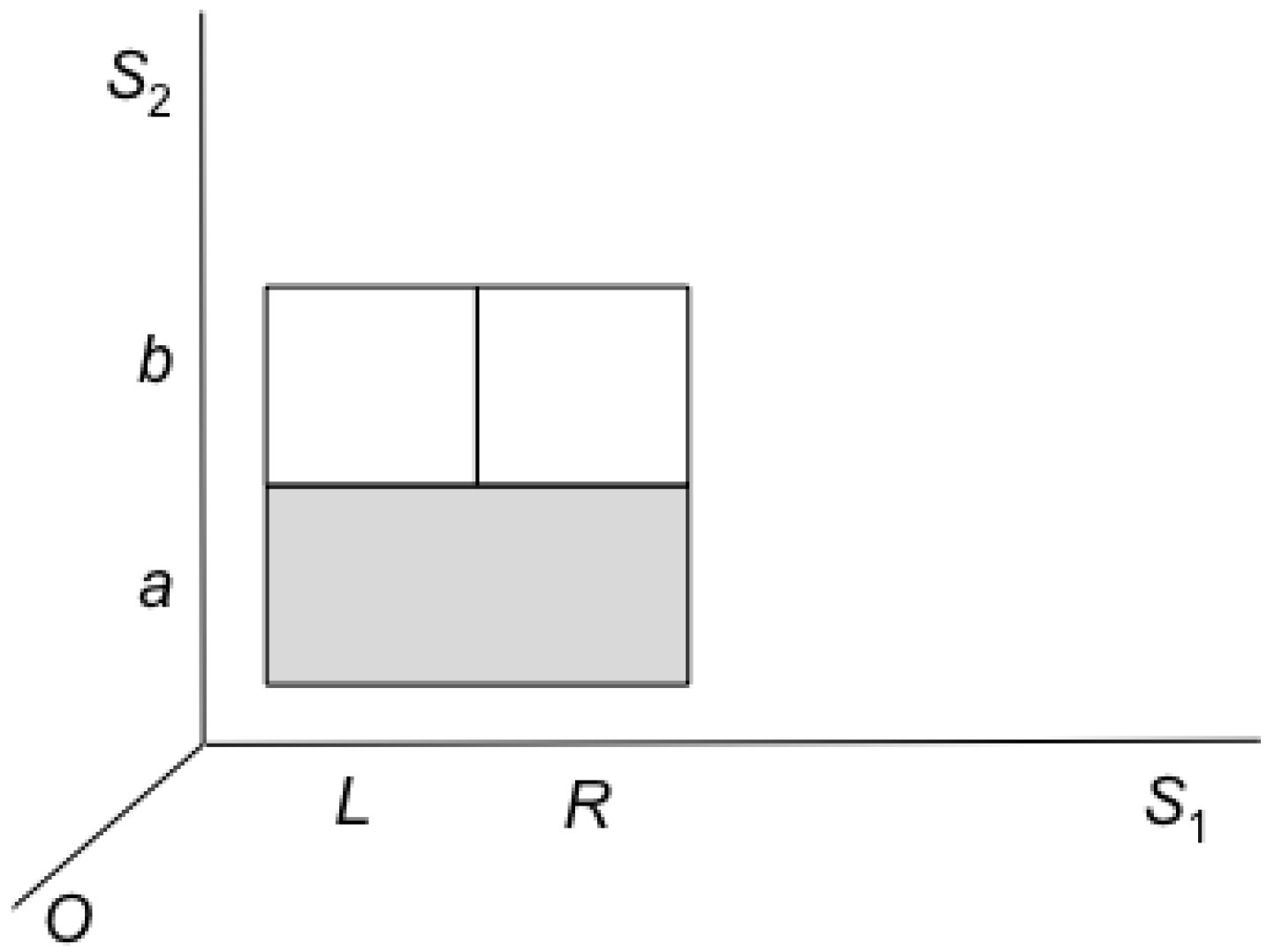
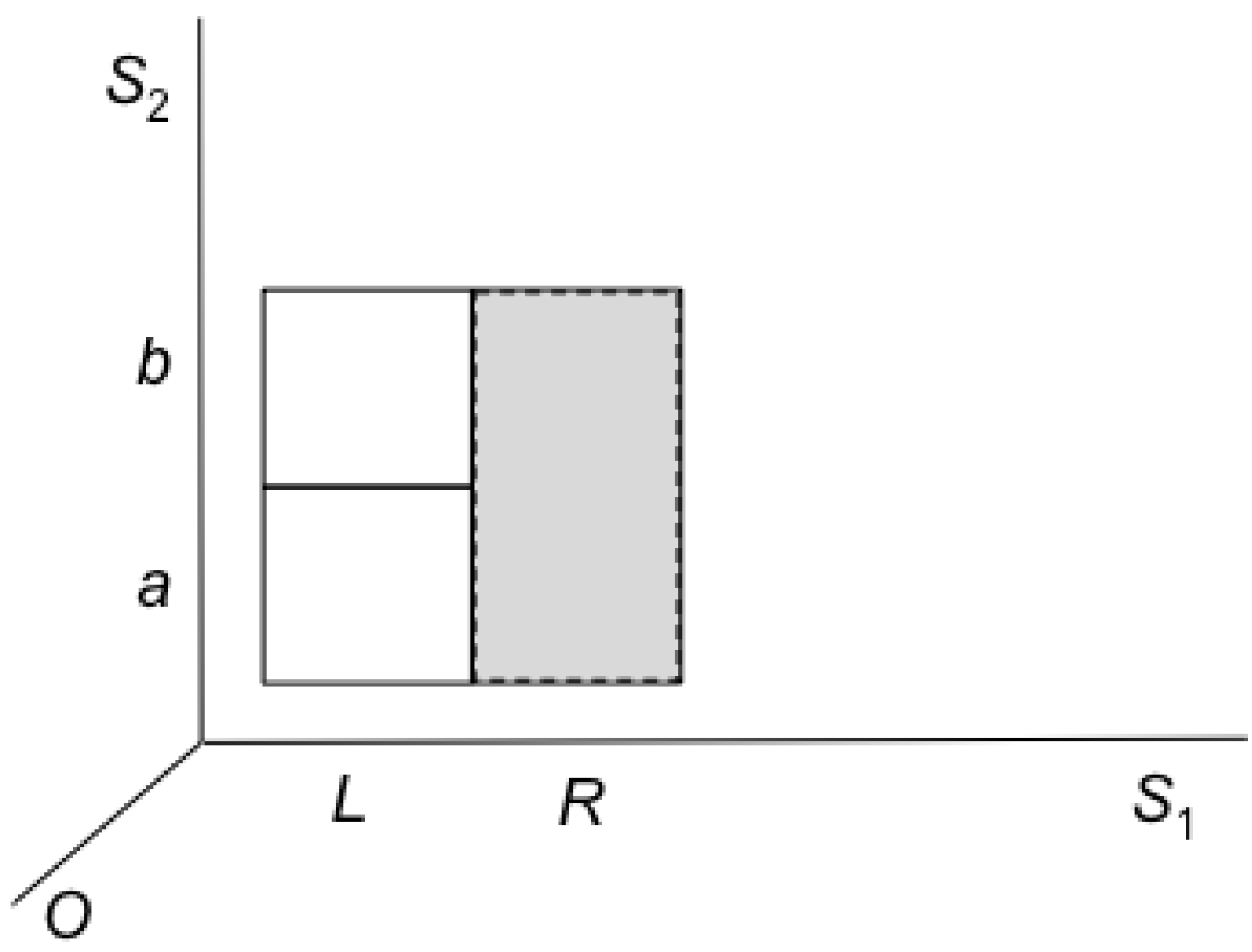
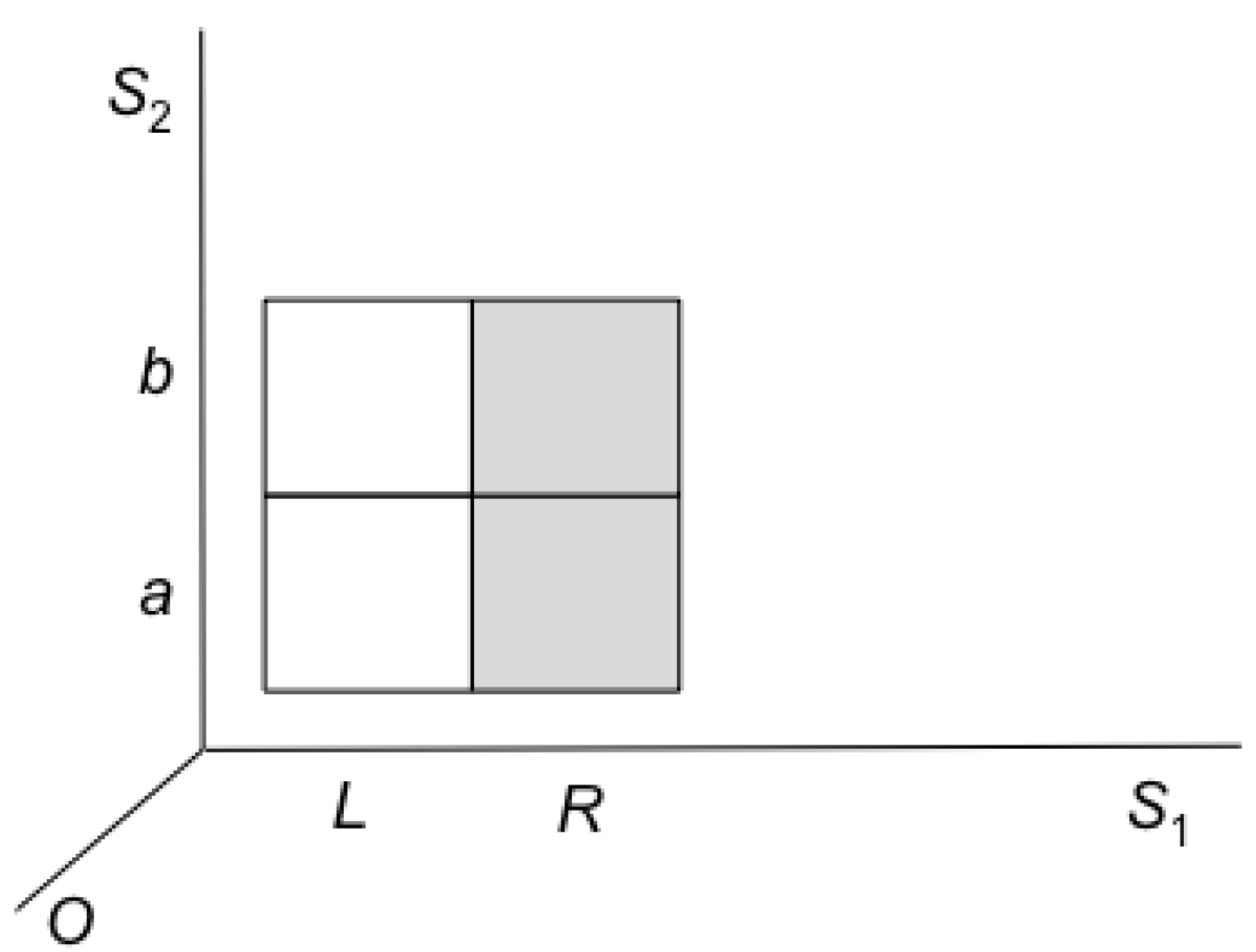
Finally the above analysis of erasure holds also for the special case of erasure as restore-to-one, as can be seen in
Figure 10, where
S1 is Landauer’s information-bearing degree of freedom. Here, restoring to one does not result in an entropy increase, due to the partition to macrostates on the
S2 (non information bearing) degree of freedom.
In familiar thermodynamic situations there seem to be fixed limitations on the observation capabilities of human observers and, in this sense, one can perhaps introduce a maximally fine-grained partition to thermodynamic macrostates (see Earman [
15]) which results in some specific entropy of post-erasure macrostates. But the details of these macrostates are a contingent matter of fact. In particular, the principles of mechanics entail no specific relation between the pre-erasure and post-erasure entropy of the universe. This means that whether or not the LB thesis is true for the familiar thermodynamic situations is a question of contingent fact as well. In any case, our analysis of erasure demonstrates that, contrary to the conventional wisdom,
the LB thesis is not a theorem in classical mechanics (nor is it a theorem in quantum mechanics; see our [
10], Appendix B.3).
Figure 10.
Restore-to-one.
Figure 10.
Restore-to-one.
4. Erasure of Random Data
Up to now our account focused on the erasure of data
known to the observer, as opposed to
unknown or random data (see Bennett [
3,
4] for these terms). (Bennett’s [
3] and Feynman’s [
16] analyses of an erasure using a bi-stable well are special cases of our analysis; see our [
10], Chapter 12.) In the literature erasure is often described in terms that pertain to information bearing degrees of freedom
vs. other degrees of freedom. Let us re-describe our account of erasure in the previous section in these terms. Consider first the erasure dynamics described in
Figure 11 and
Figure 12. Here
S1 is the information-bearing degree of freedom and
S2 is the other non-information degree of freedom. In
Figure 11 and
Figure 12 the dynamics maps the initial macrostates
La and
Ra to the final macrostate
Rab. As can be seen in the two figures the Lebesgue measure of
Rab is equal to the sum of the Lebesgue measures of the initial macrostates
La and
Ra, as required in this case by Liouville’s theorem. It can easily be seen that this dynamics is
blending since one cannot infer from the final macrostate
R of
S1 the initial macrostates
L or
R of
S1. This dynamics, however, results in an
increase of the total entropy of the universe
S1 +
S2, and in particular the dynamics increases the entropy of the non-information bearing degree of freedom
S2.
Figure 11.
Erasure of known data: Case a.
Figure 11.
Erasure of known data: Case a.
Figure 12.
Erasure of known data: Case b.
Figure 12.
Erasure of known data: Case b.
However, this entropy increase is
not necessary. Suppose, for example, that in the case of
Figure 11 the observer carries out a measurement on the post-erasure blob in order to find out whether the system is in the macrostate
Ra or
Rb. The outcome of this measurement is either the one in
Figure 13 or the one in
Figure 14. Similarly for the case of
Figure 12: here, too, the outcome of the measurement will be either the one in
Figure 13 or the one in
Figure 14. And note that this measurement can be finished at the same time that the erasure (in
Figure 11 and
Figure 12) ends. In these cases,
the post-erasure macrostate has the same entropy as the pre-erasure macrostate. And of course
other changes of entropy are possible, depending on the partition of the state space into macrostates at the same time (that is, the time at which the erasure is finished), according to the details of the correlations between the observer and the system.
Figure 13.
Post-erasure macrostate Rb.
Figure 13.
Post-erasure macrostate Rb.
Figure 14.
Post-erasure macrostate Ra.
Figure 14.
Post-erasure macrostate Ra.
However, Landauer [
1] insisted that the interesting case of erasure (namely the one that is relevant for analyzing computation and for applying the LB thesis) is that of
unknown or random data. This case is described in
Figure 15,
Figure 16 and
Figure 17.
Figure 15.
Erasure of random data: Part 1.
Figure 15.
Erasure of random data: Part 1.
Figure 16.
Erasure of random date: Part 2.
Figure 16.
Erasure of random date: Part 2.
Figure 17.
Erasure of random data: Part 3.
Figure 17.
Erasure of random data: Part 3.
In the initial state in
Figure 15 the observer cannot distinguish between
La and
Ra and therefore the initial macrostate is
La +
Ra. In some sense one can say that in this case there is nothing to be erased since at the initial time before the erasure there is no information that is known to the observer. The only way to make sense of erasure of random data is in terms of counterfactuals. That is, if the observer were to know the initial data, then the erasing dynamics would result in a final macrostate from which the observer would not be able to recover his memory. Here is a dynamics that implements an erasure of this sort. In
Figure 16 the dynamics takes all the trajectories in the macrostate
La +
Ra to the final macrostate
Ra +
Rb. In this case although there is no explicit blending it is not in fact required since as we said there is no information that is known to the observer that is finer than the initial macrostate
L +
R along
S1. In the counterfactual sense we proposed above the dynamics maps
L +
R onto
R, while expanding along
S2 (which is necessary due to Liouville’s theorem). Although in this case the total entropy of the universe
S1 +
S2 is conserved, the entropy of
S2 increases. However, even this increase is not necessary. Consider
Figure 17. Here the dynamics results in erasing (counterfactually) the information stored in
S1, by mapping the initial macrostate
La +
Ra to two different macrostates
Ra and
Rb of
S2, which in this case are distinguishable by the observer. That is, the blending in this case takes place
across different macrostates of
S2, while in the previous case (of
Figure 16) the blending takes place within a single macrostate of
S2. Whether the macrostates
L and
R of
S1 (and similarly the macrostates
a and
b of
S2) are distinguishable by an observer is a question of
fact, and therefore cannot be settled universally by any principle of mechanics.
This completes our account of the notion of blending, which is both necessary and sufficient for erasure in classical mechanics. Our analysis can easily be generalized to all logically irreversible operations (see [
10], Chapter 12).